Transverse Electric Guided Wave Propagation in a Plane Waveguide with Kerr Nonlinearity and Perturbed Inhomogeneity in the Permittivity Function
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Statement of the Problem
3.2. Problem
3.3. Problem
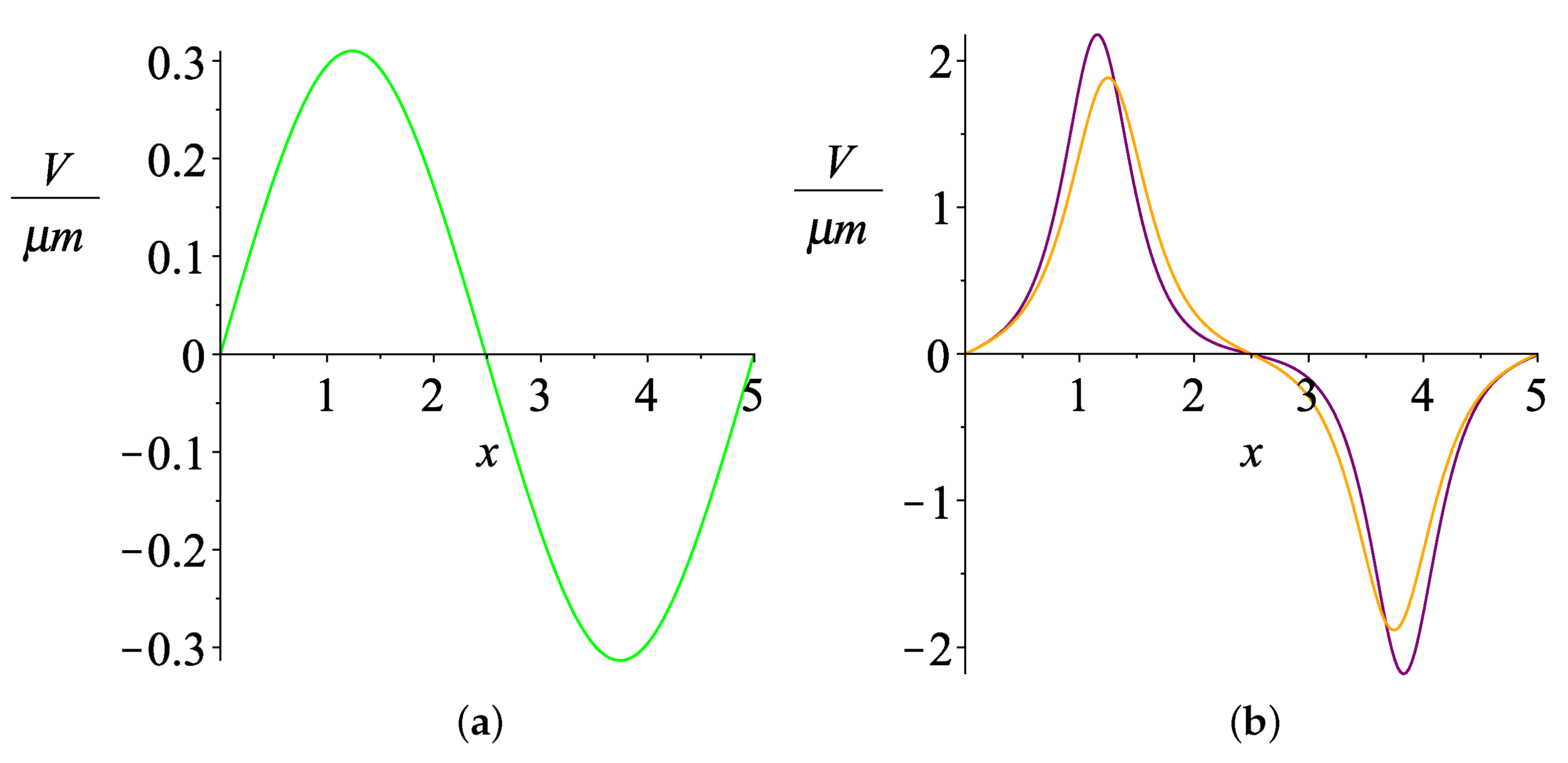
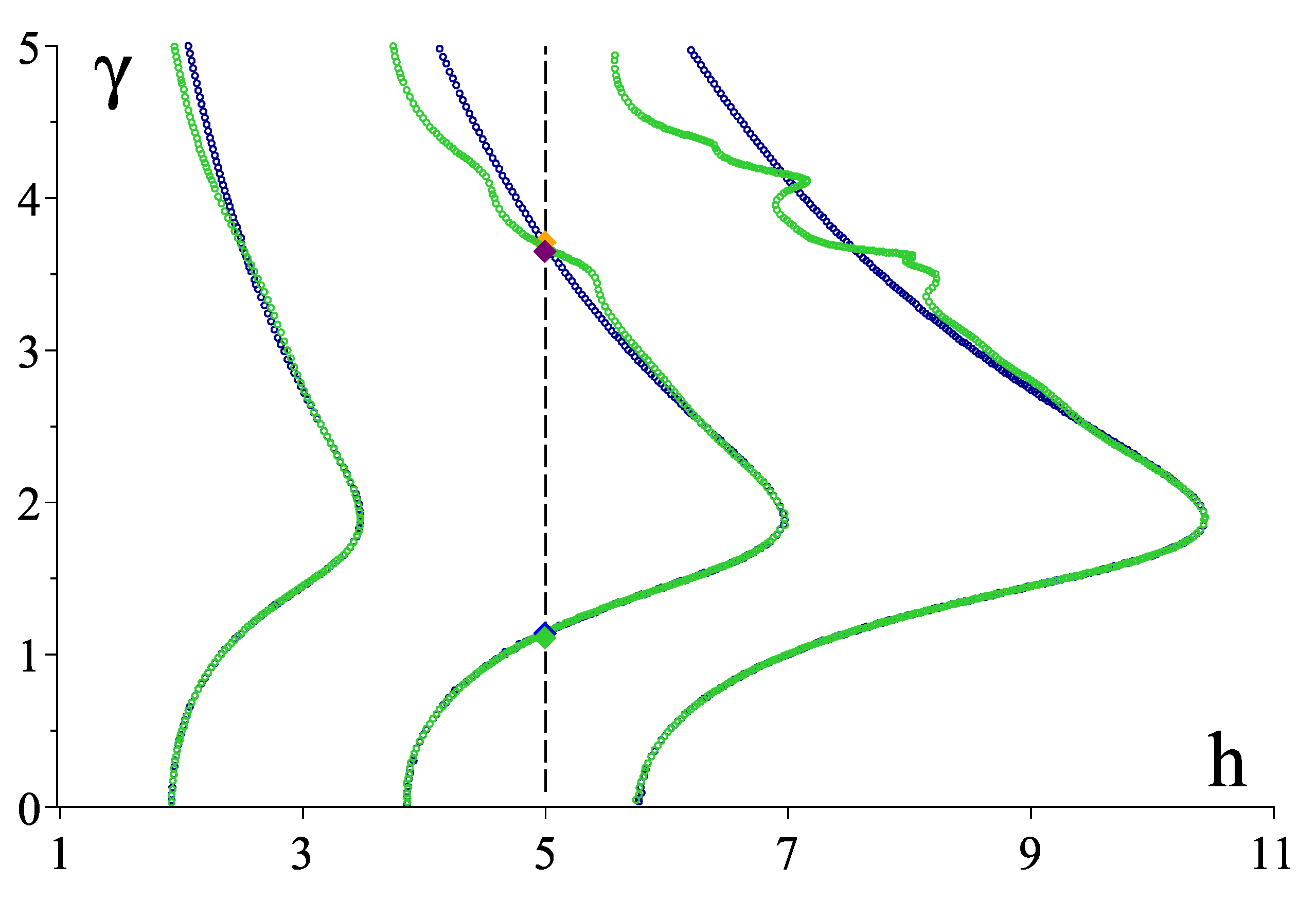
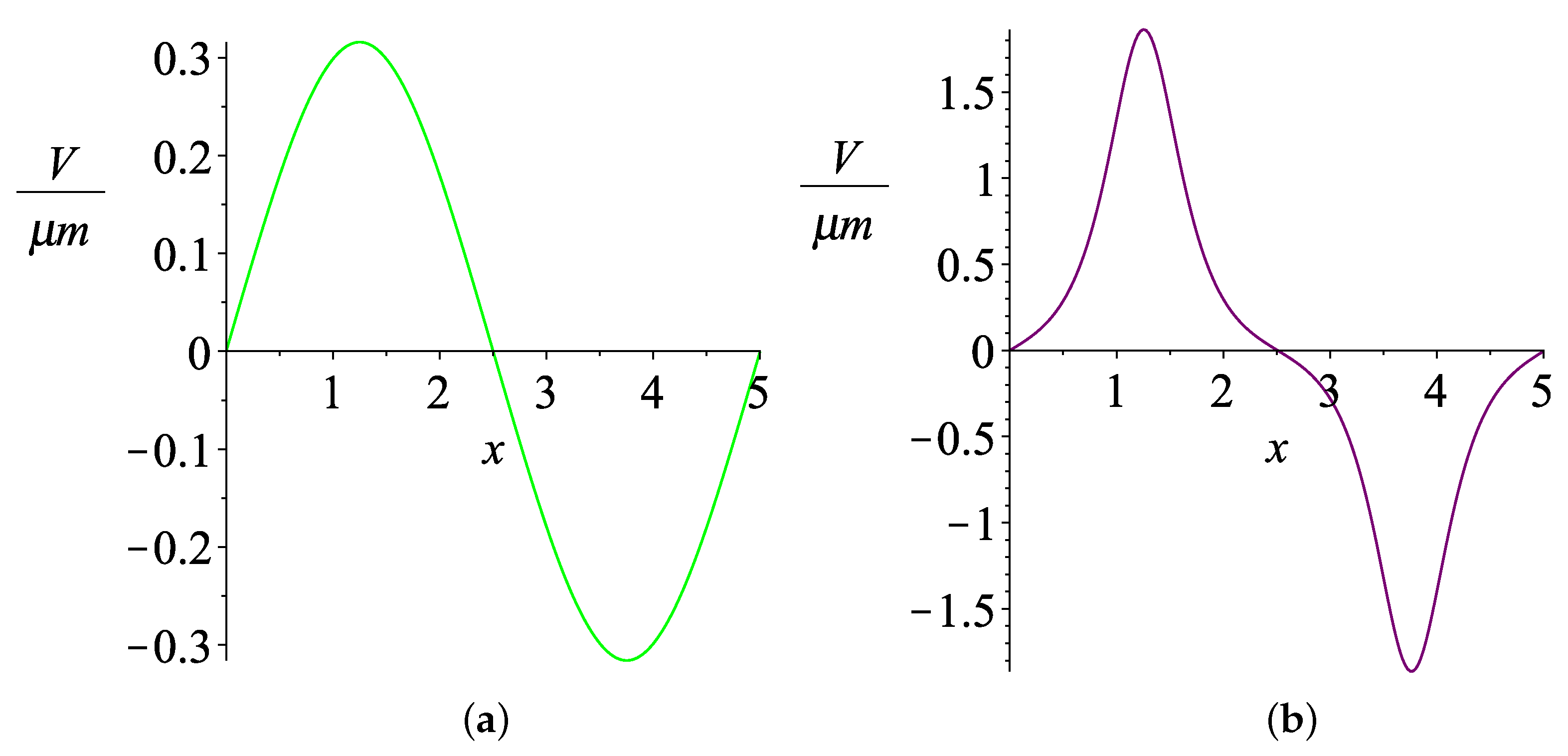
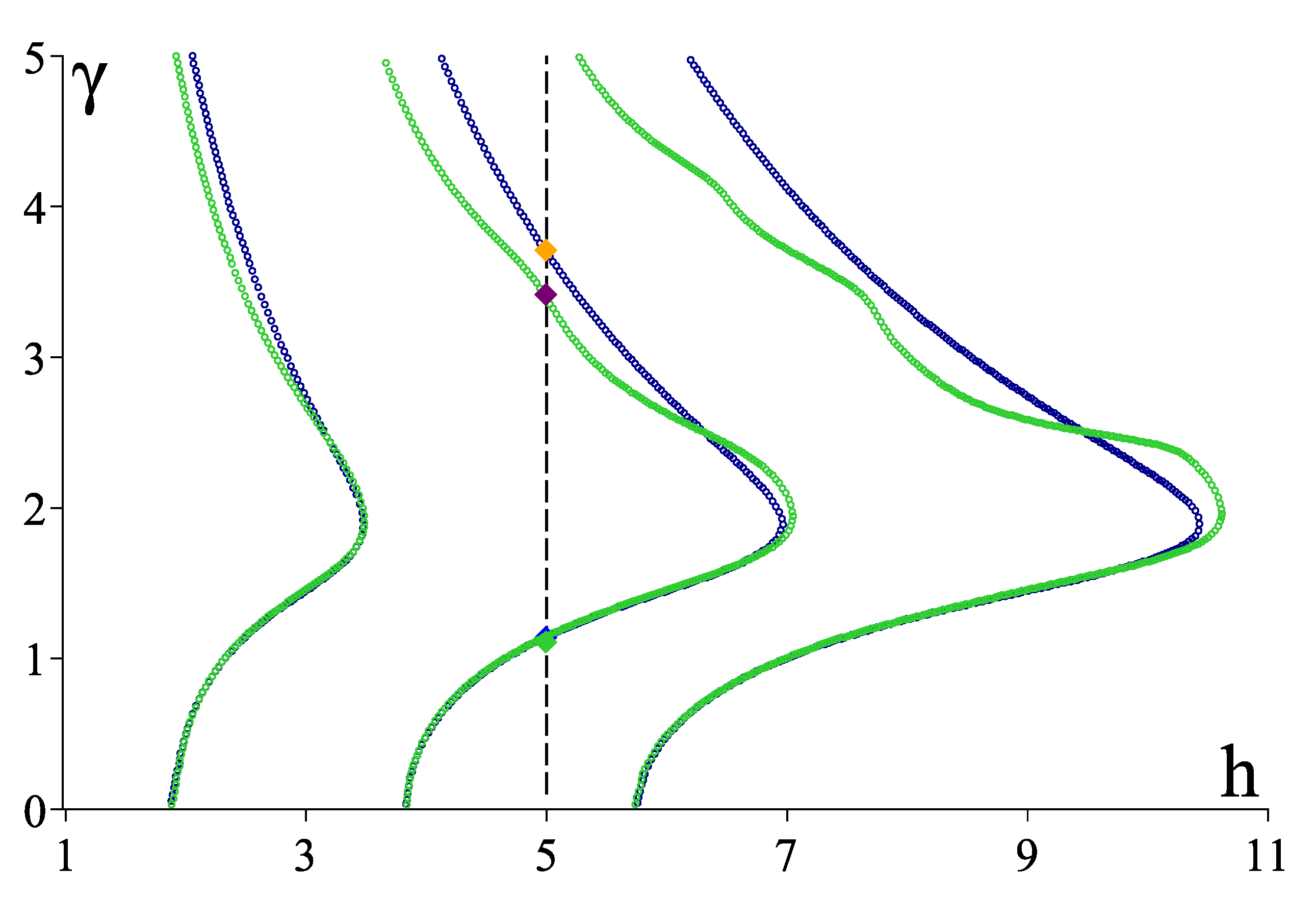
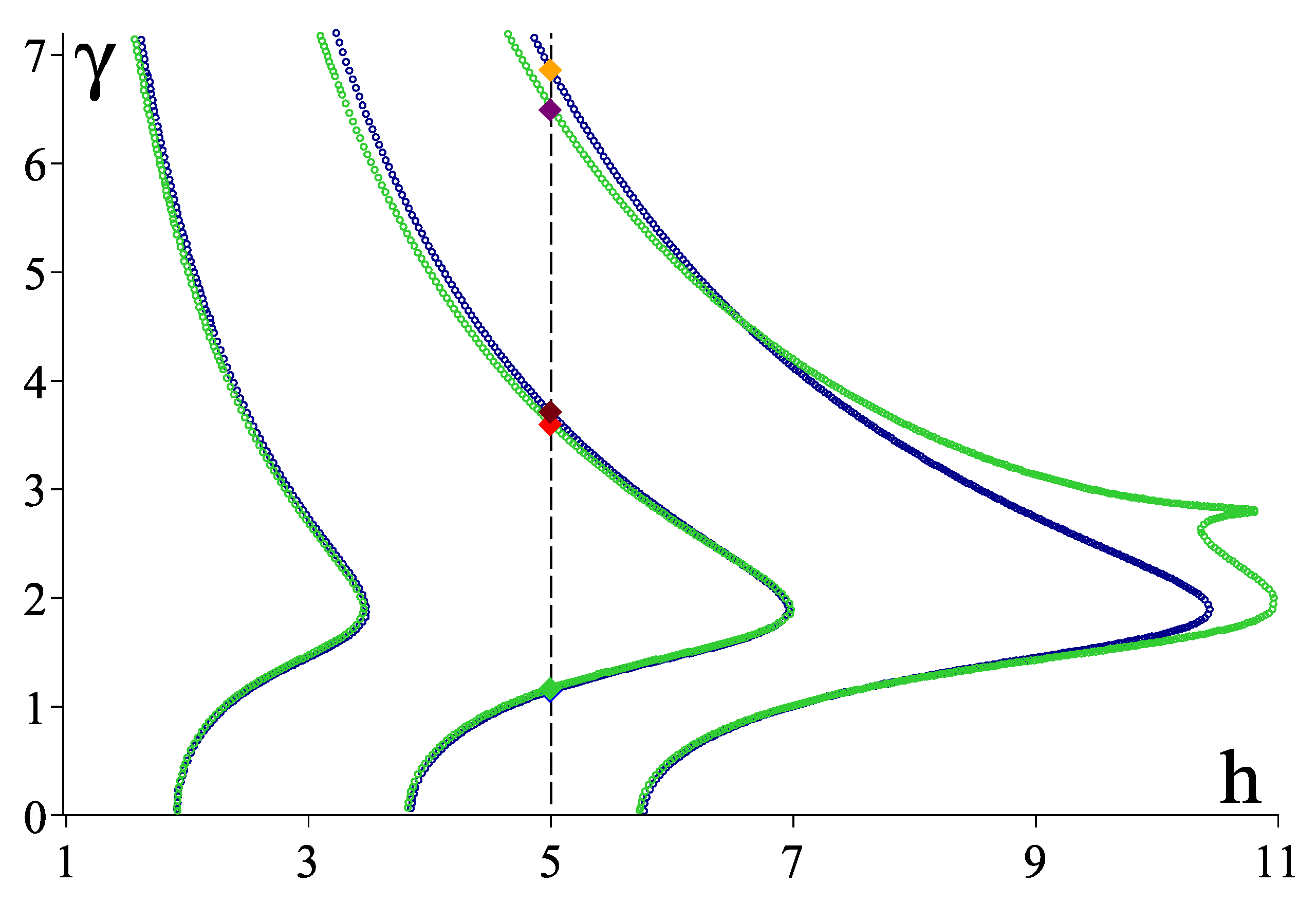
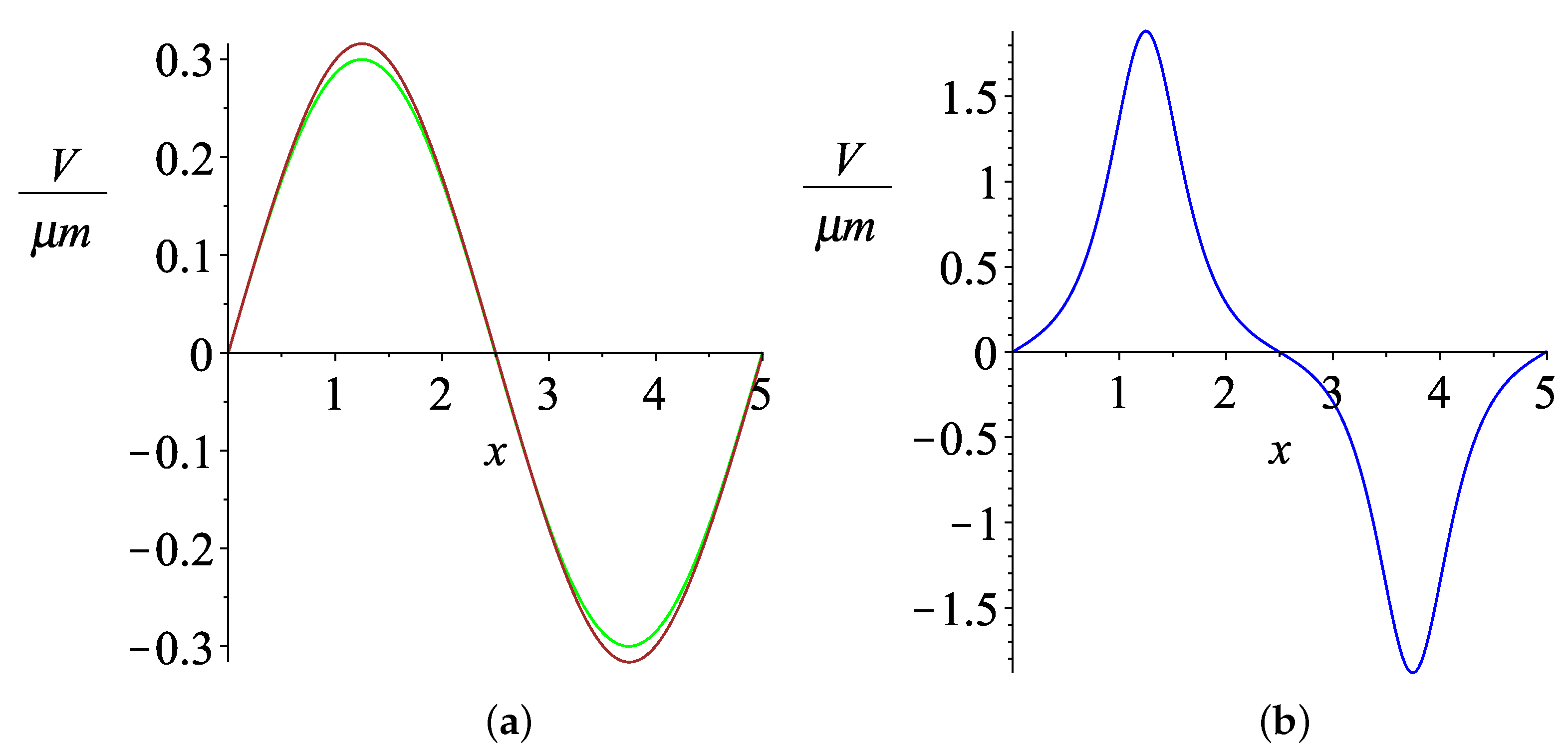
3.4. Numerical Results
3.5. Proofs
3.5.1. Proof of Statement 4
3.5.2. Proof of Statement 5
3.5.3. Proof of Statement 6
3.5.4. Proof of Theorem 2
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Unger, H.G. Planar Optical Waveguides and Fibres; Clarendon Press: Oxford, UK, 1977. [Google Scholar]
- Snyder, A.; Love, J. Optical Waveguide Theory; Chapman and Hall: London, UK, 1983. [Google Scholar]
- Sodha, M.S.; Ghatak, A.K. Inhomogeneous Optical Waveguides; Optical Physics and Engineering; Plenum Press: New York, NY, USA; London, UK, 1977. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M.; Pitaevskii, L.P. Course of Theoretical Physics (vol.8). Electrodynamics of Continuous Media; Butterworth-Heinemann: Oxford, UK, 1993. [Google Scholar]
- Akhmediev, N.N.; Ankevich, A. Solitons, Nonlinear Pulses and Beams; Chapman and Hall: London, UK, 1997. [Google Scholar]
- Boardman, A.D.; Egan, P.; Lederer, F.; Langbein, U.; Mihalache, D. Third-Order Nonlinear Electromagnetic TE and TM Guided Waves. In Nonlinear Surface Electromagnetic Phenomena; Ponath, H.-E., Stegeman, G.I., Eds.; Elsevier Science Publisher: North-Holland, The Amsterdam; London, UK; New York, NY, USA; Tokyo, Japan, 1991. [Google Scholar]
- Boyd, R.W. Nonlinear Optics, 2nd ed.; Academic Press: New York, NY, USA; London, UK, 2003. [Google Scholar]
- Mills, D.L. Nonlinear Optics: Basic Concepts; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Zakery, A.; Elliott, S.R. Optical Nonlinearities in Chalcogenide Glasses and Their Applications; Springer Series in Optical Sciences; Springer: Berlin/Heidelberg, Germany, 2007; Volume 135. [Google Scholar]
- Li, C. Nonlinear Optics Principles and Applications; Shanghai Jiao Tong University Press: Shanghai, China; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Khoo, I.C. Nonlinear optics, active plasmonics and metamaterials with liquid crystals. Prog. Quantum Electron. 2014, 38, 77–117. [Google Scholar] [CrossRef]
- Borghi, M.; Castellan, C.; Signorini, S.; Trenti, A.; Pavesi, L. Nonlinear silicon photonics. J. Opt. 2017, 19, 093002. [Google Scholar] [CrossRef]
- Schürmann, H.W. On the theory of TE-polarized waves guided by a nonlinear three-layer structure. Z. Phys. B 1995, 97, 515–522. [Google Scholar] [CrossRef]
- Smirnov, Y.G.; Valovik, D.V. Guided electromagnetic waves propagating in a plane dielectric waveguide with nonlinear permittivity. Phys. Rev. A 2015, 91, 013840. [Google Scholar] [CrossRef]
- Valovik, D.V. Novel propagation regimes for TE waves guided by a waveguide filled with Kerr medium. J. Nonlinear Opt. Phys. Mater. 2016, 25, 1650051. [Google Scholar] [CrossRef]
- Said, A.A.; Wamsley, C.; Hagan, D.J.; Stryland, E.W.V.; Reinhardt, B.A.; Roderer, P.; Dillard, A.G. Third- and fifth-order optical nonlinearities in organic materials. Chem. Phys. Lett. 1994, 228, 646–650. [Google Scholar] [CrossRef]
- Tan, C.; Li, N.; Xu, D.; Chen, Z. Spatial focusing of surface polaritons based on cross-phase modulation. Results Phys. 2021, 27, 104531. [Google Scholar] [CrossRef]
- Schürmann, H.W.; Smirnov, Y.G.; Shestopalov, Y.V. Propagation of TE-waves in Cylindrical Nonlinear Dielectric Waveguides. Phys. Rev. E 2005, 71, 016614. [Google Scholar] [CrossRef] [PubMed]
- Smirnov, Y.G.; Valovik, D.V. Coupled Electromagnetic TE-TM Wave Propagation in a Layer with Kerr Nonlinearity. J. Math. Phys. 2012, 53, 123530. [Google Scholar] [CrossRef]
- Valovik, D.V. Nonlinear multi-frequency electromagnetic wave propagation phenomena. J. Opt. 2017, 19, 115502. [Google Scholar] [CrossRef]
- Valovik, D.V. On a nonlinear eigenvalue problem related to the theory of propagation of electromagnetic waves. Differ. Equ. 2018, 54, 168–179. [Google Scholar] [CrossRef]
- Valovik, D.V. On spectral properties of the Sturm–Liouville operator with power nonlinearity. Monatshefte Math. 2019, 188, 369–385. [Google Scholar] [CrossRef]
- Moskaleva, M.A.; Kurseeva, V.Y.; Valovik, D.V. Asymptotical analysis of a nonlinear Sturm–Liouville problem: Linearisable and non-linearisable solutions. Asymptot. Anal. 2020, 119, 39–59. [Google Scholar]
- Adams, M.J. An Introduction to Optical Waveguides; John Wiley & Sons: Chichester, UK; New York, NY, USA; Brisbane, Australia; Toronto, ON, Canada, 1981. [Google Scholar]
- Marcuse, D. Theory of Dielectric Optical Waveguides, 2nd ed.; Academic Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Courant, R.; Hilbert, D. Methods of Mathematical Physics; Interscience Publishers Inc.: New York, NY, USA, 1953; Volume 1. [Google Scholar]
- Pontryagin, L.S. Ordinary Differential Equations; Pergamon Press: Oxford, UK, 1962. [Google Scholar]
- Mihalache, D.; Stegeman, G.I.; Seaton, C.T.; Wright, E.M.; Zanoni, R.; Boardman, A.D.; Twardowki, T. Exact dispersion relations for transverse magnetic polarized guided waves at a nonlinear interface. Opt. Lett. 1987, 12, 187–189. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; Wang, Z.H. Exact dispersion relations for TM waves guided by thin dielectrics films bounded by nonlinear media. Opt. Lett. 1993, 18, 260–262. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.H.; Chang, R.; Leung, P.T.; Tsai, D.P. Nonlinear dispersion relation for surface plasmon at a metal-Kerr medium interface. Opt. Commun. 2009, 282, 1412–1415. [Google Scholar] [CrossRef]
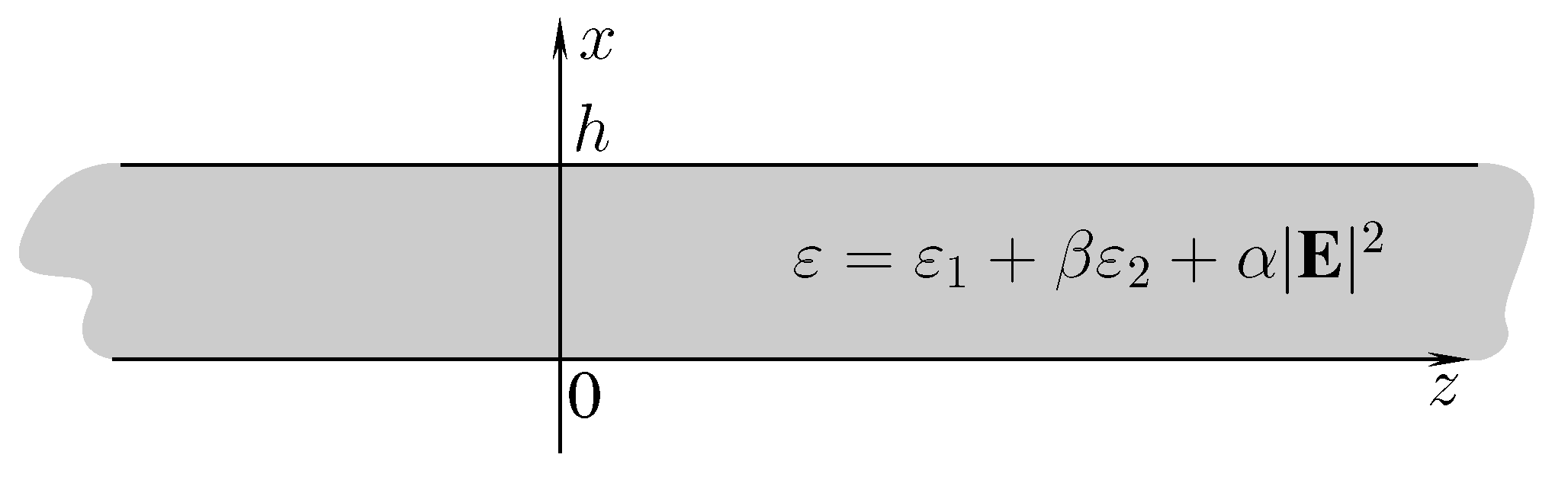


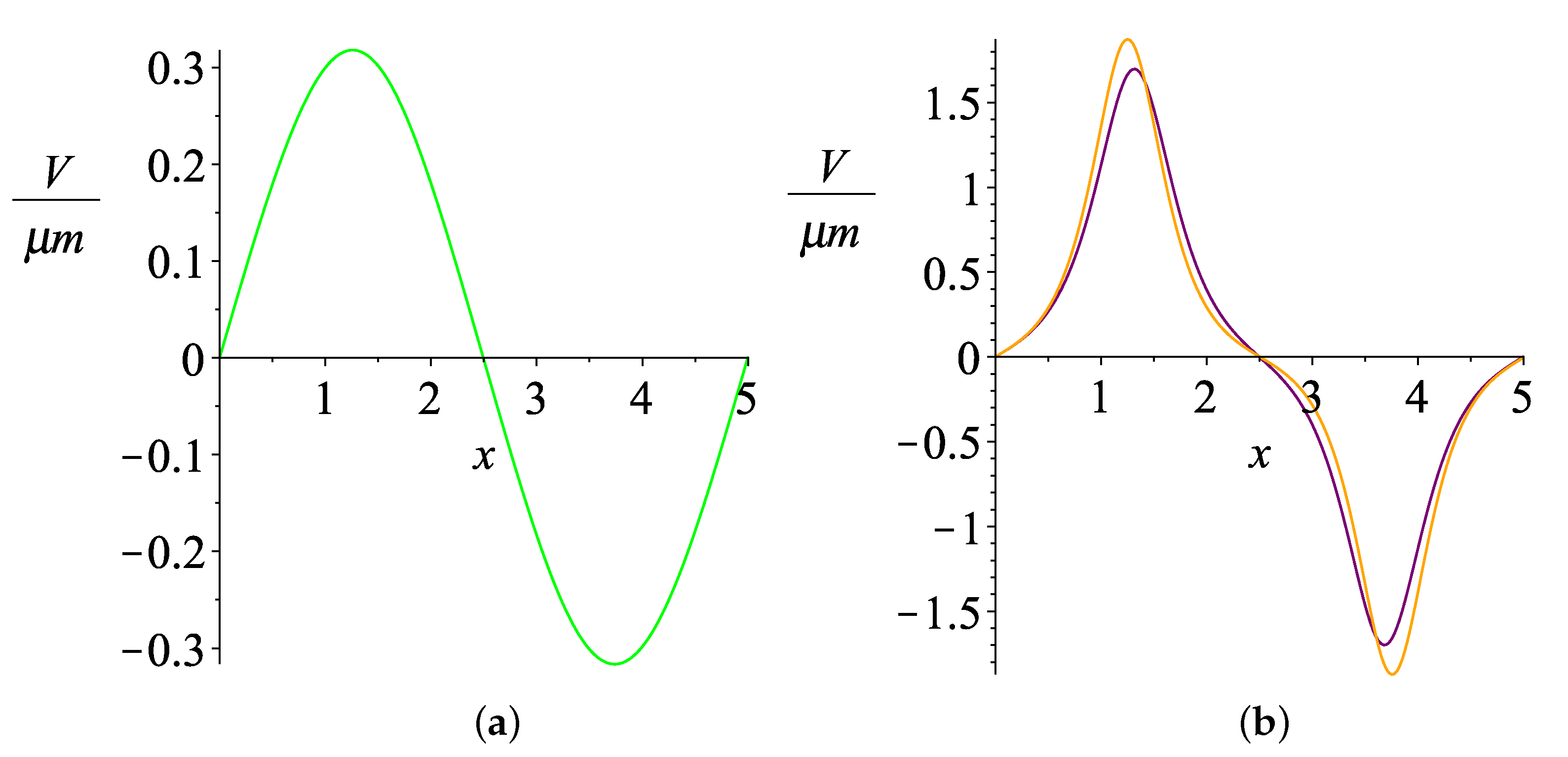
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dyundyaeva, A.; Tikhov, S.; Valovik, D. Transverse Electric Guided Wave Propagation in a Plane Waveguide with Kerr Nonlinearity and Perturbed Inhomogeneity in the Permittivity Function. Photonics 2023, 10, 371. https://doi.org/10.3390/photonics10040371
Dyundyaeva A, Tikhov S, Valovik D. Transverse Electric Guided Wave Propagation in a Plane Waveguide with Kerr Nonlinearity and Perturbed Inhomogeneity in the Permittivity Function. Photonics. 2023; 10(4):371. https://doi.org/10.3390/photonics10040371
Chicago/Turabian StyleDyundyaeva, Anna, Stanislav Tikhov, and Dmitry Valovik. 2023. "Transverse Electric Guided Wave Propagation in a Plane Waveguide with Kerr Nonlinearity and Perturbed Inhomogeneity in the Permittivity Function" Photonics 10, no. 4: 371. https://doi.org/10.3390/photonics10040371
APA StyleDyundyaeva, A., Tikhov, S., & Valovik, D. (2023). Transverse Electric Guided Wave Propagation in a Plane Waveguide with Kerr Nonlinearity and Perturbed Inhomogeneity in the Permittivity Function. Photonics, 10(4), 371. https://doi.org/10.3390/photonics10040371




