Strategy for Attacking the Key Parameters of Electro-Optic Self-Feedback Phase Encryption System

Abstract

In this paper, we propose a method for cracking the key parameters of an electro-optic self-feedback temporal optical phase encryption system and experimentally demonstrate the feasibility of the scheme. By scanning a tunable dispersion compensation (TDC) module at the receiver, the time delay signature (TDS) of an encrypted signal can be exposed, making it possible to extract other key parameters of the system and reconstruct a decryption setup. The TDS characteristics for three typical modulation formats are investigated, revealing that while such an encryption system is secure against power detection attack, there is a risk of TDS leakage. The findings can guide the design of advanced optical encryption schemes with TDS suppression for security enhancement.

1. Introduction

As the demand for confidential information sharing and data interconnection grows dramatically, guaranteeing the data security in the optical network is of paramount importance [1]. Traditional approaches mainly use digital encryption algorithms to encrypt the upper layer confidential data, and such algorithms, which rely solely on computational complexity, will face serious potential threat from quantum computers in the near future. Therefore, secure optical signal transmission in the physical layer becomes an urgent need [2,3]. A variety of strategies based on optical domain encryption have been proposed and demonstrated previously [4,5,6,7,8,9,10,11], including coherent time spreading optical encoding based on super-structured fiber Bragg grating (SSFBG) [4], spectral phase encoding time spreading based on spatial light modulator (SLM) [5,6], XOR logical encryption based on semiconductor optical amplifier [7], optic chaos encryption [8,9,10], and stimulated Brillouin scattering (SBS) based optical gain or loss encryption [11]. All those approaches can be realized purely by hardware components in the optical domain and effectively protect the data confidentiality but still suffer from the problems of limited achievable bit rate lower than 25 Gb/s, requiring additional encryption channels and specially designed optical transmitters that are not fully compatible with modern fiber-optic communication systems.

Recently, a novel hardware encryption scheme based on an electro-optic time-delayed feedback loop has been proposed and demonstrated for various bit rates [12,13], which exhibits superior advantages of enabling high bit rate operation and being fully pluggable and compatible with fiber-optic systems; more importantly, the signal can be self-encrypted without additional encryption channels. It has been successfully proved that this type of optical encryption scheme is very efficient in defending against direct power detection attack [13]. However, it is worthy of concern that, in the case of a public-known encryption structure, this method of encrypting data based on the physical layer needs to rely on the eavesdropping resistance of the key parameters, and the cracking of the system key parameters will directly threaten the system security. Therefore, it is quite essential to explore whether such an encryption scheme is resistant to other kinds of sophisticated eavesdropping attacks.

In this paper, we experimentally investigate the security of the electro-optic self-feedback temporal phase encryption scheme against statistical autocorrelation function (ACF) analysis attack for three typical optical modulation formats. It has been revealed that such an encryption scheme exhibits certain security vulnerability by extracting the time delay signature (TDS) from the ACF curve when an eavesdropper is equipped with a proper interception setup. A cracking method for a malicious eavesdropper has been provided for hardware key parameter extraction and decryption setup reconstruction.

2. Principle and Experimental Setup

The experimental setup to investigate the security issue of the electro-optic self-feedback temporal phase encryption scheme is illustrated in Figure 1. At the transmitter side, a 40 GHz Fujitsu Mach-Zehnder modulator (MZM) is employed to modulate a continuous-wave optical carrier centering at 1550.1 nm to produce a 28 Gb/s intensity modulated on-off-keying (OOK) or 4-level pulse amplitude modulation (PAM4) signal, which is directed into the subsequent electro-optic self-feedback temporal phase encryption module. The encryption module consists of a chromatic dispersion component (D1), an electro-optic feedback phase encryption loop (EOFPL) followed by another chromatic dispersion component (D2). Both dispersion fiber and conventional chirped fiber Bragg grating (CFBG) can be utilized for the dispersion component (D1 and D2). After passing through the first dispersion component D1, the modulated optical signal is temporally spread and distorted due to chromatic dispersion, whose output signal can be described in the time domain as:

$$E_1\left(\mathrm{t}\right)=F^{-1}(F\left(E_0\left(\mathrm{t}\right)\right)·(exp\left(j\frac{B}{2}{(\omega -{\omega }_0)}^2\right))),$$

(1)

where B is the dispersion coefficient, ${\omega }_0$ is the original angular frequency, and $E_0\left(\mathrm{t}\right)$ is the electric field of the intensity modulated signal. F and $F^{-1}$ denote the Fourier transform and Fourier inverse transform, respectively. Then, after the EOFPL for self-feedback phase encryption, the output optical signal can be expressed as

$$E_2\left(t\right)=E_1\left(t\right)exp\left(j\frac{V\left(t\right)}{V_{\pi }}\pi \right),$$

(2)

where $V_{\pi }$ is the half-wave voltage of the phase modulator and $V\left(t\right)$ is the drive voltage of the phase modulator, which can be obtained from the following differential delay equation:

$$\frac{1}{\theta }{\int }_{{}_{t_0}}^{t}V\left(\xi \right)d\xi +V\left(t\right)+\tau \frac{dV\left(t\right)}{dt}=\eta {\left|E_1(t-t_d)\right|}^2,$$

(3)

where $t_d$ is the TDS of the EOFPL, $\eta$ is the normalized loop gain, and $\left|·\right|$ is the modular operation. The left side of the Equation (3) is a band-pass filter function, where $\theta$ and $\tau$ are the integral response time and differential response time. The band-pass filter function is used to approximately represent the feedback path consisting of a phase modulator (PM1), a photodetector (PD1), and a radio frequency amplifier (AMP1). After that, the self-feedback phase encrypted signal is further temporally scrambled by using another chromatic dispersion component (D2) based on phase-to-intensity conversion to generate the encrypted signal, which is transmitted over a span of transmission fiber including ~20 km standard single mode fiber (SSMF) and ~2.2 km corresponding dispersion compensation fiber. A CFBG is utilized to act as D2 in the setup. At the legitimate receiver side, a symmetric decryption structure is employed to perform temporal phase decryption followed by direct power detection to recover the confidential optical signal.

In the EOFPL encryption system, the hardware key parameters include the dispersion values of the dispersive component D1 and D2, the modulation depth of the PM1, and the roundtrip delay time of the feedback phase loop, which contribute to the hardware key space together. Then, the key measurement parameters of this experiment are shown in

Table 1. Table of key measurement parameters.

Key Parameters	Key Measurement Parameters
The TDS of EOFPL	Encrypted signals, autocorrelation information of signals
Modulation depth of modulator (MD)	preset value (0~1.5)
Dispersion value of SSMF	D4 (−1400~400 ps/nm)
Dispersion value of CFBG	D3 (−1400~0 ps/nm)

. Specifically, the dispersion value of D1 is set as 1000 ps/nm, D2 is 500 ps/nm, the modulation depth of the PM1 is set as 0.81, and the roundtrip delay time of the EOFPL is 65.12 ns, in the experiment. Among them, the delay time of EOFPL is the most critical key parameter since it could be intentionally varied in a relatively large range and contributes to most of the hardware key space. Once the delay time is revealed to an eavesdropper, it becomes possible for her to reconstruct a decryption EOFPL structure and retrieve the confidential data. Hence, it is of vital importance to guarantee the security of the delay time of the EOFPL for the whole encryption scheme.

To emulate an eavesdropper’s malicious attack on extracting the key hardware parameters, especially the delay time via statistical ACF analysis, a portion of the encrypted signal is tapped from the transmission link and then directed into an interception setup, which consists of an erbium-doped fiber amplifier (EDFA), an optical filter, a commercial tunable dispersion compensator (D5), and another photodetector (PD4). We use a commercial maximum adjustable dispersion module (−3000~3000 ps/nm) to dynamically scan the dispersion values and investigate the TDS characteristics of the corresponding ACF at different dispersion compensation values, which will transform the temporally phase encrypted signal to different temporal profiles due to the phase intensity conversion by the chromatic dispersion. Finally, a 40 GHz photodetector is used to detect the intercepted signal with different dispersion value settings, and the temporal waveforms are collected and processed offline with a digital sampling oscilloscope (DSO) with a sampling rate of 100 GSa/s to perform ACF analysis.

3. Results and Discussion

In the electro-optic self-feedback temporal phase hardware encryption system, the security of the whole system depends firstly on the confidentiality of the hardware key parameters and then on the hardware key space that adds the difficulty of the brute-force attack. Although it is extremely difficult to extract the values of key hardware parameters directly from the temporal waveform of the encrypted signal that exhibits as a noise-like signal, it is potentially possible for an eavesdropper to record the intercepted waveform and perform statistical analysis, particularly calculating the ACF to extract the key parameters. In the ACF analysis method, relative to the time series $v\left(t\right)$, the background $Q_{ACF}$ can be defined as [14]:

$$\begin{array}{c}{Q}_{ACF}=\left[P_{lower,ACF},P_{uppper,ACF}\right]\\ \\ P_{lower,ACF}=mean\left\{ACF\left(s\right)\right\}-SD\left\{ACF\left(s\right)\right\}\\ \\ P_{upper,ACF}=mean\left\{ACF\left(s\right)\right\}+SD\left\{ACF\left(s\right)\right\},\end{array}$$

(4)

where $SD$ represents the operation of solving for the standard deviation, the mean represents averaging the data, s denotes the time shift, $P_{uppper,ACF}$ is the upper threshold of ACF background, and $P_{lower,ACF}$ is the lower threshold of ACF background. The function of ACF can be obtained by [14]

$$ACF\left(s\right)=\frac{〈\left[v\left(t\right)-〈v\left(t\right)〉\right]\left[v(t+s)-〈v\left(t\right)〉\right]〉}{\sqrt{〈{(v\left(t\right)-〈v\left(t\right)〉)}^2〉〈{(v(t+s)-〈v\left(t\right)〉)}^2〉}},$$

(5)

Firstly, the ACF characteristic of the encrypted signal for conventional OOK modulation format is investigated, as illustrated in Figure 2. It is clear that when the dispersion value of D5 for an eavesdropper is set to 0 ps/nm, the TDS is submerged in the ACF background and no TDS peak can be extracted from the ACF curve of the intercepted signal, as depicted in Figure 2a with blue solid line. The TDS peak value here refers to the autocorrelation coefficient at TDS (65.12 ns) obtained after ACF analysis of the signal, which reflects the degree of correlation between the original signal and signal after a delay of 65.12 ns. A larger absolute value indicates a greater degree of correlation. From the results, it can be seen that the EOFPL encryption scheme is capable of providing hardware security against both direct detection attack and TDS attack if the eavesdropper directly record the encrypted signal and perform statistical ACF analysis. In contrast, if a sophisticated eavesdropper attempts to crack the system by employing another separate dispersion module with a dispersion value of −2000 ps/nm or 1200 ps/nm, a distinct TDS peak will be observed in the ACF curve, which is located exactly at the delay time of 65.12 ns inside the EOFPL. Hence, one of the key hardware parameters can be extracted by the eavesdropper, and security vulnerability is revealed in such an attack scenario. To further quantify the TDS peak value, the relationship between the applied dispersion D5 for an eavesdropper and the TDS peak of the encrypted signal with two typical phase modulation depths (MD) of 0.41 and 0.81 is depicted in Figure 2b. It is evident that when the dispersion of D5 is properly selected, the TDS peak can be popped out from the upper and lower ACF background and leaked to an eavesdropper. Since the two curves of MD = 0.41 and MD = 0.81 have similar change patterns, we can take MD = 0.41 as an example. If D5 lies between −3000~−2000 ps/nm, the TDS peak shows an increasing trend. At the dispersion value of around −2000 ps/nm, a maximum TDS peak of ~0.07 is obtained. As D5 shifts towards the range of −2000 to −500ps/nm, the TDS peak shows a gradually decreasing trend. When D5 is −500~1700 ps/nm, the TDS peak is between the upper and lower ACF background, indicating that the TDS peak cannot be effectively detected at this time, i.e., there is no time delay leakage. As D5 continues to increase, the TDS peak will persist in being exposed and show an increasing trend. Hence, a sophisticated eavesdropper is possible to crack the delay time parameter of the encryption system by detecting the TDS if blind scanning the dispersion of D5 to be in the region, where the corresponding TDS peak is outside the lower and upper ACF thresholds. It is worth noting that the leakage of the TDS peak for the MD of 0.81 is more prominent than that of the MD of 0.41. The larger the MD, the higher the security against direct power detection attack due to enhanced signal encryption effect, but the stronger the TDS leaked is, indicating the tradeoff between signal encryption and TDS leakage. We then further investigate the effect of changing the non-return-to-zero (NRZ) signal rate on TDS leakage, and the experimental results are shown in Figure 2c. One can observe the overall trend in which the TDS peak becomes more and more visible as the NRZ signal rate decreases. And at different rates, the TDS peak is higher than the exhibited significant TDS leakage, which is especially obvious when the dispersion value is set to −2000 ps/nm.

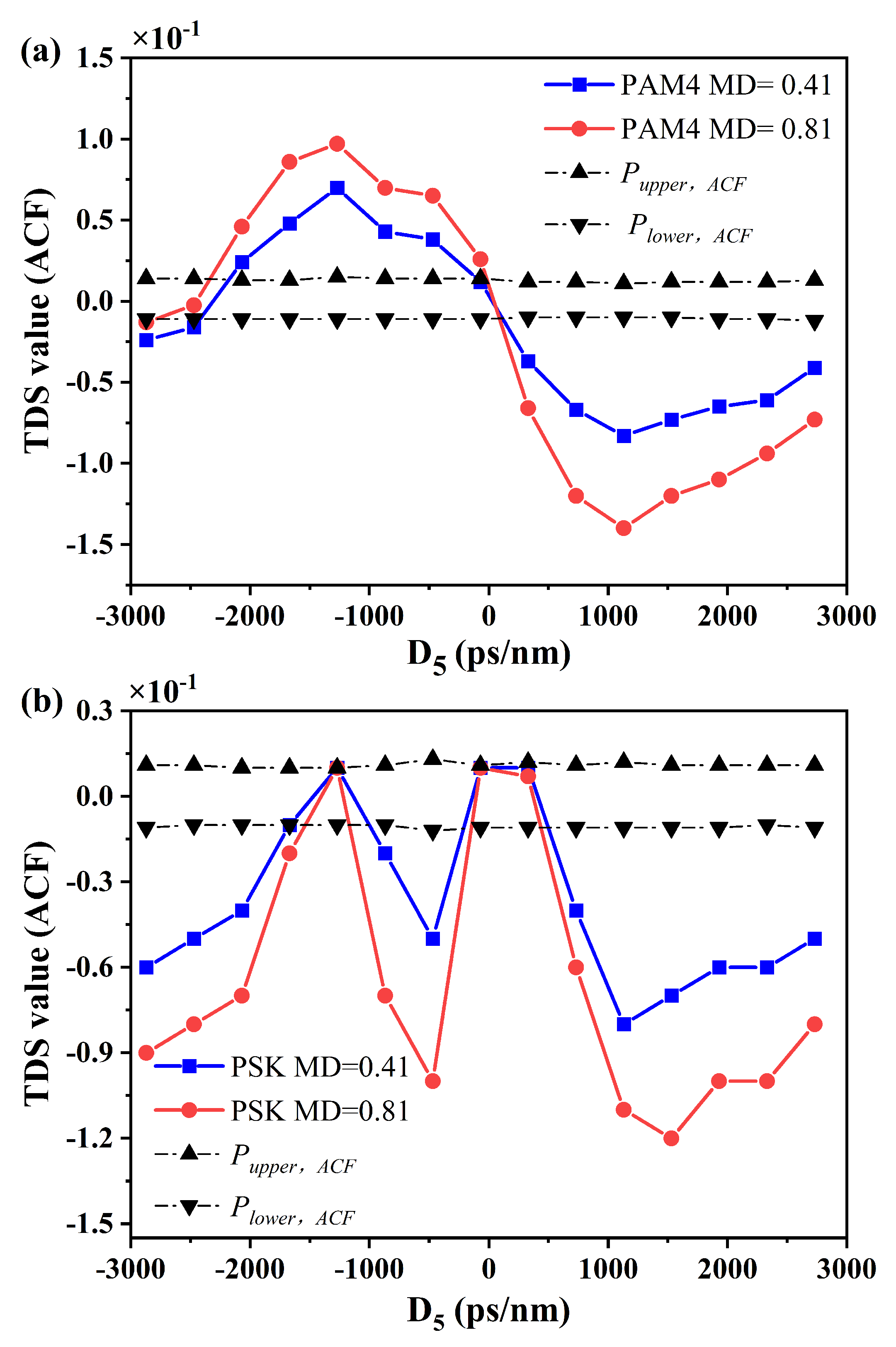
In addition, the relationship between the TDS peak and the dispersion D5 is also investigated for the high-order PAM4 modulation format, as shown in Figure 3a. The dependence of TDS value versus the D5 exhibits similar a tendency to that of the NRZ modulation format, but the PAM4 signal has a more pronounced TDS peak and the dispersion range of D5 for TDS exposure is greatly expanded, showing that it is much easier to detect the TDS of a PAM4 signal for a malicious eavesdropper. Furthermore, when the phase-shift-keying (PSK) modulation format is employed by replacing the MZM into a PM in the setup, it is found that the behavior of TDS for the PSK data is distinctly different from that of the NRZ and PAM4 intensity modulated data, as shown in Figure 3b. The TDS peak of the feedback loop for a PSK data is negative, and it is exposed outside the lower ACF background intermittently in the dispersion regions of −900 to −100 ps/nm, −3000 to −1600 ps/nm and 500 to 3000 ps/nm for D5, which demonstrates that the delay time of the self-feedback encryption phase loop can be extracted by detecting the TDS peak value regardless of the applied modulation formats.

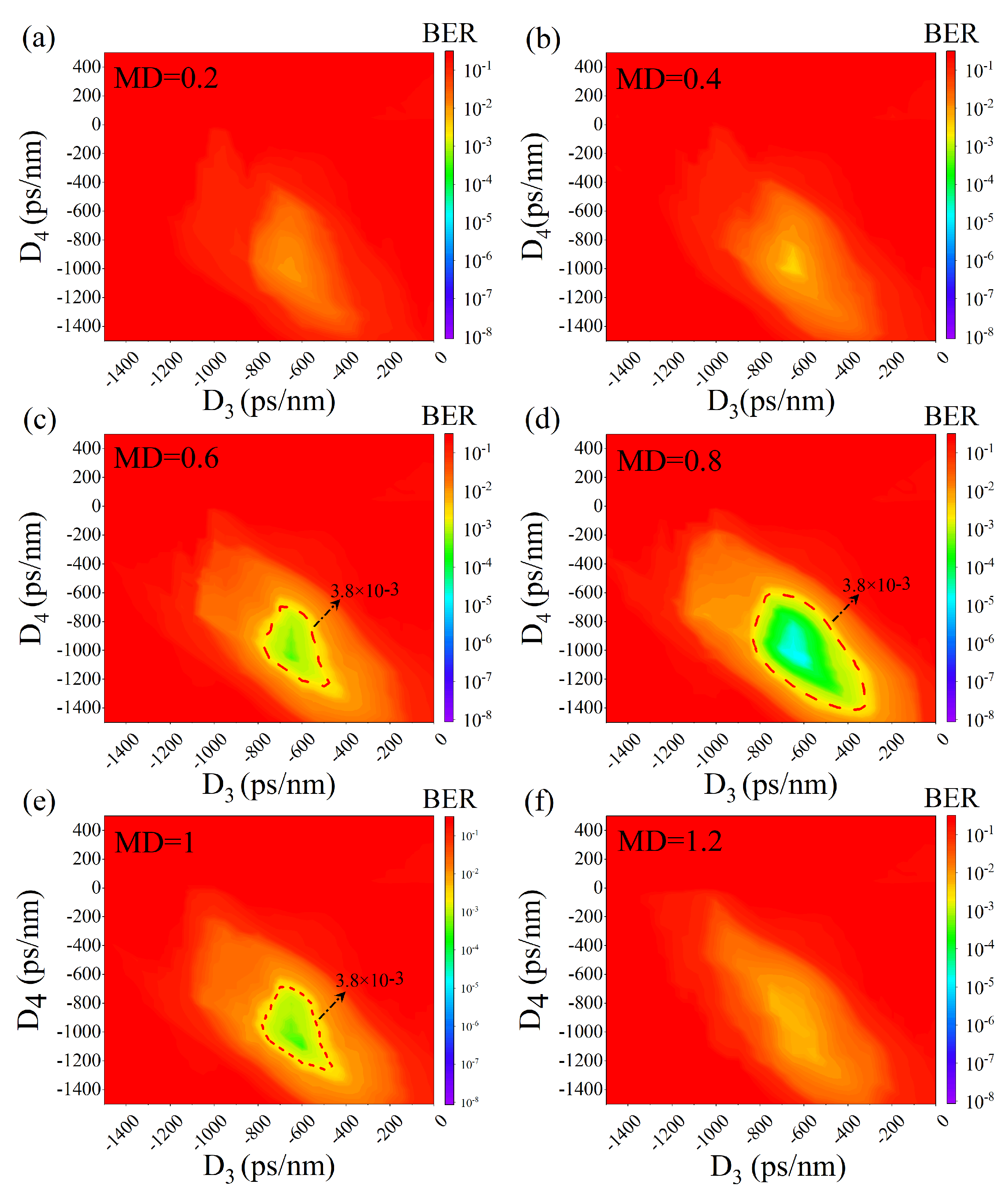
After extracting the TDS of the feedback loop from the encrypted signal, attention is now turned into investigate whether it is possible for an eavesdropper to reconstruct an identical decryption module by brute-force cracking the remaining hardware parameters. Since the key space for the phase MD is relatively small, an eavesdropper is feasible to firstly fix the delay time of the loop and then select a MD value before brute-force scanning the dispersion values of D3 and D4 for decryption until they are matched with the counterpart dispersion values of D1 and D2. Figure 4a–f depict the contour plots of the measured BER versus the dispersion values of D3 and D4 for different cases of phase MDs. It is clear that when the MD is selected as 0.81 and the dispersion of D3 and D4 are scanned through the values of −500 ps/nm and −1100 ps/nm, a BER lower than the hard-decision forward error correction (HD-FEC) threshold can be obtained, indicating that all of the remaining hardware key parameters are cracked, as shown in Figure 4d. Figure 5a,b further depict the waveforms and eye diagrams of the original NRZ signal and the encryption signal intercepted from the transmission link, which clearly show that the original confidential signal can be encrypted in the time domain and it is not easily recovered by simply detecting the waveform and eye diagram. Figure 5c,d show the waveforms and eye diagrams after reconstructing a decryption self-feedback loop based on the extracted TDS value but without (c) and with (d) the correct dispersion values of D3 and D4. It can be clearly seen that the waveform of the recovered data resembles with the original data quite well, and the corresponding eye diagram is open after the TDS extraction and brute-force hardware parameter attacks.

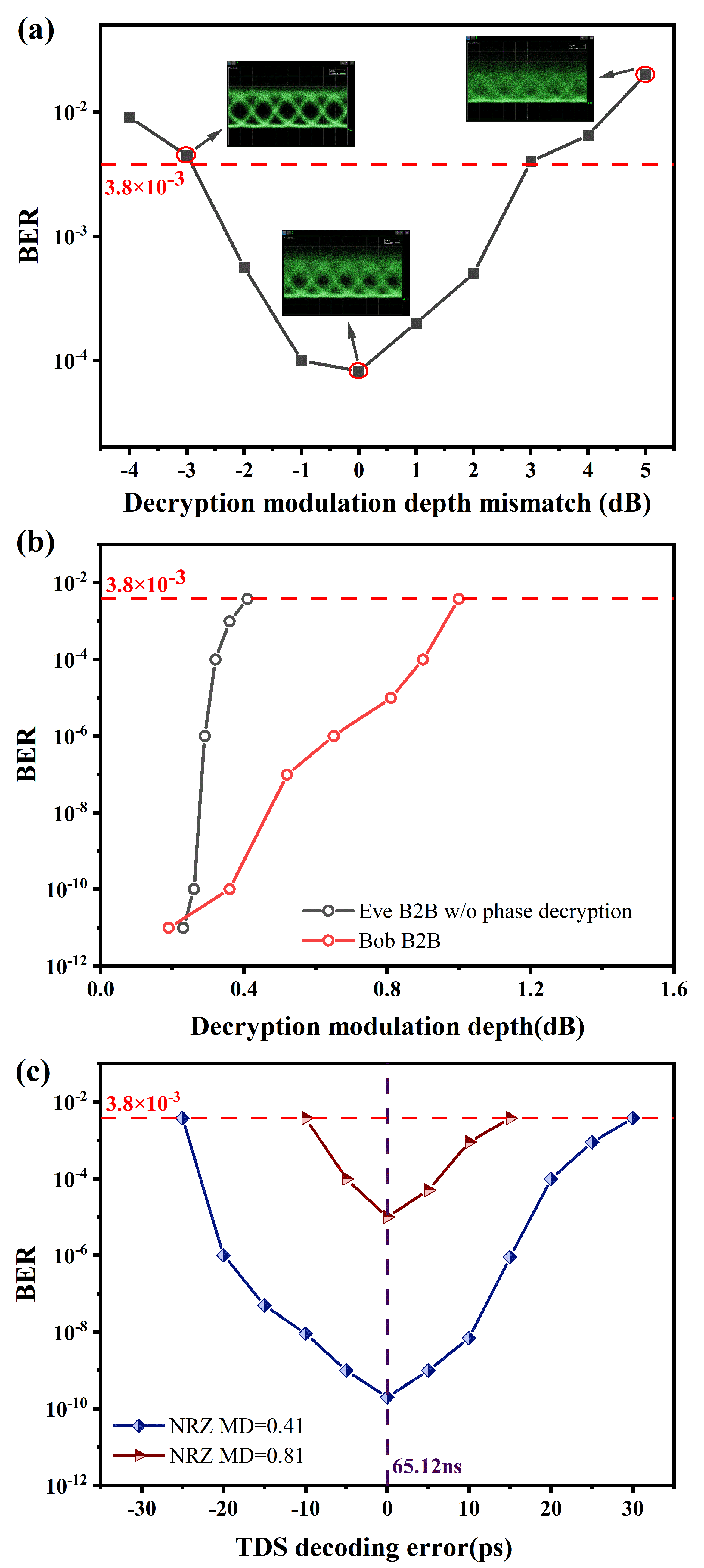
In addition, the tolerance of phase MD of the reconstructed decryption feedback loop is also investigated, as shown in Figure 6a. It is clear that the decryption phase MD mismatch of ~±3dB can be tolerated for a 28 Gb/s NRZ signal when the phase MD is set as 0.81. BER lower than the HD-FEC threshold can be achieved for an eavesdropper, indicating the security vulnerability of such a system against powerful statistical ACF analysis. In the paper, we also discuss the result that the range of TDS leakage becomes smaller as the modulation depth decreases, followed by a discussion on whether a critical modulation depth exists for the system that maintains the communication quality while masking the TDS. As shown in Figure 6b, the red curve represents the BER versus phase modulation depth for legitimate users, while for eavesdroppers who have cracked the system dispersion without reconfiguring the EOFPL, the relationship is shown in the gray curve. Finally, we also discussed the effect of the TDS parameter deciphering deviation on the accuracy of decrypted signals for different modulation depths, and the results are shown in Figure 6c. The allowable range of TDS deciphering deviation is −25~30ps when MD = 0.41, and −10~15ps when MD = 0.81, beyond which the signals cannot be decrypted correctly.

4. Conclusions

In summary, we experimentally demonstrate the security vulnerability of the electro-optic self-feedback temporal phase encryption scheme by detecting the time delay signature of the encrypted signal for three typical optical modulation formats. The key extraction strategy for four hardware parameters is also provided based on statistic ACF analysis and brute-force attack, which makes is possible for an eavesdropper to reconstruct a decryption module and intercept the confidential data. It is desirable to develop innovative novel electro-optic self-feedback encryption schemes with eliminated TDS to guarantee the system security against both power detection and TDS detection attacks in future.