Effect of Surface Nonlinearity Distribution on Second Harmonic Generation under Tightly Focused Beams
Abstract
1. Introduction
2. Theory
3. Results and Discussion
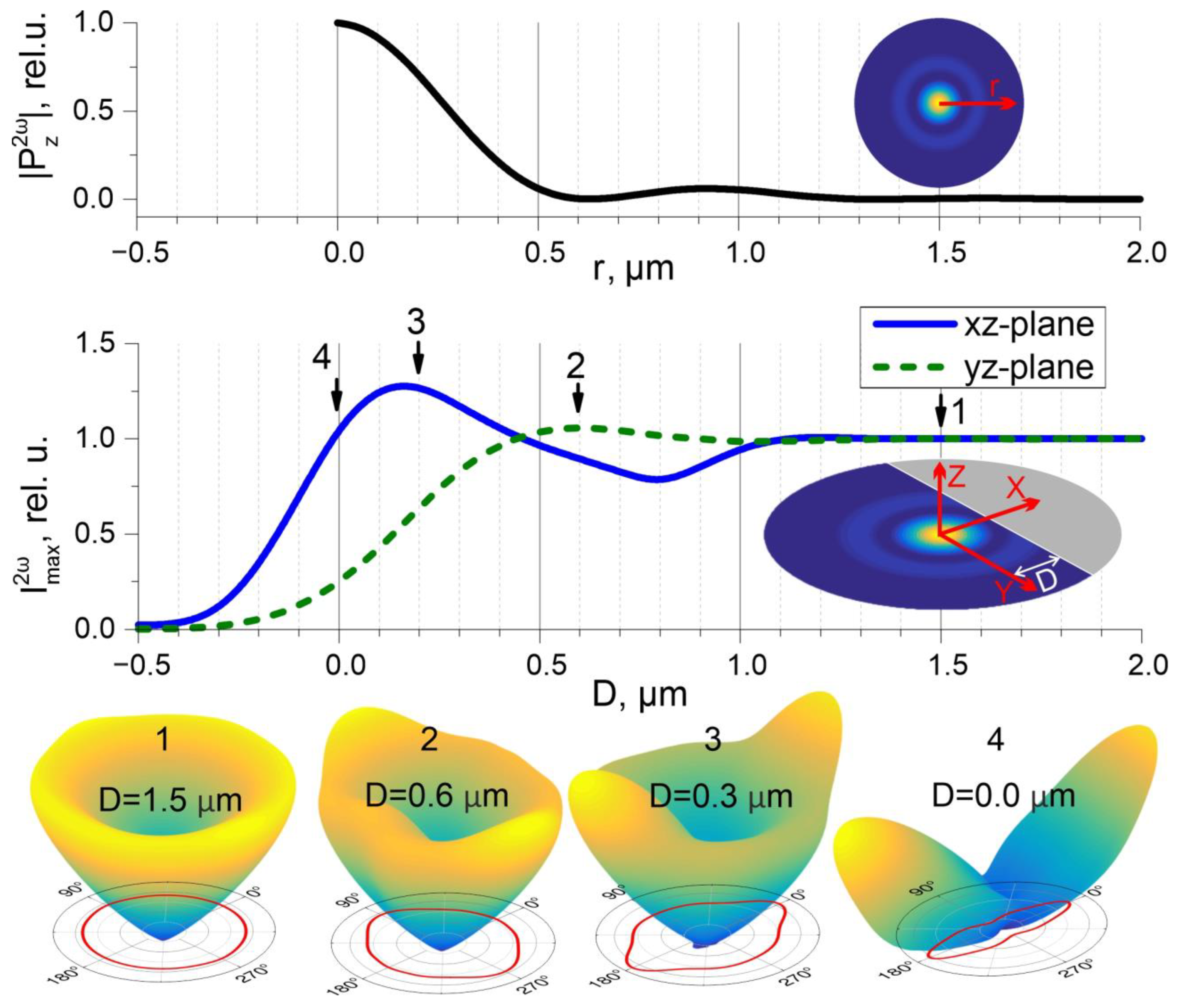
3.1. χ(2)zzz-Component
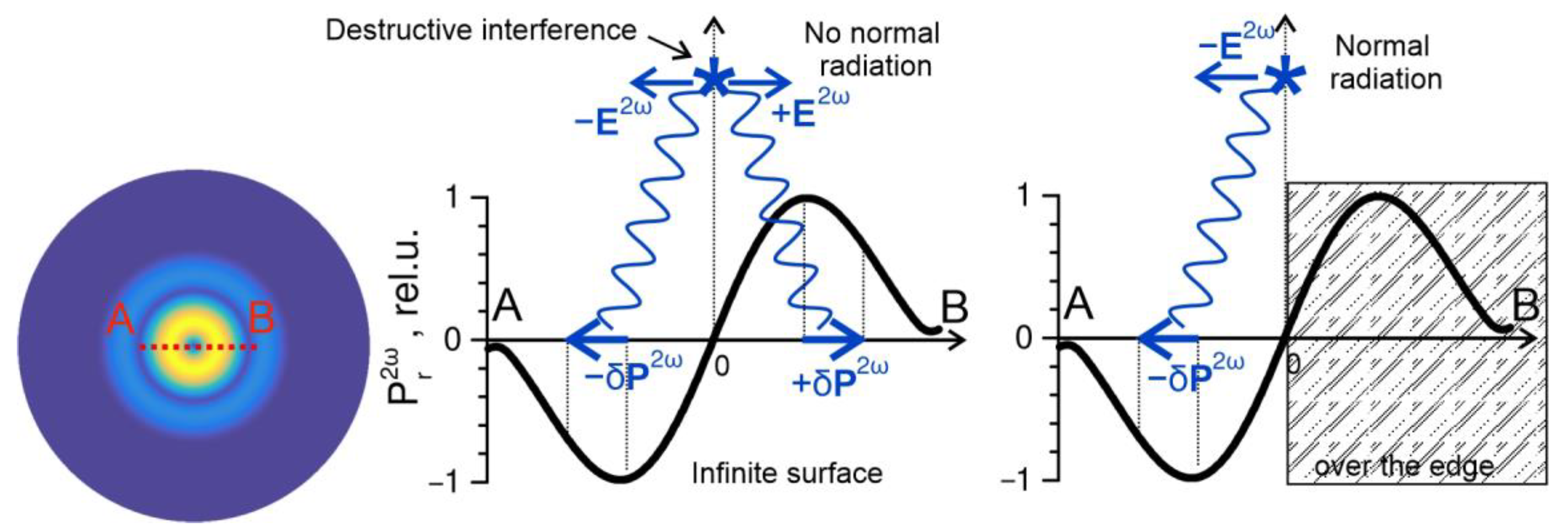
3.2. χ(2)xzx-Component and Normal Radiation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Franken, P.A.; Hill, A.E.; Peters, C.W.; Weinreich, G. Generation of optical harmonics. Phys. Rev. Lett. 1961, 7, 118–119. [Google Scholar] [CrossRef]
- Ren, Y.; Zhao, X.; Hagley, E.W.; Deng, L. Ambient-condition growth of high-pressure phase centrosymmetric crystalline KDP microstructures for optical second harmonic generation. Sci. Adv. 2016, 2, e1600404. [Google Scholar] [CrossRef]
- Kauranen, M.; Zayats, A.V. Nonlinear plasmonics. Nat. Photonics 2012, 6, 737–748. [Google Scholar] [CrossRef]
- Liu, T.; Xiao, S.; Li, B.; Gu, M.; Luan, H.; Fang, X. Third- and Second-Harmonic Generation in All-Dielectric Nanostructures: A Mini Review. Front. Nanotechnol. 2022, 4, 891892. [Google Scholar] [CrossRef]
- Krause, D.; Teplin, C.W.; Rogers, C.T. Optical surface second harmonic measurements of isotropic thin-film metals: Gold, silver, copper, aluminum, and tantalum. J. Appl. Phys. 2004, 96, 3626–3634. [Google Scholar] [CrossRef]
- Wang, X.; Shen, S.; Sun, J.; Fan, F.; Chang, S. Surface and bulk second-harmonic responses from a glass slide using tightly focused radially polarized light. Opt. Lett. 2016, 41, 5652–5655. [Google Scholar] [CrossRef] [PubMed]
- Butet, J.; Russier-Antoine, I.; Jonin, C.; Lascoux, N.; Benichou, E.; Brevet, P.F. Sensing with multipolar second harmonic generation from spherical metallic nanoparticles. Nano Lett. 2012, 12, 1697–1701. [Google Scholar] [CrossRef]
- Tran, R.J.; Sly, K.L.; Conboy, J.C. Applications of Surface Second Harmonic Generation in Biological Sensing. Annu. Rev. Anal. Chem. 2017, 10, 387–414. [Google Scholar] [CrossRef]
- Xia, C.; Sun, J.; Wang, Q.; Chen, J.; Wang, T.; Xu, W.; Zhang, H.; Li, Y.; Chang, J.; Shi, Z.; et al. Label-Free Sensing of Biomolecular Adsorption and Desorption Dynamics by Interfacial Second Harmonic Generation. Biosensors 2022, 12, 1048. [Google Scholar] [CrossRef]
- Wunderlich, S.J. Second Harmonic Light Scattering from Dielectric and Metallic Spherical Nanoparticles. Ph.D. Thesis, Der Friedrich-Alexander-Universität Erlangen-Nürnberg, Erlangen, Germany, 2014. [Google Scholar]
- Thyagarajan, K.; Rivier, S.; Lovera, A.; Martin, O.J.F. Enhanced second-harmonic generation from double resonant plasmonic antennae. Opt. Express 2012, 20, 12860–12865. [Google Scholar] [CrossRef]
- Frizyuk, K.; Volkovskaya, I.; Smirnova, D.; Poddubny, A.; Petrov, M. Second-harmonic generation in Mie-resonant dielectric nanoparticles made of noncentrosymmetric materials. Phys. Rev. B 2019, 99, 075425. [Google Scholar] [CrossRef]
- Scherbak, S.A.; Lipovskii, A.A. Understanding the Second-Harmonic Generation Enhancement and Behavior in Metal Core–Dielectric Shell Nanoparticles. J. Phys. Chem. C 2018, 122, 15635–15645. [Google Scholar] [CrossRef]
- Lerman, G.M.; Levy, U. Effect of radial polarization and apodization on spot size under tight focusing conditions. Opt. Express 2008, 16, 4567–4581. [Google Scholar] [CrossRef]
- Butet, J.; Russier-Antoine, I.; Jonin, C.; Lascoux, N.; Benichou, E.; Brevet, P.-F. Nonlinear Mie theory for the second harmonic generation in metallic nanoshells. J. Opt. Soc. Am. B 2012, 29, 2213–2221. [Google Scholar] [CrossRef]
- Rodríguez, F.J.; Wang, F.X.; Canfield, B.K.; Cattaneo, S.; Kauranen, M. Multipolar tensor analysis of second-order nonlinear optical response of surface and bulk of glass. Opt. Express 2007, 15, 8695–8701. [Google Scholar] [CrossRef]
- Scherbak, S.A.; Reshetov, I.V.; Zhurikhina, V.V.; Lipovskii, A.A. Second Harmonic Generation By Surface of Poled Glasses: Modeling and Measurement of Maker Fringes. St. Petersbg. State Polytech. Univ. J. Phys. Math. 2021, 14, 95–113. [Google Scholar] [CrossRef]
- Melik-Gaykazyan, E.V.; Kruk, S.S.; Camacho-Morales, R.; Xu, L.; Rahmani, M.; Zangeneh Kamali, K.; Lamprianidis, A.; Miroshnichenko, A.E.; Fedyanin, A.A.; Neshev, D.N.; et al. Selective Third-Harmonic Generation by Structured Light in Mie-Resonant Nanoparticles. ACS Photonics 2018, 5, 728–733. [Google Scholar] [CrossRef]
- Bautista, G.; Huttunen, M.J.; Kontio, J.M.; Simonen, J.; Kauranen, M. Third- and second-harmonic generation microscopy of individual metal nanocones using cylindrical vector beams. Opt. Express 2013, 21, 21918–21923. [Google Scholar] [CrossRef]
- Zhang, W.; Xue, T.; Lu, F.; Zhang, L.; Meng, C.; Wang, J.; Mei, T. Second-order surface optical nonlinear response of plasmonic tip axially excited via ultrafast vector beams. Appl. Phys. Express 2020, 13, 032002. [Google Scholar] [CrossRef]
- Biss, D.P.; Brown, T.G. Polarization-vortex-driven second-harmonic generation. Opt. Lett. 2003, 28, 923–925. [Google Scholar] [CrossRef]
- Ohtsu, A. Second-harmonic wave induced by vortex beams with radial and azimuthal polarizations. Opt. Commun. 2010, 283, 3831–3837. [Google Scholar] [CrossRef]
- Pakhomov, A.V.; Löchner, F.J.F.; Zschiedrich, L.; Saravi, S.; Hammerschmidt, M.; Burger, S.; Pertsch, T.; Setzpfandt, F. Far-field polarization signatures of surface optical nonlinearity in noncentrosymmetric semiconductors. Sci. Rep. 2020, 10, 10545. [Google Scholar] [CrossRef]
- Sun, J.; Wang, X.; Chang, S.; Zeng, M.; Shen, S.; Zhang, N. Far-field radiation patterns of second harmonic generation from gold nanoparticles under tightly focused illumination. Opt. Express 2016, 24, 7477–7487. [Google Scholar] [CrossRef] [PubMed]
- Scherbak, S.A.; Lipovskii, A.A. Optical second-harmonic response of axially symmetric media under tightly focused excitation: Linear versus radial polarization. J. Opt. Soc. Am. B 2022, 39, 2237–2245. [Google Scholar] [CrossRef]
- An, H.; Fleming, S. Second-order optical nonlinearity and accompanying near-surface structural modifications in thermally poled soda-lime silicate glasses. J. Opt. Soc. Am. B 2006, 23, 2303–2309. [Google Scholar] [CrossRef]
- Chervinskii, S.; Sevriuk, V.; Reduto, I.; Lipovskii, A. Formation and 2D-patterning of silver nanoisland film using thermal poling and out-diffusion from glass. J. Appl. Phys. 2013, 114, 224301. [Google Scholar] [CrossRef]
- Fleming, L.A.H.; Goldie, D.M.; Abdolvand, A. Imprinting of glass. Opt. Mater. Express 2015, 5, 1674–1681. [Google Scholar] [CrossRef]
- Dussauze, M.; Rodriguez, V.; Adamietz, F.; Yang, G.; Bondu, F.; Lepicard, A.; Chafer, M.; Cardinal, T.; Fargin, E. Accurate Second Harmonic Generation Microimprinting in Glassy Oxide Materials. Adv. Opt. Mater. 2016, 4, 929–935. [Google Scholar] [CrossRef]
- Dadap, J.I.; Shan, J.; Heinz, T.F. Theory of optical second-harmonic generation from a sphere of centrosymmetric material: Small-particle limit. J. Opt. Soc. Am. B 2004, 21, 1328–1347. [Google Scholar] [CrossRef]
- Hermans, A.; Kieninger, C.; Koskinen, K.; Wickberg, A.; Solano, E.; Dendooven, J.; Kauranen, M.; Clemmen, S.; Wegener, M.; Koos, C.; et al. On the determination of χ(2) in thin films: A comparison of one-beam second-harmonic generation measurement methodologies. Sci. Rep. 2017, 7, 44581. [Google Scholar] [CrossRef]
- Drevinskas, R.; Zhang, J.; Beresna, M.; Gecevičius, M.; Kazanskii, A.G.; Svirko, Y.P.; Kazansky, P.G. Laser material processing with tightly focused cylindrical vector beams. Appl. Phys. Lett. 2016, 108, 221107. [Google Scholar] [CrossRef]
- Biss, D.P.; Brown, T.G. Cylindrical vector beam focusing through a dielectric interface. Opt. Express 2001, 9, 490–497. [Google Scholar] [CrossRef] [PubMed]
- Richards, B.; Wolf, E. Electromagnetic diffraction in optical systems, II. Structure of the image field in an aplanatic system. Proc. R. Soc. London. Ser. A. Math. Phys. Sci. 1959, 253, 358–379. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scherbak, S.; Reshetov, I.; Kan, G.; Lipovskii, A. Effect of Surface Nonlinearity Distribution on Second Harmonic Generation under Tightly Focused Beams. Photonics 2023, 10, 350. https://doi.org/10.3390/photonics10040350
Scherbak S, Reshetov I, Kan G, Lipovskii A. Effect of Surface Nonlinearity Distribution on Second Harmonic Generation under Tightly Focused Beams. Photonics. 2023; 10(4):350. https://doi.org/10.3390/photonics10040350
Chicago/Turabian StyleScherbak, Sergey, Ilya Reshetov, Gennadiy Kan, and Andrey Lipovskii. 2023. "Effect of Surface Nonlinearity Distribution on Second Harmonic Generation under Tightly Focused Beams" Photonics 10, no. 4: 350. https://doi.org/10.3390/photonics10040350
APA StyleScherbak, S., Reshetov, I., Kan, G., & Lipovskii, A. (2023). Effect of Surface Nonlinearity Distribution on Second Harmonic Generation under Tightly Focused Beams. Photonics, 10(4), 350. https://doi.org/10.3390/photonics10040350




