Influence of Off-Axis Noncanonical Vortex on the Dynamics of Energy Flux
Abstract
1. Introduction
2. Theoretical Background
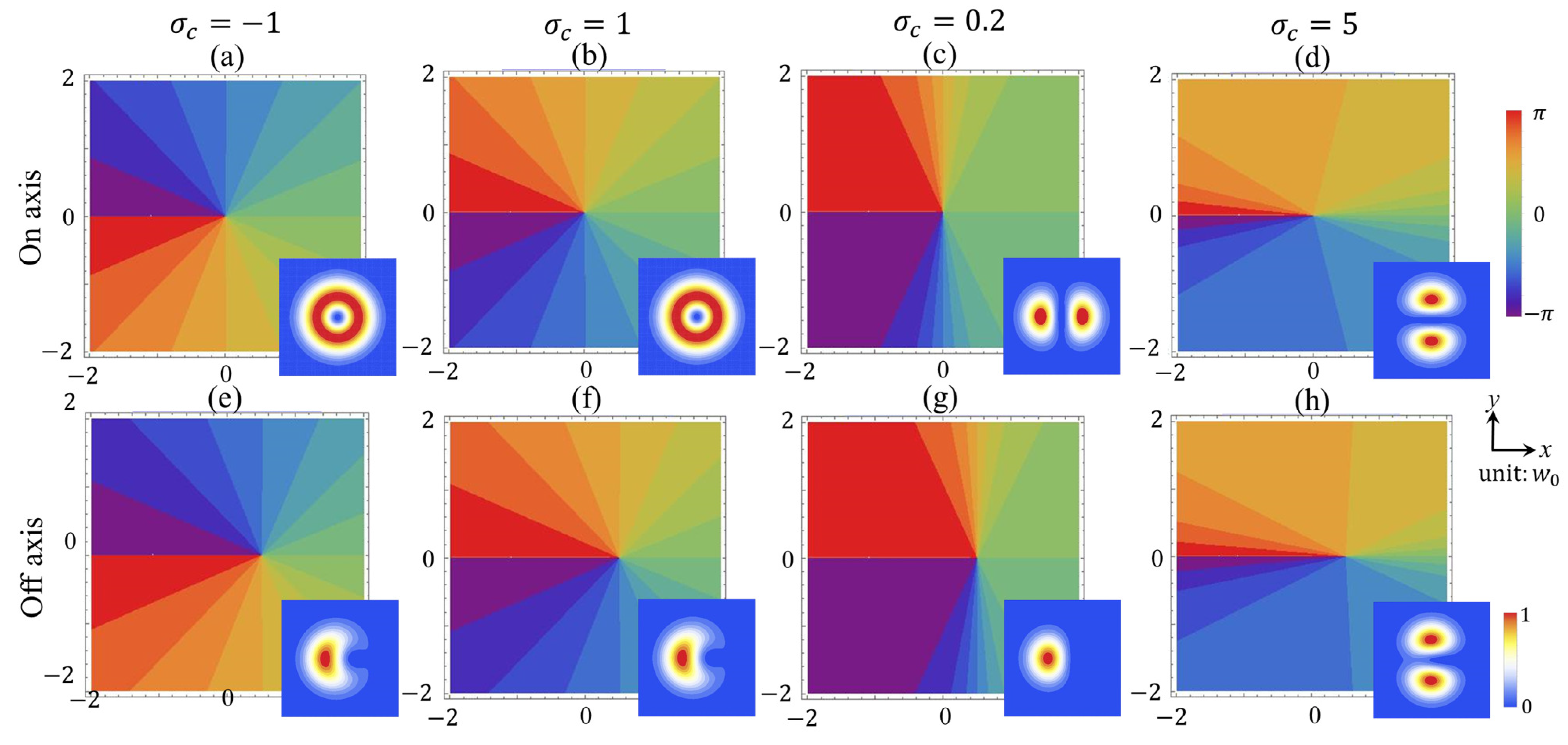
2.1. Noncanonical Vortex
2.2. Electric Field, Magnetic Field and Energy Flux
3. Results and Discussions
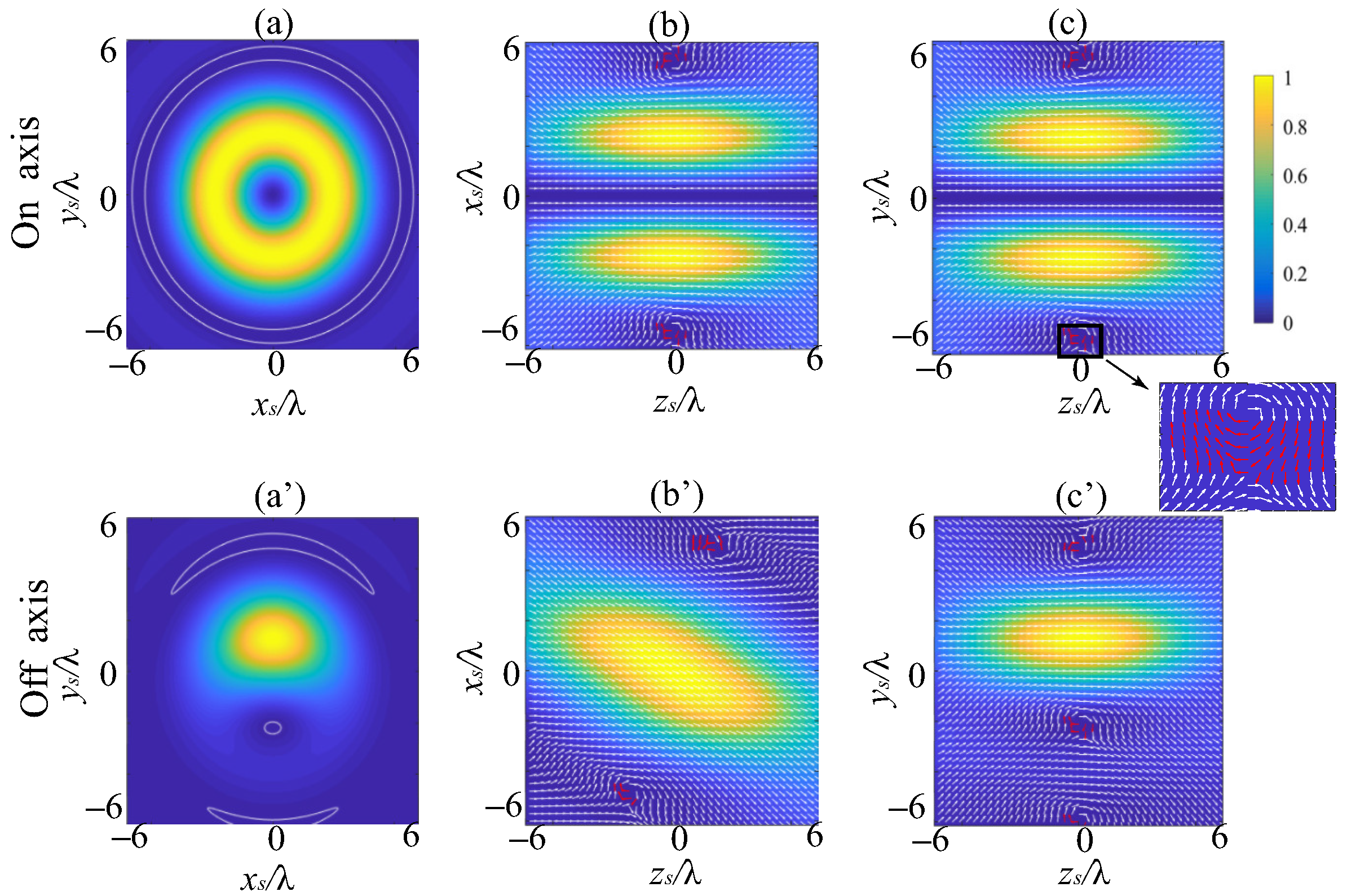
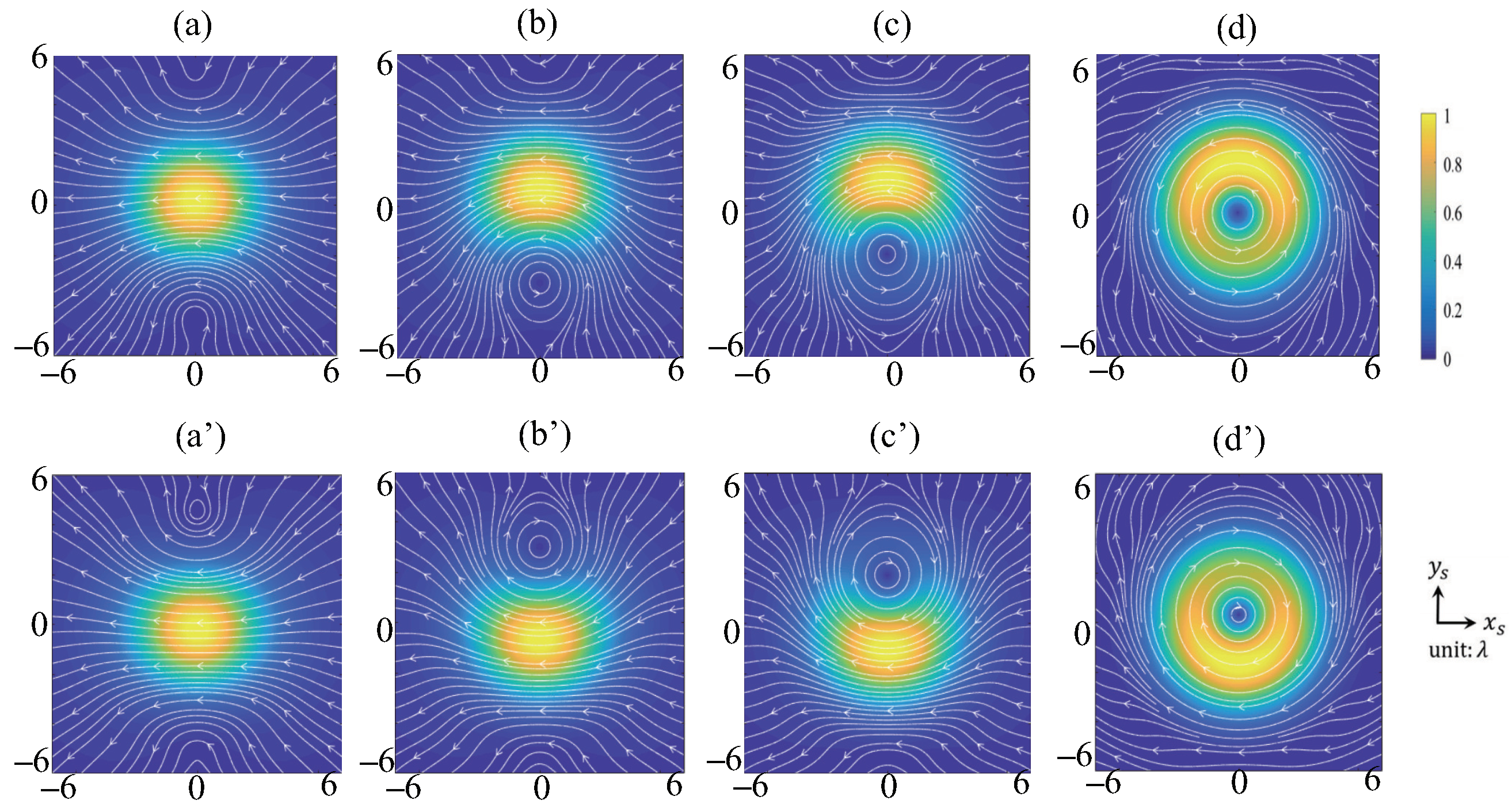
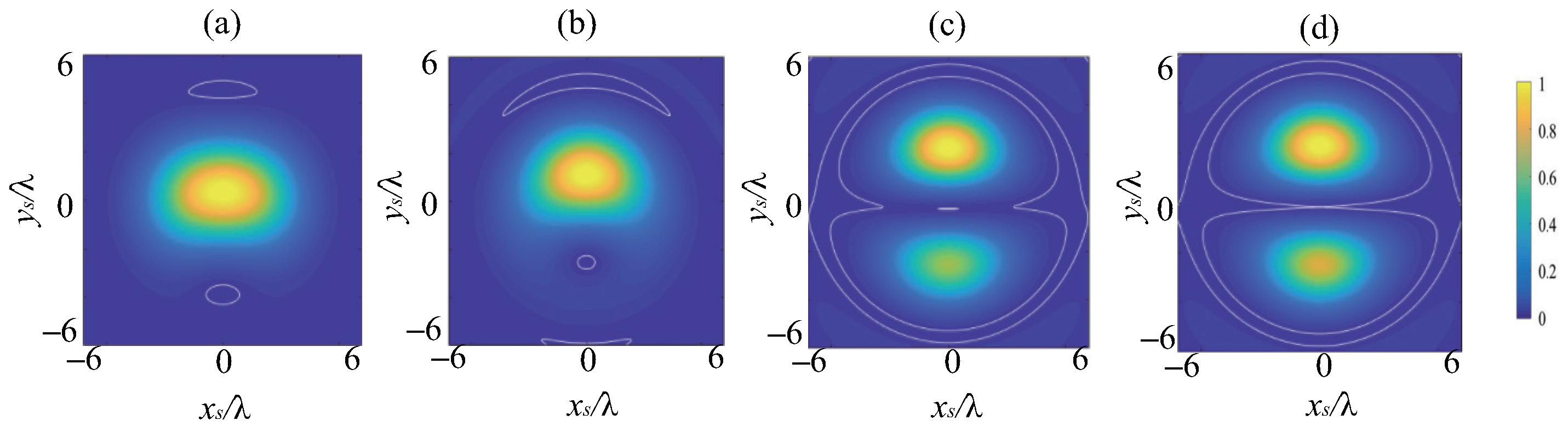
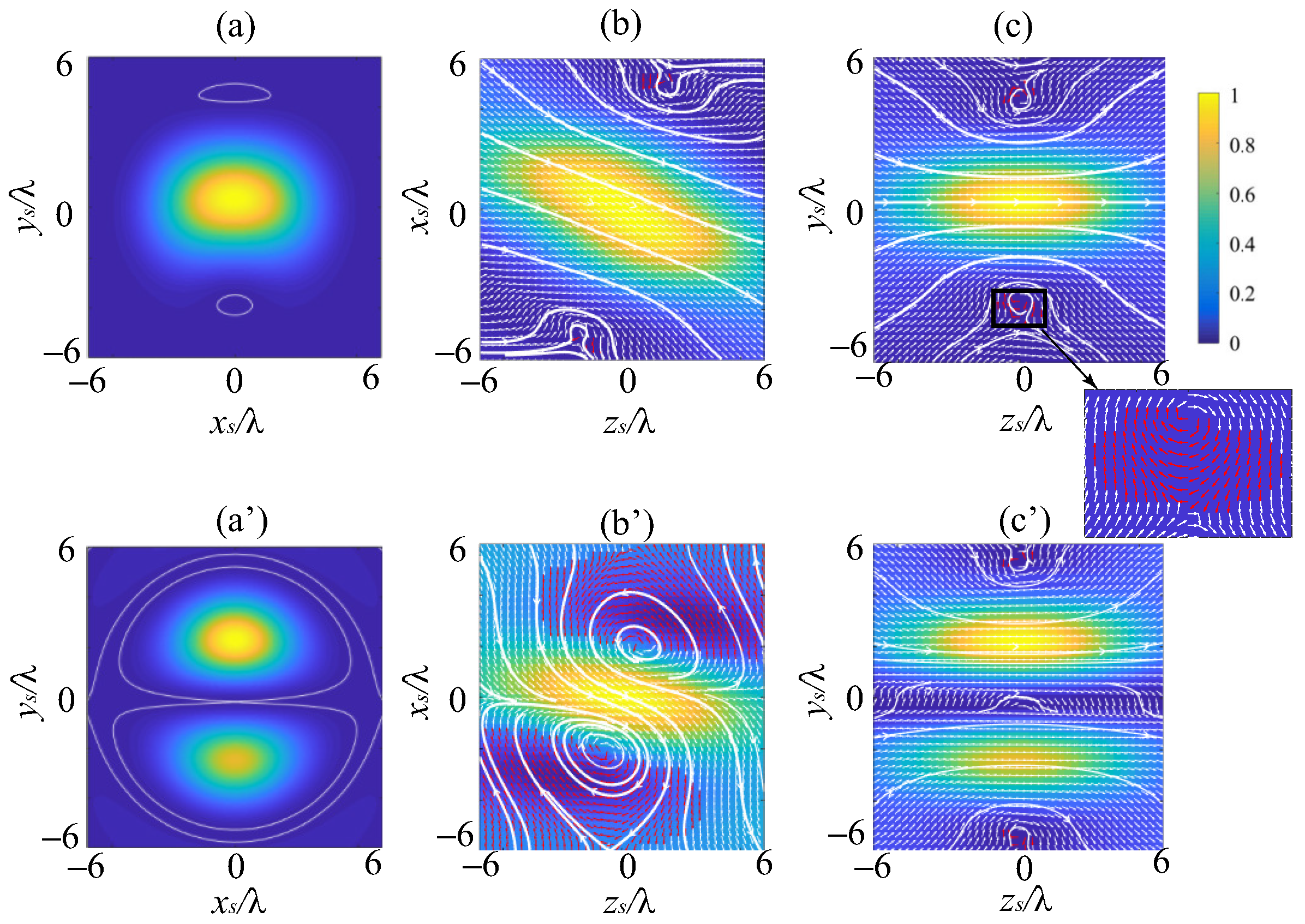
3.1. Energy Flux: The Canonical Vortex Case
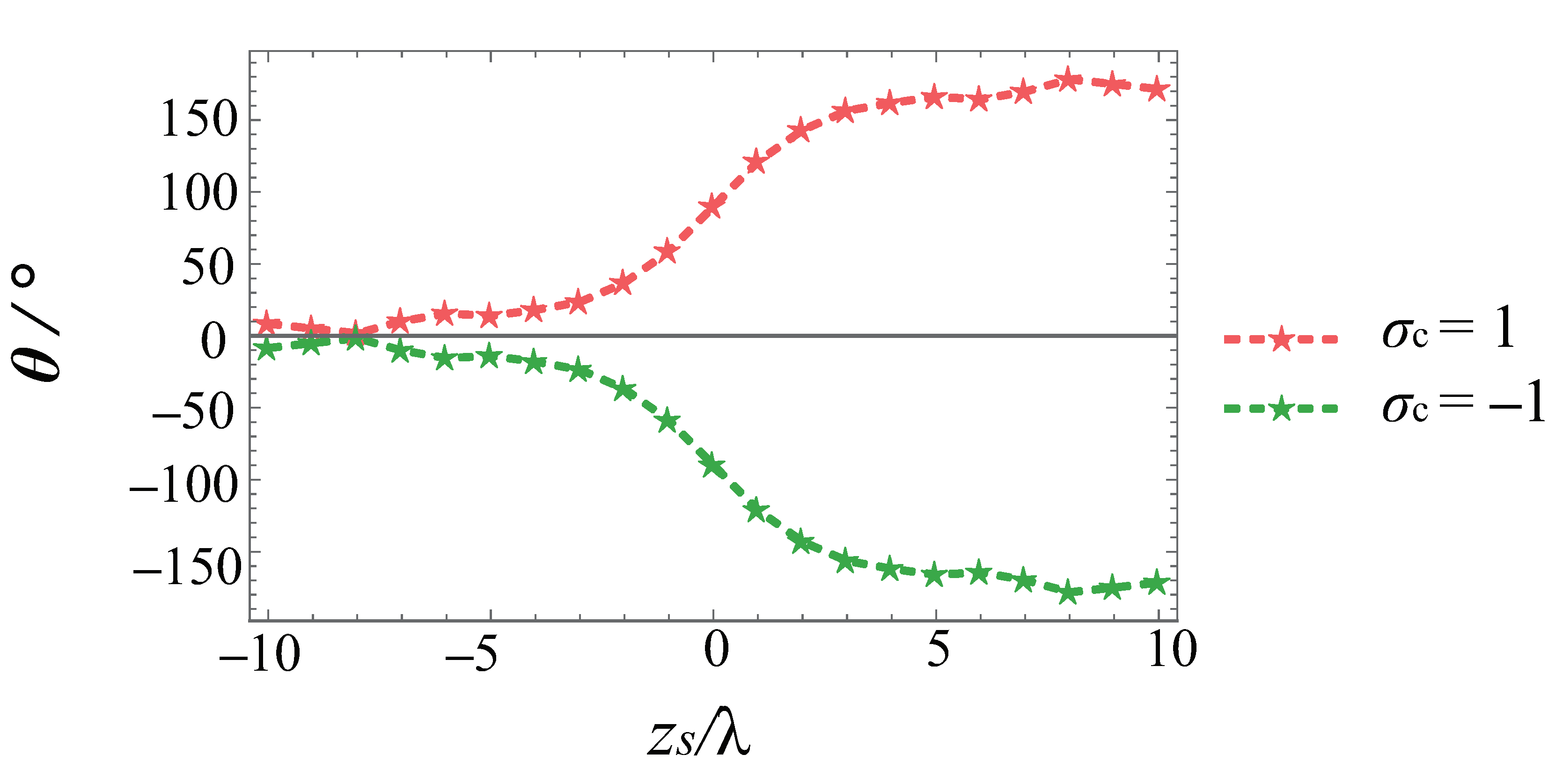
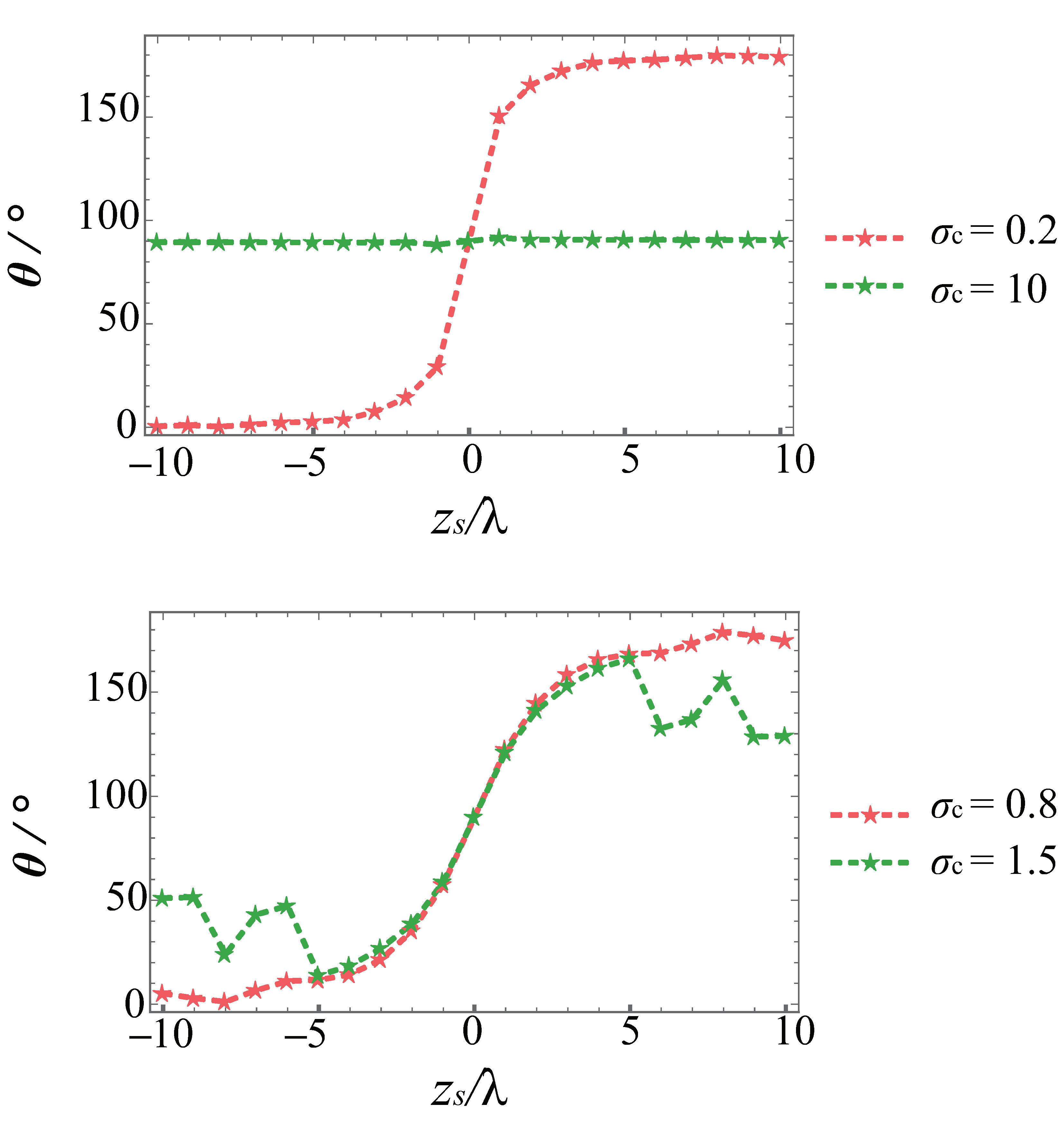
3.2. Energy Flux: The Noncanonical Vortex Case
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Soskin, M.S.; Vasnetsov, M.V. Singular Optics. In Progress in Optics; Wolf, E., Ed.; Elsevier: Amsterdam, The Netherlands, 2001; Volume 42, pp. 219–276. [Google Scholar] [CrossRef]
- Gbur, G.J. Singular Optics; Chemical Rubber Company: Boca Raton, FL, USA, 2017. [Google Scholar] [CrossRef]
- Otte, E.; Tekce, K.; Denz, C. Tailored intensity landscapes by tight focusing of singular vector beams. Opt. Express 2017, 25, 20194–20201. [Google Scholar] [CrossRef]
- Zhao, X.; Pang, X.; Zhang, J.; Wan, G. Transverse Focal Shift in Vortex Beams. IEEE Photon. J. 2018, 10, 1–17. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Kovalev, A.A.; Stafeev, S.S.; Nalimov, A.G.; Rasouli, S. Tightly focusing vector beams containing V-point polarization singularities. Opt. Laser. Technol. 2022, 145, 107479. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Stafeev, S.S.; Nalimov, A.G. Sharp Focusing of a Hybrid Vector Beam with a Polarization Singularity. Photonics 2021, 8, 227. [Google Scholar] [CrossRef]
- Dong, M.; Zhao, C.; Cai, Y.; Yang, Y. Partially coherent vortex beams: Fundamentals and applications. Sci. China Phys. Mech. 2021, 64, 224201. [Google Scholar] [CrossRef]
- Chen, J.; Liu, X.; Yu, J.; Cai, Y. Simultaneous determination of the sign and the magnitude of the topological charge of a partially coherent vortex beam. Appl. Phys. B-Lasers O 2016, 122, 201. [Google Scholar] [CrossRef]
- Angelsky, O.V.; Bekshaev, A.Y.; Maksimyak, P.P.; Maksimyak, A.P.; Hanson, S.G.; Zenkova, C.Y. Orbital rotation without orbital angular momentum: Mechanical action of the spin part of the internal energy flow in light beams. Opt. Express 2012, 20, 3563–3571. [Google Scholar] [CrossRef]
- Angelsky, O.V.; Bekshaev, A.Y.; Maksimyak, P.P.; Maksimyak, A.P.; Zenkova, C.Y.; Gorodynska, N.V. Circular motion of particles by the help of the spin part of the internal energy flow. In Proceedings of the ROMOPTO 2012: Tenth Conference on Optics: Micro- to Nanophotonics III, Bucharest, Romania, 3–6 September 2012; Vlad, V.I., Ed.; International Society for Optics and Photonics, SPIE: Bucharest, Romania, 2013; Volume 8882, p. 88820A. [Google Scholar] [CrossRef]
- Taylor, M.A.; Waleed, M.; Stilgoe, A.B.; Rubinsztein-Dunlop, H.; Bowen, W.P. Enhanced optical trapping via structured scattering. Nature Photon. 2015, 9, 669–673. [Google Scholar] [CrossRef]
- Padgett, M.J.; Molloy, J.; McGloin, D. Optical Tweezers: Methods and Applications; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar] [CrossRef]
- Bozinovic, N.; Yue, Y.; Ren, Y.; Tur, M.; Kristensen, P.; Huang, H.; Willner, A.E.; Ramachandran, S. Terabit-scale orbital angular momentum mode division multiplexing in fibers. Science 2013, 340, 1545–1548. [Google Scholar] [CrossRef]
- Freund, I.; Shvartsman, N.; Freilikher, V. Optical dislocation networks in highly random media. Opt. Commun. 1993, 101, 247–264. [Google Scholar] [CrossRef]
- Tong, R.; Dong, Z.; Chen, Y.; Wang, F.; Cai, Y.; Setälä, T. Fast calculation of tightly focused random electromagnetic beams: Controlling the focal field by spatial coherence. Opt. Express 2020, 28, 9713–9727. [Google Scholar] [CrossRef] [PubMed]
- Pang, X.; Xiao, W.; Zhang, H.; Feng, C.; Zhao, X. X-type vortex and its effect on beam shaping. J. Opt. 2021, 23, 125604. [Google Scholar] [CrossRef]
- Molina-Terriza, G.; Wright, E.M.; Torner, L. Propagation and control of noncanonical optical vortices. Opt. Lett. 2001, 26, 163–165. [Google Scholar] [CrossRef]
- Roux, F.S. Coupling of noncanonical optical vortices. J. Opt. Soc. Am. B 2004, 21, 664–670. [Google Scholar] [CrossRef]
- Kim, G.H.; Lee, H.J.; Kim, J.U.; Suk, H. Propagation dynamics of optical vortices with anisotropic phase profiles. J. Opt. Soc. Am. B 2003, 20, 351–359. [Google Scholar] [CrossRef]
- Lopez-Mago, D.; Perez-Garcia, B.; Yepiz, A.; Hernandez-Aranda, R.I.; Gutiérrez-Vega, J.C. Dynamics of polarization singularities in composite optical vortices. J. Opt. 2013, 15, 044028. [Google Scholar] [CrossRef]
- Gong, L.; Wang, X.; Zhu, Z.; Lai, S.; Feng, H.; Wang, J.; Gu, B. Transversal energy flow of tightly focused off-axis circular polarized vortex beams. Appl. Opt. 2022, 61, 5076–5082. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Li, P.; Liu, S.; Wei, B.; Qi, S.; Fan, X.; Wang, S.; Zhang, Y.; Zhao, J. Autofocusing of ring Airy beams embedded with off-axial vortex singularities. Opt. Express 2020, 28, 7953–7960. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.H.; Kim, H.S.; Han, I.; Bae, J.Y.; Yeo, W.J.; Jeong, S.K.; Jeon, M.; Choi, H.J.; Kim, D.U.; Lee, K.S.; et al. Generation of wavelength-tunable optical vortices using an off-axis spiral phase mirror. Opt. Lett. 2021, 46, 4216–4219. [Google Scholar] [CrossRef]
- Ignatowsky, V.S. Diffraction by a lens of arbitrary aperture. Trans. Opt. Inst. 1919, 1, 1–36. [Google Scholar]
- Richards, B.; Wolf, E. Electromagnetic Diffraction in Optical Systems. II. Structure of the Image Field in an Aplanatic System. Proc. R. Soc. Lond. A 1959, 253, 358–379. [Google Scholar] [CrossRef]
- Monteiro, P.B.; Neto, P.A.M.; Nussenzveig, H.M. Angular momentum of focused beams: Beyond the paraxial approximation. Phys. Rev. A 2009, 79, 033830. [Google Scholar] [CrossRef]
- Novitsky, A.V.; Novitsky, D.V. Negative propagation of vector Bessel beams. J. Opt. Soc. Am. A 2007, 24, 2844–2849. [Google Scholar] [CrossRef] [PubMed]
- Kotlyar, V.V.; Kovalev, A.A.; Nalimov, A.G. Energy density and energy flux in the focus of an optical vortex: Reverse flux of light energy. Opt. Lett. 2018, 43, 2921–2924. [Google Scholar] [CrossRef]
- Youngworth, K.S.; Brown, T.G. Focusing of high numerical aperture cylindrical-vector beams. Opt. Express 2000, 7, 77–87. [Google Scholar] [CrossRef]
- Zhan, Q.; Leger, J.R. Focus shaping using cylindrical vector beams. Opt. Express 2002, 10, 324–331. [Google Scholar] [CrossRef]
- Zhan, Q. Cylindrical vector beams: From mathematical concepts to applications. Adv. Opt. Photon. 2009, 1, 1–57. [Google Scholar] [CrossRef]
- Dogariu, A.; Sukhov, S.; Sáenz, J. Optically induced ‘negative forces’. Nat. Photon. 2013, 7, 24–27. [Google Scholar] [CrossRef]
- Petersen, J.; Volz, J.; Rauschenbeutel, A. Chiral nanophotonic waveguide interface based on spin-orbit interaction of light. Science 2014, 346, 67–71. [Google Scholar] [CrossRef]
- Huang, S.Y.; Zhang, G.L.; Wang, Q.; Wang, M.; Tu, C.; Li, Y.; Wang, H.T. Spin-to-orbital angular momentum conversion via light intensity gradient. Optica 2021, 8, 1231–1236. [Google Scholar] [CrossRef]
- Geng, T.; Li, M.; Guo, H. Orbit-induced localized spin angular momentum of vector circular Airy vortex beam in the paraxial regime. Opt. Express 2021, 29, 14069–14077. [Google Scholar] [CrossRef]
- Otte, E.; Rosales-Guzmán, C.; Ndagano, B.; Denz, C.; Forbes, A. Entanglement beating in free space through spin–orbit coupling. Light Sci. Appl. 2018, 7, 18009. [Google Scholar] [CrossRef] [PubMed]
- Onoda, M.; Murakami, S.; Nagaosa, N. Hall effect of light. Phys. Rev. Lett. 2004, 93, 083901. [Google Scholar] [CrossRef] [PubMed]
- Zhu, W.; Zheng, H.; Zhong, Y.; Yu, J.; Chen, Z. Wave-vector-varying Pancharatnam-Berry phase photonic spin Hall effect. Phys. Rev. Lett. 2021, 126, 083901. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Zhang, J.; Pang, X.; Wan, G. Properties of a strongly focused Gaussian beam with an off-axis vortex. Opt. Commun. 2017, 389, 275–282. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Liang, H.; Wu, G.; Pang, X. Influence of Off-Axis Noncanonical Vortex on the Dynamics of Energy Flux. Photonics 2023, 10, 346. https://doi.org/10.3390/photonics10030346
Zhao X, Liang H, Wu G, Pang X. Influence of Off-Axis Noncanonical Vortex on the Dynamics of Energy Flux. Photonics. 2023; 10(3):346. https://doi.org/10.3390/photonics10030346
Chicago/Turabian StyleZhao, Xinying, Huijian Liang, Gaofeng Wu, and Xiaoyan Pang. 2023. "Influence of Off-Axis Noncanonical Vortex on the Dynamics of Energy Flux" Photonics 10, no. 3: 346. https://doi.org/10.3390/photonics10030346
APA StyleZhao, X., Liang, H., Wu, G., & Pang, X. (2023). Influence of Off-Axis Noncanonical Vortex on the Dynamics of Energy Flux. Photonics, 10(3), 346. https://doi.org/10.3390/photonics10030346






