Abstract
Here, we experimentally demonstrate a straightforward-to-implement scheme that enables the rotating velocimetry of a noncooperative target at large deflection angles. This scheme is based upon the combination of digital modal decomposition with the rotational Doppler effect of orbital angular momentum (OAM)-carried light modes. To achieve this, we first theoretically analyzed the tilt effect of a rotating surface on the OAM complex spectra and rotational Doppler spectrum. Our findings validate that the tilted surface causes not only the broadening of OAM power and phase spectra, but also the broadening of the scattered Doppler spectrum. Furthermore, we introduce a compensation phase for tilted OAM light that effectively suppresses the sidebands of the OAM power spectrum, thereby restraining the sideband amplitudes of the Doppler spectrum. As a consequence, the rotating velocimetry can be extended to cover larger tilt angles (as large as 70 degrees) than those of existing systems. Our outcomes have the advantages of providing, in addition to profound insight into the interaction between OAM-carrying light and object motion, potential opportunities for noncontact optical metrology and the telemetry of angular speeds, particularly in meteorological applications.
1. Introduction
The Doppler effect characterizes the variation in a wave’s frequency between a source in motion and an observer, which essentially is a vector with a magnitude from several hertz to several megahertz per meter per second, and the direction relies upon the illumination and the geometry collection systems [1]. Understanding of the Doppler effect plays a vital role in a myriad of realms [2,3,4,5], and thus gives rise to a plethora of applications, such as fire lidar, wind tunnel, and artificial intelligence, to name a few [6,7,8]. Particularly, in an ad hoc, laser-based, Doppler-effect-using remote sensing setup, the optical Doppler shift in the light of incident light wavefront structures and motional fashions typically falls into two types: linear Doppler shift and rotational Doppler shift (RDS). More intriguingly, these two shifts share a common root [9]. Despite its many uses, the linear Doppler shift is primarily used to gain the velocity component in the line of sight. The RDS arises from either the rotation of the light source carrying orbital angular momentum (OAM) [5,10] or the entity’s rotation [11,12,13,14,15,16]. The metrology of the RDS is considered to be a promising avenue for tackling the aforesaid onrushing technology challenge. The RDS has been observed by exploiting spin angular momentum [17,18], OAM [5,14,15], spin-orbit coupling [19], and coherent detection [20]. It has been applied to developing an OAM complex spectrum analyzer [21], measuring vorticity in fluid flows [11,12], tracking astronomical objects [22], and modifying real remote sensing [23]. An OAM-dependent observable has also allowed researchers to sense rotational angular velocity [13,15], hence becoming topical and arousing widespread attention owing to urgently practical demands and potential applications.
There exist numerous efforts dedicated to this topic, including observation of the angular velocity value through various OAM-carrying spatial light modes [24,25,26,27,28,29], discrimination of the speed directions via distinct strategies [30,31,32], measurement of non-uniform rotational velocity [33,34], and detection of complicated deviations between light and a rotor, while embracing lateral and angular deviations [35,36,37]. As the first attempt suggests, even though various illuminated spatial light modes with OAM, comprising Laguerre-Gaussian (LG) mode [24], Bessel-Gaussian mode [25], perfect vortex beam [26], ring Airy Gaussian vortex beam [27], perfect LG mode [28], and white light [29], have unambiguously experimentally verified the relationship between OAM-dependent rotational Doppler shift and the angular velocity, the vector nature of the rotating velocity is neglected as a consequence of using the absolute value of the Doppler shift and detectors’ property itself. To address this issue, the heterodyne detection strategy [30], dual-frequency vortex protocol [31], and vectorial Doppler metrology approach [32] can be recognized as powerful solutions to enable the metrology of the angular velocity vector. Additionally, time–frequency analysis technology has been adopted as an efficient knob to implement non-stationary signal processing, thereby facilitating the measurement of rotational angular acceleration/deceleration [33,34]. Despite the excellent detection performance, on one hand, the above-mentioned probing frameworks typically need to severely realign the light axis and the rotary shaft, thereby enormously hindering the practical implementations. In relation to this challenge, rotating velocimetry in the case of lateral misalignment has been demonstrated [35,36]. On the other hand, the incident optical axis more often needs to be strictly orthogonal to the motional surface, which is not practical within real-world scenarios. Namely, there inevitably exists a tilt angle between the optical axis and rotary shaft in practice. As such, while previous work by Qiu et al. has analyzed the effect of angular deviation on rotating velocimetry [37], how to develop a compensating strategy to effectively improve the RDS spectrum at larger tilt angles has remained elusive until now, which hinders potential applications of rotating Doppler velocimetry in practical scenarios.
In this work, we experimentally investigated laser Doppler rotating velocimetry using a spinning disk with off-axis angles as large as 70 degrees. More specifically, we achieved this based upon the combination of digital modal decomposition with the rotational Doppler effect of OAM-carrying light modes. In this regard, we first highlight the mechanism of the modal decomposition and introduce the RDS resulting from the rotor. Subsequently, a proof-of-principle experiment was implemented for the demonstration of our hypothesis. The results reveal that rotating velocity of a surface at larger tilt angles can be unambiguously determined. Moreover, we validated that a tilted rotating surface results in the Doppler spectrum broadening, which is rooted in the eigen bases of the tilted rotating surface corresponding to the OAM components of the multiple tilted-light-mode induced RDSs in the Doppler power spectrum. Furthermore, we introduce a modulation technique to enhance the capability of rotating velocimetry at larger tilt angles. Our validated scheme and findings could pave the way for noncontact optical metrology, remote measurement, and beyond.
2. Theoretical Analyses
Figure 1a shows when a LG light mode is directed along z-direction onto a tilted rotating target surface with tilt angle γ versus a planar surface, the resultant light mode displays an ellipsis-shaped distribution. This scenario is equivalent to a tilted light beam with the same tilt angle γ being emitted onto a planar rotating target surface [38], as shown in Figure 1b. The tilted OAM-carried light mode can be given in the cylindrical coordinates (r, φ, z) at z = 0 [38]:
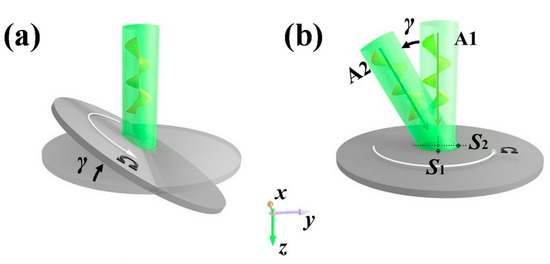
Figure 1.
Schematic of probing rotating velocity of a tilted target. (a) Realistic scenarios with tilted rotor illuminated by OAM-carried light modes along z-direction; (b) equivalent conditions with non-inclination rotor illuminated by oblique OAM-carried light modes. Ω: rotating angular velocity of a rotor; γ: tilt angle, A1 and A2: optical axis of normal and inclined light beams; S1 and S2: a target’s feature points in an elliptical light ring.
Here, σ = (x2 + y2)1/2 with x = rcosφ and y = rsinφcosγ. E0 is the amplitude factor, and w0 denotes the beam waist radius. Bnl stands for the binomial coefficient. The Laguerre polynomial Lp|l| possesses the OAM index l and radial modal index p. δ = (2n − l)φ is the azimuthal phase of tilted OAM light. Note that the tilted OAM light possesses the azimuthal index of 2n − l, which is equivalent to the eigen bases of the tilted surface. In addiion, the relevant interferential modes also can be easily garnered by the superimposition of its conjugate modes with the OAM index of −l, described by:
Equation (2) means that the interferometric mode is subject to a cosine modulation in the azimuthal direction by OAM index l, hence leading to petal-like elliptical patterns.
Having obtained the tilted OAM-carried modes, we proceed to the analyses of the tilted effect of a rotating surface on the OAM complex spectra, before implementing associated rotational Doppler velocimetry. Based upon the digital modal decomposition technique, the tilted OAM modes can be expanded by a set of chosen basis modes according to [39,40]:
with r = (x, y) being the spatial coordinates; Ci = ρiexp(iΔφi) is the normalized weighting coefficient with the amplitude ρi and the intramodal phase Δφi. Φi(r) is the i-th spatial basis modes that are orthogonal each other in the Hilbert space, which can be the vector elements or the scalar ones, and N is the expanded mode number. Here, we select LG modes with p = 0 as the basis modes, and the weighting coefficient can be ascertained by the operation of inner products, manifested as
where “*” denotes the operation of the complex conjugate. with foreknown amplitude Al and phase φl can be encoded as the digital holograms that can be loaded upon a diffractive optical device, such as SLM. We here draw upon an exact complex amplitude modulation technology to generate the digital holograms with a transmission function [41]:
where F(Al) = 1 + sinc−1(Al), in which sinc−1(·) is the inverse function of the sinc(·). G(r) = g·r is a phase-ramp function with the grating frequencies g = (gx, gy) along the horizontal and vertical directions, respectively. Mod[·] stands for the modulus function. The inner product Cl can be measured by the intensity measurements on the optical axis. As such, the on-axis highest intensity proportional to the norm of the weighting coefficient possesses the magnitude of Il, which can be called the OAM power spectrum [42]:
The OAM intermodal phase spectrum can also be acquired following three on-axis intensity measurements recorded on a camera in sequence, expressed as
where Isin and Icos are, respectively, the intensity of the inner products and , and I0 is the intensity of inner products of the referenced Gaussian light on the axis. Note that the transmission functions , and can be individually encoded on SLM, with no need for the extra build of reference arms [43,44]. Once a set of the complex coefficients Ci that depend on the amplitude ρi and the intramodal phase Δφi are obtained, the inclined OAM light fields and the phase distributions can be reconstructed according to Equation (3). Additionally, the corresponding OAM complex spectra can be determined by Equations (6) and (7).
Now that we have detailed how to measure the OAM power and phase spectra, we can proceed to carry on corresponding rotational Doppler spectrum analysis. Generally, the expression of RDSs covering 360-degree rotation angles can be given by [37]:
where θ denotes the angle of a point on the rotor versus x-axis in the xoy plane. As shown in Figure 1b, we can derive the RDS at the two extreme points on the rotating surface illuminated with the elliptical mode, S1 and S2, respectively. From Equation (8), we can obtain the tilt-and-rotation-induced Doppler shift at S1 point when θ = 0 as:
In Equation (9), the oblique RDS can be viewed as an extreme minimum. On the other hand, at the point of S2, we can also derive the extreme maximum of the RDS from Equation (8) when θ = π/2:
Equations (9) and (10) indicates that the multiple RDSs are distributed in a specific bandwidth (i.e., between the minimum and maximum RDSs). Namely, the rotational Doppler spectrum are broadened. Such Doppler-spectrum spreading stems from OAM spectrum broadening of the tilted light. With the Doppler spectrum spreading, the peak values of Doppler signals will gradually decrease. In addition, the center frequency in the broadening Doppler spectrum can also be obtained, which can be employed to determine the rotating velocity [37]:
Having introduced the rotational Doppler spectrum, we proceed to develop a modulation technique to extend the rotating velocimetry to cover larger tilt angles than previous work [37]. To achieve this, one needs to suppress the broadening of the Doppler power spectrum. This can be achieved by suppressing the sidebands of the OAM power spectrum via modulation technology. The modulation technology essentially is to inversely compensate for the phase change caused by the optical path change within the tilted OAM light. As such, we introduce a compensation phase φc = 2πysinγ/λ into the azimuthal phase term δ in Equation (1) with OAM components. As a result, the corrected azimuthal phase can be rewritten as:
From Equation (12), each of OAM component can be modulated by the introduced φc. By substituting Equation (12) into Equation (1) and repeatedly performing the modal decomposition process from Equations (3)–(7), we can obtain the modulated OAM power and phase spectra. Only if the sidebands of modulated OAM power spectrum can be effectively reduced, the suppression of Doppler spectrum broadening can be achieved, thereby realizing rotating velocimetry of a surface at larger tilt angles.
3. Experiment
3.1. Experiment Setup
We designed an experimental setup to validate above protocol at the proof-of-principle level, as shown in Figure 2. Light from a 532 nm laser (Coherent OBIS FP 532LS) was firstly coupled into a single-mode optical fiber (SMF) with a microscope objective (MO). After exiting the SMF, it passed a half-wave plate (HWP) combined with a linear polarizer (LP) to control the optical power and the polarization. Subsequently, this adjusted light was reflected by a mirror (M) onto a phase-only liquid-crystal-on-silicon spatial light modulator (SLM1) operating in reflection mode for on-demand generation of conjugated superimposed OAM-carried light modes, where we preloaded the digital hologram of the tilted light modes with OAM indices of ±10 and a tilt angle of 30° for an example in SLM1, as shown in Figure 3a. Such generated beams were relayed onto the first beam splitter (BS1) through a 4f system consisting of the two plan-convex lenses and a SLM2 operating in transmissive mode. The SLM2 was used to realize a digital spatial filter with much higher purity than that of the physical filter [45], and the uploaded mask is shown in Figure 3b. Afterwards, the beams were split into two paths: the reflective path after BS1 was applied to achieve a digital OAM complex spectrum analyzer. To be specific, with the help of a transmission-type SLM3, the spatial basis vectors or the match filters could firstly be well uploaded, and a set of exemplary digital holograms are illustrated in Figure 3c–f. Then, Fourier lens L3 and CCD were used for light field reconstructions and OAM power and phase spectrum analyses. The transmission path after passing through the second beam splitter (BS2) was impinged onto a high-speed rotor with a rough surface mounted on a revolving stage. Here, the radius of OAM light mode before the rotor was about 2.5 mm. Additionally, the backscattered light was delivered to a rotational velocity sensor for the purpose of sensing rotating velocity. More specifically, the backscattered light was first focused by a lens L4 on a photodetector (PD). In order to collect and record the beating signals, we then combined an oscilloscope (OSC) with this PD together with a computer, such that the collected beating signals could be used to obtain associated rotational Doppler power spectra by carrying out the fast Fourier transform.
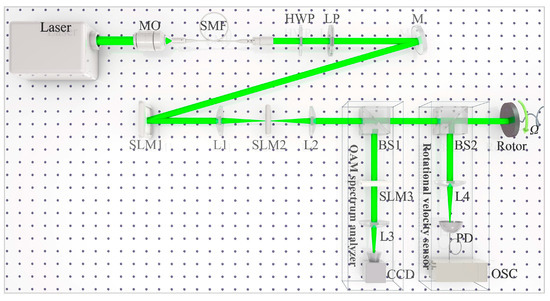
Figure 2.
Experimental setup for the generation and reconstruction of OAM-carried light modes and the characterization of the OAM complex spectrum and rotating velocity detection. MO: microscopic objective; SMF: single mode fiber; LP: linear polarizer; HWP: half wave plate; M: mirror; SLM: spatial light modulator; L: lens; BS: beam splitter; CCD: charge coupled device; PD: photodevice; Osc: oscilloscope.
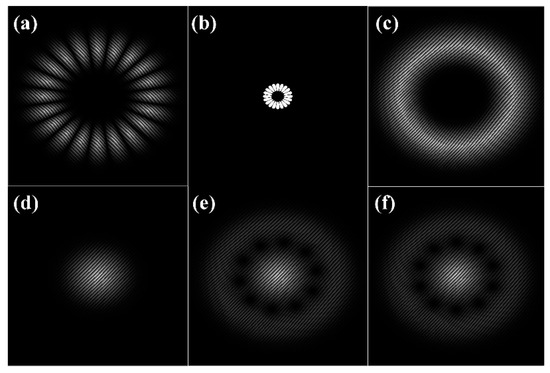
Figure 3.
(a) Digital hologram of superimposed OAM-carried light mode at tilt angle 30° loaded upon SLM1. (b) The mask at the Fourier plane loaded on SLM2. (c–f) The digital holograms of a set of basis vectors uploaded on SLM3 for OAM complex spectrum analysis and light-mode analysis and its phase reconstructions, with (c) LG*0,10, (d) LG*0,0, (e) LG*0,10 + iLG*0,0 and (f) LG*0,10 + LG*0,0.
3.2. Experimental Results
To measure rotational Doppler power spectra for the deduction of rotating velocity of a tilted surface, we can firstly analyze the incident light patterns along with phase distributions and associated OAM power and phase spectra. Towards this end, we theoretically simulate and experimentally reconstruct corresponding light modes and phase distributions and OAM power spectra |ρl|2 and phase spectra Δφl at tilt angles of 15°, 30° and 45°, respectively. The results are displayed in Figure 4a–c, respectively. We here select ±10-order OAM modes as an example to illustrate our measurement scheme, and the higher-order OAM modes can induce a higher sensibility. Figure 4a–c show that the superimposed OAM-carrying light modes show petal-like distributions as expected by Equation (2). Additionally, with the increased tilt angles, the petal-shaped patterns vary from circular to elliptical structures. Meanwhile, the reconstructed light fields are in well agreement with theoretical counterparts, with 2-dimensional (2D) correlation coefficients between them are 99.1%, 91% and 87% at 15°, 30° and 45°, respectively. The definition of the 2D correlation coefficient has been given in literature [46]. It is worth mentioning that the experimental OAM light fields are reconstructed by the measured OAM power and phase spectra via mode-superposition principle in Equation (3). In addition, we can observe in the bottom of Figure 4a–c that the corresponding OAM power spectra suffer from diffusion effects or inter-modal crosstalk. To be specific, the larger the tilt angle, the more salient the diffused effect, and the lower the power magnitude. Further, the OAM power spectra are distributed symmetrically around 0-th OAM mode, and they are asymmetrical around the ±10th modes. More crucially, there exists the difference of two between the adjacent broadening OAM indices, i.e., ln-ln-1 = 2, with ln being the n-th OAM index, consistent with theoretical analysis of azimuthal phase δ in Equation (1).
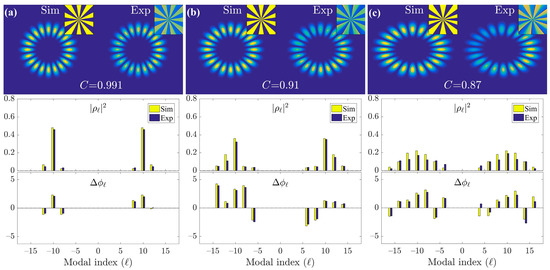
Figure 4.
Theoretical simulations and experimental reconstructions of light mode and phase distributions and matched OAM power spectra |ρl|2 and phase spectra Δφl of superimposed OAM-carried light modes with tilt angles of (a) 15°, (b) 30° and (c) 45°, respectively. C denotes the 2D correlation coefficient between simulated and reconstructed light modes.
Having analyzed light field properties and OAM modal distributions for a tilted rotor, we proceed to the associated rotational Doppler velocimetry. For this purpose, we measured the Doppler power spectra of the beat frequency induced by the rotor with tilt angles of 15°, 30° and 45°, respectively, as plotted in Figure 5a–c, wherein the central RDS is 954.15 Hz. It is evident that the experimentally measured RDS generated by the tilted rotor is in good agreement with the theory. Thus, a rotating velocity can be measured following Equation (11). More significantly, Figure 5 shows that the measured Doppler power spectra were subjected to the broadenings. The broadenings indicate the spreading of the envelope consisting of multiple Doppler signal peaks, as represented by the red circles in Figure 5. This broadening effect is consistent with the theoretical analysis in Equations (9) and (10). As the tilt angle increases, the spreading effect becomes more salient. Such Doppler spectrum spreading is mainly ascribed to the diffused OAM power and phase spectra of tilted light, as illustrated in Figure 4.

Figure 5.
Experimentally measured RDS power spectra, induced by a rotor at tilt angles of (a) 15°, (b) 30° and (c) 45°, respectively. The preset rotating velocity of the rotor was 300 rad/s.
To achieve the rotating velocimetry of a surface at larger tilt angles, we introduced the compensation phase φc in Equation (12) into the original tilted OAM light. The φc can be obtained by compensated optical paths when the tilt angles are known. Subsequently, we measured the OAM power and phase spectra at a tilt angle of 45 degrees again, as shown in Figure 6a,b. Compared to the case in the absence of modulation in Figure 4c, the presence of the phase modulation in Figure 6a,b shows the salient difference in OAM modal distributions. For the former, as shown in Figure 4c, the sideband components versus central main band (+10 and 10-order modes) in the OAM power spectrum possess significantly higher weightings. In contrast, for the latter, the weightings of the sideband components in the OAM power spectrum were effectively reduced by φc, thereby possessing relative low power weighting. Since the broadening sidebands of OAM power and phase spectra caused the spreading rotating Doppler spectrum, the suppression effect for the weightings of the sideband components in OAM power spectrum can effectively suppress the rotating Doppler spectrum. The suppression effect on the rotating Doppler spectrum is shown in Figure 6c. This effect makes the central main band in Doppler spectrum clearer, thereby leading to the improved measurement accuracy at larger tilt angles. Additionally, we can see in Figure 4 and Figure 6a,b that there exist slight discrepancies between the simulations and experiments in the OAM power and phase spectrum of each OAM modal index. These small differentials stem mainly from the imperfect energy efficiency of SLM3 in the OAM spectrum analyzer. Yet, these imperfections do not affect the basic distribution laws of measured modal spectra and the eventual accuracy of rotating velocimetry.
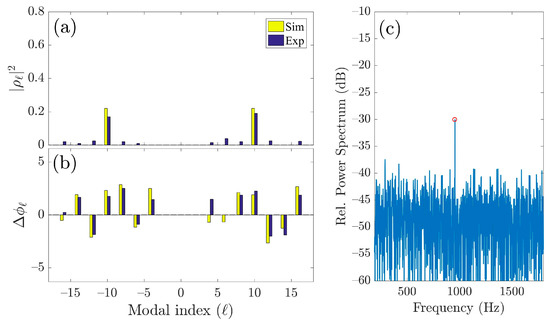
Figure 6.
OAM (a) power and (b) phase spectra with the compensation phase φc. (c) The sideband-suppressed rotational Doppler power spectrum.
Furthermore, we measured the rotating velocity at various tilt angles, with prescribed rotating velocity of 300 rad/s. The experimental results are shown in Figure 7. Clearly, the unmodulated OAM light modes can achieve rotating velocimetry at 50 degrees, whereas the modulated OAM light modes can realize the rotating velocimetry of surface to cover as much as 70 degrees. This is due to the compensation phase introduced into modulated scheme, which restrains the sideband amplitudes of the Doppler spectrum, thereby leading to a relatively higher signal-to-noise ratio (SNR) over a larger range of tilt angles compared to the unmodulated cases. In all measurements, the difference between adjacent OAM indices determined the resolution of OAM spectrum, which was Δl = 2 in our measurement. Meanwhile, the resolution of the Doppler power spectrum indicates the lowest frequency interval Δf, which was determined by the sampling duration. We used a time length of 0.1 s to perform the fast Fourier transform, thereby giving a frequency resolution of Δf = 10 Hz. Additionally, with the varying rotating velocity values, the magnitudes of the rotational Doppler shifts would synchronously change along the frequency axis. However, the amplitudes of corresponding Doppler spectrums remained constant, as these values are dependent on the emitted light power of the specific modal components [21]. Hence, the maximum detectable tilt angle will not be affected by the change in rotation speed.
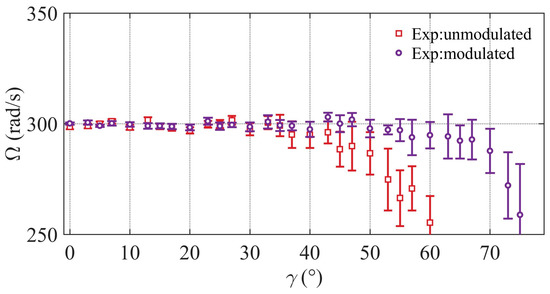
Figure 7.
Experimentally measured rotating velocity as a function of the tilt angles with the unmodulated and modulated OAM light fields. The disk spun with a constant angular speed of 300 rad/s.
To clearly clarify the advantage of our reported system, we further compared existing measuring systems with our validated system via the OAM indices of the probe beams and the largest tilt angle of the object, as shown in Table 1. We can see in Table 1 that in the previous work in ref. [37], the system could measure the rotating velocity of a surface with the maximum tilt angle of less than 50 degrees, in which they used emitted 18-order OAM light modes. In our reported system, the unmodulated OAM light modes with 10- and 18-order OAM indices separately enable rotating velocimetry of a surface with the comparable largest tilt angles, under the same circumstances. On the contrary, when we use the modulated OAM modes with the same indices as the emitted light, the rotating velocity of the surface at tilt angles as large as 70 degrees can be measured. It is demonstrated that with our system, the rotating velocity of a surface can be detected at larger tilt angles than by other systems and unmodulated systems.

Table 1.
Comparison of previously published works with this work on the rotating velocimetry of a tilted object using OAM light fields.
4. Discussions
When the tilt angle is unknown, this case is equivalent to unmodulated situations, as shown in Figure 7 (red date points), where rotating velocity fails to be measured at larger tilt angles (>50 degrees). If the measured tilt angle is inaccurate, the phase-compensated scheme can still effectively measure rotating velocity. This is because the phase-compensated scheme in essence aims to improve the SNR of the Doppler spectrum (the vertical axis in the RDS-spectrum diagram) and does not affect the RDS value (the horizontal axis in RDS-spectrum diagram), which determines the result of the rotating velocimetry. However, the extent of improvement depends on the magnitude of the tilt angle. For instance, as shown in Figure 7 (purple date points), when the evaluated tilt angle is less than 70 degrees, the modulated scheme can still measure rotating velocity at larger tilt angles. On the contrary, if the evaluated tilt angle is greater than 70 degrees, the modulated scheme gradually loses effectiveness as the signals are submerged into noise. Therefore, the result of the phase-compensated scheme can still be effective when the tilt angle is below 70 degrees.
The presented rotating velocimetry with a compensating strategy may found applications in a wide range of fields, such as aviation, fluid dynamics, and biological sciences. For example, in the aviation industry, during take-off or landing of a large passenger aircraft, its two wingtips will generate large vortices with diameters reaching several meters. In such scenarios, the rotating velocimetry for these vortices is crucial for ensuring flight safety. Furthermore, in fluid dynamics, it can be used to study the vorticity-field distribution in fluids. In biological sciences, it can be used to study the microfluidic behaviors of biological cells and microorganisms. However, in these scenarios, the objects being measured are often tilted at various angles, making it challenging to obtain accurate velocity measurements. Therefore, an effective compensating strategy for larger tilt angles would greatly enhance the accuracy of the rotating velocimetry. Moreover, to address the issue of determining the tilted angle in real practice, researchers can utilize various methods, such as image analysis techniques, geometrical measurements, or machine learning algorithms. Another possible method is to use the measured OAM spectrum, as different tilted angles correspond to different broadening widths of OAM spectra.
5. Conclusions
To summarize, we have proposed and experimentally validated a compensating scheme to detect the rotating velocity of a rotor at large tilt angles. This was achieved by combining digital modal decomposition and the rotational Doppler effect. We first unveiled that the tilt of a rotating surface causes both the diffusion of OAM power and that of phase spectra. It is the spreading OAM modal spectrum that gives rise to the broadening and reduced central component in the rotational Doppler power spectrum. With higher tilt angles, the accuracy of the rotating velocimetry gradually decreases, which results from the reduced Doppler signals. A compensation phase is including to effectively suppress the sidebands of OAM power spectrum, thereby leading to the reduced sideband signals in the rotational Doppler power spectrum while maintaining the magnitude of the central component. As a consequence, the rotating velocimetry of a tilted surface can be extended to cover larger tilt angles than in existing systems—up to 70 degrees. Our demonstrated findings not only help to researchers understand the interaction of OAM-carrying light with macroscopic objects, but also may find practical applications in tornado and whirlpool forewarning, astronomical surveys, lidar countermeasures, and remote sensing systems.
Author Contributions
Conceptualization, Y.Z. (Yanxiang Zhang) and Z.Z.; methodology, Z.Z.; software, Y.Z. (Yanxiang Zhang); validation, Y.Z. (Yanxiang Zhang), Z.Z. and Y.Z. (Yuan Zhao); formal analysis, Y.Z. (Yanxiang Zhang); investigation, Y.Z. (Yanxiang Zhang); resources, Y.Z. (Yanxiang Zhang); data curation, Y.Z. (Yuan Zhao); writing—original draft preparation, Y.Z. (Yanxiang Zhang); writing—review and editing, Z.Z.; visualization, Y.Z. (Yanxiang Zhang); supervision, Z.Z.; project administration, L.L.; funding acquisition, Z.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (Grant No. 62075049) and the Fundamental Research Funds for the Central Universities (FRFCU5710050722) (AUEA5770500522).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Charrett, T.O.H.; James, S.W.; Tatam, R.P. Optical fibre laser velocimetry: A review. Meas. Sci. Technol. 2012, 23, 032001. [Google Scholar] [CrossRef]
- Yeh, Y.; Cummings, H.Z. Localised fluid flow measurements with a He–Ne spectrometer. Appl. Phys. Lett. 1964, 4, 176–178. [Google Scholar] [CrossRef]
- Mayor, M.; Lovis, C.; Santos, N.C. Doppler spectroscopy as a path to the detection of Earth-like planets. Nature 2014, 513, 328–335. [Google Scholar] [CrossRef]
- Doppler, C. Ueber das Farbige Licht der Doppelsterne und Einiger Anderer Gestirne des Himmels: Versuch Einer das Bradley’sche Aberrations-Theorem Als Integrirenden Theil in Sich Schliessenden Allgemeineren Theorie; Commission bei Borrosch & André: Prague, Czech Republic, 1842. [Google Scholar]
- Courtial, J.; Robertson, D.A.; Dholakia, K.; Allen, L.; Padgett, M.J. Rotational frequency shift of a light beam. Phys. Rev. Lett. 1998, 81, 4828–4830. [Google Scholar] [CrossRef]
- Amzajerdian, F.; Pierrottet, D.; Hines, G.D.; Petway, L.B.; Barnes, B.W. Doppler lidar sensor for precision navigation in GPS-deprived environment. Laser Radar Technology and Applications XVIII. Int. Soc. Opt. Photonics 2013, 8731, 87310G. [Google Scholar]
- Ristić, S. Laser Doppler anemometry and its application in wind tunnel tests. Sci. Technol. Rev. 2007, 57, 64. [Google Scholar]
- Watrasiewicz, B.M.; Rudd, M.J. Laser Doppler Measurements; Butterworths: London, UK, 1976. [Google Scholar]
- Fang, L.; Padgett, M.J.; Wang, J. Sharing a common origin between the rotational and linear Doppler effects. Laser Photonics Rev. 2017, 11, 1700183. [Google Scholar] [CrossRef]
- Nienhuis, G. Doppler effect induced by rotating lenses. Opt. Commun. 1996, 132, 8–14. [Google Scholar] [CrossRef]
- Belmonte, A.; Rosales-Guzmán, C.; Torres, J.P. Measurement of flow vorticity with helical beams of light. Optica 2015, 2, 1002–1005. [Google Scholar] [CrossRef]
- Vasnetsov, M.V.; Torres, J.P.; Petrov, D.V.; Torner, L. Observation of the orbital angular momentum spectrum of a light beam. Opt. Lett. 2003, 28, 2285–2287. [Google Scholar] [CrossRef]
- Rosales-Guzmán, C.; Hermosa, N.; Belmonte, A.; Torres, J.P. Experimental detection of transverse particle movement with structured light. Sci. Rep. 2013, 3, 2815. [Google Scholar] [CrossRef] [PubMed]
- Rosales-Guzmán, C.; Hermosa, N.; Belmonte, A.; Torres, J.P. Measuring the translational and rotational velocities of particles in helical motion using structured light. Opt. Express 2014, 22, 16504–16509. [Google Scholar] [CrossRef] [PubMed]
- Lavery, M.P.J.; Speirits, F.C.; Barnett, S.M.; Padgett, M.J. Detection of a spinning object using light’s orbital angular momentum. Science 2013, 341, 537–540. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.L.; Fu, D.; Dong, J.; Zhang, P.; Zhang, X. Theoretical analysis and experimental verification on optical rotational Doppler effect. Opt. Express 2016, 24, 10050–10056. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Zentgraf, T.; Zhang, S. Rotational Doppler effect in nonlinear optics. Nat. Phys. 2016, 12, 736–740. [Google Scholar] [CrossRef]
- Li, K.F.; Deng, J.H.; Liu, X.; Li, G. Observation of rotational doppler effect in second harmonic generation in reflection mode. Laser Photonics Rev. 2018, 12, 1700204. [Google Scholar] [CrossRef]
- Georgi, P.; Schlickriede, C.; Li, G.; Zhang, S.; Zentgraf, T. Rotational Doppler shift induced by spin-orbit coupling of light at spinning metasurfaces. Optica 2017, 4, 1000–1005. [Google Scholar] [CrossRef]
- Anderson, A.Q.; Strong, E.F.; Heffernan, B.M.; Siemens, M.E.; Rieker, G.B.; Gopinath, J.T. Detection technique effect on rotational Doppler measurements. Opt. Lett. 2020, 45, 2636–2639. [Google Scholar] [CrossRef]
- Zhou, H.L.; Fu, D.Z.; Dong, J.J.; Zhang, P.; Chen, D.X.; Cai, X.L.; Li, F.; Zhang, X.L. Orbital angular momentum complex spectrum analyzer for vortex light based on the rotational Doppler effect. Light Sci. Appl. 2017, 6, e16251. [Google Scholar] [CrossRef] [PubMed]
- Neo, R.; Leon-Saval, S.; Bland-Hawthorn, J.; Molina-Terriza, G. OAM interferometry: The detection of the rotational Doppler shift. Opt. Express 2017, 25, 21159–21170. [Google Scholar] [CrossRef]
- Zhang, W.; Gao, J.; Zhang, D.; He, Y.; Xu, T.; Fickler, R.; Chen, L. Free-space remote sensing of rotation at the photon-counting level. Phys. Rev. Appl. 2018, 10, 044014. [Google Scholar] [CrossRef]
- Zhai, Y.; Fu, S.; Zhang, J.; Lv, Y.; Zhou, H.; Gao, C. Remote detection of a rotator based on rotational Doppler effect. Appl. Phys. Express 2020, 13, 022012. [Google Scholar] [CrossRef]
- Fu, S.; Wang, T.; Zhang, Z.; Zhai, Y.; Gao, C. Nondiffractive Bessel-Gauss beams for the detection of rotating object free of obstructions. Opt. Express 2017, 25, 20098–20108. [Google Scholar] [CrossRef]
- Qiu, S.; Ren, Y.; Liu, T.; Chen, L.; Wang, C.; Li, Z.; Shao, Q. Spinning object detection based on perfect optical vortex. Opt. Lasers Eng. 2020, 124, 105842. [Google Scholar] [CrossRef]
- Qiu, S.; Ren, Y.; Sha, Q.; Ding, Y.; Wang, C.; Li, Z.; Liu, T. Observation of the rotational doppler shift of the ring airy gaussian vortex beam. Opt. Commun. 2021, 490, 126900. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Z.; Liu, L.; Zhao, Y. Measurement of rotational velocity enabled by novel perfect Laguerre-Gaussian modes. Opt. Express 2022. To be published. [Google Scholar]
- Lavery, M.P.; Barnett, S.M.; Speirits, F.C.; Padgett, M.J. Observation of the rotational Doppler shift of a white-light, orbital-angular-momentum-carrying beam backscattered from a rotating body. Optica 2014, 1, 1–4. [Google Scholar] [CrossRef]
- Rosales-Guzmán, C.; Hermosa, N.; Belmonte, A.; Torres, J.P. Direction-sensitive transverse velocity measurement by phase-modulated structured light beams. Opt. Lett. 2014, 39, 5415–5418. [Google Scholar] [CrossRef]
- Li, Z.; Liu, T.; Ren, Y.; Qiu, S.; Wang, C.; Wang, H. Direction-sensitive detection of a spinning object using dual-frequency vortex light. Opt. Express 2021, 29, 7453–7463. [Google Scholar] [CrossRef]
- Fang, L.; Wan, Z.; Forbes, A.; Wang, J. Vectorial doppler metrology. Nat. Commun. 2021, 12, 4186. [Google Scholar]
- Zhai, Y.; Fu, S.; Yin, C.; Zhou, H.; Gao, C. Detection of angular acceleration based on optical rotational Doppler effect. Opt. Express 2019, 27, 15518–15527. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Zhang, Y.; Wang, F.; Zhao, Y. Measuring the rotational velocity and acceleration based on orbital angular momentum modulation and time–frequency analysis method. Opt. Commun. 2022, 502, 127414. [Google Scholar] [CrossRef]
- Qiu, S.; Liu, T.; Li, Z.; Wang, C.; Ren, Y.; Shao, Q.; Xing, C. Influence of lateral misalignment on the optical rotational Doppler effect. Appl. Opt. 2019, 58, 2650–2655. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Cen, L.; Zhang, J.D.; Hu, J.; Wang, F.; Zhao, Y. Rotation velocity detection with orbital angular momentum light spot completely deviated out of the rotation center. Opt. Express 2020, 28, 6859–6867. [Google Scholar] [CrossRef]
- Qiu, S.; Liu, T.; Ren, Y.; Li, Z.; Wang, C.; Shao, Q. Detection of spinning objects at oblique light incidence using the optical rotational Doppler effect. Opt. Express 2019, 27, 24781–24792. [Google Scholar] [CrossRef]
- Ding, Y.; Ren, Y.; Liu, T.; Qiu, S.; Wang, C.; Li, Z.; Liu, Z. Analysis of misaligned optical rotational Doppler effect by modal decomposition. Opt. Express 2021, 29, 15288–15299. [Google Scholar] [CrossRef]
- Litvin, I.A.; Dudley, A.; Roux, F.S.; Forbes, A. Azimuthal decomposition with digital holograms. Opt. Express 2012, 20, 10996–11004. [Google Scholar] [CrossRef]
- Flamm, D.; Naidoo, D.; Schulze, C.; Forbes, A.; Duparré, M. Mode analysis with a spatial light modulator as a correlation filter. Opt. Lett. 2012, 37, 2478–2480. [Google Scholar] [CrossRef]
- Bolduc, E.; Bent, N.; Santamato, E.; Karimi, E.; Boyd, R.W. Exact solution to simultaneous intensity and phase encryption with a single phase-only hologram. Opt. Lett. 2013, 38, 3546–3549. [Google Scholar] [CrossRef]
- Schulze, C.; Dudley, A.; Flamm, D.; Duparre, M.; Forbes, A. Measurement of the orbital angular momentum density of light by modal decomposition. New J. Phys. 2013, 15, 073025. [Google Scholar] [CrossRef]
- D’Errico, A.; D’Amelio, R.; Piccirillo, B.; Cardano, F.; Marrucci, L. Measuring the complex orbital angular momentum spectrum and spatial mode decomposition of structured light beams. Optica 2017, 4, 1350–1357. [Google Scholar] [CrossRef]
- Fu, S.; Zhai, Y.; Zhang, J.; Liu, X.; Song, R.; Zhou, H.; Gao, C. Universal orbital angular momentum spectrum analyzer for beams. PhotoniX 2020, 1, 19. [Google Scholar] [CrossRef]
- Pinnell, J.; Klug, A.; Forbes, A. Spatial filtering of structured light. Am. J. Phys. 2020, 88, 1123–1131. [Google Scholar] [CrossRef]
- Neto, A.M.; Victorino, A.C.; Fantoni, I.; Zampieri, D.E.; Ferreira, J.V.; Lima, D.A. Image processing using Pearson’s correlation coefficient: Applications on autonomous robotics. In Proceedings of the IEEE International Conference on Autonomous Robot Systems and Competitions, 13th International Conference on Autonomous Robot Systems, Lisbon, Portugal, 24 April 2013; pp. 1–6. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).