Performance Study of Generalized Space Time Block Coded Enhanced Fully Optical Generalized Spatial Modulation System Based on Málaga Distribution Model

Abstract

This paper proposes a generalized space time block coded (GSTBC) enhanced fully optical generalized spatial modulation (EFOGSM) system based on Málaga (M) turbulent channel. GSTBC-EFOGSM adopts the hybrid concept of generalized space time block coded and optical spatial modulation to further utilize the high transmission rate of EFOGSM and the diversity advantage of GSTBC in free space optical (FSO) communication systems. Considering the combined effects of path loss, pointing error and atmospheric turbulence, the Meijer G function is used to derive the closed-form expression for the average bit error rate (ABER) of GSTBC-EFOGSM. Then, the ABER performance, data transmission rate, energy efficiency and computational complexity at the receiver of GSTBC-EFOGSM are compared with other optical spatial modulation schemes by simulation. In addition, the effects of key factors, such as data transmission rate, encoding ratio, number of photodetectors and modulation order, on the ABER performance of the system are also analyzed via simulation. Monte Carlo (MC) simulation is used to verify the correctness of the numerical simulation. The simulation results show that the GSTBC-EFOGSM system has better ABER performance and good performance gain.

1. Introduction

Free space optical (FSO) communication technology is a kind of communication technology that transmits in the atmosphere and uses laser as a medium. In recent years, it has been widely studied by the research community due to its large transmission bandwidth, strong confidentiality, low implementation cost, and having no spectrum license [1]. FSO has made great achievements in the application of metropolitan area network expansion, cellular system backhaul and military secure communication [2]. However, the advantages of FSO communications are not without cost. The atmospheric turbulence encountered by the beam along the propagation path and the aiming error between the communication equipment will cause the optical signal to flicker and distort in amplitude and phase, which will degrade the communication performance of the FSO system [3,4]. The gas molecules and particles in the atmospheric channel (such as rain, fog, dust) will have an atmospheric absorption effect on the laser, which will attenuate the power of the laser signal, that is, the path loss [5]. For many years, in order to better study the effect of atmospheric turbulence state on the communication quality of FSO systems, the research community has been trying to develop general models that can be applied to any type of atmospheric turbulence conditions. In 2011, Jurado et al. proposed a generalized model called Málaga (M) distribution, which provides a good fit with experimental data and has good advantages in atmospheric channel modeling [6]. In order to overcome the above problems and limitations, multiple input multiple output (MIMO) technology has become the main technology of FSO because it can improve the transmission capacity and signal quality of the system [7,8,9].

As a novel optical multiple input multiple output technology, optical spatial modulation (OSM) uses digital modulation constellation and laser index to transmit and carry information at the same time, and also creates a mapping relationship between input bit information and laser to carry and transmit information [10]. In 2014, Pham et al. combined OSM with Pulse Position Modulation (PPM) and proposed a Spatial Pulse Position Modulation (SPPM) system suitable for FSO communication [11]. The research shows that OSM has both signal domain and spatial domain, which greatly improves the spectral efficiency of the system. OSM not only effectively avoids the problem of strong interference between channels and difficult synchronization between antennas in MIMO technology, but also reduces the link cost and the complexity of signal detection at the receiver [12]. In 2019, Jaiswal et al. proposed a differential optical spatial modulation and analyzed its BER performance under Gamma–Gamma and negative exponential channel models [13]. However, OSM only activates one laser at a time to send information, which also causes a waste of space resources. In addition, OSM must require the number of lasers in the system to be set to the integer power of 2, which greatly increases the cost of the system and limits the application of the system. In order to overcome these shortcomings, optical generalized spatial modulation (OGSM) has been further proposed by the research community [14,15,16]. In 2019, Cao’s team improved the minimum mean square error (MMSE) algorithm by using the balance factor to solve the problem of high complexity of the Maximum Likelihood (ML) decoding algorithm and modified the weights according to the characteristics of the OGSM signal activating a certain number of lasers [14]. However, they did not study the performance problem of OSM system in atmospheric channel. In 2020, Wang Huiqin et al., based on pulse position modulation and pulse amplitude modulation suitable for intensity modulation/direct detection (IM/DD), focused on how to improve the rate of traditional OSM [15]. However, they did not study the power efficiency of OSM, the computational complexity at the receiver or the issue of how to effectively improve its ABER performance. In 2021, Wang Yi et al. combined OGSM and serial relay system, and added convolutional coding to form an optical spatial modulation scheme suitable for FSO communication. Research shows that OGSM FSO system with serial relay has better performance [16]. However, they did not investigate more advanced upgrade schemes for optical spatial modulation to achieve lower BER, and the OGSM scheme did not consider the limitation that the system is subjected to in terms of transmission rate. The research gap in the literature survey expresses that modern FSO communication systems still require higher spectral efficiency. At present, the research community has not conducted performance analysis for any superior optical generalized spatial modulation for FSO communication, which motivates us to propose more innovative optical generalized spatial modulation schemes for FSO communication systems.

Enhanced fully optical generalized spatial modulation (EFOGSM) scheme transmits information not only by the index of the laser, but also by using the type bearing of the signal constellation. That is, a constellation type is added so that the primary constellation and the secondary constellation are used to increase the number of combinations between the modulation and the laser. At the same time, EFOGSM makes full use of all possible laser combinations when the total number of lasers is unchanged, thus breaking the limit of the logarithmic scale relationship between the transmission rate of OGSM system and the number of lasers. It is known that EFOGSM technology has not yet appeared and has not been reported in FSO communication system.

In order to further mitigate fading effects, provide diversity gain and enhance the advantages of optical spatial modulation in FSO systems, the integration of space time block coding (STBC) and OSM has been considered as a particularly promising modulation scheme in recent years. At present, only Ferhat’s team have studied the STBC-OSM scheme in FSO communication system in 2017. They derived the bit error rate (BER) expressions of the system under lognormal and double generalized gamma fading channels, and the simulation results show that the system has a significant improvement in BER performance compared with OSM [17]. The results show that STBC-OSM can also achieve high diversity gain by transmitting the same data information in different time slots, while maintaining high energy efficiency and low complexity. However, the STBC-OSM scheme can only use two lasers in the transmission cycle and transmit a pair of symbols of the STBC matrix at the same time, which greatly wastes the space resources. The system needs to use an arbitrary number of lasers to achieve higher spectral efficiency, which makes the STBC-OSM system need further optimization, that is, the STBC-EFOGSM scheme appears. However, the selection process of laser combinations becomes complicated when multiple lasers are used in STBC-EFOGSM. Since the information bits are transmitted through an activated laser combination based on different modulation symbols, this complicates the mapping process from bits to modulation symbols. More importantly, when the number of lasers increases, the design of STBC space code-word becomes more complex, and the diversity gain will also decrease. Therefore, this paper proposes a generalized space time block coded enhanced fully optical generalized spatial modulation (GSTBC-EFOGSM) system to overcome this complexity. At present, GSTBC-EFOGSM system has not been reported in FSO communication system.

Based on the above facts, this paper proposes the EFOGSM scheme and the GSTBC-EFOGSM system. Under M distribution model, considering the combined effects of path loss, pointing error and atmospheric turbulence on the GSTBC-EFOGSM system, the Meijer’s G form closed expression of the average bit error rate (ABER) of the system is derived. On the basis of theoretical derivation, the simulation compares GSTBC-EFOGSM with other optical spatial modulation schemes in terms of ABER, data transmission rate, energy efficiency and computational complexity of the receiver. In addition, the effects of key factors, such as data transmission rate, encoding ratio, number of photodetectors (PD) and modulation order, on the ABER of the system are also analyzed via simulation. Monte Carlo (MC) simulation is used to verify the correctness of the numerical simulation.

The rest of this paper is organized as follows. Section 2 proposes and introduces the EFOGSM scheme and the EFOGSM mapping rules. Section 3 proposes and introduces the GSTBC-EFOGSM system model. Section 4 presents the channel fading model for the M distribution. Section 5 derives a Meijer-G form closed expression for the GSTBC-EFOGSM system ABER. In Section 6, the ABER performance of GSTBC-EFOGSM and other OSM schemes are analyzed and compared through simulations, as well as the performance comparison analysis, such as data transmission rate, energy efficiency and computational complexity of the receiver. Section 7 concludes the paper.

2. The EFOGSM Scheme

In this section, the EFOGSM scheme is proposed and introduced.

Figure 1 shows the system chart of EFOGSM including the modulator and demodulator. The incoming data are split into two groups after serial–parallel conversion. The first group contains data bits ${\log }_2{P}_M+{\log }_2{S}_{\raisebox{1ex}{$M$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$, where $P_M$ represents the primary signal constellations and $S_{\raisebox{1ex}{$M$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$ represents the secondary signal constellations. The second group represents spatial bit $⌊{\log }_2{\displaystyle \sum _{N_u=2}^{Nt}\left(\begin{array}{c}{N}_t\\ N_u\end{array}\right)}⌋$, where $N_{\mathrm{u}}$ denotes the number of lasers that activate transmission of the primary and secondary signal constellations, and $N_t$ denotes the number of lasers used to select the laser subset for transmitting constellation symbol information. The laser subset can vary from activating only two lasers to multiple or all lasers. In all laser subsets, one or more lasers transmit symbols based on the main signal constellation $P_M$, while other lasers transmit symbols based on the secondary signal constellation $S_{\raisebox{1ex}{$M$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$. The space bit is used to select the active laser combination. Typically, the transmitted information bits are based on three groups: the primary signal constellation, the secondary signal constellation and the activated laser combination mapping. First, the information bits are transmitted through the main signal constellation at a data transmission rate of ${\log }_2{P}_M$. Second, the secondary signal constellation is used to transmit information bits at a transmission rate of ${\log }_2{S}_{\raisebox{1ex}{$M$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$. Finally, the transmission rate of $⌊{\log }_2{\displaystyle \sum _{N_u=2}^{Nt}\left(\begin{array}{c}{N}_t\\ N_u\end{array}\right)}⌋$ can be obtained using the spatial combination of laser and digital modulation constellation. Therefore, the data transmission rate of the proposed EFOGSM can be expressed as follows:

$$R_p^{EFOGSM}={\log }_2{P}_M+⌊{\log }_2{\displaystyle \sum _{N_u=2}^{Nt}\left(\begin{array}{c}{N}_t\\ N_u\end{array}\right)}⌋+{\log }_2{S}_{\raisebox{1ex}{$M$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$$

(1)

In the above equation, $\lfloor \rfloor$ represents rounded down.

Table 1. EFOGSM system mapping table.

Data Bits	Laser Combination	Signal Constellation	DATA BITS	Laser Combination	Signal Constellation
0000	L1L2	PM:SM/2	1000	L1L2	SM/2: PM
0001	L1L3	PM:SM/2	1001	L1L3	SM/2: PM
0010	L1L4	PM:SM/2	1010	L1L4	SM/2: PM
0011	L2L3	PM:SM/2	1011	L2L3	SM/2: PM
0100	L2L4	PM:SM/2	1100	L2L4	SM/2: PM
0101	L3L4	PM:SM/2	1101	L3L4	SM/2: PM
0110	L1L2L3	PM:SM/2:SM/2	1110	L1L2L3	SM/2: PM: PM
0111	L1L2L4	PM:SM/2:SM/2	1111	L1L2L4	SM/2: PM: PM

illustrates the transport mapping process of EFOGSM. The system uses a 4-pulse amplitude modulation (PAM) modulator for the primary signal constellation and a 2-PAM for the secondary signal constellation. With a transmission rate of Rp = 8 bpcu and $N_t=N_{\mathrm{r}}=4$ ($N_t$ is the number of lasers, and $N_{\mathrm{r}}$ is the number of photodetectors). The data bits to be transmitted are [101 1110]. The first three bits [101] are transmitted through both the primary and secondary signal constellations. [10] is sent via the primary signal constellation and is equivalent to ${\log }_2{P}_M$, while the remaining [1] is transmitted through the secondary signal constellation and is equivalent to ${\log }_2{S}_{\raisebox{1ex}{$M$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$. The remaining four bits [1110] are transmitted through the laser index L₁L₂L₃, the secondary signal constellation bits are transmitted through laser L₁, and the primary signal constellation bits are transmitted through lasers L₂ and L₃. Therefore, the emission vector of EFOGSM is $x={[S_{\raisebox{1ex}{$M$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{ \mathrm{P}}_M{ \mathrm{P}}_M 0]}^{\mathrm{T}}$, which is $N_t\times 1$ in size.

3. System Model

This paper proposes a novel GSTBC-EFOGSM architecture consisting of N_t lasers and N_r photodetectors operating over M distributed channels across T time slots. Figure 2 shows the system model of GSTBC-EFOGSM, where the information bits of length B were divided into K blocks to map K EFOGSM symbols, which were then called into the OSTBC structure for encoding with a coding ratio R = K/T. This innovative approach enables communication over long distances with minimal distortion, making it an ideal choice for a wide range of applications. Explicitly, for the kth block, the information bit of length $B_k=⌊{\log }_2{\displaystyle \sum _{N_u=2}^{Nt}\left(\begin{array}{c}{N}_t\\ N_u\end{array}\right)}⌋+M_{\mathrm{k}}$ was further divided into two parts for the combination of the selected activation laser and the $M_{\mathrm{k}}$-PAM modulation mapping EFOGSM symbol $x_k$, respectively. Where $M_{\mathrm{k}}={\log }_2{P}_{M_k}+{\log }_2{S}_{\raisebox{1ex}{$M_k$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$, $P_{M_k}$ and $S_{\raisebox{1ex}{$M_k$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$ stand for primary and secondary signal constellations, respectively.

After using the EFOGSM mapping, the K EFOGSM symbols were then called into the OSTBC structure for encoding. Consequently, the data transmission rate $R_p^{\prime }$ of the proposed GSTBC-EFOGSM scheme can be expressed as follows:

$$R_p^{\prime }=\frac{{\displaystyle \sum _{k=1}^K⌊{\log }_2{\displaystyle \sum _{N_u=2}^{Nt}\left(\begin{array}{c}{N}_t\\ N_u\end{array}\right)}⌋}+M_{\mathrm{k}}}{T}$$

(2)

Due to the availability of numerous OSTBC codes with varying coding ratios, the proposed GSTBC-EFOGSM architecture can offer flexible transmission rates and diversity orders that are tailored to the specific GSTBC configuration, and the number of lasers employed. In the subsequent section, we introduce the proposed GSTBC-EFOGSM scheme via an alternative GSTBC scheme, thereby highlighting the versatility and adaptability of the proposed approach.

3.1. GSTBC-EFOGSM R = 3/4

In the case of the GSTBC-EFOGSM scheme with a coding ratio of R = 3/4 and time slot T = 4, the information bits were partitioned into three distinct groups and modulated into three EFOGSM symbols $x_1$, $x_2$ and $x_3$. Where $x_{\mathrm{k}}$ is:

$$x_k={[0,\dots ,0{, \mathrm{P}}_M,S_{\raisebox{1ex}{$M$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}, 0,\dots ,0]}^T, \mathrm{k}=1,2,3$$

(3)

These symbols were then subjected to further processing to improve the overall reliability of the system. Then, the transmitted signal was obtained by OSTBC coding. The GSTBC-EFOGSM scheme with the transmitted signal $S_{3/4}\in R^{N_t\times 4}$ could be obtained by using $x_1$, $x_2$ and $x_3$ as follows:

$$S_{3/4}={\left[\begin{array}{cccc}{x}_1& {\overline{x}}_2& x_3& 0\\ x_2& x_1& 0& x_3\\ x_3& 0& {\overline{x}}_1& {\overline{x}}_2\\ 0& x_3& x_2& x_1\end{array}\right]}_{N_t\times 4}$$

(4)

In the equation above, by using an overline notation, the complement of a signal $x_{\mathrm{k}}$ is defined by ${\overline{x}}_k={[0,\dots ,0{, \mathrm{P}}_M+M+1,S_{\raisebox{1ex}{$M$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}+M+1, 0,\dots ,0]}^{\mathrm{T}}, \mathrm{k}=1,2,3$ [14].

3.2. GSTBC-EFOGSM R = 1/2

In the case of the GSTBC-EFOGSM scheme with a coding ratio of R = 1/2 and time slot T = 8, the information bits were partitioned into four distinct groups, each of which was then mapped to a unique EFOGSM symbol, namely $x_1$, $x_2$, $x_3$ and $x_4$. Then, the transmitted signal was obtained by OSTBC coding, such as:

$$S_{4/8}={\left[\begin{array}{cccccccc}{x}_1& x_2& x_3& x_4& x_1& {\overline{x}}_2& {\overline{x}}_3& {\overline{x}}_4\\ x_2& x_1& x_4& x_3& x_2& x_1& x_4& {\overline{x}}_3\\ x_3& x_4& x_1& x_2& x_3& {\overline{x}}_4& x_1& x_2\\ x_4& x_3& x_2& x_1& x_4& x_3& {\overline{x}}_2& x_1\end{array}\right]}_{N_t\times 8}$$

(5)

In the equation above, by using an overline notation, the complement of a signal $x_{\mathrm{k}}$ is defined by ${\overline{x}}_k={[0,\dots ,0{, \mathrm{P}}_M+M+1,S_{\raisebox{1ex}{$M$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}+M+1, 0,\dots ,0]}^T, \mathrm{k}=1,2,3,4$ [14].

When the modulation signal is transmitted through the atmospheric channel, the electrical signal matrix $Y\in R^{N_r\times T}$ received by the photodetector of the system can be written as follows:

$$Y=\omega P_{t}HS+n$$

(6)

In the equation, $P_{\mathrm{t}}$ denotes the transmit power, while $\omega$ represents the detection efficiency of the photodetector. Additionally, the term $n$ represents $Nr\times T$ the additive white Gaussian noise with zero mean and variance ${\sigma }^2$. The channel gain matrix is represented by the symbol $H\in R^{Nr\times Nt}$ and can be expressed in the following manner:

$$H=\left[\begin{array}{ccccc}{h}_{11}& h_{12}& h_{13}& \cdots & h_{1N_t}\\ h_{21}& h_{22}& h_{23}& \cdots & h_{2N_t}\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ h_{N_{r}1}& h_{N_{r}2}& h_{N_{r}3}& \cdots & h_{N_r{N}_t}\end{array}\right]$$

(7)

where the symbol $h_{ij}$ represents the channel gain associated with the link between the jth laser and the ith photodetector, $j=1,2,\cdots ,N_t$, $i=1,2,\cdots ,N_r$.

To detect the transmitted signal, the receiver employed the ML decoding algorithm, which was equipped with complete information about the channel and ideal time synchronization. The criteria employed by the ML decoding algorithm can be expressed as follows:

$$\hat{S}=\underset{S\in ℂ}{\arg \min }{‖Y-HS‖}_F^2$$

(8)

where ${‖•‖}_F$ denotes the F-norm and $𝕔$ is the set of GSTBC-EFOGSM symbols.

4. Aggregated Channel Attenuation Model

In this paper, the channel model accounts for the cumulative impact of atmospheric turbulence $h_a$, path loss $h_l$ and pointing error $h_p$. Therefore, the joint channel attenuation state can be expressed as $h=h_a{h}_l{h}_p$.

4.1. Atmospheric Turbulence

The FSO channel in this paper was modeled using the M distribution. This statistical model, which has gained popularity in recent years, characterizes surface irradiance fluctuation of unbounded light waves. It is a comprehensive model that encompasses all channel conditions ranging from weak turbulence to strong turbulence and unifies most of the statistical models of irradiance fluctuation proposed worldwide, including the LN distribution and Gamma–Gamma distribution. Additionally, the M distribution demonstrated excellent agreement with experimental data [18]. The PDF of the M distribution can be expressed as:

$$f_{h_a}\left(h_a\right)=A{\displaystyle \sum _{k=1}^{\beta }{a}_k}{\left(h_a\right)}^{\frac{\alpha +k}{2}-1}{K}_{\alpha -k}\left(2\sqrt{\frac{\alpha \beta h_a}{\xi \beta +{\Omega }^{\prime }}}\right)$$

(9)

where

$$\left\{\begin{array}{c}A=\frac{2{\alpha }^{\frac{\alpha }{2}}}{{\xi }^{1+\frac{\alpha }{2}}\mathsf{\Gamma }\left(\alpha \right)}{\left(\frac{\xi \beta }{\xi \beta +{\Omega }^{\prime }}\right)}^{\beta +\frac{\alpha }{2}}\\ a_k=\left(\begin{array}{c}\beta -1\\ k-1\end{array}\right)\frac{{\left(\xi \beta +{\Omega }^{\prime }\right)}^{1-\frac{k}{2}}}{\left(k-1\right)!}{\left(\frac{{\Omega }^{\prime }}{\xi }\right)}^{k-1}{\left(\frac{\alpha }{\beta }\right)}^{\frac{k}{2}}\end{array}\right.$$

(10)

$\alpha$ represents the effective number of large-scale units in the scattering environment, $\beta$ which is related to the diffraction effect caused by small-scale eddies, and $K_v\left(\cdot \right)$ representing the modified Bessel function of order v. The classical scattering component’s average power is given by $\xi =E\left[{\left|U_S^G\right|}^2\right]=2b_0\left(1-\eta \right)$, where $U_S^C$ denotes the component of quasi-forward scattering of eddy currents along the propagation axis, $0\le \eta \le 1$ denotes the ratio between the scattered power coupled with the LOS and the power of all scattered components. The average power of the total scattering component is represented by $2b_0=E\left[{\left|U_S^C\right|}^2+{\left|U_S^G\right|}^2\right]$, where $U_S^G$ denotes the energy scattered to the receiver by the eddy current on the propagation axis. The parameter ${\Omega }^{\prime }=\Omega +2\eta {\mathrm{b}}_0+2\sqrt{2{\mathrm{b}}_0\Omega \eta }\cos \left({\varphi }_A-{\varphi }_B\right)$ represents the contribution of the coherent average power, where $\Omega$ represents the average power of the LOS, ${\varphi }_A$ and ${\varphi }_B$ are the deterministic line-of-sight component and the scattering component coupled to it, respectively. $\Gamma \left(\cdot \right)$ is the gamma function.

4.2. Path Loss

The path loss is denoted by $h_l$, and it is commonly induced by unfavorable weather conditions. FSO link transmission is minimally affected in clear weather conditions. However, harsh weather conditions such as rain, snow and haze will cause a certain attenuation in the optical link and result in a significant reduction in optical signal power during communication. The Beer–Lambert law was utilized to determine the amount of optical signal power loss in the communication path [19].

$$h_l\left(d\right)=\exp \left(-\sigma d\right)$$

(11)

where d represents the link distance, parameter $\sigma$ is the attenuation efficiency. Different weather conditions result in different values of $\sigma$. In this paper, we focused on the scenario of sunny weather.

4.3. Pointing Error

Misalignment between the transmitter and receiver due to weak earthquakes, dynamic wind loads and building sway caused by thermal expansion will cause vibration of the transmitted beam, which in turn causes aiming errors and further leads to performance degradation of the FSO system, and its expression is as follows [20]:

$$f_{h_p}\left(h_p\right)=\frac{{\gamma }^2}{A_0^{{\gamma }^2}}{\left(h_p\right)}^{{\gamma }^2-1},0\le h_p\le A_0$$

(12)

where $A_0={\left[erf\left(v\right)\right]}^2$ represents the received optical power at $\varsigma =0$ and $erf\left(\cdot \right)$ is the error function. $v=\sqrt{\pi }r/\sqrt{2}{w}_z$, where $r$ represents the radius in the transverse plane of the incident wave, $w_z$ denotes the optical beam width. $w_{zeq}^2=w_z^2\sqrt{\pi }erf\left(v\right)/2v\exp \left(-v^2\right)$ denotes the equivalent beam width. $\gamma =w_{zeq}/2{\delta }_s$, where ${\delta }_s$ denotes the standard deviation of the pointing error displacement at the receiver.

4.4. Aggregated Channel Attenuation Model

The PDF of the jointly attenuated channel gain $h$ could be obtained by evaluating the product of the PDFs of the three independent attenuation factors that affect the channel gain.

$$f_h\left(h\right)={\displaystyle \int f_{h\left|h_a\right.}\left(h\left|h_a\right.\right)}{f}_{h_a}\left(h_a\right)d{h}_a$$

(13)

where the function $f_{h\left|h_a\right.}\left(h\left|h_a\right.\right)$ represents the probability density function that depends on the atmospheric turbulence $h_a$, and it is defined as follows:

$$f_{h\left|h_a\right.}\left(h\left|h_a\right.\right)=\frac{1}{h_a{h}_l}{f}_{h_p}\left(\frac{h}{h_a{h}_l}\right)=\frac{{\gamma }^2}{A_0{}^{{\gamma }^2}{h}_a{h}_l}{\left(\frac{h}{h_a{h}_l}\right)}^{{\gamma }^2-1}, 0\le h\le A_0{h}_a{h}_l$$

(14)

By utilizing Equations (9), (13) and (14), and by applying the relevant integral formula of the Meijer G function found on the Mathematical Functions website [21], it was possible to calculate a closed-form expression for the probability density function (PDF) of the channel state $h$ in the M distribution model as follows:

$$f_h\left(h\right)=\frac{A{\gamma }^2}{2h}{\displaystyle \sum _{k=1}^{\beta }{a}_k}{\left(\frac{\alpha \beta }{\xi \beta +{\Omega }^{\prime }}\right)}^{-\frac{\alpha +k}{2}}G\begin{array}{cc}3,& 0\\ 1,& 3\end{array}\left[\frac{a\beta h}{\left(\xi \beta +{\Omega }^{\prime }\right)A_0{h}_l}\left|\begin{array}{ccc}1+{\gamma }^2& & \\ {\gamma }^2,& \alpha ,& k\end{array}\right.\right]$$

(15)

5. Performance Analysis

5.1. ABER Performance

In this section, the ABER upper bound for the GSTBC-EFOGSM system under the M distribution was derived. Assuming that the transmitted and received signals of GSTBC-EFOGSM are $S_i$ and $S_{\mathrm{j}}$ respectively, the ABER upper bound could be obtained from the following equation:

$$P_b\le \frac{1}{T{R}_P^{‘}{2}^{T{R}_P^{‘}}}{\displaystyle \sum _{i=1}^{2^{T{R}_P^{‘}}}{\displaystyle \sum _{j=1,j\ne i}^{2^{T{R}_P^{‘}}}{d}_H\left(S_i,S_j\right)P\left(S_i\to S_j\right)}}$$

(16)

where $d_H\left(S_i,S_j\right)$ represents the Hamming distance between $S_i$ and $S_{\mathrm{j}}$. $P\left(S_i\to S_j\right)$ represents the pairwise error probability (PEP) between the symbols $S_i$ and $S_{\mathrm{j}}$. Accordingly, the conditional pairwise error probability was:

$$P\left(S_i\to S_j\left|H\right.\right)=Q\left(\sqrt{\frac{\rho }{2}{‖H(S_j-S_i)‖}_F^2}\right)$$

(17)

where ${‖H(S_j-S_i)‖}_F^2={\displaystyle \sum _{\mathrm{n}=1}^{Nr}{\left|H(S_j-S_i)\right|}^2}$, $\rho$ represents the average signal to noise ratio (SNR). $Q\left(🞄\right)$ represents the Q function [22]. Let ${\alpha }_n=H(S_j-S_i)$, $G={\displaystyle \sum _{n=1}^{Nr}{\left|{\alpha }_n\right|}^2}$, Equation (17) could be written as:

$$P\left(S_i\to S_j\left|H\right.\right)=Q\left(\sqrt{\frac{\rho }{2}{\displaystyle \sum _{\mathrm{n}=1}^{Nr}{\left|{\alpha }_n\right|}^2}}\right)$$

(18)

By the approximate computation of the Gaussian Q-function $Q\left(x\right)\approx \frac{1}{12}\exp \left(-\frac{x^2}{2}\right)+\frac{1}{4}\exp \left(-\frac{2x^2}{3}\right)$ [23], Equation (18) could be further written as:

$$P\left(S_i\to S_j\left|H\right.\right)=\frac{1}{12}\exp \left(-\frac{\rho }{4}{\displaystyle \sum _{n=1}^{Nr}{\left|{\alpha }_n\right|}^2}\right)+\frac{1}{4}\exp \left(-\frac{\rho }{3}{\displaystyle \sum _{n=1}^{Nr}{\left|{\alpha }_n\right|}^2}\right)$$

(19)

Thus, the PEP could be expressed as follows [17]:

$$P\left(S_i\to S_j\right)=E\left(P\left(S_i\to S_j\left|H\right.\right)\right)$$

(20)

where $E\left(🞄\right)$ represents the expectation operator. Combined with Equations (18) and (20), PEP could be expressed as follows:

$$P\left(S_i\to S_j\right)=E\left(\frac{1}{12}\exp \left(-\frac{\rho }{4}{\displaystyle \sum _{n=1}^{Nr}{\left|{\alpha }_n\right|}^2}\right)+\frac{1}{4}\exp \left(-\frac{\rho }{3}{\displaystyle \sum _{n=1}^{Nr}{\left|{\alpha }_n\right|}^2}\right)\right)$$

(21)

Let $Y={\left|{\alpha }_n\right|}^2$, PEP can be further expressed as follows:

$$P\left(S_i\to S_j\right)=\frac{1}{12}{\displaystyle \prod _{n=1}^{Nr}{\displaystyle \underset{Y}{\int }\exp \left(-\frac{\rho }{4}Y\right)}{f}_{\mathrm{Y}}(\mathrm{Y})d\mathrm{Y}}+\frac{1}{4}{\displaystyle \prod _{n=1}^{Nr}{\displaystyle \underset{Y}{\int }\exp \left(-\frac{\rho }{3}Y\right)}{f}_{\mathrm{Y}}(\mathrm{Y})d\mathrm{Y}}$$

(22)

With the help of the Moment Generating function (MGF), the above equation could be written as follows:

$$P\left(S_i\to S_j\right)=\frac{1}{12}{\displaystyle \prod _{\mathrm{m}=1}^{Nr}{M}_{{\left|{\alpha }_n\right|}^2}\left(\frac{\rho }{4}\right)}+\frac{1}{4}{\displaystyle \prod _{\mathrm{m}=1}^{Nr}{M}_{{\left|{\alpha }_n\right|}^2}\left(\frac{\rho }{3}\right)}$$

(23)

By putting the joint channel attenuation Equations (15) and (23) into Equation (16) and using the relevant integral formula of Meijer G function in [21], the upper bound expression of ABER could be calculated as follows:

$$\begin{array}{cc}\hfill P_b\le & \frac{1}{T{R}_P^{‘}{2}^{T{R}_P^{‘}}}{\displaystyle \sum _{\mathrm{i}=1}^{2^{T{R}_P^{‘}}}{\displaystyle \sum _{j=1,\mathrm{j}\ne i}^{2^{T{R}_P^{‘}}}{d}_H\left(S_i,S_j\right)}}\left(\frac{1}{12}{\displaystyle \prod _{\mathrm{m}=1}^{Nr}{M}_{{\left|{\alpha }_n\right|}^2}\left(\frac{\rho }{4}\right)}+\frac{1}{4}{\displaystyle \prod _{\mathrm{m}=1}^{Nr}{M}_{{\left|{\alpha }_n\right|}^2}\left(\frac{\rho }{3}\right)}\right)\hfill \\ \hfill =& \frac{1}{T{R}_P^{‘}{2}^{T{R}_P^{‘}}}{\displaystyle \sum _{\mathrm{i}=1}^{2^{T{R}_P^{‘}}}{\displaystyle \sum _{j=1,j\ne i}^{2^{T{R}_P^{‘}}}{d}_H\left(S_i,S_j\right)}}\hfill \\ \hfill & \left(\begin{array}{c}\frac{1}{12}{\left(\frac{A{\gamma }^2}{4\pi }{\displaystyle \sum _{k=1}^{\beta }{a}_k{2}^{\alpha +k-1}{B}^{-\frac{\alpha +k}{2}}}G\begin{array}{cc}6,& 1\\ 3,& 6\end{array}\left[\frac{B^2}{4\rho A_0^2{h}_l^2}\left|\begin{array}{c}C\\ D\end{array}\right.\right]\right)}^{Nr}+\\ \frac{1}{4}{\left(\frac{A{\gamma }^2}{4\pi }{\displaystyle \sum _{k=1}^{\beta }{a}_k{2}^{\alpha +k-1}{B}^{-\frac{\alpha +k}{2}}}G\begin{array}{cc}6,& 1\\ 3,& 6\end{array}\left[\frac{3B^2}{16\rho A_0^2{h}_l^2}\left|\begin{array}{c}C\\ D\end{array}\right.\right]\right)}^{Nr}\end{array}\right)\hfill \end{array}$$

(24)

where $B=\alpha \beta /\left(\xi \beta +{\Omega }^{\prime }\right)$, $C=\frac{1+{\gamma }^2}{2},\frac{2+{\gamma }^2}{2},1$, $D=\frac{{\gamma }^2}{2},\frac{1+{\gamma }^2}{2},\frac{\alpha }{2},\frac{\alpha +1}{2},\frac{k}{2},\frac{k+1}{2}$.

5.2. Computational Complexity at the Receiver

The computational complexity of the receiver for different optical spatial modulations was determined by counting the total number of actual operations required for its ML decoder [24]. In a conventional OSM, the ML decoder computes ${{\displaystyle {\sum }_{i=1}^{N_{\mathrm{r}}}‖y_i-h_{i}x‖}}^2$ by computing one combined multiplication $h_{i}x$, which is four real multiplications, and four more real multiplications to compute the square norm. However, these operations require the search to be performed on a $2^{R_P}$ basis for each value of $N_r$, where R_p represents the data transmission rate achieved by each optical spatial modulation scheme. In this way, the conventional OSM ML decoder uses this definition to compute the actual operation total count, and the complexity of its receiver can be expressed as [24]:

$$C_{OSM}=8N_r\times 2^{R_p^{OSM}}$$

(25)

In the same way, the complexity of the OGSM receiver is calculated. However, since multiple lasers in OGSM are activated to emit the same constellation symbol, the complexity of its receiver is increased compared to OSM. The complexity of the OGSM receiver is expressed as follows [24]:

$$C_{OGSM}=8N_r(2(N_u-1))\times 2^{R_p^{OGSM}}$$

(26)

For EFGSM, since the ML search is divided into two separate groups, represented by a primary constellation carrying ${\log }_2{P}_M$ bits and a sub-constellation carrying ${\log }_2{S}_{\raisebox{1ex}{$M$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$ bits. Thus, the complexity of the receiver is significantly reduced by ${\log }_2\frac{M}{2}$ bits. The complexity of the EFGSM receiver is expressed as follows:

$$C_{EFOGSM}=8N_r[((2\times ⌈\frac{N_t}{2}-1⌉)\times 2^{R_p^M})+((2\times ⌈\frac{N_t}{2}-1⌉)\times 2^{R_p^S})]$$

(27)

where $R_p^M={\log }_2{P}_M$ and $R_p^S={\log }_2{S}_{\raisebox{1ex}{$M$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$ denote the primary signal constellation rate and the secondary signal constellation rate, respectively. $\lceil \rceil$ means round up.

For GSTBC-EFOGSM, similarly to the proposed EFOGSM method, the receiver complexity of its ML decoder is expressed as follows:

$$C_{GSTBC-EFOGSM}=8N_r[((2\times ⌈\frac{N_t}{2}-1⌉)\times K\times 2^{R_p^M})+((2\times ⌈\frac{N_t}{2}-1⌉)\times K\times 2^{R_p^S})]$$

(28)

6. Simulation Results and Analysis

This section presents simulation results of the GSTBC-EFOGSM FSO system with varying parameters. The performance of the proposed system was compared to that of the EFOGSM, OGSM, and OSM systems. Monte-Carlo simulations were employed to validate the numerical results. Under the M-distributed integrated atmospheric channel, each parameter selection of system is shown in

Table 2. Selection of simulation parameters for GSTBC-EFOGSM FSO system.

System Parameters	Symbol	Value
Light wavelength	$\lambda$	1550 nm
Link distance	d	1000 m
the beam bandwidth	$w_z/r$	25
the jitter error	${\delta }_s/r$	3
Path loss	$h_l$	0.937
a positive parameter related to effective large-scale cells in the scattering process	$\alpha$	6.37727
a natural number representing the number of fading parameters	$\beta$	5
represents the amount of scattered power coupled with the LOS	$\eta$	0.5
The average power of the total scatter components	$2b_0$	0.5
the average optical power of the LOS term	$\Omega$	0.5
The difference between the determined phase of LOS and coupled to the LOS scattering term	${\mathsf{\varphi }}_{\mathrm{A}}-{\mathsf{\varphi }}_{\mathrm{B}}$	$\pi /2$

.

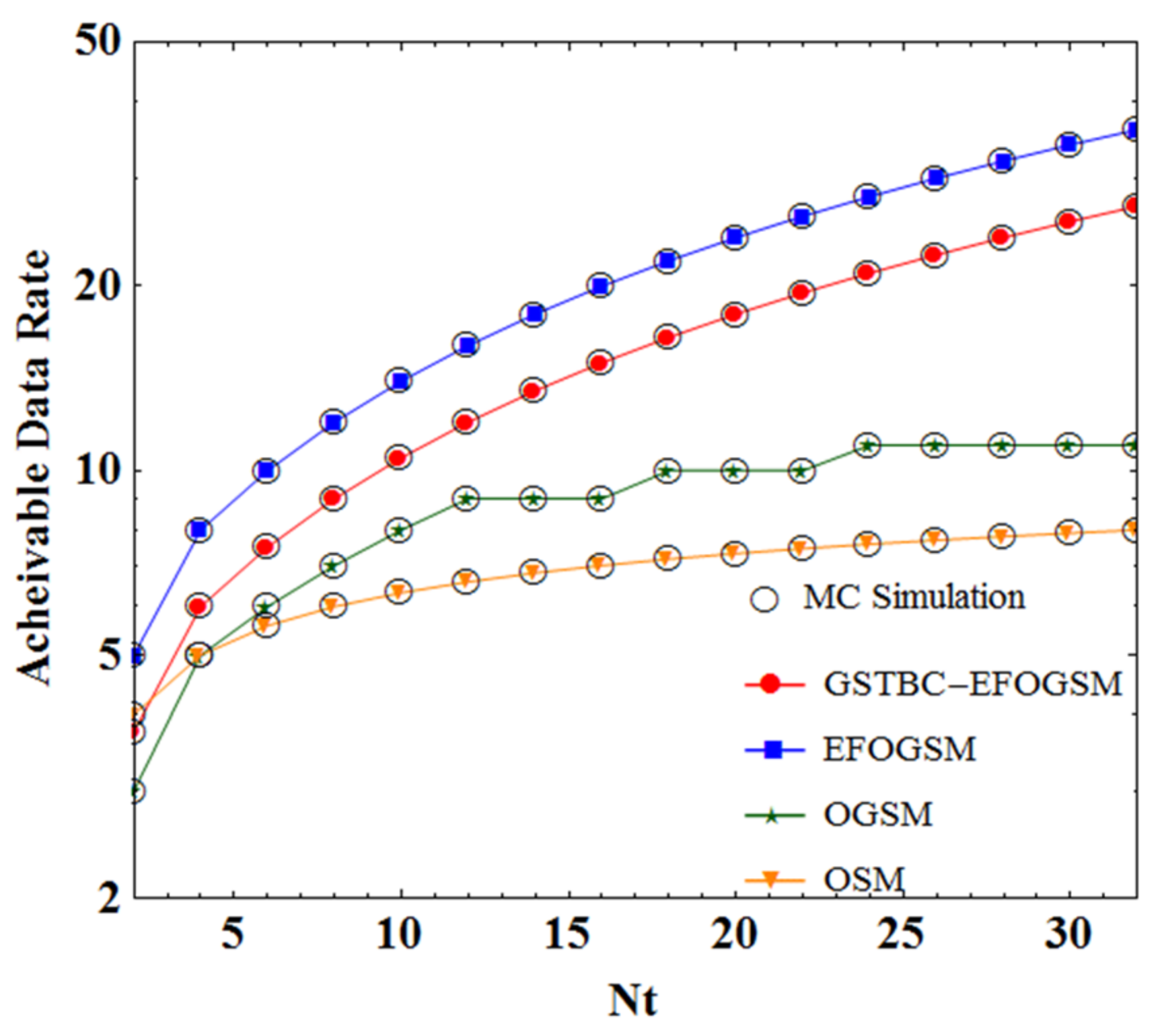
Figure 3 shows the data transmission rate $R_P^{‘}$ simulation for different optical spatial modulation schemes with different number of lasers N_t.. For OSM, OGSM and the main signal constellation of EFOGSM and GSTBC-EFOGSM, the modulation order of M-PAM is M = 8. 4-PAM was used as a secondary signal constellation for EFOGSM and GSTBC-EFOGSM. When N_t = 10, the figure illustrates that the transmission rates for OSM, OGSM, EFOGSM, and GSTBC-EFOGSM schemes were 6 bpcu, 8 bpcu, 14 bpcu and 10.5 bpcu, respectively. The data transmission rate of GSTBC-EFOGSM and EFOGSM schemes was higher than that of OSM and OGSM. In addition, Figure 3 shows that the data transfer rate improvement of OSM and OGSM was limited when N_t increased. The transmission rate of EFOGSM and GSTBC-EFOGSM could be made faster with an increase in N_t. This is because all possible laser combinations were fully utilized in GSTBC-EFOGSM and EFOGSM, and the transmission rate was improved by the change of the digital signal constellation and the number of lasers. Although the transmission rate of GSTBC-EFOGSM was slightly lower than that of EFOGSM, this is because the GSTBC-EFOGSM system divided the input bit into K blocks and performed EFOGSM modulation at the same time, so the transmission rate of GSTBC-EFOGSM system was lower than that of EFOGSM system using only one modulation. However, GSTBC-EFOGSM had a higher and faster transmission rate than other OSM schemes, and also had higher diversity gain than EFOGSM in performance. Therefore, by comparing these schemes, we can see that GSTBC-EFOGSM has a higher data transmission rate.

Figure 4 shows the simulation graph of ABER performance comparison of GSTBC-EFOGSM, EFOGSM and OGSM schemes at the same data transmission rate. In order to achieve a data transmission rate of 9 bpcu, the GSTBC-EFOGSM system used $\left(M,N_t,K,T\right)=\left(16,16,3,4\right)$ and $\left(M,N_t,K,T\right)=\left(256,16,4,8\right)$, respectively, when the coding ratio R = 0.75 and 0.5. The accuracy of numerical calculations was confirmed by the results of MC simulation. From the simulation results, we can see that the GSTBC-EFOGSM scheme had better ABER performance than EFOGSM and OGSM. When the Signal-to-Noise Ratio (SNR) of GSTBC-EFOGSM R = 0.75 was 13 dB, the obtained ABER was about 10⁻¹⁰. In order to obtain the same ABER, the SNR under EFOGSM and OGSM schemes were 40 dB and 45 dB, respectively. The EFOGSM scheme outperformed OGSM, because the laser combination of EFOGSM changed, which was fully conducive to the redundancy of laser combination so that the same data could be transmitted through multiple lasers. The GSTBC-EFOGSM scheme performed better than the other regular OSM schemes because the GSTBC technique was added to the EFOGSM scheme, which achieved a significant enhancement in performance over the EFOGSM scheme alone. Furthermore, the simulation results demonstrated that in order to achieve an ABER of 10⁻²⁰ orders of magnitude, the SNR required for the GSTBC-EFOGSM system was 23 dB and 36 dB for coding ratios of 0.75 and 0.5, respectively. That is, when the coding ratio was changed from 0.75 to 0.5, the SNR of the system increased by 13 dB. By increasing the coding rate, the cost of engineering implementation can be effectively reduced, channel coding redundancy can be decreased and transmission efficiency can be improved. In this system, R = 0.75 is the more suitable option. Thus, through a comparison of these schemes, it becomes apparent that the GSTBC-EFOGSM scheme with R = 0.75 provides better performance gains.

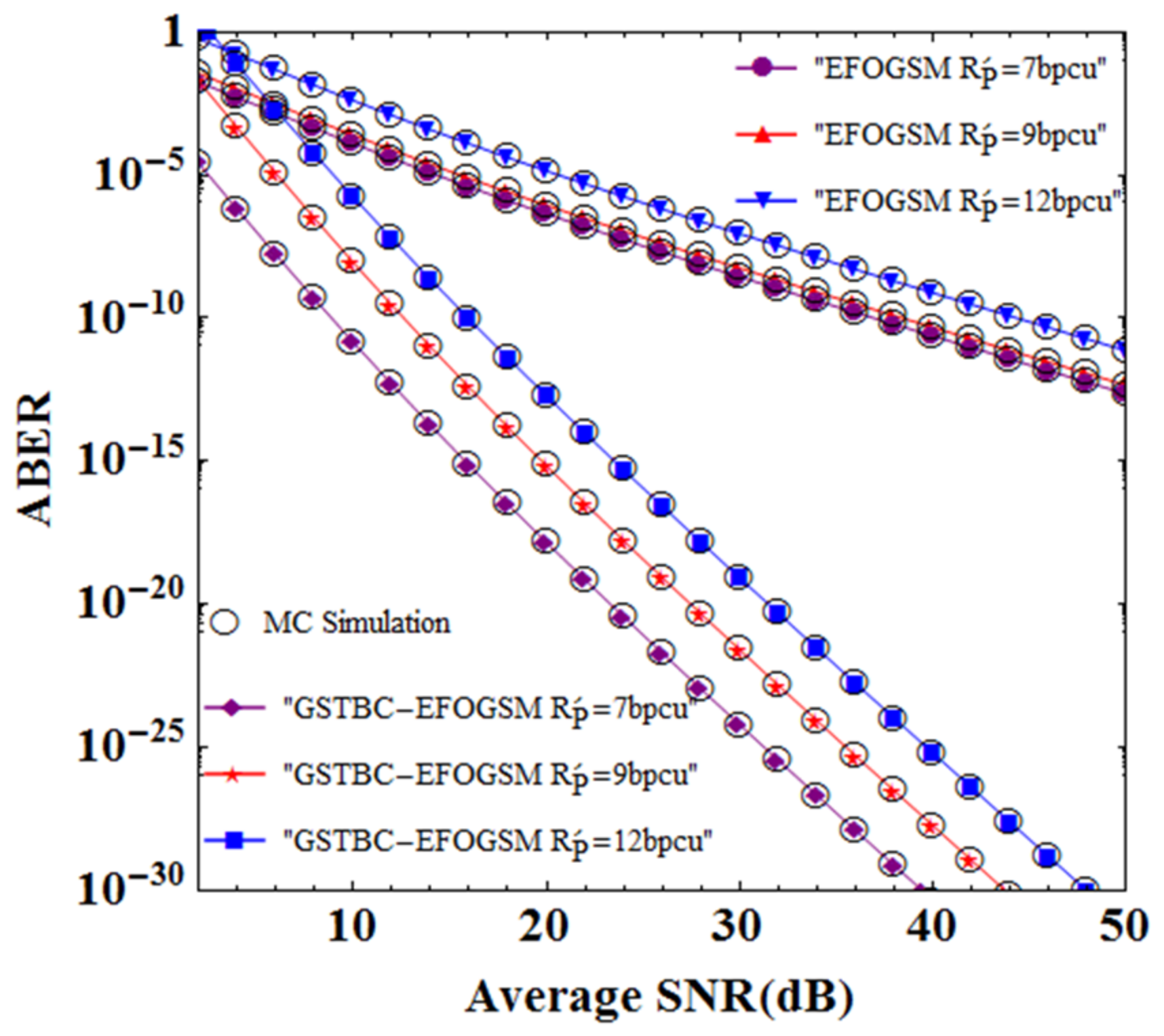
Figure 5 describes the ABER simulation diagram of GSTBC-EFOGSM and EFOGSM schemes under different data transmission rate $R_P^{‘}$. The coding ratio of GSTBC-EFOGSM was set to 0.75. In order to achieve data transmission rates of 7 bpcu, 9 bpcu and 12 bpcu, respectively, $\left(M,N_t,K,T\right)=\left(8,16,3,4\right)$, $\left(M,N_t,K,T\right)=\left(16,16,3,4\right)$ and $\left(M,N_t,K,T\right)=\left(64,16,3,4\right)$ were used in the proposed GSTBC-EFOGSM system, while $\left(M,N_t\right)=\left(7,4\right)$, $\left(M,N_t\right)=\left(8,4\right)$ and $\left(M,N_t\right)=\left(32,4\right)$ were used in the EFOGSM system. The MC simulation results were used to confirm the accuracy of the numerical calculations. As shown in

Table 3. Table of ABER performance comparison between EFOGSM and GSTBC-EFOGSM with SNR = 30.

Rp	EFOGSM	GSTBC-EFOGSM
7 bpcu	$7.46\times {10}^{-9}$	$1.09\times {10}^{-23}$
9 bpcu	$1.49\times {10}^{-8}$	$4.64\times {10}^{-21}$
12 bpcu	$2.39\times {10}^{-7}$	$1.48\times {10}^{-18}$

, when SNR = 30, the ABER of EFOGSM and GSTBC-EFOGSM systems gradually increased with the increase in Rp, and when the value of fixed Rp was 7 bpcu, the ABER of GSTBC-EFOGSM system was significantly smaller than that of EFOGSM system. Therefore, it can be concluded that increasing the transmission rate will also reduce the anti-interference ability of the system and increase the ABER of the system, so it is not possible to blindly increase the transmission rate of the system and thus lose the ABER of the system. Furthermore, the implementation of GSTBC coding technique substantially diminished the ABER of the GSTBC-EFOGSM system in contrast to the EFOGSM system. For instance, in achieving a 10⁻¹⁰ ABER, the GSTBC-EFOGSM system yielded a coding gain of roughly 26 dB. This outcome highlights the superiority of utilizing the GSTBC technique in FSO systems.

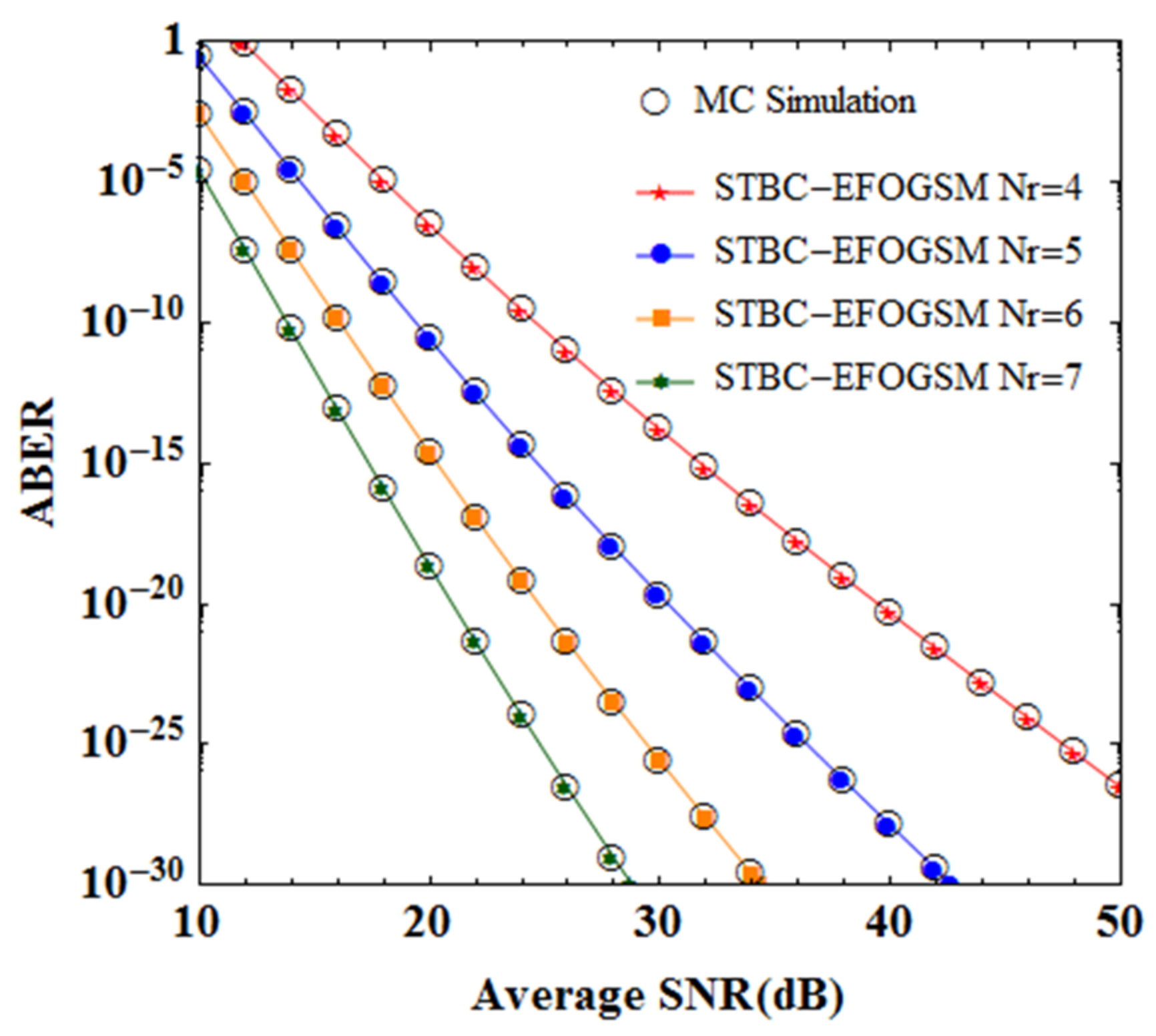
Figure 6 depicts the ABER simulation of the GSTBC-EFOGSM system with R = 0.75, featuring different photodetector numbers. The simulation results exhibited a satisfactory agreement with the MC simulation results, thereby verifying the accuracy of the proposed approach. As illustrated in Figure 6, when the photodetector number was Nr = 4, the system necessitated an SNR of 32 dB to achieve an ABER of 10⁻¹⁵. However, when the number of photodetectors was appropriately augmented, for example, when Nr = 5, 6 and 7, the SNE of the system was 24 dB, 20 dB and 18 dB, respectively, for attaining the same ABER. Thus, the system attained performance gains of 8 dB, 12 dB and 14 dB, respectively. This outcome indicates that increasing the photodetector number can effectively enhance the system’s performance. Moreover, the decline trend of the system’s ABER became more pronounced with an increase in the photodetector number, signifying that a greater number of photodetectors leads to more prominent performance advantages for the system.

Figure 7 shows the energy efficiency of different optical spatial modulation systems under the condition of M = 256. In the optical spatial modulation mapping, the required transmission bits of the system part were transmitted in the spatial domain to improve the energy efficiency in the communication transmission. As shown in Figure 7, when N_t = 6, the energy efficiency of OSM, OGSM, EFOGSM and GSTBC-EFOGSM iwa 24%, 33%, 87% and 50%, respectively. For N_t = 8, OSM, OGSM, EFOGSM and GSTBC-EFOGSM can achieve 27%, 38%, 112% and 67% energy savings, respectively. The energy efficiency of EFOGSM and GSTBC-EFOGSM was significantly higher than that of other conventional OSM schemes, and this high performance was a feature brought by the low number of bits transmitted by the system communication. This is because EFOGSM and GSTBC-EFOGSM schemes used two signal constellations in the modulation process. Therefore, their spatial domain used two sets of laser mapping combination to transmit information bits, while other optical spatial modulation schemes only used one set of laser mapping combination scheme to index information. Although the energy efficiency of GSTBC-EFOGSM was slightly lower than that of EFOGSM, it was also 1.5 times of that of OGSM. Moreover, the coding technology added in GSTBC-EFOGSM brought about a stronger overall performance of the system. Therefore, by comparing these schemes, we can see that GSTBC-EFOGSM has higher energy efficiency.

The computational complexity analysis of the ML decoder in the receiver for various optical spatial modulation systems is illustrated in Figure 8. All schemes had an R_P of 9 bpcu and used the same number of lasers. Figure 8 shows that when N_r = 4, the computational complexities of EFOGSM, GSTBC-EFOGSM, OSM and OGSM schemes were 864, 12,096, 18,432 and 36,864, respectively. The EFOGSM scheme obviously greatly reduced the receiver computational complexity of the conventional OSM scheme, which was reduced by more than 90% compared with OSM and OGSM. The reason for this is that EFOGSM offered orthogonal signals that minimized the complexity of the ML decoder by transmitting two distinct signal constellations. Therefore, the computational complexity of the receiver was significantly lower than that of other OSM schemes. Although GSTBC-EFOGSM was less complex than EFOGSM, it was 34% less complex than OSM and 67% less complex than OGSM. Moreover, GSTBC-EFOGSM had the performance advantage of diversity gain compared to EFOGSM, which also compensated for its slightly higher complexity. Therefore, by comparing these schemes, it is clear that GSTBC-EFOGSM has lower receiver computational complexity.

7. Conclusions

The present study proposes a GSTBC-EFOGSM system that operates over atmospheric joint attenuation channels with M distribution. The average bit error rate performance of the system was evaluated while considering the combined impact of path loss, pointing errors and irradiance.

Table 4. Parameter variable.

System Parameters	Symbol	System Parameters	Symbol	System Parameters	Symbol	System Parameters	Symbol
the primary signal constellations	$P_M$	the secondary signal constellations	$S_{\raisebox{1ex}{$M$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$	the transmitted signal	$S$	Light wavelength	$\lambda$
EFOGSM signal	$x_{\mathrm{k}}$	Coding ratio	R	modulation order	M	Link distance	d
the complement of a signal	${\overline{x}}_{\mathrm{k}}$	the data transmission rate	Rp	the average signal to noise ratio	$\rho$	Optical beam width	$w_z$
The number of activated lasers	$N_{\mathrm{u}}$	the number of lasers	$N_t$	the detection efficiency of the photodetector	$\omega$	the attenuation efficiency	$\sigma$
the transmit power	$P_{\mathrm{t}}$	The classical scattering component’s average power	$\xi$	the additive white Gaussian noise	$n$	Path loss	$h_l$
the modified Bessel function of order v	$K_v\left(\cdot \right)$	the standard deviation of the pointing error displacement at the receiver	${\delta }_s$	Pointing error	$h_p$	a positive parameter related to effective large-scale cells in the scattering process	$\alpha$
the channel gain	$H$	the received optical power	$A_0$	slot time	T	a natural number representing the number of fading parameters	$\beta$
the Hamming distance	$d_H\left(x_i,x_j\right)$	Deterministic line-of-sight component	${\mathsf{\varphi }}_{\mathrm{A}}$	Component of scattering	${\mathsf{\varphi }}_{\mathrm{B}}$	the equivalent beam width	$w_{zeq}$
the average optical power of the LOS term	$\Omega$	The average power of the total scatter components	$2b_0$	the radius in the transverse plane of the incident wave	r	represents the amount of scattered power coupled with the LOS	$\eta$

shows the parameter variables in the full paper. An upper bound for the Meijer-G form of the ABER expression of the system was derived, and the theoretical results were subsequently validated via Monte Carlo simulations. Compared with OSM, OGSM and EFOGSM methods, GSTBC-EFOGSM showed great superiority in system performance. The simulation outcomes demonstrate that the GSTBC-EFOGSM scheme is successful in enhancing the ABER performance of the system and offering higher data transmission rates, energy efficiency and lower receiver computational complexity. In addition, the influence of key factors, such as data transmission rate, coding ratio and the number of photodetectors on the system, was also studied in the simulation. The simulation results show that the GSTBC-EFOGSM scheme with encoding ratio R = 0.75 can provide significant performance gains. In addition, the anti-jamming ability of the system will decrease with the increase in the data transmission rate. Therefore, the data transmission rate of the system cannot be blindly increased to lose the ABER of the system. Moreover, the system’s performance advantage can become more prominent by augmenting the number of photodetectors. In conclusion, GSTBC-EFOGSM is a promising technology, which provides a good measure for the implementation of free-space optical communication with large capacity, high rate and high diversity gain.