Local Field Enhancement Due to the Edge States of Nanoplasmonic Crystal
Abstract
1. Introduction
2. Structure Design
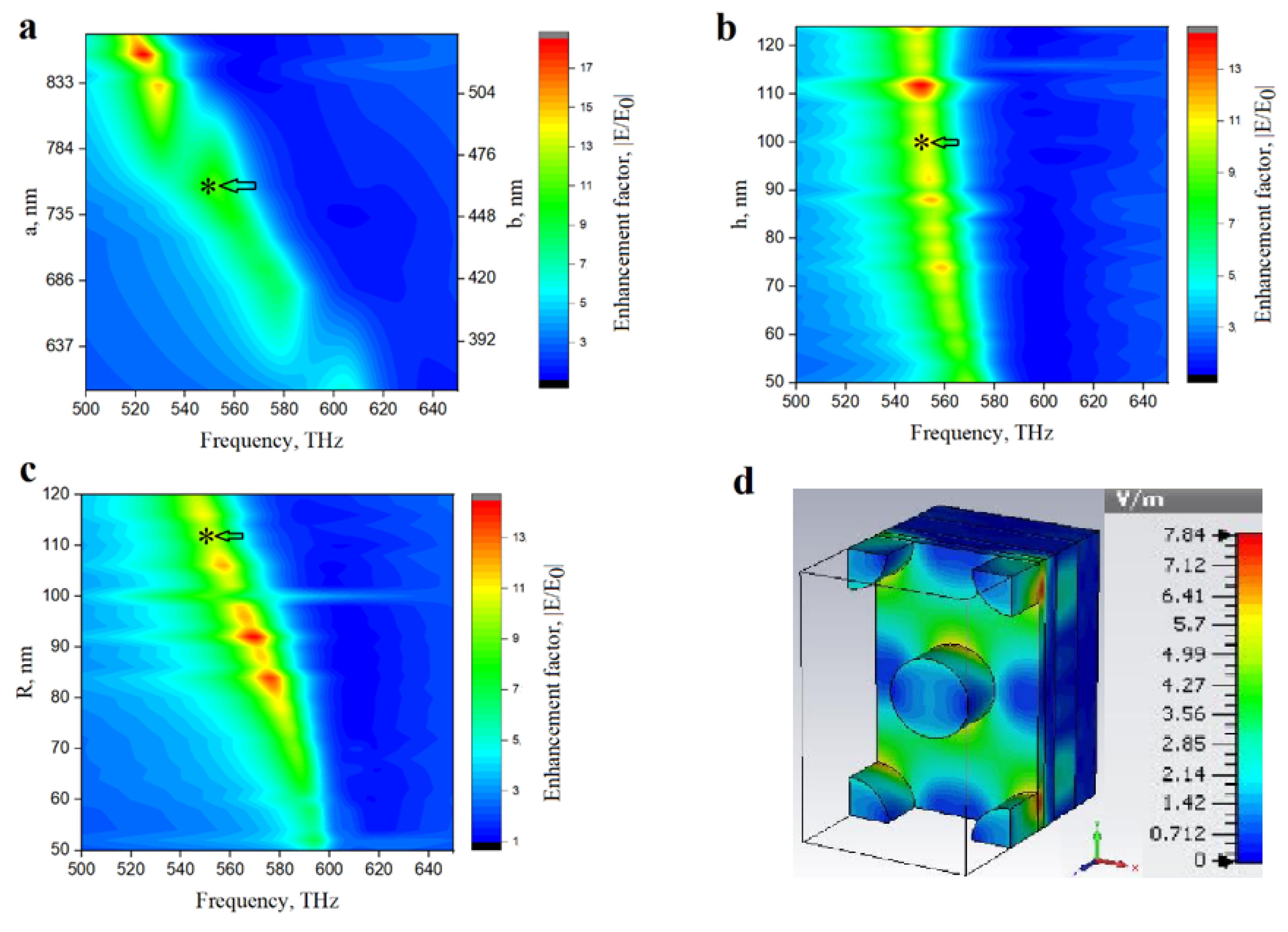
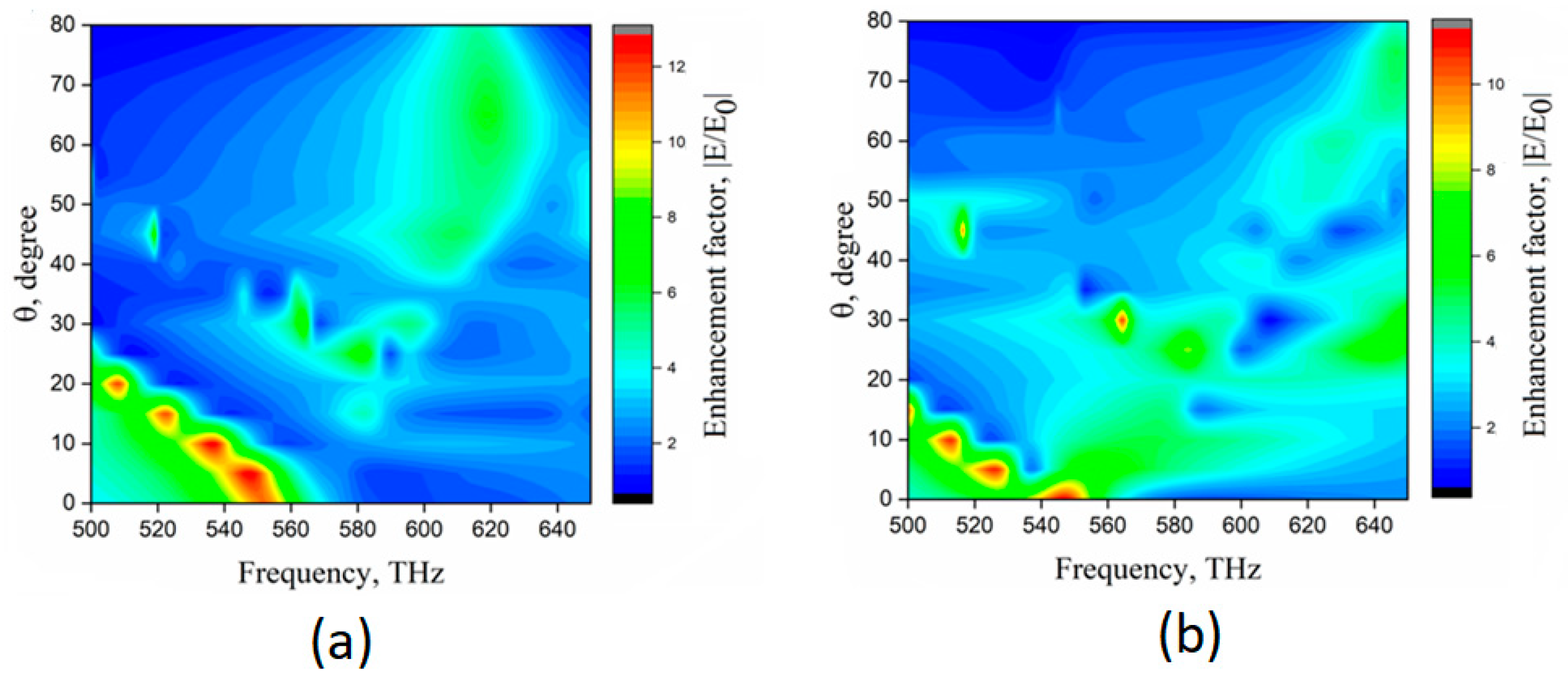
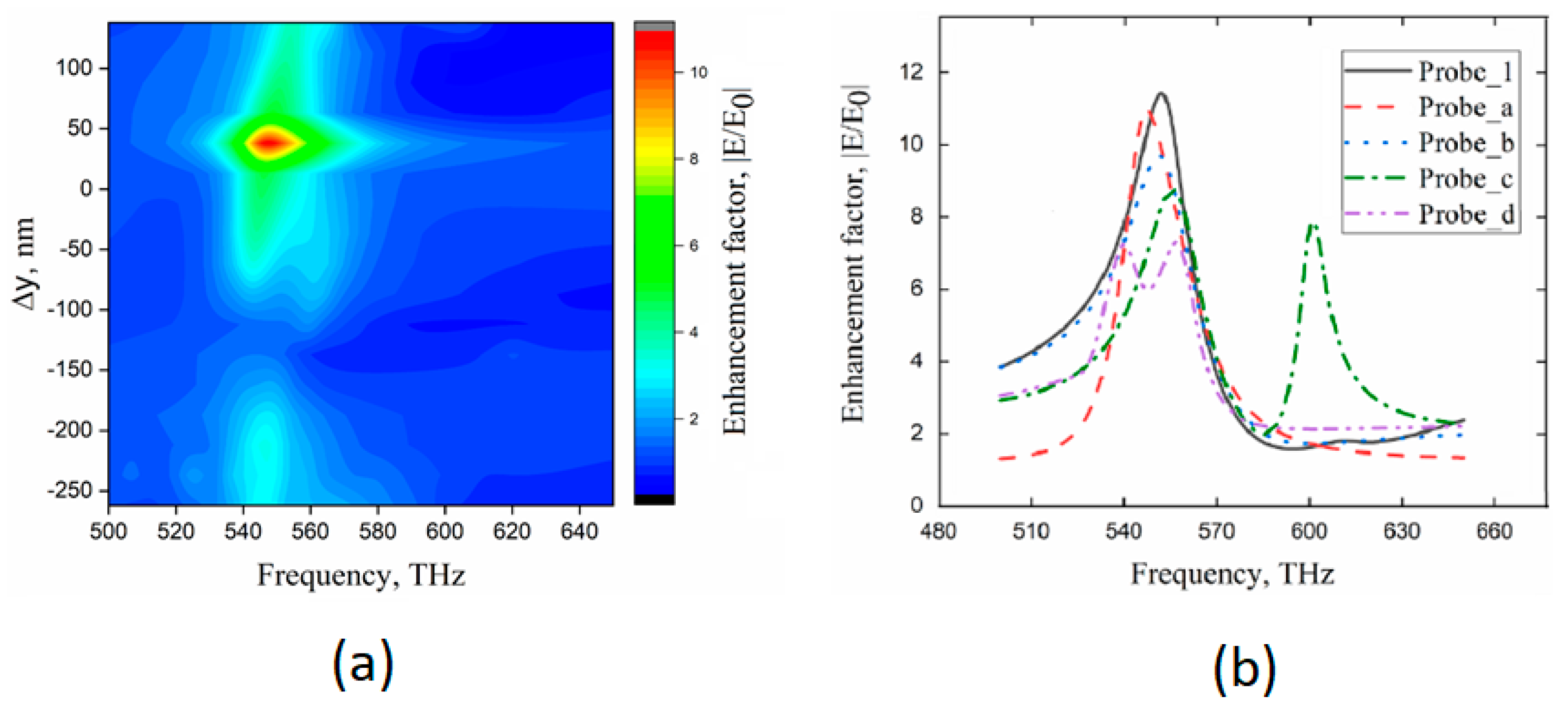
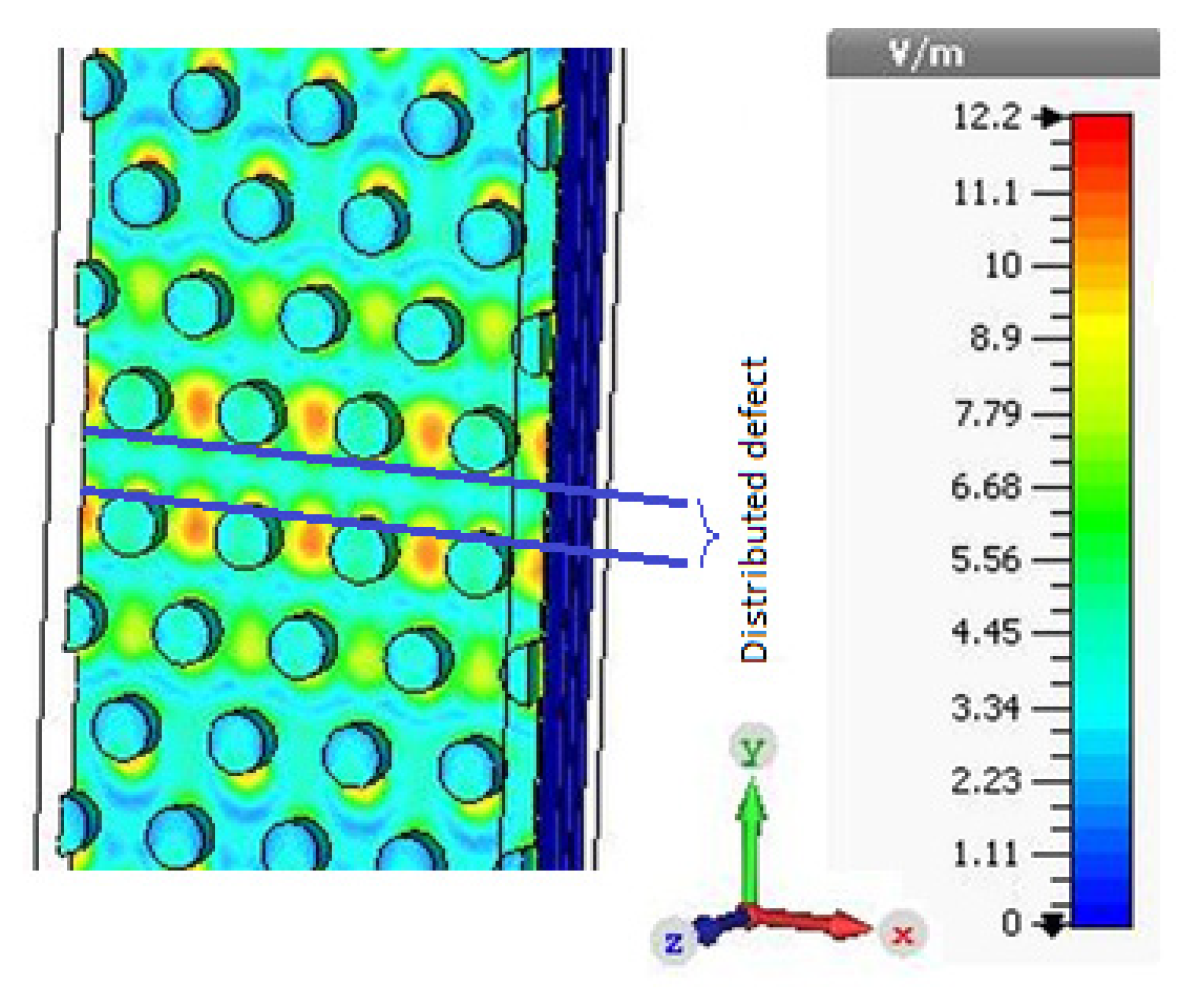
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sarychev, A.K.; Ivanov, A.; Lagarkov, A.; Barbillon, G. Light concentration by metal-dielectric micro resonators for SERS sensing. Materials 2019, 12, 103. [Google Scholar] [CrossRef] [PubMed]
- Kukushkin, V.; Grishina, Y.V.; Egorov, S.V.; Solov’Ev, V.V.; Kukushkin, I.V. Combined dielectric and plasmon resonance for giant enhancement of Raman scattering. JETP Lett. 2016, 103, 508512. [Google Scholar] [CrossRef]
- Lagarkov, A.; Budashov, I.; Chistyaev, V.; Ezhov, A.; Fedyanin, A.; Ivanov, A.; Kurochkin, I.; Kosolobov, S.; Latyshev, A.; Nasimov, D.; et al. SERS-active dielectric metamaterials based on periodic nanostructures. Opt. Express 2016, 24, 7133–7150. [Google Scholar] [CrossRef] [PubMed]
- Le Ru, E.C.; Blackie, E.; Meyer, M.; Etchegoin, P.G. Surface enhanced Raman scattering enhancement factors: A comprehensive study. J. Phys. Chem. C 2007, 111, 13794. [Google Scholar] [CrossRef]
- Fedotova, Y.; Kukushkin, V.; Solovyev, V.V.; Kukushkin, I.V. Spoof plasmons enable giant Raman scattering enhancement in near-infrared region. Opt. Express 2019, 27, 32578–32586. [Google Scholar] [CrossRef] [PubMed]
- Kukushkin, V.I.; Vankov, A.B.; Kukushkin, I.V. Long-range manifestation of surface-enhanced Raman scattering. JETP Lett. 2013, 98, 64–69. [Google Scholar] [CrossRef]
- Jin, B.; Argyropoulos, C. Enhanced four-wave mixing with nonlinear plasmonic metasurfaces. Sci. Rep. 2016, 6, 28746. [Google Scholar] [CrossRef]
- Smirnova, D.; Leykam, D.; Chong, Y.; Kivshar, Y. Nonlinear topological photonics. Appl. Phys. Rev. 2020, 7, 021306. [Google Scholar] [CrossRef]
- Fedotova, A.; Younesi, M.; Sautter, J.; Vaskin, A.; Lochner, F.J.F.; Steinert, M.; Geiss, R.; Pertsch, T.; Staude, I.; Setzpfandt, F. Second-harmonic generation in resonant nonlinear metasurfaces based on lithium niobate. Nano Lett. 2020, 20, 8608–8614. [Google Scholar] [CrossRef]
- Smirnova, D.; Kruk, S.; Leykam, D.; Melik-Gaykazyan, E.; Choi, D.-Y.; Kivshar, Y. Third-harmonic generation in photonic topological metasurfaces. Phys. Rev. Lett. 2019, 123, 103901. [Google Scholar] [CrossRef]
- Yuan, Q.; Gu, L.; Fang, L.; Gan, X.; Chen, Z.; Zhao, J. Giant enhancement of nonlinear harmonic generation in a silicon topological photonic crystal nanocavity chain. Laser Photonics Rev. 2022, 16, 2100269. [Google Scholar] [CrossRef]
- Butet, J.; Brevet, P.-F.; Martin, O.J.F. Optical second harmonic generation in plasmonic nanostructures: From fundamental principles to advanced applications. ACS Nano 2015, 9, 10545–10562. [Google Scholar] [CrossRef]
- Bandres, M.A.; Wittek, S.; Harari, G.; Parto, M.; Ren, J.; Segev, M.; Christodoulides, D.N.; Khajavikhan, M. Topological insulator laser: Experiments. Science 2018, 359, eaar4005. [Google Scholar] [CrossRef]
- You, J.W.; Lan, Z.; Panoiu, N.C. Four-wave mixing of topological edge plasmons in graphene metasurfaces. Sci. Adv. 2020, 6, eaaz3910. [Google Scholar] [CrossRef]
- Barik, S.; Karasahin, A.; Flower, C.; Cai, T.; Miyake, H.; DeGottardi, W.; Hafezi, M.; Waks, E. A topological quantum optics interface. Science 2018, 359, 666–668. [Google Scholar] [CrossRef]
- Barik, S.; Miyake, H.; DeGottardi, W.; Waks, E.; Hafezi, M. Two-dimensionally confined topological edge states in photonic crystals. New J. Phys. 2016, 18, 113013. [Google Scholar] [CrossRef]
- He, X.-T.; Liang, E.-T.; Yuan, J.-J.; Qiu, H.-Y.; Chen, X.-D.; Zhao, F.-L.; Dong, J.-W. A silicon-on-insulator slab for topological valley transport. Nat. Commun. 2019, 10, 872. [Google Scholar] [CrossRef]
- Yang, Y.; Jiang, H.; Hang, Z.H. Topological valley transport in two-dimensional honeycomb photonic crystals. Sci. Rep. 2018, 8, 1588. [Google Scholar] [CrossRef]
- Barik, S.; Karasahin, A.; Mittal, S.; Waks, E.; Hafezi, M. Chiral quantum optics using a topological resonator. Phys. Rev. B 2020, 101, 205303. [Google Scholar] [CrossRef]
- Ota, Y.; Liu, F.; Katsumi, R.; Watanabe, K.; Wakabayashi, K.; Arakawa, Y.; Iwamoto, S. Photonic crystal nanocavity based on a topological corner state. Optica 2019, 6, 786–789. [Google Scholar] [CrossRef]
- El Hassan, A.; Kunst, F.K.; Moritz, A.; Andler, G.; Bergholtz, E.J.; Bourennane, M. Corner states of light in photonic waveguides. Nat. Photonics 2019, 13, 697–700. [Google Scholar] [CrossRef]
- Palik, E.D. Handbook of Optical Constants of Solids, 3rd ed.; Academic Press: Cambridge, MA, USA, 1998. [Google Scholar]
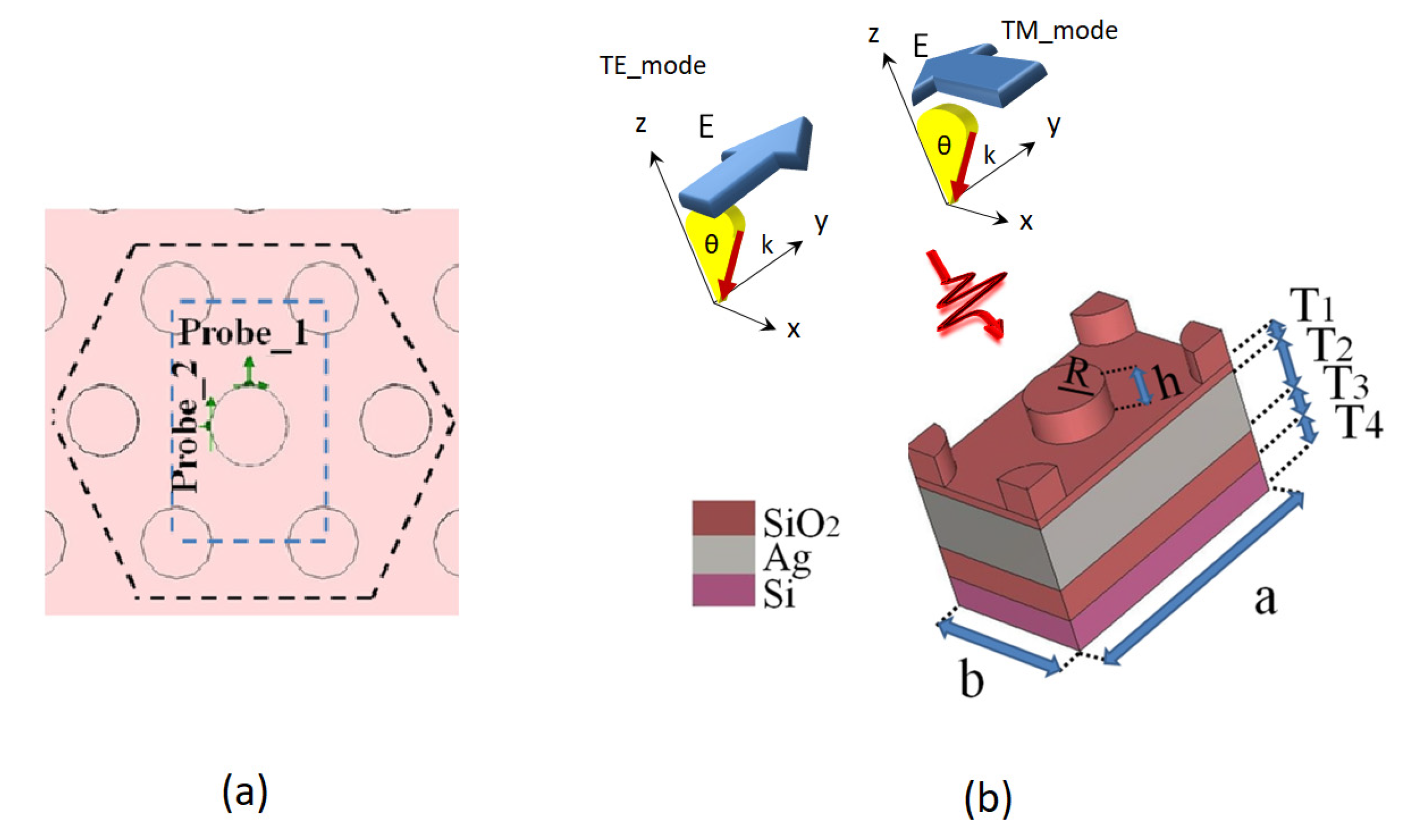
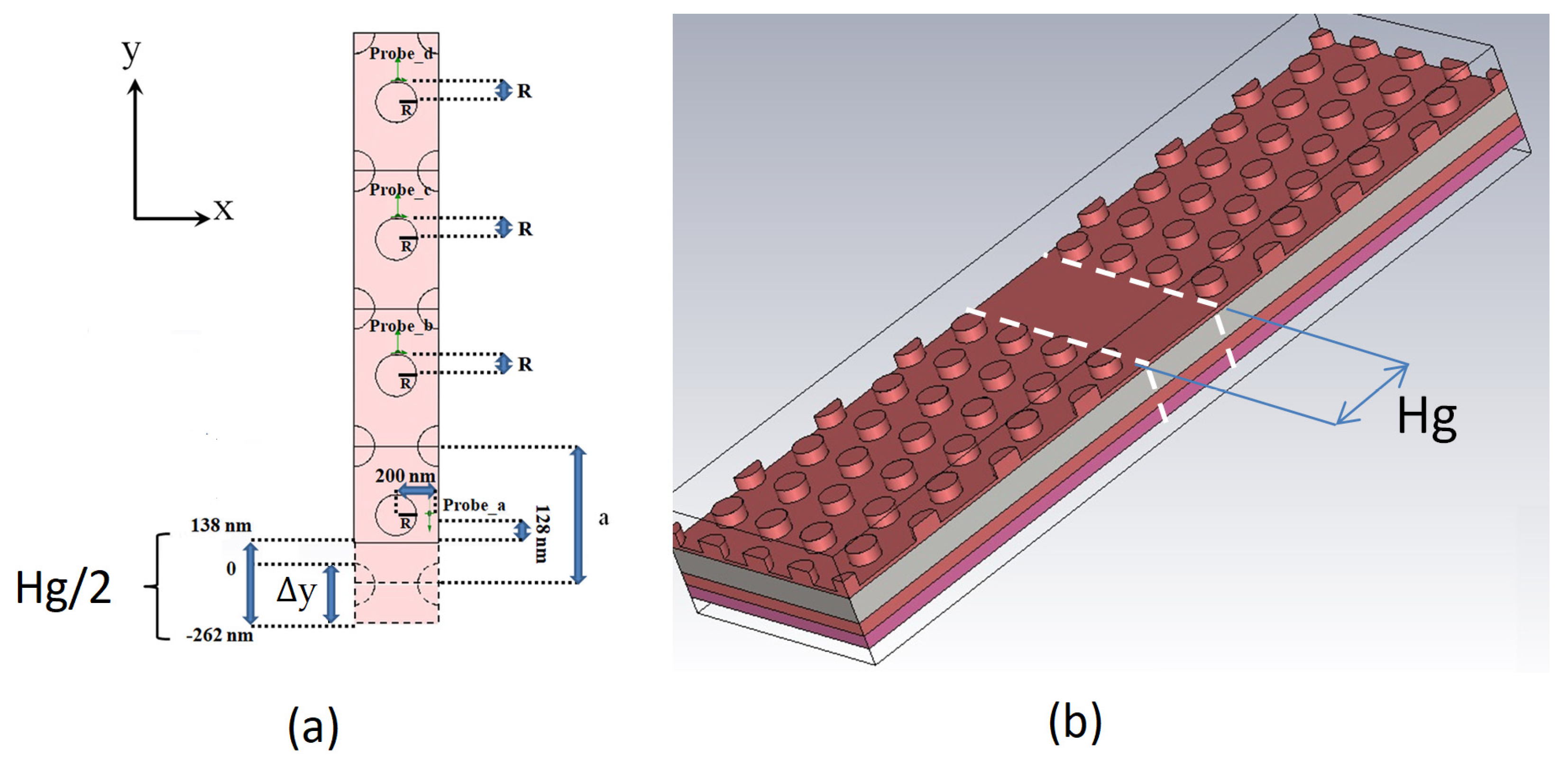
| Parameter | Symbol | Value (nm) |
|---|---|---|
| Cylindrical dielectric radius | 112 | |
| Cylindrical dielectric height | ||
| The top SiO2 thickness | ||
| Ag thickness | ||
| SiO2 thickness perching on Si | ||
| Si thickness | ||
| Length of the unit cell | 756 | |
| Width of the unit cell | b | 462 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beiranvand, B.; Khabibullin, R.A.; Sobolev, A.S. Local Field Enhancement Due to the Edge States of Nanoplasmonic Crystal. Photonics 2023, 10, 263. https://doi.org/10.3390/photonics10030263
Beiranvand B, Khabibullin RA, Sobolev AS. Local Field Enhancement Due to the Edge States of Nanoplasmonic Crystal. Photonics. 2023; 10(3):263. https://doi.org/10.3390/photonics10030263
Chicago/Turabian StyleBeiranvand, Behrokh, Rustam A. Khabibullin, and Alexander S. Sobolev. 2023. "Local Field Enhancement Due to the Edge States of Nanoplasmonic Crystal" Photonics 10, no. 3: 263. https://doi.org/10.3390/photonics10030263
APA StyleBeiranvand, B., Khabibullin, R. A., & Sobolev, A. S. (2023). Local Field Enhancement Due to the Edge States of Nanoplasmonic Crystal. Photonics, 10(3), 263. https://doi.org/10.3390/photonics10030263





