Abstract
We study the tight focus of generalized (hybrid) Poincaré beams. A conventional Poincaré beam is a coaxial superposition of two optical vortices, one with left circular polarization and a topological charge (TC) of m, while the other has a right circular polarization and a TC of −m. The generalized Poincaré beams are also composed of two optical vortices, but their TCs are different, for instance, p and q. Here, we theoretically investigate the generalized Poincaré beams with the TCs p = m + 1 and q = −m in tight focus. In this case, both transverse components of the strength vector of the initial electric field have a topological charge of 1/2, and the beam itself is a cylindrical vector beam of fractional order m + 1/2. Analytical expressions are derived for the components of the strength vectors of the electric and magnetic field at the focus as well as for the intensity distribution, the longitudinal component of the spin angular momentum (SAM), and for the components of the Poynting vector (energy flow density). We show that the intensity at the focus has 2m − 1 local maxima residing evenly in a certain circle radius with the center on the optical axis. We also demonstrate that the radial spin and orbital Hall effects occur at the focus, i.e., the longitudinal SAM component has different signs in the circles of different radii, and the azimuthal component of the transverse Poynting vector also has different signs.
1. Introduction
Poincaré beams, whose polarization state is related to the polarization Poincaré sphere [1,2,3], are actively studied in optics, starting with works [3,4,5,6]. In a general case, a Poincaré beam is a superposition of two optical vortices with different topological charges (TC) p and q and with orthogonal polarizations. For the optical vortices, the conventional Laguerre–Gaussian beams of different indices [7,8,9] can be chosen, or diffraction-free Bessel beams, or the Bessel–Gaussian beams generated by axicons [10,11,12]. The Poincaré beams can be generated similarly to all the other vector beams, by using liquid-crystal light modulators, half-wave and quarter-wave plates [13,14,15], or by using lasers and q-plates [16], and metasurfaces [12]. In Ref. [17], the polarization singularity index (Poincaré–Hopf index) of the Poincaré beams was studied. In Ref. [18], the optical Hall effect was theoretically discovered in the tight focus of the Poincaré beams. The optical (or photonic) Hall effect is divided into spin [19,20] and orbital [21,22]. Usually, the Hall effect in optics is observed when a light field is reflected from an interface between media [21,22], or when it passes through multilayered media [23], crystals [24,25], or through a metasurface [26]. There are known works investigating the Hall effect in the tight focus of a laser radiance [27,28] or the vicinity of the focal plane [29]. We note that the abovementioned works do not contain theoretically obtained key characteristics of the generalized Poincaré beams in tight focus using the Richards–Wolf formalism [30]: amplitudes of the electric and magnetic vectors, intensity distribution, distributions of components of the Poynting vector, and the spin angular momentum (SAM) vector.
In this work, adopting the Richards–Wolf approach, we obtain analytical expressions, describing key characteristics of the generalized Poincaré beams in a case when the topological charges (TC) of the two optical vortices with left and right circular polarization are equal with respect to p = m + 1 and q = −m. We demonstrate that at the focus of such beams, radial spin and orbital Hall effects take place. We note that in [31], we demonstrated the spin Hall effect for fractional-order cylindrical vector beams at the focus plane. In the current work, at p = m + 1 and q = −m, there is also a cylindrical vector beam with a fractional order of m + 1/2. Therefore, we can expect that there is also the spin Hall effect at the focus of such a generalized Poincaré beam. The work of [31] does not contain analytical expressions for electric field components at the focus of fractional-order cylindrical vector beams. In the current work, we derive such analytical expressions.
In our previous work [32], we have shown that the orbital Hall effect occurs before and after the focus of the conventional vectorial cylindrical beams, which are a special case of Poincaré beams when the optical vortices have the TCs m and −m, and that local areas in the beam cross section, where the transverse energy flow is rotating clockwise or counterclockwise, reside in pairs on a certain circle radius with the center on the optical axis. In this work, energy flows, rotating clockwise or counterclockwise, reside on circles with different radii. Therefore, this orbital Hall effect is called radial.
We note that the Richards–Wolf formalism [30] adequately describes the light field only near the focus. The work of [33] investigates the behavior of light at the focus by using an exact solution of the Helmholtz equation in the spherical coordinates, which is correct in the whole space. However, generating such a light field at the focus requires generating in the initial plane all three components of the electric vector. This is a challenging problem. In our case, only the transverse components of the electric field should be generated in the initial plane, which is easy to implement in practice.
2. Vector Field in the Initial Plane
We consider here the following Jones vector of the initial light field:
with (r, φ) being the polar coordinates in the initial plane, and a, and b being complex constants. If p = −n and q = n, the beam from Equation (1) reduces to a conventional Poincaré beam [4,5,6]. If , then the field (1) becomes maximally inseparable [18]:
When p = q, the field (1) reduces to a linearly polarized optical vortex with the topological charge (TC) q. When p = −q, the field (1) is a cylindrical vector beam of the order q [34]. When p = −m and q = m + 1, the field (2) is given by
The field (3) is interesting because it is a cylindrical vector beam of a half-integer order. In Ref. [35], the beam (3) is not quite correctly called a vector vortex beam with a fractional topological charge. As was already shown in [31], in the tight focus of the fractional-order cylindrical vector beams, subwavelength areas are generated with elliptic polarization of different handedness, that is, the polarization vector in these areas is rotating clockwise or counterclockwise. We note that the initial light field (3) is linearly polarized at each point of its cross section. Therefore, similarly to [31], it should be expected that the focused field (3) should also contain the areas with elliptic polarization of different handedness. It is also seen from Equation (3) that the initial field is a coaxial superposition of two optical vortices with left and right circular polarization and with different topological charges of m + 1 and –m. Since these topological charges do not compensate for each other, it is reasonable to expect circular energy flow at the focus. This means that at the focus, a nonzero distribution of the axial component of the angular momentum vector should be present. Below, we show that this is indeed so.
3. Components of the Strength Vector of the Electric Field at the Focus
The Richards–Wolf formalism [30] allows access to all components of the strength vector of the electric field at the tight focus of the initial field (3):
where
where k = 2π/λ is the wavenumber of light with the wavelength λ, f is the focal length of an aplanatic system (ideal spherical lens), ν = 0, 1, and 2, Jμ(ξ) is the μth-order Bessel function of the first kind, ξ = krsinθ, θ is the polar angle that defines the tilt of the optical axis of rays converging into the focus, θ0 is the maximal angle that defines the numerical aperture of the aplanatic system (NA = sinθ0), (r, φ, z) is the cylindrical coordinate system with the origin at the focus (z = 0 is the focus plane), and A(θ) is the amplitude of the initial circularly symmetric field (real-valued function).
4. Intensity Distribution of the Electric Field at the Focus
From the components of the electric vector (4), we can derive the intensity distribution of the light field at the focus plane (z = 0):
where the first two terms in the round brackets describe the transverse intensity , whereas the third term in the round brackets describes the longitudinal intensity Iz. As seen from Equation (6), the intensity is a nonnegative function (I ≥ 0) since each term in the round brackets in Equation (6) is nonnegative, for the sum of two squared numbers is equal to or greater than their doubled product. Equation (6) also follows that the intensity distribution contains 2m − 1 local maxima and 2m − 1 local minima (or intensity nulls) that reside on a certain circle radius with the center on the optical axis. Thus, the number of these intensity maxima and nulls is always odd (2m − 1).
5. Longitudinal Component of the Spin Angular Momentum Vector at the Focus
Using the components of the electric field vector at the focus (4), we can derive the longitudinal component of the spin angular momentum (SAM) vector of the field (3), since the longitudinal SAM component Sz is equal to the third Stokes parameters S3, whose magnitude indicates the presence of elliptic or circular polarization in the beam cross section. The SAM vector is defined by the following expression [28]:
with ω being the angular frequency of light. Below, we omit the constant factor 1/(16πω) for brevity. It can be seen from Equation (7) that the longitudinal SAM component (without the constant) coincides with the nonnormalized third component of the Stokes vector:
Substitution of expressions (4) for the electric field components into Equation (8) yields
A comparison of Equations (6) and (9) reveals that if the transverse intensity is a sum of two positive terms A and B, then
and the longitudinal SAM component is a difference between these terms:
According to Equation (9), similarly to the intensity distribution in Equation (6), the SAM distribution also has 2m − 1 local maxima and 2m − 1 local minima. As seen from Equation (11), if B > A, then Sz > 0 (polarization vector is rotating counterclockwise), and vice versa, if B < A, then Sz < 0 (polarization vector is rotating clockwise). In the areas where B = A (Sz = 0), the polarization is linear. The points in the beam cross section at the focus, where Sz = 0, are called [36] topological spin defects. Thus, it follows from Equations (9) and (11) that there are areas with different spins at the focus: positive (Sz > 0) and negative (Sz < 0). The spatial separation of areas with left circular and right circular polarization is called the spin Hall effect [27,28,29]. In the Simulation section below, these conclusions are confirmed by concrete examples.
6. Energy Flow Density at the Focus
Here we derive the Poynting vector (energy flow density) at the focus of the field (3). To do this, we should first obtain the components of the strength vector of the magnetic field at the focus. In the same way, as we obtained the components of the electric vector (4) by using the Richards–Wolf theory [30], we can also obtain the magnetic vector:
The Poynting vector is defined by the well-known formula [30]:
where c is the vacuum speed of light, Re is the real part of a complex number, E × H is the cross product, and * is the complex conjugation. Below, we omit the constant c/(8π) for brevity. Substituting components (4) and (12) into Equation (13), we obtain the components of the Poynting vector at the focus of the field (3):
Passing to the polar components Pr and Pφ of the transverse Poynting vector, we obtain:
As seen from Equation (14), the longitudinal component of the Poynting vector at the focus has a circularly symmetric distribution and does not depend on the azimuthal angle φ. It is also seen from Equation (14) that if m = 1 or m = 2 then there is a reverse energy flow on the optical axis since for m = 1 or m = 2, we obtain the following on the optical axis:
Equation (15) indicates that the transverse energy flow at the focus is rotating along a closed trajectory with the center on the optical axis, clockwise if Q(r) > 0, and counterclockwise if Q(r) < 0. Since the function Q(r) is of different signs on different radii r, it can be stated that the radial orbital Hall effect occurs at the focus of the light field (3). This also follows on from the expression for the longitudinal component of the angular momentum vector J of field (3) when it is written by definition using the azimuthal component of the energy flow [28]:
The energy flow at the focus is rotating along a spiral around the optical axis since the topological charges of the two optical vortices, which are present in the superposition in the initial field (3), do not compensate for each other as they have different magnitudes: m + 1 and −m.
7. Simulation
Using the Richards–Wolf formalism [30], we computed the distributions of intensity and the longitudinal component of the SAM vector (spin density) at the tight focus of the light field using the initial distribution given by Equation (3). We supposed that the field amplitude in the initial plane was constant, i.e., A(θ) = 1, wavelength λ = 532 nm, focal length f = 10 μm, and the numerical aperture NA = 0.95. Figure 1 shows the distributions of the longitudinal component of the spin angular momentum Sz (Figure 1a–d) (red and blue colors denote positive and negative values), the intensity I (Figure 1e–h) (black and yellow colors denote zero and maximal values), and the angular component of the Poynting vector Pφ (Figure 1i–l) (red and blue colors denote positive and negative values) of a light beam with polarization (3) of different order m at the tight focus. The beam orders in Figure 1 are m = 1 (Figure 1a,e,i), m = 2 (Figure 1b,f,j), m = 3 (Figure 1c,g,k), and m = 5 (Figure 1d,h,l). The arrows in Figure 1i–l illustrate the directions of the angular energy flow. The scale mark in each figure denotes 1 μm.
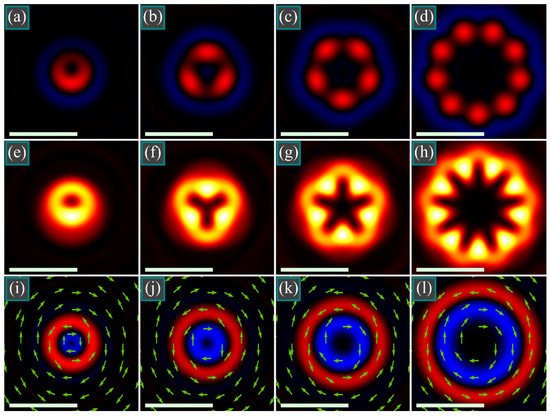
Figure 1.
Distributions of the longitudinal component of the spin angular momentum (a–d) (red and blue color denote, respectively, positive and negative values), intensity (e–h) (black means zero and yellow means maximum), and the angular component of the Poynting vector (i–l) (red means positive and blue means negative values) of a light beam with polarization (3) and with a different order at the tight focus. Arrows (i–l) denote the directions of the angular energy flow. The scale mark in each figure denotes 1 μm.
As seen in Figure 1 (2nd row), the number of local maxima in the intensity distribution at the focus is consistent with the theory [Equation (6)] and is equal to 2m − 1: 1 (Figure 1e), 3 (Figure 1f), 5 (Figure 1g), and 9 (Figure 1h). It is also seen in Figure 1 (1st row), that, according to Equation (9), the SAM distribution also contains 2m − 1 local maxima (red color in Figure 1a–d), where Sz > 0, which reside on a certain circle with the center on the optical axis. On a circle with a larger radius, (blue color in Figure 1a–d), Sz < 0. The black color in Figure 1a–d denotes the areas with zero spin, i.e., where polarization is linear. Since the brightness of the blue color in Figure 1a–d is 2–3 times lower than that of the red color, elliptic polarization in the areas of positive spin is closer to circular polarization, whereas the polarization ellipses in the areas of negative spin are more elongated and closer to linear polarization. Nevertheless, the spatial separation of the areas with positive and negative spin at the focus demonstrates the spin Hall effect.
Figure 1i–l (3rd row) confirms theoretical predictions [Equation (15)] and demonstrates that the transverse energy flow at the focus plane rotates. On a circle closer to the optical axis (blue color in Figure 1i–l), Pφ < 0, i.e., the transverse energy flow is rotating clockwise. On a larger circle radius (red ring in Figure 1i–l), Pφ > 0, and the energy flow is rotating counterclockwise. The spatial separation of the orbital energy flux in opposite directions is a manifestation of the radial orbital Hall effect at the focus.
8. Discussion of the Results
Here, we compare the transverse components of the electric field in the initial plane (3) and the focus plane (4). Although in the initial plane, the components Ex and Ey of the field (3) have the same phase, and thus the field has inhomogeneous linear polarization, at the focus, the transverse components of field (4) acquire a relative phase delay of π/2 or 3π/2. This leads to the areas with elliptic polarization at the focus. On the other hand, the longitudinal SAM component (7) in the initial plane is equal to zero Sz = 0, while the energy flow (13) has only one longitudinal component, which is equal to the unit: Pz = 1. At the focus plane, the SAM density is given by Equation (9), but if the function Sz is integrated over the whole focus plane, then it is equal to zero. Thus, the full longitudinal SAM component is conserved and equal to zero. The field (3) in the initial plane has a nonzero density of the longitudinal component of the orbital angular momentum (OAM) vector [37]:
If the OAM density (17) is integrated over the angle φ from 0 to 2π, then the full OAM in the initial plane is nonzero and equal to half of the initial beam power W/2.
At the focus plane, the longitudinal OAM component can also be obtained:
According to Equation (18), the OAM density depends on the angle as sin(2m − 1)φ. This means that on a certain circle radius with the center on the optical axis, the OAM has (2m − 1) local maxima and minima, similar to the SAM distribution (9). It can be shown that if the OAM density is integrated over the whole focus plane, then this also yields half of the initial beam power W/2. Thus, in this case, the full SAM and OAM are conserved separately. Therefore, it can be concluded that the spin Hall effect at the focus of the beam (3) arises due to the conservation of the full longitudinal SAM of the beam. Since the longitudinal SAM of the whole beam is zero, the areas with the spin of a different sign should arise in pairs. In the same way, the radial orbital Hall effect at the focus occurs due to the conservation of the full longitudinal OAM of the beam.
Summing the SAM (9) and OAM (18) densities, we obtain:
The comparison of the density of the longitudinal component of the angular momentum (AM) vector in Equation (16) with the sum of the longitudinal SAM and OAM components in Equation (19) reveals that they are not equal to each other: Jz ≠ Lz + Sz. We considered the reason for this inequality earlier in [37].
In concluding this section, we consider the difference between the Hall effect near the tight focus [18,31,32,37] and the Hall effect which occurs when light is reflected off the interface between two media [22,38]. As was shown in [22], when an optical vortex is reflected from a plane glass surface, the annular intensity distribution becomes inhomogeneous. For the optical vortices with the topological charges m and −m, the intensity maxima on the ring appear in different places, i.e., shifted relative to each other (orbital Hall effect). In Ref. [38], it was shown that when a p-polarized Gaussian beam (polarization vector is in the incidence plane) is reflected from the glass surface under an angle close to the Brewster angle, the spin Hall effect occurs when the reflected light is split into two beams with opposite spins in the direction orthogonal to the incidence plane. In the tight focus [18,31,32,37], spin and orbital Hall effects occur due to the conservation of the full angular momentum. The light with opposite spins and/or with opposite energy rotation at the focus plane is concentrated in different places. A different manifestation of the Hall effect at the focus, as investigated in the different works [18,31,32,37], is explainable since the different types of the initial vector fields were considered. In Ref. [18], the focusing of the conventional Poincaré beams was considered, while [31] dealt with the focusing of fractional-order cylindrical vector beams. In Ref. [32], the Hall effect of the cylindrical vector beams of an integer order arises before and beyond the focus, whereas it is absent at the focus itself. In Ref. [37], the Hall effect was studied at the focus of a circularly polarized optical vortex. In contrast to these works, we here studied the tight focusing of a generalized Poincaré beam, whose topological charge is equal to 1/2 and whose order of inhomogeneous linear polarization is equal to m + 1/2. It is impossible to predict in advance, based on the initial light field, whether or not the Hall effect will arise at the tight focus. Thus, each new type of initial vector beam should be considered separately.
9. Conclusions
Based on the Debye integrals [30], we have investigated both theoretically and numerically generalized (hybrid) Poincaré beams at a tight focus. A generalized Poincaré beam is a coaxial superposition of two optical vortices with left and right circular polarization and with the TC of p and q. For certainty, we studied the case when p = m + 1 and q = −m [Equation (3)]. Simple analytical expressions have been obtained for the components of the electric and magnetic strength vectors at the focus [Equations (4) and (12)], for the intensity distribution [Equation (6)], for the longitudinal component of the spin angular momentum [Equation (9)], and for the components of the Poynting vector [Equation (14)]. It has been shown that the intensity at the focus has 2m − 1 local maxima, residing evenly on a certain circle radius with the center on the optical axis. In addition, radial spin and orbital Hall effects have been demonstrated. This means that the longitudinal SAM component has different signs on circles with different radii in the focal plane, and the azimuthal component of the transverse Poynting vector also has different signs (Figure 1). Such beams can be used for the simultaneous trapping of several micro- or nanoparticles (Figure 1h) into the local intensity maxima that should simultaneously rotate around their centers of mass (Figure 1d) and move along the ring (Figure 1l). In addition, when moving along the ring, the particles will need to overcome the ‘breaks’ in the intensity distribution (Figure 1h).
Author Contributions
Conceptualization, V.V.K.; methodology, V.V.K.; software, A.A.K. and A.M.T.; validation, V.V.K.; formal analysis, V.V.K.; investigation, V.V.K. and A.A.K.; resources, V.V.K.; data curation, V.V.K.; writing—original draft preparation, V.V.K.; writing—review and editing, V.V.K.; visualization, A.A.K. and A.M.T.; supervision, V.V.K.; project administration, V.V.K.; funding acquisition, V.V.K. and A.A.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research (theory) was funded by the Russian Science Foundation, grant number 22-12-00137.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We acknowledge the support of the Ministry of Science and Higher Education of the Russian Federation within a government project of the FSRC “Crystallography and Photonics” RAS (simulation).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Holleczek, A.; Aiello, A.; Gabriel, C.; Marquardt, C.; Leuchs, G. Classical and quantum properties of cylindrically polarized states of light. Opt. Express 2011, 19, 9714–9736. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Zhou, X.; Liu, Y.; Ling, X.; Luo, H.; Wen, S. Generation of arbitrary cylindrical vector beams on the higher order Poincaré sphere. Opt. Lett. 2014, 39, 5274–5276. [Google Scholar] [CrossRef] [PubMed]
- Yi, X.; Liu, Y.; Ling, X.; Zhou, X.; Ke, Y.; Luo, H.; Wen, S.; Fan, D. Hybrid-order Poincaré sphere. Phys. Rev. A 2015, 91, 023801. [Google Scholar] [CrossRef]
- Beckley, A.M.; Brown, T.G.; Alonso, M.A. Full Poincaré beams. Opt. Express 2010, 18, 10777–10785. [Google Scholar] [CrossRef]
- Milione, G.; Sztul, H.I.; Nolan, D.A.; Alfano, R.R. Higher-order Poincaré sphere, Stokes parameters, and the angular momentum of light. Phys. Rev. Lett. 2011, 107, 053601. [Google Scholar] [CrossRef]
- Milione, G.; Evans, S.; Nolan, D.A.; Alfano, R.R. Higher Order Pancharatnam-Berry Phase and the Angular Momentum of Light. Phys. Rev. Lett. 2012, 108, 190401. [Google Scholar] [CrossRef]
- Galvez, E.J.; Khadka, S. Poincare modes of light. Proc. SPIE 2012, 8274, 82740Y. [Google Scholar] [CrossRef]
- Galvez, E.J.; Khadka, S.; Schubert, W.H.; Nomoto, S. Poincare-beam patterns produced by nonseparable superpositions of Laguerre-Gauss and polarization modes of light. Appl. Opt. 2012, 51, 2925. [Google Scholar] [CrossRef]
- Lopez-Mago, D. On the overall polarisation properties of Poincaré beams. J. Opt. 2019, 21, 115605. [Google Scholar] [CrossRef]
- Boucher, P.; Del Hoyo, J.; Billet, C.; Pinel, O.; Labroille, G.; Courvoisier, F. Generation of high conical angle Bessel–Gauss beams with reflective axicons. Appl. Opt. 2018, 57, 6725–6728. [Google Scholar] [CrossRef]
- Li, D.; Feng, S.; Nie, S.; Chang, C.; Ma, J.; Yuan, C. Generation of arbitrary perfect Poincaré beams. J. Appl. Phys. 2019, 125, 073105. [Google Scholar] [CrossRef]
- Liu, M.; Huo, P.; Zhu, W.; Zhang, C.; Zhang, S.; Song, M.; Zhang, S.; Zhou, Q.; Chen, L.; Lezec, H.J.; et al. Broadband generation of perfect Poincaré beams via dielectric spin-multiplexed metasurface. Nat. Commun. 2021, 12, 2230. [Google Scholar] [CrossRef]
- Gu, Z.; Yin, D.; Gu, F.; Zhang, Y.; Nie, S.; Feng, S.; Ma, J.; Yuan, C. Generation of concentric perfect Poincaré beams. Sci. Rep. 2019, 9, 15301. [Google Scholar] [CrossRef]
- Alpmann, C.; Schlickriede, C.; Otte, E.; Denz, C. Dynamic modulation of Poincaré beams. Sci. Rep. 2017, 7, 8076. [Google Scholar] [CrossRef]
- Fu, S.; Gao, C.; Wang, T.; Zhai, Y.; Yin, C. Anisotropic polarization modulation for the production of arbitrary Poincaré beams. J. Opt. Soc. Am. B 2018, 35, 1–7. [Google Scholar] [CrossRef]
- Naidoo, D.; Roux, F.S.; Dudley, A.; Litvin, I.; Piccirillo, B.; Marrucci, L.; Forbes, A. Controlled generation of higher-order Poincaré sphere beams from a laser. Nat. Photonics 2016, 10, 327–332. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Kovalev, A.A.; Stafeev, S.S.; Zaitsev, V.D. Index of the Polarization Singularity of Poincare Beams. Bull. Russ. Acad. Sci. Phys. 2022, 86, 1158–1163. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Stafeev, S.S.; Zaitsev, V.D.; Telegin, A.M. Poincaré Beams at the Tight Focus: Inseparability, Radial Spin Hall Effect, and Reverse Energy Flow. Photonics 2022, 9, 969. [Google Scholar] [CrossRef]
- Ling, X.; Yi, X.; Zhou, X.; Liu, Y.; Shu, W.; Luo, H.; Wen, S. Realization of tunable spin-dependent splitting in intrinsic photonic spin Hall effect. Appl. Phys. Lett. 2014, 105, 151101. [Google Scholar] [CrossRef]
- Yin, X.; Ye, Z.; Rho, J.; Wang, Y.; Zhang, X. Photonic spin Hall effect at metasurfaces. Science 2013, 339, 1405–1407. [Google Scholar] [CrossRef]
- Kumar, R.N.; Gupta, S.D.; Ghosh, N.; Banerjee, A. Probing the rotational spin-Hall effect in a structured Gaussian beam. Phys. Rev. A 2022, 105, 023503. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, X.X.; Ling, X.H.; Chen, S.Z.; Luo, H.L.; Wen, S.C. Orbit-orbit interaction and photonic orbital Hall effect in reflection of a light beam. Chin. Phys. B 2014, 23, 064215. [Google Scholar] [CrossRef]
- Kavokin, A.; Malpuech, G.; Glazov, M. Optical spin Hall effect. Phys. Rev. Lett. 2005, 95, 136601. [Google Scholar] [CrossRef] [PubMed]
- Fadeyeva, T.A.; Rubass, A.F.; Volyar, A.V. Transverse shift of a high-order paraxial vortex-beam induced by a homogeneous anisotropic medium. Phys. Rev. A 2009, 79, 053815. [Google Scholar] [CrossRef]
- Fu, S.; Guo, C.; Liu, G.; Li, Y.; Yin, H.; Li, Z.; Chen, Z. Spin-orbit optical Hall effect. Phys. Rev. Lett. 2019, 123, 243904. [Google Scholar] [CrossRef]
- Zhang, F.; Guo, Y.H.; Pu, M.B.; Li, X.; Ma, X.L.; Luo, X.G. Metasurfaces enabled by asymmetric photonic spin-orbit interactions. Opto-Electr. Eng. 2020, 47, 200366. [Google Scholar] [CrossRef]
- Shu, W.; Lin, C.; Wu, J.; Chen, S.; Ling, X.; Zhou, X.; Luo, H.; Wen, S. Three-dimensional spin Hall effect of light in tight focusing. Phys. Rev. A 2020, 101, 023819. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Ostrovskaya, E.A.; Alonso, M.A.; Rodríguez-Herrera, O.G.; Lara, D.; Dainty, C. Spin-to-orbital angular momentum conversion in focusing, scattering, and imaging systems. Opt. Express 2011, 19, 26132–26149. [Google Scholar] [CrossRef]
- Man, Z.; Xi, Z.; Yuan, X.; Burge, R.E.; Urbach, H.P. Dual coaxial longitudinal polarization vortex structures. Phys. Rev. Lett. 2020, 124, 103901. [Google Scholar] [CrossRef]
- Richards, B.; Wolf, E. Electromagnetic diffraction in optical systems, II. Structure of the image field in an aplanatic system. Proc. R. Soc. Lond. A 1959, 253, 358–379. [Google Scholar] [CrossRef]
- Stafeev, S.S.; Nalimov, A.G.; Zaitsev, V.D.; Kotlyar, V.V. Tight focusing cylindrical vector beams with fractional order. J. Opt. Soc. Am. B 2021, 38, 1090–1096. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Stafeev, S.S.; Kovalev, A.A.; Zaitsev, V.D. Spin Hall Effect before and after the Focus of a High-Order Cylindrical Vector Beam. Appl. Sci. 2022, 12, 12218. [Google Scholar] [CrossRef]
- Volyar, A.V.; Shvedov, V.G.; Fadeeva, T.A. Structure of a nonparaxial gaussian beam near the focus: III. Stability, eigenmodes, and vortices. Opt. Spectrosc. 2001, 91, 235–245. [Google Scholar] [CrossRef]
- Zhan, Q. Cylindrical vector beams: From mathematical concepts to applications. Adv. Opt. Photon. 2009, 1, 1–57. [Google Scholar] [CrossRef]
- Weng, X.; Miao, Y.; Wang, G.; Zhan, Q.; Dong, X.; Qu, J.; Gao, X.; Zhuang, S. Light beam carrying natural non-integer orbital angular momentum in free space. arXiv 2021, arXiv:2105.11251. [Google Scholar] [CrossRef]
- Wang, H.; Wojcik, C.C.; Fan, S. Topological spin defects of light. Optica 2022, 9, 1417–1423. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Kovalev, A.A.; Telegin, A.M. Angular and Orbital Angular Momenta in the Tight Focus of a Circularly Polarized Optical Vortex. Photonics 2023, 10, 160. [Google Scholar] [CrossRef]
- Li, S.-M.; Chen, J. Spin Hall effect of reflected light from an air-glass interface around the Brewster’s angle. Appl. Phys. Lett. 2012, 100, 071109. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).