High Extinction Ratio 4 × 2 Encoder Based on Electro-Optical Graphene Plasma Structure

Abstract

In this paper, a plasmonic electro-optical encoder based on graphene at THz frequency is proposed. The surface plasmon polaritons (SPPs) in the graphene–insulator–metal structure are excited by an incident TM wave with a wavelength of 9.3 μm. Graphene plasma waveguides have extremely high confinement, relatively low losses, and high tunability. The switching mechanism is based on the application of an external voltage to locally change the chemical potential of the graphene for encoding. Setting the chemical potential to 1 eV allows SPPs to propagate while lowering the chemical potential to 0.1 eV prevents the SPPs from propagating. A 4 × 2 encoder with a minimum encoding extinction ratio (ER) of 37 dB, a maximum modulation depth (MD) of 99.99%, and a structure area of 0.8 μm² is proposed based on the design rules and simulations using the finite-difference time-domain (FDTD) method. In terms of the obtained results, the proposed structure can be used in optical integrated circuits.

1. Introduction

The prospective of computing applications inclines to the use of optical processing [1,2]. Compared to conventional electronic computing apparati, which are susceptible to extensive limitations of interconnect delays and high thermal sensitiveness [3,4], optical waveguide technology offers solutions for miniaturization of computing applications with parallel processing, low latency, thermal stability, large bandwidth, and real-time transmission [5,6,7,8]. However, limitations by diffraction limits prevent the integration of photonic circuits on their electrical scale [9,10]. Due to the ability to confine electromagnetic waves to the subwavelength dimension, plasma technology is a promising contestant for the realization of photonic integrated circuits. The SPPs are collective electromagnetic waves that are excited at the boundary between the dielectric layer and the metal [11]. Usually, two main types of plasma structures, metal–insulator–metal (MIM) and insulator–metal–insulator (IMI), are used for the conduction of plasma waves [12,13,14]. However, common conventional plasma metals such as Au and Ag have high ohmic and radiation losses and are not suitable for far infrared (FIR) and terahertz (THz) frequencies. In addition, the tunability of SPP in plasma MIM and IMI structures is a challenging problem [15]. With the emergence of graphene as a 2D material with promising optical and electrical properties, graphene–insulator–metal (GIM) structures have been introduced for a wide range of frequency applications in the mid-infrared (MIR) to THz [16]. The most important feature that distinguishes graphene from other plasma materials is the change in the optical properties of graphene through the application of chemical doping and electrostatic fields [16,17]. Although different tunable plasma devices based on noble metals have been reported so far, the tunable properties of these devices are mainly based on the thermo-optical [18], magneto-optical [19], and electro-optical properties of dielectric materials [20]. Therefore, graphene is a suitable material for designing tunable plasmonics for high-speed optoelectronic devices. So far, different graphene-based optical devices have been reported, such as waveguides [21,22], modulators [23,24], switches [25,26], logic gates [27,28], and sensors [29,30]. Among logic circuits, encoders have a very important role in communication networks. In recent years, different schemes of encoders have been constructed [31,32,33,34,35,36,37,38,39,40,41,42,43,44]. Recently, Haddadan et al. proposed an optoelectronic encoder using a graphene-Al₂O₃ stack [45]. However, the area is a little bit large. The large size of 4 × 2 encoders based on photonic crystals has caused a significant disadvantage for integration. The current research on photonic crystal-based plasma devices is becoming increasingly popular [46,47]. If our research on 4 × 2 encoders is based on photonic crystals, the large size poses a significant disadvantage for integration. In the field of plasmonic device, an encoder using gold nano-ridge graphene has achieved a breakthrough in terms of size. However, the gold nano-ridge makes it undoubtedly more difficult in terms of integration [48]. Exploiting the plasmonic properties of graphene is an effective method for designing optoelectronic devices. In this paper, a switching operation of a graphene plasma waveguide based on terahertz frequency is designed. The encoding operation of the plasma waveguide encoder is achieved by controlling the state of the graphene waveguide switch, and the designed encoder is relatively small in size compared to other works. The 4 × 2 encoder proposed in this paper operates at 9.3 µm and has a sub-wavelength structure size. Its minimum extinction ratio is about 37 dB, and the maximum modulation depth is 99.99%.

The rest of this paper is organized as follows. Section 2 describes the basic principles of the design of the 4 × 2 encoder structure as well as the structure and operating principle of the design. The corresponding simulation results of the 4 × 2 encoder are given in Section 3. Finally, the conclusion is in Section 4.

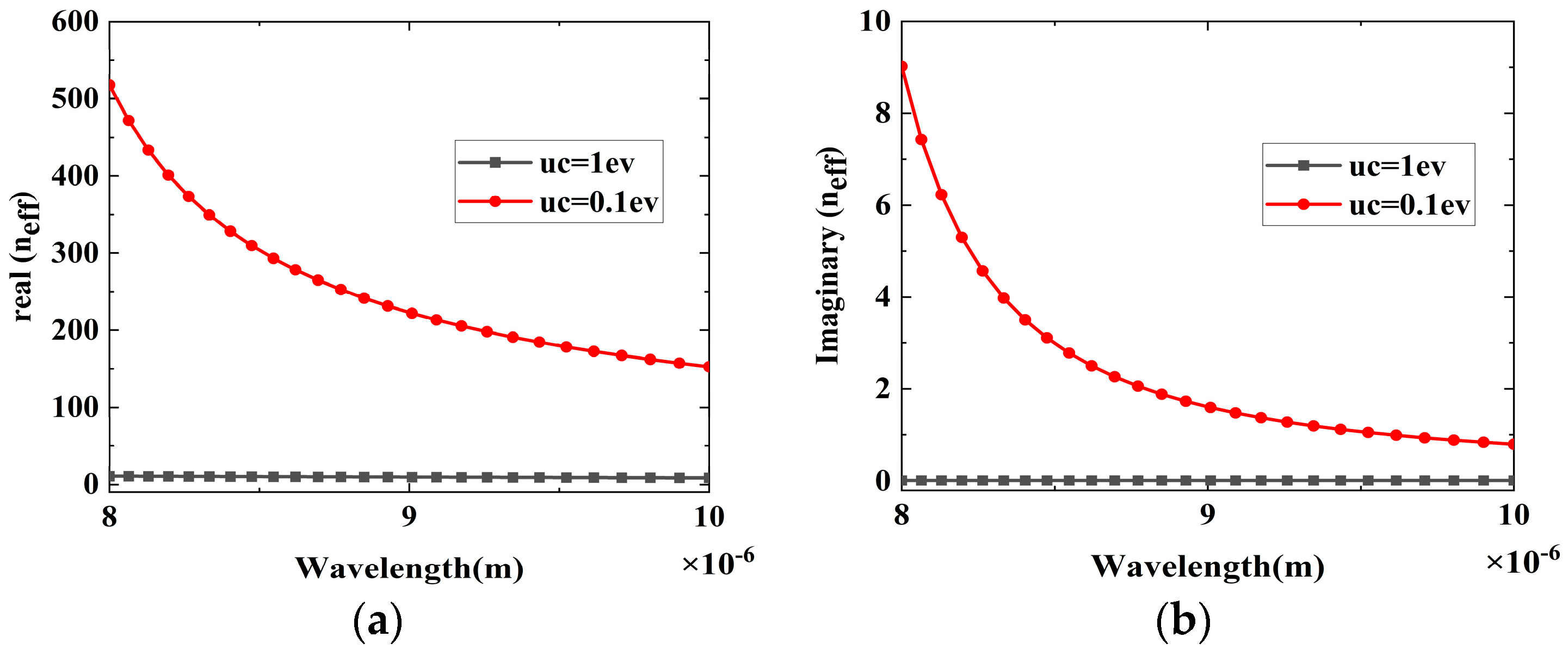
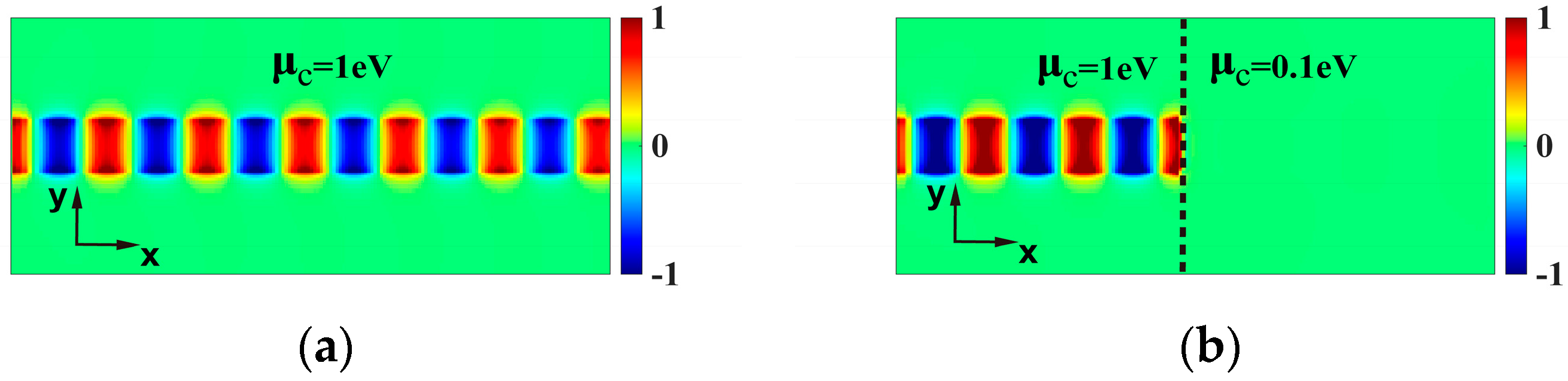
2. Design and Modeling

Precious metals are reported to be suitable plasma materials in the visible and near-infrared (NIR) regions. However, they have high losses in the far-infrared (FIR) and terahertz (THz) regions. Graphene plasma waveguides have extremely high confinement, relatively low losses, and high tunability compared to conventional plasma waveguides based on noble metals [49,50]. Graphene has good electro-optical properties, especially at FIR and THz frequencies, and is a top plasmonic material [17].

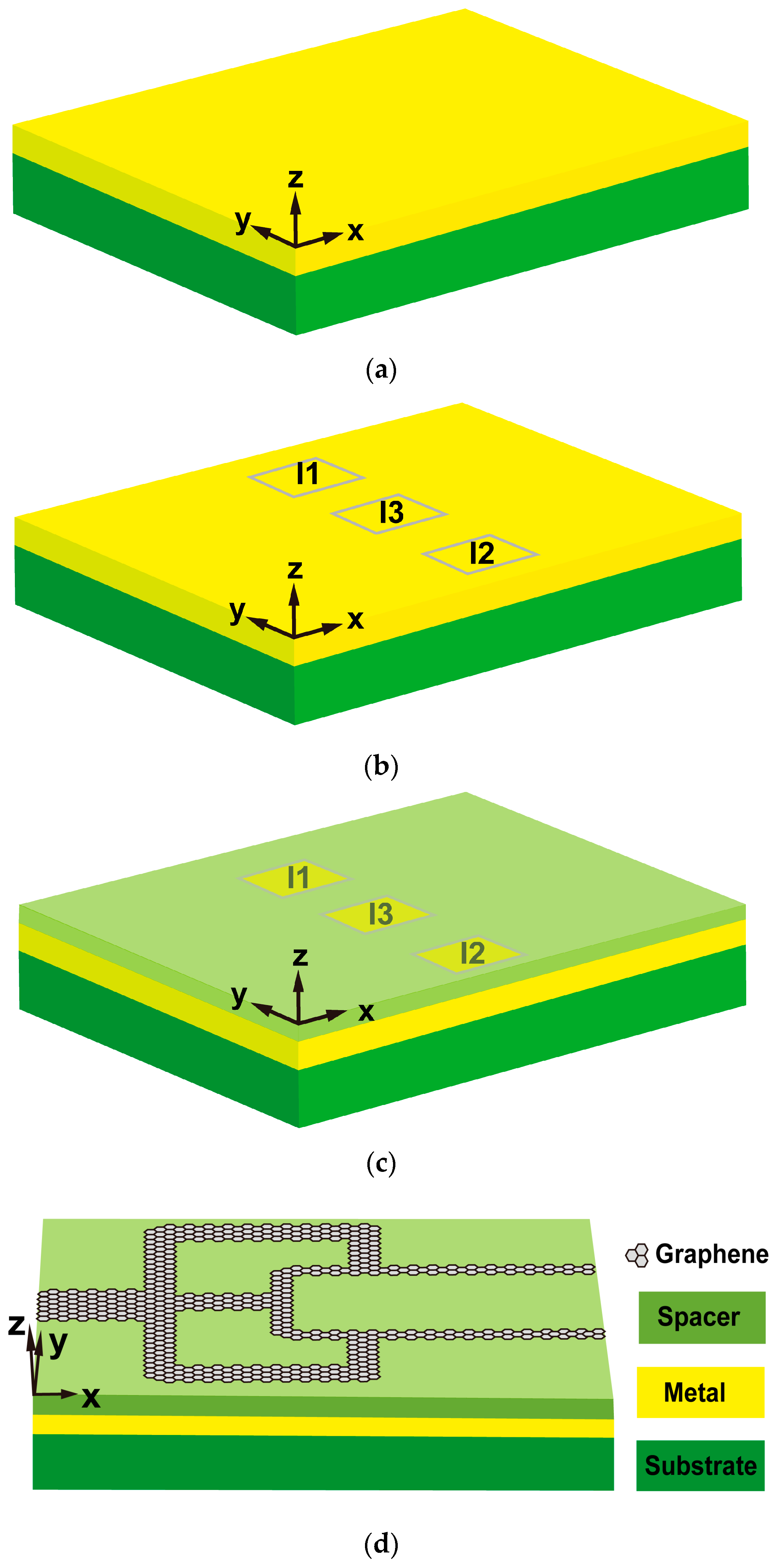
2.1. The Basic Principles of Design

The optical properties of graphene are extremely dependent on its surface conductivity. Graphene is a two-dimensional material with a thickness of 0.34 nm, and its surface conductivity can be easily changed by doping methods. The optical properties of graphene depend on the angular frequency $\omega$ scattering rate $\Gamma$, the chemical potential ${\mu }_{\mathrm{c}}$, and the temperature $T$. The complex surface conductivity of graphene is composed of intraband and interband contributions. It is modeled by the Kubo formula as follows [51]:

$$\sigma \left(\omega ,\Gamma ,{\mu }_{\mathrm{c}},T\right)={\sigma }_{inter}\left(\omega ,\Gamma ,{\mu }_{\mathrm{c}},T\right)+{\sigma }_{intra}\left(\omega ,\Gamma ,{\mu }_{\mathrm{c}},T\right)$$

(1)

$${\sigma }_{inter}=\frac{i{e}^2}{4\pi \hslash }ln\frac{2\left|{\mu }_{\mathrm{c}}\right|-\left(\omega +i2\Gamma \right)\hslash }{2\left|{\mu }_{\mathrm{c}}\right|+\left(\omega +i2\Gamma \right)\hslash }$$

(2)

$${\sigma }_{intra}=\frac{i{e}^2{k}_{B}T}{\pi {\hslash }^2\left(\omega +i2\Gamma \right)}\left[\frac{{\mu }_c}{k_{B}T}+2In\left(1+e^{-\frac{{\mu }_c}{k_{B}T}}\right)\right]$$

(3)

where $e$ is the electron charge, $\hslash$ is the approximate Planck constant, and $k_B$ is the Boltzmann constant. The scattering rate is related to the electron relaxation time ($\tau$) through $2\Gamma ={\tau }^{-1}$. In the far-infrared and THz wavelengths, the influence of intraband jumps dominates, while in the visible and near-infrared regions, interband jumps are the decisive phenomenon [16]. Figure 1 shows the intraband and interband portions of the graphene surface conductivity at ${\mu }_{\mathrm{c}}$ = 1 eV. It is clear that the total graphene surface conductivity is almost equal to the intraband contribution, and the effect of interband jumps is negligible.

For $\left|{\mu }_{\mathrm{c}}\right|>\hslash \omega /2$, the imaginary part of the graphene surface conductivity is positive and the graphene behaves similarly to an ultrathin metal. In this case, the TM mode SPP propagates along the graphene dielectric layer. For $\left|{\mu }_c\right|<\hslash \omega /2$, the imaginary part of the graphene surface conductivity is negative and the graphene behaves similarly to a dielectric [17,52]. In this case, the TE mode SPP is excited. In addition, the ultrathin metallic properties of graphene under TM-polarized SPP conditions are the focus of this paper.

In this paper, the temperature $T$, scattering rate $\Gamma$, and operating wavelength λ are 300 K, 0.11 meV, and 9.3 μm, respectively. The relationship between graphene conductivity on chemical potential and wavelength is shown in Figure 2. The relationship between the chemical potential and the required external voltage is given by [53].

$${\mu }_c\approx \hslash v_F\sqrt{\pi a_0\left|V_{ext}-V_{Dirac}\right|}$$

(4)

where $v_F=0.9\times {10}^6$ m/s is the Fermi velocity, $V_{ext}$ is the external voltage applied to the graphene layer, $V_{Dirac}$ is the natural doping-induced voltage shift, and $a_0$ = 9 × 10¹⁶ m⁻²·V⁻¹ is a constant estimated from a single capacitor model [53]. Whenever the chemical potential of graphene changes, the dielectric constant of the structure also changes. The complex permittivity of graphene is expressed in terms of surface conductivity as follows [54].

$$\epsilon ={\epsilon }_0-\frac{Im\left(\sigma \right)}{\omega \mathsf{\Delta }}+i\frac{Re\left(\sigma \right)}{\omega \mathsf{\Delta }}$$

(5)

where ${\epsilon }_0$, $\mathsf{\Delta }$, $Re\left(\sigma \right)$, and $Im\left(\sigma \right)$ are the free space permittivity, the effective thickness of the graphene layer, and the real and imaginary parts of the graphene conductivity, respectively. Similarly, the effective index ($n_{eff}$) of the structure changes when the chemical potential of graphene changes. Figure 3 shows the $n_{eff}$ of a graphene layer surrounded by air. Therefore, the dielectric constant of graphene as well as the $n_{eff}$ of the structure depends on the chemical potential of graphene.

Usually, when the chemical potential decreases, the imaginary part of $n_{eff}$ increases, leading to higher losses and lower propagation lengths. This phenomenon paves the way for the design of graphene-based plasma switches. The wavelength (λ_SPP) and the propagation length (L_SPP) of the SPP depend on the effective refractive index and are obtained by the following equation [17]:

$${\lambda }_{SPP}=\frac{{\lambda }_0}{Re\left(n_{eff}\right)}$$

(6)

$$L_{SPP}=\frac{{\lambda }_0}{2\pi Im\left(n_{eff}\right)}$$

(7)

For a single graphene layer surrounded by air, the effective refractive index of the TM wave at λ = 9.3 μm is 9.2712 + 0.0153i when the chemical potential is 1 Ev, which results in λ_SPP = 1.003 μm and L_SPP = 96.74 μm. In addition, when the chemical potential is 0.1 Ev, the effective refractive index is 194.38 + 1.23i, which causes the SPP to propagate at λ_SPP = 0.048 μm and L_SPP = 1.20 μm.The higher the real part of $n_{eff}$, the smaller the λ_SPP. In addition, by decreasing the imaginary part of $n_{eff}$, L_SPP increases. Figure 4 shows the distribution of the z-component of the electric field at 0.1 Ev and 1 Ev chemical potential. When the chemical potential is 1 Ev, the SPP can propagate to the output port (“ON” state). In addition, when the chemical potential becomes 0.1 Ev, the SPP is not allowed to propagate (“OFF” state) and a large number of waves are reflected. It can be seen that when the chemical potential changes from 1 Ev to 0.1 Ev, the λ_SPP increases while the L_SPP decreases severely. This behavior suggests that a graphene-based plasma switch can be designed by applying an external voltage.

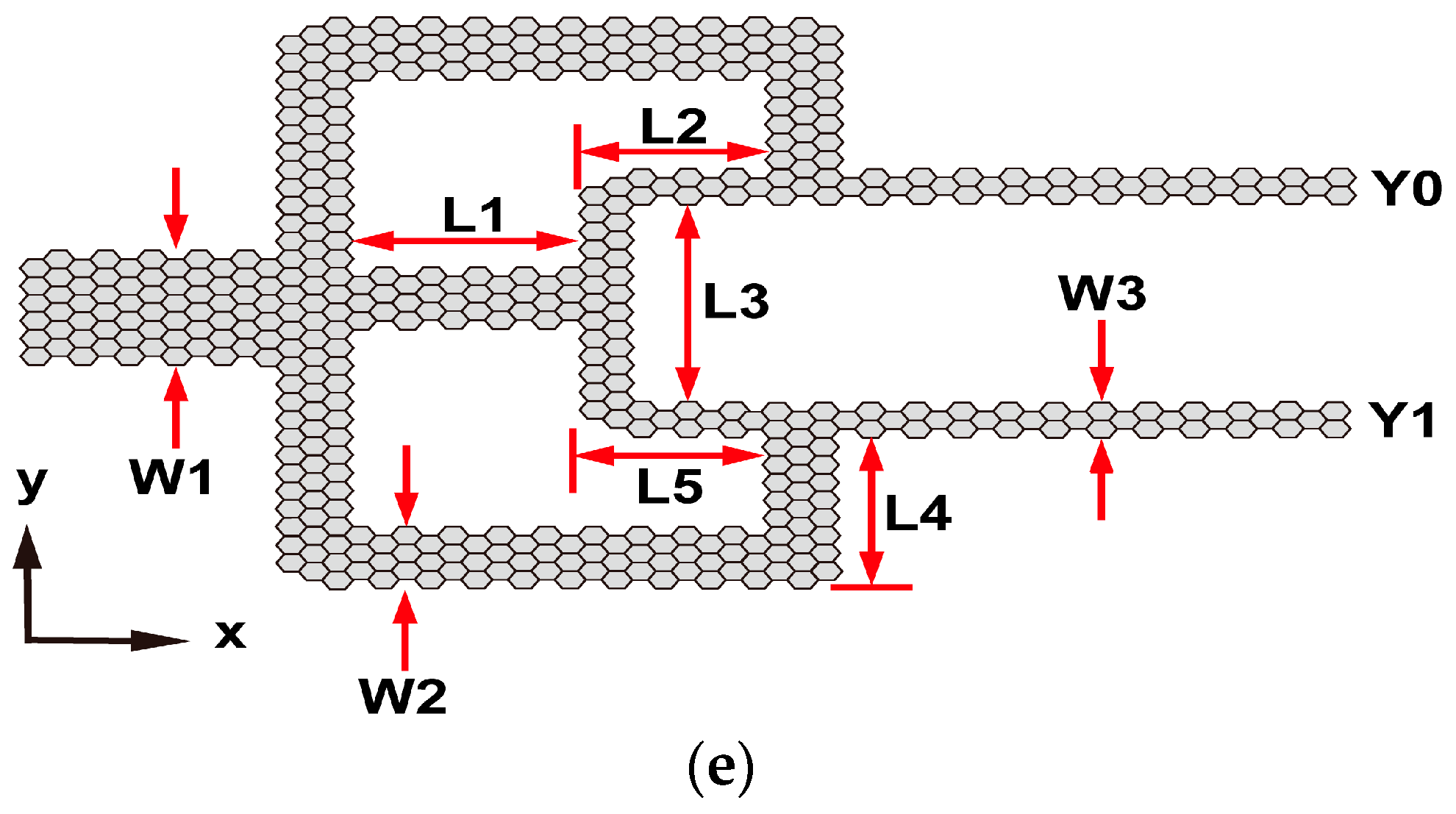
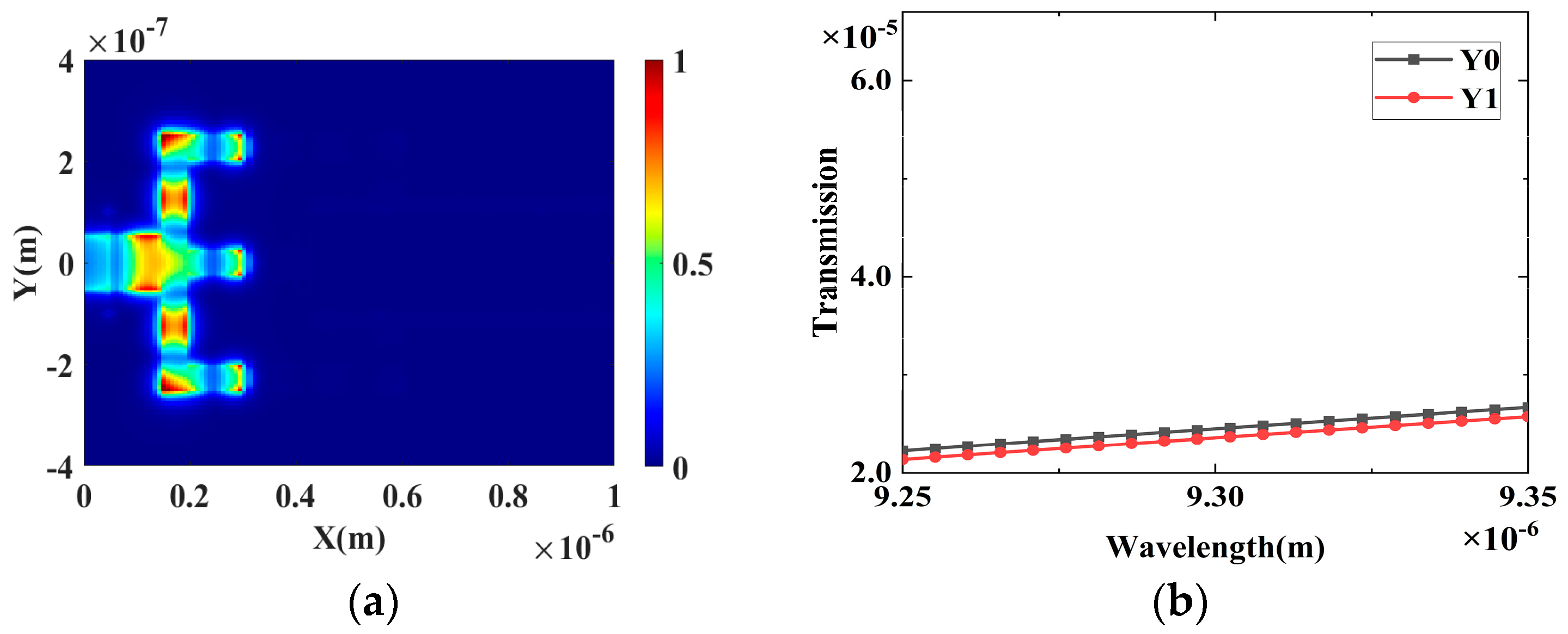
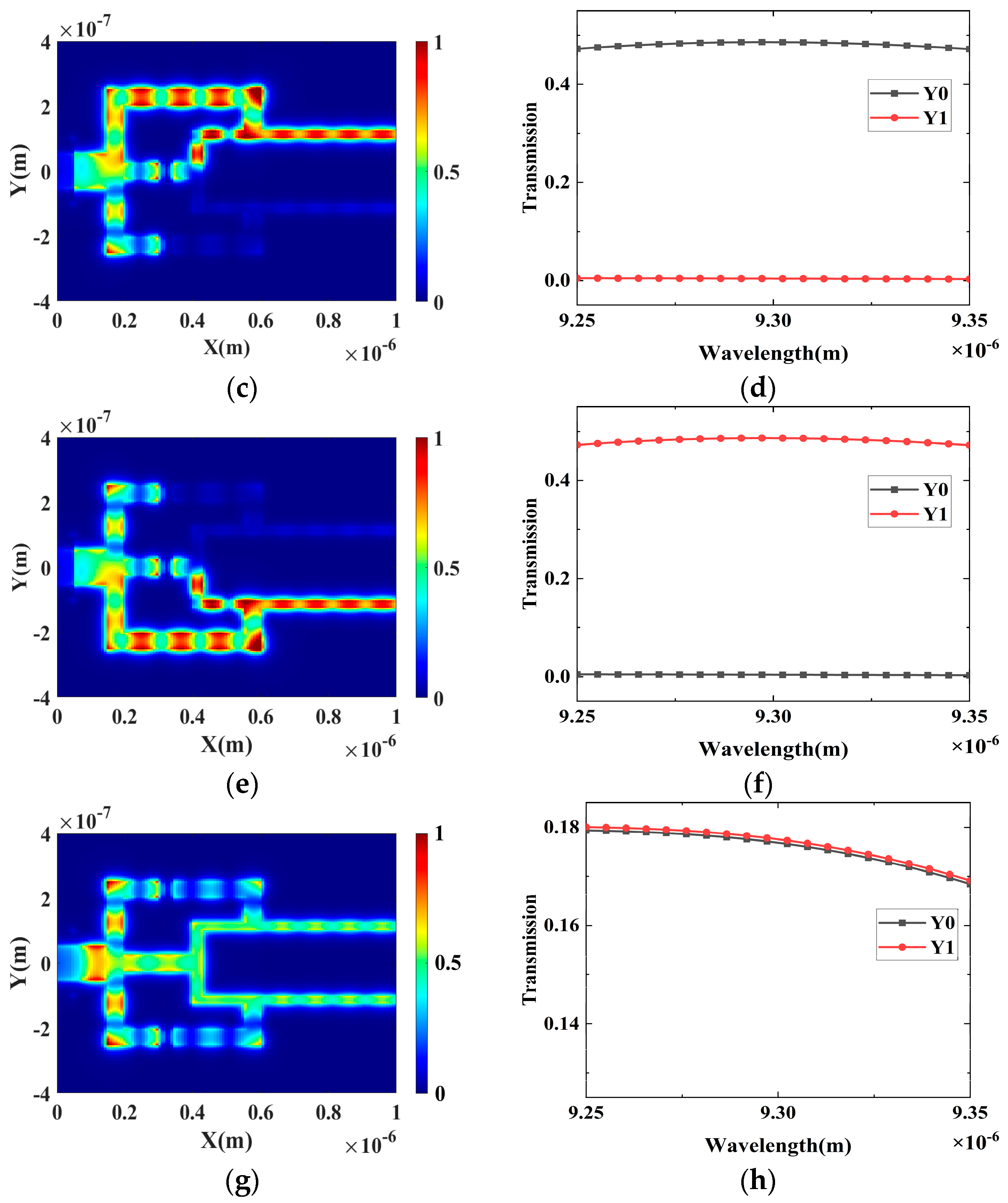
2.2. The Proposed 4 × 2 Encoder

The basic structure schematic for implementing a graphene-based SPPs electro-optical 4 × 2 encoder is shown in Figure 5. Au of 30 nm thickness is deposited on the dielectric substrate. A review of the literature shows that gold is more effective than other metallic materials [55]. This metal layer can be used as a selective contact for applying external voltages while increasing the light confinement in the spacer layer. A dielectric layer of 20 nm thickness is located on the metal layer as a spacer layer, and graphene nanoribbons are deposited on the spacer layer. The dielectric layer has a dielectric constant of 1.4. The geometry of the graphene nanoribbon is shown in Figure 5e. Figure 5 illustrates the feasible fabrication process of the proposed 4 × 2 encoder. First, the metal layer is deposited on the dielectric substrate by electron beam evaporation (Figure 5a) [56]. Metal nanopick contacts can be produced by standard photolithography and wet etching (Figure 5b) [57]. Then, the spacer layer is deposited on top of the patterned metal layer and polished to obtain a thick surface with the desired thickness (Figure 5c). Finally, the graphene nanoribbons grown on copper are transferred to the spacer layer by employing a wet transfer method (Figure 5d) [58]. Combining graphene with metal makes the wave number of plasmonic wave modes increase, thus further enhancing the plasmonic waveguide confinement [59]. The graphene-based waveguide can support two modes, including an edge mode and a waveguide mode [60]. For low-width graphene nanoribbons, the waveguide is in single mode and only supports the edge mode. In this mode, the power is concentrated at the edges of the graphene layers. When the width of the graphene nanoribbon increases, the higher-order modes are also excited and the waveguide becomes multimode. To maximize the transmission [61], the widths of the graphene nanoribbons were chosen to be W1 = 100 nm, W2 = 45 nm, and W3 = 20 nm. Figure 6a shows the normalized total transmission coefficients of the three output branches G_U, G_D, and G_M as a function of W2 for an input width W1 = 100 nm at a wavelength of 9.3 µm. Due to the symmetry of the graphene structure, the G_U and G_D normalized total transmission coefficients are nearly equal. To further illustrate the selection of the optimal width W2, define $K=\left|\frac{T_{G\_U}-T_{G\_M}}{T_{G\_U}+T_{G\_D}+T_{G\_M}}\right|$, as shown in Figure 6b; if the value of K is closer to 0, this means that the width of W2 is selected more reasonably, and vice versa, it means that the selection of W2 is not reasonable. It is clear from Figure 6a,b that the total transmission coefficient of each branch of the three-branch graphene structure is most similar when W2 is taken to be 45 nm. Figure 6c shows the total transmission coefficient of the electro-optical 4 × 2 encoder Y0 as a function of L2 at a wavelength of 9.3 µm with only the selective contact I1 in the on state. Similarly, when only the selective contact I2 is in the on state, the total transmission coefficient results are the same as those in Figure 6c, due to the symmetry of the structure. Figure 6d shows the total transmission coefficient of the electro-optical 4 × 2 encoder Y0 as a function of L2 at a wavelength of 9.3 µm with only the selective contact I3 in the on state. Similarly, due to the symmetry of the structure, the total transmission coefficient of Y1 is the same as that of Y0 at this time, and the total transmission coefficient of Y0 is used as a reference for the comparison of Figure 6c,d. Obviously, from Figure 6a,b, the total transmission coefficient of the output can be taken as the best value when L2 is around 157 nm and only one of the selected contacts I1, I2, and I3 is opened. This also indirectly shows that a small error in the graphene waveguide structure of the electro-optical 4 × 2 encoder due to the manufacturing process will not affect the function of the plasma electro-optical 4 × 2 encoder. By applying an external voltage to the selector contact, the chemical potential of the graphene layer is changed and the light can be propagated through the waveguide or blocked by using the properties of the graphene plasma switch. By adjusting the selector contact voltage to keep the chemical potential at 1 eV, the SPP can propagate within the boundary of the graphene dielectric layer and indicate a logical “1” state (“ON” state). In addition, when the chemical potential changes to 0.1 eV, the SPP propagation distance decreases significantly and indicates a logical “0” state (“OFF” state).

Figure 5. (a) Deposition of the metal layer on the dielectric substrate. (b) Process of patterning the selected contact electrodes to form the input electrode. (c) Deposition of the spacer layer on the patterned metal layer. (d) Transfer of graphene nanoribbons on top of the spacer layer and realization of the proposed 4 × 2 encoder. (e) Top view of the graphene waveguide. The geometric parameters are shown in

Table 1. Table of graphene pattern layer geometries (nm).

W1	W2	W3	L1	L2	L3	L4	L5
100	45	20	205	157	210	125	157

. The dimensions are not to scale.

Figure 5. (a) Deposition of the metal layer on the dielectric substrate. (b) Process of patterning the selected contact electrodes to form the input electrode. (c) Deposition of the spacer layer on the patterned metal layer. (d) Transfer of graphene nanoribbons on top of the spacer layer and realization of the proposed 4 × 2 encoder. (e) Top view of the graphene waveguide. The geometric parameters are shown in Table 1. The dimensions are not to scale.

The working principles of the 4 × 2 encoder are as follows:

(1)

The chemical potential of the input electrodes in the three selective contact regions of the graphene layer can be changed. Each region acts as a switch.

(2)

The propagation of SPP in each input waveguide depends on the voltage applied to each switching electrode.

(3)

When any one of I1, I2, and I3 is ON, the state of I0 is logic “0”.

(4)

When I1 is ON, I2 and I3 are OFF.

(5)

When I2 is ON, I1 and I3 are OFF.

(6)

When I3 is ON, I1 and I2 are OFF.

(7)

When I1, I2, and I3 are OFF, it means I0 is in the logic “1” state.

Under this condition, the electro-optical 4 × 2 encoder is implemented. The truth table of the proposed 4 × 2 encoder is given in

Table 2. Truth table of the proposed 4 × 2 encoder.

Input				Output
I0	I1	I2	I3	Y0	Y1
1	0	0	0	0	0
0	1	0	0	1	0
0	0	1	0	0	1
0	0	0	1	1	1

.

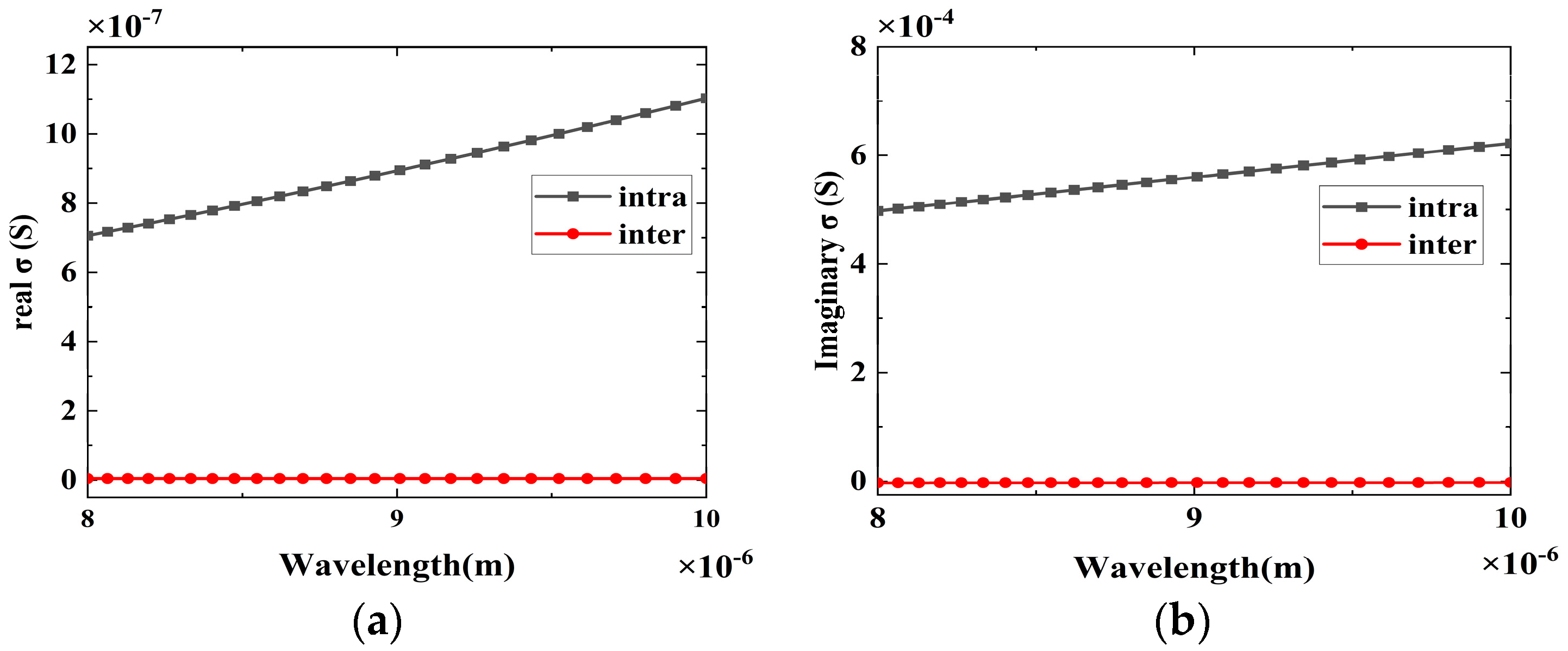
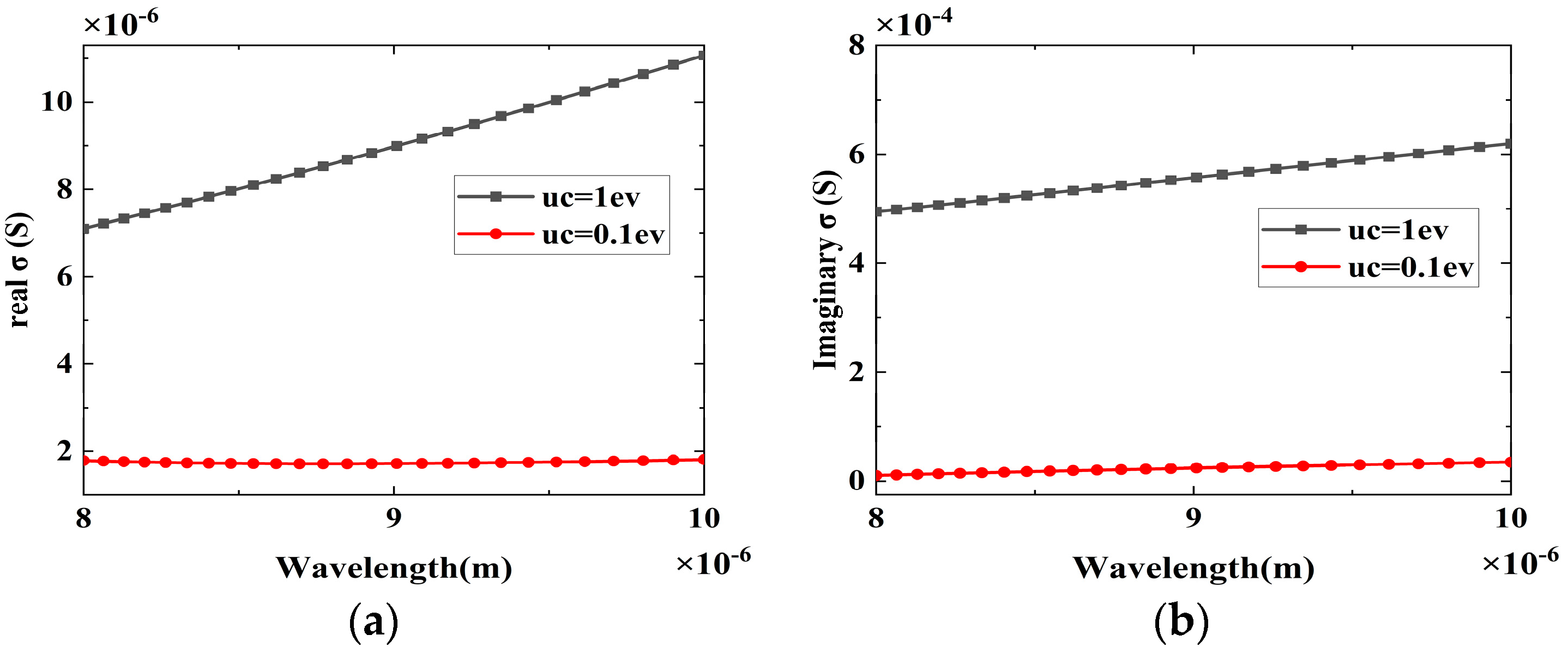
3. Results and Discussion

The proposed optoelectronic 4 × 2 encoder was simulated using the three-dimensional finite-dimensional time-domain difference (FDTD) method from Lumerical Solutions Canada, version 2020 R2. Compared to the spectral element method (SEM) [62], which focuses more on the mechanism, FDTD is more convenient for visualizing the electric field intensity distribution of the proposed structure. In the simulation, the grid size in the z-direction around the graphene layer is fixed at 0.1 nm and gradually increases outside the graphene layer. In addition, the grid sizes in the x and y directions are set to 8 nm and 4 nm, respectively. In addition, a perfectly matched layer (PML) boundary condition is used in the simulation. The structure is also excited by TM mode light waves with a wavelength of 9.3 μm and a bandwidth of 0.1 μm. Figure 7 shows the intensity of the electric field distribution for different encoding states. Different external voltages are applied to the plasma switches on the optical waveguide branches according to the selective contacts to characterize the four-bit code. The applied external voltage is 1 ev in the branch where the graphene plasma switch is located, and then I1, I2, and I3 are in the “ON” state and are defined as code “1”. Similarly, the applied external voltage is 0.1 ev in the branch where the graphene plasma switch is located, and the branch where I1, I2, and I3 are located is “OFF” and is defined as code “0”. In this way, when the plasma switch on the waveguide branch is coded “1”, the optical signal can be passed through the waveguide branch. According to the working principle of Section 3 and the true value of Table 2, the coding function of 4 × 2 is realized. As shown in Figure 7a, when I1, I2, and I3 are “OFF”, the default I0 is “ON”, and the four-bit coding flag is defined as “1000 “(I0 I1 I2 I3 I4). As there are no light signals in the output of Y0 and Y1, the 2-bit outputs is are“00” (Y0Y1). Figure 7c is the electric field intensity distribution, when only I1 is “ON”. Figure 7e is the electric field intensity distribution, when only I2 is “ON”. Figure 7g is the electric field intensity distribution, when only I3 is “ON”.

Table 3. Normalized transmission under different coding conditions.

Input				Output
I0	I1	I2	I3	Y0	Y1
1	0	0	0	2.69389 × 10−5	2.69155 × 10−5
0	1	0	0	0.483541	0.00436279
0	0	1	0	0.00436611	0.483586
0	0	0	1	0.176601	0.176639

summarizes the normalized transmission under different coding conditions, which leads to two important parameters for the evaluation of the encoder.

In order to have a criterion to evaluate the coding performance, the parameter of the minimum extinction ratio ($E{R}_{min}$) is defined as follows [63]:

$$E{R}_{min}=10\log \left(\frac{T_{1,min}}{T_{0,max}}\right)$$

(8)

Here, $T_{1,min}$ is the minimum normalized transmission for the logic gate logic “1” state, while $T_{0,max}$ is the maximum normalized transmission for the logic gate logic “0” state. In addition, the modulation depth (MD) can be found in Refs [64,65].

$$M{D}_{max}=\frac{T_{1,max}-T_{0,min}}{T_{1,max}}$$

(9)

Here, $T_{1,max}$ is the maximum normalized transmission in the logic gate logic “1” state, while $T_{0,min}$ is the minimum normalized transmission in the logic gate logic “0” state.

Table 4. Minimum ER of the proposed 4 × 2 encoder logic gate.

Input				Minimum ER (dB)	Maximum MD (%)
I0	I1	I2	I3
1	0	0	0	~	~
0	1	0	0	47.0726	99.99
0	0	1	0	47.0736	99.99
0	0	0	1	37.0002	99.98

summarizes the minimum extinction ratio and the maximum modulation depth for different encoding conditions. In order to evaluate the proposed encoder, the area, minimum extinction ratio, and maximum modulation depth are compared with the other optical encoders in

Table 5. Comparison of the obtained results with other works.

Description	ER (dB)	MD (%)	Area (μm2)	Ref
Nonlinear PhC	16.33	98.04	612	[33]
PhC	7.32	94.90	880	[34]
PhC	12.92	91.38	~	[35]
PhC ring resonators	9.54	~	757	[36]
Triangular lattice shape PhC	11.76	96.84	723	[37]
PhC	9.03	~	200	[38]
PhC ring resonators	9.24	89.94	792	[39]
2D PhC ring resonators	~	99.49	1225	[40]
PhC	17.78	~	744	[41]
Silica-based PhC fiber	13.76	97.78	150	[42]
2D PhC	16.53	97.80	132.7	[43]
PhC using the graphene–Al2O3 stacks	7.6	91	127	[45]
Graphene-based plasmonic using Au nano-ridge	14.44	~	0.36	[48]
Graphene plasmonic waveguides	37	99.99	0.8	This work

. References [31,32,33,34,35,36,37,38,39,40,41] are all-optical and do not have the ability to adjust the transmission after fabrication, while in the proposed structure, the light transmission through the waveguide can be controlled by applying an appropriate voltage to the graphene layer and changing the chemical potential. In addition, the area of the proposed structure is small compared to other structures. Table 5 shows that the minimum extinction ratio of the designed encoder is greater than that of the references [31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46]. Thus, the small size and high extinction ratio are the main advantages of the device and guarantee the capability of the designed encoder in optical circuit applications.

4. Conclusions

A graphene-based plasmonic electro-optical 4 × 2 encoder at THz frequency has been designed and analyzed. The proposed plasmonic subwavelength structure in a graphene–insulator–metal (GIM) configuration has the advantages of optical properties such as the ultra-compact size, high brightness, high extinction ratio, and voltage dependence of the device. The structure achieves the desired encoding logic operation by applying different external voltages to the selector contact input electrode and thus varying the voltage of the graphene plasma switch. The minimum encoding extinction ratio and maximum modulation depth of the proposed electro-optical 4 × 2 encoder are 37 dB and 99.99%, respectively, with a structure area of 0.8 μm². The results show that the proposed plasmonic encoder can be used in optical integrated circuits. In addition, the reversible design of the electro-optical 4 × 2 encoder based on graphene plasma proposed in this paper will be the next research focus.