Abstract
An optical coherence tomography (OCT) system based on the ghost imaging (GI) technique is developed for correctly imaging in scattering media. Usually, the scattering in the media leads to a decrease in the signal-to-noise ratio of the reconstructed image. This problem can be solved by using ghost imaging-OCT(GI-OCT), but the number of patterns required for GI reconstruction depends on the concentration of the scattering media. Therefore, studying the relationship between the intensity distribution in reconstructed images and the optical properties of scattering media is essential. In this study, image reconstruction is carried out in scattering media with a concentration of 0.0% to 1.4%, diluted from processed milk. Using the structural similarity index method (SSIM) to analyze the reconstruction condition, it is found that the target image can be reconstructed correctly when the SSIM value is more than 0.7. By analyzing the intensity distribution of the reconstructed image, the results show that the extinction coefficient of the scattering media is negatively correlated with the contrast of the reconstructed image and positively correlated with the scattering intensity. Their correlation coefficients are −0.94 and 0.99, respectively.
1. Introduction
Optical coherence tomography (OCT) methods have been proposed for three decades [1]. OCT is based on the principle of low-coherence interference and has the advantage of being noncontact, noninvasive, and producing high-resolution cross-sectional images. It has been widely used commercially, with significant results in ophthalmology, such as the interior of the retina. In the last decade, it has also been increasingly used for cardiology and dermatology observations due to its excellent performance in measuring nonhomogeneous media [2,3,4,5,6]. However, in the measurement of scattering media with OCT, such as cardiovascular and skin, the disorderly distribution of the scatter causes an extinction phenomenon (absorption and scattering) [7]. It is difficult to obtain accurate optical properties in the scattering media because of light scattering [8,9,10,11].
Ghost imaging (GI) is well-known for solving the distinguishing signal and noise and has been applied to many fields. For example, in LIDAR, 3D imaging, astronomical observation of turbulent atmospheres and microscopy, and OCT [12,13,14,15,16,17,18,19,20,21]. Inspired by the achievements of GI applied in different fields [22,23,24,25,26], a GI-OCT method is proposed by using the GI technique on the measurement path of OCT [27]. This method can collect scattering light after passing through a scattering media and provide a scattered distribution image. Unlike conventional OCT, which focuses the light on a point, the GI-OCT method illuminates the light on a defined area and uses a point receiver to receive the scattering light. Generating different illumination light patterns with a digital mirror device (DMD), the interference OCT signal is detected by a single photodiode after passing through the scattering media [28,29]. Many studies of image recovery from records of diffracted field patterns have been conducted using a reference wave [30,31,32,33], while GI-OCT does use a reference wave. Then, the correlation between the light intensity and the pattern is calculated to reconstruct the scattering intensity distribution within the determined region.
GI-OCT can reconstruct each layer distribution of scattering media. The reconstructed images of scattering media are directly related to the depth limit of OCT measurement. Therefore, studying the relationship between the scattering media’s optical properties and the reconstructed image’s intensity distribution is essential. Usually, the number of patterns required for GI varies for different degrees of scattering media. Validating the number of patterns is the first step to studying the relationship between the scattering media and the reconstructed image.
In this work, the GI-OCT method is used to reconstruct the image in diluted processed milk. The SSIM method evaluates the reconstructed images’ quality and obtains the required number of patterns in the reconstructed images at different concentrations [34]. Additionally, the relationships between the optical properties of scattering media and the contrast, as well as the scattering intensity in the reconstructed image, are analyzed.
2. Experiment and Methods
2.1. Experiment Setup and Sample Target
The GI-OCT method is proposed and constructed in the referred paper [27]. In this paper, the equipment in the previous work is upgraded to measure the distribution of the flowing solution, shown in Figure 1.
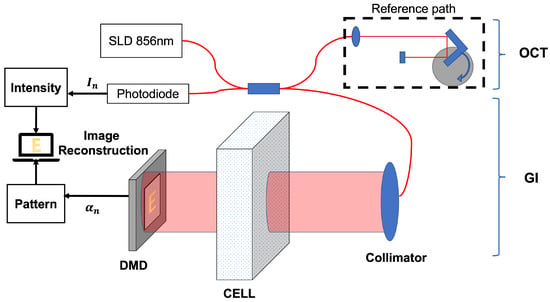
Figure 1.
Experiment setup of GI-OCT for scattering media measurement.
For the new GI-OCT, a high-power Super luminescent Diode (SLD) light source with a Gaussian distribution at a wavelength of 856 nm is used, and the equipment specifications are shown in Table 1.

Table 1.
SLD specification of GI-OCT.
The GI-OCT beam needs to spread and reflect part of the light, making illumination patterns. This study prepared a high-power SLD to validate the GI-OCT algorithm and concept in this experiment.
The reference path consists of a stable rotating motor and a fixed mirror to complete the axial scan [35]. The measurement path is equipped with an optical probe, and a varifocal collimator makes the collimator beam of 2 mm diameter. Meanwhile, the DMD chip is set in the measurement path, and its specifications are shown in Table 2.

Table 2.
DMD specification of GI-OCT.
The DMD chip has nearly 100% reflectivity for the specification reflection wavelength and 90% reflectivity for our OCT light source. The micromirrors are arranged in a matrix of 854 × 480 on the DMD chip, with a total size of 4.61 × 2.59 mm. The size of each micromirror is μm, and the deflection angle is degrees on the diagonal axis, divided into “on” and “off” states. Therefore, the DMD chip is tilted +17 degrees along the diagonal, so that the pattern light in the “on” state can be reflected back to the collimator. The solution is put in a 1 cm-thick cell and is placed between the DMD chip and the optical probe. Light passes through the cell to illuminate the DMD, and the reflected pattern light through the sample returns to the OCT probe. The DMD chip is controlled to display 10 × 10 speckle patterns in the mm DMD chip area. Each speckle has 27 × 18 micromirrors.
This experiment uses the letter “E” overlapped with the DMD illumination pattern as the target object in order to be able to focus on the scatter distribution of the solution, as shown in Figure 2. Additionally, the DMD chip is placed in the OCT’s interference area, so that the OCT’s measured light reflection is highly efficient, the light intensity is stable, and the image results can be focused on reconstructing the solution’s distribution.

Figure 2.
The sample overlapped with the DMD chip. The DMD control area is a mm area, and each speckle has 27 × 18 micromirrors.
In this paper, we prepared different concentrations: pure water (0.0%) and 0.3%, 0.6%, 1.2%, 1.3%, and 1.4% diluted form a processed milk solution. The diluted solution’s transmittances are 69%, 50%, 26%, 24%, and 18%, respectively. The different GI calculation methods can significantly affect imaging results. Therefore, the effect of different GI calculation methods on the optical properties of the solution need to be compared, which are computational ghost imaging (CGI), differential ghost imaging (DGI), pseudoinverse ghost imaging (PGI), and differential pseudoinverse ghost imaging (DPGI) [36,37,38]. Moreover, the number of light patterns in the GI calculation greatly impacts the results. We also compared the number of different measurements—400 to 2400 times.
The reconstructed results are evaluated from 3 different views: (1). GI calculation methods: CGI, DGI, PGI, DPGI. (2). Number of measurements: 400, 800, 1200, 1600, 2000, and 2400. (3). Diluted processed milk solution concentrations: 0.3%, 0.6%, 1.2%, 1.3%, 1.4%, and pure water.
2.2. Method
Peak signal-to-noise ratio (PSNR) evaluates the degree of coincidence between the original and referred images. In this study, the reconstructed image of 0.0% concentration solution (pure water) in 2400 measurements by the DPGI method is used as the original image. Additionally, the OCT beam has a Gaussian distribution, making reconstructed images overlapped on the beam distribution. The referred images are compared with the 0.0% concentration image, the overlapped beam distribution can be canceled with the image of pure water, and only the information of the scattering media is evaluated. However, the referred images are not the same concentration experiment as the original image. Therefore, the value of PSNR does not represent the degree of consistency of the reconstructed image. Furthermore, PSNR values are hard to distinguish between the images with not enough measurement numbers to reconstruct or the distribution affected by the scattering media. Only, the PSNR is not suitable for confirming image reconstruction. Here, the structural similarity index method (SSIM) is introduced to evaluate the reconstructed images. SSIM is a method for predicting the perceived quality of two images. The value of SSIM is close to 1, which means the perceived structure of the two images is consistent, and the value is close to 0, which means the images are unrelated. The subjective judgment of the clarity of the image letter “E” with the SSIM result is performed, and a successful reconstruction is defined in the SSIM value of 0.7 or more. The SSIM is used to evaluate the effect of the scattering media on the reconstructed image. We confirmed that other image letters also produce the same results. In the results section, the results of SSIM above and below 0.7 are compared for different GI calculation methods, different number of measurements, and different concentrations.
here, x and y indicate the expected result and the comparison result. is the mean value, is the standard deviation, is the covariance of x and y, , and L represents the maximum possible pixel value in the image. The experimental images are compressed between 0 and 1; here, .
3. Results
Figure 3 shows the GI-OCT reconstructed images of the 0.3% concentration solution using four different GI calculation methods with a number of measurements of 400. Figure 3a shows the result of the CGI method. Each pattern obtained little information in this result, requiring a large number of measurements (over 10,000) to obtain the recognizable target image. Figure 3b shows the result of the DGI method. Depending on the relative difference in light transmission, the signal-to-noise ratio of DGI can be several orders of magnitude higher than that of CGI. However, as a variant of CGI, the information obtained in a handful of measurements is as little as CGI, and the reconstructed image is hardly visible as a target image. Figure 3c shows the result of the PGI method. PGI can be reconstructed in small measurements, and the letter “E” can be distinguished in the image. Figure 3d shows the result of the DPGI method. The results of DPGI are similar to PGI and can also be obtained in a small number of measurements with the recognizable target image. DPGI is better than PGI reconstruction in the case of much electrical noise. The images are consistent between the two methods, indicating that there is not much noise in this experiment.

Figure 3.
The results of 0.3% concentration solution in 400 measurements by four GI methods: (a) CGI method, (b) DGI method, (c) PGI method, and (d) DPGI method.
The PSNR values obtained by comparing Figure 3a–d with the original image are 9.99, 13.37, 18.92, and 18.90, and the values of SSIM are 0.08, 0.53, 0.88, and 0.88, respectively. The reason for the small PSNR values of CGI (a) and DGI (b) is that the numbers of measurements are not enough to obtain correctly reconstructed images. In the case of small concentrations, the PSNR values of (a) (b) have a large difference compared with the PSNR values of (c) (d). The value of this SSIM is below 0.7, and the letter “E” cannot be identified. On the contrary, the PSNR results for PGI (c) and DPGI (d) are similar and greater than (a) and (b). The value of SSIM is greater than 0.7, and the letter “E” can be identified very clearly. The number of measurements required for image reconstruction differs on different GI calculation methods, resulting in the CGI and DGI methods being unable to obtain reconstructed images within the available number of measurements. In other words, the results of the CGI and DGI methods cannot be used to analyze the optical properties of images with scattering media. Among these four GI calculation methods, it is verified that the DPGI method has the best reconstruction efficiency and noise immunity. Therefore, the DPGI method results are used for the number of measurements and concentration experiments.
Figure 4 shows the reconstruction results of the DPGI method through a solution concentration of 1.2%. Additionally, it shows the reconstruction images of every 400 measurements, stepped up to 2400 measurements. In 400 measurements, the target is not clearly distinguished from the surrounding parts, and the shape of the letter “E” could not be accurately identified. In 800 measurements, the target and surrounding parts are slightly separated, and the letter “E” can be recognized. In 1200 measurements, the target is clearly distinguished from the surrounding part, but the target part still has the light intensity distribution, and the surrounding part has not changed much. In 1600 and 2000 measurements, the light intensity distribution of the target part decreases, and the surrounding part is unchanged. Finally, in 2400 measurements, there is a strong reduction in the light intensity of the target part, and the letter “E” is clearly recognized; the surrounding part looks to be fixed. The image gradually becomes more recognizable as the number of measurements increases.

Figure 4.
The results of 1.2% concentration solution by DPGI methods in different measurements.
Using the same processing as in Figure 3, the images in Figure 4 are images referred to the calculated PSNR and SSIM. The PSNR values of (a), (b), (c), (d), (e), and (f) are obtained as 12.65, 13.10, 13.84, 13.62, 13.04, and 14.20, respectively. The SSIM values are 0.60, 0.71, 0.71, 0.75, 0.75, and 0.76, respectively. As stated in the method section, the letter “E” of the reconstructed image is gradually recognizable with little difference in the PSNR values, resulting in only the PSNR values between not enough numbers of measurements or the distributions affected being hard to distinguish. The letter “E” changes from unrecognizable to recognizable, while the value of PSNR does not change much, indicating that the effect of the scattering media makes the reconstructed image’s PSNR value go down. It is not easy to distinguish from the values of PSNR, but from the value of SSIM it is easy to know the difference for recognizability from 0.60 and 0.71, which proves the reliability of SSIM for this image reconstruction.
Figure 5 shows the reconstructed results of the DPGI method through different concentrations at the number of 2400 measurements. It results from (a) pure water (0.00%) and diluted solutions of (b) 0.3%, (c) 0.6%, (d) 1.2%, (e) 1.3%, and (f) 1.4% of processed milk. In the 0.0% solution, the letter “E” has the largest contrast between the target and surrounding parts. In the 0.3% solution, the target and surrounding parts are slightly affected and can be found to be different from (a). In the 0.6%, 1.2%, and 1.3% solutions, the target and surrounding part gradually deteriorate, but the letter “E” can still be distinguished. There are no significant changes in the distribution of the target part, but the distribution of the surrounding parts appears to be deteriorating. Additionally, in the 1.4% solution, the target part is no longer distinguishable from the surrounding part. There are deteriorations in the results of the reconstructed target part with increased concentrations for the same number of measurements.

Figure 5.
The results of each concentration solution (diluted milk) by DPGI methods in 2400 measurements.
The PSNR is used to evaluate Figure 5 using the same way as before, and the values of (b), (c), (d), (e), and (f) were obtained as 19.06, 15.82, 14.20, 14.10, and 11.68, respectively. The SSIM values are 0.93, 0.86, 0.76, 0.78, and 0.37, respectively. The values of PSNR can be used to distinguish the concentrations for the same number of measurements at different concentrations. However, SSIM has a more obvious distinction. For the values of SSIM higher than 0.70, the letter “E” can be identified. When (e) comparing (f) in Figure 5, the value of PSNR has only a small decrease in the unidentifiable image, but SSIM has a large decrease. The PSNR values are 14.10 and 11.68, which is only a 10% change, even for the good quality image of PSNR value 30, while the SSIM values are 0.78 and 0.37, with a difference of about 50%. For the same number of measurements, the results of the reconstructed target fraction deteriorate with increasing concentrations.
Figure 6 summarizes the results of the SSIM and PSNR methods for the DPGI calculation method at different concentrations for the different measurements. In Figure 6a, the PSNR values of each concentration change with the number of measurements. The results for each concentration of PSNR are separated in Figure 6a, all tending to be straight lines. In the same concentration, it does not change more than 3. The PSNR method is difficult to distinguish between the images with not enough numbers of measurements or the distribution affected, and they both have low values. However, in Figure 6b, the SSIM values of each concentration change with the number of measurements. The results of SSIM have a large change, with a significant rise after a certain number of measurements, after which all concentrations are straight lines. For example, the solutions at 1.2% and 1.3%, which have the results of the PSNR values that do not distinguish the image reconstruction in the number of measurements but can be distinguished in the SSIM, are shown in Figure 7 for the reconstructed results. There are significant improvements after a certain number of measurements.
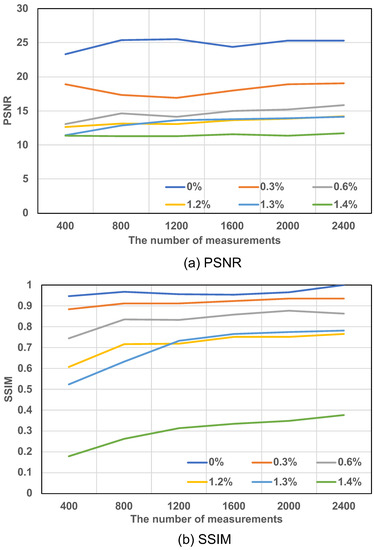
Figure 6.
Calculation results of reconstruction images with PSNR and SSIM: (a) the PSNR results for 400∼2400 measurements and 0.0%, 0.3%, 0.6%, 1.2%, 1.3%, and 1.4% concentrations and (b) the SSIM results for 400∼2400 measurements and 0.0%, 0.3%, 0.6%, 1.2%, 1.3%, and 1.4% concentrations.

Figure 7.
The reconstructed image by the DPGI method with an SSIM value of 0.7 as the boundary: (a) 1.2% concentration, left: 400 measurements, right: 800 measurements; (b) 1.3% concentration, left: 800 measurements, right: 1200 measurements.
Figure 7 shows the reconstructed images with the SSIM value of 0.7 as the threshold. Figure 7a shows the image in 1.2% concentration solution of 400 measurements compared with 800 measurements, with the SSIM values of 0.60 and 0.71, respectively. There is a big difference between the SSIM values of 0.6 and 0.7 in recognition of the target. However, the PSNR value of 13.04 with 400 measurements, and that of 13.10 with 800 measurements, represents only a small difference. Figure 7b shows the images in a 1.3% concentration solution with the SSIM values. The letter “E” is still difficult to recognize at an SSIM value of 0.61 with 800 measurements, but it is easily recognizable at an SSIM value of 0.71 with 1200 measurements. The related PSNR values are 13.64 and 13.79, respectively, and again with only a small difference. The value of SSIM is consistent with that in (a), where 0.7 is the boundary of the recognition.
To summarize, it is difficult to distinguish image reconstruction with the PSNR method because of the large sensitivity to each pixel. Additionally, the solution has a random scattering, which may affect each pixel, while the SSIM method has a structural comparison and can judge whether the image reconstruction with the letter “E” is recognizable. A high concentration of the solution will increase the number of measurements required for reconstruction.
4. Discussion
Figure 8 shows the relationship between the extinction coefficient of the solution and the target-surrounding parts’ contrast of the reconstructed image. From reconstructed images, the contrast of the letter “E” varies with the scattering of the solution. The target-surrounding parts’ contrast is the ratio of the reconstructed image’s target and the surrounding parts’ light intensities. The results of the DPGI method are obtained by comparing 2400 measurement images with different concentrations. The horizontal axis is the extinction coefficient with different concentrations of solution, and the vertical axis is the contrast of the light intensity of the target and surrounding parts. The extinction coefficient is calculated by Beer–Lambert law, which is the ratio of incident light to transmitted light intensities. The incident light intensity is the OCT interference light intensity through the pure water, and the transmitted light intensity is the transmitted light OCT interference intensity through each concentration solution. The following formula is used to calculate the contrast:
where, and represent the surrounding and target parts’ average light intensity. The larger value of the contrast indicates that the target part of the reconstructed image is receiving less scattered light. The closer the contrast value is to 0, the less the intensity difference between the target and the surrounding parts, and the more scattered the target part affected. The correlation coefficient obtained is −0.94, indicating that the extinction coefficient is significantly and negatively correlated with the contrast of the light intensity of the target part to that of the surrounding part of the reconstructed image. The correlation coefficient is the ratio of the covariance and standard deviation of the two different data. The optical properties of the scattering media can be determined from the contrast between the target and the surrounding parts of the reconstructed image.
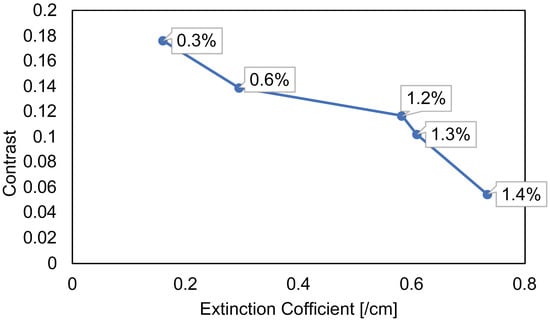
Figure 8.
The relationship between the extinction coefficient and the target-surrounding parts’ contrast in 2400 measurements by the DPGI method.
The optical properties of the solution are discussed by combining OCT interference intensity with reconstructed images. Figure 9 shows the relationship between the extinction coefficient of the solution and the scattered intensity of the reconstructed image’s average pixel. The horizontal axis is the extinction coefficient with different solution concentrations, and the vertical axis is the scattered intensity of the reconstructed image. The scattered intensity of the reconstructed image is shown in the following:
where is the OCT interference intensity of pure water and is the pixel intensity of the reconstruction image of pure water. is the transmitted OCT interference intensity of each concentration, and is the pixel intensity of the reconstruction image at each concentration. N and M are the number of horizontal and vertical speckles, which is 10. The correlation coefficient was 0.99. The extinction coefficient is significantly correlated with the scattered light intensity of the reconstructed image. The average value of the pixel of the reconstructed image in the DPGI method is certificated by the actual OCT interference light intensity. The total light intensity of the solution is adapted to the result of GI reconstruction, which can rearrange the solution’s actual OCT interference scattered light intensity distribution. The combination with OCT interference light intensity gives the solution’s scattered light intensity distribution.
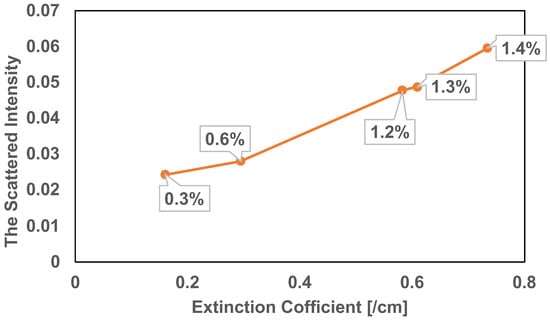
Figure 9.
The relationship between the extinction coefficient and the scattered light intensity.
The next work is to complete the mathematical models. Mathematical models require more precise resolution and a large amount of experimental data. However, to get to this step, solving computation and measurement time problems is necessary. A higher resolution will require more measurement time to obtain a good result, and the amount of calculation will also increase exponentially. When discussing the cross-sectional resolution limits of the method, the resolution can reach a single micromirror size of the DMD, and it is μm. However, it will require so much measurement time and a longer computation time. The DMD currently in use is a usual commercial device, and its maximum output frame rate is limited to 240 Hz. Using a special DMD will improve measurement speed and accuracy, as well as shorten measurement times. At the same time, a large amount of measurement data can use deep learning to speed up the calculation. GI-OCT has great potential in the medical field under the measurement’s resolution, and speed is improved. It has an important role in the observation of skin and cardiovascular structures. In addition, GI-OCT has been used to analyze the optical properties of subcutaneous capillaries, teeth, and other scattering media. It is used to identify symptoms such as broken blood vessels, tooth decay, and periodontitis [39,40,41].
5. Conclusions
To obtain the relationship between the light intensity distribution in the reconstructed images and the optical properties of the scattering media, the reconstructed images are evaluated by using GI-OCT for different concentrations of solutions with different measurements. The reconstructed images are evaluated by using PSNR and SSIM. When the reconstructed result obtains an SSIM value of over 0.7, it can be confirmed that the image is fully reconstructed, even if in the scattering media. The contrast of the target and surrounding parts in the reconstructed image is evaluated with the extinction coefficient of the scattering media, and the correlation coefficient is negatively correlated to −0.94. Moreover, the correlation coefficient between the scattered light intensity of the reconstructed image and the extinction coefficient of the scattering media is 0.99.
The relationship between the contrast and the scattered light intensity of the reconstructed image was obtained in a known solution. It can be used as a method to evaluate the optical properties of the solution in a certain concentration.
Author Contributions
Conceptualization, methodology, formal analysis, and funding acquisition, D.H. and T.S.; writing—review and editing, D.H., N.L., and T.S.; software, validation, investigation, resources, data curation, writing—original draft preparation, visualization, supervision, and project administration, D.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by JST SPRING, Grant Number JPMJSP2109.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Huang, D.; Swanson, E.A.; Lin, C.P.; Schuman, J.S.; Stinson, W.G.; Chang, W.; Hee, M.R.; Flotte, T.; Gregory, K.; Puliafito, C.A.; et al. Optical coherence tomography. Science 1991, 254, 1178–1181. [Google Scholar] [CrossRef] [PubMed]
- Gambichler, T.; Moussa, G.; Sand, M.; Sand, D.; Altmeyer, P.; Hoffmann, K. Applications of optical coherence tomography in dermatology. J. Dermatol. Sci. 2005, 40, 85–94. [Google Scholar] [CrossRef]
- Sinclair, H.; Bourantas, C.; Bagnall, A.; Mintz, G.S.; Kunadian, V. OCT for the identification of vulnerable plaque in acute coronary syndrome. JACC Cardiovasc. Imaging 2015, 8, 198–209. [Google Scholar] [CrossRef] [PubMed]
- Schwartz, M.; Levine, A.; Markowitz, O. Optical coherence tomography in dermatology. Cutis 2017, 100, 163–166. [Google Scholar] [CrossRef] [PubMed]
- Spaide, R.F.; Fujimoto, J.G.; Waheed, N.K.; Sadda, S.R.; Staurenghi, G. Optical coherence tomography angiography. Prog. Retin. Eye Res. 2018, 64, 1–55. [Google Scholar] [CrossRef]
- Vabre, L.; Dubois, A.; Boccara, C.; Vabre, L.; Dubois, A.; Boccara, C.; Vabre, L.; Dubois, A.; Boccara, A.C. Thermal-light full-field optical coherence tomography. Opt. Lett. 2002, 27, 530–532. [Google Scholar]
- Kirillin, M.Y.; Priezzhev, A.V.; Myllylä, R. Role of multiple scattering in formation of OCT skin images. Quantum Electron. 2008, 38, 570–575. [Google Scholar] [CrossRef]
- Tamaki, T.; Yuan, B.; Raytchev, B.; Kaneda, K.; Mukaigawa, Y. Multiple-scattering optical tomography with layered material. In Proceedings of the 2013 International Conference on Signal-Image Technology and Internet-Based Systems, SITIS 2013, Kyoto, Japan, 2–5 December 2013; pp. 93–99. [Google Scholar] [CrossRef]
- Tearney, G.J.; Brezinski, M.E.; Bouma, B.E.; Hee, M.R.; Southern, J.F.; Fujimoto, J.G. Determination of the refractive index of highly scattering human tissue by optical coherence tomography. Opt. Lett. 1995, 20, 2258. [Google Scholar] [CrossRef]
- Levitz, D.; Thrane, L.; Frosz, M.H.; Andersen, P.E.; Andersen, C.B.; Andersson-Engels, S.; Valanciunaite, J.; Swartling, J.; Hansen, P.R. Determination of optical scattering properties of highly-scattering media in optical coherence tomography images. Opt. Express 2004, 12, 249. [Google Scholar] [CrossRef]
- Choi, Y.; Hillman, T.R.; Choi, W.; Lue, N.; Dasari, R.R.; So, P.T.; Choi, W.; Yaqoob, Z. Measurement of the time-resolved reflection matrix for enhancing light energy delivery into a scattering medium. Phys. Rev. Lett. 2013, 111, 243901. [Google Scholar] [CrossRef]
- Lindell, D.B.; Wetzstein, G. Three-dimensional imaging through scattering media based on confocal diffuse tomography. Nat. Commun. 2020, 11, 4517. [Google Scholar] [CrossRef]
- Shapiro, J.H. Computational ghost imaging. Phys. Rev. A 2008, 78, 061802. [Google Scholar] [CrossRef]
- Katkovnik, V.; Astola, J. Compressive sensing computational ghost imaging. J. Opt. Soc. Am. A 2012, 29, 1556. [Google Scholar] [CrossRef] [PubMed]
- Bromberg, Y.; Katz, O.; Silberberg, Y. Ghost imaging with a single detector. Phys. Rev. A 2009, 79, 053840. [Google Scholar] [CrossRef]
- Ryczkowski, P.; Barbier, M.; Friberg, A.T.; Dudley, J.M.; Genty, G. Ghost imaging in the time domain. Nat. Photonics 2016, 10, 167–170. [Google Scholar] [CrossRef]
- Devaux, F.; Moreau, P.A.; Denis, S.; Lantz, E. Computational temporal ghost imaging. Optica 2016, 3, 698. [Google Scholar] [CrossRef]
- Zhao, C.; Gong, W.; Chen, M.; Li, E.; Wang, H.; Xu, W.; Han, S. Ghost imaging lidar via sparsity constraints. Appl. Phys. Lett. 2012, 101, 141123. [Google Scholar] [CrossRef]
- Chen, W.; Chen, X. Ghost imaging for three-dimensional optical security. Appl. Phys. Lett. 2013, 103, 221106. [Google Scholar] [CrossRef]
- Olivieri, L.; Gongora, J.S.T.; Peters, L.; Cecconi, V.; Cutrona, A.; Tunesi, J.; Tucker, R.; Pasquazi, A.; Peccianti, M. Hyperspectral terahertz microscopy via nonlinear ghost imaging. Optica 2020, 7, 186. [Google Scholar] [CrossRef]
- Miot, C.A.G.A.; Yczkowski, P.I.R.; Riberg, A.R.I.T.F.; Udley, J.O.H.N.M.D.; Enty, G.O.G. Ghost optical coherence tomography. Opt. Express 2019, 27, 24114–24122. [Google Scholar]
- Li, F.; Zhao, M.; Tian, Z.; Willomitzer, F.; Cossairt, O. Compressive ghost imaging through scattering media with deep learning. Opt. Express 2020, 28, 17395. [Google Scholar] [CrossRef] [PubMed]
- Gong, W.; Han, S. Correlated imaging in scattering media. Opt. Lett. 2011, 36, 394. [Google Scholar] [CrossRef]
- Vellekoop, I.M.; Mosk, A.P. Focusing coherent light through opaque strongly scattering media. Opt. Lett. 2007, 32, 2309. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Ryczkowski, P.; Friberg, A.; Dudley, J.M.; Genty, G. Temporal ghost imaging with wavelength conversion. In Proceedings of the 2019 Conference on Lasers and Electro-Optics Europe & European Quantum Electronics Conference (CLEO/Europe-EQEC), Munich, Germany, 23–27 June 2019; pp. 1–5. [Google Scholar]
- Popoff, S.M.; Lerosey, G.; Carminati, R.; Fink, M.; Boccara, A.C.; Gigan, S. Measuring the transmission matrix in optics: An approach to the study and control of light propagation in disordered media. Phys. Rev. Lett. 2010, 104, 100601. [Google Scholar] [CrossRef] [PubMed]
- Huyan, D.; Lagrosas, N.; Shiina, T. Target imaging in scattering media using ghost imaging optical coherence tomography. APL Photonics 2022, 7, 086104. [Google Scholar] [CrossRef]
- Dudley, D.; Duncan, W.M.; Slaughter, J. Emerging digital micromirror device (DMD) applications. MOEMS Disp. Imaging Syst. 2003, 4985, 14. [Google Scholar] [CrossRef]
- Hellman, B.; Takashima, Y. Angular and spatial light modulation by single digital micromirror device for multi-image output and nearly-doubled étendue. Opt. Express 2019, 27, 21477. [Google Scholar] [CrossRef]
- Zhang, Y.; Situ, G.; Pedrini, G.; Wang, D.; Javidi, B.; Osten, W. Application of short-coherence lensless Fourier-transform digital holography in imaging through diffusive medium. Opt. Commun. 2013, 286, 56–59. [Google Scholar] [CrossRef]
- Stsepuro, N.; Kovalev, M.; Krasin, G.; Podlesnykh, I.; Gulina, Y.; Kudryashov, S. Surface Depth-Mapping of Material via the Transport-of-Intensity Equation. Photonics 2022, 9, 815. [Google Scholar] [CrossRef]
- Li, J.; Zhou, N.; Sun, J.; Zhou, S.; Bai, Z.; Lu, L.; Chen, Q.; Zuo, C. Transport of intensity diffraction tomography with non-interferometric synthetic aperture for three-dimensional label-free microscopy. Light. Sci. Appl. 2022, 11, 154. [Google Scholar] [CrossRef]
- Chernomyrdin, N.V.; Skorobogatiy, M.; Gavdush, A.A.; Musina, G.R.; Katyba, G.M.; Komandin, G.A.; Khorokhorov, A.M.; Spektor, I.E.; Tuchin, V.V.; Zaytsev, K.I. Quantitative super-resolution solid immersion microscopy via refractive index profile reconstruction. Optica 2021, 8, 1471. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Shiina, T.; Moritani, Y.; Ito, M.; Okamura, Y. Long-optical-path scanning mechanism for optical coherence tomography. Appl. Opt. 2003, 42, 3795. [Google Scholar] [CrossRef] [PubMed]
- Don, M. An Introduction to Computational Ghost Imaging with Example Code; CCDC Army Research Laboratory: Aberdeen Proving Ground, MD, USA, 2019. [Google Scholar]
- Ferri, F.; Magatti, D.; Lugiato, L.A.; Gatti, A. Differential ghost imaging. Phys. Rev. Lett. 2010, 104, 253603. [Google Scholar] [CrossRef]
- Zhang, C.; Guo, S.; Cao, J.; Guan, J.; Gao, F. Object reconstitution using pseudo-inverse for ghost imaging. Opt. Express 2014, 22, 30063. [Google Scholar] [CrossRef]
- Agrawal, P.; Sanikop, S.; Patil, S. New developments in tools for periodontal diagnosis. Int. Dent. J. 2012, 62, 57–64. [Google Scholar] [CrossRef]
- Tanaka, M.; Hirano, M.; Murashima, K.; Obi, H.; Yamaguchi, R.; Hasegawa, T. 17-mm Spectroscopic Spectral-Domain Optical Coherence Tomography for Imaging Lipid Distribution Within Blood Vessel. Opt. Express 2015, 23, 6645. [Google Scholar] [CrossRef]
- Hsieh, Y.S.; Ho, Y.C.; Lee, S.Y.; Chuang, C.C.; che Tsai, J.; Lin, K.F.; Sun, C.W. Dental optical coherence tomography. Sensors 2013, 13, 8928–8949. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).