Abstract
Spatial division multiplexed (SDM) transmission systems with coherence communication technology have become an important issue in meeting the demands for the capacity of fiber. However, research on the phase noise from lasers is mainly focused on single-channel systems or single-carrier SDM systems. In this paper, a phase noise model comprising common laser phase noise, in addition to the core phase drifts induced by the SDM, is introduced and analyzed for a coherence orthogonal frequency-division multiplexing (CO-OFDM) spatial-division multiplexed transmission (SDM) system. Based on the phase noise model, the applicability of the blind phase search algorithm and the pilot-aided phase estimation algorithm is discussed and demonstrated via simulation. The results show that these two algorithms can work well when considering combined laser linewidths with core phase drifts for CO-OFDM 7-core multi-core fiber (MCF). The results mean that with the SDM phase noise model, phase noise estimation in other cores can be transferred from one core to lower the complexity with the help of the model. This research provides a proper application of the phase noise analysis of large-capacity optical communication based on a weak-coupled MCF.
1. Introduction
In order to meet the increasing demand for optical communications, spatial division multiplexed (SDM) systems have attracted much attention worldwide because of their potential to satisfy the demands for the capacity of fiber, sharing digital signal processing (DSP) resources, and integrating optical devices [1,2,3,4,5]. Moreover, to maximize the capacity and transmission length of the system, a coherent optical orthogonal frequency-division multiplexing (CO-OFDM) system with multi-level modulation formats, such as M-ary quadrature amplitude modulation (M-QAM), has been utilized as a promising candidate for long-haul optical systems because of its inherent spectral efficiency (SE) and excellent tolerance to linear impairments such as residual chromatic dispersion (CD) and polarization mode dispersion [6,7,8,9]. However, CO-OFDM systems with relatively long symbol durations can increase the sensitivity to various transmission impairments, especially serious laser phase noise (LPN), which is mainly due to imperfect linewidths of lasers at both the transmitter and the receiver. Both carrier phase error (CPE) and inter-carrier interference (ICI), due to the LPN, result in performance degradation as the orthogonality is damaged in the CO-OFDM system [10,11]. The impact of the LPN increases as the number of carriers increases. In particular, for an SDM transmission link using multi-core fibers (MCFs), the LPN is common among the SDM channels if all the channels are shared with the same light source at both the transmitter and the receiver [12]. However, temperature variations and imperfections or certain properties in different SDM links can cause phase drifts that are specific to cores. The core phase drifts can further damage the transmission performance of the CO-OFDM system. Fortunately, several papers have proposed a phase noise model considering the laser phase noise and a core phase drifts model for a single-carrier system [13,14]. The results show that these phase drifts, which are different in the optical MCF cores, are correlated with LPN. Therefore, the correlation between the laser phase noise and the core phase noise can be exploited to compensate for the LPN, especially for phase-noise-sensitive OFDM systems.
Several techniques have been presented in recent papers that deal with CPE for CO-OFDM systems with a single-core, single-mode fiber. The most widely used methods are blind phase-noise estimation (BPNE) and pilot-aided (PA) methods [15,16,17,18,19,20,21,22,23]. PA methods estimate the phase noise by transmitting pre-known data in OFDM symbols with low computational effort [15,16,17]. However, PA methods cause a loss of SE because some carriers carry pre-known symbols instead of useful data. Some techniques, such as the complex conjugate method, design the pilot to decrease the loss of SE. To further increase the SE, BPNEs, such as the blind phase search (BPS) algorithm and the Kalman Filter algorithm, have been proposed in papers [18,19,20,21,22,23]. However, the complexity of BPNEs is higher than that of PA algorithms by a factor of hundreds or even thousands. Furthermore, they also require a phase tracking scheme, either a feedback loop or digital phase tracking, for phase unwrapping to avoid the phase-uncertainty issue. In previous papers, we also proposed several PA algorithms to increase the phase compensation performance for multi-carrier systems [24,25,26]. CPE has also been analyzed for various super-channel transmission links, such as multi-core fibers, multi-mode fibers, and wavelength-division multiplexed transmission [12,27,28,29,30]. These papers for MCF hold that temperature variations, other external perturbations, and imperfections will cause phase drifts that are specific to cores. The phase shift will have a high degree of spatial correlation across the channels. The correlation can be exploited to lower the required computational complexity in DSP. These papers have demonstrated that, with the help of a new phase noise model, the algorithm for multi-core can be transferred one by one, and the complexity is lower. So far, the phase noise model with phase shift has only been analyzed in the single carrier systems. Multi-carrier systems, which are deeply affected by phase noise, are rarely reported [31].
In order to analyze the phase noise for the multi-carrier system in SDM channels, the phase noise model for single carriers systems in papers 12, 13, and 28 are introduced and modified for a CO-OFDM MCF transmission system. Based on this phase noise model, the phase noise with core-phase drifts for the multi-carrier OFDM optical transmission is deducted and analyzed. Then, the traditional estimation and compensation algorithms for OFDM are demonstrated with this phase model.
2. Phase Noise Model for the CO-OFDM SDM System
The principle and the block diagram of the CO-OFDM system for SDM transmission are shown in Figure 1. For simplicity, all the signal distortions are ideally compensated with the exception of phase noise and amplified spontaneous emission noise, which is approximated as the random walk and additive white Gaussian noise (AWGN). In addition, the phase noise and the core phase noise are highly correlated, and all the cores in the SDM share the same transmitter and local oscillator (LO) [28]. Furthermore, a baseband CO-OFDM with one polarization is considered in this paper, noting that the analysis can also be easily extended to passband optical transmission with dual-polarized OFDM systems without any difficulties.
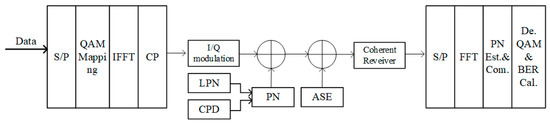
Figure 1.
Block diagram based on the proposed phase noise model for a CO-OFDM SDM system.
In this paper, the phase noise contains laser phase noise (LPN) , which is introduced by the lasers at the transmitter and local oscillator at the receiver, in addition to CPD , which is caused by the differences of the core in SDM transmission. For SDM transmission, the index D is the spatial channel. The LPN and CPD are statistically independent components and can be approximated as random walks [28]. Therefore, the discrete-time model of the laser phase noise on the n-th sample of the m-th OFDM symbol can be expressed as
where and represent the independently incremental movement of the phase noise at time i and are Gaussian distributed with zero mean and variance and . In particular, the laser phase noise is modeled as the Wiener model and , where is the combined linewidth of the transmitter and LO lasers and is the sample time. The CPD is related to the LPN, and these variances determined their corresponding phase drifts. The phase noise is statistically independent of the AWGN and other distortions and unknown at the transmitter. However, the phase noise and the relation can be estimated at the receiver. Thanks to the previous research on the SDM, the phase noise can be described as a multidimensional random walk [28]. Therefore, Equation (1) can be expressed as
where is a multivariate zero-mean Gaussian random variable with a covariance matrix [14]
In CO-OFDM systems, the m-th symbol and n-th sample time-domain OFDM symbol at the transmitter can be written as
where is the data on the k-th carrier of the m-th symbol. We assume that the chromatic dispersion is ideally compensated before the FFT on the receiver side. For simplicity, only the ASE noise and the phase noise are considered, and the received OFDM symbol can be expressed as
where is the total ASE noise generated in the optical fiber and the device in the transmission link. We assume that inter-symbol interference is absent because of the cycle period (CP). After the DFT operation, the frequency domain OFDM symbol is
where the ICI is defined as
Additionally, is given as
In Equations (6) and (8), the term is referred to as the common phase error (CPE), as it is a time-average of the phase noise drift during one OFDM symbol. Additionally, the phase-noise estimation algorithms are mainly focused on the CPE [19].
Additionally, is expressed as [19]
Based on Equations (1)–(3) and (10), also contains the laser phase noise and the core phase drift, with zero mean Gaussian noise. In addition, the variance in the LPN is modified as , where is the OFDM symbol duration. From this variance, the OFDM system is more sensitive to phase noise than single-carrier systems and has a great influence on the number of carriers because of the phase noise.
The second and third terms in Equation (6) are called the equalization-enhanced phase noise (EEPN) and are normally treated as zero mean Gaussian noise. If we write the EEPN as
Equation (6) can then be expressed as
Thus, the OFDM distortions from the phase noise can be characterized by two separate parts: one is CPE, which is the pure noise rotation from the OFDM symbol, and a mean phase deviation in one OFDM symbol. The second part is called ICI, which changes faster in one OFDM symbol and can be treated as zero mean Gaussian noise. In this case, the CO-OFDM system in the SDM transmission link with laser phase noise, in addition to the core phase drifts, converges to the linear OFDM system model with contrast-phase offset. The phase noise in SDM is a multidimensional random walk with zero mean and variance. Based on this model, CPE in the CO-OFDM SDM system can be estimated with the blind phase noise estimation algorithms and the pilot-aided phase estimation algorithms. Figure 2 shows a schematic diagram of phase noise models for the traditional MCF phase noise model and the multivariate Gaussian model.
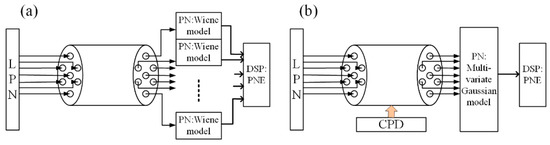
Figure 2.
Schematic diagram of phase noise model (a) traditional MCF and (b) multivariate Gaussian model.
3. Phase Noise Estimation Algorithms
The CPE in OFDM system in the standard single-mode fiber is usually estimated by BPNE or PA algorithms and compensated with good performance. However, in the SDM transmission link, the phase noise contains not only the laser phase noise but also the core phase noise, which is influenced by different core characteristics. The phase noise in the MCF is a multidimensional random walk and is rather complex compared to the SSMF. Fortunately, from the phase model proposed in Section 2, the CPE in the OFDM SDM system also has an extra phase added to the OFDM symbol, which is the same as the OFDM signal in SMF transmission. Therefore, we try to apply a blind phase search algorithm and pilot-added phase noise estimation algorithm to compensate for the phase noise.
3.1. Blind Phase Noise Estimation Algorithm
In CO-OFDM systems, BPNE can be implemented without differential bit encoding because the pre-known training sequences are inserted for channel estimation, providing the initial phase value. However, M-ary quadrature amplitude modulation (MQAM) is also utilized to increase the SE for optical transmission. In these conditions, the BPNE algorithm only estimates the phase noise [−π/4, π/4], so a phase tracking scheme is required for phase unwrapping to avoid phase uncertainty issues. Furthermore, in the SDM transmission link, the CPD is introduced to the phase noise model to increase the corrections to the phase noise in a spatial channel. As analyzed in a previous paper, the CPD is about 10–3 times greater than LPN and is affected by many parameters [28]. These reasons increase the demand for the phase noise estimation algorithm.
For common analysis, the blind phase search algorithm (BPS) is demonstrated briefly in this paper. The BPS algorithm can be proper for many modulation formats and is widely used in optical transmission. Therefore, in this paper, we apply the BPS algorithm as the BPNE to estimate the phase noise for the OFDM SDM system. From Equation (12), the OFDM signal has the same phase noise and can be treated as one data point like a single carrier system. The block diagram of BPS for the OFDM system is shown in Figure 3. The received signals contain N sample signals in one OFDM symbol. As for the BPS algorithm, in one OFDM symbol is firstly rotated by B test phase angles .
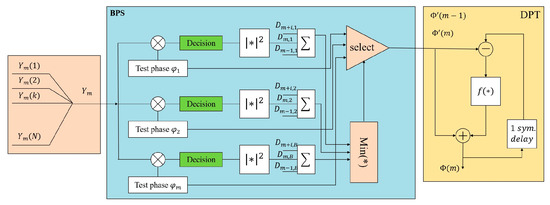
Figure 3.
Block of BPS algorithm.
Then, all rotated symbols are sent into the hard decision circuit, and the distance to the closest constellation point is calculated at the complex plane:
where represents the closest constellation point based on the hard decision. To reduce the influence of the ASE noise on the phase noise estimation, the number of this distance around the test symbol is calculated as
Based on the best distance to the constellation point, the best test phase can be selected. However, as mentioned above for BPNE, the BPNE algorithm only estimates the phase noise [−π/4, π/4]. Furthermore, the phase noise in the SDM transmission is a multidimensional random walk, which makes the PNE complex. Therefore, a phase-tracking scheme is required for phase unwrapping to avoid the phase-uncertainty issue. In this paper, digital phase tracking is analyzed and utilized in this paper for an SDM phase tracking scheme. The phase unwrapping in the OFDM system can be expressed as
3.2. Pilot-Aided Phase Noise Estimation
The pilot-aided phase noise estimation algorithm can estimate the phase noise by transmitting several pilots in each OFDM symbol, which is pre-known to the receiver. To compare the inserted pilots and the received pilots, the CPE can be approximated as [7]
where is the number of the inserting pilots, is the received l-th pilot of the m-th symbol, and is the transmitted l-th pilot of m-th symbol. Obviously, the accuracy of the CPE depends on the number of pilots with the cost of the SE.
4. Results
To evaluate the performance of the BPNE and PA algorithm for estimation in the CO-OFDM SDM transmission link, we performed the simulation using VPI TransmissionMaker and Matlab. The OFDM symbol has the same zero carriers for frequency protection and for preventing the DC influence. After 16QAM mapping, CP addition, and IFFT, the phase noise, which contains LPN in addition to CPD, is added to the time-domain OFDM symbol for transmitting. The transmission link is assumed as a seven-core weak-coupled fiber with crosstalk of -50 dB; therefore, the dimension of the PN with CPD is seven. At the receiver, after coherent detection, the OFDM signal is sent into the DSP for serial-to-parallel conversion, FFT, and OFDM demodulation. The 16QAM signal, followed by PN estimation and compensation, converts the complex signal into data bits. The received bits are compared with the transmitted bits to estimate BER.
Figure 4 compares the PN compensation with PA and BPS algorithms in terms of the required SNR against the normalized linewidth (NLW) containing laser phase noise, with the addition of core phase drifts for 128 -subcarrier 16 QAM CO-OFDM SDM systems. The required SNRs at different NLWs are the tested SNRs when the BERs achieve 3.8 × 10−3 (7% HD-FEC threshold). Different pilots (2, 4, and 8) are input instead of the data subcarriers to estimate the phase noise. In general, CPD is about 10−3 times the LPN and is used in this section. As can be seen in Figure 4, the required SNR of BPS with the DPT algorithm is always lower than that of the PA algorithm with insert pilots. The pilots are inserted evenly in this simulation. The required SNR of BPS is about 1.4 dB, 2.7 dB, and 4 dB better than that of eight pilots, four pilots, and two pilots, respectively. The more inserted pilots there are for the PA algorithm, the better the performance of the PN compensation is (as Equation (12) shows). However, the tolerances of the PA are better than those of the BPS. For the 1 dB SNR penalty, the tolerances of the NLW are 1.5 × 10−3 and 3 × 10−3 for the BPS and PA methods. When the tolerance of NLW is reached, the performance of the BPS method decreases greatly compared with PA, which is due to the fact that the PN exceeds the tested phase of BPS.
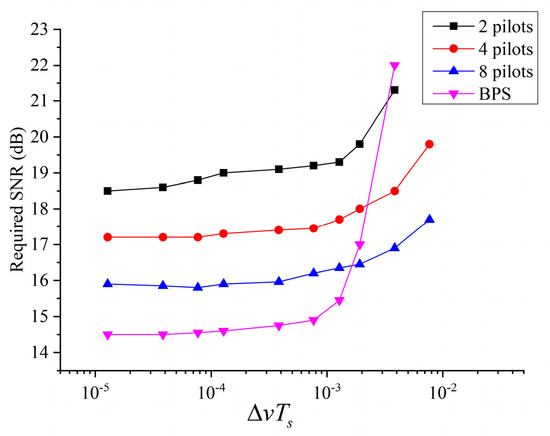
Figure 4.
The comparison for phase noise estimation with PA and BPS for the 128-sub-carrier CO-OFDM SDM system. The required SNR is tested at BER of 3.8 × 10−3 (7% HD-FEC threshold).
Next, we analyze the performance of the PN compensation for 16 QAM CO-OFDM SDM transmission links under different subcarriers. The BERs as a function of SNR are simulated at the same NLW of 2.56 × 10−4 for 64, 128, and 256 subcarriers. Figure 5a–c show that the PN compensation performances are almost the same under different subcarriers. When the HD-FEC threshold is achieved, the required SNRs are about 14.5 dB, 15.9 dB, and 17.3 dB for BPS, four insert pilots’ PA, and eight insert pilots’ PA, respectively. The performance of BPS is better than that of PA (about 1.4 dB for eight insert pilots and 3 dB for four insert pilots) for random subcarriers. The results indicate that the PN compensation performance mainly depends on the PNE algorithm and is little affected by the number of subcarriers. In order to deeply analyze the influence of the subcarriers on the PN compensation, BERs as a function of SNR under different carriers are demonstrated with BPS and PA with eight insert pilots. The required SNR for different subcarriers is almost the same (less than 0.1 dB) at the HD-FEC. Thus, the BPS-DPT with the 32-test-phase algorithm has a better performance compared with the PA algorithm. Additionally, the performance under the same NLW is almost the same under different subcarriers with the same PNE algorithm.
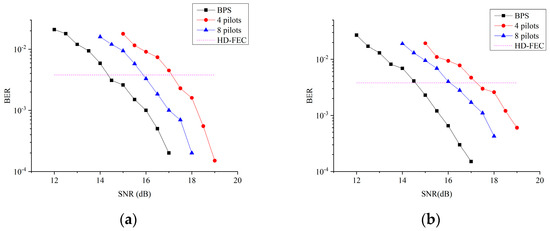
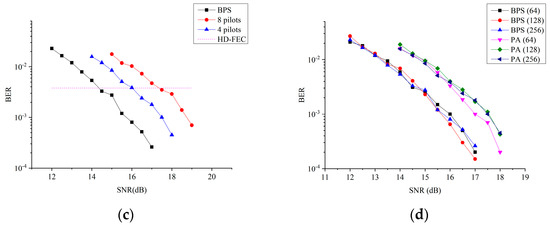
Figure 5.
BER as a function of SNR for the CO-OFDM SDM transmission link under different subcarriers ((a): 64 subcarriers, (b): 128 subcarriers, (c): 256 subcarriers, and (d): performance under different subcarriers). (a) N = 64. (b) N = 128. (c) N = 256.
In general, the laser phase noise, which mainly depends on the linewidths of the lasers at the transmitters and the LO at the receivers, needs the PNE algorithm to compensate for it. Nowadays, the linewidths of commercial lasers are about 100 kHz for extra-cavity lasers (ECLs) or 1 MHz for distributed-feedback lasers (DFBs). Therefore, a comfortable PNE algorithm should cover the linewidths of the lasers, and a larger NLW tolerance is better. In the SDM transmission link, the CPD, which is added to LPN, makes the system more sensitive. The required SNRs under different NLWs for 16 CO-OFDM SDM systems with LPN and CPD are compared between BPS-DPT and the PA algorithm for eight inserted pilots in Figure 6. The CPD is set to 10-3 of the LPN for coherent seven-core MCFs, which means the covariance of the PN with LPN and CPD is a seven-dimensional matrix. The BPS performs about 1.5 dB better than the PA algorithm. The number of carriers has little influence on the PN compensation, and only a 0.2 dB SNR penalty is needed between 64 and 256 subcarriers. The results show that BPS performs better in terms of required OSNR, while PA performs better in terms of tolerance NLW. The tolerance NLW is the linewidth at which the 1 dB SNR penalty is used when the BER achieves HD-FEC. This means that with lower SNR for long-haul transmissions, the BPS is preferred, and with a larger-linewidth laser, the PA algorithm may be preferred.
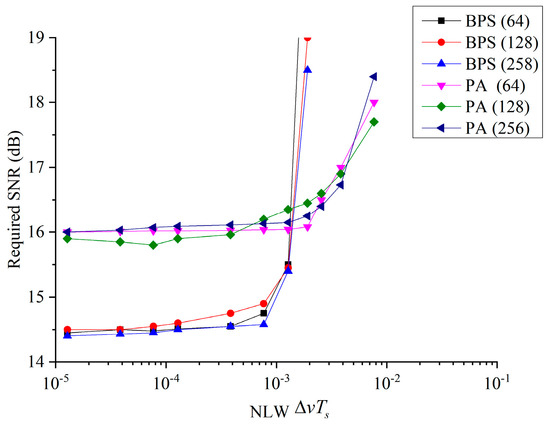
Figure 6.
NLW tolerance for the PA and BPS algorithms under different subcarriers.
For the SDM transmission link, the PN contains LPN and CPD, which is a multidimensional random walk. As is analyzed in a previous paper, is a normal value for weak-coupled multi-core fiber coherent transmission. However, the CPD introduced by the crosstalk in the cores of the MCF is different for different MCF distances. The BER as a function of the SNR with the difference between CPD and LPN is demonstrated in Figure 7. The ratios of LPN and CPD are set to 5 × 102, 1 × 103, 2 × 103, and 4 × 103, respectively. Figure 7a–c show that the performance of the ratio and the subcarrier is almost the same. The main difference in the performance comes from the algorithm. With different ratios of LPN and CPD, the required SNRs are almost equal. A faint SNR difference in the ratio was shown between different numbers of subcarriers, namely that the required SNR for 256 changed less than that of 64 subcarriers.
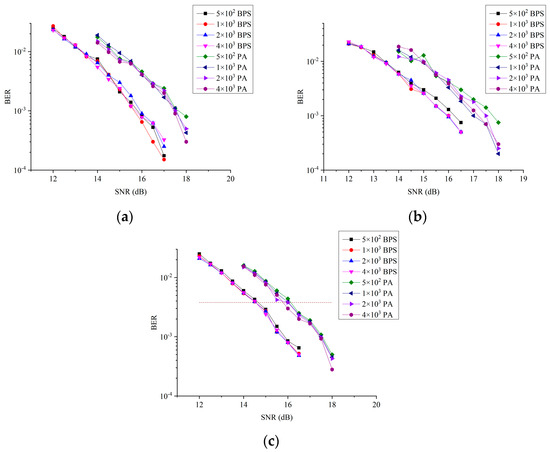
Figure 7.
BER vs. SNR with the difference between CPD and LPN. (a) N = 64. (b) N = 128. (c) N = 256.
In order to assess the complexity of the BPNE and the PA algorithm, we estimated the real-valued multiplications because multiplication costs more hardware resources than adders, sign changes, and other operations. In general, a complex-value multiply operation should occupy four real-value multiplications. As stated in the above introduction, we can calculate the complexity of the BPS and the PA algorithm. In this paper, we apply BPS with DPT as the BPNE for phase noise estimation and fix the number of test phases to 32 for 16QAM. In BPS, the number of test phases has the most importance to the accuracy of the CPE. However, the larger number of test phases can greatly increase the complexity. In general, for BPS in traditional transmission links, there should be at least 16 test phases for 16QAM to obtain acceptable performance. For OFDM’s SDM transmission link, considering the complexity of the phase noise with CPD, we apply 32 test phases to estimate the phase noise. For comparison, the step of reducing the ASE noise in the BPS is neglected. To sum up, the complexity descriptions of the BPS-DPT and the PA algorithm are shown in Table 1. The table shows that BPS has more complexity than PA for multiplications. Furthermore, through simple calculation, the number of adders is also bigger than that achieved by using the PA algorithm.

Table 1.
Complexity comparison and SE loss between the BPS-DFT algorithm and the PA algorithm in terms of the multiplications.
5. Conclusions
In this paper, the carriers’ phase-noise estimation for the CO-OFDM system with an SDM transmission link is studied. The phase-noise model, which can be seen as a multidimensional random walk, is demonstrated with laser phase noise in addition to the core phase drift. With the proposed multidimensional phase noise model, the transmission performance is simulated and analyzed based on the blind phase estimation algorithm (BPS) and the pilot-aided algorithm with a different number of insert pilots for 16QAM CO-OFDM 7-core multi-core fibers. The results show that the different performance under different parameters mainly comes from the algorithms and about 1.4 dB SNR penalties between BPS-DPT and eight inserted pilots’ PA. However, the PA has a better tolerance NLW than BPS from 1.5 × 10−3 to 3 × 10−3. Furthermore, the ratio of LPN and CPD, the number of subcarriers, and the number of inserted pilots are also demonstrated in this paper. The results show that the traditional phase-noise algorithms can also perform well for multi-carrier SDM systems considering the core phase drift. This means that with the SDM phase noise model, only multi-channel parallel phase noise algorithms can be considered without the difference between the cores for weak-coupled SDMs. These studies can also help to redesign the phase-noise compensation algorithms based on the traditional algorithms and the correlation between the cores of MCFs. The results and discussions may have a better influence on the CPE research for SDM transmission links.
Author Contributions
All authors contributed extensively to the work presented in this paper. Conceptualization, L.Y.; methodology, G.J.; software, G.J. and L.Y.; validation, G.J. and L.Y.; formal analysis, L.Y.; investigation, G.J.; resources, G.J. and L.Y.; data curation, L.Y.; writing—original draft preparation, G.J. and L.Y.; writing—review and editing, G.J. and L.Y.; supervision, L.Y.; project administration, G.J. and L.Y.; funding acquisition, G.J. and L.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China 62001181 and the Knowledge Innovation Program of Wuhan-Shuguang Project 202201080102335.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data can be requested from the authors by email.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Puttnam, B.J.; Luis, R.S.; Mendinueta, J.-M.D.; Sakaguchi, J.; Klaus, W.; Awaji, Y.; Wada, N.; Kanno, A.; Kawanishi, T. Long Distance Transmission in a Multi-Core Fiber with Self-Homodyne Detection. In Proceedings of the Optical Fiber Communication Conference, Los Angeles, CA, USA, 22–26 March 2015; p. Th1D.5. [Google Scholar]
- Richardson, D.J.; Fini, J.M.; Nelson, L.E. Space-division multiplexing in optical fibers. Nat. Photonics 2013, 7, 354–362. [Google Scholar] [CrossRef]
- Agrawal, G.P.; Mumtaz, S.; Essiambre, R.J. Nonlinear Performance of SDM Systems Designed with Multimode or Multicore Fibers. In Proceedings of the Optical Fiber Communication Conference and Exposition and the National Fiber Optic Engineers Conference (OFC/NFOEC), Anaheim, CA, USA, 17–21 March 2013. [Google Scholar]
- Puttnam, B.J.; Luis, R.; Delgado-Mendinueta, J.-M.; Sakaguchi, J.; Klaus, W.; Awaji, Y.; Wada, N.; Kanno, A.; Kawanishi, T. High-capacity self-homodyne PDM-WDM-SDM transmission in a 19-core fiber. Opt. Express 2014, 22, 21185. [Google Scholar] [CrossRef] [PubMed]
- Antonelli, C.; Mecozzi, A.; Golani, O.; Shtaif, M. Nonlinear Propagation in Fibers for Space Division Multiplexing. In CLEO: Science and Innovations, Proceedings of the Lasers and Electro-Optics, San Jose, CA, USA, 14–19 May 2017; Optica Publishing Group: Washington, WA, USA, 2017. [Google Scholar]
- Chen, X.; He, J.; Che, D.; Shieh, W. Hybrid Modulated Multiband Coherent Optical OFDM for Low-Complexity Phase Noise Compensation. J. Light. Technol. 2015, 33, 126–132. [Google Scholar] [CrossRef]
- Le, S.T.; Kanesan, T.; Giacoumidis, E.; Doran, N.J.; Ellis, A.D. Quasi-Pilot Aided Phase Noise Estimation for Coherent Optical OFDM Systems. IEEE Photonics Technol. Lett. 2014, 26, 504–507. [Google Scholar] [CrossRef]
- You, B.; Yang, L.; Luo, F.; Yang, S.; Chen, D.; Ni, Y.; Li, B.; Liu, D. Pilot-based Extended Kalman Filter for Phase Noise Estimation in CO-FBMC/OQAM Systems. Opt. Commun. 2019, 443, 116–122. [Google Scholar] [CrossRef]
- Tomba, L. On the effect of Wiener phase noise in OFDM systems. IEEE Trans. Commun. 1998, 46, 580–583. [Google Scholar] [CrossRef]
- Hong, X.; Hong, X.; Zhang, J.; He, S. Low-complexity linewidth-tolerant time domain sub-symbol optical phase noise suppression in CO-OFDM systems. Opt. Express 2016, 24, 4856. [Google Scholar] [CrossRef]
- Taylor, M.G. Phase Estimation Methods for Optical Coherent Detection Using Digital Signal Processing. J. Light. Technol. 2009, 27, 901–914. [Google Scholar] [CrossRef]
- Feuer, M.D.; Nelson, L.E.; Zhou, X.; Woodward, S.L.; Isaac, R.; Zhu, B.; Taunay, T.F.; Fishteyn, M.; Fini, J.M.; Yan, M.F. Joint Digital Signal Processing Receivers for Spatial Superchannels. IEEE Photonics Technol. Lett. 2012, 24, 1957–1960. [Google Scholar] [CrossRef]
- Souto, D.V.; Olsson, B.-E.; Larsson, C.; Mello, D.A.A. Joint-Polarization and Joint-Subchannel Carrier Phase Estimation for 16-QAM Optical Systems. J. Light. Technol. 2012, 30, 3185–3191. [Google Scholar] [CrossRef]
- Alfredsson, A.F.; Agrell, E.; Wymeersch, H.; Puttnam, B.J.; Rademacher, G.; Luis, R.S.; Karlsson, M. Pilot-Aided Joint-Channel Carrier-Phase Estimation in Space-Division Multiplexed Multicore Fiber Transmission. J. Light. Technol. 2019, 37, 1133–1142. [Google Scholar] [CrossRef]
- Hussin, S.; Puntsri, K.; Noe, R. Analysis of Partial Pilot Filling Phase Noise Compensation for CO-OFDM Systems. IEEE Photonics Technol. Lett. 2013, 25, 1099–1102. [Google Scholar] [CrossRef]
- Chen, X.; He, J.; Che, D.; Shieh, W. Low Complexity Phase Noise Compensation for Multiband Coherent Optical OFDM. In Proceedings of the 2014 OptoElectronics and Communication Conference and Australian Conference on Optical Fibre Technology, Melbourne, VIC, Australia, 6–10 July 2014. [Google Scholar]
- Zhou, X.; Yang, X.; Li, R.; Long, K. Efficient Joint Carrier Frequency Offset and Phase Noise Compensation Scheme for High-Speed Coherent Optical OFDM Systems. J. Light. Technol. 2013, 31, 1755–1761. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Le, S.T.; Wuilpart, M.; Yakusheva, T.; Mégret, P. Simplified extended Kalman filter phase noise estimation for CO-OFDM trans-missions. Opt. Express 2017, 25, 27247–27261. [Google Scholar] [CrossRef]
- Le, S.T.; Haigh, P.A.; Ellis, A.D.; Turitsyn, S.K. Blind Phase Noise Estimation for CO-OFDM Transmissions. J. Light. Technol. 2016, 34, 745–753. [Google Scholar] [CrossRef]
- Colavolpe, G.; Foggi, T.; Forestieri, E.; Secondini, M. Impact of Phase Noise and Compensation Techniques in Coherent Optical Systems. J. Light. Technol. 2011, 29, 2790–2800. [Google Scholar] [CrossRef]
- Xiang, M.; Fu, S.; Deng, L.; Tang, M.; Shum, P.; Liu, D. Low-complexity feed-forward carrier phase estimation for M-ary QAM based on phase search acceleration by quadratic approximation. Opt. Express 2015, 23, 19142–19153. [Google Scholar] [CrossRef]
- Yankov, M.P.; Fehenberger, T.; Barletta, L.; Hanik, N. Low-Complexity Tracking of Laser and Nonlinear Phase Noise in WDM Optical Fiber Systems. J. Light. Technol. 2015, 33, 4975–4984. [Google Scholar] [CrossRef]
- Zhou, X.; Zhong, K.; Gao, Y.; Lu, C.; Lau, A.P.T.; Long, K. Modulation-format-independent blind phase search algorithm for coherent optical square M-QAM systems. Opt. Express 2014, 22, 24044–24054. [Google Scholar] [CrossRef]
- You, B.; Luo, F.; Yang, L.; Yang, S.; Chen, D.; Ni, Y.; Li, B.; Liu, D. Joint Carrier Frequency Offset and Phase Noise Compensation Scheme for Coherent Optical FBMC/OQAM Systems. In Proceedings of the Second Symposium on Novel Technology of X-Ray Imaging, Beijing, China, 10 May 2019; Volume 11068. [Google Scholar]
- You, B.; Yang, L.; Luo, F.; Fu, S.; Yang, S.; Li, B.; Liu, D. Joint Carrier Frequency Offset and Phase Noise Estimation Based on Pseudo-Pilot in CO-FBMC/OQAM System. IEEE Photonics J. 2019, 11, 1–11. [Google Scholar] [CrossRef]
- Hu, H.; Luo, F.; Yang, L.; Yang, S.; Li, B. RF-pilot-based partition phase correction for CO-OFDM system phase noise mitigation. Opt. Eng. 2018, 57, 056111. [Google Scholar] [CrossRef]
- Uden, R.G.H.; Okonkwo, C.M.; Sleiffe, V.A.J.M.; Kuschnerov, M.; Waardt, H.d.; Koonen, A.M.J. Single DPLL Joint Carrier Phase Compensation for Few-Mode Fiber Transmission. IEEE Photonics Technol. Lett. 2013, 25, 1381–1384. [Google Scholar] [CrossRef]
- Alfredsson, A.; Agrell, E.; Wymeersch, H. Iterative Decoding and Phase-Noise Compensation for Multichannel Optical Transmission. IEEE Trans. Commun. 2018, 67, 5532–5543. [Google Scholar] [CrossRef]
- Mazur, M.; Lorences-Riesgo, A.; Schroeder, J.; Andrekson, P.A.; Karlsson, M. High Spectral Efficiency PM-128QAM Comb-Based Superchannel Trans-mission Enabled by a Single Shared Optical Pilot Tone. J. Light. Technol. 2018, 36, 1318–1325. [Google Scholar] [CrossRef]
- Lundberg, l.; Mazur, M.; Lorences-Riesgo, A.; Karlsson, M.; Andrekson, P.A. Joint carrier recovery for DSP complexity reduction in frequency comb-based superchannnel transceivers. In Proceedings of the 2017 European Conference on Optical Communication (ECOC), Gothenburg, Sweden, 17–21 September 2017; p. Th1D.3. [Google Scholar]
- Alfredsson, A.F.; Agrell, E.; Wymeersch, H.; Karlsson, M. Phase noise compensation for spatial division multiplexed transmission. In Proceedings of the Optical Fiber Communication Conference, Los Angeles, CA, USA, 19–23 March 2017; p. Th4C.7. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).