On the Possibility of Intense Unipolar THz Pulses Formation in Nonhomogeneous Nonequilibrium Nitrogen Plasma Channels
Abstract
1. Introduction
2. 3D Model
3. Results and Discussion
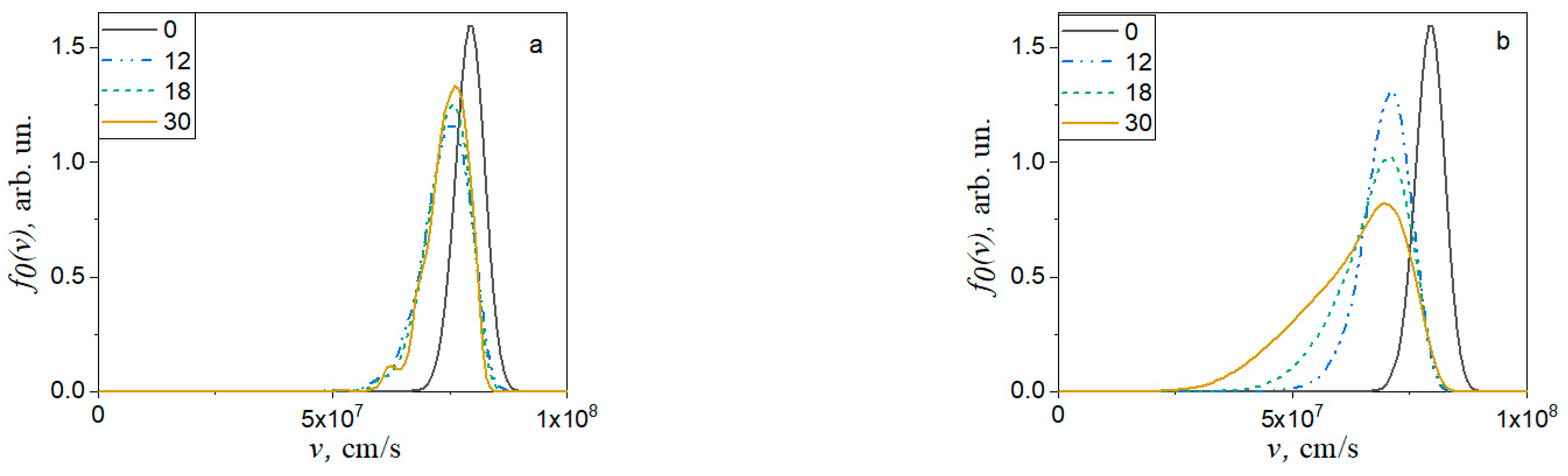
3.1. Amplification in the Nonequilibrium Plasma Channel and Formation of the Unipolar THz pulses
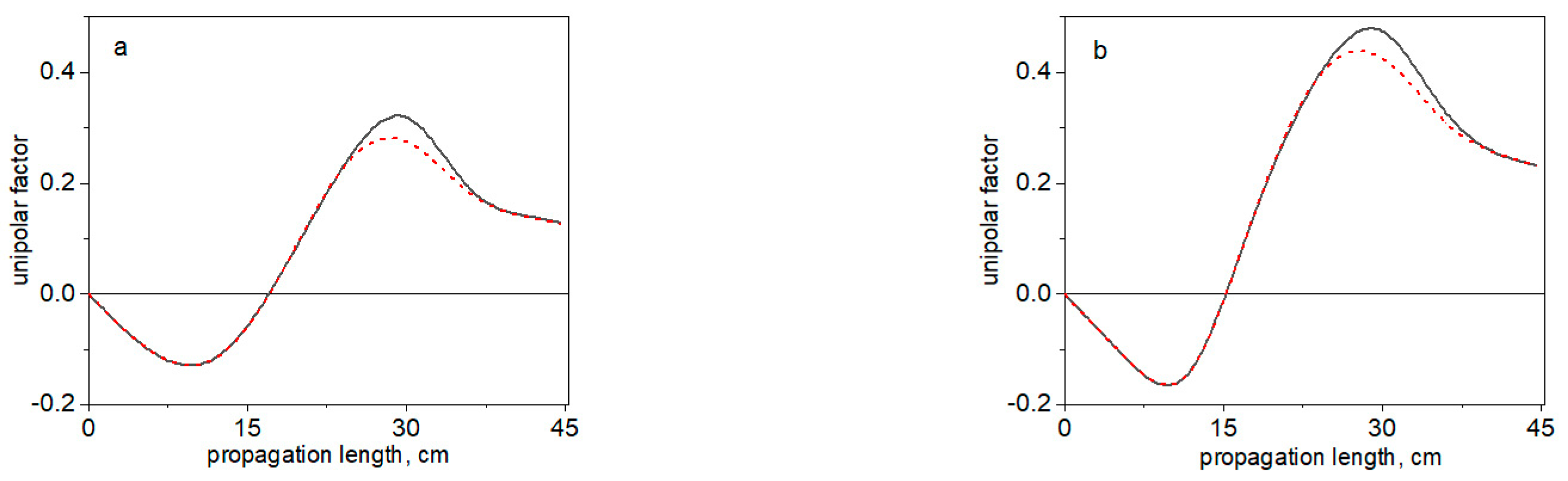
3.2. Transferring of the Unipolar THz Pulse out of Plasma Channel
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Manzoni, C.; Mucke, O.D.; Cirmi, G.; Fang, S.; Moses, J.; Huang, S.W.; Hong, K.H.; Cerullo, G.; Kartner, F.X. Coherent pulse synthesis: Towards sub-cycle optical waveforms. Laser Photon. Rev. 2015, 9, 129. [Google Scholar] [CrossRef]
- Hassan, M.; Luu, T.; Moulet, A.; Raskazovskaya, O.; Zhokhov, P.; Garg, M.; Karpowicz, N.; Zheltikov, A.M.; Pervak, V.; Krausz, F.; et al. Optical attosecond pulses and tracking the nonlinear response of bound electrons. Nature 2016, 530, 66–70. [Google Scholar] [CrossRef] [PubMed]
- Yoshioka, K.; Igarashi, I.; Yoshida, S.; Arashida, Y.; Katayama, I.; Takeda, J.; Shigekawa, H. Subcycle mid-infrared coherent transients at 4 MHz repetition rate applicable to light-wave-driven scanning tunneling microscopy. Opt. Lett. 2019, 44, 5350–5353. [Google Scholar] [CrossRef] [PubMed]
- Arkhipov, R.; Arkhipov, M.; Pakhomov, A.; Babushkin, I.; Rosanov, N. Half-cycle and unipolar pulses (Topical Review). Las. Phys. Lett. 2022, 19, 043001. [Google Scholar] [CrossRef]
- Chai, X.; Ropagnol, X.; Raeis-Zadeh, S.M.; Reid, M.; Safavi-Naeini, S.; Ozaki, T. Subcycle Terahertz Nonlinear Optics. Phys. Rev. Lett. 2018, 121, 143901. [Google Scholar] [CrossRef]
- Arkhipov, R.; Pakhomov, A.; Arkhipov, M.; Babushkin, I.; Demircan, A.; Morgner, U.; Rosanov, N. Unipolar subcycle pulse-driven nonresonant excitation of quantum systems. Opt. Lett. 2019, 44, 1202–1205. [Google Scholar] [CrossRef] [PubMed]
- Arkhipov, R.; Pakhomov, A.; Arkhipov, M.; Demircan, A.; Morgner, U.; Rosanov, N.; Babushkin, I. Selective ultrafast control of multi-level quantum systems by subcycle and unipolar pulses. Opt. Express. 2020, 28, 17020–17034. [Google Scholar] [CrossRef] [PubMed]
- Ramasesha, K.; Leone, S.R.; Neumark, D.M. Real-time probing of electron dynamics using attosecond time-resolved spectroscopy. Ann. Rev. Phys. Chem. 2016, 67, 41. [Google Scholar] [CrossRef]
- Rosanov, N. On acceleration of a relativistic particle by a radiation pulse. Opt. Spectrosc. 2019, 126, 140–143. [Google Scholar] [CrossRef]
- Rosanov, N.; Tumakov, D.; Arkhipov, M.; Arkhipov, R. Criterion for the yield of micro-object ionization driven by few- and subcycle radiation pulses with nonzero electric area. Phys. Rev. A 2021, 104, 063101. [Google Scholar] [CrossRef]
- Sajadi, M.; Wolf, M.; Kampfrath, T. Transient birefringence of liquids induced by terahertz electric-field torque on permanent molecular dipoles. Nat. Commun. 2017, 8, 14963. [Google Scholar] [CrossRef] [PubMed]
- Pakhomov, A.; Arkhipov, M.; Rosanov, N.; Arkhipov, R. Ultrafast control of vibrational states of polar molecules with subcycle unipolar pulses. Phys. Rev. A 2022, 105, 043103. [Google Scholar] [CrossRef]
- Arkhipov, R.; Arkhipov, M.; Rosanov, N. Unipolar light: Existence, generation, propagation, and impact on microobjects. Quantum Electron. 2020, 50, 801–815. [Google Scholar] [CrossRef]
- You, D.; Bucksbaum, P.H. Propagation of half-cycle far infrared pulses. J. Opt. Soc. Am. B 1997, 14, 1651–1655. [Google Scholar] [CrossRef]
- Arkhipov, M.; Arkhipov, R.; Rosanov, N. Obtaining Unipolar Pulses at Far Field Zone of the Source. Opt. Spectrosc. 2021, 129, 1193–1195. [Google Scholar] [CrossRef]
- Bessonov, E.G. On a class of electromagnetic waves. Sov. Phys. JETP 1981, 53, 433. [Google Scholar]
- Rosanov, N. Area of ultimately short light pulses. Opt. Spectrosc. 2009, 107, 721–725. [Google Scholar] [CrossRef]
- Bogatskaya, A.; Volkova, E.; Popov, A. Unipolar terahertz pulse formation in a nonequilibrium plasma channel formed by an ultrashort uv laser pulse. Phys. Rev. E 2021, 104, 025202. [Google Scholar] [CrossRef]
- Arkhipov, R.; Pakhomov, A.; Arkhipov, M.; Babushkin, I.; Tolmachev, Y.; Rosanov, N. Generation of unipolar pulses in nonlinear media. JETP Lett. 2017, 105, 408–418. [Google Scholar] [CrossRef]
- Sazonov, S. Soliton-like unipolar objects in nonequilibrium dissipative media. Laser Phys. Lett. 2021, 18, 105401. [Google Scholar] [CrossRef]
- Shou, Y.; Hu, R.; Gong, Z.; Yu, J.; Chen, J.; Mourou, G.; Yan, X.; Ma, W. Cascaded generation of isolated sub-10 attosecond half-cycle pulses. N. J. Phys. 2021, 23, 053003. [Google Scholar] [CrossRef]
- Bogatskaya, A.; Volkova, E.; Popov, A. New method of unipolar THz pulse generation in photoionised xenon plasma. Plasma Sources Sci. Technol. 2021, 30, 085001. [Google Scholar] [CrossRef]
- Zhang, D.; Bai, Y.; Zeng, Y.; Ding, Y.; Li, Z.; Zhou, C.; Leng, Y.; Song, L.; Tian, Y.; Li, R. Towards high-repetition-rate intense terahertz source with metal wire-based plasma. IEEE Photon. J. 2022, 14, 5910605. [Google Scholar] [CrossRef]
- Sychugin, S.; Novokovskaya, A.; Bakunov, M. Propagation dynamics of optically generated unipolar electromagnetic pulses. Phys. Rev. A 2022, 105, 053528. [Google Scholar] [CrossRef]
- Bogatskaya, A.; Popov, A. On the possibility of the amplification of subterahertz electromagnetic radiation in a plasma channel created by a high intensity ultrashort laser pulse. JETP Lett. 2013, 97, 388. [Google Scholar] [CrossRef]
- Bogatskaya, A.; Smetanin, I.; Volkova, E.; Popov, A.M. Guiding and amplification of microwave radiation in a plasma channel created in gas by intense ultraviolet laser pulse. Las. Part. Beams 2015, 33, 17. [Google Scholar] [CrossRef]
- Bogatskaya, A.; Bin, H.; Popov, A.; Smetanin, I. Nonequilibrium laser plasma of noble gases: Prospects for amplification and guiding of the microwave radiation. Phys. Plasmas 2016, 23, 093510. [Google Scholar] [CrossRef]
- Phelps, A.; Pitchford, L. Anisotropic scattering of electrons by N2 and its effect on electron transport. Phys. Rev. A 1985, 31, 2932. [Google Scholar] [CrossRef]
- Bogatskaya, A.; Volkova, E.; Popov, A. On the possibility of a short subterahertz pulse amplification in a plasma channel created in air by intense laser radiation. J. Phys. D 2014, 47, 185202. [Google Scholar] [CrossRef]
- Bogatskaya, A.; Volkova, E.; Popov, A. Nonequilibrium plasma channel in gaseous media formed by powerful UV laser as a waveguide for transportation and amplification of short microwave pulses. Laser Phys. Lett. 2015, 12, 035301. [Google Scholar] [CrossRef]
- Bogatskaya, A.; Volkova, E.; Popov, A. The response of nonequilibrium nonstationary plasma created by an intense femtosecond UV laser pulse in rare gases to the emission of the THz frequency band. Laser Phys. Lett. 2019, 16, 066008. [Google Scholar] [CrossRef]
- Bogatskaya, A.; Volkova, E. 3D modeling of short THz pulse propagation and amplification in the nonequilibrium plasma channel. JOSA B 2022, 39, 299. [Google Scholar] [CrossRef]
- Seifert, T.; Jaiswal, S.; Sajadi, M.; Jakob, G.; Winner, S.; Wolf, M.; Kläui, M.; Kampfrath, T. Ultrabroadband single-cycle terahertz pulses with peak fields of 300 kV cm−1 from a metallic spintronic emitter. Appl. Phys. Lett. 2017, 110, 252402. [Google Scholar] [CrossRef]
- Balčiūnas, T.; Lorenc, D.; Ivanov, M.; Smirnova, O.; Zheltikov, A.; Dietze, D.; Unterrainer, K.; Rathje, T.; Paulus, G.; Baltuška, A.; et al. CEP-stable tunable THz-emission originating from laser-waveform-controlled sub-cycle plasma-electron bursts. Opt. Express 2015, 23, 15278. [Google Scholar] [CrossRef] [PubMed]
- Ginzburg, V.; Gurevich, A. Nonlinear phenomena in a plasma located in an altering electromagnetic field. Sov. Phys. Usp. 1960, 3, 115. [Google Scholar] [CrossRef]
- Raizer, Y. Laser-Induced Discharge Phenomena; Consultants Bureau: New York, NY, USA, 1977. [Google Scholar]
- Zvorykin, V.D.; Goncharov, S.A.; Ionin, A.A.; Mokrousova, D.V.; Ryabchuk, S.V.; Seleznev, L.V.; Sunchugasheva, E.S.; Ustinovskii, N.N.; Shutov, A.V. Experimental capabilities of the GARPUN MTW Ti: Sapphire—KrF laser facility for investigating the interaction of subpicosecond UV pulses with targets. Quantum Electron. 2017, 47, 319. [Google Scholar] [CrossRef]
- Shipilo, D.E.; Panov, N.A.; Suchungasheva, E.S.; Mokrousova, D.V.; Shutov, A.V.; Zvorykin, V.D.; Ustinovskii, N.N.; Seleznev, L.V.; Savel’ev, A.B.; Kosareva, O.G.; et al. Fifteen meter long uninterrupted filaments from sub-terawatt ultraviolet pulse in air. Opt. Express 2017, 25, 25386. [Google Scholar] [CrossRef] [PubMed]
- Chekalin, S.V.; Kandidov, V.P. From self-focusing light beams to femtosecond laser pulse filamentation. Phys. Usp. 2013, 56, 123. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bogatskaya, A.V.; Volkova, E.A.; Popov, A.M. On the Possibility of Intense Unipolar THz Pulses Formation in Nonhomogeneous Nonequilibrium Nitrogen Plasma Channels. Photonics 2023, 10, 113. https://doi.org/10.3390/photonics10020113
Bogatskaya AV, Volkova EA, Popov AM. On the Possibility of Intense Unipolar THz Pulses Formation in Nonhomogeneous Nonequilibrium Nitrogen Plasma Channels. Photonics. 2023; 10(2):113. https://doi.org/10.3390/photonics10020113
Chicago/Turabian StyleBogatskaya, Anna V., Ekaterina A. Volkova, and Alexander M. Popov. 2023. "On the Possibility of Intense Unipolar THz Pulses Formation in Nonhomogeneous Nonequilibrium Nitrogen Plasma Channels" Photonics 10, no. 2: 113. https://doi.org/10.3390/photonics10020113
APA StyleBogatskaya, A. V., Volkova, E. A., & Popov, A. M. (2023). On the Possibility of Intense Unipolar THz Pulses Formation in Nonhomogeneous Nonequilibrium Nitrogen Plasma Channels. Photonics, 10(2), 113. https://doi.org/10.3390/photonics10020113




