Cascaded Stimulated Polariton Scattering in a Single-Pass KTP Crystal under Picosecond Pumping
Abstract
1. Introduction
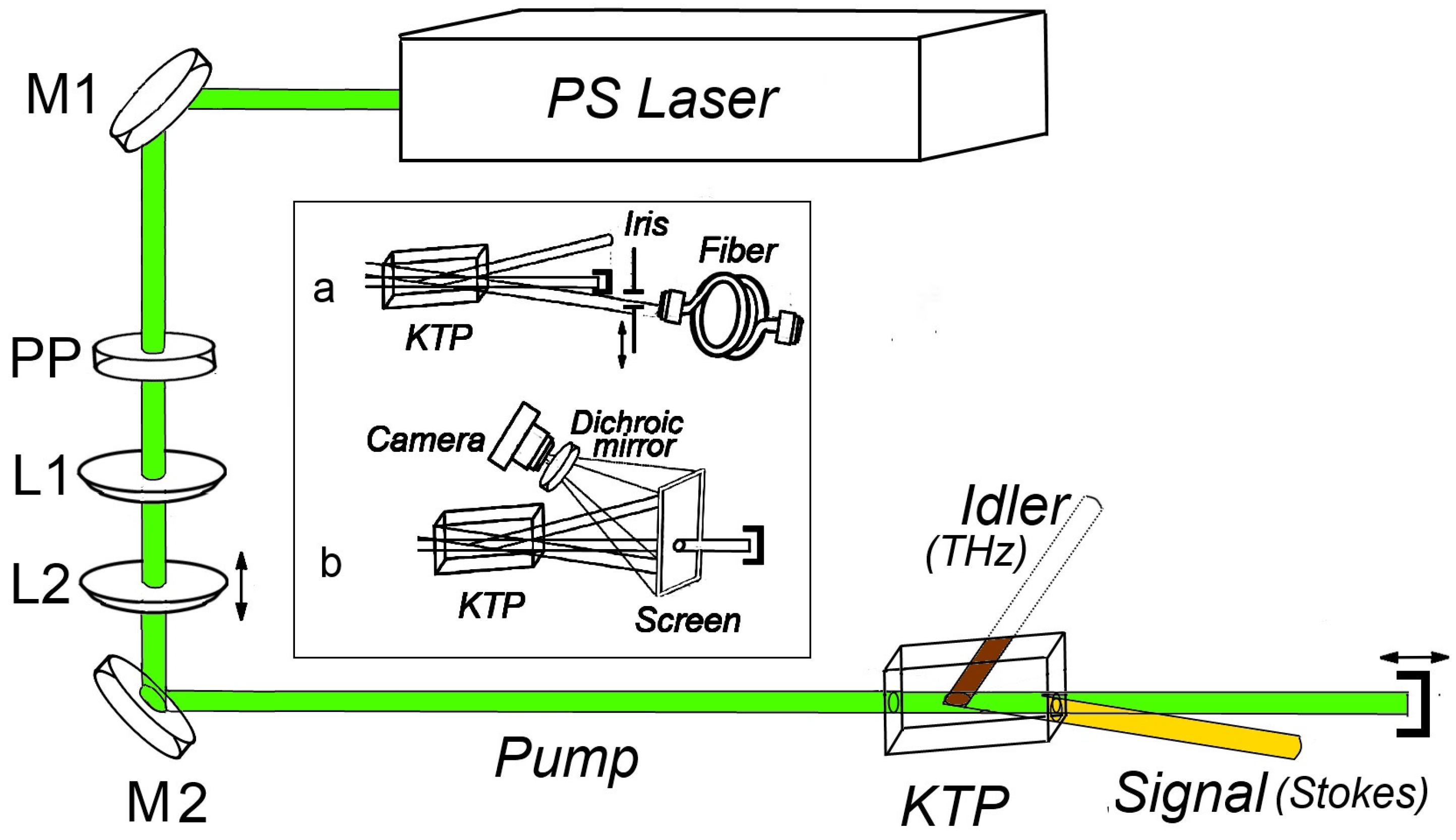
2. Materials and Methods
3. Results
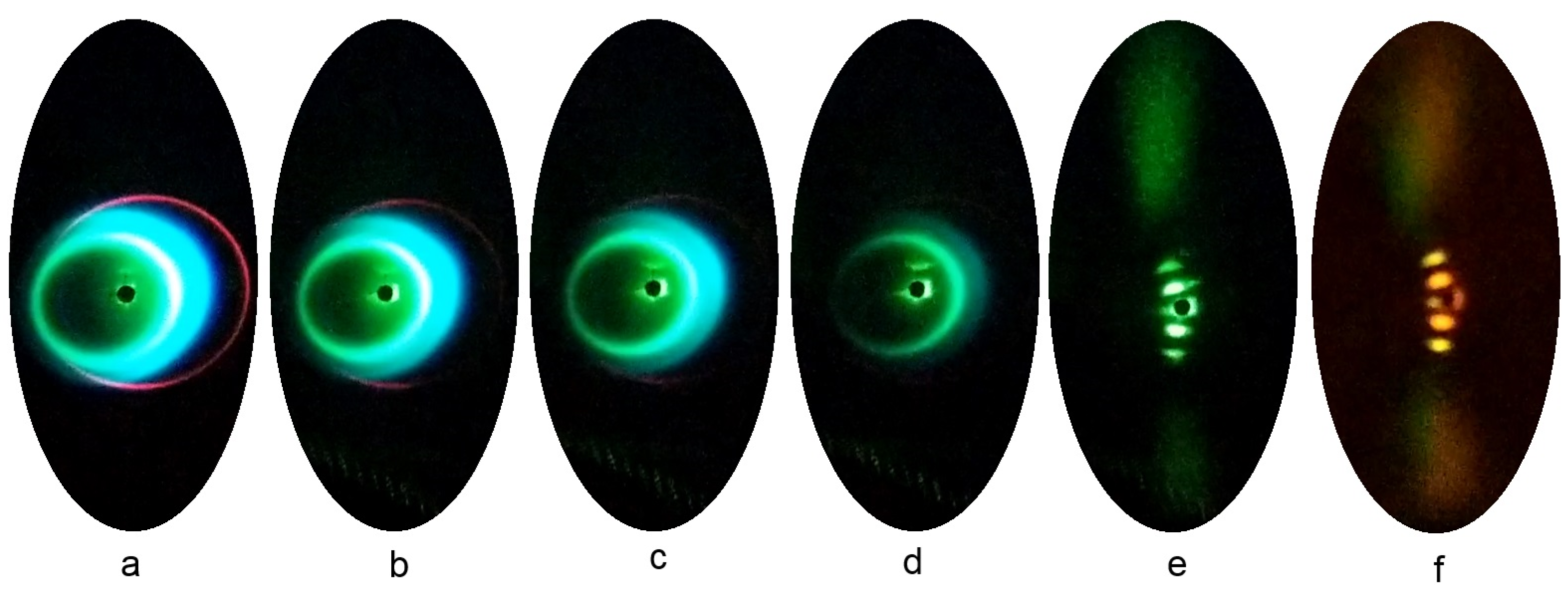
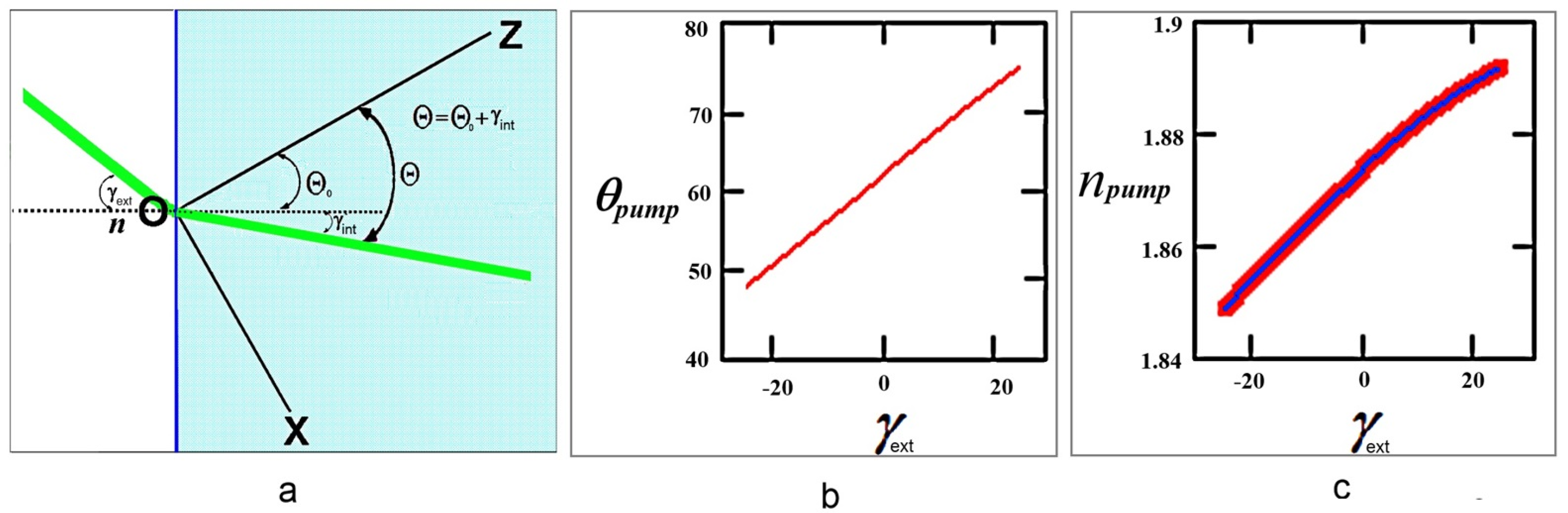
3.1. Outside the Crystal
3.2. Inside the Crystal
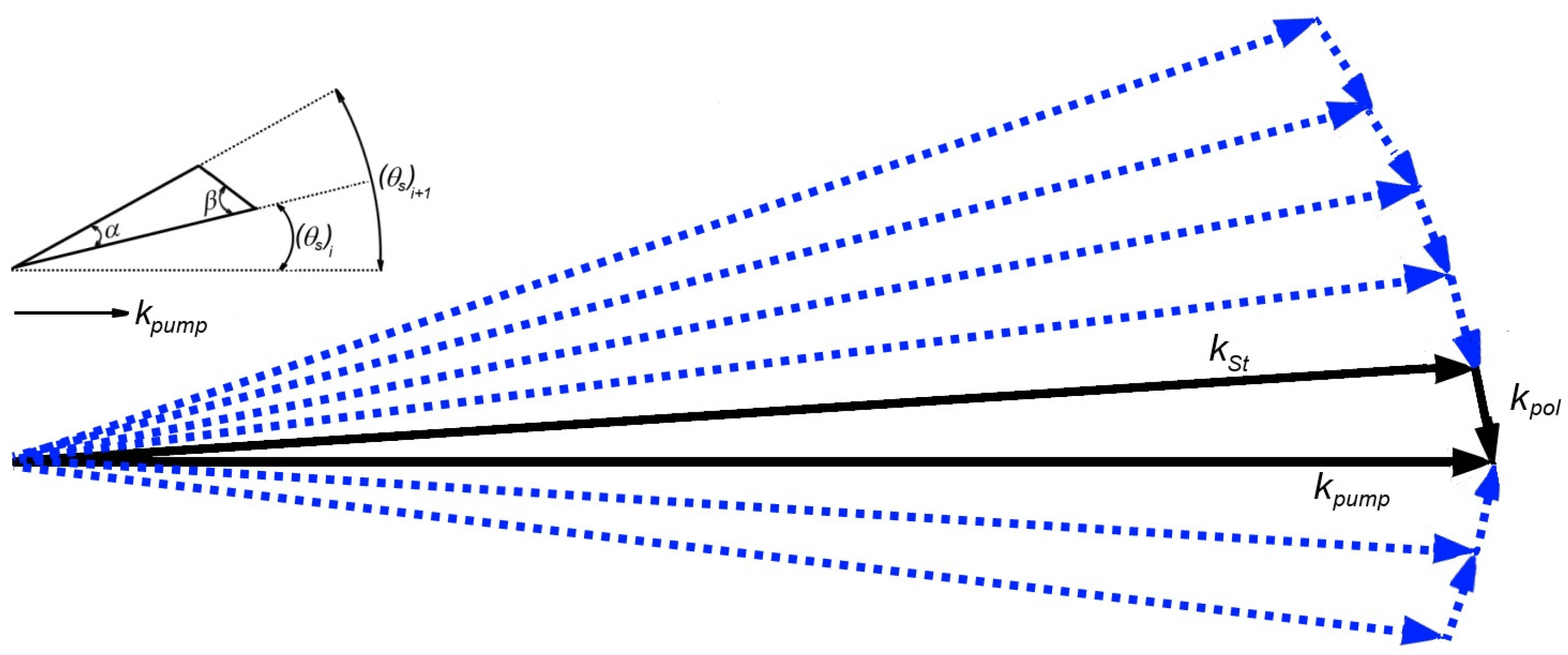
3.2.1. Rays in the Principal Plane XOZ
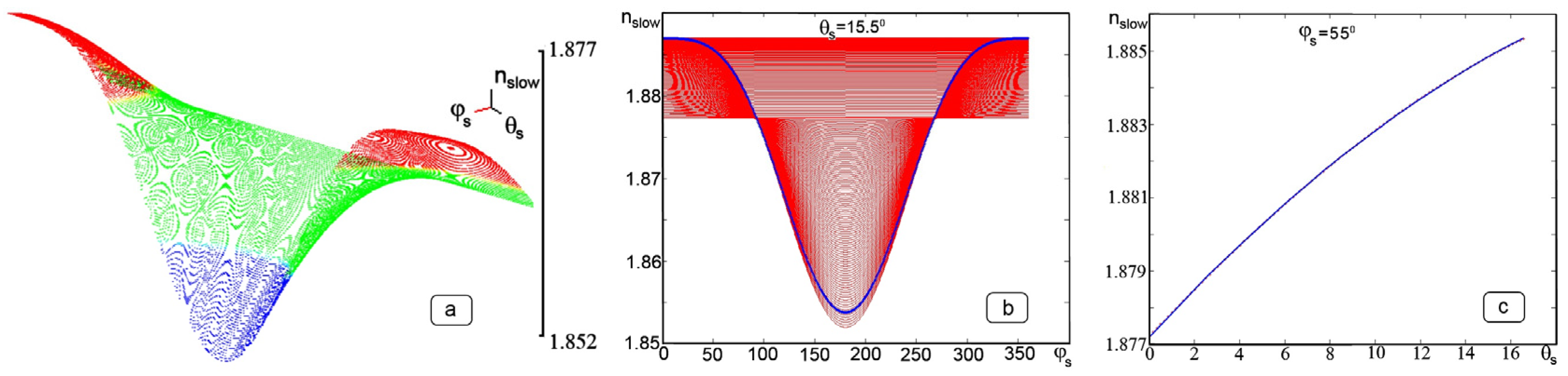
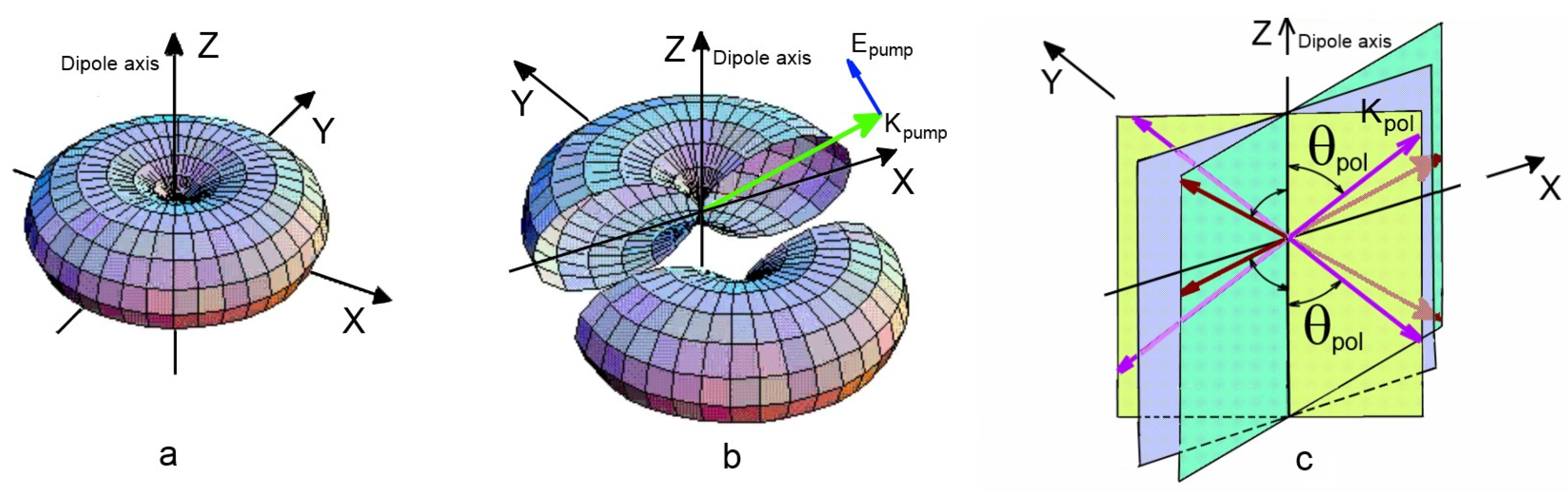
3.2.2. Rays in Any Direction
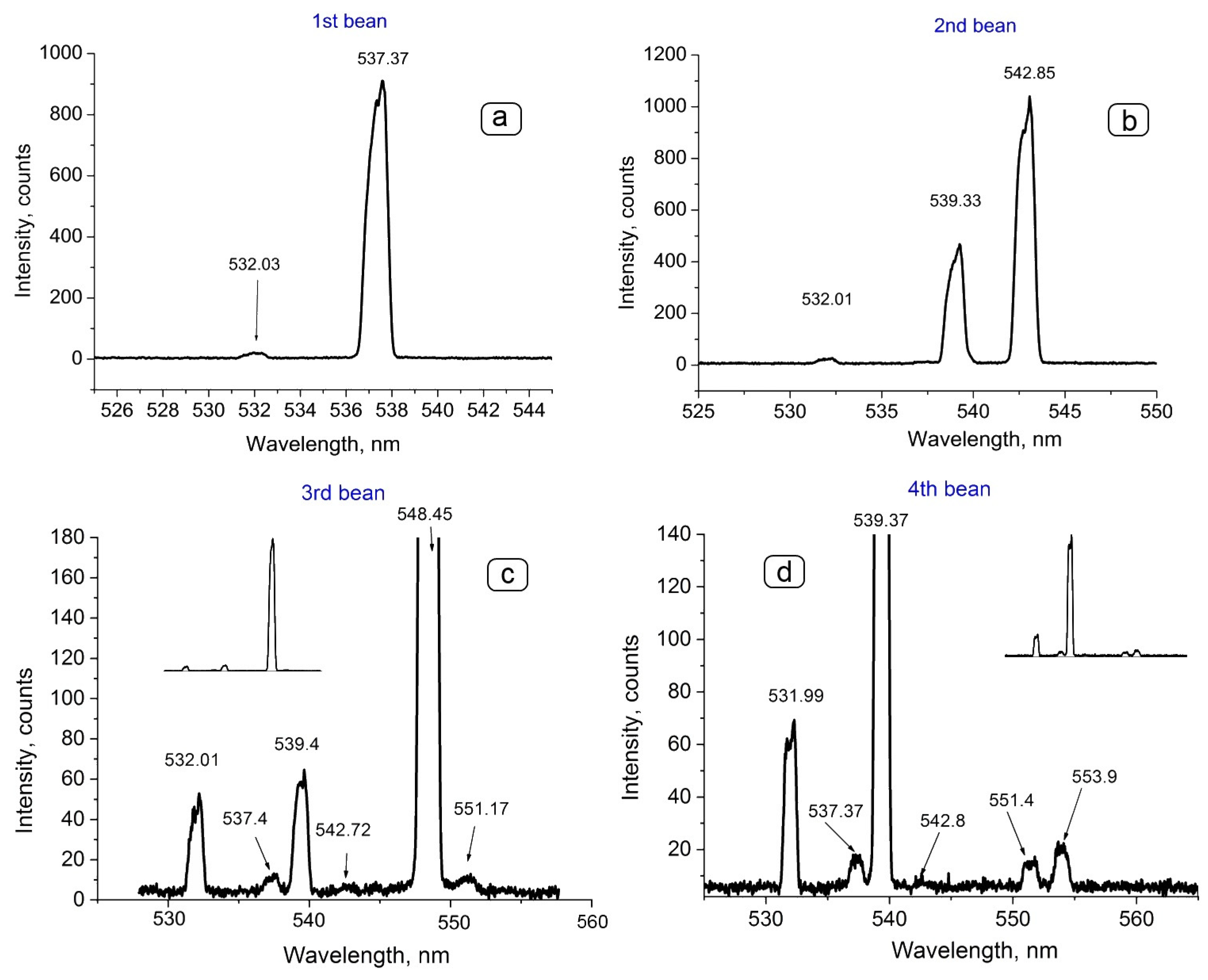
3.2.3. Characters of the Polariton Waves
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ikari, T.; Zhang, X.; Minamide, H.; Ito, H. THz-wave parametric oscillator with a surface emitted configuration. Opt. Express 2006, 14, 1604–1610. [Google Scholar] [CrossRef] [PubMed]
- Kawase, K.; Shikata, J.; Ito, H. Thz wave parametric source. J. Phys. D Appl. Phys. 2002, 35, R1–R14. [Google Scholar] [CrossRef]
- Lee, A.J.; Pask, H.M. Cascaded stimulated polariton scattering in a Mg:LiNbO3 THz laser. Opt. Express 2015, 23, 8687–8698. [Google Scholar] [CrossRef] [PubMed]
- Thomson, C.L.; Dunn, M.H. Observation of a cascaded process in intracavity terahertz optical parametric oscillator based on lithium niobate. Opt. Express 2013, 21, 17647–17658. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Gao, F.; Zhang, X.; Cong, Z.; Liu, Z.; Chen, X.; Qin, Z.; Wang, P.; Xu, J.; Wang, Z.; Ming, N. Enhancement of intracavity pumped THz parametric oscillator power by adopting diode side pumped configuration based on KTP crystal. Crystals 2019, 9, 666. [Google Scholar] [CrossRef]
- Jiang, S.; Chen, X.; Cong, Z.; Zhang, X.; Qin, Z.; Liu, Z.; Wang, W.; Li, N.; Fu, Q.; Lu, Q.; et al. Tunable Stokes laser generation based on the stimulated polariton scattering in KTP crystal. Opt. Express 2015, 23, 20187–20194. [Google Scholar] [CrossRef] [PubMed]
- Wang, N.T.; Cong, Z.; Chen, X.; Zhang, X.; Qin, Z.; Tang, G.; Li, N.; Wang, C.; Lu, Q. Terahertz parametric oscillator based on KTP crystal. Opt. Lett. 2014, 39, 3706–3709. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Zhang, X.; Cong, Z.; Liu, Z.; Chen, X.; Qin, Z.; Ming, N.; Guo, Q. Tunable Stokes laser based on KTP crystal. Crystals 2020, 10, 974. [Google Scholar] [CrossRef]
- Gao, F.; Zhang, X.; Cong, Z.; Liu, Z.; Chen, X.; Qin, Z.; Wang, P.; Xu, J. Tunable Stokes laser based on the cascaded stimulated polariton scattering and stimulated Raman scattering in RTP crystal. Opt. Lett. 2020, 45, 861–864. [Google Scholar] [CrossRef]
- Zang, J.; Cong, Z.; Chen, X.; Zhang, X.; Qin, Z.; Liu, Z.; Lu, J.; Wu, D.; Fu, Q.; Jiang, S.; et al. Tunable KTA Stokes laser based on stimulated polariton scattering and its intracavity frequency doubling. Opt. Express 2016, 24, 7558–7565. [Google Scholar] [CrossRef]
- Hayashi, S.; Nawata, K.; Sakai, H.; Taira, T.; Minamide, H.; Kawase, K. High-power, single-longitudinal-mode terahertz-wave generation pumped by a microchip Nd:YAG laser. Opt. Express 2012, 20, 2881–2886. [Google Scholar] [CrossRef] [PubMed]
- Zhao, G.; Yang, Y.; Huang, Y.; Liu, F.; Feng, L.; Huang, S.; Liu, K. High repetition rate and high power picosecond terahertz parametric amplifier with a KTP crystal. Appl. Phys. Lett. 2020, 116, 131107. [Google Scholar] [CrossRef]
- Oshima, Y.; Naganawa, T.; Zen, H.; Kii, T.; Ohgaki, H. Synchronously pumped THz parametric oscillator driven by amplified picosecond mode-locked laser. In Proceedings of the 45th International Conference on Infrared, Millimeter and Terahertz Waves, Buffalo, NY, USA, 8–13 November 2020. [Google Scholar] [CrossRef]
- Warrier, A.M.; Lin, J.; Pask, H.M.; Lee, A.J.; Spence, D.J. Multiwavelength ultrafast LiNbO3 Raman laser. Opt. Express 2015, 23, 25582. [Google Scholar] [CrossRef] [PubMed]
- Warrier, A.M.; Li, R.; Lin, J.; Lee, A.J.; Pask, H.M.; Spence, D.J. Tunable THz generation in the picosecond regime from the stimulated polariton scattering in a LiNbO3 crystal. Opt. Lett. 2016, 41, 4409–4412. [Google Scholar] [CrossRef]
- Corletti, L.; McDonnel, G.; Leon, U.; Rocco, D.; Finazzi, M.; Toma, A.; Ellenbogen, T.; Della Valle, G.; Celebrano, M.; De Angelis, C. Nonlinear THz generation through optical rectification enhanced by phonon-polariton in lithium niobate thin films. ACS Photonics 2023, 10, 1419–1425. [Google Scholar] [CrossRef] [PubMed]
- Kitaeva, G.; Safronenkov, D.; Starkova, N. An improvement of the Cherenkov THz generation scheme using convex silicon prism-lens adapters. Photonics 2023, 10, 1145. [Google Scholar] [CrossRef]
- Kitaeva, G.; Markov, D.; Safronenkov, D.; Starkova, N. Prism couplers with convex output surfaces for nonlinear Cherenkov terahertz radiation. Photonics 2023, 10, 450. [Google Scholar] [CrossRef]
- Wu, M.-H.; Chiu, Y.-C.; Wang, T.D.; Zhao, G.; Zukauskas, A.; Laurell, F.; Huang, Y.-C. THz parametric generation and amplification from KTP in comparison with lithium niobate and lithium tantalate. Opt. Express 2016, 24, 25964–25973. [Google Scholar] [CrossRef]
- Kondratyuk, N.V.; Shagov, A.A. Stimulated light scattering and optical parametric oscillation in noncollinear wave interactions in the XY plane of a KTP crystal excited by the second harmonic of a Nd:YAG laser. Quantum Electron. 1999, 29, 729. [Google Scholar] [CrossRef]
- Pasiskevicius, V.; Canalias, C.; Laurell, F. Highly efficient SRS of picosecond pulses in KTP. Appl. Phys. Lett. 2006, 88, 041110. [Google Scholar] [CrossRef]
- Labruyere, A.; Shalby, B.M.; Krupa, K.; Couderc, V.; Tonello, A.; Baronio, F. Simulteneous broadband Raman cascading and parametric conversion in KTP. Opt. Lett. 2013, 38, 3758–3761. [Google Scholar] [CrossRef] [PubMed]
- Leifenstorfer, A.; Moskalenko, A.S.; Kampfrath, T.; Kono, J.; Castro-Camus, E.; Peng, K.; Qureshi, N.; Turchinovich, D.; Tanaka, K.; Markelz, A.G.; et al. The 2023 terahertz science and technology roadmap. J. Phys. D Appl. Phys. 2023, 56, 223001. [Google Scholar] [CrossRef]
- Kiwa, T.; Tonouchi, M. Special issue “Terahertz (THz) science in advanced materials, devices and systems”. Photonics 2023, 10, 1024. [Google Scholar] [CrossRef]
- Vereshchagin, A.К.; Vereshchagin, K.A.; Morozov, V.B.; Tunkin, V.G. Non-collinear optical parametric amplifier for time-resolved broadband picosecond CARS. J. Raman Spectrosc. 2014, 45, 507. [Google Scholar] [CrossRef]
- Vereshchagin, K.A.; Vereshchagin, A.K.; Morozov, V.B.; Tunkin, V.G. Combined parametric down- and up-conversion noncollinear processes under picosecond pumping in KTP, controlled by injection seeding. J. Raman Spectrosc. 2021, 52, 1651. [Google Scholar] [CrossRef]
- Huo, G.-W.; Zhang, T.Y.; Wan, R.G.; Zhang, M.Z.; Cheng, G.H.; Zhao, W. Optimizing the phase-matching parameters of a BIBO crystal for ultrafast spontaneous parametric down conversion. Proc. SPIE 2012, 8333, 833313. [Google Scholar] [CrossRef]
- Nikogosyan, D. Nonlinear Optical Crystals: A Complete Survey; Springer Science+Business Media, Inc.: New York, NY, USA, 2005; pp. 56–58. [Google Scholar]
- Yariv, A.; Yev, P. Optical Waves in Crystals; John Wiley & Sons: New York, NY, USA, 1984. [Google Scholar]
- Boeuf, N.; Branning, D.; Chaperot, I.; Dauler, E.; Gueґin, S.; Jaeger, G.; Muller, A.; Migdall, A. Calculating characteristics of noncollinear phase matching in uniaxial and biaxial crystals. Opt. Eng. 2000, 39, 1016–1024. [Google Scholar] [CrossRef]
- Ortega, T.A.; Pask, H.M.; Lee, A.J. Competition effects between stimulated Rasman and polariton scattering in intracavity KTP crystal. In Proceedings of the Advaced Solid State Lasers Conference, ASSL, Berlin/Heidelberg, Germany, 4–9 October 2015. [Google Scholar]
- Lee, C.Y.; Chang, C.C.; Sung, C.L.; Chen, Y.F. Intracavity continuous-wave multiple stimulated Raman-scattering emissions in a KTP crystal pumped by a Nd:YVO4 laser. Opt. Express 2015, 23, 22765–22770. [Google Scholar] [CrossRef]
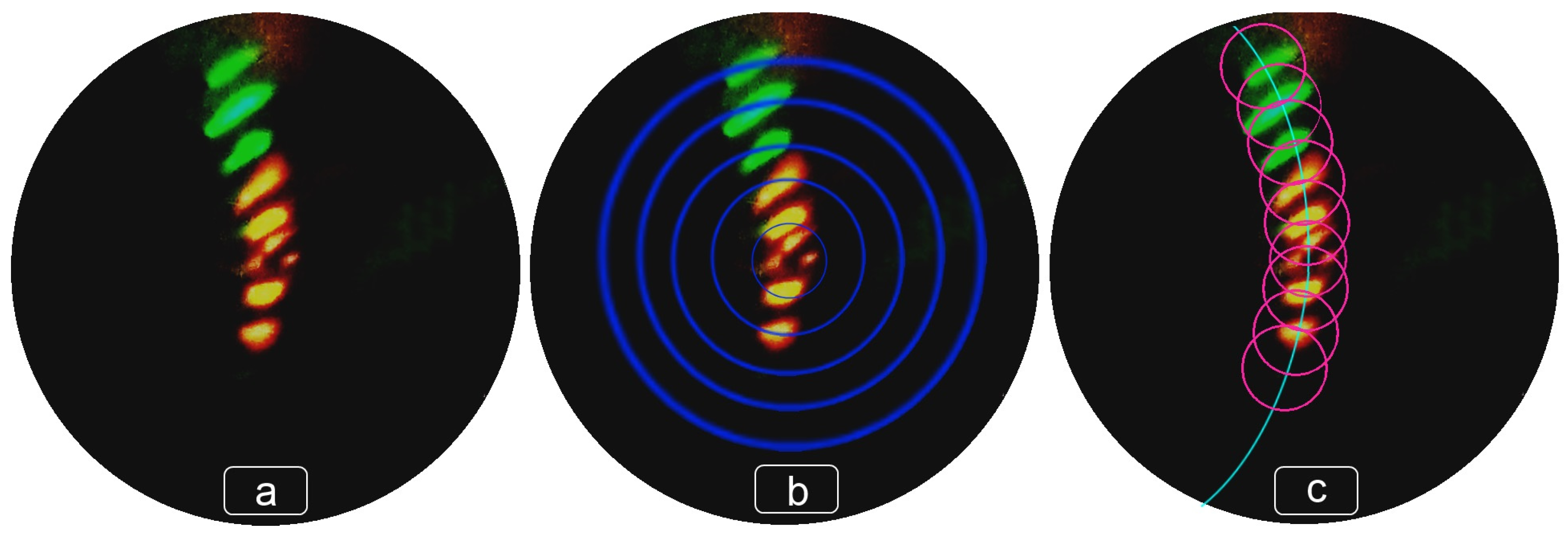
| Bean Number | R, mm | Polar Angle, Grad | Azimuth Angle, Grad | Wavelength, nm |
|---|---|---|---|---|
| 1 | 12.9 ± 0.3 | 3.76 ± 0.10 | −84.3 ± 1.0 | 537.37 ± 0.02 |
| 2 | 24.8 ± 0.2 | 7.64 ± 0.04 | −84.4 ± 1.0 | 542.85 ± 0.05 |
| 3 | 36.7 ± 0.2 | 11.02 ± 0.04 | −81.9 ± 1.0 | 548.45 ± 0.05 |
| 4 | 50.6 ± 0.2 | 14.87 ± 0.04 | −78.9 ± 1.0 | 553.90 ± 0.05 |
| 5 | 63.4 ± 0.2 | 18.31 ± 0.04 | −76.7 ± 1.0 | - |
| −1 | 11.2 ± 0.3 | 3.28 ± 0.10 | 79.5 ± 1.0 | 537.37 ± 0.02 |
| −2 | 24.5 ± 0.2 | 7.16 ± 0.04 | 82.2 ± 1.0 | 542.85 ± 0.05 |
| Bean Number | nslow | θ, Grad | φ, Grad | Wavelength, nm |
|---|---|---|---|---|
| Pump | 1.890 | 74.430 | 0 | 532.00 ± 0.02 |
| 1 | 1.877 | 73.245 | 2.080 | 537.37 ± 0.02 |
| 2 | 1.875 | 72.993 | 3.974 | 542.85 ± 0.05 |
| 3 | 1.873 | 72.211 | 5.609 | 548.45 ± 0.05 |
| 4 | 1.871 | 71.790 | 7.752 | 553.90 ± 0.05 |
| −1 | 1.877 | 73.216 | −1.724 | 537.37 ± 0.02 |
| −2 | 1.875 | 72.993 | −3.974 | 542.85 ± 0.05 |
| Bean * Number | npol | α **, Grad | β ***, Grad | Frequency, cm−1/THz |
|---|---|---|---|---|
| 1 | 7.281 | 2.0 | 62.9 | 187.84 ± 0.70/5.64 ± 0.02 |
| 2 | 6.265 | 1.8 | 69.8 | 187.86 ± 1.00/5.64 ± 0.03 |
| 3 | 5.949 | 1.7 | 68.3 | 188.09 ± 0.03/5.640 ± 0.001 |
| 4 | 7.181 | 2.0 | 72.2 | 179.40 ± 0.03/5.380 ± 0.001 |
| −1 | 6.321 | 1.7 | 58.7 | 187.84 ± 0.70/5.64 ± 0.02 |
| −2 | 7.283 | 2.1 | 72.5 | 187.86 ± 1.00/5.64 ± 0.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vereshchagin, K.A.; Vereshchagin, A.K.; Morozov, V.B.; Tunkin, V.G. Cascaded Stimulated Polariton Scattering in a Single-Pass KTP Crystal under Picosecond Pumping. Photonics 2023, 10, 1355. https://doi.org/10.3390/photonics10121355
Vereshchagin KA, Vereshchagin AK, Morozov VB, Tunkin VG. Cascaded Stimulated Polariton Scattering in a Single-Pass KTP Crystal under Picosecond Pumping. Photonics. 2023; 10(12):1355. https://doi.org/10.3390/photonics10121355
Chicago/Turabian StyleVereshchagin, Konstantin A., Alexey K. Vereshchagin, Vyacheslav B. Morozov, and Vladimir G. Tunkin. 2023. "Cascaded Stimulated Polariton Scattering in a Single-Pass KTP Crystal under Picosecond Pumping" Photonics 10, no. 12: 1355. https://doi.org/10.3390/photonics10121355
APA StyleVereshchagin, K. A., Vereshchagin, A. K., Morozov, V. B., & Tunkin, V. G. (2023). Cascaded Stimulated Polariton Scattering in a Single-Pass KTP Crystal under Picosecond Pumping. Photonics, 10(12), 1355. https://doi.org/10.3390/photonics10121355





