Frequency Acquisition Approach in Polarization-Modulated Ranging Based on Lock-in Analysis

Abstract

In this study, we propose a frequency measurement and estimation approach based on a lock-in analysis for precise frequency determination in polarization-modulated ranging signals. In this method, the modulation signal of an electro-optic modulator (EOM) is manipulated to introduce an intermediate frequency (IF) component into the detected signal. Subsequently, the detected signal is analyzed using lock-in analysis techniques to extract the necessary frequency component, and a new swept frequency waveform is generated, facilitating the frequency acquisition and distance calculation. We conducted theoretical derivations, simulations and experiments to validate the effectiveness of this method. The research findings suggest that our method can enhance the accuracy of frequency measurements by a factor of approximately ten when compared to a direct detection approach, leading to a corresponding improvement in ranging precision. Furthermore, even with larger sweep step sizes and smaller modulation frequencies, the proposed approach can achieve superior ranging results.

1. Introduction

Laser-ranging technology, distinguished by its high resolution, robust coherence and exceptional interference resistance, finds extensive application in aerospace, large-scale equipment production, energy-related equipment and manufacturing processes [1,2,3]. Common laser-ranging techniques encompass the timed pulse method [4], phase comparison method [5], frequency-modulated continuous wave (FMCW) method [6,7,8,9,10,11,12] and femtosecond frequency comb method [13,14,15,16]. The timed pulse method, while widely used, offers a limited resolution; therefore, it is not suitable for industrial applications. The phase comparison method has a rapid response and robust anti-interference capabilities but is marred by challenges such as 2$\mathsf{\pi }$ entanglement and intensity interference, making it unsuitable for high-precision measurements. FMCW ranging has the advantages of high accuracy and no ranging blind areas but is constrained by the modulation bandwidth and light source linearity, resulting in a limited measuring range. Conversely, the femtosecond optical comb ranging method demonstrates exceptional ranging accuracy and range capabilities. However, the system’s complexity and the associated maintenance costs make it less suitable for engineering applications.

Table 1. Advantages and disadvantages of ranging methods.

Ranging Method	Advantages	Disadvantages
Timed pulse method	Extensive measuring range, rapid measurement speed, suitable for motion target identification	Achieves accuracy at the centimeter level
Phase comparison method	Rapid response, extensive range, robust anti-interference capabilities	Presence of a fuzzy distance, limits phase measurement accuracy to sub-meter level in distance measurement
Frequency-modulated continuous wave method	Simple structure, high accuracy, no ranging blind areas	Limited measuring range, potential for distance-Doppler coupling
Femtosecond frequency comb method	High accuracy, large operational range	Expensive equipment, immature technology, challenging to promote in industry

shows the advantages and disadvantages of each ranging method.

Polarization-modulated ranging technology possesses significant engineering applicability as it eliminates the need for phase identification, mitigates distance blurring and exhibits robust resistance to interference. This technique employs an electro-optic modulator to perform two successive frequency-sweep polarization modulations on the measurement light, followed by interference demodulation. Distance information is computed through capturing the adjacent modulation frequencies corresponding to the optical intensity minima of the output signal. Achieving distance measurement accuracy relies on several factors, including a high modulation frequency, a small sweep step size and precise frequency extraction corresponding to the light intensity minima. However, accurately extracting the frequency relies on accurately detecting the minimum intensity, which may not be achieved through direct detection due to the lowest signal-to-noise ratio and limited measurement resolution at very low intensity values. Furthermore, while finer sweep frequencies can enhance the frequency measurement accuracy, they can adversely affect the ranging speed. As a result, it is crucial to strike a balance that suits the sweep step and the accuracy of measurements.

The polarization-modulated ranging method was originally introduced by Kern & Co., Ltd., Aarau, Switzerland, and found its initial application in the commercial distance meter ME5000 [17,18]. Since then, Leica Geosystems has introduced μ-base rangefinders, which dramatically improve the range repeatability by boosting the modulation frequency to 2.4 GHz [19,20]. Following that, technicians conducted thorough research on technologies related to polarization-modulated ranging. In 2014, Hei Kefei [21] from Tianjin University confirmed the principle of polarization modulation ranging, successfully implementing the proposed system. In 2016, Xiao Yang [22] derived and validated the relationship between the ranging accuracy and the modulation frequency, enhancing accuracy through elevating the modulation frequency to 7.9 GHz; however, this increase led to heightened equipment costs and complexity. In 2018, Zhao Boya [23] employed the ‘swing method’ as a strategy to bypass the need for a direct measurement of the minimum intensity. Nevertheless, the stability of the distance measurement system remained suboptimal. In 2019, Gao Shuyuan [24] demonstrated the effect of a thermally induced phase difference on the demodulated waveform of a body phase modulator and proposed enhancing frequency extraction accuracy through bi-directional sweeping, but this increased the measurement time. In 2022, Gao Chao [25] and his team at the Institute of Microelectronics, the Chinese Academy of Sciences, scrutinized the causes of modulated signal waveform distortion. They introduced an IMLS fitting algorithm to rectify the inaccurate extraction of minimum point frequencies resulting from waveform distortions. However, their method involves intricate computational steps. Although researchers have significantly advanced the field through numerous remarkable contributions, most of the previous work has not directly addressed the issues of the low signal-to-noise ratio and frequency measurement resolution at the minimum signal intensity.

Table 2. Previous works, with their contributions, advantages and shortcomings.

Year	Author	Contribution	Advantages	Disadvantages
2014	Hei Kefei [21]	Confirmed polarization modulation ranging principle.
2016	Xiao Yang [22]	Verified the relationship between measurement precision and modulation frequencies.	Improved precision with higher frequencies	Heightened equipment costs and complexity
2018	Zhao Boya [23]	Introduced sweep strategy of the ‘swing method’.	Bypassed the need for a direct measurement of the minimum.	Distance measurement precision needs to be improved
2019	Gao Shuyuan [24]	Introduced sweep strategy of ‘bi-directional sweeping’	Reduced the effect of thermal-induced waveform distortions on the measurement of the minimum-point frequency	Increased cost of time
2022	Gao Chao [25]	Introduced IMLS algorithm to estimate minimum-point frequency	Minimized the impact of waveform distortions on the estimation of the minimum-point frequency	Increased algorithm complexity

summarizes previous works for their contributions, with advantages and shortcomings.

This study introduces a frequency extraction method using a lock-in amplifier (LIA) analysis for polarization-modulated ranging. Lock-in amplifiers (LIAs) are widely employed in various scientific domains, including metrology [26], biomedicine [27], seismic monitoring [28], detection [29,30] and others [31,32,33,34], due to their exceptional noise reduction capabilities. In our research, we apply frequency modulation to the modulator’s drive signal, thereby modulating the detection signal into an AC signal to mitigate the impact of wideband noise, particularly detector 1/f noise. Subsequently, we utilize a lock-in amplifier to demodulate the signal, enhancing the measurement resolution from the minimum to the maximum value at the point of minimum optical intensity. Finally, we verified the effectiveness of this approach through numerical simulations and experimental tests. The major contributions of the paper are as follows:

• We modulate the frequency of the polarization-modulated signal, allowing us to extract specific frequency components from the detected signal. This modulation transforms the measurement point from a state with near-zero resolution to the highest resolution, resulting in a 40,000-fold increase in the signal’s peak-to-peak value near the minima.
• By applying a lock-in analysis technique to the signal extraction, the noise rejection of the signal is enhanced, and the noise amplitudes at very small signal values are reduced by a factor of 1000.
• The proposed method efficiently acquires signals with linear properties near the minima, even under large sweep steps. This streamlines signal processing and analysis, potentially increasing the speed of measurements.

The article is organized as follows: Section 2 discusses the principle of polarization-modulated ranging technology as well as the principle of the lock-in analysis technique applied to the ranging system. In Section 3, we conducted simulations of the proposed method and the original direct detection method. The experimental measurements of the two methods are presented in Section 4. A brief conclusion is provided in Section 5, followed by a detailed conclusion in Section 6.

2. Theoretical Analyses

2.1. Theory of Polarization-Modulated Ranging Technology

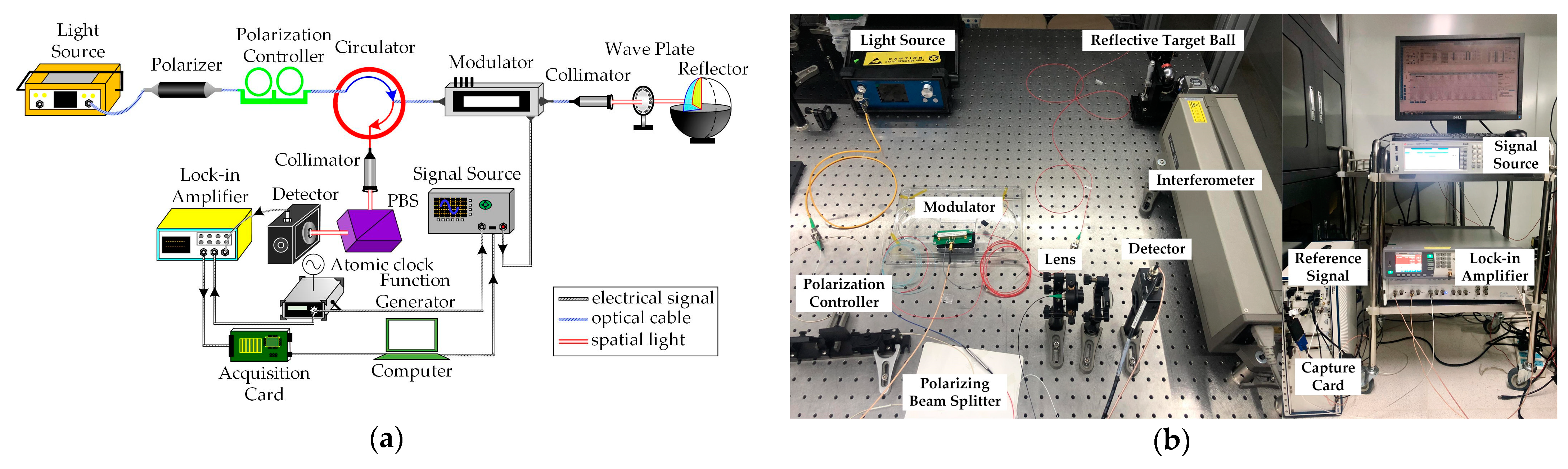
A schematic diagram of the polarization-modulated ranging system is shown Figure 1. In this system, continuous linearly polarized light emitted by the laser passes through an isolator and a polarizing beam splitter (PBS) angled at 45 degrees from the x-axis, resulting in equal-amplitude polarization components in both the x- and y-axes as the light enters the EOM. The EOM introduces a sinusoidal phase delay between these two components, with a linearly varying frequency. The quarter-wave plate (QWP) has its fast axis oriented at 45 degrees to the x-axis, allowing light to travel to the target and return along the same path before being demodulated by the EOM. After the demodulated light reaches the PBS, polarization interference occurs, and then the resulting optical signal is converted into an electrical signal by a photodetector. Subsequently, the signal undergoes AD conversion and is then computed for the measured distance with a microprocessor.

By establishing a Jones matrix polarization model of the optical path, we have the following (Equation (1)):

$$\left[\begin{array}{c}{\mathrm{E}}_x\\ {\mathrm{E}}_y\end{array}\right]=\frac{1}{2}·\left[\begin{array}{cc}1& 1\\ 1& 1\end{array}\right] \left[\begin{array}{cc}1& 0\\ 0& {\mathrm{e}}^{\mathit{iM}\cos \left(\omega t+\phi \right)}\end{array}\right]·\frac{1}{\sqrt{2}} \left[\begin{array}{cc}1& -i\\ -i& 1\end{array}\right] · \left[\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right] \frac{1}{\sqrt{2}} \left[\begin{array}{cc}1& i\\ i& 1\end{array}\right] \left[\begin{array}{cc}1& 0\\ 0& {\mathrm{e}}^{\mathit{iM}\cos \left(\omega t\right)}\end{array}\right] \frac{1}{\sqrt{2}} \left[\begin{array}{c}1\\ 1\end{array}\right]$$

(1)

where M represents the modulation depth of the EOM and φ represents the phase delay of the modulation signal due to the time of flight. The terms E_x and E_y represent the electric field strength in the x-direction and y-direction, respectively.

Due to the polarization interference between the x- and y--axis components of the reflected light on the PBS, the total electric field intensity is the squared modulus of the vector sum of these two electric fields, so we have

$$I =\widetilde{{\mathrm{E}}_x}·\widetilde{{\mathrm{E}}_x^{*}}+\widetilde{ {\mathrm{E}}_y}·\widetilde{{\mathrm{E}}_y^{*}}=\frac{1}{2} \left\{1-\cos \left[M\cos \left(\omega t+\phi \right)-M\cos \left(\omega t\right)\right]\right\}$$

(2)

Expanding Equation (2) in series with the Bessel functions of the first kind, we obtain Equation (3):

$$I=\frac{1}{2}\left\{\begin{array}{c}1 -J_0\left(2M\sin \frac{\phi }{2}\right)\\ -{\sum }_{n=1}^{\infty }{J}_{2n} \left(2M\cos \frac{\phi }{2} \right)\cos \left(2n\sin \frac{2\omega t+\phi }{2}\right)\\ +{\sum }_{n=1}^{\infty }{J}_{2n-1} \left(2M\cos \frac{\phi }{2} \right) \sin \left( \left(2n-1\right)\sin \frac{2\omega t+\phi }{2}\right)\end{array}\right\}$$

(3)

Since the photodetector integrates the optical intensity signal, the final expression can be obtained as follows:

$$I=\frac{M^2}{2}\left[1 -\cos \left(\phi \right)\right]$$

(4)

where, in the relationship between the phase difference and the measured optical path, the lengths L is as follows:

$$\phi =\frac{4\mathsf{\pi }L}{\mathrm{c}} \mathrm{n}f$$

(5)

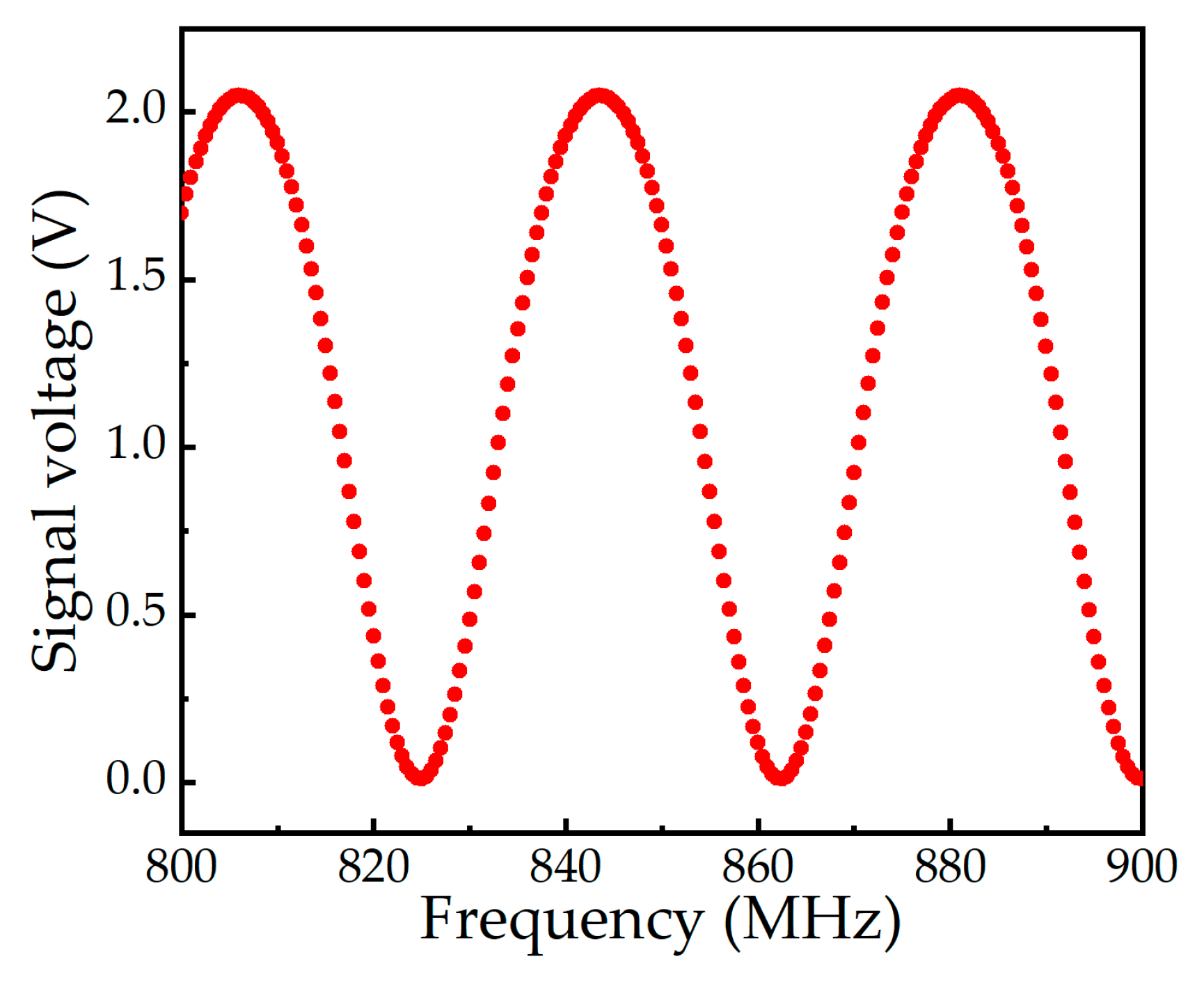
where ‘c’ denotes the speed of light, ‘f’ signifies the modulation frequency, ‘n’ is the air refractive index and ‘L’ denotes the distance to be measured. When continuously adjusting the modulation frequency, the light intensity, I, varies with the modulation frequency, f, in a cosine relationship, as depicted in Figure 2.

When φ is an integer multiple of 2π, it signifies that the modulation waves passing through the EOM are in phase. This implies that the entire optical path length is commensurate with an integer multiple of the modulation half-wavelengths. Consequently, the intensity of the detected light should theoretically correspond to a local minimum on the overall intensity variation curve; then, we can obtain:

$$L=N \frac{\mathrm{c}}{2\mathrm{n}{f}_1}$$

(6)

where N represents a multiple of the measuring distance and the modulation wavelength. To obtain the value of N, the frequency should be increased in small steps until a zero-phase difference is again detected, at which frequency the path contains N + l of these new half-wavelengths:

$$L=\left(N+1\right) \frac{\mathrm{c}}{2 \mathrm{n} f_2}$$

(7)

By combining the above two expressions, the distance, L, can be calculated through the frequency values corresponding to the minimal intensities, denoted as ‘f₁’ and ‘f₂’:

$$L=\left[ \frac{f_1}{f_2-f_1} \right] · \frac{\mathrm{c}}{2 \mathrm{n}{f}_1}$$

(8)

where [ ] represents the floor function.

Differentiating Expression (7) highlights that the ranging accuracy relies on the precision of the frequency measurement at zero phase difference, as indicated in Expression (9):

$$\frac{∆L}{L}=-\frac{∆f}{f}$$

(9)

Therefore, methods aimed at improving the ranging accuracy involve enhancements in the modulation frequency and frequency extraction precision of the intensity minima. However, at the point of zero phase difference, the complete demodulation of the measured light occurs, resulting in the immersion of the detected light within background noise, including the 1/f noise and dark current of the detector, thermal noise and the shot noise inside electronic circuits, etc. Throughout the entire waveform, parameters such as the amplitude, signal-to-noise ratio and measurement resolution reach their minimum values. Consequently, the effort to capture minima through a direct measurement of the signal strength faces challenges.

2.2. Principle of Lock-in Analysis Technique

In order to apply the lock-in analysis technique, we introduce frequency modulation to the modulation signal of the EOM, as depicted by the following expression: cos (2 π f_m t). Consequently, the instantaneous frequency of the EOM undergoes a transformation to the following form (10):

$$f=f_c+∆f·\cos \left( 2 \mathsf{\pi } f_m t \right)$$

(10)

where f_m is the modulation frequency, Δf is the maximum frequency deviation of the FM signal and f_c is the center frequency, still incremented by a small step size.

Based on the relationship between phase and frequency, the instantaneous phase difference between the emitted and reflected light can be written as Function (11):

$$\phi =2 \mathsf{\pi } \left( f_c+∆f·\cos \left( 2 \mathsf{\pi } f_{m}t\right)\right)$$

(11)

So, the light intensity signal can be written as Expression (12):

$$I_F=\frac{M^2}{2} \left\{1 -\cos \left[ a \left( f_c+∆f·\cos \left( 2 \mathsf{\pi } f_m t \right)\right)\right]\right\}$$

(12)

where ‘a’ represents the expression of 4πnL/c. Expanding Equation (12) in series with the Bessel functions of the first kind, we obtain Equation (13):

$$\begin{gathered} I_F=\frac{M^2}{2}-\frac{M^2}{2} \cos \left( a f_c \right)·J_0\left( a∆f \right) \\ -M^2 \cos \left( a{f}_c \right)\sum _{n=1}^{\infty }{\left(-1\right)}^n{J}_{2n}\left( a∆f \right)\cos \left(2\mathrm{n}·2\mathsf{\pi }{f}_{m}t\right) \\ -M^2\sin \left( a f_c \right)\sum _{n=1}^{\infty }{\left(-1\right)}^n{J}_{2n-1}\left( a∆f \right)\cos \left(\left(2n-1\right)\right)·2\mathsf{\pi }{f}_{m}t \end{gathered}$$

(13)

with n ∈ 1, 2, 3…, where $J_k(a∆f)$ is the kth-order Bessel function of the first kind.

For the signal I_F, its first harmonic at the frequency f_m is expressed as follows:

$$I_F\left({ f}_m,t \right)={ M}^{ 2} \sin \left( a f_c \right){ J}_1\left( a∆f \right)\cos \left( 2 \mathsf{\pi } f_m t \right)=A(t) \times \cos \left( 2 \mathsf{\pi }{ f}_m t \right)$$

(14)

As demonstrated in Equation (14), the amplitude of the first harmonic, A(t), is characterized by a sinusoidal function of f_c. This implies that when the outgoing and reflected light are in phase, the signal resolution of A(t) is the highest in the whole waveform.

The frequency resolution of A(t) is mathematically expressed as:

$$R=M^2·\cos ({a f}_c ) ·{ J}_1\left( \frac{2 \mathsf{\pi } \mathrm{n} L}{\mathrm{c}}·∆f \right)·\frac{2 \mathsf{\pi } \mathrm{n} L}{\mathrm{c}}$$

(15)

Consequently, the derivative of A(t) concerning f_c reaches its maximum value when the phase difference is zero, aligning with the signal’s peak resolution throughout the frequency sweep. This enhancement significantly improves the accuracy of the measured frequency values associated with a phase difference of zero. According to the equation above, the system resolution, R, can be optimized when the parameter $J_1( \frac{2\mathsf{\pi } \mathrm{n} L}{\mathrm{c}}·∆f )$ reaches its peak value. Consequently, it is essential to perform an optimal estimation of Δf before applying frequency modulation to enhance the measurement resolution of the frequency.

By combining the expressions from Equations (6) and (7), we can derive the relationship between L and the frequencies of two adjacent light intensity minima (f₂ $-$f₁) as:

$$L=\frac{\mathrm{c}}{2 n ({ f}_2-f_1 )}$$

(16)

When the distance to be measured, L, remains constant, the difference between the frequencies corresponding to adjacent minima becomes a fixed value that we refer to as ‘period T’. This ‘T’ value can be obtained from the initial sweep’s light intensity signal. By substituting Equation (16) into the expression for the first-order Bessel function above, we can conclude that the theoretical range of values for Δ f can be selected from 0 to 0.58604 times ‘T’, with the optimal value being approximately 0.58604 times ‘T’.

By optimizing the modulation parameters, it is possible to obtain a first harmonic signal with an enhanced resolution. Then A(t) can be demodulated using a lock-in amplifier equipped with a narrow-band filtering function to remove the wideband background noise and substantially enhance the signal-to-noise ratio of the demodulated signal.

2.3. Methodological Steps

The methodological processing steps are as follows:

• Generate the signal, ${\mathrm{S}}_d=\cos \left( 2 \mathsf{\pi }{f}_{c}t\right),$ to drive the EOM. Continuously and linearly vary f_c, and after each frequency shift, record f_c and the averaged amplitude I of the signal received by the detector.
• Compute the difference between consecutive values in the I-f_c sequence. Identify the frequency values corresponding to two consecutive minimum amplitudes, denoted as f₁ and f₂, and calculate the period, T = f₂ − f₁, and Δf = T/4.
• Generate a frequency-modulated signal, ${\mathrm{S}}_m=\cos \left( 2 \mathsf{\pi } f_{m}t\right),$ to modulate ${\mathrm{S}}_d$. This results in a new swept-frequency signal, $I_F=\cos \left( 2 \mathsf{\pi } (f_c+∆f·\cos \right( 2 \mathsf{\pi } f_{m}t\left)t\right)$. Re-drive the EOM and collect the output signal, I_F.
• Multiply the reference signal, ${\mathrm{S}}_m,$ with I_F and apply a low-pass filter to obtain the DC component, $A\left(t\right)$.
• Continuously and linearly vary the frequency, f_c. After each frequency shift, record f_c and the averaged amplitude, $A\left(t\right)$, of the signal received by the detector and obtain the $A\left(t\right)$−f_c sequence
• Identify the minimum points in the $A\left(t\right)$−f_c sequence, retaining the initial frequencies of the minimum intensity, f₁ and f₂.
• Locate the first minimum point in the signal and perform a linear regression on the three points before and after it to obtain two linear models.
• Determine the intersection point of the two linear models and calculate its corresponding frequency value, i.e., the final value of the frequency obtained.
• Repeat steps 7–8 to obtain the second minimum frequency value.
• Utilize Formula (16) to compute the final distance value.

3. Simulation

We assessed two frequency evaluation methodologies, one based on direct detection and the other on a lock-in analysis, through simulation experiments. For this evaluation, we considered a measurement distance of 100 m. The original signal driving the EOM is a sinusoidal signal with a variable frequency, linearly increasing from 5 MHz to 8 MHz over a 2 s sweep period, with a step size of 500 Hz. The signal-to-noise ratio (SNR) is set at 0 dB. The sampling frequency is fixed at 80 MHz, resulting in a total of 160 million sampling points. The theoretical relative ranging accuracy at this sweep step is 6.25 × 10⁻⁵.

The analysis using direct measurements comprises several steps: The calculation of the light intensity expression begins with the use of Expressions (2) and (5), incorporating noise at a signal-to-noise ratio of 0 dB. The modulation frequency is varied, and the average light intensity is computed at each frequency, treating this computation as a form of low-pass filtering. This process yields a sequence of light intensity values across different frequencies. Following this, the minimum values of the sequence, along with the two points preceding and succeeding each minimum point, are identified. Segmented binomial fittings are then applied to determine the frequency values corresponding to the minimized value of the fitted function. Finally, the distance value is computed according to Expression (8).

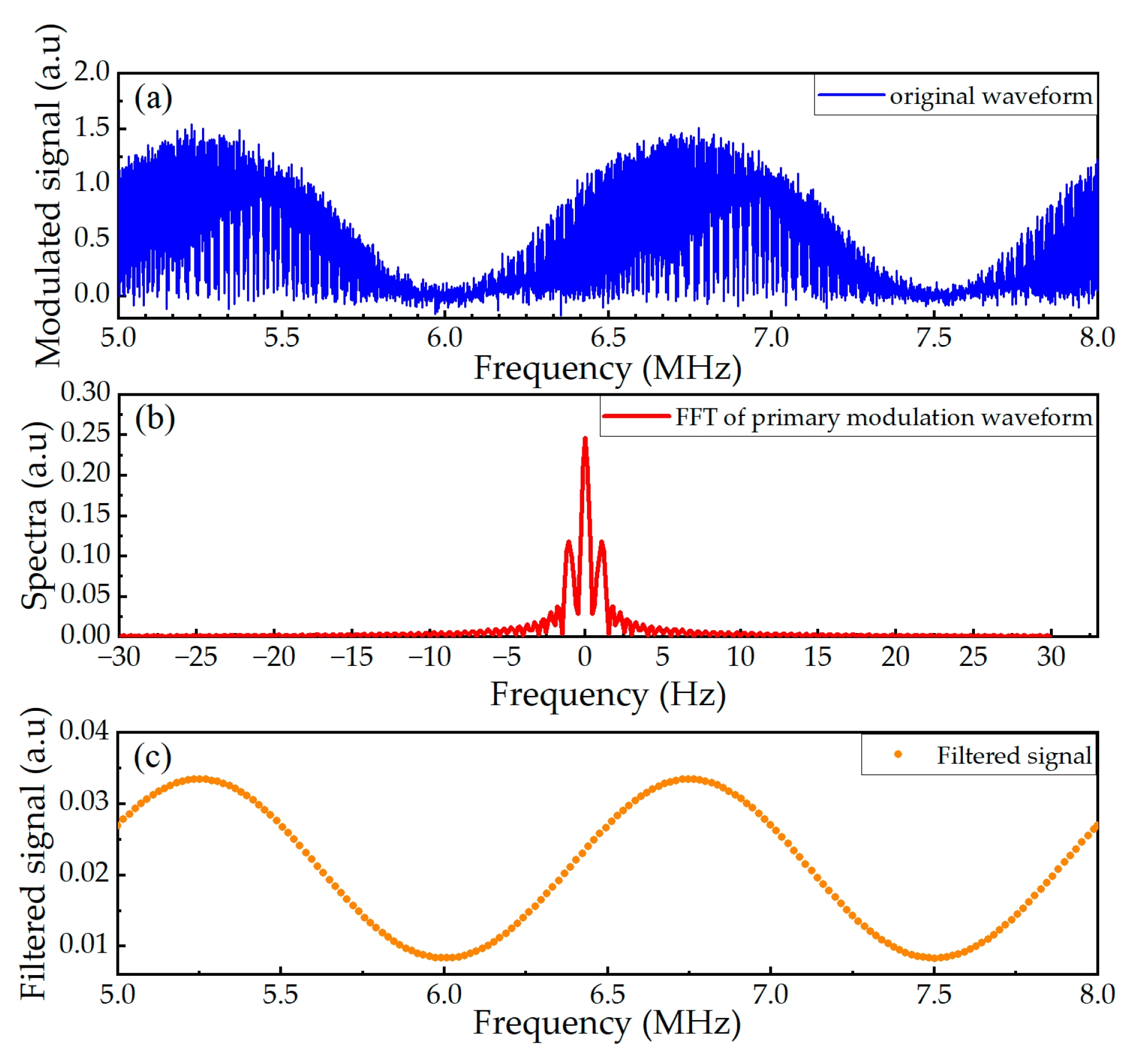
Figure 3a displays the raw intensity signal obtained through direct detection, encompassing various frequency components. In practice, it undergoes integration processing by the photodetector to effectively filter out high-frequency constituents. Figure 3b illustrates the low-frequency components of the direct detection signal’s spectrum. It exhibits two peaks at DC (direct current) and 0.75 Hz. The DC component represents the constant voltage offset resulting from EOM demodulation at each frequency. The 0.75 Hz component is related to the frequency sweeping process. Upon applying a low-pass filter, the intensity–frequency waveform is illustrated in Figure 3c. By identifying the frequency values corresponding to the two minima of this curve, we calculated a distance of 100.000805 m using Expression (5). This computation results in an absolute error of 0.805 mm, with a relative error of 8.05 × 10⁻⁶.

In lock-in analysis-based measurements, the phase difference resulting from the double passage of measured light through the modulator is calculated using Equation (11). Subsequently, this phase difference is integrated into Equation (4) to derive a numerical solution for the light intensity where the modulation frequency, f_m, is set at 2 kHz and the maximum frequency deviation, Δf, is 1.5 MHz. While varying the frequency (f_c), the obtained light intensity sequence is multiplied by the modulating signal, sin(w_m × t), at each frequency, and the multiplied results are averaged as a low-pass filtering computation to obtain its DC component. This process generates the light intensity-frequency sequence. Subsequently, the minimum value of the light intensity-frequency sequence is identified, along with the three points preceding and following each minimum-value point. These points are used for segmented linear fitting to determine the frequency value corresponding to the intersection point of the fitted function. Finally, the distance value is calculated according to Equation (8).

The temporal waveform of the optical intensity signal is depicted in Figure 4a, which also contains various frequency components. A spectral analysis of the intensity signal detected for specific frequency components of the scanned signal reveals that, in the low-frequency part, the signal can be expanded by a Fourier series that includes frequency components such as f_m, 2 f_m, 3 f_m, etc., as shown in Figure 4b. Figure 4c shows the amplitude curve of the 2 kHz component of the detected signal as a function of frequency during the frequency sweep. Notably, this waveform presents four troughs positioned along the frequency axis, aligning with the frequencies at which the light intensity of the original signal experiences its maxima and minima. By determining the in-phase frequency values, which are 6 MHz and 7.5 MHz, corresponding to the two minima of the original intensity curve, respectively, an absolute error of 6.246 × 10⁻² mm is calculated, with a relative error of 6.246 × 10⁻⁷.

4. Experimental Setup and Results

The experimental setup is shown in Figure 5. It includes a super luminescent diode (SLED) light source operating at a central wavelength of 1550 nm. Accompanying the light source are a polarizer and a polarization controller, enabling precise polarization adjustment along the x- and y-axes.

Additionally, the configuration involves a circulator, an EOM (COERI, Chongqing, China, DC-300 MHz), a QWP, a collimator, a reflector, a PBS and a detector. A function generator (Agilent, New York, USA, 81150A) produces a stable, fixed-frequency reference signal used to modulate the frequency-swept signal sourced from the source (Keysight, Santa Clara, CA, USA, N5171B). This modulated signal is employed to drive the EOM for polarization modulation. A PBS is used to split the returned measurement light, and a photodetector (Thorlabs, Newton, NJ, USA, APD130C) is used to convert the optical signal into an electrical signal. The converted signal, in conjunction with the reference signal generated by the function generator, enters the lock-in amplifier (Zurich Instruments, Zurich, Switzerland, HF2LI) for demodulation. Subsequent to demodulation and acquisition through a data acquisition card, the resultant signal is transmitted to the computer for the distance calculation.

First, we compare the accuracy of the direct detection and lock-in analysis methods in measuring the frequency of optical in-phase points. To obtain the intensity-frequency signal covering an in-phase point, we performed a localized segmented sweep of the electro-optical modulator (EOM) with a sweep step of 4 kHz, collecting a total of 50 data points. Then, we applied least-squares fitting to determine the horizontal coordinates corresponding to the very small values in this waveform, i.e., the in-phase point frequencies to be estimated.

Figure 6a illustrates the discrete signal and its fitted waveform acquired through the direct detection method. Significant random noise is visible at the bottom of the image, resulting in signal jitter, while the upper half of the image shows even more jitter, affecting the accuracy of the fit. The amplitude of this random noise, estimated from the amplitude at the bottom of the graph, is about 0.15 V. Figure 6b shows the frequency values obtained from 20 measurements with a standard deviation of about 11,500 Hz. This frequency measurement error and the modulation frequency range, as indicated by Equation (9), lead to a relative distance measurement standard deviation of roughly 9 × 10⁻⁵.

In contrast, Figure 6c shows the time-domain signal and its fitted waveform obtained through the lock-in analysis method, where it can be seen that the sampling points have very good linearity over a large swept frequency range, which remains true even for very small swept frequencies range near the minima, indicating that the method provides sufficient resolution. Segments of the waveform encompassing the minima and a 560 Hz range before and after were extracted from the fitted curves of the two methods. Their peak-to-peak values were computed, and the direct measurement yielded 4.7 × 10⁻² μV peak-to-peak values, while the lock-in analysis resulted in 2.1 mV, indicating a 40,000-fold enhancement in the peak-to-peak signal amplitude. As the light is fully demodulated at the light intensity minima, the measured light intensity after the PBS should approach zero. Therefore, the signal amplitude at the minima reflects the noise magnitude. Comparing the test results of the methods, the direct amplitude measurement yielded a value of 148.7 mV, while the lock-in analysis resulted in 1.52 mV, indicating a 1000-fold reduction in noise amplitude. This demonstrates that the lock-in analysis eliminated most of the random noise.

These two aspects are sufficient to ensure the measurement accuracy of the frequency at the in-phase point, and excellent frequency measurement results can be obtained even with a large sweep step. Figure 6d shows the frequency values obtained from 20 measurements conducted through the lock-in analysis method. These measurements exhibit a standard deviation of approximately 1687 Hz, leading to a relative distance measurement standard deviation of approximately 1.3 × 10⁻⁵. Notably, this represents an almost ten-fold improvement over the conventional method.

The signal source generates a frequency sweep signal covering a range of 117 MHz to 200 MHz, with a step size of 20 kHz and a power of 18 dBm. The frequency modulation signal has a modulation frequency of 1 MHz and produces a frequency offset of 500 kHz. The time constant of the lock-in amplifier is set to 0.2 ms. Figure 7 depicts the detected waveform resulting from the lock-in analysis processing.

To evaluate the system’s distance measurement accuracy, we conducted precision comparison experiments using a dual-frequency laser interferometer (Keysight, Santa Clara, CA, USA, 5519) featuring a calibration accuracy of 0.07 µm + 0.07 ppm. The retro-reflectors of both the ranging system and the interferometer are mounted back-to-back on a mobile displacement table, ensuring the co-linearity of the interferometer’s optical path with the spatial optical path of the system in the test. During the test, the retro-reflectors were moved along the displacement stage, and readings from both the interferometer and ranging system were recorded. Following the linear fitting of the interferometric and absolute ranging readings during the motion of the target reflector, the difference between the fitted outcomes and the interferometer readings can be utilized to deduce the ranging accuracy of the system. Figure 8 represents the experimental results of the absolute distance measurement based on the lock-in analysis. Figure 8a shows the residuals, and Figure 8b depicts the linearity test result for the measured absolute distance. The measurement difference between the interferometer and our absolute distance system was found to be less than 0.198 mm (P.V.). This comparative test confirms that the linearity of the absolute distance measurement is within a possible maximum fluctuation of 0.118 mm in terms of the standard deviation, as shown in Table 3. Figure 9 shows the experimental results of the direct measurement method, which has a maximum residual of 0.587 mm and a standard deviation of error of 0.360 mm.

As per Equation (9), when the modulation frequency is approximately 100 MHz and the sweep step is 20 kHz, the theoretical relative error of the ranging system is 2 × 10⁻⁴. This theoretical value is consistent with the accuracy obtained through the direct measurement method. However, the maximum relative error observed in the lock-in analysis experiment is 2.9 × 10⁻⁵, surpassing the theoretical measurement accuracy. This suggests that the current method can achieve improved ranging results even when employing a larger sweep step. If we increase the modulation frequency of the scan by a factor of 10, the ranging accuracy will increase accordingly.

Figure 8. Distance measurement results of the lock-in analysis.

Figure 8. Distance measurement results of the lock-in analysis.

Table 3. Comparison between the distances measured by the interferometer and the proposed system.

RDM by Interferometer (mm)	ADM (mm)	Residual (mm)
1.355	6496.484
2.367	6495.399	0.122
3.378	6494.759	−0.198
4.451	6493.628	−0.055
5.588	6492.400	0.130
7.647	6490.538	0.075
11.405	6487.171	−0.059
Mean value		0.002
Standard deviation		0.118

Table 3. Comparison between the distances measured by the interferometer and the proposed system.

RDM by Interferometer (mm)	ADM (mm)	Residual (mm)
1.355	6496.484
2.367	6495.399	0.122
3.378	6494.759	−0.198
4.451	6493.628	−0.055
5.588	6492.400	0.130
7.647	6490.538	0.075
11.405	6487.171	−0.059
Mean value		0.002
Standard deviation		0.118

Figure 9. Distance measurement results of the direct measurement method.

Figure 9. Distance measurement results of the direct measurement method.

5. Discussion

The measurement uncertainty of this system consists of the refractive index uncertainty in the optical path, which depends on the temperature, atmospheric pressure, partial pressure of water vapor and carbon dioxide content, and its fluctuations. Since the refractive index was not corrected during the experiment, this is a source of uncertainty to be considered.

In addition, the uncertainties in the frequency measurements and estimates include the frequency reference uncertainty, the light intensity measurement uncertainty and the frequency estimation uncertainty. The frequency reference uncertainty is of the order of 10⁻¹⁵, so it is not a major source of measurement uncertainty for this experiment. When detecting the light intensity minima, the light intensity measurement uncertainty and frequency estimation uncertainty are mainly affected by system noise. It should be emphasized that the lock-in analysis method has the advantage of suppressing the generalized noise, especially the 1/f noise, which improves the signal-to-noise ratio and the signal resolution, thus optimizing the above two uncertainties. In addition, the LIA method allows the sweep step size to be further reduced to increase the number of fitted sampling points and improve the accuracy of the frequency estimation.

However, the main shortcoming of the current lock-in analysis method is its slow analysis speed, especially after refining the sweep step, which is due to the long time required for signal integration and the filtering of the LIA. Therefore, our next work will focus on optimizing the sweep control strategy to reduce the number of sweep points and improving the signal processing method of the lock-in amplifier to improve the filtering speed.

6. Conclusions

To address the challenge of achieving high-resolution frequency measurements associated with the light intensity minima of polarization-modulated ranging signals, we proposed a frequency measurement and estimation technique for polarization modulation ranging based on a lock-in analysis. The approach involves frequency modulating the modulation signal of the EOM in the system and introducing an IF component into the detection signal. Following the extraction of this IF component through the lock-in analysis, a new swept frequency waveform is generated. This process not only enhances the frequency resolution for the target point, elevating it from the lowest level across the entire waveform to the highest level, but also efficiently mitigates the impact of wideband noise, notably 1/f noise. Consequently, it substantially enhances the precision of both frequency measurements and estimations. We conducted a theoretical derivation to validate the effectiveness of this method. Then, we carried out simulations and experiments to conduct comparative frequency measurements and ranging trials. The findings reveal that our method can enhance the precision of both frequency and distance measurements by a factor of ten when contrasted with conventional techniques, and improved ranging outcomes are achievable even with large sweep increments.