Ultra-Broadband, Compact Arbitrary-Ratio Multimode Power Splitter Based on Tilted Subwavelength Gratings

Abstract

Mode division multiplexing (MDM) technology is an effective solution for high-capacity optical interconnection, and multimode power splitters, as essential components in MDM systems, have attracted widespread attention. However, supporting a wide range of modes and arbitrary power splitting ratios with large bandwidth in power splitters remains a significant challenge. In this paper, we designed a power splitter based on a subwavelength grating (SWG) structure with tilted placement on a silicon-on-insulator (SOI) substrate. We achieve arbitrary TE₀–TE₉ mode-insensitive power distribution by altering the filling coefficient of the SWG. Thanks to our specific selection of cladding materials and compensatory design for the optical wave transmission and reflection shifts induced by SWG, our device demonstrates low additional loss (EL < 1.1 dB) and inter-mode crosstalk (−18.8 < CT < −60 dB) for optical modes ranging from TE₀ to TE₉, covering a wavelength range from 1200 nm to 1700 nm. Furthermore, our proposed device can be easily extended to higher-order modes with little loss of device performance, offering significant potential in MDM platforms.

1. Introduction

With the development of artificial intelligence technology, various industries are deeply integrating with intelligent information technology. Due to the increasing prominence of issues such as the slowing of Moore’s Law, the “power wall” [1], and the “von Neumann bottleneck” [2,3] in traditional electronic integrated circuits, silicon-based optoelectronic platforms are emerging as promising new technologies in the “post-Moore’s Law” era [4]. These can greatly reduce the limitations on the development and application of artificial intelligence technology and have become the main direction of widespread attention and breakthroughs in the industry at home and abroad [5]. In the optical interconnect and optical computing network of the silicon-based photonic platform, a large number of passive devices are employed for controlling the transmission [6,7,8], coupling [9,10], and power distribution of light. Among these, optical splitters, as essential components in ultra-compact photonic integrated circuits, play a crucial role in various domains, including sensors, optical switches, logic gates, modulators, signal processing, and more. Additionally, the rapid advancement of MDM technology enables power splitters supporting multiple modes to enhance the transmission and processing speed of high-capacity information greatly. Presently, common multimode power splitters include devices such as multimode interference couplers (MMI) [11,12] and directional couplers (DC) [9,13]. These couplers have limited-wavelength bandwidth support and require complex designs to achieve arbitrary power splitting ratios (PSRs), which significantly restricts their utility in on-chip MDM applications. Therefore, designing a broadband multimode splitter with arbitrary PSRs remains a challenging and strategically significant endeavor.

In this work, inspired by geometric optical prisms, we propose a novel multimode 2 × 2 power splitter. When light waves pass through the etched subwavelength grating (SWG) in this multimode beam splitter, they undergo frustrated total internal reflection (FTIR), which enables the transmission of some light waves while reflecting others. Moreover, by adjusting the filling coefficient of the SWG material, we can flexibly control the PSR between the reflected and transmitted light waves. We employ 2.5 D Variational Finite-difference time-domain (VARFDTD) simulations and optimization to design the structure of this power splitter, aiming to achieve high-performance broadband power distribution for multimode signals while reducing the device’s dependence on etching processes. On the one hand, to enhance device performance, we have designed slight offsets for our SWG and the output ports for transmission relative to the intersection point of the input and reflector waveguide centers to compensate for the effects of Goos–Hänchen (GH) shift and the transmission offset generated by the SWG layer. On the other hand, to simplify device fabrication, we investigate the impact of grating filling materials and device cladding materials on device performance and grating dimensions. Ultimately, our proposed multimode power splitter achieves power distribution of TE₀–TE₉-mode light waves at arbitrary ratios within the wavelength range of 1200 nm to 1700 nm. Furthermore, the power splitter exhibits EL of less than 1.1 dB for various mode light waves, and the insertion loss (IL) variation and inter-mode CT for different mode light waves at the same wavelength and output port are both less than 1 dB and −18.8 dB, respectively.

2. Device Design

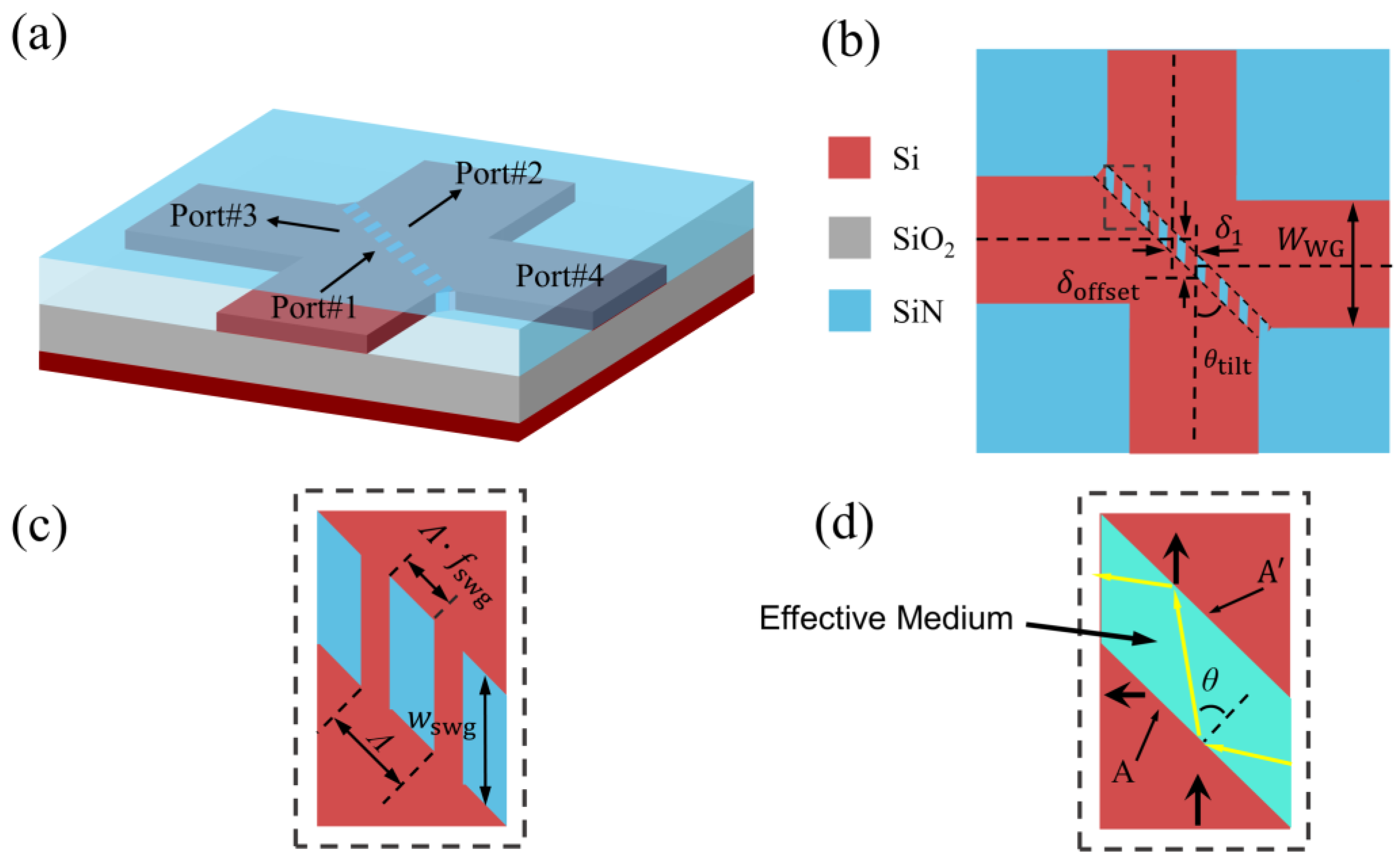
The multimode power splitter is designed on a standard silicon-on-insulator (SOI) substrate with a 220 nm thick top Si layer and a 2 μm thick buried oxide. It is covered by a 2 μm thick Si₃N₄ material, which serves as both the cladding structure and the filling material for the SWG, as shown in Figure 1a. Figure 1b shows that the core of the device consists mainly of a cross-shaped Si waveguide with a width of $W_{\mathrm{WG}}$ and a centrally tilted (${\theta }_{\mathrm{tilt}}$ = 45°) SWG. The multimode power splitter draws inspiration from the structure of a spectral prism, which gives it characteristics similar to those of a spectral prism. Specifically, the light wave mode incident from input port #1 is divided into two beams by the SWG, exiting from port #2 and port #3, respectively. Likewise, if light enters from port #2, it is divided into two beams, exiting from port #1 and port #4, with the PSR remaining unchanged.

To prevent the shift of light waves caused by transmission and reflection through the SWG layer from affecting the performance of the output ports, there is a longitudinal offset ${\delta }_{offset}$ and a lateral offset ${\delta }_1$ between SWG and port #2 relative to the intersection points of port #1 and port #3 waveguide centers, as illustrated in Figure 1b. We provide a detailed definition of the SWG period $\Lambda$ and the SWG filling coefficient $f_{swg}$ in Figure 1c. According to the characteristics of the SWG and the principles of geometric optics, the SWG can be considered equivalent to a single-layer dielectric [see Figure 1d].

According to the Fresnel formula, the reflectance and transmittance of TE-polarized mode incident waves on a single-layer dielectric layer can be expressed as:

$$R_{TE}=\frac{{\left[n_{co}^2{cos}^2{\theta }_0/\left(n_{swg}cos\theta \right)-n_{swg}cos\theta \right]}^2{sin}^2\delta }{4n_{co}^2{{cos}^2{\theta }_{0}cos}^2\delta +{\left[n_{co}^2{cos}^2{\theta }_0/\left(n_{swg}cos\theta \right)+n_{swg}cos\theta \right]}^2{sin}^2\delta },$$

(1)

$$T_{TE}=\frac{4n_{co}^2{cos}^2{\theta }_0}{4n_{co}^2{{\mathrm{c}\mathrm{o}\mathrm{s}}^2{\mathsf{\theta }}_{0}cos}^2\delta +{\left[n_{co}^2{cos}^2{\theta }_0/\left(n_{swg}cos\theta \right)+n_{swg}cos\theta \right]}^2{sin}^2\delta },$$

(2)

where $n_{co}$ is the refractive index of the Si waveguide core layer, $n_{swg}$ is the refractive index corresponding to the SWG equivalent to a single-layer dielectric, ${\theta }_0$ is the incident angle of the beam, $\theta$ is the angle of refraction and reflection at interfaces $\mathrm{A}$ and ${\mathrm{A}}^{\mathrm{’}}$ within the equivalent single-layer dielectric, and $\delta$ is the phase shift within the effective dielectric layer. According to Equations (1) and (2), the PSR of the SWG reflector is obtained as:

$${PSR}_{swg}=\frac{T_{TE}}{R_{TE}+T_{TE}}=\frac{4n_{co}^2{cos}^2{\theta }_0}{4n_{co}^2{cos}^2{\theta }_0{cos}^2\delta +{\left[n_{co}^2{cos}^2{\theta }_0/\left(n_{swg}cos\theta \right)+n_{swg}cos\theta \right]}^2{sin}^2\delta },$$

(3)

The $n_{swg}$ in Equations (4)–(6) can be obtained using the Rytov [14] formula:

$$n_{swg}^2=n_{//}^2{n}_{\perp }^2/\left(n_{\perp }^2{sin}^2\theta +n_{//}^2{cos}^2\theta \right),$$

(4)

$$1/n_{\perp }^2=\left(1-f_{swg}\right)/n_{Si}^2+f_{swg}/n_f^2,$$

(5)

$$n_{//}^2=\left(1-f_{swg}\right)n_{Si}^2+f_{swg}{n}_f^2,$$

(6)

where $n_{//}$ and $n_{\perp }$ represent the ordinary/extraordinary effective medium indices, indicating that SWG is essentially birefringent [15]. $n_f$ is the refractive index of the filling medium in SWG. The Rytov formula is derived using a zeroth-order approximation, assuming $\lambda /\Lambda \to \mathrm{\infty }$. For smaller values of $\lambda /\Lambda$, higher-order approximation expressions of the Rytov formula [16,17] can be used to improve accuracy.

As shown in Figure 1d, due to the half-wave loss generated when light is incident from an optically sparse medium and reflected from an optically dense medium, resulting in additional optical path difference, the phase shift $\delta$ within the effective dielectric layer can be obtained from the following equation [18]:

$$\delta =k_{eff}{w}_{swg}sin{\theta }_{tilt}\mathit{cos}\theta ,$$

(7)

where $k_{eff}$ is the effective wave vector ($k_{eff}=k_0{n}_{swg}$, where $k_0$ is the wave vector of incident light in vacuum), and $w_{swg}$ is the width of the SWG [see Figure 1c]. According to Equation (7), δ is influenced by $n_{swg}$ and $w_{swg}$, Moreover, Equations (1)–(7) reveal that $R_{TE}$, $T_{TE}$, and ${\mathrm{P}\mathrm{S}\mathrm{R}}_{swg}$ are all dependent on $n_{swg}$ associated with $f_{swg}$. Consequently, the PSR between the reflected wave and the transmitted wave can be flexibly designed by adjusting $f_{swg}$ and $w_{swg}$ of the SWG reflector in Equations (4)–(7).

3. Simulation and Analysis

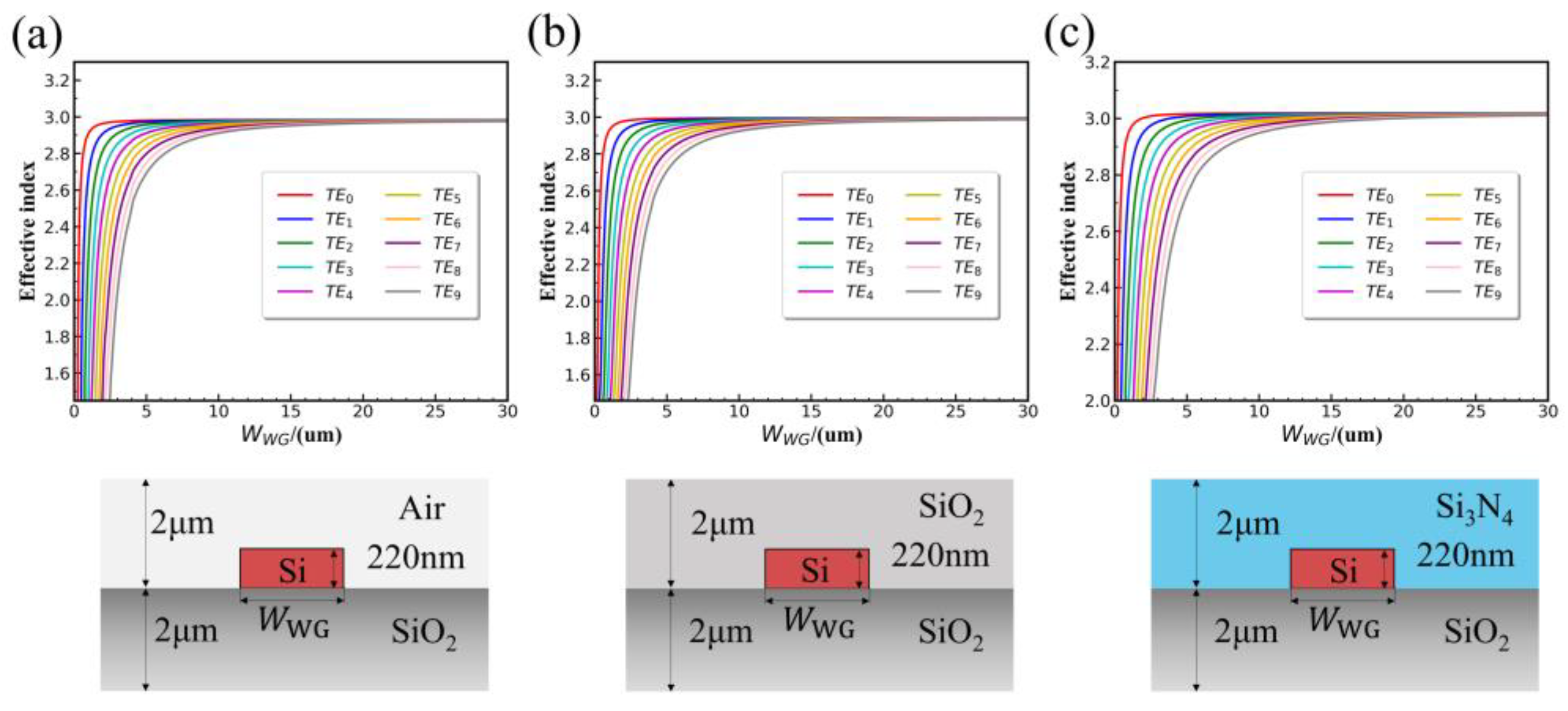
Due to the excellent compatibility of SiO₂ and Si₃N₄ with the SOI platform and the mature growth process on Si, they can serve as ideal cladding materials. Furthermore, since other photonic devices in our research project primarily operate around a wavelength of 1310 nm, we used the finite element method (FEM) to simulate the effect of changing the Si waveguide width on the effective refractive index of TE₀–TE₉ mode light in different cladding scenarios at this wavelength. The simulation results in Figure 2 show that when the cladding structures are Air, ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$, and Si₃N₄, as the central waveguide width $W_{\mathrm{W}\mathrm{G}}$ increases, the effective refractive index of TE₀–TE₉ modes in the waveguide gradually approaches equality. When $W_{\mathrm{W}\mathrm{G}}$ > 8 μm, the effective refractive index of low-order modes TE₀–TE₃ becomes closer. Considering that overly large dimensions would dramatically increase the subsequent simulation and modeling time for the device, we chose to investigate the output characteristics of ports #2 and #3 of the power splitter in TE₀–TE₃ modes for these three cladding structures with $W_{\mathrm{W}\mathrm{G}}$ = 8 μm.

Based on the diffraction theory of gratings, when the grating period is much smaller than the operating wavelength, only zero-order diffraction will occur. At this point, the SWG can be effectively considered to be a single-layer dielectric, and its effective refractive index is influenced by the SWG filling structure. Therefore, specific PSRs can be achieved by designing the SWG filling structure appropriately. To ensure that the light emitted from port #2 and port #3 undergoes only zero-order diffraction, both the diffraction angles (including reflection and transmission) and the angle of incidence of the grating must be equal. Only specular reflection and direct transmission occur with no backward reflection. Therefore, to suppress backward reflection, the following conditions [19] should be satisfied:

$$\Lambda <\frac{{\lambda }_0}{n_{eff}\left[1+sin{\theta }_{tilt}\right]}={\Lambda }_c,$$

(8)

where $n_{eff}$ is the effective refractive index of the given mode, and ${\lambda }_0$ is the operating wavelength. From Formula (8), it can be observed that as $n_{eff}$ increases and ${\lambda }_0$ decreases, the value of the maximum grating period ${\Lambda }_c$ decreases accordingly. To meet the requirements of all three cladding structures for suppressing backward reflection, the scenario with the maximum ${\mathrm{n}}_{eff}$ value is chosen to be used in Equation (8) for calculations. As shown in Figure 3, when $W_{\mathrm{WG}}$ > 8 μm, the $n_{eff}$ for TE₀–TE₃ mode waves in devices with the three cladding structures are quite close. Therefore, we study the impact of the three cladding structures on the power splitter performance at this width. Since under the same $W_{\mathrm{WG}}$ conditions, the waveguide’s $n_{eff}$ using SiO₂ and Air cladding structures is lower compared to Si₃N₄, plugging in the $n_{eff}$ value for TE₀–TE₃ modes under the Si₃N₄ cladding structure ($n_{eff}$ = 3.018) into Equation (8) yields a value of ${\Lambda }_c$ = 0.25 μm. Taking into consideration the suppression of backward reflection for shorter wavelength light waves, ${\Lambda }_c$ = 0.2 μm is chosen.

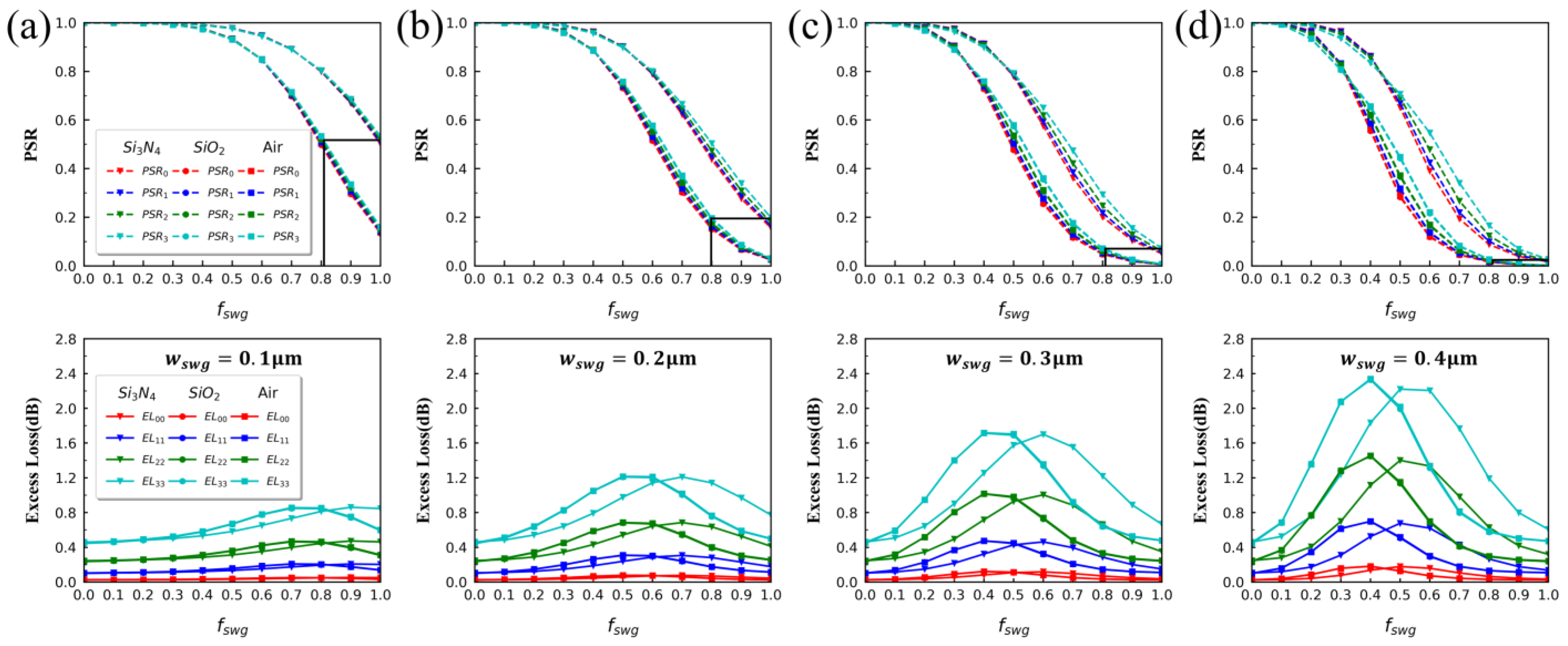
Without considering grating transmission offset and GH shift, we employ the VARFDTD method to simulate the effects of varying $f_{swg}$ and $w_{swg}$ on the PSR and EL of TE₀–TE₃ modes in devices with three cladding structures when 1310 nm wavelength light waves are incident, as shown in Figure 3a–c. To meet simulation accuracy requirements, the grid resolution at the SWG is set to dx = dy = dz = 10 nm. The formulas for calculating EL and PSR are as follows:

$${EL}_{ij}=-10{\mathit{log}}_{10}\left(T_{ij2}+T_{ij3}\right)\left(i=j\right),$$

(9)

$${PSR}_i=\frac{T_{ii2}}{T_{ii2}+T_{ii3}},$$

(10)

where $T_{ijk}$ is the transmittance of input mode TE_i (i = 0, 1, 2, 3) generating mode TE_j (j = 0, 1, 2, 3) at ports k (k = 2, 3). ${PSR}_i$ here denotes the PSR when the corresponding emission mode is TE_i. It can be observed that the ${PSR}_i$ varies with changes in $f_{swg}$, $\Lambda$, and $w_{swg}$. However, for i = 0, 1, 2, 3, the ${PSR}_i$ changes are nearly identical due to the similarity in effective refractive indices of these modes, as shown in Figure 3a.

The simulation and calculations in Figure 3 reveal that only at $w_{swg}$ ≥ 0.3 μm, there is a significant difference in the PSR of TE₃ mode compared to other lower-order modes. This is due to the significant difference in the $n_{eff}$ of TE₃ mode compared to other lower-order modes in the simulated Si waveguide structure, and this effect can be reduced by increasing $W_{\mathrm{W}\mathrm{G}}$. Furthermore, from Figure 3, it is evident that in multimode power splitters with Air and SiO₂ cladding structures, the EL and PSR curves for TE_i (i = 0, 1, 2, 3) almost coincide. In contrast, for multimode power splitters with Si₃N₄ cladding structures, there is a noticeable deviation in the EL and PSR curves compared to the other two cladding structures. This difference is reflected in two aspects: first, when Si₃N₄ is used as the cladding structure, the PSR exhibits a smoother transition above the horizontally marked line in Figure 3a–d compared to the other two cladding structures. It is less sensitive to changes in $f_{swg}$ and thus achieves superior etching tolerance for the device. Second, when the three cladding structures achieve the same PSR in the power splitter, as shown in Figure 3a–d EL curves, it can be seen that the EL of ${\mathrm{T}\mathrm{E}}_i$ in the power splitter with Si₃N₄ cladding is smaller than in the other two cladding structures, indicating lower loss. The reason for the aforementioned differences is that, in these two structures, the effective refractive index curves of mode ${\mathrm{T}\mathrm{E}}_i$ in the Si waveguide are nearly identical, and both differ significantly from the effective refractive index curve in the Si₃N₄ structure, as can be seen in Figure 2a,b.

The above results and analysis indicate that using Si₃N₄ as the cladding structure for multimode power splitters performs better in etching processes and device performance compared to the other two cladding structures. To achieve a wide range of PSR, low EL, and lower mode sensitivity, we ultimately selected $w_{swg}$ as 0.2 μm and 0.3 μm for the subsequent simulation.

On the one hand, due to the presence of GH shift, the actual reflection interface experiences displacement relative to interface A [see Figure 1d], resulting in a mode–field mismatch between the output mode and port #3 (reflection port). It is necessary to eliminate this mode–field mismatch to avoid additional losses and PSR errors. For TE-polarized modes, the required mirror offset ${\delta }_{offset}$ to compensate for GH offset can be derived as [8]:

$${\delta }_{offset}=\frac{sin{\theta }_0}{k_0\sqrt{n_{eff}^{2}s{in}^2{\theta }_0-n_{swg}^{\prime 2}}},$$

(11)

where $k_0$ is the wave vector of incident light in a vacuum, with a value of $2\pi /{\lambda }_0$. $n_{swg}^{\prime }$ represent the effective refractive indices of the corresponding mode in the SWG layer, respectively. By combining Equation (4), it becomes evident that in multimode simulation scenarios, the value ${\delta }_{offset}$ is influenced by $f_{swg}$.

On the other hand, as light is input from port #1 and undergoes reflection and refraction within the SWG before being output from port #2, the presence of SWG leads to an optical wave experiencing a transmission offset as it passes through the equivalent dielectric layer. This transmission offset distance can be calculated using the steady-state phase theory [20,21]:

$$\left\{\begin{array}{c}A=\frac{n_{eff}^2{cos}^2{\theta }_0}{n_{swg}^{\prime }cos\theta }-n_{swg}^{\prime }cos\theta \\ B=\frac{n_{eff}^2{cos}^2{\theta }_0}{n_{swg}^{\prime }cos\theta }+n_{swg}^{\prime }cos\theta \\ {\delta }_1={2w}_{swg}cos{\theta }_{0}sin{\theta }_0\left[\frac{1}{2}-\frac{B{n}_{eff}^2{cos}^2{\theta }_0-A^2\mathit{sin}\left(2\delta \right)/2\delta }{4n_{eff}^2{cos}^2{\theta }_0+A^2{sin}^2\delta }\right]\end{array}\right.,$$

(12)

where A and B represent coefficients associated with $n_{eff}$, $n_{swg}^{\prime }$, $\theta$, and ${\theta }_0$. it can be seen that ${\delta }_1$, relative to ${\delta }_{offset}$, is influenced not only by $f_{swg}$ but also affected by $w_{swg}$.

From Figure 3b, it can be observed that when $w_{swg}$ = 0.2 μm and $f_{swg}$ = 0.8, or $w_{swg}$ = 0.3 μm and $f_{swg}$ = 0.65, the PSR of the four modes is around 0.5, indicating even power splitting at both output ports. We can more easily observe the impact of grating transmission offset and GH displacement on the two output ports in this situation. Using Snell’s law $n_{si}sin{\theta }_0$ = $n_{swg}sin\theta$ and Equations (4)–(6), we can calculate the value of $\theta$ by substituting $f_{swg}$, $n_f$, and $n_{si}$, and then determine the value of $n_{swg}$. With the value of $n_{swg}$ and the SWG cladding structure, we can use FEM to calculate that $n_{swg}^{\prime }$ is 2.04 and 2.18 under the two conditions. 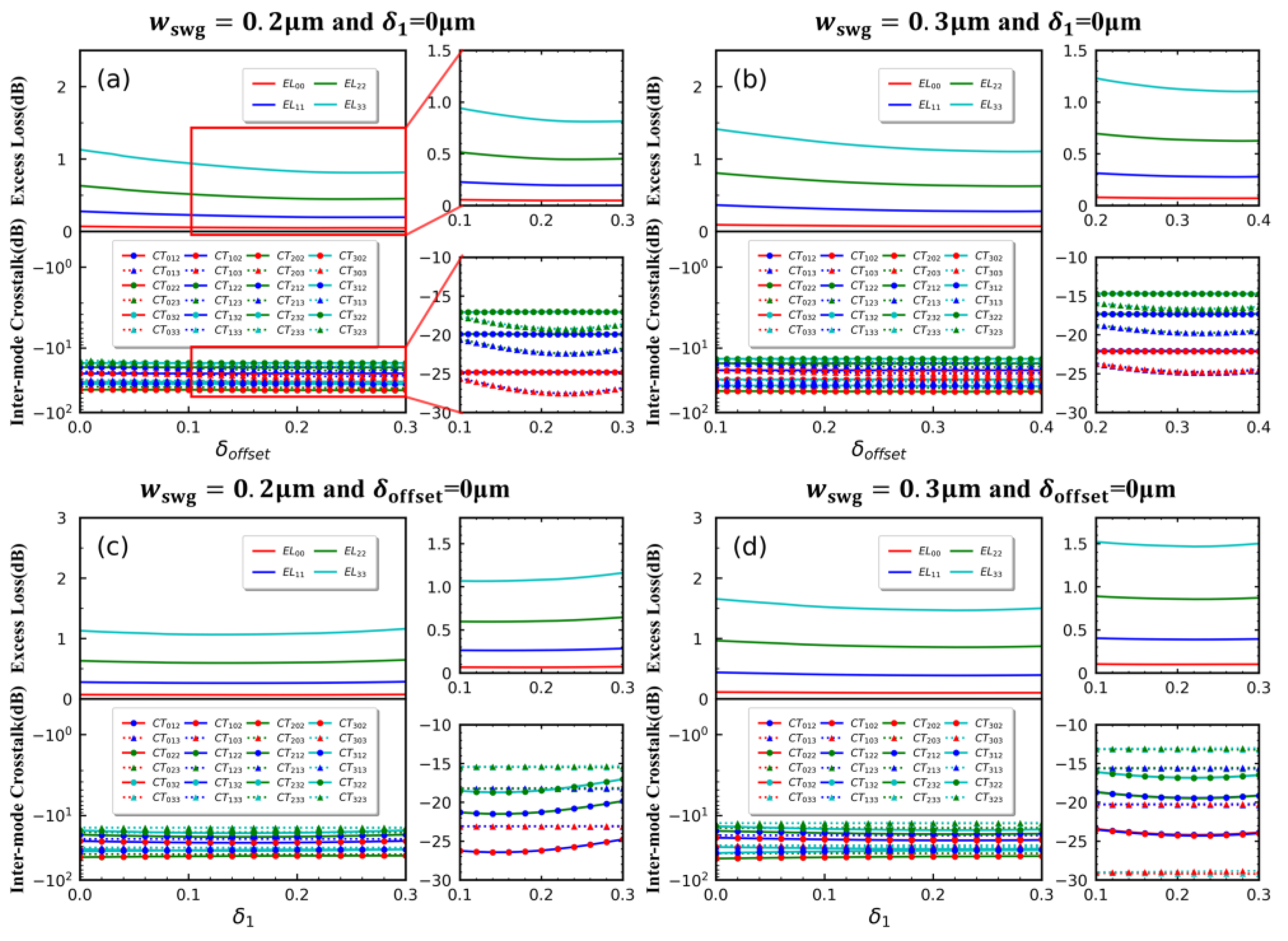Plugging these values into Equations (11) and (12) yields ${\delta }_{offset}$ and ${\delta }_1$ values of 0.23 μm, 0.17 μm, and 0.32, 0.25 μm, respectively. To validate the accuracy of this calculation, we conducted simulations using the VARFDTD method to assess the impact of ${\delta }_{offset}$ and ${\delta }_1$ displacements on the ELs and inter-mode CTs of ${\mathrm{T}\mathrm{E}}_i$ modes at output ports #2 and #3 in the entire device, with the grid resolution at SWG set to dx = dy = dz = 10 nm, and the simulation results are shown in Figure 4. CT is derived from the following equation:

$${CT}_{ijk}=10{\mathit{log}}_{10}{T}_{ijk}\left(i\ne j\right),$$

(13)

Where ${CT}_{ijk}$ represents the crosstalk of mode TE_j (j = 0, 1, 2, 3) relative to mode TE_i (i = 0, 1, 2, 3) at ports k (k = 2, 3). From Figure 4a,b, it can be observed that when ${\delta }_{offset}$ is 0.23 μm and 0.32 μm, the CT effects on the four modes are weakest, and the values of ELs are minimized. The increase in ${\delta }_{offset}$ has a much larger impact on the CTs of modes output from port #3 compared to those output from port #2. From Figure 4c,d, it can be seen that when ${\delta }_1$ is 0.16 μm and 0.24 μm, the ELs for the two modes are minimal. Additionally, unlike the impact of ${\delta }_{offset}$ on port #3, the variation of ${\delta }_1$ has a more significant effect on the CTs of modes at port #2. Considering the simulation step size, these simulation results are consistent with the GH shift behavior predicted by Equation (11) and the transmission shift behavior predicted by Equation (12). Furthermore, from Figure 4a–d, it can be observed that when ${\delta }_{offset}$ and ${\delta }_1$ deviations relative to the target values are within 20 nm, and the changes in EL and CTs are less than 0.02 dB and 0.5 dB, respectively, indicating good manufacturing robustness of the device. When $W_{\mathrm{W}\mathrm{G}}$ > 8 μm, it can be observed from Figure 2c that changing the $W_{\mathrm{W}\mathrm{G}}$ has a very small impact on $n_{eff}$, and similarly, the value of $n_{swg}^{\prime }$ remains nearly unchanged. Therefore, at $W_{\mathrm{W}\mathrm{G}}$ = 30 μm, the values of ${\delta }_{offset}$ and ${\delta }_1$ influenced by this factor also do not change significantly. To compensate for the GH shift and transmission shift, ${\delta }_{offset}$ and ${\delta }_1$ can be selected as 0.23 μm and 0.17 μm, respectively, at $w_{swg}$ = 0.2 μm, or 0.32μm and 0.25μm, respectively, at $w_{swg}$ = 0.3 μm to achieve optimal device performance.

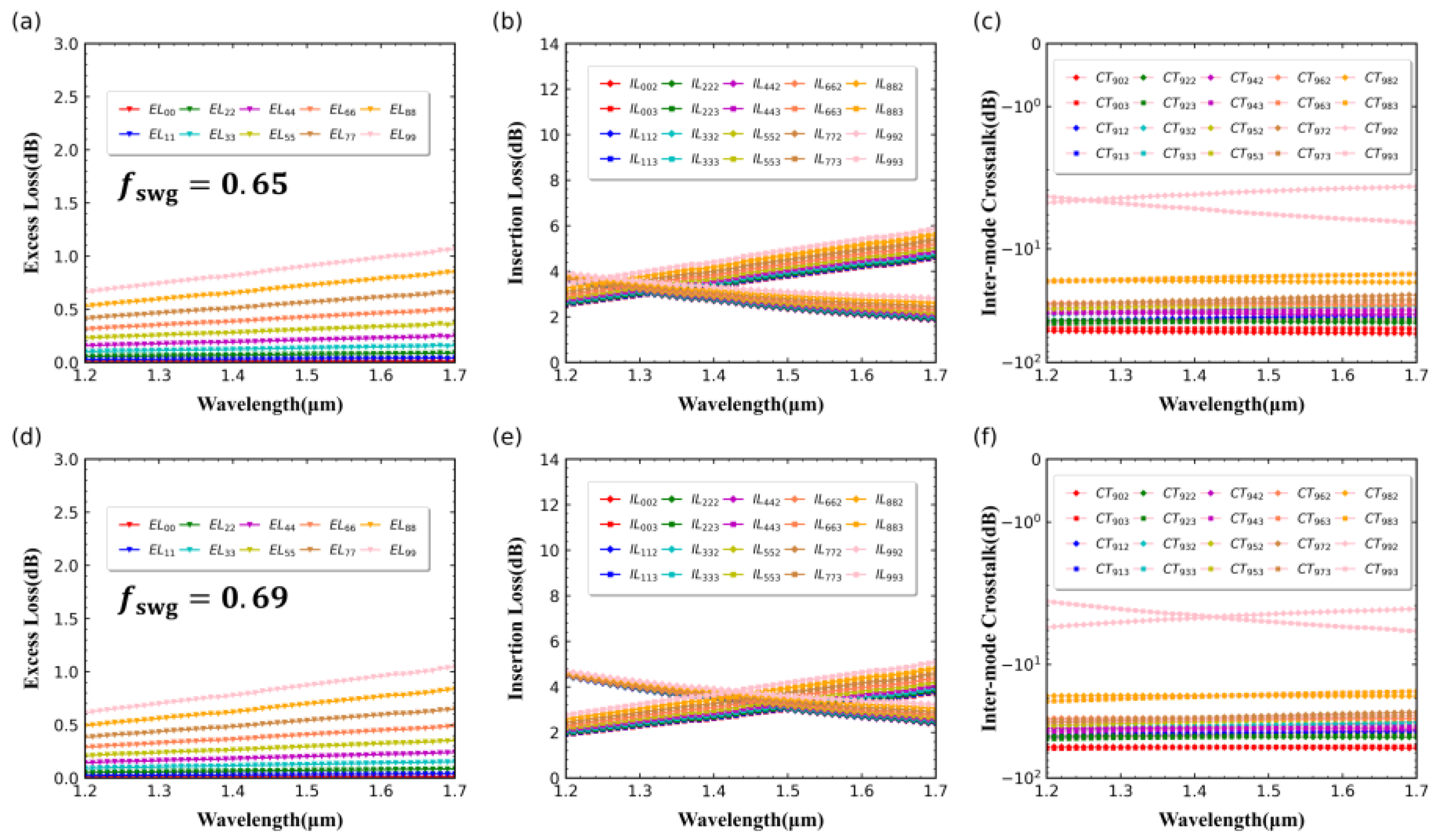
To visually demonstrate the multimode scalability of the power splitter, we used the VARFDTD method to simulate the ILs, ELs for each mode, and inter-mode CTs for TE₀–TE₉ modes in the multimode power splitter at $W_{\mathrm{W}\mathrm{G}}$ = 30 μm, $w_{swg}$ = 0.3 μm, and $w_{swg}$ values of 0.65 and 0.69 over a wavelength range of 1200–1700 nm at output ports #2 and #3 relative to the input port. The results are shown in Figure 5. The IL can be determined using the following formula:

$${IL}_{ijk}=10{\mathit{log}}_{10}{T}_{ijk}\left(i=j\right),$$

(14)

where ${IL}_{ijk}$ represents the insertion loss of mode TE_j (j = 0, 1, 2, 3) relative to mode TE_i (i = 0, 1, 2, 3) at ports k (k = 2, 3).

As shown in Figure 3c earlier, at $f_{swg}$ = 0.65, the multimode power splitter achieves uniform power splitting for TE₀–TE₃ optical waves at 1310 nm wavelength with $W_{\mathrm{W}\mathrm{G}}$ = 8 μm. In Figure 5a–c, it can be observed that at $W_{\mathrm{W}\mathrm{G}}$ = 30 μm, the device achieves uniform power splitting for TE₀–TE₅ and even higher-order modes at 1310 nm wavelength, demonstrating excellent multimode expansion performance. Figure 5d–f reveals that at $f_{swg}$ = 0.69, the device achieves relatively uniform power splitting for TE₀–TE₅ at 1450 nm wavelength, with ELs for TE₀–TE₅ modes below 0.5 dB across the simulated wavelength range of 1200–1700 nm, and their IL curves largely overlap. however, ELs for TE₆–TE₉ modes increase significantly. 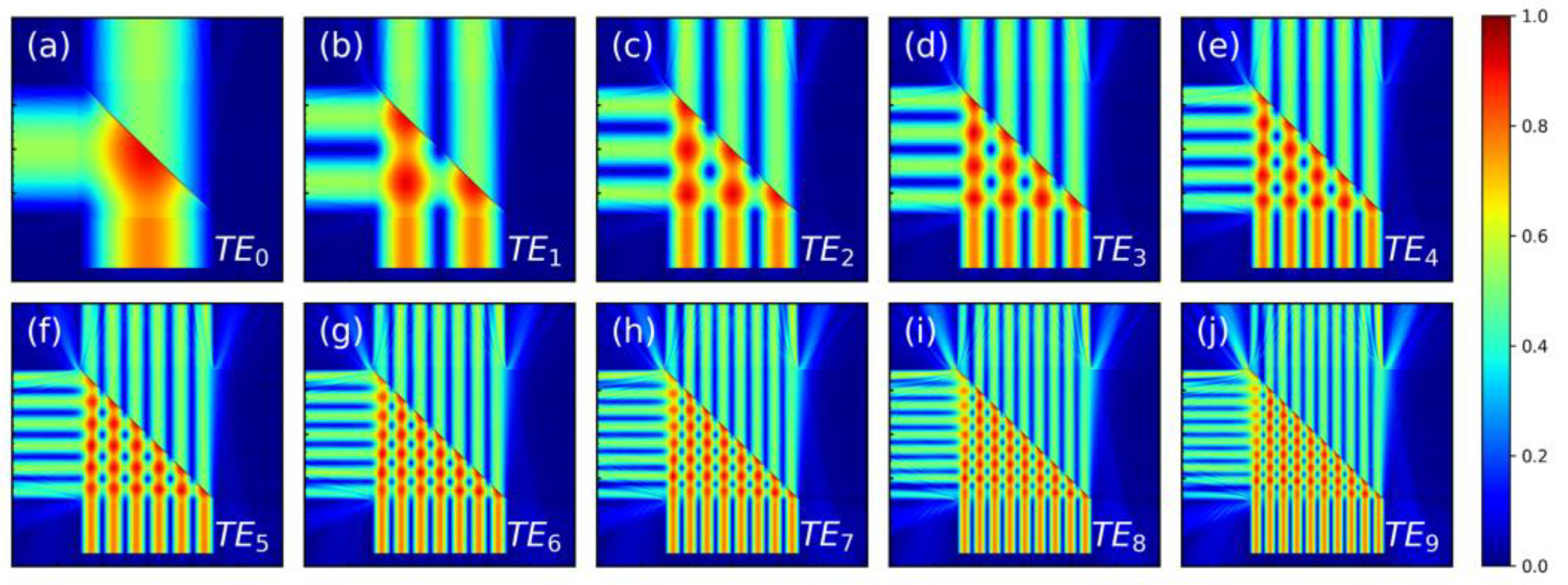Figure 6g–j illustrates the electric field distribution of TE₆–TE₉ modes at 1450 nm wavelength and $f_{swg}$ = 0.69, showing that TE₆–TE₉ modes leak noticeably into the cladding due to reduced confinement at the SWG grating in the Si waveguide. This leakage can be improved by reducing the $n_{eff}$ difference of higher-order modes. By increasing the $W_{\mathrm{W}\mathrm{G}}$ width, it is easy to expand the device to more modes, which can significantly reduce the losses and differences mentioned above.

4. Discussion

In the optimization process, we employed the VARFDTD method to simulate the entire device. We set the grid resolution at the SWG to dx = dy = dz = 10 nm and utilized the TE₀–TE₉ modes for excitation. The wavelength range of the light source was set to 1200–1700 nm. In

Table 1. The simulated result of the design power splitters.

Modes	PSR	EL (dB)	CT (dB)	${\left|△{\mathbf{I}\mathbf{L}}_{0-9}\right|\left(\mathbf{d}\mathbf{B}\right)}^{\mathbf{a}}$	${\left|△\mathbf{I}\mathbf{L}\right|\left(\mathbf{d}\mathbf{B}\right)}^{\mathbf{a}}$	${\mathbf{B}\mathbf{W}\left(\mathbf{n}\mathbf{m}\right)}^{\mathbf{a}}$
10	Arbitrary	<1.1	<−18.8	<1.1	<2	500

^a$\left|△{\mathrm{I}\mathrm{L}}_{0-9}\right|$ represents the IL difference of different ${\mathrm{T}\mathrm{E}}_0$ –${\mathrm{T}\mathrm{E}}_9$ modes at the same wavelength and the same output port, $\left|△\mathrm{I}\mathrm{L}\right|$ refers to the absolute value of the actual IL difference between the two output ports for all modes relative to the reference IL difference, and BW represents the bandwidth.

, we summarized the data from Figure 5d–f and presented detailed device data. From Table 1, it can be seen that our proposed multimode power splitter exhibits extremely low excess loss (EL < 1.1 dB) and relatively small inter-mode crosstalk (−18.8 < CT < −60 dB) for all TE₀–TE₉ modes in the wavelength range of 1200–1700 nm. Furthermore, when the PSR is around 0.5, the actual IL is within 2 dB of the target IL of 3 dB, and the maximum IL difference between different TE₀–TE₉ modes is less than 1.1 dB.

In the subsequent manufacturing process, our proposed device will be manufactured based on commercial SOI chips with a top Si layer of 220 nm and a buried oxide layer of 2 μm in thickness. We will employ electron beam lithography (EBL) for waveguide patterning and perform inductively coupled plasma (ICP) etching on the masked chip. The Si layer will be etched completely to a depth of 220 nm, thus achieving a complete waveguide structure. Once the waveguide structure is etched and the mask is completely removed, the device fabrication will be completed by depositing a silicon nitride film using ion-assisted pulsed DC reactive magnetron sputtering. Before the device fabrication, Figure 4 demonstrates that the variations in EL and CTs are both less than 0.02 dB and 0.5 dB, respectively, when the compensations for transmissive and reflective optical wave displacements deviate from the target values by less than 20 nm.

The comparison between the currently reported state-of-the-art on-chip multimode power splitters and the simulation results of our work is presented in

Table 2. Performance comparison of several on-chip multimode power splitters.

Structures	PSR	Modes	Device Size (μm)	EL (dB)		CT (dB)		BW (nm)
				Sim.	Exp.	Sim.	Exp.	Sim.	Exp.
[18]	0~1	3	315	0.5	/	<−20.0	/	415	/
[23]	0.5	4	800	<0.4	/	<−18.5	/	165	/
[22]	0~1	9	40	<0.9	/	<−16.3	/	400	/
This work	0~1	10	40	<1.1	/	<−18.8	/	500	/

. The results indicate that compared to other multimode power splitters, our proposed SWG-based multimode power splitter with arbitrary PSR supports more transmission modes, has a smaller footprint, and possesses an ultra-wide operating bandwidth covering O, E, S, C, L, and U bands. In the past, devices often could only achieve spectral splitting for a few modes with PSR = 0.5, and the wavelength range and device size could not be balanced. Additionally, for the same device size and identical excitation modes (such as TE₀–TE₈), compared to Ref. [22], due to our use of Si₃N₄ cladding structure and compensation for the transmission and reflection shifts of optical waves caused by SWG, the proposed structure in this paper can achieve lower ELs (<0.92 dB) and inter-mode CTs (<−18.8 dB) over a wider wavelength range (>500 nm). Overall, our research demonstrates significant potential in the application of large-scale silicon systems.

5. Conclusions

In conclusion, we have proposed and demonstrated a multimode subwavelength grating power splitter on the SOI platform that can achieve arbitrary PSRs. By optimizing the waveguide cladding material and compensating for the transmission and reflection offsets of the light waves, this power splitter can achieve low-loss, mode-insensitive spectral splitting for TE₀–TE₉ modes. It can cover an extremely wide wavelength range from 1200 nm to 1700 nm, with very low excess loss (EL < 1.1 dB) and inter-mode crosstalk (−18.8 < CT < −60 dB). The SWG-based splitter presented here can also be used as a 2 × 2 coupler and within Mach–Zehnder modulators. Furthermore, by adjusting the duty cycle, this structure can be employed for multimode waveguide bends, covering almost all optical communication bands. Therefore, it holds great potential for large-scale on-chip MDM systems.