Cherenkov-Type Terahertz Generation by Long-Wavelength Ultrafast Laser Excitation of a GaP Crystal
Abstract
:1. Introduction
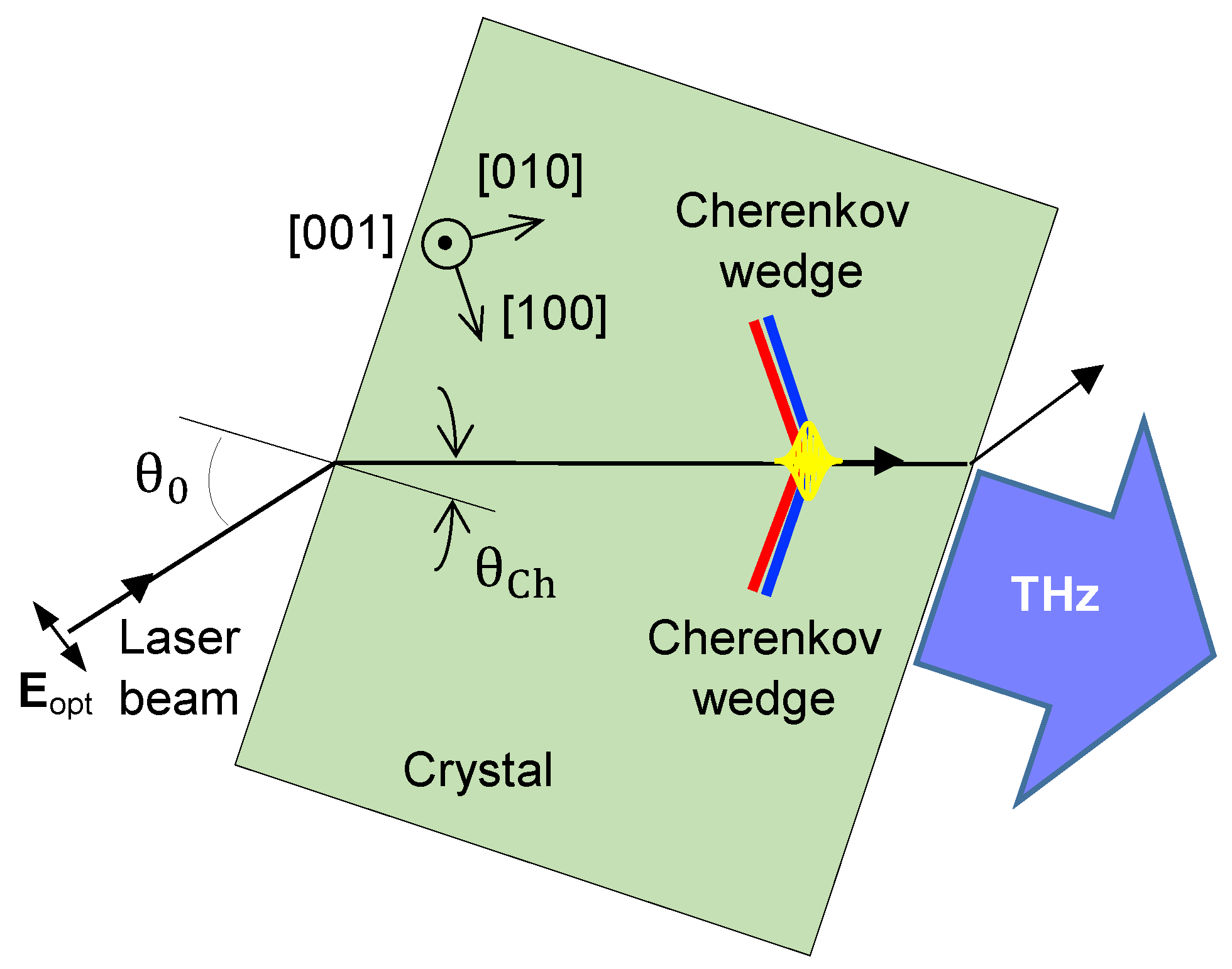
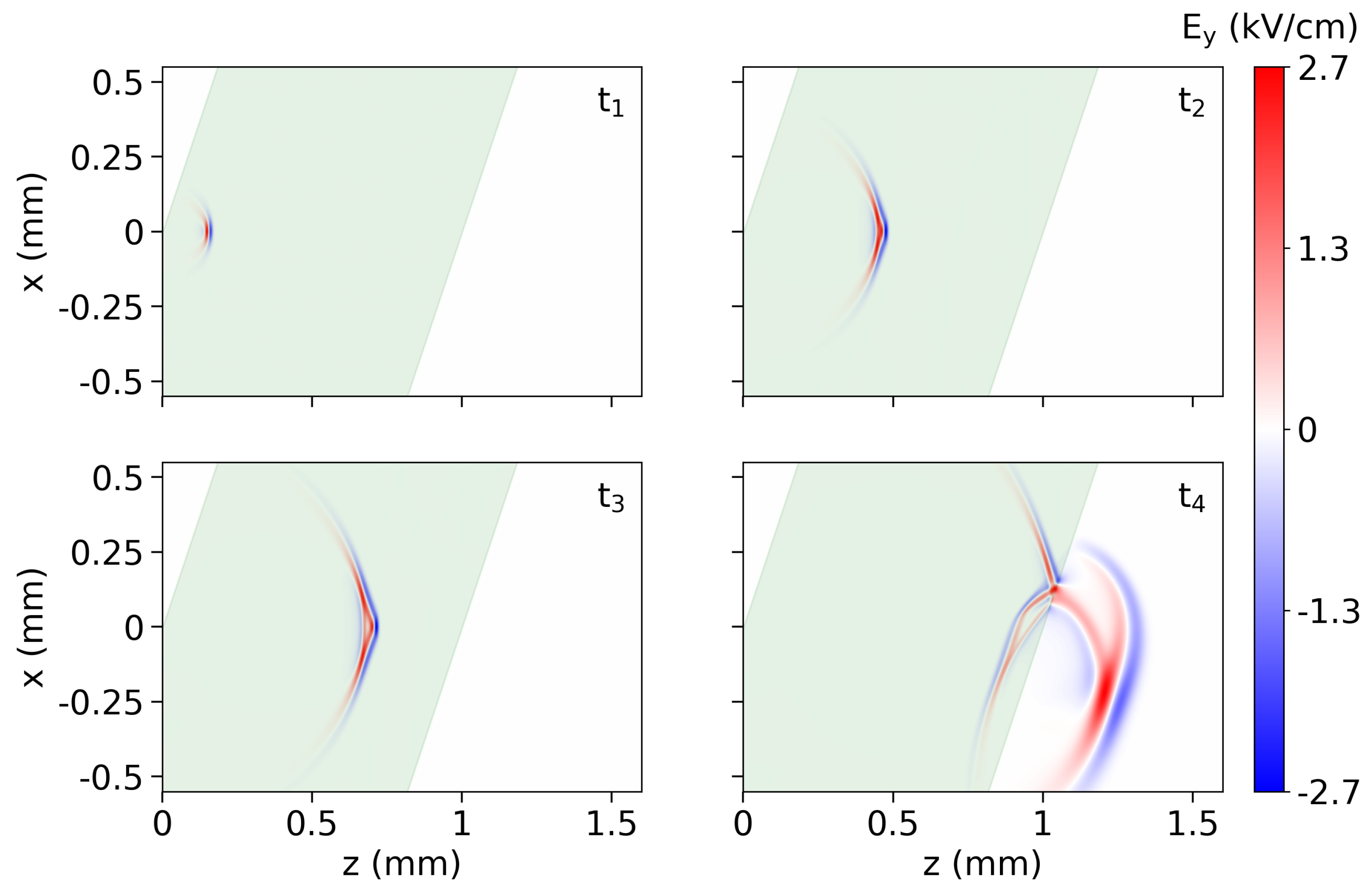
2. Generation Scheme and Modelling
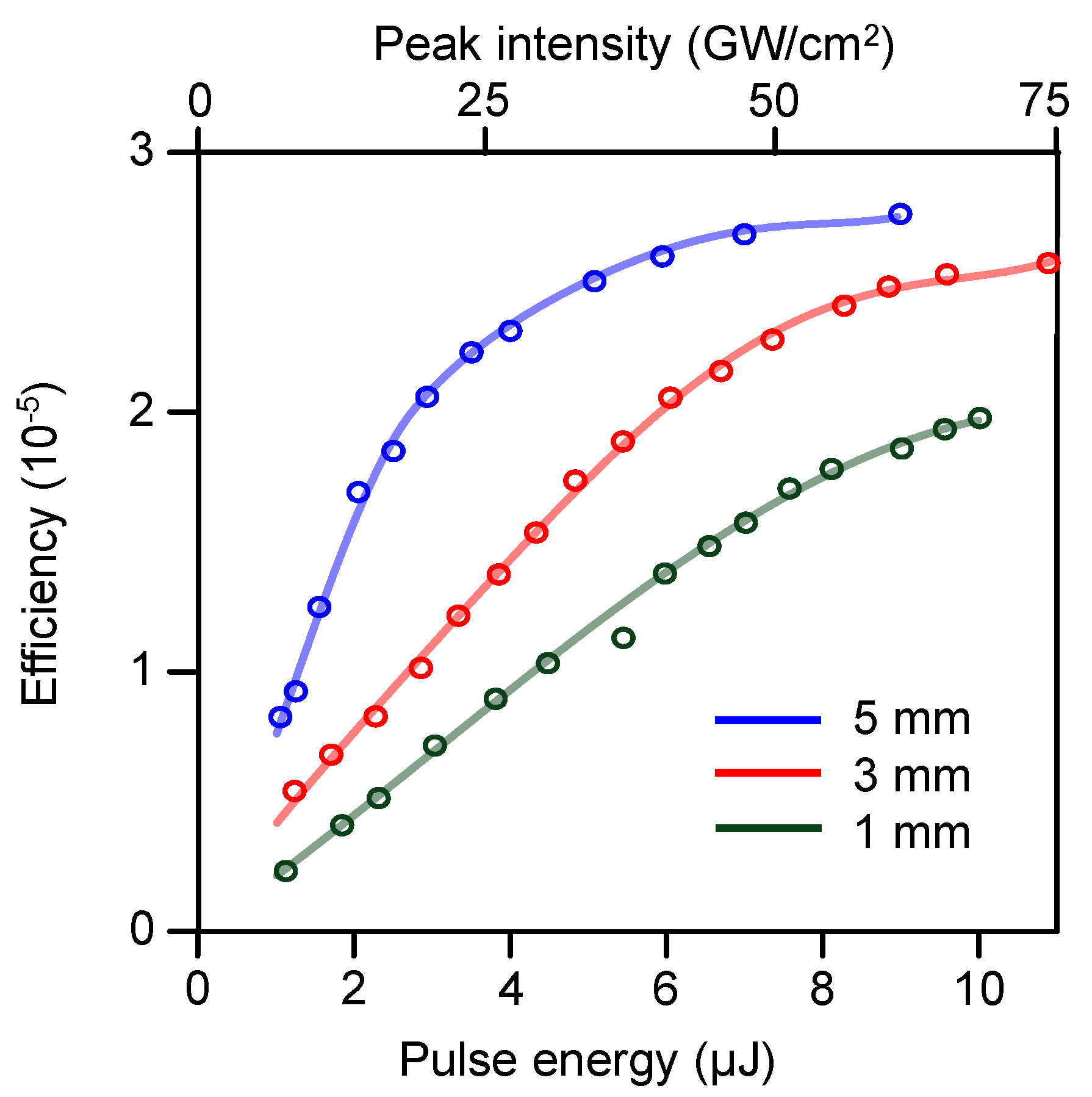
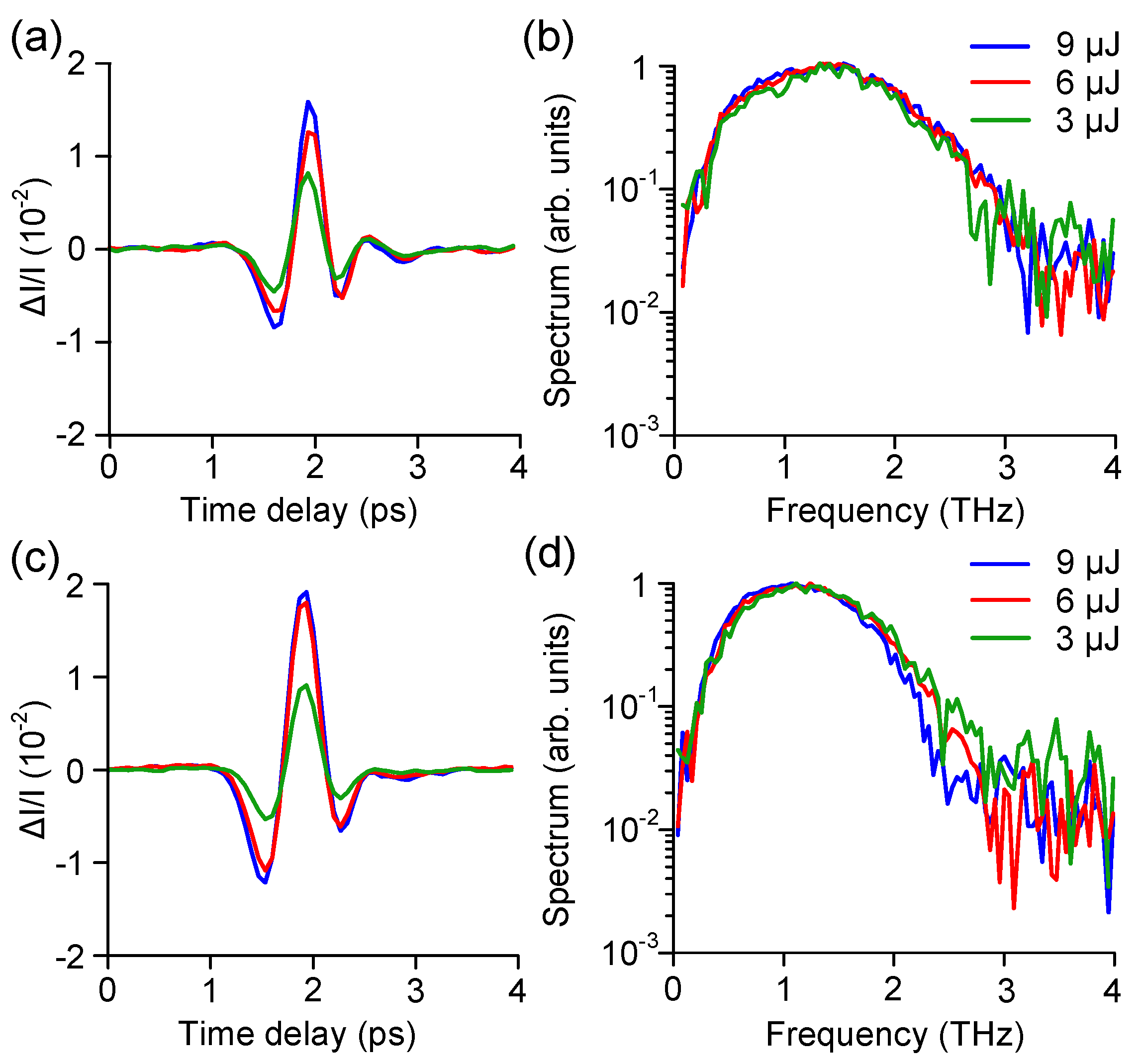
3. Experimental Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bagdasaryan, D.A.; Makaryan, A.O.; Pogosyan, P.S. Cerenkov radiation from a propagating nonlinear polarization wave. JETP Lett. 1983, 37, 594–596. [Google Scholar]
- Auston, D.H. Subpicosecond electro-optic shock waves. Appl. Phys. Lett. 1983, 43, 713–715. [Google Scholar] [CrossRef]
- Auston, D.H.; Cheung, K.P.; Valdmanis, J.A.; Kleinman, D.A. Cherenkov Radiation from Femtosecond Optical Pulses in Electro-Optic Media. Phys. Rev. Lett. 1984, 53, 1555–1558. [Google Scholar] [CrossRef]
- Askar’yan, G.A. Cerenkov radiation and transition radiation from electromagnetic waves. Sov. Phys. JETP 1962, 15, 943–946. [Google Scholar]
- Askar’yan, G.A. Cherenkov Radiation from Optical Pulses. Phys. Rev. Lett. 1986, 57, 2470. [Google Scholar] [CrossRef] [PubMed]
- Tomasino, A.; Parisi, A.; Stivala, S.; Livreri, P.; Cino, A.C.; Busacca, A.C.; Peccianti, M.; Morandotti, R. Wideband THz Time Domain Spectroscopy based on Optical Rectification and Electro-Optic Sampling. Sci. Rep. 2013, 3, 3116. [Google Scholar] [CrossRef] [PubMed]
- Nagai, M.; Tanaka, K.; Ohtake, H.; Bessho, T.; Sugiura, T.; Hirosumi, T.; Yoshida, M. Generation and detection of terahertz radiation by electro-optical process in GaAs using 1.56 μm fiber laser pulses. Appl. Phys. Lett. 2004, 85, 3974–3976. [Google Scholar] [CrossRef]
- Polónyi, G.; Monoszlai, B.; Gäumann, G.; Rohwer, E.J.; Andriukaitis, G.; Balciunas, T.; Pugzlys, A.; Baltuska, A.; Feurer, T.; Hebling, J.; et al. High-energy terahertz pulses from semiconductors pumped beyond the three-photon absorption edge. Opt. Express 2016, 24, 23872–23882. [Google Scholar] [CrossRef]
- Theuer, M.; Torosyan, G.; Rau, C.; Beigang, R.; Maki, K.; Otani, C.; Kawase, K. Efficient generation of Cherenkov-type terahertz radiation from a lithium niobate crystal with a silicon prism output coupler. Appl. Phys. Lett. 2006, 88, 071122. [Google Scholar] [CrossRef]
- Stepanov, A.G.; Hebling, J.; Kuhl, J. THz generation via optical rectification with ultrashort laser pulse focused to a line. Appl. Phys. B 2005, 81, 23–26. [Google Scholar] [CrossRef]
- Carnio, B.N.; Moutanabbir, O.; Elezzabi, A.Y. Nonlinear Photonic Waveguides: A Versatile Platform for Terahertz Radiation Generation (a Review). Laser Photon. Rev. 2023, 17, 2200138. [Google Scholar] [CrossRef]
- Bakunov, M.I.; Efimenko, E.S.; Gorelov, S.D.; Abramovsky, N.A.; Bodrov, S.B. Efficient Cherenkov-type optical-to-terahertz converter with terahertz beam combining. Opt. Lett. 2020, 45, 3533–3536. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, M.C.; Yeh, K.-L.; Hebling, J.; Nelson, K.A. Efficient terahertz generation by optical rectification at 1035 nm. Opt. Express 2007, 15, 11706–11713. [Google Scholar] [CrossRef] [PubMed]
- Fülöp, J.A.; Pálfalvi, L.; Almási, G.; Hebling, J. Design of high-energy terahertz sources based on optical rectification. Opt. Express 2010, 18, 12311–12327. [Google Scholar] [CrossRef] [PubMed]
- Bakunov, M.I.; Bodrov, S.B. Terahertz generation with tilted-front laser pulses in a contact-grating scheme. J. Opt. Soc. Am. B 2014, 31, 2549–2557. [Google Scholar] [CrossRef]
- Blanchard, F.; Schmidt, B.E.; Ropagnol, X.; Thiré, N.; Ozaki, T.; Morandotti, R.; Cooke, D.G.; Légaré, F. Terahertz pulse generation from bulk GaAs by a tilted-pulse-front excitation at 1.8 μm. Appl. Phys. Lett. 2014, 105, 241106. [Google Scholar] [CrossRef]
- Fülöp, J.A.; Polónyi, G.; Monoszlai, B.; Andriukaitis, G.; Balciunas, T.; Pugzlys, A.; Arthur, G.; Baltuska, A.; Hebling, J. Highly efficient scalable monolithic semiconductor terahertz pulse source. Optica 2016, 3, 1075–1078. [Google Scholar] [CrossRef]
- Cui, W.; Yalavarthi, E.K.; Radhan, A.V.; Bashirpour, M.; Gamouras, A.; Ménard, J.-M. High-field THz source centered at 2.6 THz. Opt. Express 2023, 31, 32468–32477. [Google Scholar] [CrossRef]
- Saito, K.; Tanabe, T.; Oyama, Y.; Suto, K.; Kimura, T.; Nishizawa, J. Terahertz-wave absorption in GaP crystals with different carrier densities. J. Phys. Chem. Solids 2008, 69, 597–600. [Google Scholar] [CrossRef]
- Chen, Q.; Tani, M.; Jiang, Z.; Zhang, X.-C. Electro-optic transceivers for terahertz-wave applications. J. Opt. Soc. Am. B 2001, 18, 823–831. [Google Scholar] [CrossRef]
- Shugurov, A.I.; Mashkovich, E.A.; Bodrov, S.B.; Tani, M.; Bakunov, M.I. Nonellipsometric electro-optic sampling of terahertz waves in GaAs. Opt. Express 2018, 26, 23359–23365. [Google Scholar] [CrossRef] [PubMed]
- Hebling, J.; Yeh, K.-L.; Hoffmann, M.C.; Bartal, B.; Nelson, K.A. Generation of high-power terahertz pulses by tilted-pulse-front excitation and their application possibilities. J. Opt. Soc. Am. B 2008, 25, B6–B19. [Google Scholar] [CrossRef]
- Casalbuoni, S.; Schlarb, H.; Schmidt, B.; Schmüser, P.; Steffen, B.; Winter, A. Numerical studies on the electro-optic detection of femtosecond electron bunches. Phys. Rev. ST Accel. Beams 2008, 11, 072802. [Google Scholar] [CrossRef]
- Khmelevskaia, D.; Markina, D.I.; Fedorov, V.V.; Ermolaev, G.A.; Arsenin, A.V.; Volkov, V.S.; Goltaev, A.S.; Zadiranov, Y.M.; Tzibizov, I.A.; Pushkarev, A.P.; et al. Directly grown crystalline gallium phosphide on sapphire for nonlinear all-dielectric nanophotonics. Appl. Phys. Lett. 2021, 118, 201101. [Google Scholar] [CrossRef]
- Efimenko, E.S.; Abramovsky, N.A.; Bakunov, M.I. Strong spectral broadening of Cherenkov-type terahertz radiation by free carrier generation. Phys. Rev. A 2023, 107, 013526. [Google Scholar] [CrossRef]
- Nathan, V.; Guenther, A.H.; Mitra, S.S. Review of multiphoton absorption in crystalline solids. J. Opt. Soc. Am. B 1985, 2, 294–316. [Google Scholar] [CrossRef]
- Kleinman, D.A.; Auston, D.H. Theory of Electrooptic Shock Radiation in Nonlinear Optical Media. IEEE J. Quantum Electron. 1984, 20, 964–970. [Google Scholar] [CrossRef]
- Barbiero, G.; Wang, H.; Brons, J.; Chen, B.-H.; Pervak, V.; Fattahi, H. Broadband terahertz solid-state emitter driven by Yb:YAG thin-disk oscillator. J. Phys. B 2020, 53, 125601. [Google Scholar] [CrossRef]
- Reimann, K. Table-top sources of ultrashort THz pulses. Rep. Prog. Phys. 2007, 70, 1597–1632. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bodrov, S.B.; Shugurov, A.I.; Efimenko, E.S.; Kurnikov, M.A.; Ilyakov, I.E.; Shishkin, B.V.; Bakunov, M.I. Cherenkov-Type Terahertz Generation by Long-Wavelength Ultrafast Laser Excitation of a GaP Crystal. Photonics 2023, 10, 1309. https://doi.org/10.3390/photonics10121309
Bodrov SB, Shugurov AI, Efimenko ES, Kurnikov MA, Ilyakov IE, Shishkin BV, Bakunov MI. Cherenkov-Type Terahertz Generation by Long-Wavelength Ultrafast Laser Excitation of a GaP Crystal. Photonics. 2023; 10(12):1309. https://doi.org/10.3390/photonics10121309
Chicago/Turabian StyleBodrov, S. B., A. I. Shugurov, E. S. Efimenko, M. A. Kurnikov, I. E. Ilyakov, B. V. Shishkin, and M. I. Bakunov. 2023. "Cherenkov-Type Terahertz Generation by Long-Wavelength Ultrafast Laser Excitation of a GaP Crystal" Photonics 10, no. 12: 1309. https://doi.org/10.3390/photonics10121309
APA StyleBodrov, S. B., Shugurov, A. I., Efimenko, E. S., Kurnikov, M. A., Ilyakov, I. E., Shishkin, B. V., & Bakunov, M. I. (2023). Cherenkov-Type Terahertz Generation by Long-Wavelength Ultrafast Laser Excitation of a GaP Crystal. Photonics, 10(12), 1309. https://doi.org/10.3390/photonics10121309




