Dynamic Secure Key Distribution Based on Dispersion Equalization and Cellular Automata for Optical Transmission
Abstract
:1. Introduction
2. Operating Principle
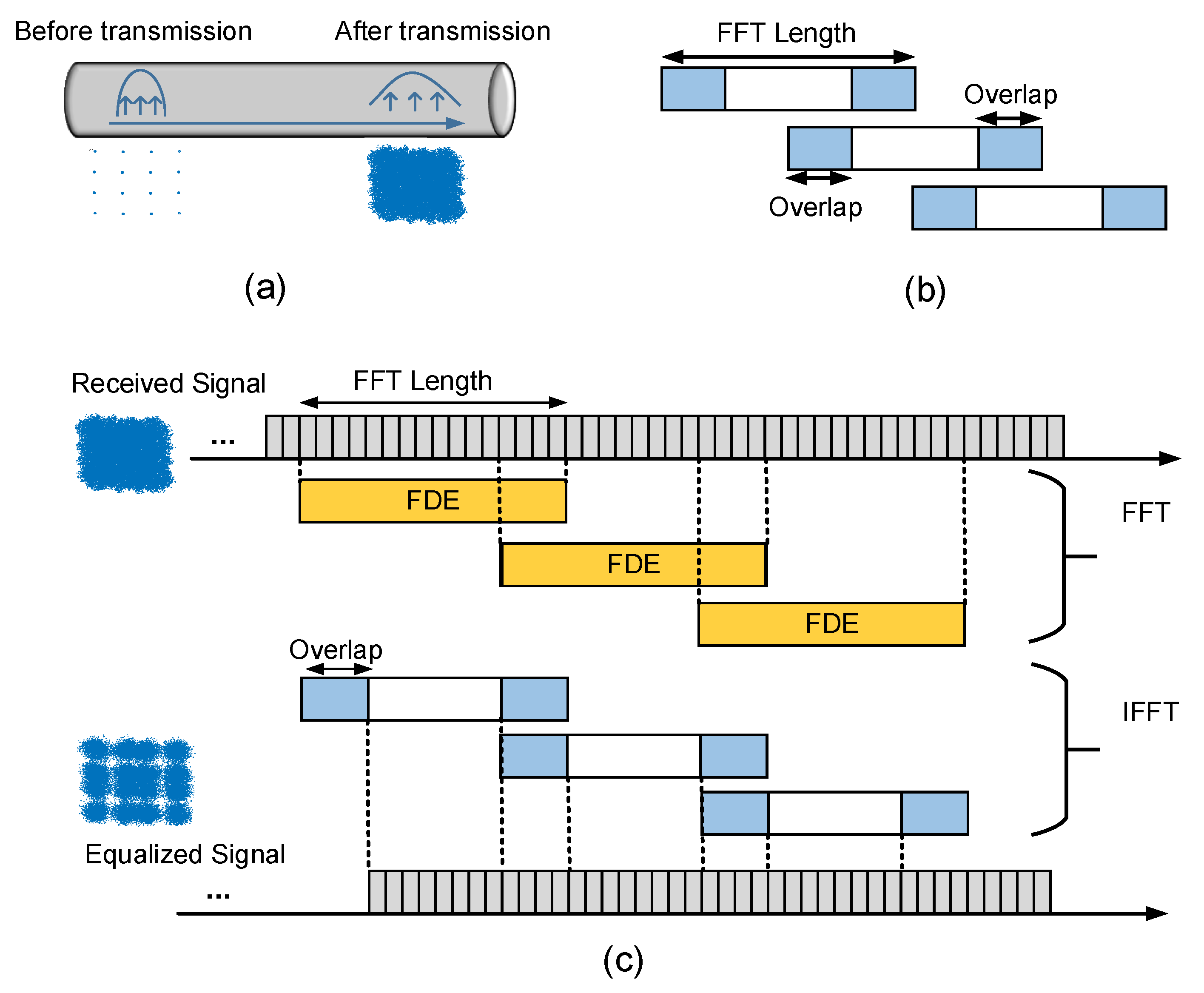
2.1. FDE Algorithm
2.2. CA Iteration
3. Simulations and Discussions
3.1. FDE Algorithm Performance
3.2. Effective Elimination of Key Inconsistency
3.3. Proof of Security under Eavesdropping Attack Situations
3.4. Dynamic Key Generation
3.4.1. Operation of Input Parameter Variation Interval
3.4.2. Operation of Local Fiber
3.4.3. Operation of CA Iteration
3.5. Analysis of Security Enhancement
3.6. Assessment of Overall Scheme
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Forutan, V.; Elschner, R.; Schmidt-Langhorst, C.; Schubert, C.; Fischer, R.F. Towards information-theoretic security in optical networks. In Proceedings of the Photonic Networks, 18. ITG-Symposium, Leipzig, Germany, 11–12 May 2017; VDE: Berlin, Germany, 2017; pp. 1–7. [Google Scholar]
- Dahan, D.; Mahlab, U. Security threats and protection procedures for optical networks. IET Optoelectron. 2017, 11, 186–200. [Google Scholar] [CrossRef]
- Skorin-Kapov, N.; Furdek, M.; Zsigmond, S.; Wosinska, L. Physical-layer security in evolving optical networks. IEEE Commun. Mag. 2016, 54, 110–117. [Google Scholar] [CrossRef]
- Fok, M.P.; Wang, Z.; Deng, Y.; Prucnal, P.R. Optical layer security in fiber-optic networks. IEEE Trans. Inf. Forensics Secur. 2011, 6, 725–736. [Google Scholar] [CrossRef]
- Shakiba-Herfeh, M.; Chorti, A.; Poor, H.V. Physical Layer Security: Authentication, Integrity, and Confidentiality. In Physical Layer Security; Springer: Berlin/Heidelberg, Germany, 2021; pp. 129–150. [Google Scholar]
- Bellare, M.; Rogaway, P. Introduction to modern cryptography. Ucsd Cse 2005, 207, 207. [Google Scholar]
- Wang, Y.; Zhang, H.; Wang, H. Quantum polynomial-time fixed-point attack for RSA. China Commun. 2018, 15, 25–32. [Google Scholar] [CrossRef]
- Deshpande, P.; Santhanalakshmi, S.; Lakshmi, P.; Vishwa, A. Experimental study of Diffie-Hellman key exchange algorithm on embedded devices. In Proceedings of the 2017 International Conference on Energy, Communication, Data Analytics and Soft Computing (ICECDS), Chennai, India, 1–2 August 2017; pp. 2042–2047. [Google Scholar]
- Yassein, M.B.; Aljawarneh, S.; Qawasmeh, E.; Mardini, W.; Khamayseh, Y. Comprehensive study of symmetric key and asymmetric key encryption algorithms. In Proceedings of the 2017 international conference on engineering and technology (ICET), Antalya, Turkey, 21–23 August 2017; pp. 1–7. [Google Scholar]
- Patra, B.; Incandela, R.M.; Van Dijk, J.P.; Homulle, H.A.; Song, L.; Shahmohammadi, M.; Staszewski, R.B.; Vladimirescu, A.; Babaie, M.; Sebastiano, F.; et al. Cryo-CMOS circuits and systems for quantum computing applications. IEEE J. Solid-State Circuits 2017, 53, 309–321. [Google Scholar] [CrossRef]
- Montanaro, A. Quantum algorithms: An overview. npj Quantum Inf. 2016, 2, 15023. [Google Scholar] [CrossRef]
- Wu, Y.; Khisti, A.; Xiao, C.; Caire, G.; Wong, K.K.; Gao, X. A survey of physical layer security techniques for 5G wireless networks and challenges ahead. IEEE J. Sel. Areas Commun. 2018, 36, 679–695. [Google Scholar] [CrossRef]
- Eriksson, T.A.; Trinh, P.V.; Endo, H.; Takeoka, M.; Sasaki, M. Secret key rates for intensity-modulated dual-threshold detection key distribution under individual beam splitting attacks. Opt. Express 2018, 26, 20409–20419. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Zhang, J.; Li, Y.; Gao, G.; Zhao, Y.; Zhang, H. Single-carrier QAM/QNSC and PSK/QNSC transmission systems with bit-resolution limited DACs. Opt. Commun. 2019, 445, 29–35. [Google Scholar] [CrossRef]
- Jiao, H.; Pu, T.; Zheng, J.; Xiang, P.; Fang, T. Physical-layer security analysis of a quantum-noise randomized cipher based on the wire-tap channel model. Opt. Express 2017, 25, 10947–10960. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Chen, Z.; Pirandola, S.; Wang, X.; Zhou, C.; Chu, B.; Zhao, Y.; Xu, B.; Yu, S.; Guo, H. Long-distance continuous-variable quantum key distribution over 202.81 km of fiber. Phys. Rev. Lett. 2020, 125, 010502. [Google Scholar] [CrossRef] [PubMed]
- Fang, X.T.; Zeng, P.; Liu, H.; Zou, M.; Wu, W.; Tang, Y.L.; Sheng, Y.J.; Xiang, Y.; Zhang, W.; Li, H.; et al. Implementation of quantum key distribution surpassing the linear rate-transmittance bound. Nat. Photonics 2020, 14, 422–425. [Google Scholar] [CrossRef]
- Zhang, J.; Marshall, A.; Woods, R.; Duong, T.Q. Efficient key generation by exploiting randomness from channel responses of individual OFDM subcarriers. IEEE Trans. Commun. 2016, 64, 2578–2588. [Google Scholar] [CrossRef]
- Kravtsov, K.; Wang, Z.; Trappe, W.; Prucnal, P.R. Physical layer secret key generation for fiber-optical networks. Optics Express 2013, 21, 23756–23771. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Hajomer, A.A.; Yang, X.; Hu, W. Error-free secure key generation and distribution using dynamic Stokes parameters. Opt. Express 2019, 27, 29207–29216. [Google Scholar] [CrossRef] [PubMed]
- Hajomer, A.A.; Yang, X.; Sultan, A.; Sun, W.; Hu, W. Key Generation and Distribution Using Phase Fluctuation in Classical Fiber Channel. In Proceedings of the 2018 20th International Conference on Transparent Optical Networks (ICTON), Bucharest, Romania, 1–5 July 2018; pp. 1–3. [Google Scholar]
- Zhang, L.; Hajomer, A.; Yang, X.; Hu, W. Secure Key Generation and Distribution Using Polarization Dynamics in Fiber. In Proceedings of the 2020 22nd International Conference on Transparent Optical Networks (ICTON), Bari, Italy, 19–23 July 2020; pp. 1–4. [Google Scholar]
- Kudo, R.; Kobayashi, T.; Ishihara, K.; Takatori, Y.; Sano, A.; Miyamoto, Y. Coherent optical single carrier transmission using overlap frequency domain equalization for long-haul optical systems. J. Light. Technol. 2009, 27, 3721–3728. [Google Scholar] [CrossRef]
- Kudo, R.; Kobayashi, T.; Ishihara, K.; Takatori, Y.; Sano, A.; Yamada, E.; Masuda, H.; Miyamoto, Y.; Mizoguchi, M. Two-stage overlap frequency domain equalization for long-haul optical systems. In Proceedings of the Optical Fiber Communication Conference, Optical Society of America, San Diego, CA, USA, 22–26 March 2009; p. OMT3. [Google Scholar]
- Niyat, A.Y.; Moattar, M.H.; Torshiz, M.N. Color image encryption based on hybrid hyper-chaotic system and cellular automata. Opt. Lasers Eng. 2017, 90, 225–237. [Google Scholar] [CrossRef]
- Naskar, P.K.; Bhattacharyya, S.; Nandy, D.; Chaudhuri, A. A robust image encryption scheme using chaotic tent map and cellular automata. Nonlinear Dyn. 2020, 100, 2877–2898. [Google Scholar] [CrossRef]
- Aldaghri, N.; Mahdavifar, H. Physical layer secret key generation in static environments. IEEE Trans. Inf. Forensics Secur. 2020, 15, 2692–2705. [Google Scholar] [CrossRef]
- Cheng, L.; Li, W.; Ma, D.; Wei, J.; Liu, X. Moving window scheme for extracting secret keys in stationary environments. IET Commun. 2016, 10, 2206–2214. [Google Scholar] [CrossRef]
- Obara, T.; Takeda, K.; Adachi, F. Performance analysis of single-carrier overlap FDE. In Proceedings of the 2010 IEEE International Conference on Communication Systems, Singapore, 17–19 November 2010; pp. 446–450. [Google Scholar]
- Tomasin, S. Overlap and save frequency domain DFE for throughput efficient single carrier transmission. In Proceedings of the 2005 IEEE 16th International Symposium on Personal, Indoor and Mobile Radio Communications, Berlin, Germany, 11–14 September 2005; Volume 2, pp. 1199–1203. [Google Scholar]
- Huang, C.; Ma, P.Y.; Blow, E.C.; Mittal, P.; Prucnal, P.R. Accelerated secure key distribution based on localized and asymmetric fiber interferometers. Opt. Express 2019, 27, 32096–32110. [Google Scholar] [CrossRef] [PubMed]
- Tu, Z.; Zhang, J.; Li, Y.; Zhao, Y.; Lei, C.; Yang, X.; Sun, Y. Experiment demonstration of physical layer secret key distribution with information reconciliation in digital coherent optical OFDM system. In Proceedings of the 2019 Asia Communications and Photonics Conference (ACP), Chengdu, China, 2–5 November 2019; pp. 1–3. [Google Scholar]
- Melki, R.; Noura, H.N.; Mansour, M.M.; Chehab, A. An efficient OFDM-based encryption scheme using a dynamic key approach. IEEE Internet Things J. 2018, 6, 361–378. [Google Scholar] [CrossRef]
- Dang, T.N.; Vo, H.M. Advanced AES algorithm using dynamic key in the Internet of things system. In Proceedings of the 2019 IEEE 4th International Conference on Computer and Communication Systems (ICCCS), Singapore, 23–25 February 2019; pp. 682–686. [Google Scholar]
- Sirakoulis, G.C. Hybrid DNA cellular automata for pseudorandom number generation. In Proceedings of the 2012 International Conference on High Performance Computing & Simulation (HPCS), Madrid, Spain, 2–6 July 2012; pp. 238–244. [Google Scholar]
- Babaei, A.; Motameni, H.; Enayatifar, R. A new permutation-diffusion-based image encryption technique using cellular automata and DNA sequence. Optik 2020, 203, 164000. [Google Scholar] [CrossRef]
- Wang, Y.; Li, X.W.; Wang, Q.H. Integral Imaging Based Optical Image Encryption Using CA-DNA Algorithm. IEEE Photonics J. 2021, 13, 1–12. [Google Scholar] [CrossRef]














| 000 | 1 | 100 | 0 |
| 001 | 1 | 101 | 0 |
| 010 | 0 | 110 | 0 |
| 011 | 1 | 111 | 0 |
| TTT | A | TTG | C | TTC | G | TTA | T |
| TGT | C | TGG | A | TGC | T | TGA | G |
| TCT | A | TCG | C | TCC | G | TCA | T |
| TAT | C | TAG | A | TAC | T | TAA | G |
| GTT | T | GTG | G | GTC | C | GTA | A |
| GGT | G | GGG | T | GGC | A | GGA | C |
| GCT | G | GCG | T | GCC | A | GCA | C |
| GAT | T | GAG | G | GAC | C | GAA | A |
| CTT | C | CTG | A | CTC | T | CTA | G |
| CGT | A | CGG | C | CGC | G | CGA | T |
| CCT | T | CCG | G | CCC | C | CCA | A |
| CAT | G | CAG | T | CAC | A | CAA | C |
| ATT | T | ATG | G | ATC | C | ATA | A |
| AGT | G | AGG | T | AGC | A | AGA | C |
| ACT | C | ACG | A | ACC | T | ACA | G |
| AAT | A | AAG | C | AAC | G | AAA | T |
| Index | p-Value |
|---|---|
| Frequency | 0.455228 |
| Block frequency | 0.042503 |
| Runs | 0.746962 |
| Longest Run | 0.901933 |
| Rank | 0.270256 |
| FFT | 0.574617 |
| Non-Overlapping Template | 0.999999 |
| Overlapping Template | 0.592848 |
| Universal | 0.638407 |
| Linear Complexity | 0.704754 |
| Serial | 0.959372 |
| Approximate Entropy | 0.993281 |
| Cumulative sum | 0.226876 |
| Random Excursions | 0.390989 |
| Random Excursion Variant | 0.114968 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, J.; Kong, W.; Liu, Z.; Ji, Y. Dynamic Secure Key Distribution Based on Dispersion Equalization and Cellular Automata for Optical Transmission. Photonics 2023, 10, 1308. https://doi.org/10.3390/photonics10121308
Cui J, Kong W, Liu Z, Ji Y. Dynamic Secure Key Distribution Based on Dispersion Equalization and Cellular Automata for Optical Transmission. Photonics. 2023; 10(12):1308. https://doi.org/10.3390/photonics10121308
Chicago/Turabian StyleCui, Jiabin, Wei Kong, Zhaoyang Liu, and Yuefeng Ji. 2023. "Dynamic Secure Key Distribution Based on Dispersion Equalization and Cellular Automata for Optical Transmission" Photonics 10, no. 12: 1308. https://doi.org/10.3390/photonics10121308
APA StyleCui, J., Kong, W., Liu, Z., & Ji, Y. (2023). Dynamic Secure Key Distribution Based on Dispersion Equalization and Cellular Automata for Optical Transmission. Photonics, 10(12), 1308. https://doi.org/10.3390/photonics10121308





