Enhanced Measurement of Vortex Beam Rotation Using Polarization-Assisted Particle Swarm Optimization for Phase Retrieval
Abstract
:1. Introduction
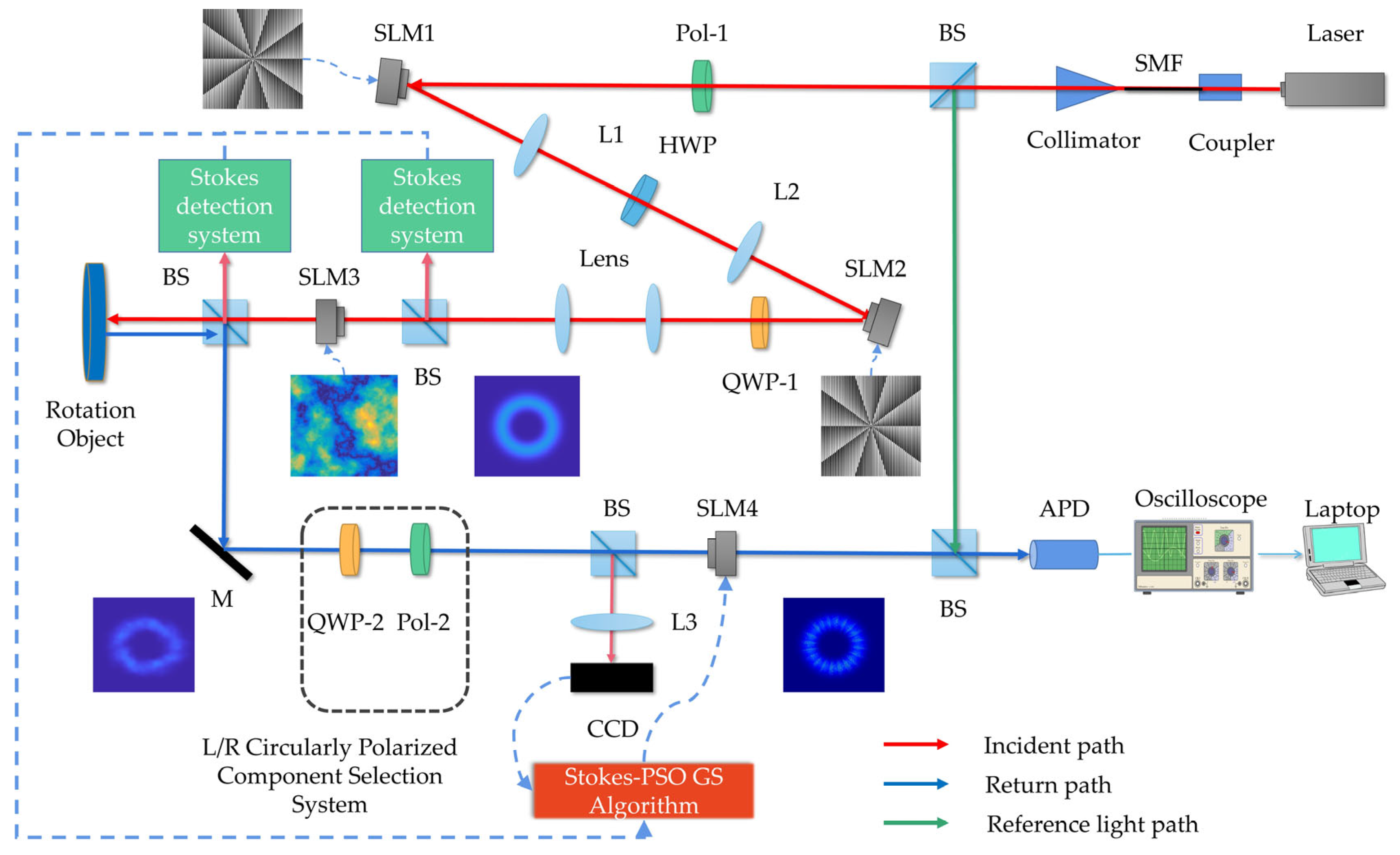
2. System Design
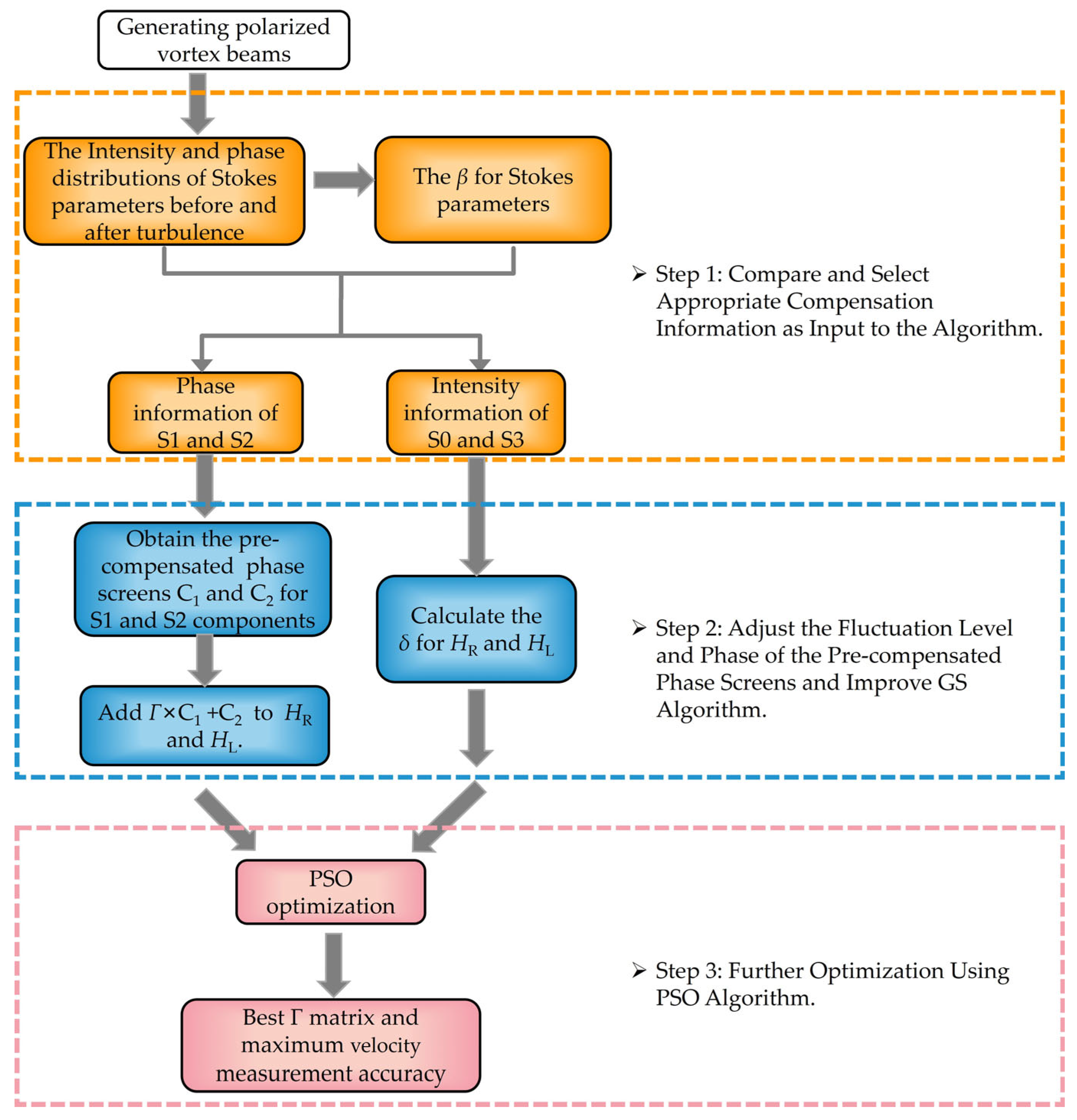
3. Stokes-PSO GS Algorithm
4. Results and Analysis
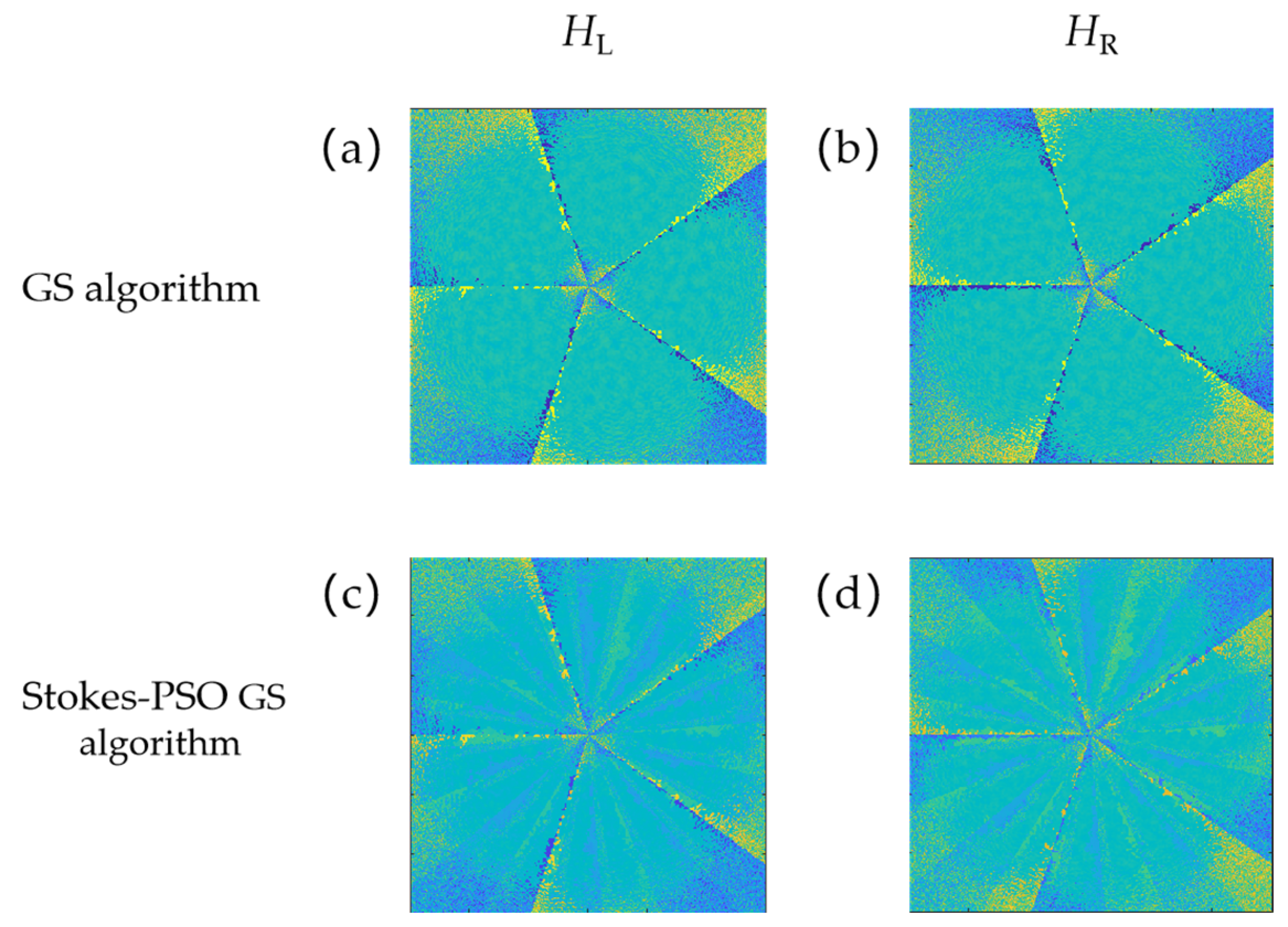
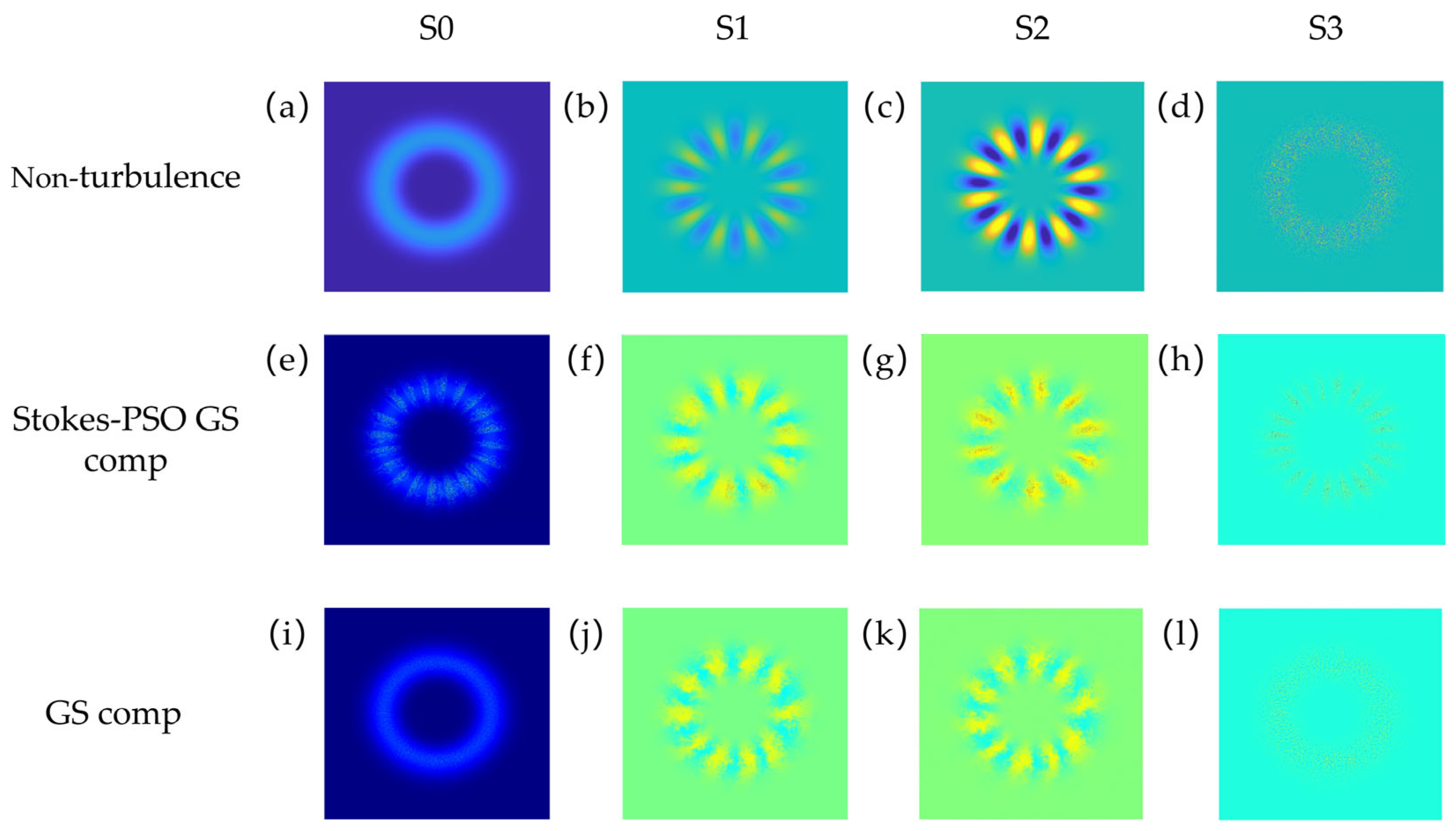
4.1. Optical Field Recovery
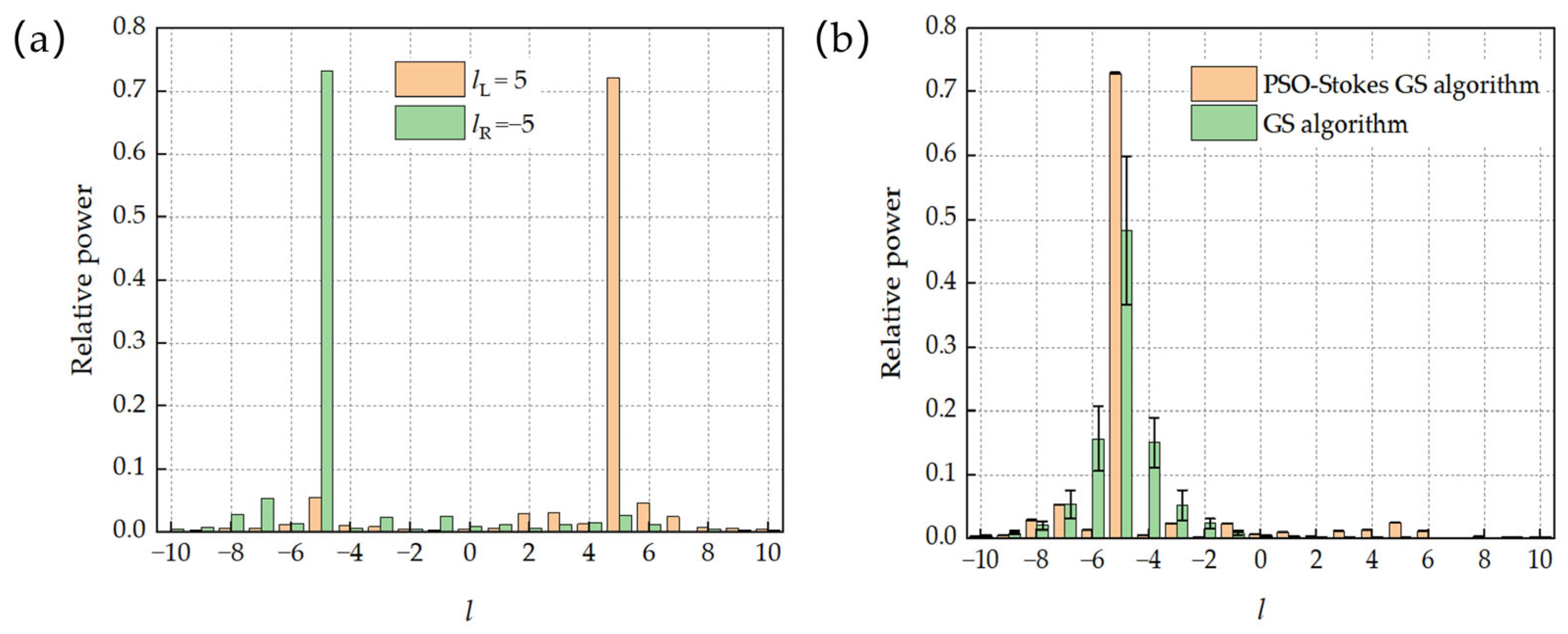
4.2. Enhancement of Orbital Angular Momentum Spectrum Purity
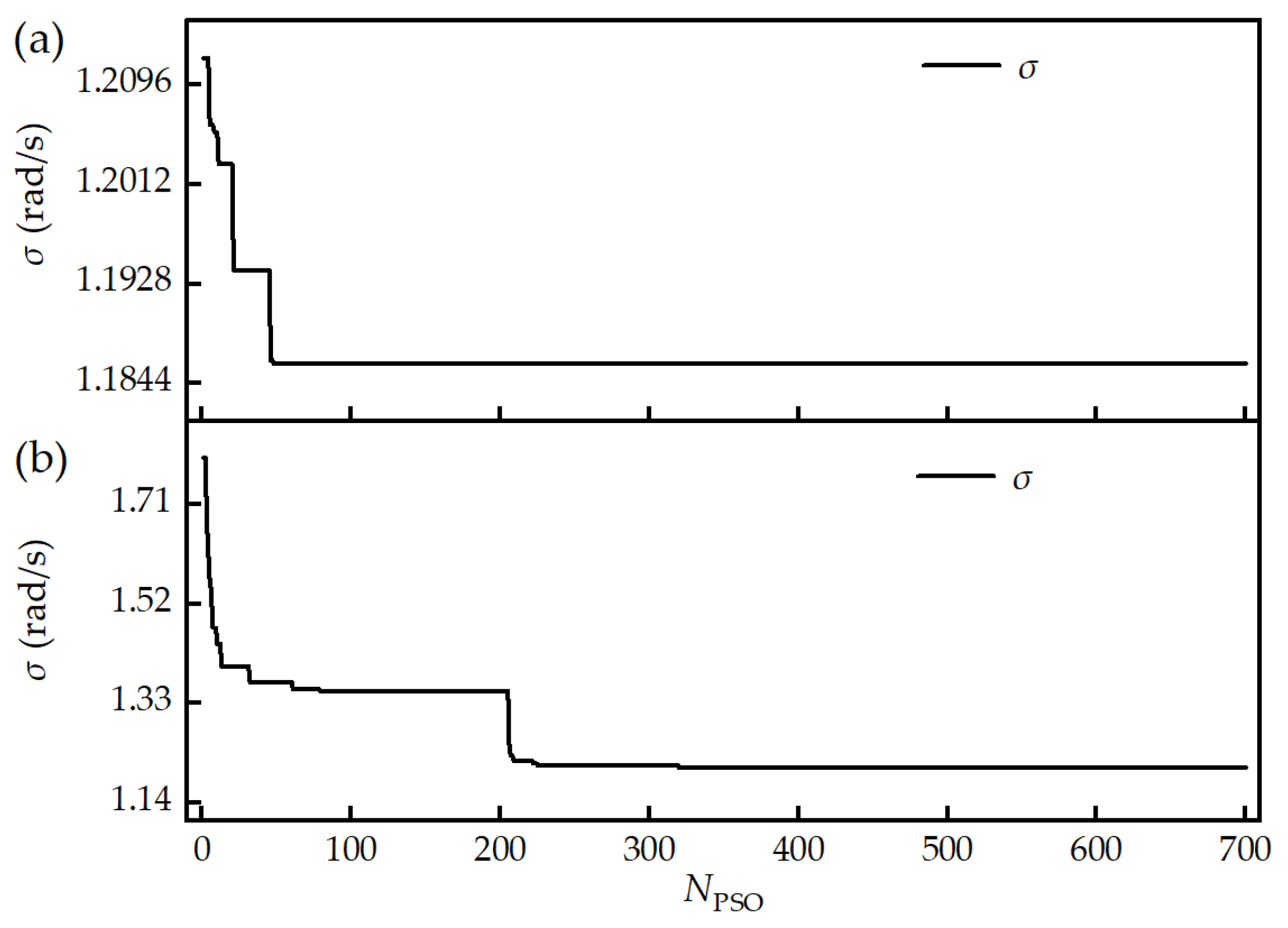
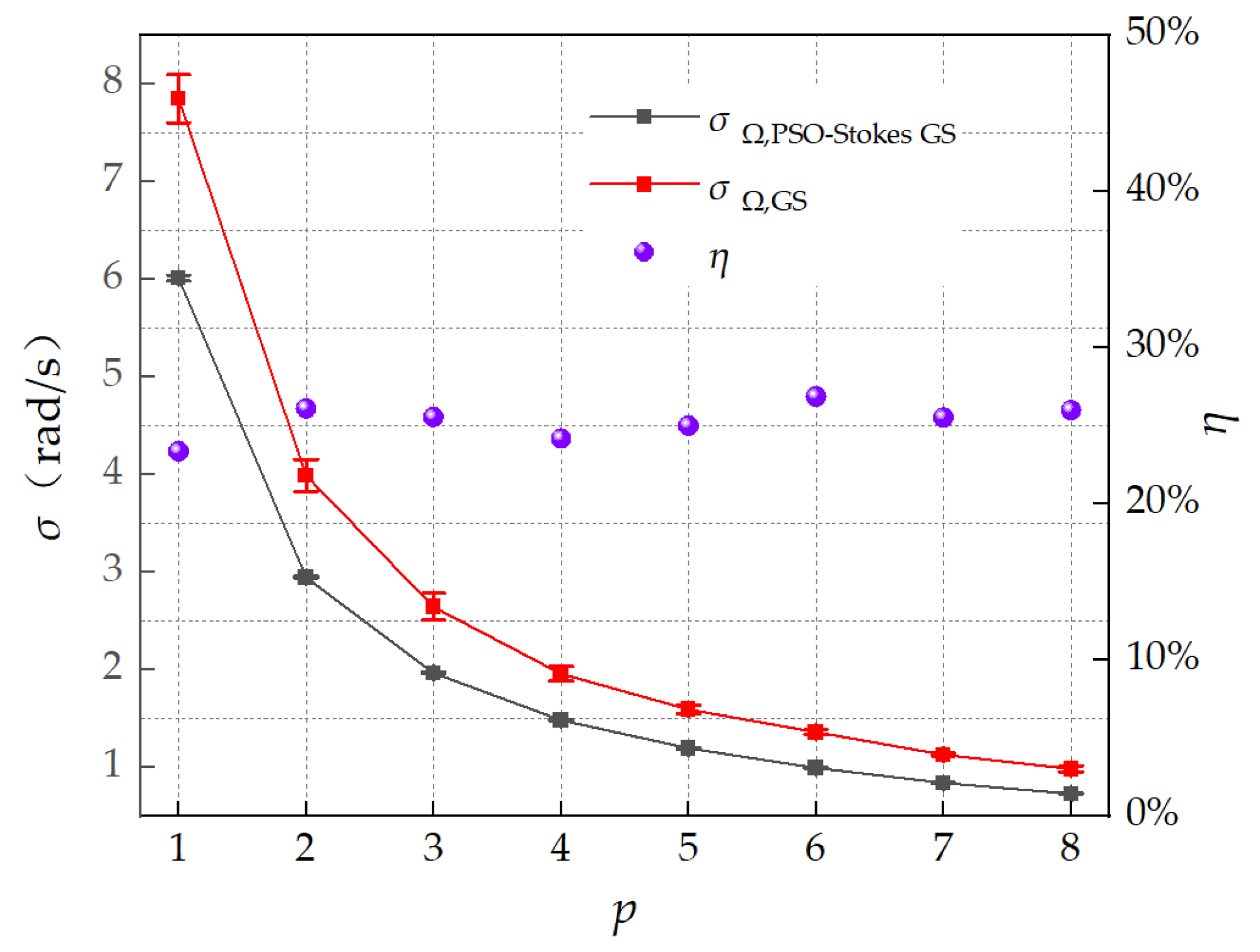
4.3. Improvement in Velocity Measurement Accuracy
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.; Woerdman, J. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Cen, L.; Wang, F.; Zhao, Y. Tiny velocity measurement using the rotating petal-like mode of orbital angular momentum. Opt. Lett. 2021, 46, 4805–4808. [Google Scholar] [CrossRef]
- Lavery, M.P.; Speirits, F.C.; Barnett, S.M.; Padgett, M.J. Detection of a spinning object using light’s orbital angular momentum. Science 2013, 341, 537–540. [Google Scholar] [CrossRef] [PubMed]
- Anderson, A.Q.; Strong, E.F.; Coburn, S.C.; Rieker, G.B.; Gopinath, J.T. Orbital angular momentum-based dual-comb interferometer for ranging and rotation sensing. Opt. Express 2022, 30, 21195–21210. [Google Scholar] [CrossRef] [PubMed]
- Qiu, S.; Ding, Y.; Liu, T.; Liu, Z.; Ren, Y. Rotational object detection at noncoaxial light incidence based on the rotational Doppler effect. Opt. Express 2022, 30, 20441–20450. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Z.; Lin, H.; Nie, Z.; Feng, R.; Zhao, Y.; Jia, B. Dual-point noncoaxial rotational Doppler effect towards synthetic OAM light fields for real-time rotating axis detection. Light Adv. Manuf. 2023, 4, 27. [Google Scholar] [CrossRef]
- Zhou, H.-L.; Fu, D.-Z.; Dong, J.-J.; Zhang, P.; Chen, D.-X.; Cai, X.-L.; Li, F.-L.; Zhang, X.-L. Orbital angular momentum complex spectrum analyzer for vortex light based on the rotational Doppler effect. Light Sci. Appl. 2017, 6, e16251. [Google Scholar] [CrossRef]
- Qiu, S.; Liu, T.; Ren, Y.; Li, Z.; Wang, C.; Shao, Q. Detection of spinning objects at oblique light incidence using the optical rotational Doppler effect. Opt. Express 2019, 27, 24781–24792. [Google Scholar] [CrossRef]
- Zhang, Z.; Cen, L.; Zhang, J.; Hu, J.; Wang, F.; Zhao, Y. Rotation velocity detection with orbital angular momentum light spot completely deviated out of the rotation center. Opt. Express 2020, 28, 6859–6867. [Google Scholar] [CrossRef]
- Ding, Y.; Liu, T.; Liu, Z.; Qiu, S.; Xu, L.; Ren, Y. Detection of a spinning object with circular procession using an optical vortex beam. Opt. Lett. 2022, 47, 2398–2401. [Google Scholar] [CrossRef]
- Deng, J.; Li, K.F.; Liu, W.; Li, G. Cascaded rotational Doppler effect. Opt. Lett. 2019, 44, 2346–2349. [Google Scholar] [CrossRef]
- Sha, Q.; Wang, W.; Liu, T.; Liu, Z.; Qiu, S.; Ren, Y. Analysis of rotational velocity measurement accuracy and signal-to-noise ratio of balanced detection based on vortex beam. Infrared Laser Eng. 2021, 50, 20210616-1–20210616-9. [Google Scholar]
- Guo, K.; Lei, S.; Lei, Y.; Zhou, H.; Guo, Z. Research on Detecting Targets’ Accelerations Based on Vortex Electromagnetic Wave in Non-Line-of-Sight Scenario. IEEE Sens. J. 2023, 23, 4078–4084. [Google Scholar] [CrossRef]
- Guo, K.; Lei, S.; Lei, Y.; Zhou, H.; Guo, Z. Study on detection accuracy of targets’ accelerations based on vortex electromagnetic wave in keyhole space. Chin. Phys. B 2023. [Google Scholar] [CrossRef]
- Guo, H.; Qiu, X.; Qiu, S.; Hong, L.; Lin, F.; Ren, Y.; Chen, L. Frequency upconversion detection of rotational Doppler effect. Photonics Res. 2022, 10, 183–188. [Google Scholar] [CrossRef]
- Yao, A.M.; Padgett, M.J. Orbital angular momentum: Origins, behavior and applications. Adv. Opt. Photonics 2011, 3, 161–204. [Google Scholar] [CrossRef]
- Aftab, M.; Choi, H.; Liang, R.; Kim, D.W. Adaptive Shack-Hartmann wavefront sensor accommodating large wavefront variations. Opt. Express 2018, 26, 34428–34441. [Google Scholar] [CrossRef]
- Zhou, S.; Zhang, Q.; Gao, R.; Chang, H.; Xin, X.; Li, S.; Pan, X.; Tian, Q.; Tian, F.; Wang, Y. High-accuracy atmospheric turbulence compensation based on a Wirtinger flow algorithm in an orbital angular momentum-free space optical communication system. Opt. Commun. 2020, 477, 126322. [Google Scholar] [CrossRef]
- Fu, S.; Zhang, S.; Wang, T.; Gao, C. Pre-turbulence compensation of orbital angular momentum beams based on a probe and the Gerchberg–Saxton algorithm. Opt. Lett. 2016, 41, 3185–3188. [Google Scholar] [CrossRef] [PubMed]
- Song, L.; Lam, E.Y. Fast and robust phase retrieval for masked coherent diffractive imaging. Photonics Res. 2022, 10, 758–768. [Google Scholar] [CrossRef]
- Li, M.; Li, Y.; Han, J. Gerchberg–Saxton algorithm based phase correction in optical wireless communication. Phys. Commun. 2017, 25, 323–327. [Google Scholar] [CrossRef]
- Dedo, M.I.; Wang, Z.; Guo, K.; Sun, Y.; Shen, F.; Zhou, H.; Gao, J.; Sun, R.; Ding, Z.; Guo, Z. Retrieving performances of vortex beams with GS algorithm after transmitting in different types of turbulences. Appl. Sci. 2019, 9, 2269. [Google Scholar] [CrossRef]
- Chang, H.; Yin, X.-l.; Cui, X.-z.; Zhang, Z.-c.; Ma, J.-x.; Wu, G.-h.; Zhang, L.-j.; Xin, X.-j. Adaptive optics compensation of orbital angular momentum beams with a modified Gerchberg–Saxton-based phase retrieval algorithm. Opt. Commun. 2017, 405, 271–275. [Google Scholar] [CrossRef]
- Dedo, M.I.; Wang, Z.; Guo, K.; Guo, Z. OAM mode recognition based on joint scheme of combining the Gerchberg–Saxton (GS) algorithm and convolutional neural network (CNN). Opt. Commun. 2020, 456, 124696. [Google Scholar] [CrossRef]
- Cao, J.; Zhao, X.; Li, Z.; Liu, W.; Gu, H. Modified artificial fish school algorithm for free space optical communication with sensor-less adaptive optics system. J. Korean Phys. Soc. 2017, 71, 636–646. [Google Scholar] [CrossRef]
- Li, Z.; Su, J.; Zhao, X. Atmospheric turbulence compensation with sensorless AO in OAM-FSO combining the deep learning-based demodulator. Opt. Commun. 2020, 460, 125111. [Google Scholar] [CrossRef]
- Kumar, N.; Khandelwal, V. Compensation of wavefront aberration using oppositional-breeding artificial fish swarm algorithm in free space optical communication. J. Opt. 2022, 52, 1370–1380. [Google Scholar] [CrossRef]
- Gao, Y.; Guan, L.; Wang, T.; Sun, Y. A novel artificial fish swarm algorithm for recalibration of fiber optic gyroscope error parameters. Sensors 2015, 15, 10547–10568. [Google Scholar] [CrossRef]
- Li, Z.; Cao, J.; Zhao, X.; Liu, W. Atmospheric compensation in free space optical communication with simulated annealing algorithm. Opt. Commun. 2015, 338, 11–21. [Google Scholar] [CrossRef]
- Sun, T.; Hu, J.; Zhu, X.; Xu, F.; Wang, C. Broadband Single-Chip Full Stokes Polarization-Spectral Imaging Based on All-Dielectric Spatial Multiplexing Metalens. Laser Photonics Rev. 2022, 16, 2100650. [Google Scholar] [CrossRef]
- Fu, S.; Gao, C.; Wang, T.; Zhang, S.; Zhai, Y. Simultaneous generation of multiple perfect polarization vortices with selective spatial states in various diffraction orders. Opt. Lett. 2016, 41, 5454–5457. [Google Scholar] [CrossRef]
- Arlt, J.; Dholakia, K.; Allen, L.; Padgett, M. The production of multiringed Laguerre–Gaussian modes by computer-generated holograms. J. Mod. Opt. 1998, 45, 1231–1237. [Google Scholar] [CrossRef]
- Tatarski, V.I. Wave Propagation in a Turbulent Medium; Courier Dover Publications: Mineola, NY, USA, 2016. [Google Scholar]
- Lane, R.; Glindemann, A.; Dainty, J. Simulation of a Kolmogorov phase screen. Waves Random Media 1992, 2, 209. [Google Scholar] [CrossRef]
- Kishikawa, H.; Kishimoto, H.; Sakashita, N.; Goto, N.; Liaw, S.-K. Pilot beam-assisted adaptive compensation for atmospheric turbulence in free-space optical transmission of beams carrying orbital angular momentum. Jpn. J. Appl. Phys. 2020, 59, SOOD03. [Google Scholar] [CrossRef]
- Yin, X.; Chang, H.; Cui, X.; Ma, J.-X.; Wang, Y.-J.; Wu, G.-H.; Zhang, L.; Xin, X. Adaptive turbulence compensation with a hybrid input–output algorithm in orbital angular momentum-based free-space optical communication. Appl. Opt. 2018, 57, 7644–7650. [Google Scholar] [CrossRef]
- Van den Bergh, F.; Engelbrecht, A.P. A cooperative approach to particle swarm optimization. IEEE Trans. Evol. Comput. 2004, 8, 225–239. [Google Scholar] [CrossRef]
- Hsieh, S.-T.; Sun, T.-Y.; Liu, C.-C.; Tsai, S.-J. Efficient population utilization strategy for particle swarm optimizer. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2008, 39, 444–456. [Google Scholar] [CrossRef] [PubMed]
- Wei, B.; Xia, X.; Yu, F.; Zhang, Y.; Xu, X.; Wu, H.; Gui, L.; He, G. Multiple adaptive strategies based particle swarm optimization algorithm. Swarm Evol. Comput. 2020, 57, 100731. [Google Scholar] [CrossRef]
- Padgett, M.; Allen, L. The Poynting vector in Laguerre-Gaussian laser modes. Opt. Commun. 1995, 121, 36–40. [Google Scholar] [CrossRef]
- Belmonte, A.; Torres, J.P. Optical Doppler shift with structured light. Opt. Lett. 2011, 36, 4437–4439. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Ding, Y.; Qiu, S.; Liu, T.; Ren, Y. Rotational frequency detection of spinning objects at general incidence using vortex beam (Invited). Infrared And Laser Eng. 2021, 50, 20210451–20210457. [Google Scholar]
- Jelalian, A.V. Laser Radar Systems; Artech House Publishers: Norwood, MA, USA, 1992. [Google Scholar]

| σΩ | σΩ, GS | σΩ, Stokes-PSO GS | η1 | η2 | ||
|---|---|---|---|---|---|---|
| 1.676 | 1.587 a | 1.184 a | 29.36% a | 29.12% | 25.39% a | 25.93% |
| 1.621 b | 1.192 b | 28.88% b | 26.47% b |
| Items | Ref. [23] | Ref. [26] | Ref. [36] | Our Work |
|---|---|---|---|---|
| Algorithm | Spatial phase perturbation (SPP) GS | AO and CNN | AO and HIOA | Stokes-PSO GS |
| 5 × 10−15 m−2/3 | 1 × 10−13 m−2/3 | 3 × 10−14 m−2/3 | 1 × 10−14 m−2/3 | |
| l | 3 | −5 | 3 | lL= 5, lR = −5 |
| OAM purity improvement (w/o comp d→comp) | <20% → <50% c | 19% → 61% | ~20% → <70% c | 11.51% → 72.93% |
| Others | z = 100 m λ = 1550 nm w = 0.01 m | z = 1.2 km λ = 1550 nm w = 0.02 m | z = 500 m λ = 1550 nm w = 0.0157 m | zST = 200 m λ = 532 nm w = 0.003 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Zhang, Z.; Wang, Q.; Feng, R.; Zhao, Y. Enhanced Measurement of Vortex Beam Rotation Using Polarization-Assisted Particle Swarm Optimization for Phase Retrieval. Photonics 2023, 10, 1293. https://doi.org/10.3390/photonics10121293
Wang H, Zhang Z, Wang Q, Feng R, Zhao Y. Enhanced Measurement of Vortex Beam Rotation Using Polarization-Assisted Particle Swarm Optimization for Phase Retrieval. Photonics. 2023; 10(12):1293. https://doi.org/10.3390/photonics10121293
Chicago/Turabian StyleWang, Hongyang, Zijing Zhang, Qingfeng Wang, Rui Feng, and Yuan Zhao. 2023. "Enhanced Measurement of Vortex Beam Rotation Using Polarization-Assisted Particle Swarm Optimization for Phase Retrieval" Photonics 10, no. 12: 1293. https://doi.org/10.3390/photonics10121293
APA StyleWang, H., Zhang, Z., Wang, Q., Feng, R., & Zhao, Y. (2023). Enhanced Measurement of Vortex Beam Rotation Using Polarization-Assisted Particle Swarm Optimization for Phase Retrieval. Photonics, 10(12), 1293. https://doi.org/10.3390/photonics10121293





