Abstract
Features of the diffraction of Gaussian beams and Laguerre–Gaussian modes on subwavelength optical 3D microstructures with variable relief heights are calculated and studied in this paper. Silicon subwavelength ring gratings and diffraction axicons were considered as such optical microstructures. The height of individual relief elements varied. The propagation of laser light through the proposed optical elements was simulated using the finite difference time domain (FDTD) method. It was shown that it is possible to select the height of individual relief rings of ring gratings in such a way that it is possible to reduce the size of the focal spot down to 0.36 λ, form an extended light segment (up to 5.79 λ), and form optical traps.
1. Introduction
Currently, methods for capturing and manipulating various micro-objects are being actively studied [1,2,3,4,5,6,7,8,9,10,11,12,13,14], in particular, using optical tweezers (optical traps) [13,14,15,16,17,18]. The use of optical traps has been shown to trap proteins, viruses, and vesicles not only theoretically, but also experimentally [19,20,21,22,23]. Various configurations of optical tweezers are known [24,25,26,27,28,29,30,31,32,33], such as the optothermal tweezer [27,28], optoelectronic tweezer [1,29], opto-thermo-electrohydrodynamic tweezer [28,29], and opto-refrigerative tweezer [30]. In particular, it has been shown that it is possible to reduce laser power when using optothermal tweezers [28], and the use of hypothermal opto-thermophoretic tweezers for controlled cargo delivery using plasmonic vesicles has also been demonstrated [28]. This type of optical tweezer allows the capture and dynamic manipulation of nanometer-sized objects [30]. Also interesting is the use of an opto-refrigerative tweezer to reduce photodamages to the target object [32]. In addition to the above, methods such as DMD-based optical manipulation [33,34] and holographic tweezer [35,36] should also be noted.
An optical bottle is an area with minimal light intensity, which is evenly surrounded on all sides by intensity maxima [37,38,39]. Such optical traps are used to solve applied problems in optical trapping [37,38,39,40,41,42,43], and Hermite–Gaussian and Laguerre–Gaussian beams are often used to create an optical bottle [39,40,41,43,44,45,46].
Vortex beams are laser radiation of a special structure [47,48,49,50]. Among the properties of the vortex beam, we should note the presence of orbital angular momentum [47,48], which is determined by the order of the optical vortex (also called topological charge). Such beams are used for some applications [51,52,53,54], among which, in addition to optical manipulation [50,51], one can note tight focusing [55,56], sensing [57], optical information transmission [58,59], and multiplexing of transmission channels data (when a beam with orbital angular momentum has a large number of possible quantum states) [60], and laser processing [61].
Diffraction optics are often used to form vortex beams [62,63,64,65,66,67,68,69,70,71,72,73,74,75,76], including multi-order diffractive optical elements [65,66,67], spiral phase plates [68,69,70], spiral and twisted axicons [71,72,73], and elements with a complex surface shape [73,74]. It is known that one can use spiral phase microplates manufactured at the end of a waveguide to form vortex beams in optical connector systems in data centers [76]. It should also be noted that optical bottles could be obtained using axisymmetric diffraction structures [43,46,77].
Materials made from silicon and its compounds are actively used for some applications [78,79,80,81], among which should be noted the production of diodes, integrated circuits, other semiconductor devices [78,81,82], solar cells [83,84], in medicine [85], in optics, and in photonics [86,87,88,89]. Moreover, it is worth noting the active development of silicon photonics [90,91,92], including for the implementation of new accelerators for deep learning [93,94,95].
The features of diffraction of Gaussian and super-Gaussian beams, as well as optical vortices with circular polarization on silicon 3D microstructures with variable heights of individual relief elements are studied this work for the formation of optical traps on the optical axis.
The finite difference time domain (FDTD) method [96,97,98,99,100] was used to numerically calculate the propagation of the laser radiation. The calculations were performed using the freely available Meep software [46,101,102,103,104] on a computing cluster with a capacity of 850 Gflop.
2. Materials and Methods
A change in the height of the optical elements quite expectedly affects the diffraction pattern in the near zone [46,105], which was previously shown using the example of a diffraction axicon [46,51]. It should be noted that in the case of uniform polarization, due to the redistribution of energy between the components of the electromagnetic field, a powerful longitudinal component can be formed [46,106,107].
The circular polarization of laser radiation was considered in this paper, in which the sign of the circular polarization is opposite to the sign of the introduced vortex phase singularity. Thus, a round focal spot should be formed on the optical axis, in contrast to the case when the signs of polarization and phase singularity are in the same direction [49].
The gaussian beams and Laguerre–Gaussian (1, 0) modes were considered as input laser beams, and super-Gaussian functions were considered to obtain a more uniform intensity distribution over the beam cross section [51,107]. The amplitude of such a beam of degree p is determined by Formula (1):
where σ is the beam size in µm. The amplitude of the Laguerre–super-Gaussian mode (1, 0) is given by [51]:
where σ is also beam size in µm. The values p = 2 and 10 for both types of beams were mainly considered in this paper. The input beams for values p = 2 and 10 are shown in Figure 1. For individual cases, p = 4, 6, 8 were also considered.

Figure 1.
The input beams, gaussian beams—(a) p = 2, σ = 4.3, (b) p = 10, σ = 8; the Laguerre–Gaussian modes (1, 0)—(c) p = 2, σ = 3.5, (d) p = 10, σ = 8.
The simulation was carried out using the FDTD method. In this method, to solve Maxwell’s equations, the discretization in time and space using central differences is used and then solved numerically [108,109].
The Meep software package was used for numerical modeling using the FDTD method [101,103], which used standard Yee mesh sampling.
The simulation parameters using the FDTD method were as follows: wavelength λ = 1.55 μm, size of the calculated 3D region x, y, z in the range [–5.8 λ; 5.8 λ]. The thickness of the absorbing layer PML (perfectly matched layer—PML) surrounding the computational area on all sides is 1.2 λ, the spatial sampling step is λ/30, and the time sampling step is λ/(60 s), where c is the speed of light.
The source was located inside the substrate, which occupied the entire space below the relief and was partially immersed in the PML layer.
The silicon (Si) is considered as a material with a high refractive index in this paper, n = 3.47. In this case, the height of the relief of the binary element corresponding to the phase π radians is equal to:
where n is the refractive index, λ is the wavelength of the laser radiation, and k = 2π/λ is the wave number.
The rounding of the relief height to 0.2 λ was carried out due to optimization of the used computing resources (to reduce the sampling step) and acceleration of research.
The size of the focal spot on the optical axis was estimated by the full width at half maximum (FWHM) and the depth of focus (DOF). The size of the longitudinal light segment was also estimated by half the intensity.
The subwavelength ring gratings with variable height (elements grating period 1.05 λ) and diffraction axicons were considered as elements.
The height of the binary element relief h = 0.2 λ (corresponding to the phase π radians) will be the basis for comparison (Figure 2) according to the FWHM and DOF for the corresponding laser beams.
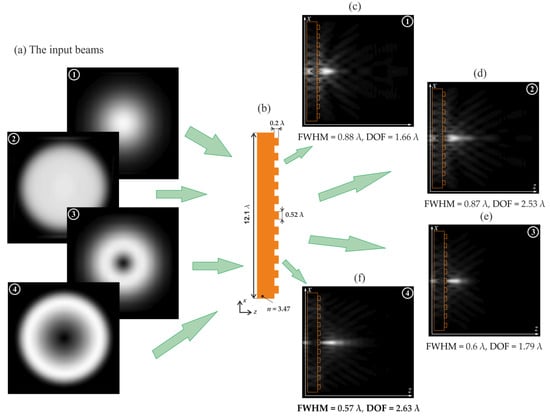
Figure 2.
The input beams’ propagation (a) through a diffraction axicon at h = 0.2 λ (b), Gaussian beams (c) p = 2, σ = 4.3 (1), (d) p = 10, σ = 8 (2); the Laguerre–Gaussian modes (1, 0) (e) p = 2, σ = 3.5 (3), (f) p = 10, σ = 8 (4).
The minimum focal spot (FWHM = 0.57 λ) and the longest light needle (DOF = 2.63 λ) were obtained for the case of the Laguerre–Gaussian mode (1.0) at p = 10 for a given height.
The heights of individual relief rings varied with steps V equal to 0.1 λ (hmax = 0.7 λ), 0.2 λ (hmax = 1.2 λ), 0.3 λ (hmax = 1.7 λ), and 0.4 λ (hmax = 2.2 λ). Thus, the heights of the grating rings were considered from 0.2 λ to 2.2 λ (Figure 3).
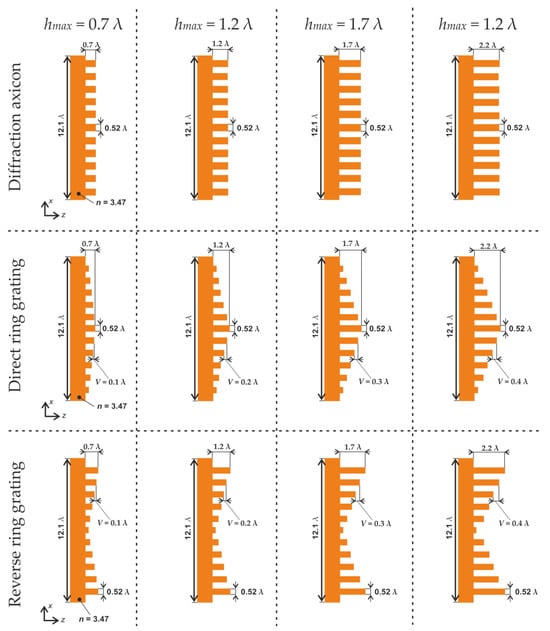
Figure 3.
The types of subwavelength optical elements.
Direct (relief height changes from maximum in the center to minimum at the edges) and reverse (relief height changes from minimum in the center to maximum at the edges) ring gratings are studied.
In addition to the standard axicon with a height h equal to 0.2 λ, axicons with a relief height corresponding to the maximum height of the gratings (0.7 λ, 1.2 λ, 1.7 λ, and 2.2 λ) were also considered.
The thickness of the substrates in the studies was fixed and amounted to λ.
3. Results
This section will discuss in detail the studies on the focusing of Gaussian laser beams and optical vortices by subwavelength silicon ring gratings of various types.
3.1. The Study of Gaussian Beams Diffraction on Silicon Ring Gratings
This section studies the diffraction of Gaussian beams at p = 2 and 10 on diffraction axicons, with direct and reverse ring gratings with relief heights of 0.7 λ, 1.2 λ, 1.7 λ, and 2.2 λ. All subsequent figures show FWHM values at the maximum intensity on the optical axis outside the element. The research results are shown in Figure 4 (for p = 2) and Figure 5 (for p = 10). It should be noted that the diffraction patterns are shown normalized to the global maximum among all studies performed.

Figure 4.
The Gaussian beams diffraction (p = 2) on a diffraction axicon, direct and reverse ring gratings with variable height at hmax = 0.7 λ (a–c), hmax = 1.2 λ (d–f), hmax = 1.7 λ (g–i), hmax = 2.2 λ (j–l).

Figure 5.
The Gaussian beams diffraction (p = 10) on a diffraction axicon, direct and reverse ring gratings with variable height at hmax = 0.7 λ (a–c), hmax = 1.2 λ (d–f), hmax = 1.7 λ (g–i), hmax = 2.2 λ (j–l).
Let us start the analysis with Figure 4. The main maxima for diffraction axicons with heights h = 0.7 λ (Figure 4a) and h = 2.2 λ (Figure 4j) for Gaussian beams with p = 2, as well as a straight annular grating with hmax = 1.7 λ (Figure 4h) and hmax = 2.2 λ (Figure 4k), are formed inside the elements. Outside the elements, in these cases, there are only local maxima, and for the case of Figure 4k, the intensity on the optical axis is so insignificant that the FWHM and DOF values are not indicated. In other cases, the main maxima are formed outside the relief.
It should be noted that the result of the calculation using the FDTD method will differ from the results obtained on the basis of geometric optics or in the model of a thin element using the Kirchhoff formulas. In particular, in the model of a thin element, with a difference in relief heights that is a multiple of 2 λ, the phase shift will be the same [110]. However, this is not true for a strict electromagnetic theory, which has been previously shown, in particular, for a diffraction axicon [51,110,111,112,113], as well as in this study (compare the cases h = 0.2 λ and h = 2.2 λ) in Figure 4 and further.
The minimum focal spot among all cases considered in Figure 4 was recorded for a direct ring grating (in the immediate vicinity of the element) at a relief height hmax = 0.7 λ (FWHM = 0.43 λ), which is 51.1% better for the same type of beam at axicon height h = 0.2 λ (FWHM = 0.88 λ).
The longest light needle (DOF = 3.92 λ) is also formed for the case of a direct ring grating at hmax = 1.2 λ, which is 2.36 times longer than the light needle formed by a diffraction axicon with h = 0.2 λ for the same type of input beam (DOF = 1.66 λ).
It should also be noted that the formation of a nonuniform electric field distribution on the optical axis (an optical trap) is observed for the case of an inverse ring grating at hmax = 1.2 λ and hmax = 2.2 λ. In addition, the formation of extended light needles is observed for the cases hmax = 0.7 λ and hmax = 1.2 λ. For the inverse ring grating, we can also note the height of cases hmax = 1.7 λ: in this case, a narrow (FWHM = 0.58 λ) light segment with DOF = 2.19 λ is formed.
Let us change the input beam by increasing p to 10 (Figure 5) and evaluate the change in this parameter on the diffraction patterns. The minimum focal spot among all cases considered in Figure 5 was recorded for a reverse ring grating at a distance of 1.8 λ from the relief at a relief height of hmax = 1.7 λ (FWHM = 0.49 λ), which is 43.6% better for the same type of beam at an axicon height of h = 0.2 λ (FWHM = 0.87 λ). Moreover, for this case, the light needle turned out to be longer than for the case of p = 2 at a similar height.
The longest light needle (DOF = 5.79 λ) was also obtained for the case of a reverse ring grating at hmax = 1.2 λ, which is 2.29 times longer than the light needle formed by a diffraction axicon with h = 0.2 λ for the same type of input beam (DOF = 2.53 λ) and 1.47 times longer than the best case for p = 2.
It should also be noted that with an increase in p, the previously observed optical traps for the inverse ring grating at hmax = 1.2 λ and hmax = 2.2 λ became more pronounced. The light segments closer to the relief became shorter, and the light segments after the minimum on the optical axis became longer (compare the cases shown in Figure 4f and Figure 4l and Figure 5f and Figure 5l, respectively).
An increase in p to 10 for a height hmax = 1.2 λ led to the movement of the maxima into the optical elements. Also worth special mention is the case of a direct ring grating at hmax = 1.2 λ: an increase in p led to the formation of a narrower and more extended light needle (FWHM = 0.79 λ, DOF = 5.53 λ) than for a similar case at p = 2 (FWHM = 0.89 λ, DOF = 3.92 λ).
Let us change the input beam. We will consider the Laguerre–Gaussian modes (1, 0) at p = 2 and p = 10 on similar optical elements.
3.2. The Study of Optical Vortex Diffraction on Silicon Ring Gratings
It was previously shown that energy redistribution between the components of the electromagnetic field for optical vortices is possible with uniform polarization of laser radiation [49,80,114,115,116]. In this way, a powerful longitudinal component can be formed [46,106,107], which has also been shown experimentally [117].
The diffraction of Laguerre–Gaussian modes (1, 0) at p = 2 (Figure 6) and p = 10 (Figure 7) on direct and reverse ring gratings and diffraction axicons with a similar previously considered relief height (0.7 λ, 1.2 λ, 1.7 λ and 2.2 λ) has been carried out in this section. The figures show the FWHM values at the maximum intensity on the optical axis outside the element.

Figure 6.
The Laguerre–Gaussian modes (1, 0) diffraction (p = 2) on a diffraction axicon, direct and reverse ring gratings with variable height at hmax = 0.7 λ (a–c), hmax = 1.2 λ (d–f), hmax = 1.7 λ (g–i), hmax = 2.2 λ (j–l).

Figure 7.
The Laguerre–Gaussian modes (1, 0) diffraction (p = 10) on a diffraction axicon, direct and reverse ring gratings with variable height at hmax = 0.7 λ (a–c), hmax = 1.2 λ (d–f), hmax = 1.7 λ (g–i), hmax = 2.2 λ (j–l).
At p = 2, basically all maxima are formed outside the elements, except for the cases of a direct ring grating at heights hmax = 1.2 λ and 2.2 λ (Figure 6e,k). The smallest focal spot for the Laguerre–Gaussian modes (1, 0) at p = 2 was obtained for a direct ring grating at a distance of 0.24 λ with a relief height hmax = 0.7 λ (FWHM = 0.36 λ), which is less than the focal spot obtained for the same beam type at axicon height h = 0.2 λ (FWHM = 0.6 λ) by 40%. It should be noted that a focal spot of comparable size was obtained for a diffraction axicon at h = 1.2 λ (FWHM = 0.37 λ) at a distance of 0.25 λ.
The longest light needle (DOF = 3.15 λ) is formed for the inverse ring grating at the relief height hmax = 2.2 λ. This is 1.76 times longer than the light needle formed by a diffraction axicon with h = 0.2 λ for the same type of input beam (DOF = 1.79 λ).
Thus, the use of the Laguerre–Gaussian mode (1, 0) at p = 2 leads to a reduction in the maximum size of the light needle and a decrease in the minimum size of the focal spot (compared to the Gaussian beam).
Also worth special mention is the case of an inverse ring grating at hmax = 1.7 λ: the formation of an optical trap is observed (Figure 6i).
Let us increase the size of p to 10 (Figure 7). Just as before, for the cases of a direct ring grating at a height of hmax = 1.2 λ and 2.2 λ, the main maxima are formed inside. The formation of the remaining maxima occurs outside the optical elements.
The minimum focal spot for the Laguerre–Gaussian modes (1.0) at p = 10 was also obtained for a direct ring grating near to the relief (0.12 λ) at the relief height hmax = 0.7 λ (FWHM = 0.36 λ). This is 36.8% smaller than the focal spot obtained for the same type of beam at an axicon height h = 0.2 λ (FWHM = 0.57 λ). Moreover, an increase in p led to an increase in the light needle for this type of element to 2.55 λ (it was DOF = 0.8 λ for p = 2).
The longest light needle (DOF = 3.16 λ) is formed for the inverse ring grating at the relief height hmax = 2.2 λ, as for the case p = 2. This is 1.2 times longer than the light needle formed by the diffraction axicon with h = 0.2 λ with the same type of input beam (DOF = 2.63 λ).
The formation of an optical trap is also observed for an inverse ring grating at hmax = 1.7 λ, and the trap is more pronounced.
Thus, it is worth noting an interesting result obtained using an inverse ring grating: the formation of optical traps was observed for both optical vortices and Gaussian beams. In fact, we can say that the central part of the ring grating focuses, and the neighboring zones defocus the laser beam. Let us consider these cases in more detail.
3.3. Formation of Optical Traps Using Inverse Ring Gratings
It was previously shown that for inverse ring gratings, both for Gaussian beams (at hmax = 1.2 λ and hmax = 2.2 λ) and for Laguerre–Gaussian (1, 0) modes (at hmax = 1.7 λ), the formation of an optical trap along the optical axis is observed. An optical trap (optical tweezers) is required to solve the problem of manipulating microscopic objects using laser light [43,46,118,119]. The invention of optical tweezers made it possible to make a qualitative leap in biological and biophysical research [14], and for a number of applied problems in optical capture, three-dimensional optical traps are used, which are a region uniformly surrounded by intensity maxima with a minimum light intensity (“optical bottle”) [42].
Let us consider the cases of the optical traps’ formation by inverse ring gratings (cases Figure 5f,l and Figure 7i) in more detail. We will vary the degree p of the beams, considering the cases p = 4, 6, 8.
The formation of optical traps by Gaussian beams using inverse annular gratings at hmax = 1.2 λ and 2.2 λ and the input beams are shown in Figure 8.
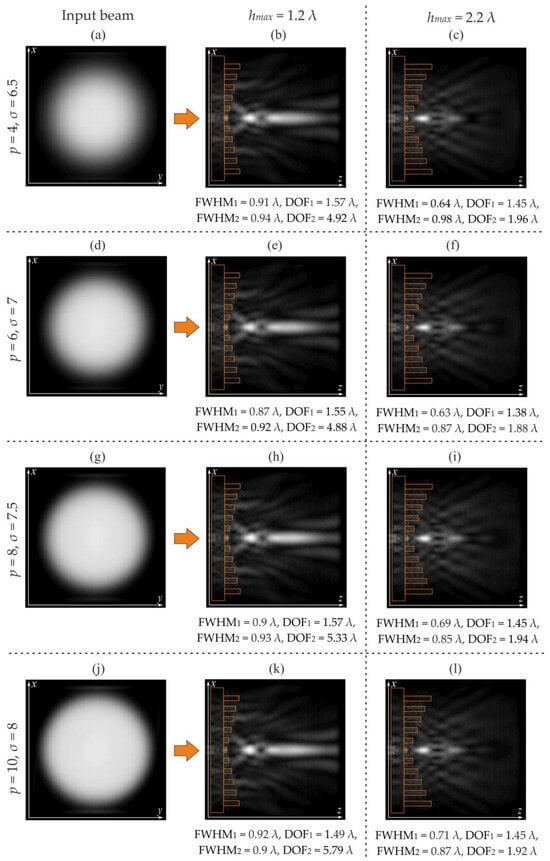
Figure 8.
The Gaussian beams diffraction, p varies from 4 to 10, input beams (a,d,g,j), reverse ring gratings, hmax = 1.2 λ (b,e,h,k), and hmax = 2.2 λ (c,f,i,l).
The minimum FWHM value at maximum was obtained in the case of p = 6, but with similar diffraction patterns, improvement of the optical trap with increasing p is visually noticeable. Let us evaluate this on the graphs.
Graphs of longitudinal and transverse sections for the extreme cases p = 4 and 10 are shown in Figure 9.
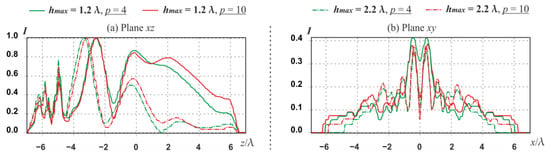
Figure 9.
Section graphs (Figure 8) for cases p = 4 and 10, and for hmax = 1.2 λ and 2.2 λ: (a) longitudinal, (b) transverse.
It is clearly visible that for p = 10, the minimum on the optical axis is less than for p = 4 for both types of elements. However, the intensity values in the transverse plane are very different from the intensity values on the optical axis, and the traps are inhomogeneous.
The formation of optical traps by Laguerre–Gaussian modes (1, 0) using inverse ring gratings at hmax = 1.7 λ is shown in Figure 10, which also shows graphs of the longitudinal section.
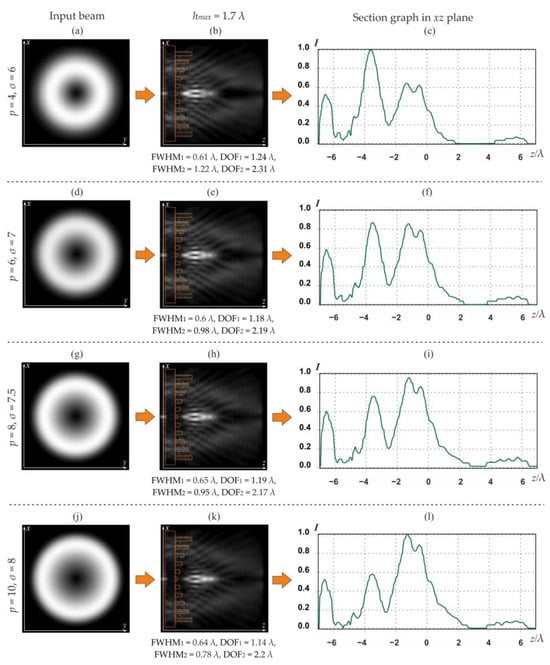
Figure 10.
The Laguerre–Gaussian modes (1, 0) diffraction, p varies from 4 to 10, input beams (a,d,g,j), inverse ring grating, hmax = 1.7 λ (b,e,h,k), and corresponding longitudinal graphs (c,f,i,l).
The case of p = 6 (line 2) stands out, where peaks of almost equal intensity are observed on the optical axis. A further increase in p leads to a redistribution of energy further from the optical element. Let us consider the case of p = 6 in more detail (Figure 11).
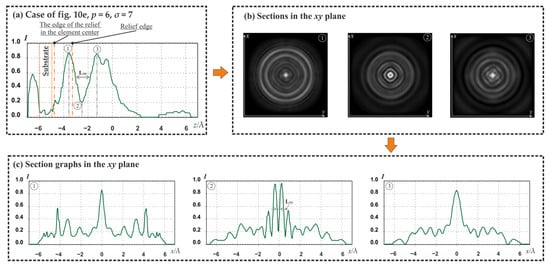
Figure 11.
The Laguerre–Gaussian modes (1, 0) diffraction on an inverse ring grating with hmax = 1.7 λ (Figure 10e), graph of the longitudinal section (a), sections in extremes 1, 2, 3 in the xy plane (b), and corresponding to extremes 1, 2, 3 (1 and 3 are the maximum points on the optical axis, 2 is the minimum point there) cross-sectional graphs (c).
In this case, the height of the maxima on the optical axis (points 1 and 3, Figure 10a) in the longitudinal plane is 85.7% and 84.9% of the maximum intensity, respectively. The length of the region of reduced intensity is Lxz = 1.12 λ.
For the cross section in the minimum region (point 2), the formation of a ring is also observed with a peak equal to 96% of the maximum intensity (off the optical axis). The width of the shadow focal spot is Lxy = 0.27 λ. The width of the ring is FWHM = 0.38 λ.
It should be noted that, for this case, it was possible to obtain a compact optical trap with a minimum range of fluctuations in the intensity values of the trap walls: from 0.8% to 11.1%.
It was previously shown that two forces act when a particle is captured by a laser beam [12,61,120]. One of them is the longitudinal component of the Poynting vector (scattering), due to which the particle moves forward along the direction of beam propagation [61]. Another force is the radiation intensity gradient (gradient), which is responsible for moving the particle to the region of maximum intensity [61]. For the calculation, we will need the field near the particle, the particle parameters, and the environment, and we will need to calculate the Poynting vector and intensity gradient. However, it should be noted that formulas [12,61] with sufficient complexity would not clearly show the effect of the trap, as well as the influence on the destruction of the rest of the field.
Let us carry out a numerical simulation where the particles will be spheres with different refractive index n (from 1.45 to 3.47). The simulation results when changing the radius of the spheres are shown in Figure 12. The spheres are shown in blue for a refractive index n = 1.45, in green for n = 2.7, and in yellow for n = 3.47.
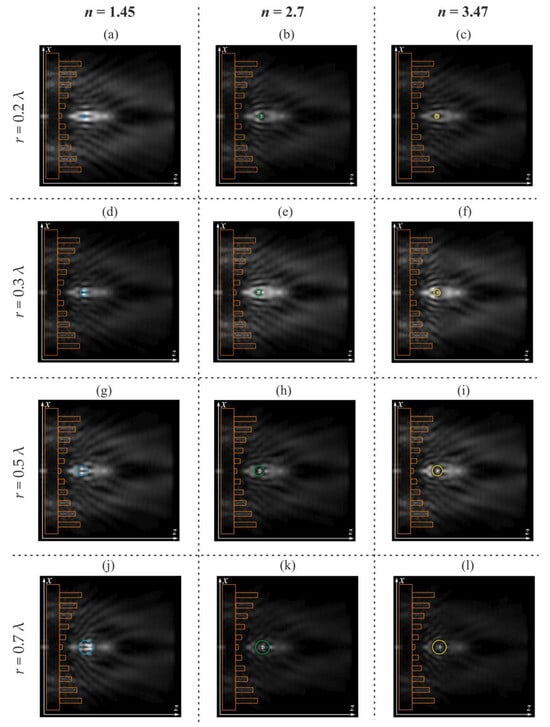
Figure 12.
The Laguerre–Gaussian modes (1, 0) diffraction (case Figure 10e) with a particle in an optical trap, n = 1.45 (a,d,g,j), n = 2.7 (b,e,h,k), n = 3.47 (c,f,i,l).
It should be noted that when the particle size is greater than 0.5 λ, destruction of the optical trap is observed, which was, in general, expected given its size. It is also clearly noticeable that as the radius increases, the intensity maximum shifts inside the sphere. It should be noted that inside the particles, an increase in the refractive index from n = 1.45 to 3.47 led to a redistribution of intensity, and the main maximum for n = 3.47 is observed on the optical axis, in contrast to the case of n = 1.45.
4. Discussion
Currently, there are a number of methods for the manufacture of optical elements, including diffractive optical elements [121,122,123,124,125]. Well-known methods include direct laser recording methods, both classical and its modifications using thermochemical and thermophysical processes [122]; lithography methods [123,125], including half-tone photolithography [123]; laser ablation [126]; and 3D printing technologies [124].
To manufacture the ring gratings considered in this paper, it is necessary to conduct experimental studies, test various methods and approaches, and vary the parameters and properties of various technological processes. It should be noted that a number of works previously demonstrated the possibility of producing a relief with an aspect ratio of more than 100 [127,128], so the production of the ring gratings studied in this article seems possible.
Initial experiments to create a ring grating with variable heights of individual relief rings were carried out with a material with a lower refractive index, namely titanium dioxide with n = 2.5, which was deposited on a quartz optical glass substrate. Preparations for the creation of the future element began with the stage of washing and cleaning the substrate. Next, a titanium film was deposited. The film thickness was controlled over time, based on the stability of the sputtering process at given parameters.
Research has shown that due to the high resolution of the structure, the method of direct laser writing with focused laser radiation is not applicable, since the resolution of the method is higher than the required structure resolution. Therefore, at this stage of recording, electron lithography was used. First, an electronic resist was applied to the surface of the titanium dioxide film in order to carry out the lithography stage. Next, using a lithography attachment, a latent image of the future structure was recorded. Next, the plasma-chemical etching was used to form rings with variable height in the titanium film. Next, the formed structure in a titanium film on a quartz substrate was subjected to annealing in a muffle furnace at the experimentally established optimal temperature and time parameters.
In the future, it is logical to continue experiments on the formation of a subwavelength micro-relief with variable height in silicon [129,130,131,132], and there is a technology for creating subwavelength cylindrical lenses [130] and subwavelength axicons [131] using the method of plasma-chemical etching (Bosch process) of the substrate surface from high-resistivity silicon [132].
5. Conclusions
The FDTD method was used in this paper to study the features of focusing Gaussian beams and optical vortices of various widths on diffraction axicons and direct and reverse ring gratings with variable height. It was shown that it is possible to select the parameters of the illuminating beam and subwavelength element in such a way that it is possible to reduce the size of the focal spot down to 0.36 λ, form an extended light needle up to 5.79 λ, and form optical traps.
Analysis of the electric field intensity patterns showed that the minimum size of the focal spot at the maximum on the optical axis for Gaussian beams was obtained for a direct ring grating (in the immediate vicinity of the element) with a relief height of hmax = 0.7 λ (FWHM = 0.43 λ, p = 2). This result is 51.1% less for the same type of beam at the axicon height h = 0.2 λ. The minimum focal spot for the Laguerre–Gaussian modes (1, 0) was also obtained for a direct ring grating at a distance of 0.24 λ with a relief height of hmax = 0.7 λ (FWHM = 0.36 λ, at p = 2). The resulting focal spot is 40% smaller than the focal spot obtained for the same type of beam at an axicon height of h = 0.2 λ (FWHM = 0.6 λ).
The longest light needle for Gaussian beams (DOF = 5.79 λ, p = 10) was obtained for the case of an inverse ring grating at hmax = 1.2 λ. This result is 2.29 times longer than the light needle formed by a diffraction axicon with h = 0.2 λ for the same type of input beam (DOF = 2.53 λ) and 1.83 times longer than the best case for Laguerre–Gaussian modes (1, 0) (DOF = 3.16 λ, p = 10).
The paper also shows the possibility of forming single optical traps using inverse subwavelength ring gratings, both for Gaussian beams and for optical vortices, and the best result was obtained for the Laguerre-Gaussian mode (1, 0) at p = 6. In this case the formation of a narrow (FWHM = 0.27 λ) and extended (Lxz = 1.12 λ) region of reduced intensity on the optical axis is observed for the maximum relief height h = 1.7 λ. The minimum range of fluctuations in the intensity values of the trap walls was obtained (from 0.8% to 11.1%) for this optical trap.
Funding
This research was funded by Ministry of Science and Higher Education within the state assignment project no. FSSS-2023-0006 in the parts “Materials and Methods”, “The study of Gaussian beams diffraction on silicon ring gratings”, and “Discussion”, as well as by the program of strategic academic leadership “Priority 2030” in other parts.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data available on request.
Conflicts of Interest
The author declares no conflict of interest.
References
- Zhang, S.; Xu, B.; Elsayed, M.; Nan, F.; Liang, W.; Valley, J.K.; Liu, L.; Huang, Q.; Wuk, M.C.; Wheeler, A.R. Optoelectronic tweezers: A versatile toolbox for nano-/micro-manipulation. Chem. Soc. Rev. 2022, 51, 9203–9242. [Google Scholar] [CrossRef]
- Vilas, N.B.; Hallas, C.; Anderegg, L.; Robichaud, P.; Winnicki, A.; Mitra, D.; Doyle, J.M. Magneto-optical trapping and sub-Doppler cooling of a polyatomic molecule. Nature 2022, 606, 70–74. [Google Scholar] [CrossRef] [PubMed]
- Wen, J.; Gao, B.; Zhu, G.; Liu, D.; Wang, L.G. Precise position and angular control of optical trapping and manipulation via a single vortex-pair beam. Opt. Lasers Eng. 2022, 148, 106773. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Tian, Z.; Samri, M.; Moh, K.; McMeeking, R.M.; Hensel, R.; Arzt, E. A bioinspired snap-through metastructure for manipulating micro-objects. Sci. Adv. 2022, 8, eadd4768. [Google Scholar] [CrossRef]
- Lu, Y.; Holland, C.M.; Cheuk, L.W. Molecular Laser Cooling in a Dynamically Tunable Repulsive Optical Trap. Phys. Rev. Lett. 2022, 128, 213201. [Google Scholar] [CrossRef] [PubMed]
- Lyu, W.; Tang, W.; Yan, W.; Qiu, M. Nanomotion of micro-objects driven by light-induced elastic waves on solid interfaces. Phys. Rev. Appl. 2023, 19, 024049. [Google Scholar] [CrossRef]
- Yang, Y.; Ren, Y.; Chen, M.; Arita, Y.; Rosales-Guzmán, C. Optical trapping with structured light: A review. Adv. Photonics 2021, 3, 34001. [Google Scholar] [CrossRef]
- Zemánek, P.; Volpe, G.; Jonáš, A.; Brzobohatý, O. Perspective on light-induced transport of particles: From optical forces to phoretic motion. Adv. Opt. Photonics 2019, 11, 577–678. [Google Scholar] [CrossRef]
- Liu, Y.; Yin, Q.; Luo, Y.; Huang, Z.; Cheng, Q.; Zhang, W.; Zhou, B.; Zhou, Y.; Ma, Z. Manipulation with sound and vibration: A review on the micromanipulation system based on sub-MHz acoustic waves. Ultrason. Sonochem. 2023, 96, 106441. [Google Scholar] [CrossRef]
- Sokolenko, B.V.; Lyakhovich, N.V.; Sidorenkova, O.S. Optical tweezers and manipulators. Modern concepts and future prospect. Phys. Usp. 2022, 65, 812–833. [Google Scholar] [CrossRef]
- Jia, Q.; Lyu, W.; Yan, W.; Tang, W.; Lu, J.; Qiu, M. Optical manipulation: From fluid to solid domains. Photonics Insights 2023, 2, R05. [Google Scholar] [CrossRef]
- Porfirev, A.P.; Fomchenkov, S.A.; Porfiriev, D.P.; Khonina, S.N.; Karpeev, S.V. Multi-plane photophoretic trapping of air-borne particles with a multi-linear optical trap. Optik 2022, 271, 170118. [Google Scholar] [CrossRef]
- Liang, Y.; Liang, G.; Xiang, Y.; Lamstein, J.; Gautam, R.; Bezryadina, A.; Chen, Z. Manipulation and assessment of human red blood cells with tunable “tug-of-war” optical tweezers. Phys. Rev. Appl. 2019, 12, 64060. [Google Scholar] [CrossRef]
- Dai, X.; Fu, W.; Chi, H.; Mesias, V.S.D.; Zhu, H.; Leung, C.W.; Liu, W.; Huang, J. Optical tweezers-controlled hotspot for sensitive and reproducible surface-enhanced Raman spectroscopy characterization of native protein structures. Nat. Commun. 2021, 12, 1292. [Google Scholar] [CrossRef] [PubMed]
- Magazzù, A.; Marcuello, C. Investigation of soft matter nanomechanics by atomic force microscopy and optical tweezers: A comprehensive review. Nanomaterials 2023, 13, 963. [Google Scholar] [CrossRef]
- Gouesbet, G. Generalized Lorenz—Mie theories and mechanical effects of laser light, on the occasion of Arthur Ashkin’s receipt of the 2018 Nobel prize in physics for his pioneering work in optical levitation and manipulation: A review. J. Quant. Spectrosc. Radiat. Transf. 2019, 225, 258–277. [Google Scholar] [CrossRef]
- Riccardi, M.; Martin, O.J. Electromagnetic forces and torques: From dielectrophoresis to optical tweezers. Chem. Rev. 2023, 123, 1680–1711. [Google Scholar] [CrossRef]
- Liu, J.; Zheng, M.; Xiong, Z.; Li, Z. 3D dynamic motion of a dielectric micro-sphere within optical tweezers. Opto-Electron. Adv. 2021, 4, 1200015. [Google Scholar] [CrossRef]
- Lin, S.; Crozier, K.B. Trapping-assisted sensing of particles and proteins using on-chip optical microcavities. ACS Nano 2013, 7, 1725–1730. [Google Scholar] [CrossRef]
- Pang, Y.; Gordon, R. Optical trapping of a single protein. Nano Lett. 2012, 12, 402–406. [Google Scholar] [CrossRef]
- Brunetti, G.; Sasanelli, N.; Armenise, M.N.; Ciminelli, C. Nanoscale optical trapping by means of dielectric bowtie. Photonics 2022, 9, 425. [Google Scholar] [CrossRef]
- Conteduca, D.; Brunetti, G.; Barth, I.; Quinn, S.D.; Ciminelli, C.; Krauss, T.F. Multiplexed Near-Field Optical Trapping Exploiting Anapole States. ACS Nano 2023, 17, 16695–16702. [Google Scholar] [CrossRef]
- Grom, F.; Kentsch, J.; Müller, T.; Schnelle, T.; Stelzle, M. Accumulation and trapping of hepatitis A virus particles by electrohydrodynamic flow and dielectrophoresis. Electrophoresis 2006, 27, 1386–1393. [Google Scholar] [CrossRef] [PubMed]
- Volpe, G.; Maragò, O.M.; Rubinsztein-Dunlop, H.; Pesce, G.; Stilgoe, A.B.; Volpe, G.; Tkachenko, G.; Truong, V.G.; Chormaic, S.N.; Kalantarifard, F.; et al. Roadmap for optical tweezers. J. Phys. Photonics 2023, 5, 022501. [Google Scholar] [CrossRef]
- Huft, P.R.; Kolbow, J.D.; Thweatt, J.T.; Lindquist, N.C. Holographic plasmonic nanotweezers for dynamic trapping and manipulation. Nano Lett. 2017, 17, 7920–7925. [Google Scholar] [CrossRef]
- Li, N.; Cadusch, J.; Liu, A.; Barlow, A.J.; Roberts, A.; Crozier, K.B. Algorithm-Designed Plasmonic Nanotweezers: Quantitative Comparison by Theory: Cathodoluminescence, and Nanoparticle Trapping. Adv. Opt. Mater. 2021, 9, 2100758. [Google Scholar] [CrossRef]
- Chen, Z.; Li, J.; Zheng, Y. Heat-mediated optical manipulation. Chem. Rev. 2021, 122, 3122–3179. [Google Scholar] [CrossRef]
- Kollipara, P.S.; Li, X.; Li, J.; Chen, Z.; Ding, H.; Kim, Y.; Huang, S.; Qin, Z.; Zheng, Y. Hypothermal opto-thermophoretic tweezers. Nat. Commun. 2023, 14, 5133. [Google Scholar] [CrossRef] [PubMed]
- Liang, S.; Cao, Y.; Dai, Y.; Wang, F.; Bai, X.; Song, B.; Zhang, C.; Gan, C.; Arai, F.; Feng, L. A versatile optoelectronic tweezer system for micro-objects manipulation: Transportation, patterning, sorting, rotating and storage. Micromachines 2021, 12, 271. [Google Scholar] [CrossRef]
- Hong, C.; Yang, S.; Ndukaife, J.C. Exosomes trapping, manipulation and size-based separation using opto-thermo-electrohydrodynamic tweezers. Nanoscale Adv. 2023, 5, 2973–2978. [Google Scholar] [CrossRef]
- Hong, C.; Yang, S.; Ndukaife, J.C. Stand-off trapping and manipulation of sub-10 nm objects and biomolecules using opto-thermo-electrohydrodynamic tweezers. Nat. Nanotechnol. 2020, 15, 908–913. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Chen, Z.; Liu, Y.; Kollipara, P.S.; Feng, Y.; Zhang, Z.; Zheng, Y. Opto-refrigerative tweezers. Sci. Adv. 2021, 7, eabh1101. [Google Scholar] [CrossRef] [PubMed]
- Xie, Q.; Yu, S.T.; Wang, X.K.; Zheng, Y.G.; Yuan, Z.S. DMD-based pure-phase superpixel method for digital holography. Appl. Phys. Express 2023, 16, 012009. [Google Scholar] [CrossRef]
- Li, J.; Hill, E.H.; Lin, L.; Zheng, Y. Optical nanoprinting of colloidal particles and functional structures. ACS Nano 2019, 13, 3783–3795. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.C.; Cheng, C.J. Holographic Optical Tweezers: Techniques and Biomedical Applications. Appl. Sci. 2022, 12, 10244. [Google Scholar] [CrossRef]
- Zhang, Y.; Min, C.; Dou, X.; Wang, X.; Urbach, H.P.; Somekh, M.G.; Yuan, X. Plasmonic tweezers: For nanoscale optical trapping and beyond. Light Sci. Appl. 2021, 10, 59. [Google Scholar] [CrossRef]
- Khonina, S.N.; Porfirev, A.P.; Volotovskiy, S.G.; Ustinov, A.V.; Fomchenkov, S.A.; Pavelyev, V.S.; Schröter, S.; Duparré, M. Generation of Multiple Vector Optical Bottle Beams. Photonics 2021, 8, 218. [Google Scholar] [CrossRef]
- Khonina, S.N.; Ustinov, A.V.; Kharitonov, S.I.; Fomchenkov, S.A.; Porfirev, A.P. Optical Bottle Shaping Using Axicons with Amplitude or Phase Apodization. Photonics 2023, 10, 200. [Google Scholar] [CrossRef]
- Wu, J.; Cai, H.; Yu, P.; Gong, P.; Man, Z.; Fu, S.; Han, K.; Ge, X.; Deng, D.; Zhang, L. The multi-consecutive optical bottles generated from the chirped elliptical Pearcey Gaussian vortex beams. Results Phys. 2022, 39, 105747. [Google Scholar] [CrossRef]
- Lamperska, W.; Masajada, J.; Drobczyński, S.; Wasylczyk, P. Optical vortex torque measured with optically trapped micro-barbells. Appl. Opt. 2020, 59, 4703–4707. [Google Scholar] [CrossRef]
- Mo, Z.; Jiang, J.; Wei, Q.; Xu, D.; Yang, H.; Huang, H.; Wu, Y.; Liu, H.; Shui, L.; Deng, D. Multiple and off-axis optical bottles from the chirped circular Pearcey Gaussian vortex beams. Opt. Express 2022, 30, 1762–1772. [Google Scholar] [CrossRef] [PubMed]
- Gong, Z.; Pan, Y.L.; Videen, G.; Wang, C. Optical trapping and manipulation of single particles in air: Principles, technical details, and applications. J. Quant. Spectrosc. Radiat. Transf. 2018, 214, 94–119. [Google Scholar] [CrossRef]
- Savelyev, D.A.; Karpeev, S.V. Development of 3D Microstructures for the Formation of a Set of Optical Traps on the Optical Axis. Photonics 2023, 10, 117. [Google Scholar] [CrossRef]
- Wei, H.; Amrithanath, A.K.; Krishnaswamy, S. 3D printing of micro-optic spiral phase plates for the generation of optical vortex beams. IEEE Photonics Technol. Lett. 2019, 31, 599–602. [Google Scholar] [CrossRef]
- He, S.; Zhang, Y.; Malomed, B.A.; Mihalache, D.; Zhang, L.; Zhang, S.; Huang, Q.; Qiu, H.; Zhao, J.; Peng, H.; et al. Generation and control of multiple optical bottles from chirped Airy–Gaussian vortex beams: Theory and experiment. Waves Random Complex Media 2022, 1–16. [Google Scholar] [CrossRef]
- Savelyev, D.A. Peculiarities of focusing circularly and radially polarized super-Gaussian beams using ring gratings with varying relief height. Comput. Opt. 2022, 46, 537–546. [Google Scholar] [CrossRef]
- Padgett, M.J. Orbital angular momentum 25 years on. Opt. Express 2017, 25, 11265–11274. [Google Scholar] [CrossRef]
- Fatkhiev, D.M.; Butt, M.A.; Grakhova, E.P.; Kutluyarov, R.V.; Stepanov, I.V.; Kazanskiy, N.L.; Khonina, S.N.; Lyubopytov, V.S.; Sultanov, A.K. Recent advances in generation and detection of orbital angular momentum optical beams—A review. Sensors 2021, 21, 4988. [Google Scholar] [CrossRef]
- Savelyev, D.A.; Khonina, S.N. Characteristics of sharp focusing of vortex Laguerre-Gaussian beams. Comput. Opt. 2015, 39, 654–662. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, X.; Xie, Z.; Min, C.; Fu, X.; Liu, Q.; Gong, M.; Yuan, X. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light Sci. Appl. 2019, 8, 90. [Google Scholar] [CrossRef]
- Savelyev, D.A. The investigation of the features of focusing vortex super-Gaussian beams with a variable-height diffractive axicon. Comput. Opt. 2021, 45, 214–221. [Google Scholar] [CrossRef]
- Paez-Lopez, R.; Ruiz, U.; Arrizon, V.; Ramos-Garcia, R. Optical manipulation using optimal annular vortices. Opt. Lett. 2016, 41, 4138–4141. [Google Scholar] [CrossRef] [PubMed]
- Dong, M.; Zhao, C.; Cai, Y.; Yang, Y. Partially coherent vortex beams: Fundamentals and applications. Sci. China Phys. Mech. Astron. 2021, 64, 224201. [Google Scholar] [CrossRef]
- Zhang, H.; Zeng, J.; Lu, X.; Wang, Z.; Zhao, C.; Cai, Y. Review on fractional vortex beam. Nanophotonics 2021, 11, 241–273. [Google Scholar] [CrossRef]
- Savelyev, D.A. The Comparison of Laser Radiation Focusing by Diffractive Axicons and Annular Gratings with Variable Height Using High-performance Computer Systems. In Proceedings of the 2021 Photonics & Electromagnetics Research Symposium (PIERS), Hangzhou, China, 21–25 November 2021; pp. 2709–2716. [Google Scholar] [CrossRef]
- Savelyev, D.; Degtyarev, S. Features of the Optical Vortices Diffraction on Silicon Ring Gratings. Opt. Mem. Neural Netw. 2022, 31, 55–66. [Google Scholar] [CrossRef]
- Sirenko, A.A.; Marsik, P.; Bernhard, C.; Stanislavchuk, T.N.; Kiryukhin, V.; Cheong, S.W. Terahertz vortex beam as a spectroscopic probe of magnetic excitations. Phys. Rev. Lett. 2019, 122, 237401. [Google Scholar] [CrossRef] [PubMed]
- Khonina, S.N.; Karpeev, S.V.; Butt, M.A. Spatial-light-modulator-based multichannel data transmission by vortex beams of various orders. Sensors 2021, 21, 2988. [Google Scholar] [CrossRef]
- Zhu, F.; Huang, S.; Shao, W.; Zhang, J.; Chen, M.; Zhang, W.; Zeng, J. Free-space optical communication link using perfect vortex beams carrying orbital angular momentum (OAM). Opt. Commun. 2017, 396, 50–57. [Google Scholar] [CrossRef]
- Bozinovic, N.; Yue, Y.; Ren, Y.; Tur, M.; Kristensen, P.; Huang, H.; Willner, A.E.; Ramachandran, S. Terabit-scale orbital angular momentum mode division multiplexing in fibers. Science 2013, 340, 1545–1548. [Google Scholar] [CrossRef]
- Khonina, S.N.; Ustinov, A.V.; Volotovskiy, S.G.; Ivliev, N.A.; Podlipnov, V.V. Influence of optical forces induced by par-axial vortex Gaussian beams on the formation of a microrelief on carbazole-containing azopolymer films. Appl. Opt. 2020, 59, 9185–9194. [Google Scholar] [CrossRef]
- Khorin, P.A.; Khonina, S.N. Influence of 3D helical microstructure shape deviations on the properties of a vortex beam generated in the near diffraction zone. J. Opt. Technol. 2023, 90, 236–241. [Google Scholar] [CrossRef]
- Savelyev, D. Optical Vortices Sharp Focusing by Silicon Ring Gratings Using High-Performance Computer Systems. Front. Artif. Intell. Appl. 2021, 345, 300–305. [Google Scholar] [CrossRef]
- Yang, Z.; Lin, X.; Zhang, H.; Ma, X.; Zou, Y.; Xu, L.; Xu, Y.; Jin, L. Design of bottle beam based on dual-beam for trapping particles in air. Appl. Opt. 2019, 58, 2471–2480. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Sun, M.; Zhu, M.; Chen, J.; Gao, X.; Ma, W.; Zhang, D. Three-dimensional shape-controllable focal spot array created by focusing vortex beams modulated by multi-value pure-phase grating. Opt. Express 2014, 22, 21354–21367. [Google Scholar] [CrossRef] [PubMed]
- Khonina, S.N.; Ustinov, A.V. Binary multi-order diffraction optical elements with variable fill factor for the formation and detection of optical vortices of arbitrary order. Appl. Opt. 2019, 58, 8227–8236. [Google Scholar] [CrossRef]
- Kazanskiy, N.L.; Khonina, S.N.; Karpeev, S.V.; Porfirev, A.P. Diffractive optical elements for multiplexing structured laser beams. Quantum Electron. 2020, 50, 629–635. [Google Scholar] [CrossRef]
- Balčytis, A.; Hakobyan, D.; Gabalis, M.; Žukauskas, A.; Urbonas, D.; Malinauskas, M.; Petruškevičius, R.; Brasselet, E.; Juodkazis, S. Hybrid curved nano-structured micro-optical elements. Opt. Express 2016, 24, 16988. [Google Scholar] [CrossRef]
- Zhou, J.; Lin, P.T. Generation of mid-infrared vortex beams by 3-D printed polymer phase plates. Opt. Laser Technol. 2022, 156, 108509. [Google Scholar] [CrossRef]
- Khonina, S.N.; Porfirev, A.P. Generation of multi-contour plane curves using vortex beams. Optik 2021, 229, 166299. [Google Scholar] [CrossRef]
- Khonina, S.N.; Kazanskiy, N.L.; Khorin, P.A.; Butt, M.A. Modern types of axicons: New functions and applications. Sensors 2021, 21, 6690. [Google Scholar] [CrossRef]
- Supp, S.; Jahns, J. Coaxial superposition of Bessel beams by discretized spiral axicons. J. Eur. Opt. Soc. Rapid Publ. 2018, 14, 18. [Google Scholar] [CrossRef]
- Sanchez-Padilla, B.; Žukauskas, A.; Aleksanyan, A.; Balčytis, A.; Malinauskas, M.; Juodkazis, S.; Brasselet, E. Wrinkled axicons: Shaping light from cusps. Opt. Express 2016, 24, 24075–24082. [Google Scholar] [CrossRef]
- Moreno, E.; Colombier, J.P. Axicon lenses with chiral-focusing properties modeling by means of analytical functions. Opt. Lasers Eng. 2023, 163, 107437. [Google Scholar] [CrossRef]
- Knyazev, B.; Cherkassky, V.; Kameshkov, O. “Perfect” terahertz vortex beams formed using diffractive axicons and prospects for excitation of vortex surface plasmon polaritons. Appl. Sci. 2021, 11, 717. [Google Scholar] [CrossRef]
- Yu, S. Potentials and challenges of using orbital angular momentum communications in optical interconnects. Opt. Express 2015, 23, 3075. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Lin, X.; Zhang, H.; Xu, Y.; Jin, L.; Zou, Y.; Ma, X. Research on the special bottle beam generated by asymmetric elliptical Gaussian beams through an axicon-lens system. Opt. Lasers Eng. 2020, 126, 105899. [Google Scholar] [CrossRef]
- Siew, S.Y.; Li, B.; Gao, F.; Zheng, H.Y.; Zhang, W.; Guo, P.; Xie, S.W.; Song, A.; Dong, B.; Luo, L.W.; et al. Review of silicon photonics technology and platform development. J. Light. Technol. 2021, 39, 4374–4389. [Google Scholar] [CrossRef]
- Cheng, L.; Mao, S.; Li, Z.; Han, Y.; Fu, H.Y. Grating couplers on silicon photonics: Design principles, emerging trends and practical issues. Micromachines 2020, 11, 666. [Google Scholar] [CrossRef]
- Savelyev, D.; Kazanskiy, N. Near-Field Vortex Beams Diffraction on Surface Micro-Defects and Diffractive Axicons for Polarization State Recognition. Sensors 2021, 21, 1973. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Feng, J.; Tian, Y.; Zhao, H.; Jin, L.; Ouyang, B.; Zhu, J.; Guo, J. Thermo-optic phase shifters based on silicon-on-insulator platform: State-of-the-art and a review. Front. Optoelectron. 2022, 15, 9. [Google Scholar] [CrossRef]
- Myny, K. The development of flexible integrated circuits based on thin-film transistors. Nat. Electron. 2018, 1, 30–39. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Y.; Wu, Y.; Yang, G.; Mazzarella, L.; Procel-Moya, P.; Tamboli, A.C.; Weber, K.; Boccard, M.; Isabella, O.; et al. High-efficiency silicon heterojunction solar cells: Materials, devices and applications. Mater. Sci. Eng. R Rep. 2020, 142, 100579. [Google Scholar] [CrossRef]
- Mortazavifar, S.L.; Salehi, M.R.; Shahraki, M.; Abiri, E. Optimization of light absorption in ultrathin elliptical silicon nanowire arrays for solar cell applications. J. Mod. Opt. 2022, 69, 368–380. [Google Scholar] [CrossRef]
- Xu, Y.; Hu, X.; Kundu, S.; Nag, A.; Afsarimanesh, N.; Sapra, S.; Mukhopadhyay, S.C.; Han, T. Silicon-based sensors for biomedical applications: A review. Sensors 2019, 19, 2908. [Google Scholar] [CrossRef] [PubMed]
- Rahim, A.; Hermans, A.; Wohlfeil, B.; Petousi, D.; Kuyken, B.; Van Thourhout, D.; Baets, R. Taking silicon photonics modulators to a higher performance level: State-of-the-art and a review of new technologies. Adv. Photonics 2021, 3, 024003. [Google Scholar] [CrossRef]
- Kazanskiy, N.L.; Butt, M.A.; Khonina, S.N. Silicon photonic devices realized on refractive index engineered subwavelength grating waveguides—A review. Opt. Laser Technol. 2021, 138, 106863. [Google Scholar] [CrossRef]
- Savelyev, D.A.; Khonina, S.N. Numerical analysis of subwavelength focusing using a silicon cylinder. Comput. Opt. 2014, 38, 638–642. [Google Scholar] [CrossRef]
- Butt, M.A.; Khonina, S.N.; Kazanskiy, N.L. Optical elements based on silicon photonics. Comput. Opt. 2019, 43, 1079–1083. [Google Scholar] [CrossRef]
- Wu, S.; Mu, X.; Cheng, L.; Mao, S.; Fu, H.Y. State-of-the-art and perspectives on silicon waveguide crossings: A review. Micromachines 2020, 11, 326. [Google Scholar] [CrossRef]
- Hsu, C.Y.; Yiu, G.Z.; Chang, Y.C. Free-space applications of silicon photonics: A review. Micromachines 2022, 13, 990. [Google Scholar] [CrossRef]
- Mu, X.; Wu, S.; Cheng, L.; Fu, H.Y. Edge couplers in silicon photonic integrated circuits: A review. Appl. Sci. 2020, 10, 1538. [Google Scholar] [CrossRef]
- Xiang, S.; Han, Y.; Song, Z.; Guo, X.; Zhang, Y.; Ren, Z.; Wang, S.; Ma, Y.; Zou, W.; Ma, B.; et al. A review: Photonics devices, architectures, and algorithms for optical neural computing. J. Semicond. 2021, 42, 023105. [Google Scholar] [CrossRef]
- Moralis-Pegios, M.; Mourgias-Alexandris, G.; Tsakyridis, A.; Giamougiannis, G.; Totovic, A.; Dabos, G.; Passalis, N.; Kirtas, M.; Rutirawut, T.; Gardes, F.Y.; et al. Neuromorphic silicon photonics and hardware-aware deep learning for high-speed inference. J. Light. Technol. 2022, 40, 3243–3254. [Google Scholar] [CrossRef]
- Shastri, B.J.; Tait, A.N.; Ferreira De Lima, T.; Pernice, W.H.; Bhaskaran, H.; Wright, C.D.; Prucnal, P.R. Photonics for artificial intelligence and neuromorphic computing. Nat. Photonics 2021, 15, 102–114. [Google Scholar] [CrossRef]
- Prather, D.W.; Shi, S. Formulation and application of the finite-difference time-domain method for the analysis of axially symmetric diffractive optical elements. JOSA A 1999, 16, 1131–1142. [Google Scholar] [CrossRef]
- Zhu, Y.; Cheng, J.; Yi, Z.; Tang, B.; Chen, J.; Zhang, J.; Hu, H.; Tang, C.; Sun, T. Spectrally selective solar absorber and thermal infrared suppression based on hollow cylindrical microstructures. Opt. Commun. 2023, 549, 129910. [Google Scholar] [CrossRef]
- Cheng, Y.; Qian, Y.; Luo, H.; Chen, F.; Cheng, Z. Terahertz narrowband perfect metasurface absorber based on micro-ring-shaped GaAs array for enhanced refractive index sensing. Phys. E Low-Dimens. Syst. Nanostruct. 2023, 146, 115527. [Google Scholar] [CrossRef]
- Li, Z.; Cheng, Y.; Luo, H.; Chen, F.; Li, X. Dual-band tunable terahertz perfect absorber based on all-dielectric InSb resonator structure for sensing application. J. Alloys Compd. 2022, 925, 166617. [Google Scholar] [CrossRef]
- Lu, W.; Yi, Z.; Zhang, J.; Xu, X.; Tang, B.; Li, G.; Zeng, L.; Chen, J.; Sun, T. A tunable broadband absorber in the terahertz band based on the proportional structure of a single layer of graphene. Diam. Relat. Mater. 2023, 140, 110481. [Google Scholar] [CrossRef]
- Hanson, J.C. Broadband rf phased array design with meep: Comparisons to array theory in two and three dimensions. Electronics 2021, 10, 415. [Google Scholar] [CrossRef]
- Urbonas, D.; Gabalis, M.; Petruskevicius, R. Numerical simulation of resonance structures with FDTD algorithms based on GPU B-CALM and CPU Meep. Opt. Quantum Electron. 2014, 46, 1021–1026. [Google Scholar] [CrossRef]
- Oskooi, A.F.; Roundy, D.; Ibanescu, M.; Bermel, P.; Joannopoulos, J.D.; Johnson, S.G. Meep: A flexible free-software package for electromagnetic simulations by the FDTD method. Comput. Phys. Commun. 2010, 181, 181687. [Google Scholar] [CrossRef]
- Montagnac, M.; Agez, G.; Patoux, A.; Arbouet, A.; Paillard, V. Engineered near-and far-field optical response of dielectric nanostructures using focused cylindrical vector beams. J. Appl. Phys. 2022, 131, 133101. [Google Scholar] [CrossRef]
- Zhuang, J.; Zhang, L.; Deng, D. Tight-focusing properties of linearly polarized circular Airy Gaussian vortex beam. Opt. Lett. 2020, 45, 296–299. [Google Scholar] [CrossRef]
- Khonina, S.N.; Kazanskiy, N.L.; Ustinov, A.V.; Volotovskiy, S.G. The lensacon: Nonparaxial effects. J. Opt. Technol. 2011, 78, 724–729. [Google Scholar] [CrossRef]
- Ding, X.; Ren, Y.; Lu, R. Shaping super-Gaussian beam through digital micro-mirror device. Sci. China Phys. Mech. Astron. 2015, 58, 1–6. [Google Scholar] [CrossRef]
- Rani, M.; Singh, U.; Kashyap, J.; Kapoor, A. Broadband light trapping in a-Si: H based plasmonic solar cells using Au core-Al2O3 shell composite nanospheres using FDTD method. Mater. Technol. 2022, 37, 2598–2607. [Google Scholar] [CrossRef]
- Taflove, A.; Hagness, S.C.; Piket-May, M. Computational electromagnetics: The finite-difference time-domain method. Electr. Eng. Handb. 2005, 3, 629–670. [Google Scholar] [CrossRef]
- Khonina, S.N.; Porfirev, A.P.; Kazanskiy, N.L. Variable transformation of singular cylindrical vector beams using anisotropic crystals. Sci. Rep. 2020, 10, 5590. [Google Scholar] [CrossRef]
- Savelyev, D.A. The comparison of the optical vortices focusing by silicon diffraction axicons and ring gratings with variable relief heights using high-performance computer systems. St. Petersburg Polytech. Univ. J. Phys. Math. 2022, 59, 172–177. [Google Scholar] [CrossRef]
- Fu, S.; Gao, C.; Wang, T.; Zhai, Y.; Yin, C. Anisotropic polarization modulation for the production of arbitrary Poincaré beams. J. Opt. Soc. Am. B 2018, 35, 1–7. [Google Scholar] [CrossRef]
- Savelyev, D.A. The investigation of the features optical vortices focusing by ring gratings with the variable height using high-performance computer systems. J. Phys. Conf. Ser. 2021, 2086, 012166. [Google Scholar] [CrossRef]
- Huang, K.; Shi, P.; Cao, G.W.; Li, K.; Zhang, X.B.; Li, Y.P. Vector-vortex Bessel–Gauss beams and their tightly focusing properties. Opt. Lett. 2011, 36, 888–890. [Google Scholar] [CrossRef]
- Khonina, S.N.; Alferov, S.V.; Karpeev, S.V. Strengthening the longitudinal component of the sharply focused electric field by means of higher-order laser beams. Opt. Lett. 2013, 38, 3223–3226. [Google Scholar] [CrossRef] [PubMed]
- Savelyev, D.A. The optical vortices focusing by subwavelength microelements with variable relief height using high-performance computer systems. Proc. SPIE 2023, 12743, 257–267. [Google Scholar] [CrossRef]
- Khonina, S.N.; Karpeev, S.V.; Alferov, S.V.; Savelyev, D.A. Experimental demonstration of generation of longitudinal component of the electric field on the optical axis by high-aperture binary axicon for linear and circular polarization of the incident beam. Comput. Opt. 2013, 37, 76–87. [Google Scholar] [CrossRef]
- Ashkin, A.; Dziedzic, J.M.; Bjorkholm, J.E.; Chu, S. Observation of a single-beam gradient force optical trap for dielectric particles. Opt. Lett. 1986, 11, 288–290. [Google Scholar] [CrossRef]
- Suarez, R.A.; Neves, A.A.; Gesualdi, M.R. Optical trapping with non-diffracting Airy beams array using a holographic optical tweezers. Opt. Laser Technol. 2021, 135, 106678. [Google Scholar] [CrossRef]
- Devi, A.; De, A.K. Unified treatment of nonlinear optical force in laser trapping of dielectric particles of varying sizes. Phys. Rev. Res. 2021, 3, 033074. [Google Scholar] [CrossRef]
- Siemion, A. The magic of optics—An overview of recent advanced terahertz diffractive optical elements. Sensors 2020, 21, 100. [Google Scholar] [CrossRef]
- Veiko, V.P.; Korolkov, V.P.; Poleshchuk, A.G.; Sinev, D.A.; Shakhno, E.A. Laser technologies in micro-optics. Part 1. Fabrication of diffractive optical elements and photomasks with amplitude transmission. Optoelectron. Instrum. Data Process. 2017, 53, 474–483. [Google Scholar] [CrossRef]
- Poleshchuk, A.G.; Korolkov, V.P.; Veiko, V.P.; Zakoldaev, R.A.; Sergeev, M.M. Laser technologies in micro-optics. Part 2. Fabrication of elements with a three-dimensional profile. Optoelectron. Instrum. Data Process. 2018, 54, 113–126. [Google Scholar] [CrossRef]
- Wang, H.; Wang, H.; Zhang, W.; Yang, J.K. Toward near-perfect diffractive optical elements via nanoscale 3D printing. ACS Nano 2020, 14, 10452–10461. [Google Scholar] [CrossRef] [PubMed]
- Lio, G.E.; Ferraro, A.; Ritacco, T.; Aceti, D.M.; De Luca, A.; Giocondo, M.; Caputo, R. Leveraging on ENZ Metamaterials to Achieve 2D and 3D Hyper-Resolution in Two-Photon Direct Laser Writing. Adv. Mater. 2021, 33, 2008644. [Google Scholar] [CrossRef]
- Kononenko, T.V.; Knyazev, B.A.; Sovyk, D.N.; Pavelyev, V.S.; Komlenok, M.S.; Komandin, G.A.; Konov, V.I. Silicon kinoform cylindrical lens with low surface roughness for high-power terahertz radiation. Opt. Laser Technol. 2020, 123, 105953. [Google Scholar] [CrossRef]
- Zhang, L.; Jiang, F.; Wu, B.; Lv, C.; Wu, M. A one-step synthesis of ultra-long silver nanowires with ultra-high aspect ratio above 2000 and its application in flexible transparent conductive electrodes. Nanotechnology 2020, 32, 105710. [Google Scholar] [CrossRef]
- Li, L.; Tuan, C.C.; Zhang, C.; Chen, Y.; Lian, G.; Wong, C.P. Uniform Metal-Assisted Chemical Etching for Ultra-High-Aspect-Ratio Microstructures on Silicon. J. Microelectromech. Syst. 2018, 28, 143–153. [Google Scholar] [CrossRef]
- Jumare, A.I.; Abou-El-Hossein, K.; Abdulkadir, L.N. Review of ultra-high precision diamond turning of silicon for infrared optics. Int. J. Sci. Res. 2017, 73, 58–123. [Google Scholar] [CrossRef]
- Kharitonov, S.I.; Pavelyev, V.S.; Kazanskiy, N.L.; Strelkov, Y.S.; Tukmakov, K.N.; Reshetnikov, A.S.; Ganchevskaya, S.V.; Gerasimov, V.V.; Knyazev, B.A. Optimization, fabrication and characterization of a binary subwavelength cylindrical lens for the terahertz range. Comput. Opt. 2023, 47, 62–67. [Google Scholar]
- Khonina, S.N.; Tukmakov, K.N.; Degtyarev, S.A.; Reshetnikov, A.S.; Pavelyev, V.S.; Knyazev, B.A.; Choporova, Y.Y. Design, fabrication and investigation of a subwavelength axicon for terahertz beam polarization transforming. Comput. Opt. 2019, 43, 756–764. [Google Scholar] [CrossRef]
- Agafonov, A.N.; Volodkin, B.O.; Kaveev, A.K.; Knyazev, B.A.; Kropotov, G.I.; Pavel’ev, V.S.; Soifer, V.A.; Tukmakov, K.N.; Tsygankova, E.V.; Choporova, Y.Y. Silicon diffractive optical elements for high-power monochromatic terahertz radiation. Optoelectron. Instrum. Data Process. 2013, 49, 189–195. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).