Enhancing Contrast of Spatial Details in X-ray Phase-Contrast Imaging through Modified Fourier Filtering
Abstract
:1. Introduction
2. Two-Distance Phase Retrieval Algorithm
3. Numerical Simulations and Experimental Data
3.1. Simulations
3.2. Experiment Data Acquisition
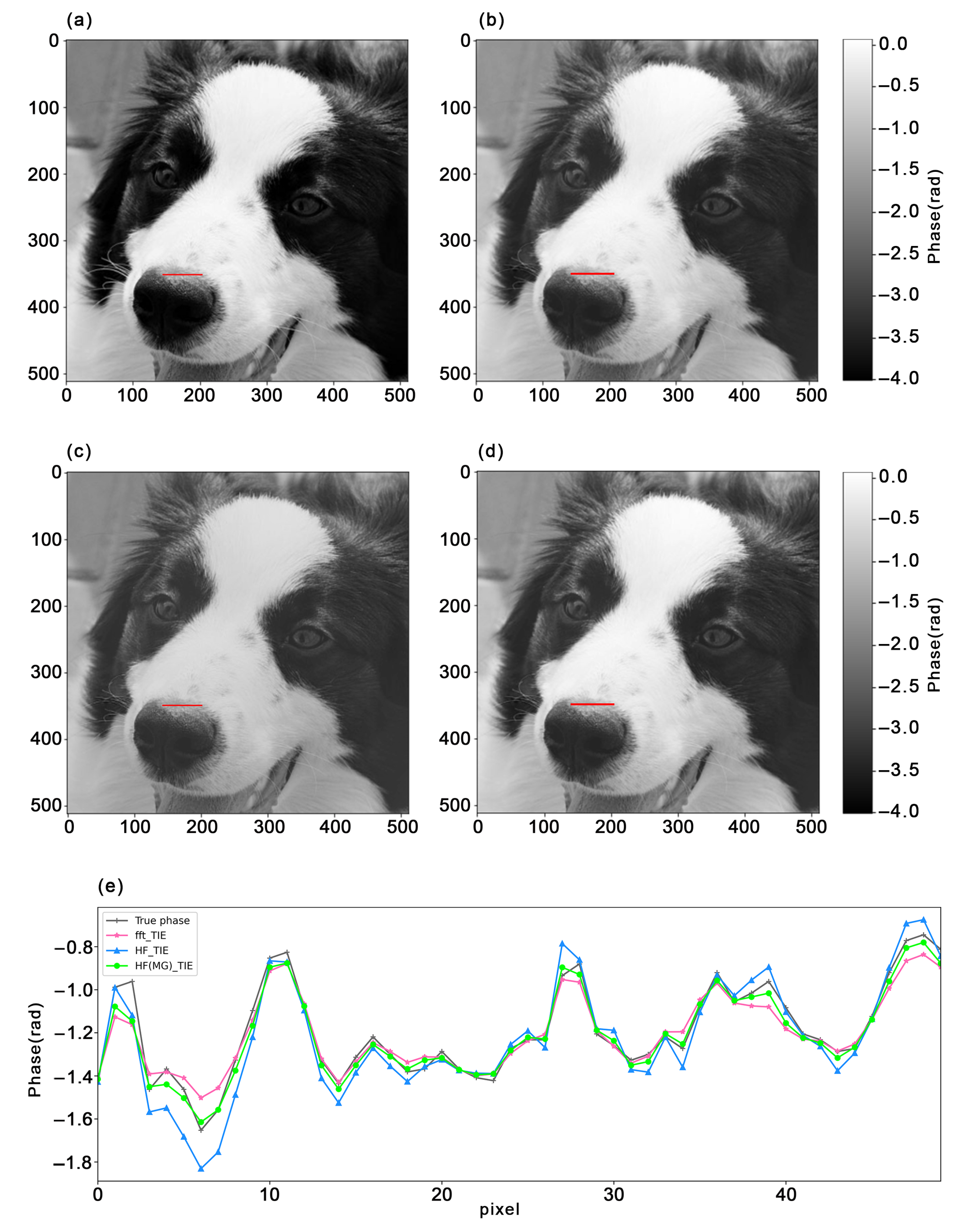
4. Results and Discussion
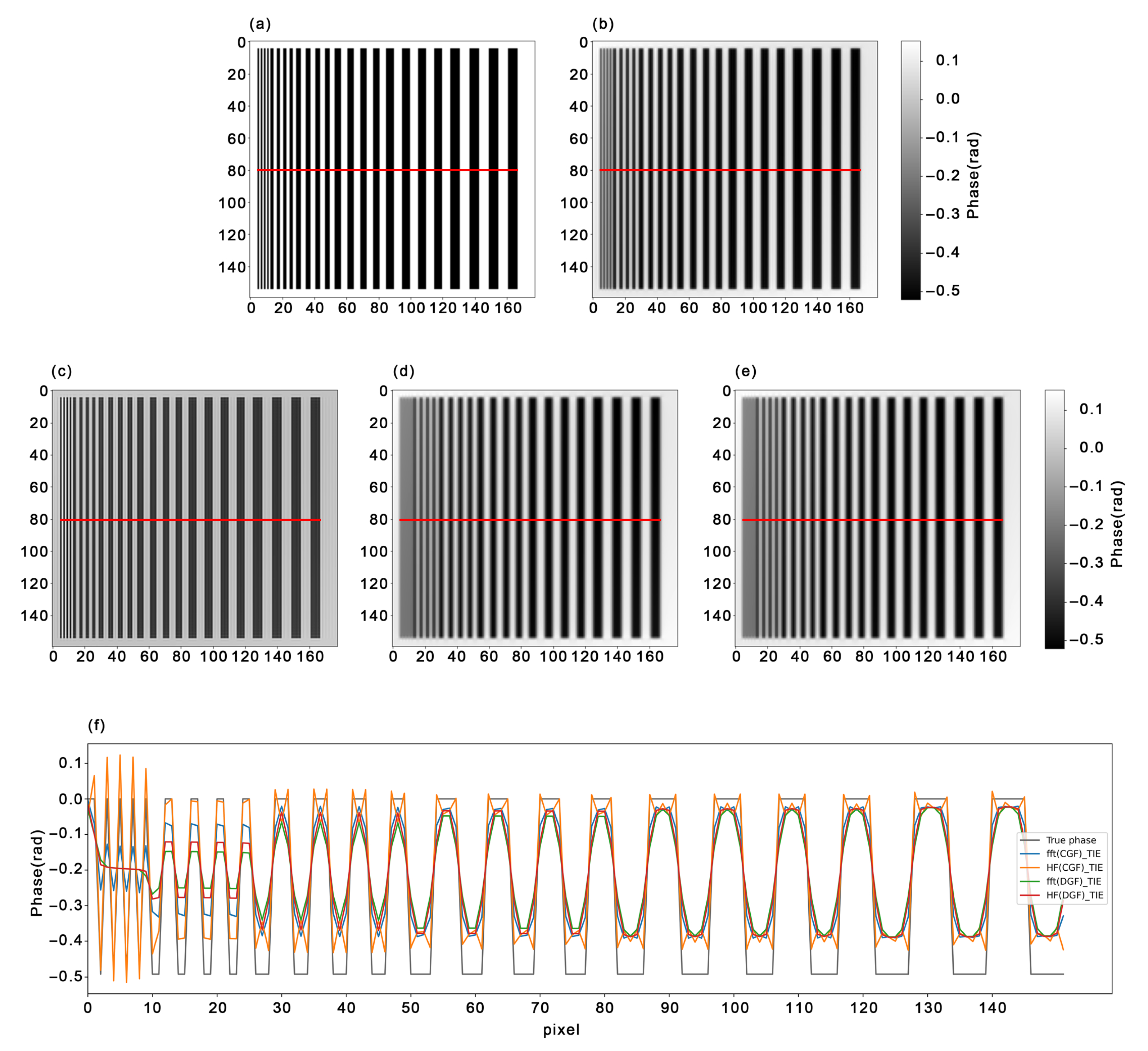
4.1. Simulated Data
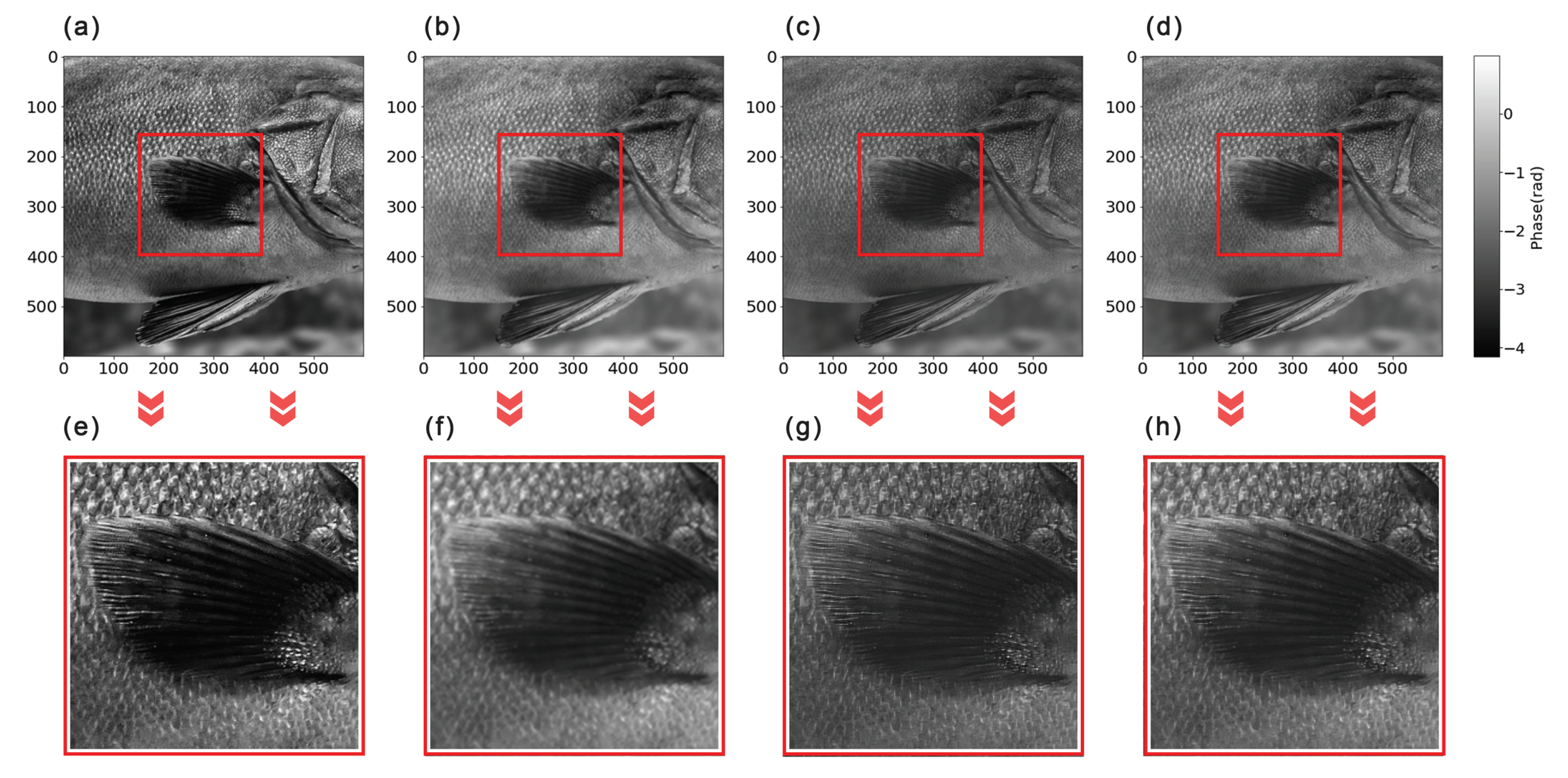
4.2. Experimental Data
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DFT | Discrete Fourier transform operator |
| IDFT | Inverse discrete Fourier transform |
| DGF | Discrete Gradient Operator Filter |
| CGF | Continuous Gradient Operator Filter |
| RMF | Reciprocal of Modified Inverse Laplacian Filter |
| ROF | Reciprocal of Original Inverse Laplacian Filter |
Appendix A. Simulation of Diverse Objects

| Dataset | FFT-TIE Method | HF(CGF)-TIE Method | HF(MG)-TIE Method |
|---|---|---|---|
| Leaves | 26.1% | 24.8% | 24.2% |
| Fish | 24.7% | 22.4% | 21.5% |
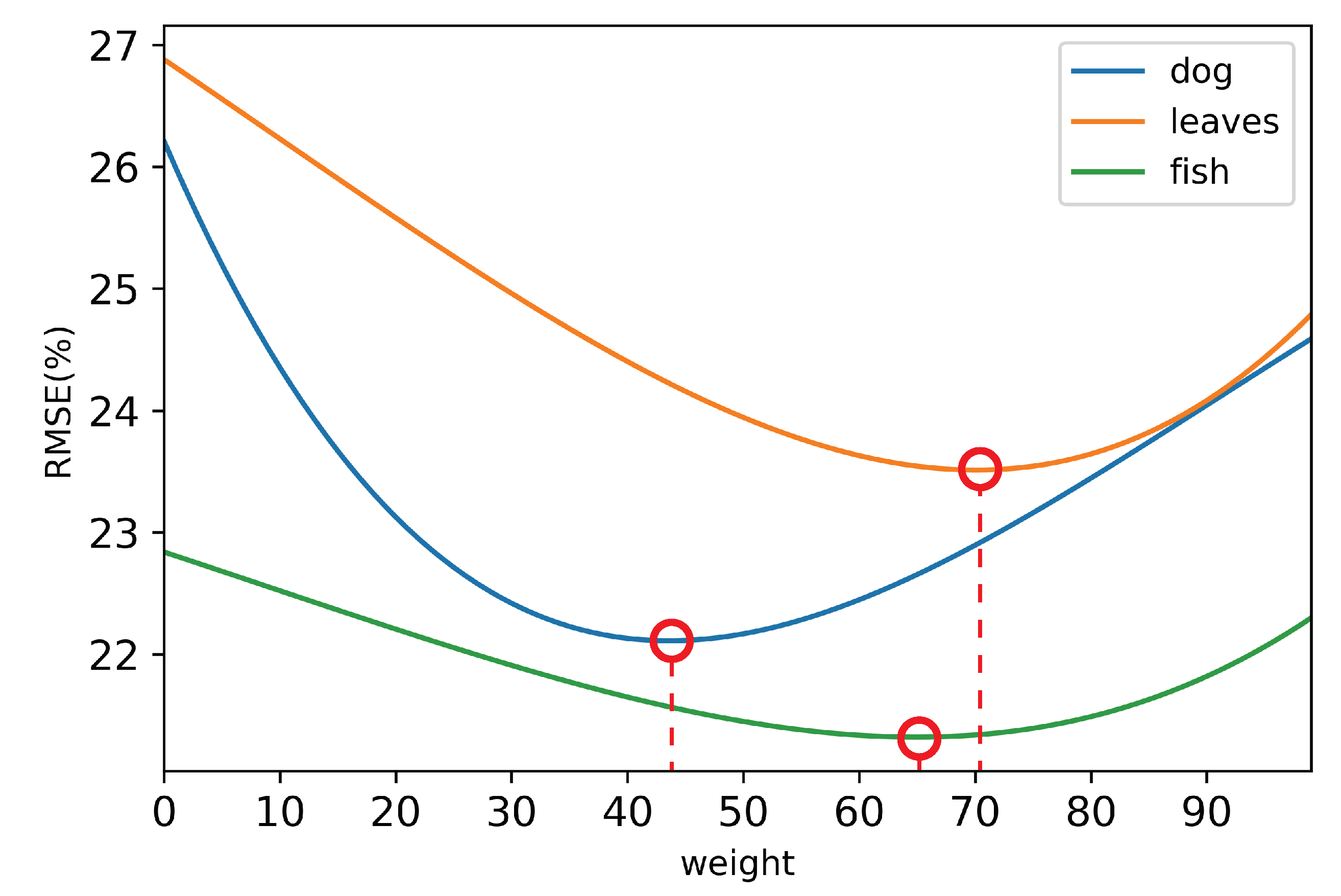
Appendix B. Weighted Analysis of CGF and DGF
References
- Momose, A. Recent advances in X-ray phase imaging. Jpn. J. Appl. Phys. 2005, 44, 6355. [Google Scholar] [CrossRef]
- Snigirev, A.; Snigireva, I.; Kohn, V.; Kuznetsov, S.; Schelokov, I. On the possibilities of X-ray phase contrast microimaging by coherent high-energy synchrotron radiation. Rev. Sci. Instrum. 1995, 66, 5486–5492. [Google Scholar] [CrossRef]
- Mayo, S.C.; Stevenson, A.W.; Wilkins, S.W. In-line phase-contrast X-ray imaging and tomography for materials science. Materials 2012, 5, 937–965. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Jiang, S.; Song, P.; Wang, R.; Yang, L.; Zhang, T.; Zheng, G. Optical ptychography for biomedical imaging: Recent progress and future directions. Biomed. Opt. Express 2023, 14, 489–532. [Google Scholar] [CrossRef] [PubMed]
- Yu, B.; Weber, L.; Pacureanu, A.; Langer, M.; Olivier, C.; Cloetens, P.; Peyrin, F. Phase retrieval in 3D X-ray magnified phase nano CT: Imaging bone tissue at the nanoscale. In Proceedings of the 2017 IEEE 14th International Symposium on Biomedical Imaging (ISBI 2017), Melbourne, Australia, 18–21 April 2017; pp. 56–59. [Google Scholar]
- Bonse, U.; Hart, M. An X-ray interferometer. Appl. Phys. Lett. 1965, 6, 155–156. [Google Scholar] [CrossRef]
- Förster, E.; Goetz, K.; Zaumseil, P. Double crystal diffractometry for the characterization of targets for laser fusion experiments. Krist. Tech. 1980, 15, 937–945. [Google Scholar] [CrossRef]
- Tkachuk, A.; Duewer, F.; Cui, H.; Feser, M.; Wang, S.; Yun, W. X-ray computed tomography in Zernike phase contrast mode at 8 keV with 50-nm resolution using Cu rotating anode X-ray source. Z. Krist.-Cryst. Mater. 2007, 222, 650–655. [Google Scholar] [CrossRef]
- Weitkamp, T.; Diaz, A.; David, C.; Pfeiffer, F.; Stampanoni, M.; Cloetens, P.; Ziegler, E. X-ray phase imaging with a grating interferometer. Opt. Express 2005, 13, 6296–6304. [Google Scholar] [CrossRef]
- Zanette, I.; Zhou, T.; Burvall, A.; Lundström, U.; Larsson, D.H.; Zdora, M.; Thibault, P.; Pfeiffer, F.; Hertz, H.M. Speckle-based X-ray phase-contrast and dark-field imaging with a laboratory source. Phys. Rev. Lett. 2014, 112, 253903. [Google Scholar] [CrossRef]
- Teague, M.R. Deterministic phase retrieval: A Green’s function solution. J. Opt. Soc. Am. 1983, 73, 1434–1441. [Google Scholar] [CrossRef]
- Zuo, C.; Li, J.; Sun, J.; Fan, Y.; Zhang, J.; Lu, L.; Zhang, R.; Wang, B.; Huang, L.; Chen, Q. Transport of intensity equation: A tutorial. Opt. Lasers Eng. 2020, 135, 106187. [Google Scholar] [CrossRef]
- Langer, M.; Cloetens, P.; Guigay, J.P.; Peyrin, F. Quantitative comparison of direct phase retrieval algorithms in in-line phase tomography. Med. Phys. 2008, 35, 4556–4566. [Google Scholar] [CrossRef] [PubMed]
- Pogany, A.; Gao, D.; Wilkins, S.W. Contrast and resolution in imaging with a microfocus X-ray source. Rev. Sci. Instrum. 1997, 68, 2774–2782. [Google Scholar] [CrossRef]
- Paganin, D.; Nugent, K.A. Noninterferometric phase imaging with partially coherent light. Phys. Rev. Lett. 1998, 80, 2586. [Google Scholar] [CrossRef]
- Schmalz, J.A.; Gureyev, T.E.; Paganin, D.M.; Pavlov, K.M. Phase retrieval using radiation and matter-wave fields: Validity of Teague’s method for solution of the transport-of-intensity equation. Phys. Rev. A 2011, 84, 023808. [Google Scholar] [CrossRef]
- Gureyev, T.; Nugent, K. Rapid quantitative phase imaging using the transport of intensity equation. Opt. Commun. 1997, 133, 339–346. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, Q.; Sun, J.; Tian, L.; Zuo, C. On a universal solution to the transport-of-intensity equation. Opt. Lett. 2020, 45, 3649–3652. [Google Scholar] [CrossRef]
- Gureyev, T.E.; Nugent, K.A. Phase retrieval with the transport-of-intensity equation. II. Orthogonal series solution for nonuniform illumination. JOSA A 1996, 13, 1670–1682. [Google Scholar] [CrossRef]
- Nugent, K.; Gureyev, T.; Cookson, D.; Paganin, D.; Barnea, Z. Quantitative phase imaging using hard X rays. Phys. Rev. Lett. 1996, 77, 2961. [Google Scholar] [CrossRef]
- Tychonoff, A.N.; Arsenin, V.Y. Solution of Ill-Posed Problems; Winston & Sons: Washington, DC, USA, 1977. [Google Scholar]
- Paganin, D.M.; Favre-Nicolin, V.; Mirone, A.; Rack, A.; Villanova, J.; Olbinado, M.P.; Fernandez, V.; da Silva, J.C.; Pelliccia, D. Boosting spatial resolution by incorporating periodic boundary conditions into single-distance hard-X-ray phase retrieval. J. Opt. 2020, 22, 115607. [Google Scholar] [CrossRef]
- Goodman, J.W. Introduction to Fourier Optics; Roberts and Company Publishers: Greenwood Village, CO, USA, 2005. [Google Scholar]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes 3rd Edition: The Art of Scientific Computing; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Paganin, D.; Mayo, S.C.; Gureyev, T.E.; Miller, P.R.; Wilkins, S.W. Simultaneous phase and amplitude extraction from a single defocused image of a homogeneous object. J. Microsc. 2002, 206, 33–40. [Google Scholar] [CrossRef]
- Gureyev, T.E.; Pogany, A.; Paganin, D.M.; Wilkins, S. Linear algorithms for phase retrieval in the Fresnel region. Opt. Commun. 2004, 231, 53–70. [Google Scholar] [CrossRef]
- Paganin, D.; Barty, A.; McMahon, P.; Nugent, K.A. Quantitative phase-amplitude microscopy. III. The effects of noise. J. Microsc. 2004, 214, 51–61. [Google Scholar] [CrossRef]


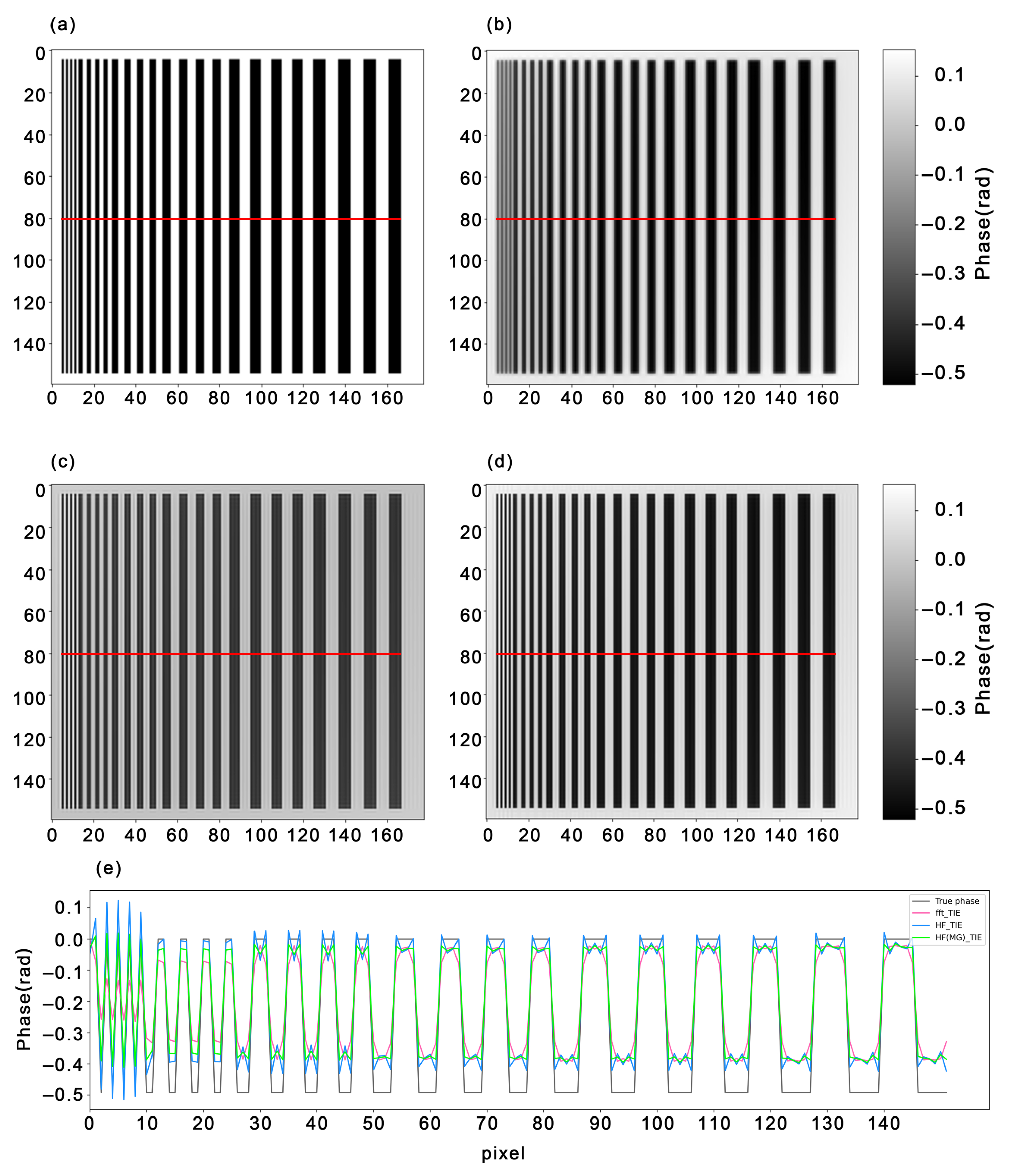

| Dataset | FFT-TIE Method | HF-TIE(CGF) Method | HF(MG)-TIE Method |
|---|---|---|---|
| 1 | 14.2% | 8.7% | 8.5% |
| 2 | 25.3% | 24.6% | 22.4% |
| Method | 1% Noise | 2% Noise | 5% Noise | 10% Noise | 20% Noise |
|---|---|---|---|---|---|
| FFT-TIE | 29.6% | 32.5% | 48.1% | 62.4% | 96.4% |
| HF(CGF)-TIE | 28.8% | 33.1% | 48.2% | 62.4% | 96.4% |
| HF(MG)-TIE | 26.7% | 31.0% | 47.6% | 62.4% | 96.3% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, B.; Li, G.; Zhang, J.; Wang, Y.; Deng, T.; Sun, R.; Huang, M.; Guaerjia, G. Enhancing Contrast of Spatial Details in X-ray Phase-Contrast Imaging through Modified Fourier Filtering. Photonics 2023, 10, 1204. https://doi.org/10.3390/photonics10111204
Yu B, Li G, Zhang J, Wang Y, Deng T, Sun R, Huang M, Guaerjia G. Enhancing Contrast of Spatial Details in X-ray Phase-Contrast Imaging through Modified Fourier Filtering. Photonics. 2023; 10(11):1204. https://doi.org/10.3390/photonics10111204
Chicago/Turabian StyleYu, Bei, Gang Li, Jie Zhang, Yanping Wang, Tijian Deng, Rui Sun, Mei Huang, and Gangjian Guaerjia. 2023. "Enhancing Contrast of Spatial Details in X-ray Phase-Contrast Imaging through Modified Fourier Filtering" Photonics 10, no. 11: 1204. https://doi.org/10.3390/photonics10111204
APA StyleYu, B., Li, G., Zhang, J., Wang, Y., Deng, T., Sun, R., Huang, M., & Guaerjia, G. (2023). Enhancing Contrast of Spatial Details in X-ray Phase-Contrast Imaging through Modified Fourier Filtering. Photonics, 10(11), 1204. https://doi.org/10.3390/photonics10111204




