Dynamics and Concealment of Time-Delay Signature in Mutually Coupled Nano-Laser Chaotic Systems
Abstract
:1. Introduction
2. Nano-Laser Dynamics
3. Results and Discussion
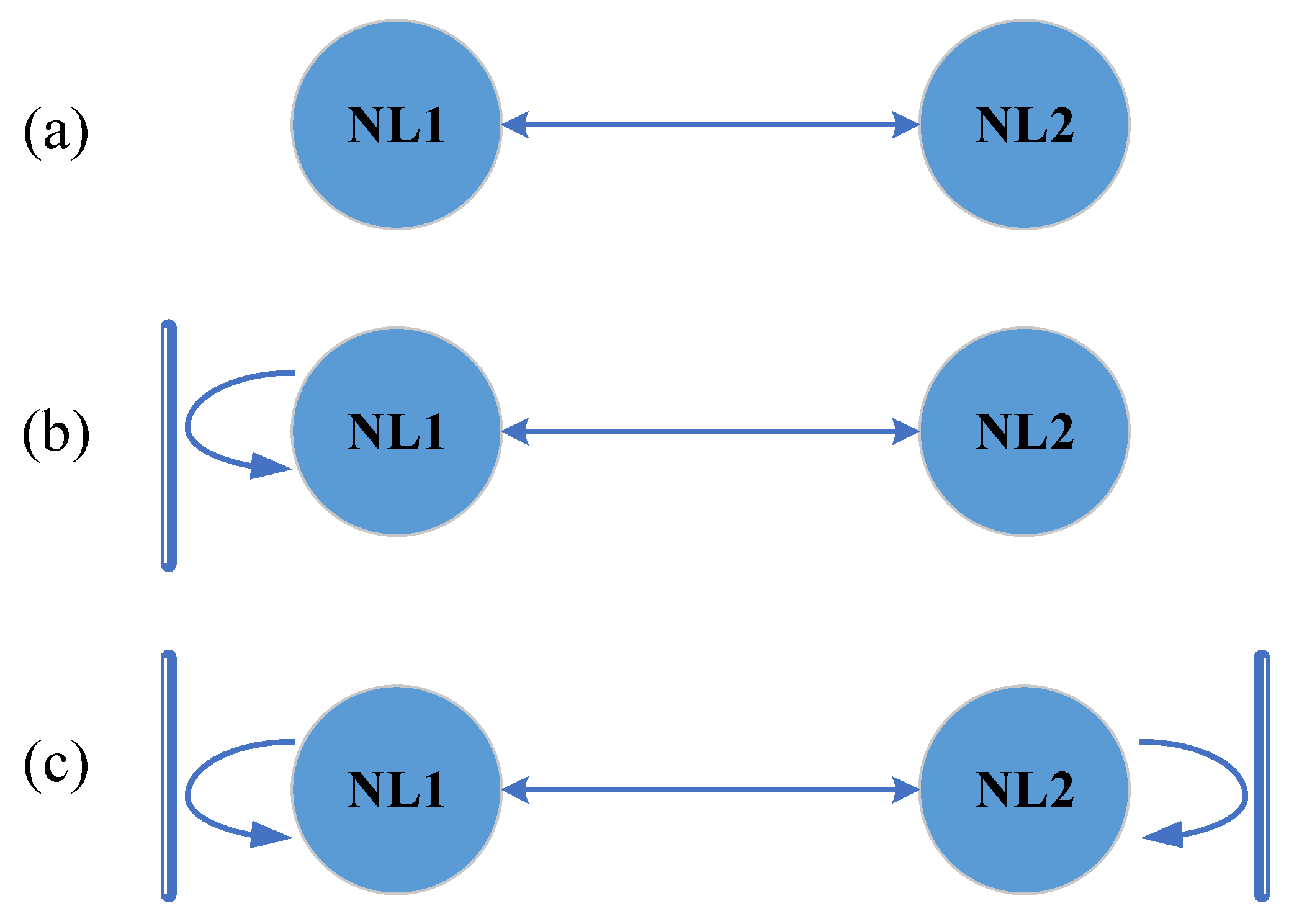
3.1. The Open-Loop Structure (without Feedback)
3.2. The Semi-Open-Loop Structure (with One Feedback)
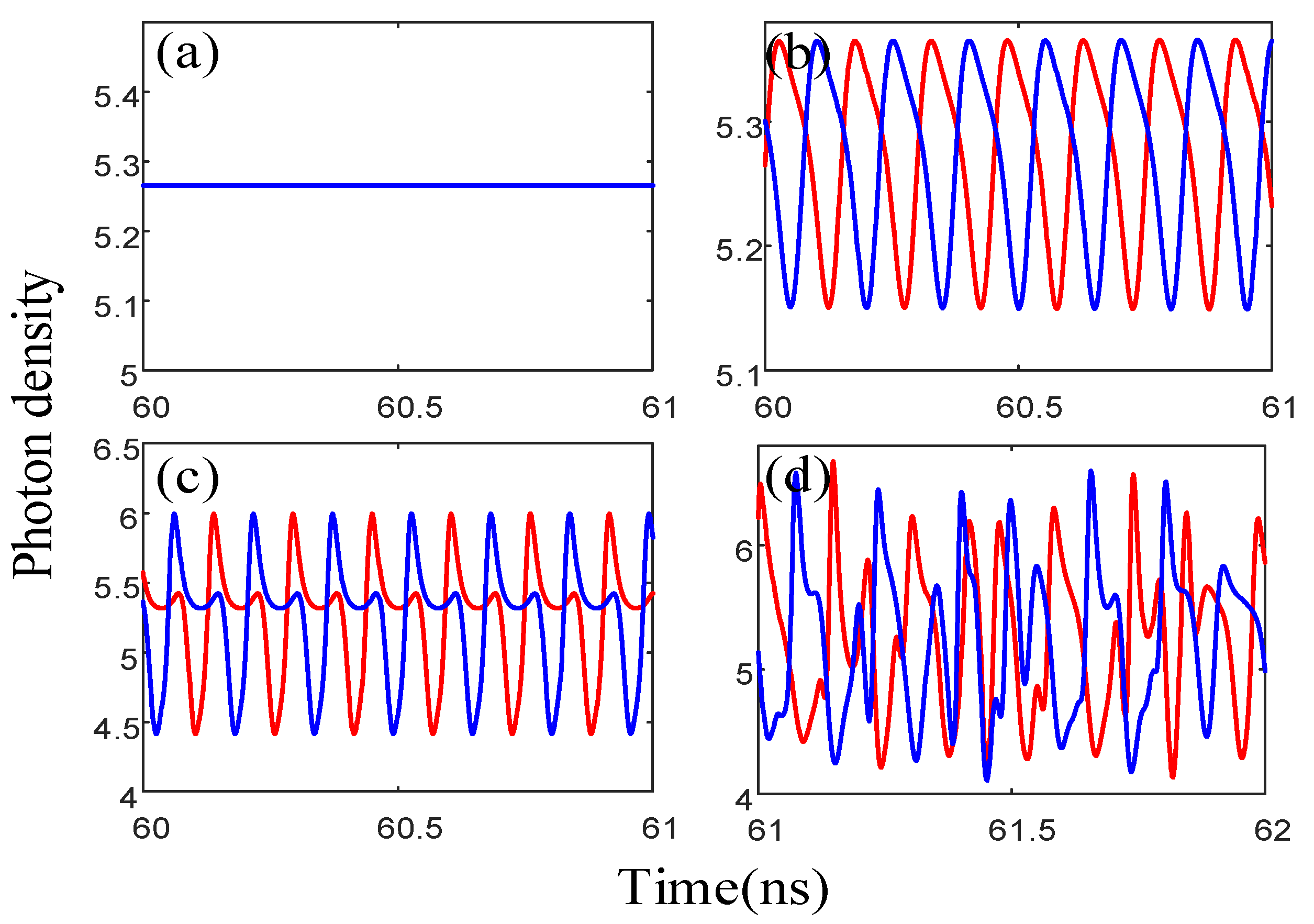
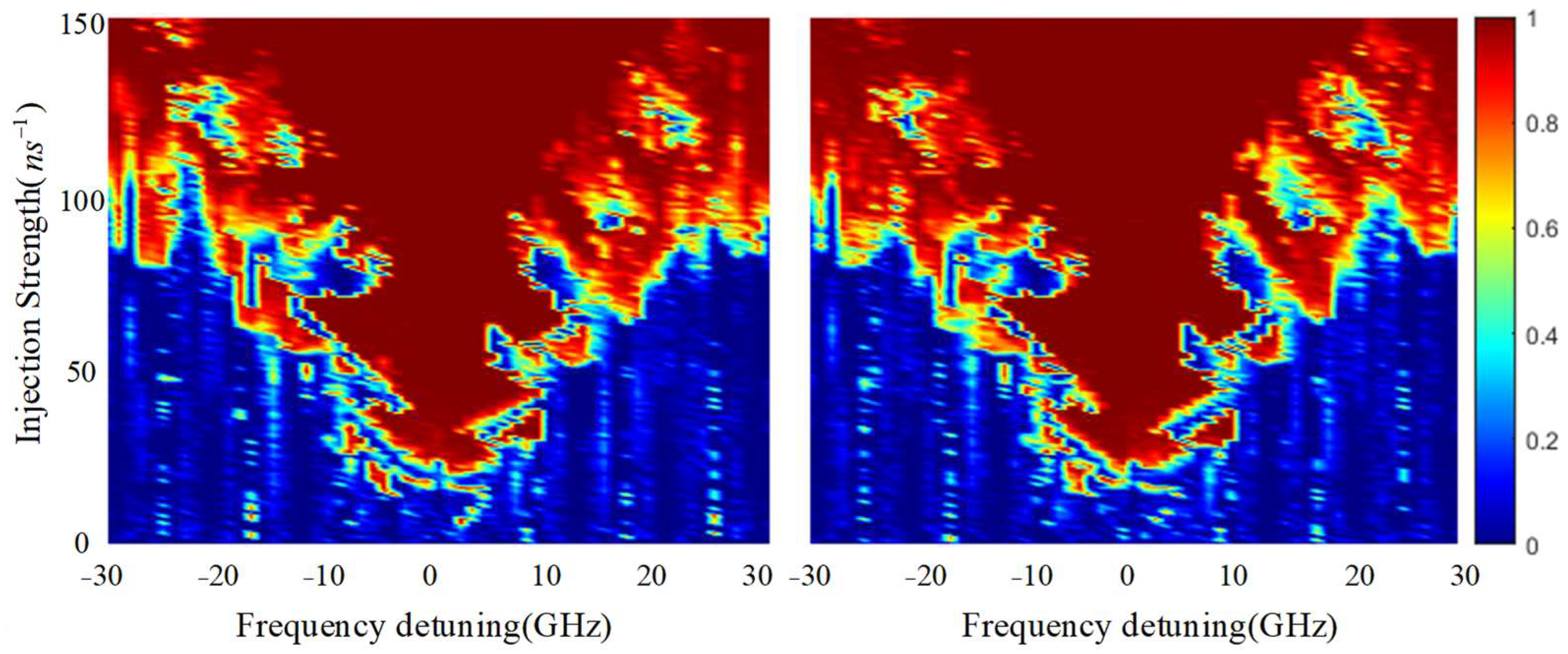
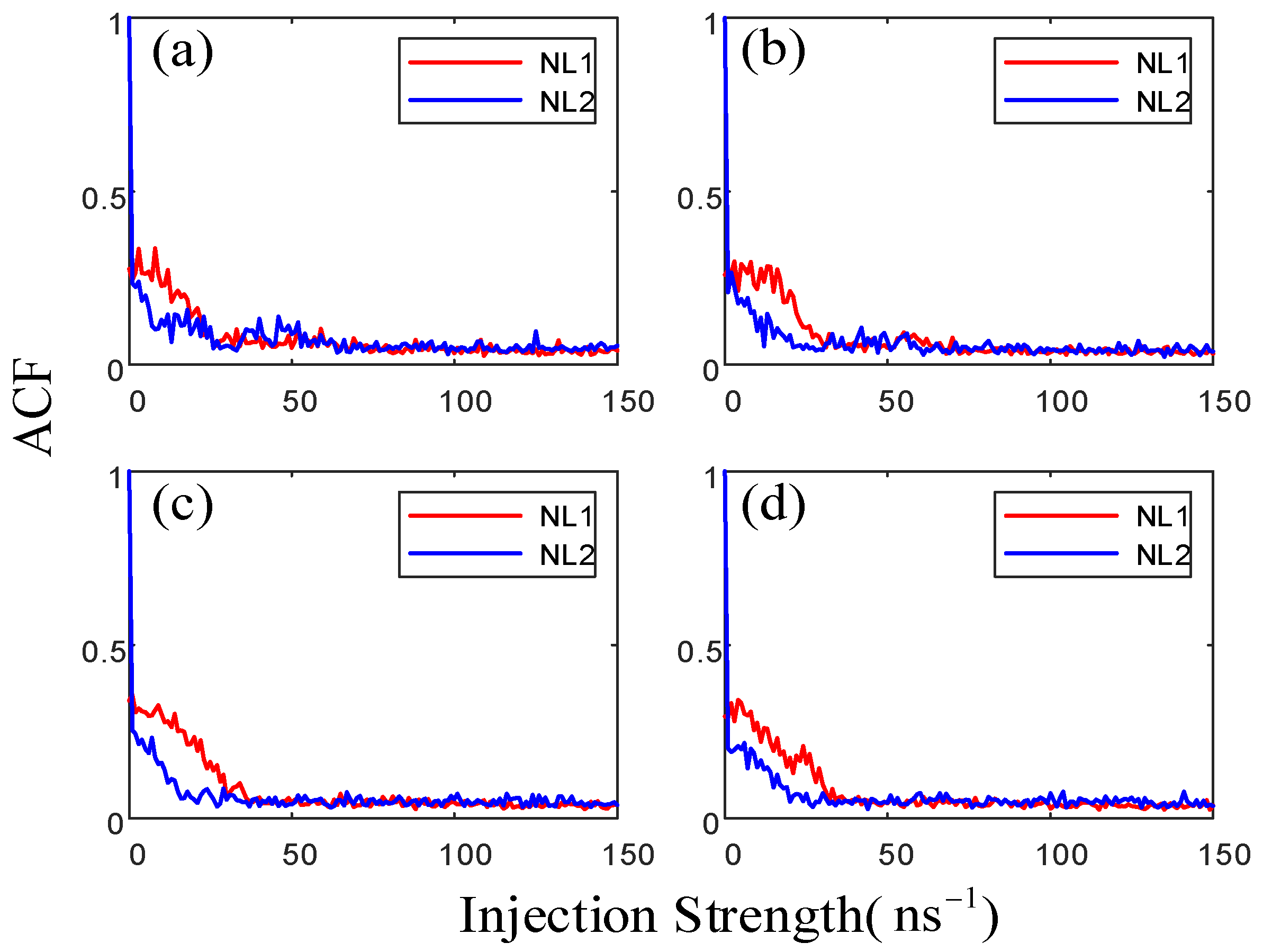
3.3. The Closed-Loop Structure (with Two Feedbacks)
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sciamanna, M.; Shore, K.A. Physics and Applications of Laser Diode Chaos. Nat. Photonics 2015, 9, 151–162. [Google Scholar] [CrossRef]
- Soriano, M.C.; García-Ojalvo, J.; Mirasso, C.R.; Fischer, I. Complex Photonics: Dynamics and Applications of Delay-Coupled Semiconductors Lasers. Rev. Mod. Phys. 2013, 85, 421–470. [Google Scholar] [CrossRef]
- Xiang, S.; Ren, Z.; Zhang, Y.; Song, Z.; Hao, Y. All-Optical Neuromorphic XOR Operation with Inhibitory Dynamics of a Single Photonic Spiking Neuron Based on a VCSEL-SA. Opt. Lett. 2020, 45, 1104–1107. [Google Scholar] [CrossRef] [PubMed]
- Yan, S.-L. Chaotic laser parallel series synchronization and its repeater applications in secure communication. Acta Phys. Sin. 2019, 68, 170502. [Google Scholar] [CrossRef]
- Li, N.; Susanto, H.; Cemlyn, B.; Henning, I.D.; Adams, M.J. Secure Communication Systems Based on Chaos in Optically Pumped Spin-VCSELs. Opt. Lett. 2017, 42, 3494–3497. [Google Scholar] [CrossRef] [PubMed]
- Li, N.; Pan, W.; Yan, L.; Luo, B.; Zou, X.; Xiang, S. Enhanced Two-Channel Optical Chaotic Communication Using Isochronous Synchronization. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 0600109. [Google Scholar] [CrossRef]
- Jiang, N.; Zhao, A.; Xue, C.; Tang, J.; Qiu, K. Physical Secure Optical Communication Based on Private Chaotic Spectral Phase Encryption/Decryption. Opt. Lett. 2019, 44, 1536–1539. [Google Scholar] [CrossRef]
- Jiang, N.; Xue, C.; Lv, Y.; Qiu, K. Physically Enhanced Secure Wavelength Division Multiplexing Chaos Communication Using Multimode Semiconductor Lasers. Nonlinear Dyn. 2016, 86, 1937–1949. [Google Scholar] [CrossRef]
- Li, P.; Sun, Y.; Liu, X.; Yi, X.; Zhang, J.; Guo, X.; Guo, Y.; Wang, Y. Fully Photonics-Based Physical Random Bit Generator. Opt. Lett. 2016, 41, 3347–3350. [Google Scholar] [CrossRef]
- Li, P.; Wang, Y.-C.; Wang, A.-B.; Wang, B.-J. Fast and Tunable All-Optical Physical Random Number Generator Based on Direct Quantization of Chaotic Self-Pulsations in Two-Section Semiconductor Lasers. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 0600208. [Google Scholar] [CrossRef]
- Xiang, S.; Wen, A.; Pan, W. Emulation of Spiking Response and Spiking Frequency Property in VCSEL-Based Photonic Neuron. IEEE Photonics J. 2016, 8, 1504109. [Google Scholar] [CrossRef]
- Robertson, J.; Wade, E.; Kopp, Y.; Bueno, J.; Hurtado, A. Toward Neuromorphic Photonic Networks of Ultrafast Spiking Laser Neurons. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 7700715. [Google Scholar] [CrossRef]
- Larger, L.; Soriano, M.C.; Brunner, D.; Appeltant, L.; Gutierrez, J.M.; Pesquera, L.; Mirasso, C.R.; Fischer, I. Photonic Information Processing beyond Turing: An Optoelectronic Implementation of Reservoir Computing. Opt. Express 2012, 20, 3241–3249. [Google Scholar] [CrossRef] [PubMed]
- Rontani, D.; Choi, D.; Chang, C.-Y.; Locquet, A.; Citrin, D.S. Compressive Sensing with Optical Chaos. Sci. Rep. 2016, 6, 35206. [Google Scholar] [CrossRef] [PubMed]
- Cheng, C.-H.; Chen, C.-Y.; Chen, J.-D.; Pan, D.-K.; Ting, K.-T.; Lin, F.-Y. 3D Pulsed Chaos Lidar System. Opt. Express 2018, 26, 12230–12241. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.-Y.; Cheng, C.-H.; Pan, D.-K.; Lin, F.-Y. Experimental Generation and Analysis of Chaos-Modulated Pulses for Pulsed Chaos Lidar Applications Based on Gain-Switched Semiconductor Lasers Subject to Optical Feedback. Opt. Express 2018, 26, 20851–20860. [Google Scholar] [CrossRef]
- Liu, B.; Jiang, Y.; Ji, H. Sensing by Dynamics of Lasers with External Optical Feedback: A Review. Photonics 2022, 9, 450. [Google Scholar] [CrossRef]
- Yarunova, E.A.; Krents, A.A.; Molevich, N.E.; Anchikov, D.A. Suppression of Spatiotemporal Instabilities in Broad-Area Lasers with Pump Modulation by External Optical Injection. Bull. Lebedev Phys. Inst. 2021, 48, 55–58. [Google Scholar] [CrossRef]
- Dmitriev, P.S.; Kovalev, A.V.; Locquet, A.; Citrin, D.S.; Viktorov, E.A.; Rontani, D. Predicting Chaotic Time Series Using Optoelectronic Feedback Laser. In Proceedings of the Semiconductor Lasers and Laser Dynamics IX, Online, 6–10 April 2020; SPIE: Bellingham, WA, USA, 2020; Volume 11356, pp. 100–105. [Google Scholar]
- Kaur, B.; Jana, S. Generation and Dynamics of One- and Two-Dimensional Cavity Solitons in a Vertical-Cavity Surface-Emitting Laser with a Saturable Absorber and Frequency-Selective Feedback. J. Opt. Soc. Am. B-Opt. Phys. 2017, 34, 1374–1385. [Google Scholar] [CrossRef]
- Spitz, O.; Wu, J.; Herdt, A.; Carras, M.; Elsäßer, W.; Wong, C.-W.; Grillot, F. Investigation of Chaotic and Spiking Dynamics in Mid-Infrared Quantum Cascade Lasers Operating Continuous-Waves and Under Current Modulation. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 1200311. [Google Scholar] [CrossRef]
- Rontani, D.; Locquet, A.; Sciamanna, M.; Citrin, D.S. Loss of Time-Delay Signature in the Chaotic Output of a Semiconductor Laser with Optical Feedback. Opt. Lett. 2007, 32, 2960–2962. [Google Scholar] [CrossRef] [PubMed]
- Nguimdo, R.M.; Colet, P.; Larger, L.; Pesquera, L. Digital Key for Chaos Communication Performing Time Delay Concealment. Phys. Rev. Lett. 2011, 107, 034103. [Google Scholar] [CrossRef]
- Soriano, M.C.; Zunino, L.; Rosso, O.A.; Fischer, I.; Mirasso, C.R. Time Scales of a Chaotic Semiconductor Laser With Optical Feedback Under the Lens of a Permutation Information Analysis. IEEE J. Quantum Electron. 2011, 47, 252–261. [Google Scholar] [CrossRef]
- Rontani, D.; Locquet, A.; Sciamanna, M.; Citrin, D.S.; Ortin, S. Time-Delay Identification in a Chaotic Semiconductor Laser with Optical Feedback: A Dynamical Point of View. IEEE J. Quantum Electron. 2009, 45, 879–1891. [Google Scholar] [CrossRef]
- Wu, J.-G.; Xia, G.-Q.; Wu, Z.-M. Suppression of Time Delay Signatures of Chaotic Output in a Semiconductor Laser with Double Optical Feedback. Opt. Express 2009, 17, 20124–20133. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Z.-Q.; Wu, Z.-M.; Xia, G.-Q. Experimental Investigation on the Time-Delay Signature of Chaotic Output from a 1550 Nm VCSEL Subject to FBG Feedback. Photonics Res. 2017, 5, 6–10. [Google Scholar] [CrossRef]
- Priyadarshi, S.; Hong, Y.; Pierce, I.; Shore, K.A. Experimental Investigations of Time-Delay Signature Concealment in Chaotic External Cavity VCSELs Subject to Variable Optical Polarization Angle of Feedback. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 1700707. [Google Scholar] [CrossRef]
- Li, N.; Pan, W.; Locquet, A.; Citrin, D.S. Time-Delay Concealment and Complexity Enhancement of an External-Cavity Laser through Optical Injection. Opt. Lett. 2015, 40, 4416–4419. [Google Scholar] [CrossRef]
- Li, N.; Pan, W.; Xiang, S.; Yan, L.; Luo, B.; Zou, X.; Zhang, L.; Mu, P. Photonic Generation of Wideband Time-Delay-Signature-Eliminated Chaotic Signals Utilizing an Optically Injected Semiconductor Laser. IEEE J. Quantum Electron. 2012, 48, 1339–1345. [Google Scholar] [CrossRef]
- Hong, Y. Experimental Study of Time-Delay Signature of Chaos in Mutually Coupled Vertical-Cavity Surface-Emitting Lasers Subject to Polarization Optical Injection. Opt. Express 2013, 21, 17894–17903. [Google Scholar] [CrossRef]
- Wu, J.-G.; Wu, Z.-M.; Xia, G.-Q.; Feng, G.-Y. Evolution of Time Delay Signature of Chaos Generated in a Mutually Delay-Coupled Semiconductor Lasers System. Opt. Express 2012, 20, 1741–1753. [Google Scholar] [CrossRef]
- Mu, P.; Pan, W.; Yan, L.; Luo, B.; Li, N.; Xu, M. Experimental Evidence of Time-Delay Concealment in a DFB Laser with Dual-Chaotic Optical Injections. IEEE Photonics Technol. Lett. 2016, 28, 131–134. [Google Scholar] [CrossRef]
- Hong, Y.; Quirce, A.; Wang, B.; Ji, S.; Panajotov, K.; Spencer, P.S. Concealment of Chaos Time-Delay Signature in Three-Cascaded Vertical-Cavity Surface-Emitting Lasers. IEEE J. Quantum Electron. 2016, 52, 2400508. [Google Scholar] [CrossRef]
- Li, N.; Pan, W.; Xiang, S.; Yan, L.; Luo, B.; Zou, X. Loss of Time Delay Signature in Broadband Cascade-Coupled Semiconductor Lasers. IEEE Photonics Technol. Lett. 2012, 24, 2187–2190. [Google Scholar] [CrossRef]
- Maslov, A.V.; Ning, C.Z. Size Reduction of a Semiconductor Nanowire Laser by Using Metal Coating. In Proceedings of the Physics and Simulation of Optoelectronic Devices XV, San Jose, CA, USA, 20–25 January 2007; SPIE: Bellingham, WA, USA, 2007; Volume 6468, pp. 138–144. [Google Scholar]
- Ding, K.; Hill, M.T.; Liu, Z.C.; Yin, L.J.; van Veldhoven, P.J.; Ning, C.Z. Record Performance of Electrical Injection Sub-Wavelength Metallic-Cavity Semiconductor Lasers at Room Temperature. Opt. Express 2013, 21, 4728–4733. [Google Scholar] [CrossRef]
- Lorke, M.; Suhr, T.; Gregersen, N.; Mørk, J. Theory of Nanolaser Devices: Rate Equation Analysis versus Microscopic Theory. Phys. Rev. B 2013, 87, 205310. [Google Scholar] [CrossRef]
- Mork, J.; Lippi, G.L. Rate Equation Description of Quantum Noise in Nanolasers with Few Emitters. Appl. Phys. Lett. 2018, 112, 141103. [Google Scholar] [CrossRef]
- Suhr, T.; Gregersen, N.; Yvind, K.; Mørk, J. Modulation Response of nanoLEDs and Nanolasers Exploiting Purcell Enhanced Spontaneous Emission. Opt. Express 2010, 18, 11230–11241. [Google Scholar] [CrossRef]
- Ding, K.; Ning, C.Z. Metallic Subwavelength-Cavity Semiconductor Nanolasers. Light Sci. Appl. 2012, 1, e20. [Google Scholar] [CrossRef]
- Abdul Sattar, Z.; Shore, K.A. External Optical Feedback Effects in Semiconductor Nanolasers. IEEE J. Sel. Top. Quantum Electron. 2015, 21, 500–505. [Google Scholar] [CrossRef]
- Sattar, Z.A.; Shore, K.A. Dynamics of Nanolasers Subject to Optical Injection and Optical Feedback. In Proceedings of the Physics and Simulation of Optoelectronic Devices XXIV, San Francisco, CA, USA, 13–18 February 2016; SPIE: Bellingham, WA, USA, 2016; Volume 9742, pp. 38–47. [Google Scholar]
- Abdul Sattar, Z.; Ali Kamel, N.; Shore, K.A. Optical Injection Effects in Nanolasers. IEEE J. Quantum Electron. 2016, 52, 1200108. [Google Scholar] [CrossRef]
- Abdul Sattar, Z.; Shore, K.A. Phase Conjugate Feedback Effects in Nano-Lasers. IEEE J. Quantum Electron. 2016, 52, 1100108. [Google Scholar] [CrossRef]
- Han, H.; Shore, K.A. Dynamical Characteristics of Nano-Lasers Subject to Optical Injection and Phase Conjugate Feedback. IET Optoelectron. 2018, 12, 25–29. [Google Scholar] [CrossRef]
- Han, H.; Shore, K.A. Zero Crosstalk Regime Direct Modulation of Mutually Coupled Nanolasers. IEEE Photonics J. 2017, 9, 1503412. [Google Scholar] [CrossRef]
- Han, H.; Shore, K.A. Analysis of High-Frequency Oscillations in Mutually-Coupled Nano-Lasers. Opt. Express 2018, 26, 10013–10022. [Google Scholar] [CrossRef] [PubMed]
- Han, H.; Shore, K.A. Modulated Mutually Coupled Nano-Lasers. IEEE J. Quantum Electron. 2017, 53, 2000208. [Google Scholar] [CrossRef]
- Elsonbaty, A.; Hegazy, S.F.; Obayya, S.S.A. Simultaneous Concealment of Time Delay Signature in Chaotic Nanolaser with Hybrid Feedback. Opt. Lasers Eng. 2018, 107, 342–351. [Google Scholar] [CrossRef]
- Romeira, B.; Fiore, A. Purcell Effect in the Stimulated and Spontaneous Emission Rates of Nanoscale Semiconductor Lasers. IEEE J. Quantum Electron. 2018, 54, 2000412. [Google Scholar] [CrossRef]
- Wu, S.; Buckley, S.; Schaibley, J.R.; Feng, L.; Yan, J.; Mandrus, D.G.; Hatami, F.; Yao, W.; Vučković, J.; Majumdar, A.; et al. Monolayer Semiconductor Nanocavity Lasers with Ultralow Thresholds. Nature 2015, 520, 69–72. [Google Scholar] [CrossRef]
- Qu, Y.; Xiang, S.; Wang, Y.; Lin, L.; Wen, A.J.; Hao, Y. Concealment of Time Delay Signature of Chaotic Semiconductor Nanolasers with Double Chaotic Optical Injections. IEEE J. Quantum Electron. 2019, 55, 2000407. [Google Scholar] [CrossRef]
- Jiang, P.; Zhou, P.; Li, N.; Mu, P.; Li, X. Optically Injected Nanolasers for Time-Delay Signature Suppression and Communications. Opt. Express 2020, 28, 26421–26435. [Google Scholar] [CrossRef] [PubMed]
- Jiang, P.; Zhou, P.; Li, N.; Mu, P.; Li, X. Characterizing the Chaotic Dynamics of a Semiconductor Nanolaser Subjected to FBG Feedback. Opt. Express 2021, 29, 17815–17830. [Google Scholar] [CrossRef] [PubMed]







| Parameter | Description | Value |
|---|---|---|
| Confinement factor | 0.645 | |
| Carrier lifetime | 1 ns | |
| Photon lifetime | 0.36 ps | |
| tr | Injection delay | 0.05 ns |
| td | Feedback delay | 0.2 ns |
| Differential gain | ||
| Transparency carrier density | ||
| Gain saturation factor | ||
| Linewidth enhancement factor | 5 | |
| Volume of active region | ||
| Wavelength of NL | 1591 nm | |
| Laser facet reflectivity | 0.85 | |
| External facet power reflectivity | 0.95 | |
| Injection ratio | 0–0.1 | |
| n | Refractive index | 3.4 |
| L | Cavity length | |
| Q | Quality factor | 428 |
| f | Feedback coupling fraction | 0–0.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Guo, G.; Liu, X.; Hu, G.; Wang, K.; Mu, P. Dynamics and Concealment of Time-Delay Signature in Mutually Coupled Nano-Laser Chaotic Systems. Photonics 2023, 10, 1196. https://doi.org/10.3390/photonics10111196
Zhang X, Guo G, Liu X, Hu G, Wang K, Mu P. Dynamics and Concealment of Time-Delay Signature in Mutually Coupled Nano-Laser Chaotic Systems. Photonics. 2023; 10(11):1196. https://doi.org/10.3390/photonics10111196
Chicago/Turabian StyleZhang, Xueting, Gang Guo, Xintian Liu, Guosi Hu, Kun Wang, and Penghua Mu. 2023. "Dynamics and Concealment of Time-Delay Signature in Mutually Coupled Nano-Laser Chaotic Systems" Photonics 10, no. 11: 1196. https://doi.org/10.3390/photonics10111196
APA StyleZhang, X., Guo, G., Liu, X., Hu, G., Wang, K., & Mu, P. (2023). Dynamics and Concealment of Time-Delay Signature in Mutually Coupled Nano-Laser Chaotic Systems. Photonics, 10(11), 1196. https://doi.org/10.3390/photonics10111196




