Vortex Beam Transmission Compensation in Atmospheric Turbulence Using CycleGAN
Abstract
:1. Introduction
2. Atmospheric Turbulence Compensation Scheme
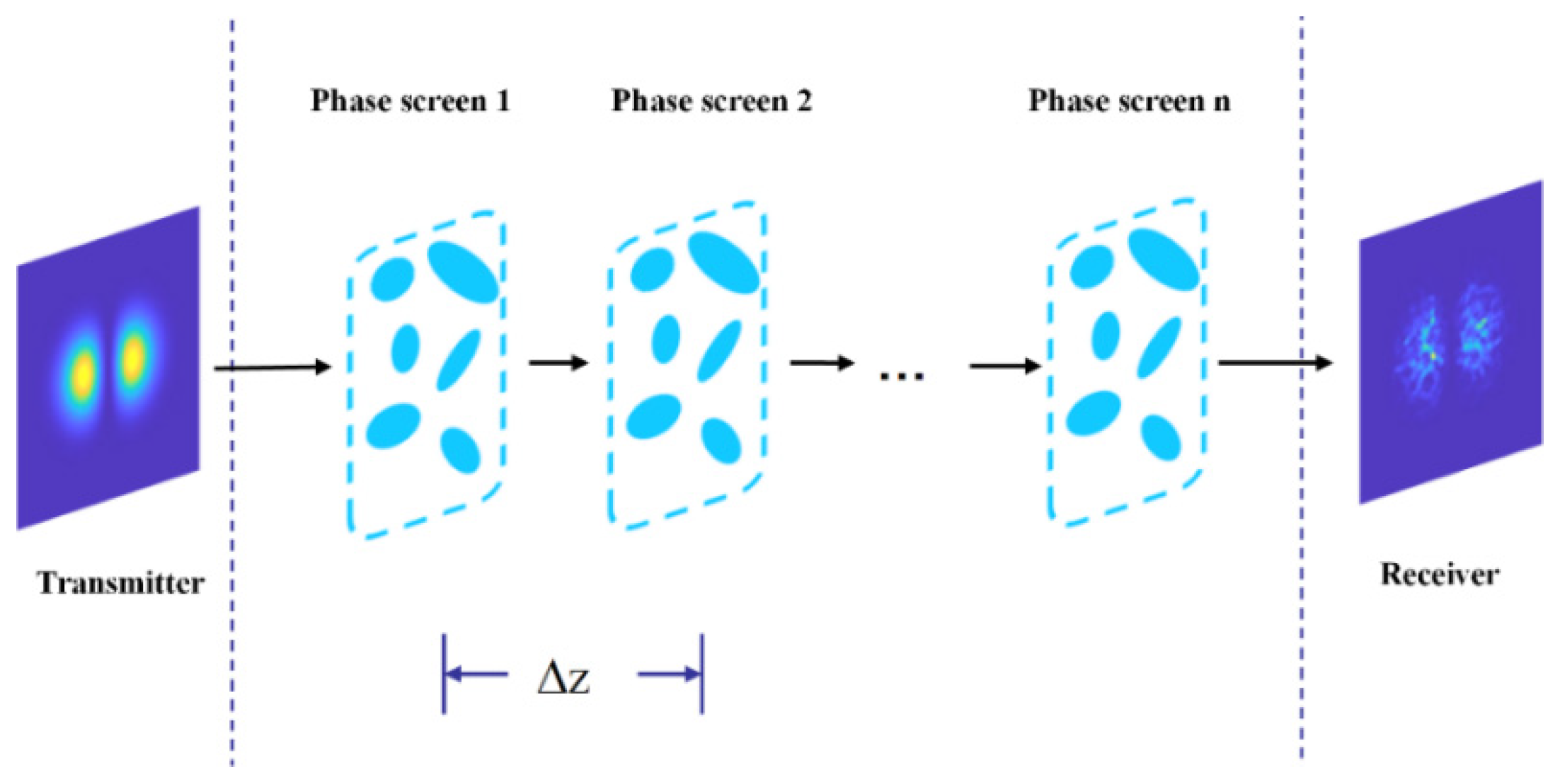
2.1. Atmospheric Turbulence Distortion Theory
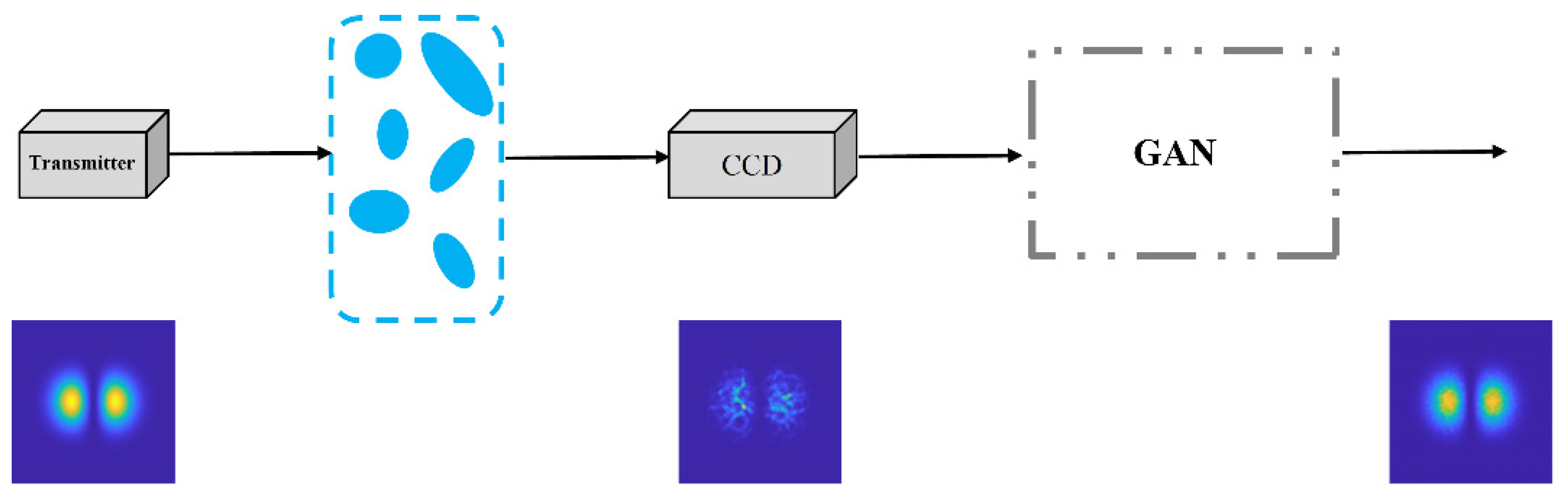
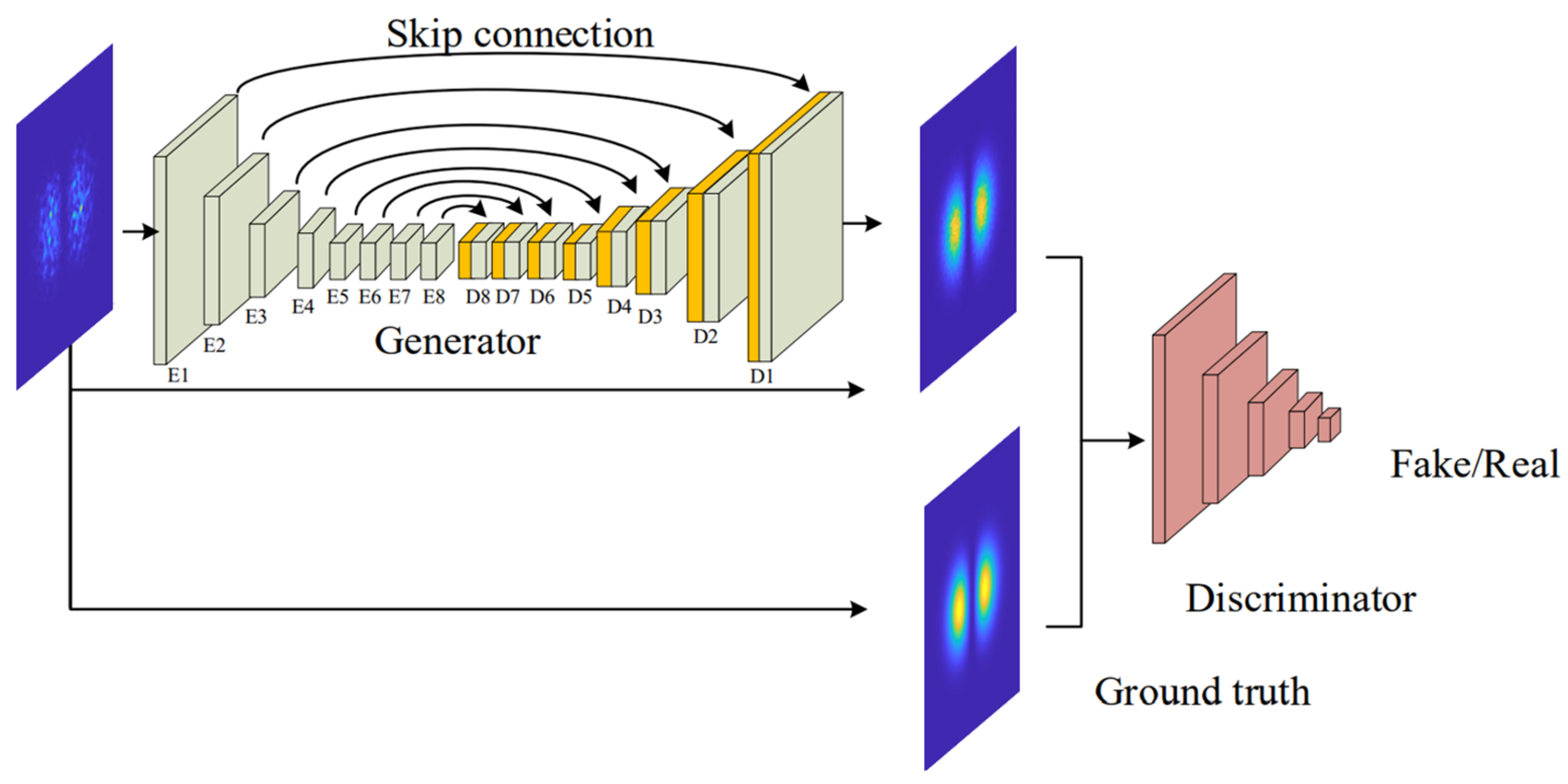
2.2. Vortex Beam Distortion Compensation Based on Pix2pix
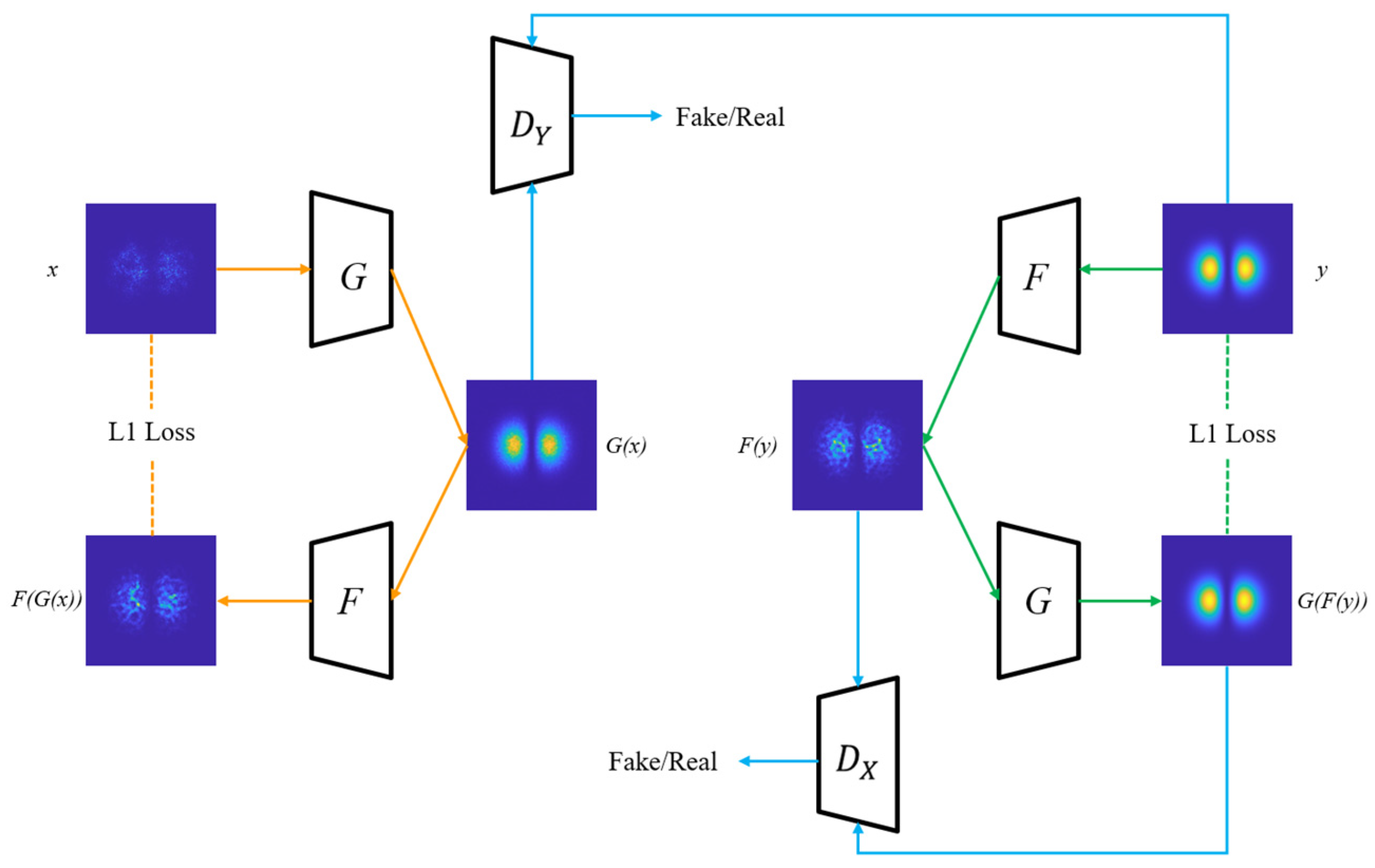
2.3. Vortex Beam Distortion Compensation Based on Improved CycleGAN
3. Results and Discussions
3.1. Evaluation Index of Turbulence Distortion Compensation
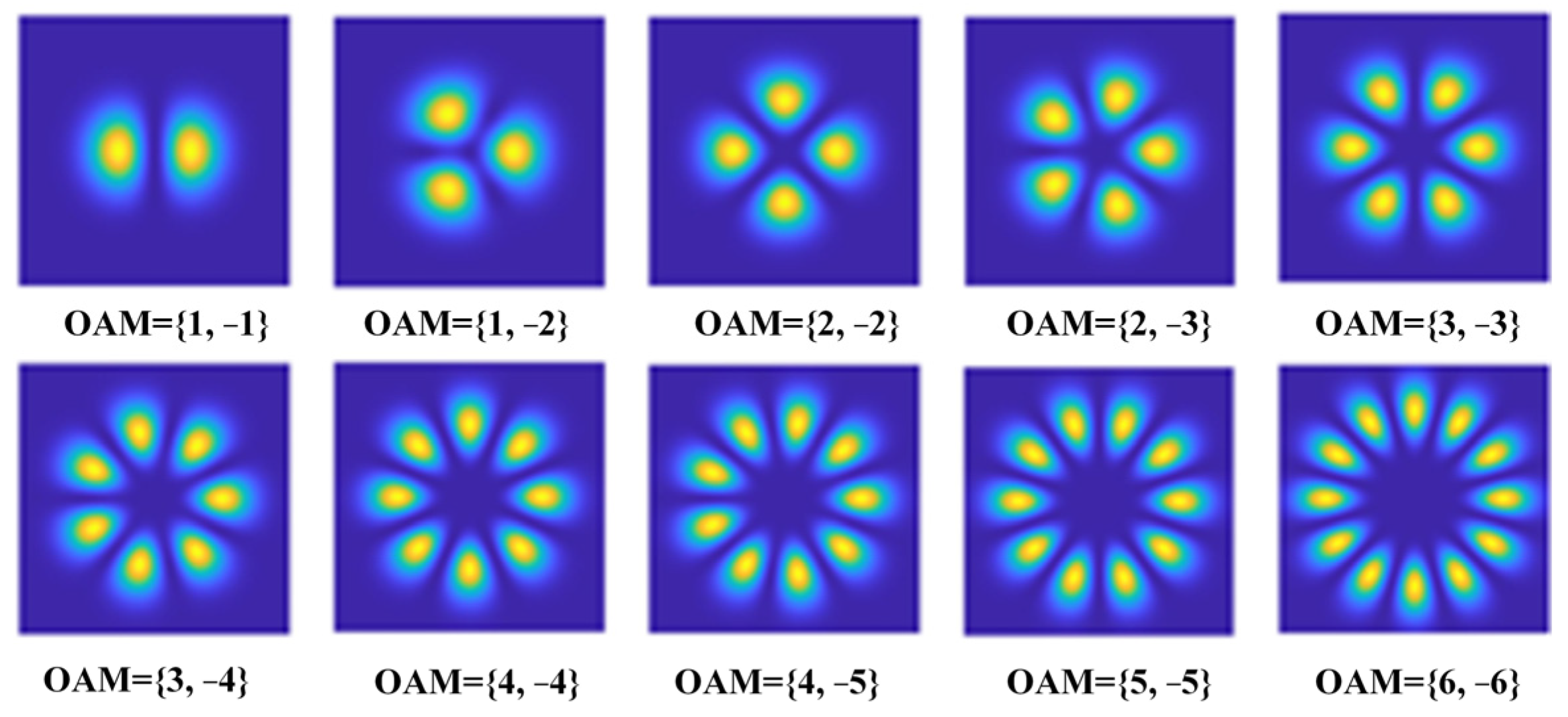
3.2. Simulation Dataset Construction
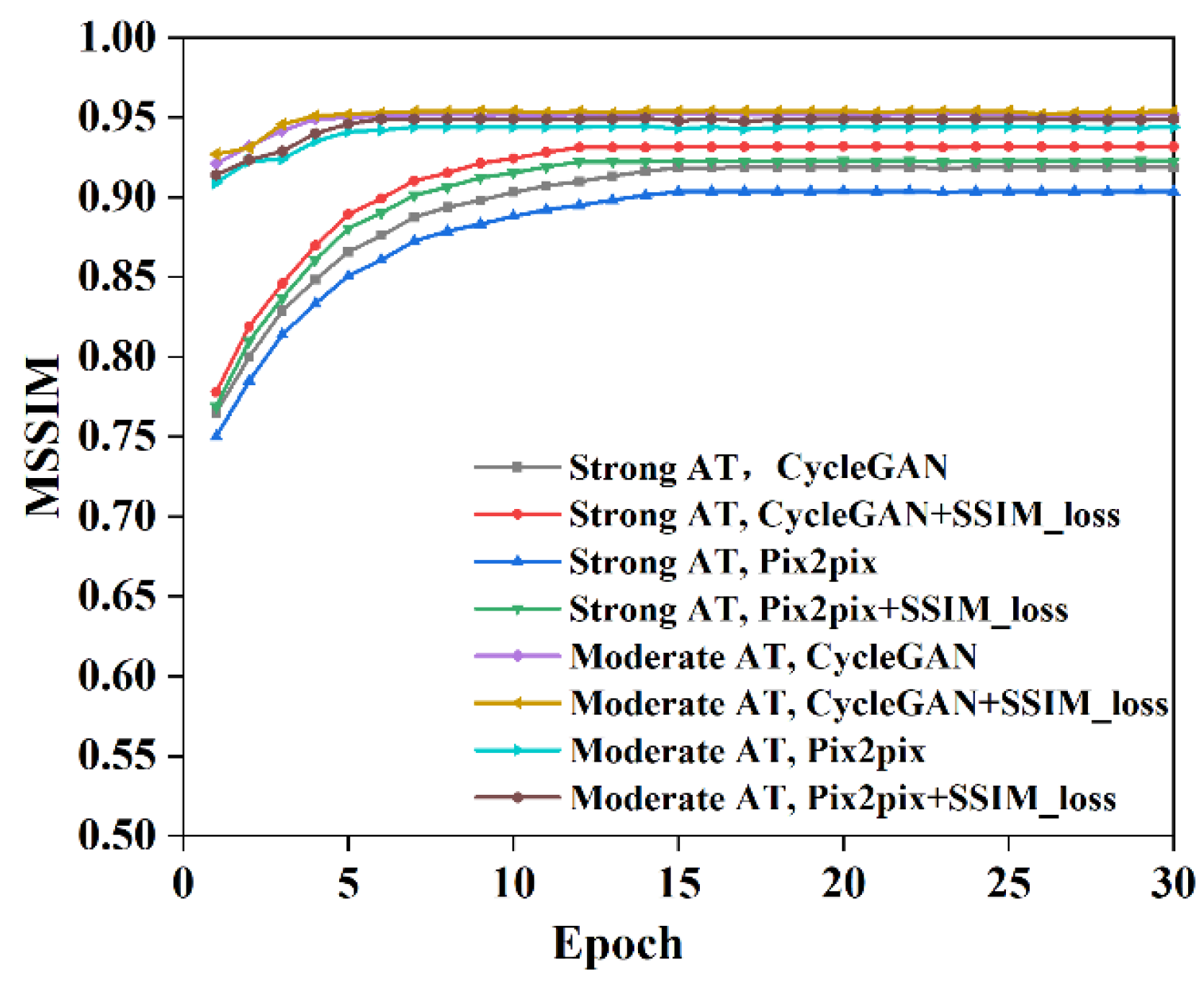
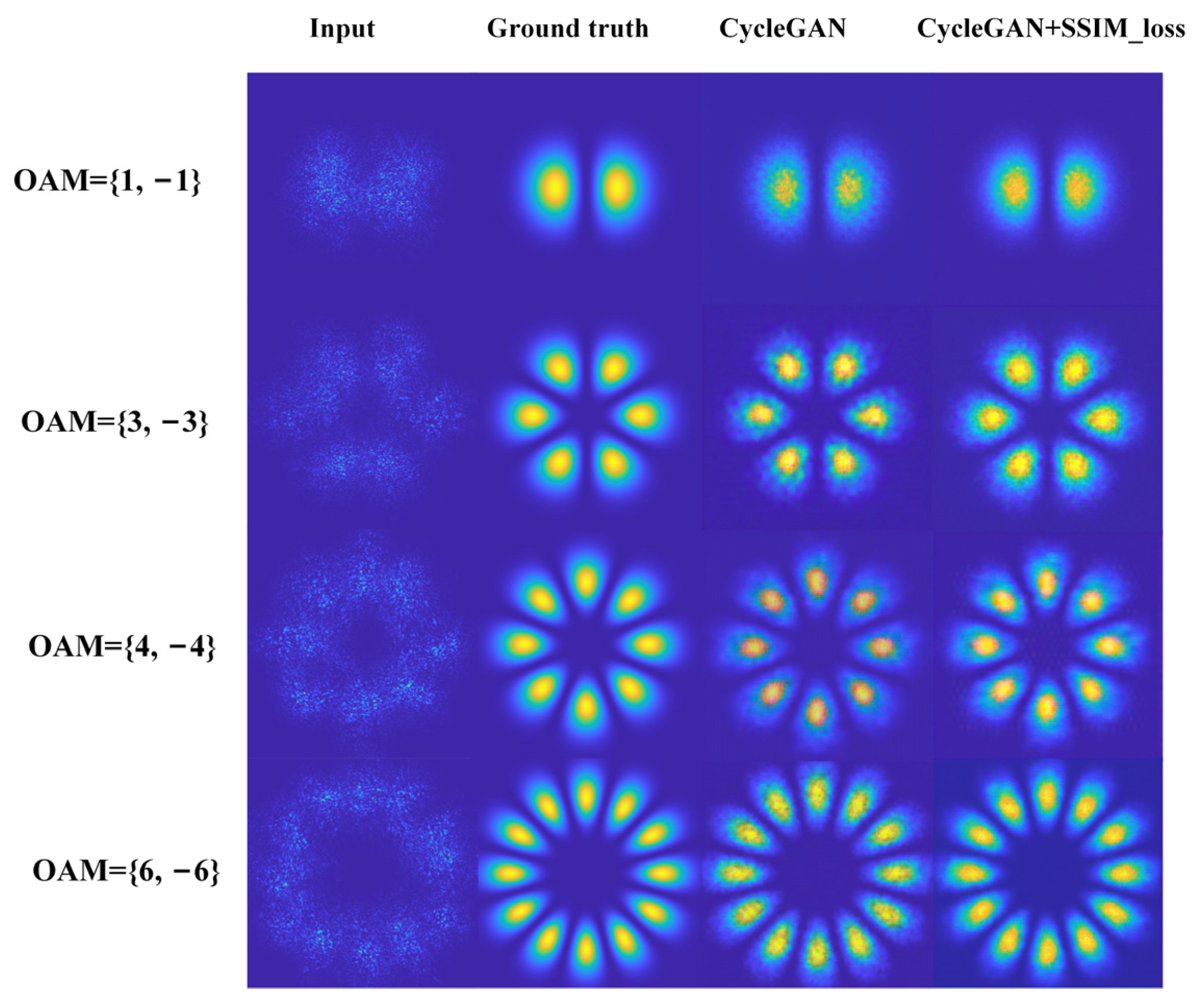
3.3. Analysis of Simulation Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, J.; Yang, J.; Fazal, I.; Ahmed, N.; Yan, Y.; Huang, H.; Ren, Y.; Yue, Y.; Dolinar, S.; Tur, M.; et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 2012, 6, 488–496. [Google Scholar] [CrossRef]
- Bozinovic, N.; Ramachandran, S. Terabit-scale orbital angular momentum mode division multiplexing in fibers. Science 2013, 340, 1545–1548. [Google Scholar] [CrossRef]
- Xie, G.; Li, L.; Ren, Y.; Huang, H.; Yan, Y.; Ahmed, N.; Zhao, Z.; Lavery, M.P.; Ashrafi, N.; Ashrafi, S.; et al. Performance metrics and design considerations for a free-space optical orbital-angular-momentum-multiplexed communication link. Optica 2015, 2, 357–365. [Google Scholar] [CrossRef]
- Willner, A. Communication with a twist. IEEE Spectr. 2016, 53, 34–39. [Google Scholar] [CrossRef]
- Ren, Y.; Wang, Z.; Liao, P.; Li, L.; Xie, G.; Huang, H.; Zhao, Z.; Yan, Y.; Ahmed, N.; Willner, A.; et al. Experimental characterization of a 400 Gbit/s orbital angular momentum multiplexed free-space optical link over 120 m. Opt. Lett. 2016, 41, 622–625. [Google Scholar] [CrossRef]
- Mair, A.; Vaziri, A.; Weihs, G.; Zeilinger, A. Entanglement of the orbital angular momentum states of photons. Nature 2001, 412, 313–316. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, Y.; Li, X.; Xu, Z.; Li, X.; Huang, L. A deep learning approach for trustworthy high-fidelity computational holographic orbital angular momentum communication. Appl. Phys. Lett. 2021, 119, 044104. [Google Scholar] [CrossRef]
- Paterson, C. Atmospheric turbulence and orbital angular momentum of single photos for optical communication. Phys. Rev. Lett. 2005, 94, 3901–3904. [Google Scholar] [CrossRef]
- Gopaul, C.; Andrews, R. The effect of atmospheric turbulence on entangled orbital angular momentum states. New J. Phy. 2007, 9, 94. [Google Scholar] [CrossRef]
- Tyler, G.; Boyd, R. Influence of atmospheric turbulence on the propagation of quantum states of light carrying orbital angular momentum. Opt. Lett. 2009, 34, 142–144. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, H.; Zhang, X.; Li, H.; Xi, L. Transmission Characteristics of Adaptive Compensation for Joint Atmospheric Turbulence Effects on the OAM-Based Wireless Communication System. Appl. Sci. 2019, 9, 901. [Google Scholar] [CrossRef]
- Bulygin, A.D.; Geints, Y.E.; Geints, I.Y. Vortex Beam in a Turbulent Kerr Medium for Atmospheric Communication. Photonics 2023, 10, 856. [Google Scholar] [CrossRef]
- Yang, P.; Xu, B.; Jiang, W.; Chen, S. Study of a genetic algorithm used in an adaptive optical system. Acta Opt. Sin. 2007, 27, 1628. [Google Scholar] [CrossRef]
- Zhao, S.; Leach, J.; Zheng, B. Correction effect of Shark-Hartmann algorithm on turbulence aberrations for free space optical communications using orbital angular momentum. In Proceedings of the 2010 IEEE 12th International Conference on Communication Technology, Nanjing, China, 11–14 November 2010; pp. 580–583. [Google Scholar] [CrossRef]
- Yu, Z.; Ma, H.; Du, S. Simulated annealing algorithm applied in adaptive near field beam shaping. Holography, Diffractive Optics, and Applications IV. SPIE 2010, 7848, 154–161. [Google Scholar] [CrossRef]
- Ren, Y.; Huang, H.; Yang, J.; Yan, Y.; Ahmed, N.; Yue, Y.; Willner, A.; Birnbaum, K.; Choi, J.; Erkmen, B.; et al. Correction of phase distortion of an OAM mode using GS algorithm based phase retrieval. In Proceedings of the 2012 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 6–11 May 2012; pp. 1–2. [Google Scholar]
- Ren, Y.; Xie, G.; Huang, H.; Bao, Y.; Ahmed, N.; Lavery, M.; Erkmen, B.; Dolinar, S.; Tur, M.; Neifeld, M.; et al. Adaptive optics compensation of multiple orbital angular momentum beams propagating through emulated atmospheric turbulence. Opt. Lett. 2014, 39, 2845–2848. [Google Scholar] [CrossRef]
- Xie, G.; Ren, Y.; Huang, H.; Lavery, M.; Ahmed, N.; Yan, Y.; Bao, C.; Li, L.; Zhao, Z.; Cao, Y.; et al. Phase correction for a distorted orbital angular momentum beam using a Zernike polynomials-based stochastic-parallel-gradient-descent algorithm. Opt. Lett. 2015, 40, 1197–1200. [Google Scholar] [CrossRef]
- Fu, S.; Zhang, S.; Wang, T.; Gao, C. Pre-turbulence compensation of orbital angular momentum beams based on a probe and the Gerchberg–Saxton algorithm. Opt. Lett. 2016, 41, 3185–3188. [Google Scholar] [CrossRef]
- Li, J.; Zhang, M.; Wang, D.; Wu, S.; Zhan, Y. Joint atmospheric turbulence detection and adaptive demodulation technique using the CNN for the OAM-FSO communication. Opt. Express 2018, 26, 10494–10508. [Google Scholar] [CrossRef]
- Tian, Q.; Lu, C.; Liu, B.; Zhu, L.; Pan, X.; Zhang, Q.; Yang, L.; Tian, F.; Xin, X. DNN-based aberration correction in a wavefront sensorless adaptive optics system. Opt. Express 2019, 27, 10765–10776. [Google Scholar] [CrossRef]
- Liu, J.; Wang, P.; Zhang, X.; He, Y.; Zhou, X.; Ye, H.; Li, Y.; Xu, S.; Chen, S.; Fan, D. Deep learning based atmospheric turbulence compensation for orbital angular momentum beam distortion and communication. Opt. Express 2019, 27, 16671–16688. [Google Scholar] [CrossRef]
- Zhai, Y.; Fu, S.; Zhang, J.; Liu, X.; Zhou, H.; Gao, C. Turbulence aberration correction for vector vortex beams using deep neural networks on experimental data. Opt. Express 2020, 28, 7515–7527. [Google Scholar] [CrossRef]
- Hao, Y.; Zhao, L.; Huang, T.; Wu, Y.; Jiang, T.; Wei, Z.; Deng, D.; Luo, A.; Liu, H. High-accuracy recognition of orbital angular momentum modes propagated in atmospheric turbulences based on deep learning. IEEE Access 2020, 8, 159542–159551. [Google Scholar] [CrossRef]
- Ke, X.; Chen, M. Recognition of orbital angular momentum vortex beam based on convolutional neural network. Microw. Opt. Technol. Lett. 2021, 63, 1960–1964. [Google Scholar] [CrossRef]
- Zhou, H.; Pan, Z.; Dedo, M.I.; Guo, Z.Y. High-efficiency and high-precision identification of transmitting orbital angular momentum modes in atmospheric turbulence based on an improved convolutional neural network. J. Opt. 2021, 23, 065701. [Google Scholar] [CrossRef]
- Xiang, Y.; Zeng, L.; Wu, M.; Luo, Z.; Ke, Y. Deep learning recognition of orbital angular momentum modes over atmospheric turbulence channels assisted by vortex phase modulation. IEEE Photonics J. 2022, 14, 8554909. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Fraley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Proc. Adv. Neural Inf. Process. Syst. 2014, 2672–2680. [Google Scholar] [CrossRef]
- Creswell, A.; White, T.; Dumoulin, V.; Arulkumaran, K.; Sengupta, B.; Bharath, A. Generative adversarial networks: An overview. IEEE Signal Proc. Mag. 2018, 35, 53–65. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farly, D.; Ozair, S.; Courvile, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Isola, P.; Zhu, J.; Zhou, T.; Efros, A. Image-to-image translation with conditional adversarial networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1125–1134. [Google Scholar] [CrossRef]
- Zhu, J.; Park, T.; Isola, P.; Efros, A. Unpaired image-to-image translation using cycle-consistent adversarial networks. In Proceedings of the 2017 IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2223–2232. [Google Scholar] [CrossRef]
- Kolmogorov, A. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1991, 434, 9–13. [Google Scholar] [CrossRef]
- Tatarskii, V.I. Theory of Fluctuation Phenomena during Propagation of Waves of a Turbulent Atmosphere; Nauka: Moscow, Russia, 1959. [Google Scholar]
- Andrews, L. An analytical model for the refractive index power spectrum and its application to optical scintillations in the atmosphere. J. Mod. Opt. 1992, 39, 1849–1853. [Google Scholar] [CrossRef]
- Martin, J.; Flatté, S. Intensity images and statistics from numerical simulation of wave propagation in 3-D random media. Appl. Opt. 1988, 27, 2111–2126. [Google Scholar] [CrossRef]
- Roddier, N. Atmospheric wavefront simulation using Zernike polynomials. Opt. Eng. 1990, 29, 1174–1180. [Google Scholar] [CrossRef]
- McGlamery, B. Restoration of turbulence-degraded images. J. Opt. Soc. Am. A 1967, 57, 293–297. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, X.; Lin, M.; Sun, J. Shufflenet: An extremely efficient convolutional neural network for mobile devices. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 6848–6856. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.; Sheikh, H.; Simoncelli, E. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]



| Distortion Compensation Network | MSSIM (Medium Turbulence) | MSSIM (Strong Turbulence) |
|---|---|---|
| Pix2pix | 0.944 | 0.903 |
| Pix2pix + SSIM_Loss | 0.949 | 0.922 |
| CycleGAN | 0.952 | 0.918 |
| CycleGAN + SSIM_Loss | 0.954 | 0.931 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, T.; Zhang, Y.; Wu, J.; Wu, Z. Vortex Beam Transmission Compensation in Atmospheric Turbulence Using CycleGAN. Photonics 2023, 10, 1182. https://doi.org/10.3390/photonics10111182
Qu T, Zhang Y, Wu J, Wu Z. Vortex Beam Transmission Compensation in Atmospheric Turbulence Using CycleGAN. Photonics. 2023; 10(11):1182. https://doi.org/10.3390/photonics10111182
Chicago/Turabian StyleQu, Tan, Yan Zhang, Jiaji Wu, and Zhensen Wu. 2023. "Vortex Beam Transmission Compensation in Atmospheric Turbulence Using CycleGAN" Photonics 10, no. 11: 1182. https://doi.org/10.3390/photonics10111182
APA StyleQu, T., Zhang, Y., Wu, J., & Wu, Z. (2023). Vortex Beam Transmission Compensation in Atmospheric Turbulence Using CycleGAN. Photonics, 10(11), 1182. https://doi.org/10.3390/photonics10111182






