A Simplified Volterra Equalizer Based on System Characteristics for Direct Modulation Laser (DML)-Based Intensity Modulation and Direct Detection (IM/DD) Transmission Systems
Abstract
:1. Introduction
2. Principle
2.1. The Second-Order Beating Terms of DML/DD Systems
2.2. Simplified VNLE
2.3. Comparison of Different Filters
2.3.1. Traditional VNLE
2.3.2. DP-VNLE
2.3.3. Proposed Simplified VNLE
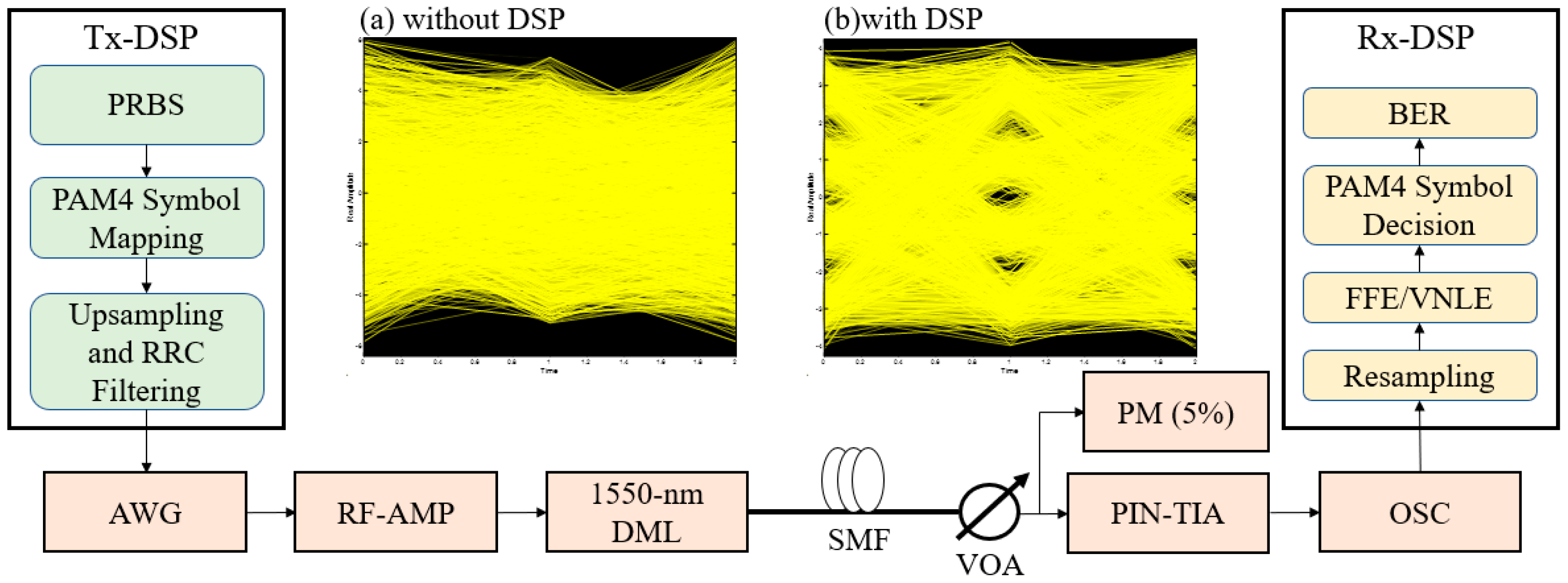
3. Experimental Setup
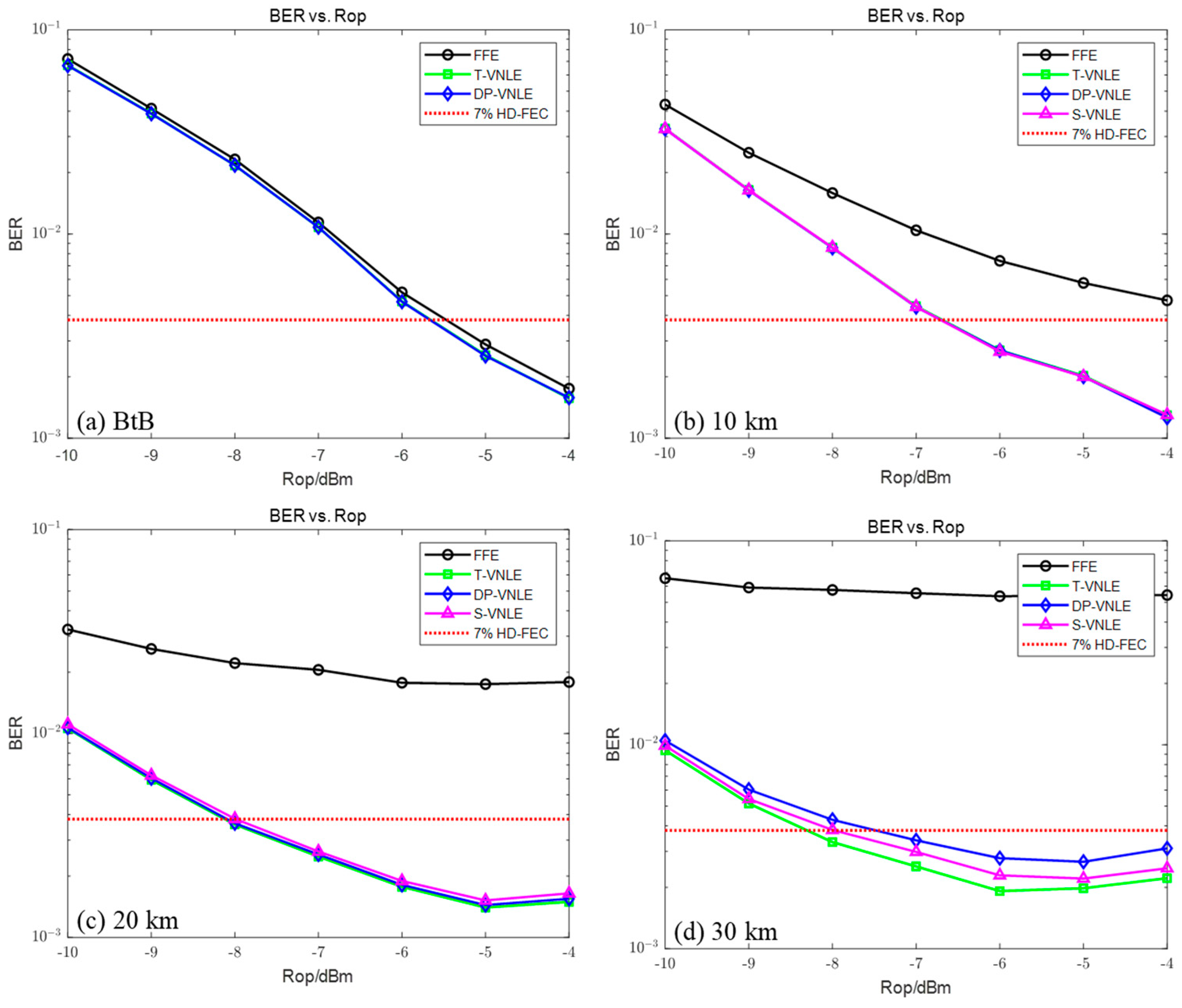
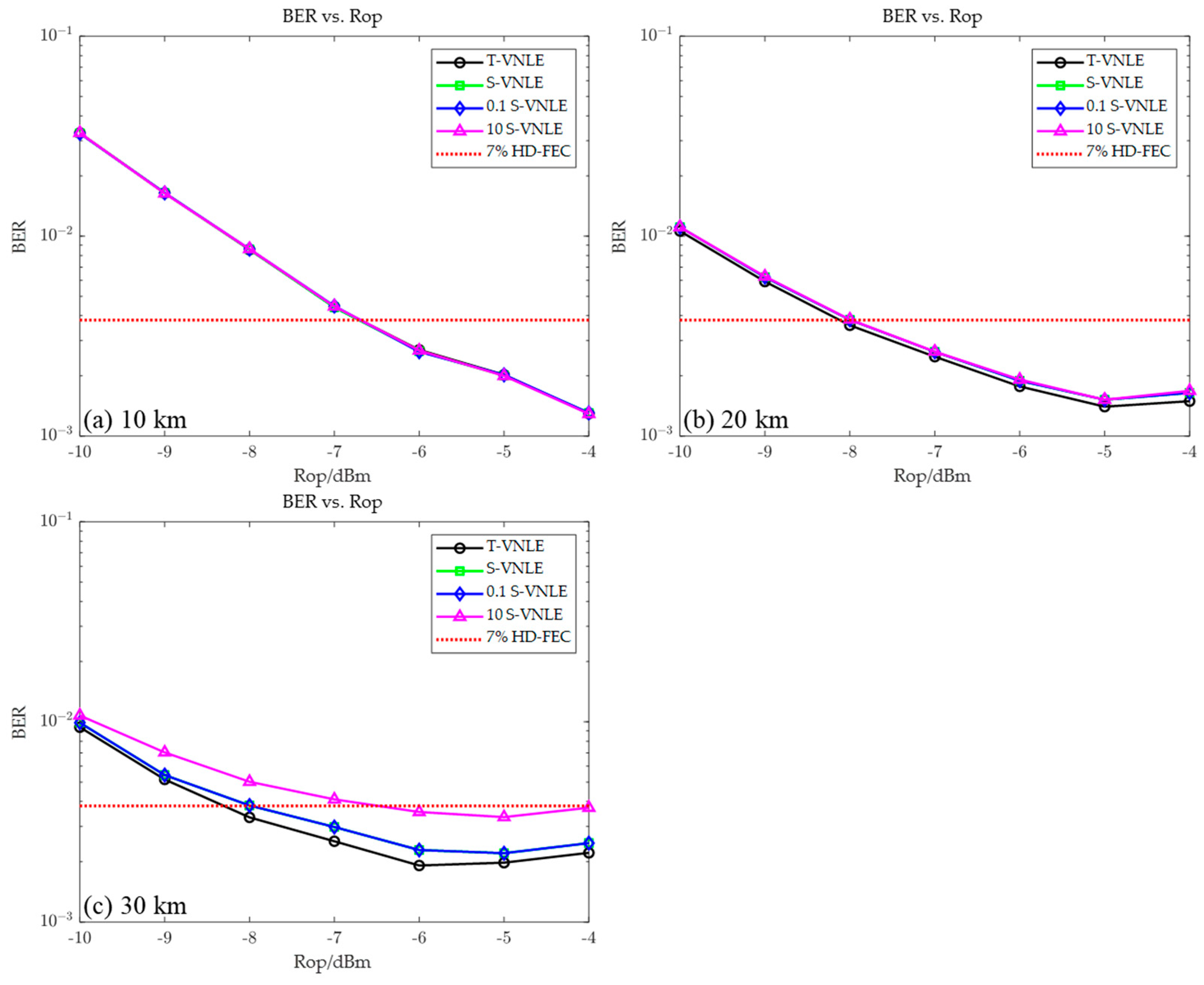
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xin, H.; Zhang, K.; Li, L.; He, H.; Hu, W. 50 Gbps PAM-4 Over Up to 80-km Transmission With C-Band DML Enabled by Post-Equalizer. IEEE Photon-Technol. Lett. 2020, 32, 643–646. [Google Scholar] [CrossRef]
- Fu, Y.; Kong, D.; Bi, M.; Xin, H.; Jia, S.; Zhang, K.; Hu, W.; Hu, H. Computationally efficient 104 Gb/s PWL-Volterra equalized 2D-TCM-PAM8 in dispersion unmanaged DML-DD system. Opt. Express 2020, 28, 7070–7079. [Google Scholar] [CrossRef] [PubMed]
- Fu, Y.; Kong, D.; Xin, H.; Jia, S.; Zhang, K.; Bi, M.; Hu, W.; Hu, H. Piecewise Linear Equalizer for DML Based PAM-4 Signal Transmission Over a Dispersion Uncompensated Link. J. Light. Technol. 2019, 38, 654–660. [Google Scholar] [CrossRef]
- Plant, D.V.; Morsy-Osman, M.; Chagnon, M. Optical Communication Systems for Datacenter Networks. In Optical Fiber Communication Conference; OSA Technical Digest (online); Optica Publishing Group: Washington, DC, USA, 2017; p. W3B.1. [Google Scholar]
- Chang, F.; Bhoja, S. New Paradigm Shift to PAM4 Signalling at 100/400G for Cloud Data Centers: A Performance Review. In Proceedings of the 2017 European Conference on Optical Communication (ECOC), Gothenburg, Sweden, 17–21 September 2017; pp. 1–3. [Google Scholar] [CrossRef]
- Zhang, K.; Zhuge, Q.; Xin, H.; Hu, W.; Plant, D.V. Performance comparison of DML, EML and MZM in dispersion-unmanaged short reach transmissions with digital signal processing. Opt. Express 2018, 26, 34288–34304. [Google Scholar] [CrossRef] [PubMed]
- He, P.; Sun, M.; Li, W.; Li, N.; Feng, Z.; Zhang, H.; Yao, C.; Sun, L.; He, Z.; Zhu, H.; et al. Demonstration of 112Gb/s PAM-4/6 Transmission Using Low-Complexity Volterra-DFE. In Proceedings of the 2022 Asia Communications and Photonics Conference (ACP), presented at Asia Communications and Photonics Conference, Shenzhen, China, 5–8 November 2022; pp. 919–923, ACP2022. [Google Scholar]
- Gao, F.; Zhou, S.; Li, X.; Fu, S.; Deng, L.; Tang, M.; Liu, D.; Yang, Q. 2 × 64 Gb/s PAM-4 transmission over 70 km SSMF using O-band 18G-class directly modulated lasers (DMLs). Opt. Express 2017, 25, 7230–7237. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Zhuge, Q.; Xin, H.; Xing, Z.; Xiang, M.; Fan, S.; Yi, L.; Hu, W.; Plant, D.V. Demonstration of 50Gb/s/λ Symmetric PAM4 TDM-PON with 10G-Class Optics and DSP-Free ONUs in the O-Band; Optical Fiber Communications Conference and Exposition (OFC): San Diego, CA, USA, 2018; pp. 1–3. [Google Scholar]
- Gao, Y.; Cartledge, J.C.; Yam, S.S.; Rezania, A.; Matsui, Y. 112 Gb/s PAM-4 Using a Directly Modulated Laser with Linear Pre-Compensation and Nonlinear Post-Compensation. In Proceedings of the ECOC 2016 42nd European Conference on Optical Communication, Dusseldorf, Germany, 18–22 September 2016; pp. 1–3. [Google Scholar]
- Bergmann, E.; Kuo, C.; Huang, S. Dispersion-induced composite second-order distortion at 1.5 mu m. IEEE Photon-Technol. Lett. 1991, 3, 59–61. [Google Scholar] [CrossRef] [PubMed]
- Kim, B.G.; Bae, S.H.; Kim, H.; Chung, Y.C. DSP-based CSO cancellation technique for RoF transmission system im-plemented by using directly modulated laser. Opt. Express 2017, 25, 12152–12160. [Google Scholar] [CrossRef] [PubMed]
- Wei, C.-C.; Cheng, H.-L.; Huang, W.-X. On Adiabatic Chirp and Compensation for Nonlinear Distortion in DML-Based OFDM Transmission. J. Light. Technol. 2018, 36, 3502–3513. [Google Scholar] [CrossRef]
- Yan, W.; Liu, B.; Li, L.; Tao, Z.; Takahara, T.; Rasmussen, J.C. Nonlinear Distortion and DSP-based Compensation in Metro and Access Networks using Discrete Multi-tone. In European Conference and Exhibition on Optical Communication; OSA Technical Digest (online); Optica Publishing Group: Washington, DC, USA, 2012. [Google Scholar]
- Stojanovic, N.; Karinou, F.; Qiang, Z.; Prodaniuc, C. Volterra and Wiener Equalizers for Short-Reach 100G PAM-4 Applications. J. Light. Technol. 2017, 35, 4583–4594. [Google Scholar] [CrossRef]
- Xia, C.; Rosenkranz, W. Nonlinear Electrical Equalization for Different Modulation Formats With Optical Filtering. J. Light. Technol. 2007, 25, 996–1001. [Google Scholar] [CrossRef]
- Yu, Y.; Choi, M.R.; Bo, T.; He, Z.; Che, Y.; Kim, H. Low-Complexity Second-Order Volterra Equalizer for DML-Based IM/DD Transmission System. J. Light. Technol. 2019, 38, 1735–1746. [Google Scholar] [CrossRef]
- Reza, A.G.; Rhee, J.-K.K. Blind nonlinearity mitigation of 10G DMLs using sparse Volterra equalizer in IM/DD PAM-4 transmission systems. Opt. Fiber Technol. 2020, 59, 102322. [Google Scholar] [CrossRef]
- Diamantopoulos, N.-P.; Nishi, H.; Kobayashi, W.; Takeda, K.; Kakitsuka, T.; Matsuo, S. On the Complexity Reduction of the Second-Order Volterra Nonlinear Equalizer for IM/DD Systems. J. Light. Technol. 2018, 37, 1214–1224. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Y.; Li, W.; Mei, M.; Feng, Z.; Wu, C.; Sun, L.; Zhu, H.; Zhao, X. 106 Gbit/s PAM4 Transmission Employing a 15 GHz Directly Modulated Laser. In Proceedings of the 2021 Asia Communications and Photonics Conference (ACP), Shanghai, China, 24–27 October 2021. [Google Scholar]
- Yu, Y.; Choi, M.R.; Bo, T.; Che, Y.; Kim, D.; Kim, H. Nonlinear Equalizer Based on Absolute Operation for IM/DD System Using DML. IEEE Photon- Technol. Lett. 2020, 32, 426–429. [Google Scholar] [CrossRef]
- Batista, E.; Seara, R. On the performance of adaptive pruned Volterra filters. Signal Process. 2013, 93, 1909–1920. [Google Scholar] [CrossRef]
- Savory, S.J. Digital filters for coherent optical receivers. Opt. Express 2008, 16, 804–817. [Google Scholar] [CrossRef] [PubMed]
- Xu, T.; Jacobsen, G.; Popov, S.; Li, J.; Vanin, E.; Wang, K.; Friberg, A.T.; Zhang, Y. Chromatic dispersion compensation in coherent transmission system using digital filters. Opt. Express 2010, 18, 16243–16257. [Google Scholar] [CrossRef] [PubMed]
- Raz, G.; van Veen, B. Baseband Volterra filters for implementing carrier based nonlinearities. IEEE Trans. Signal Process. 1998, 46, 103–114. [Google Scholar] [CrossRef]

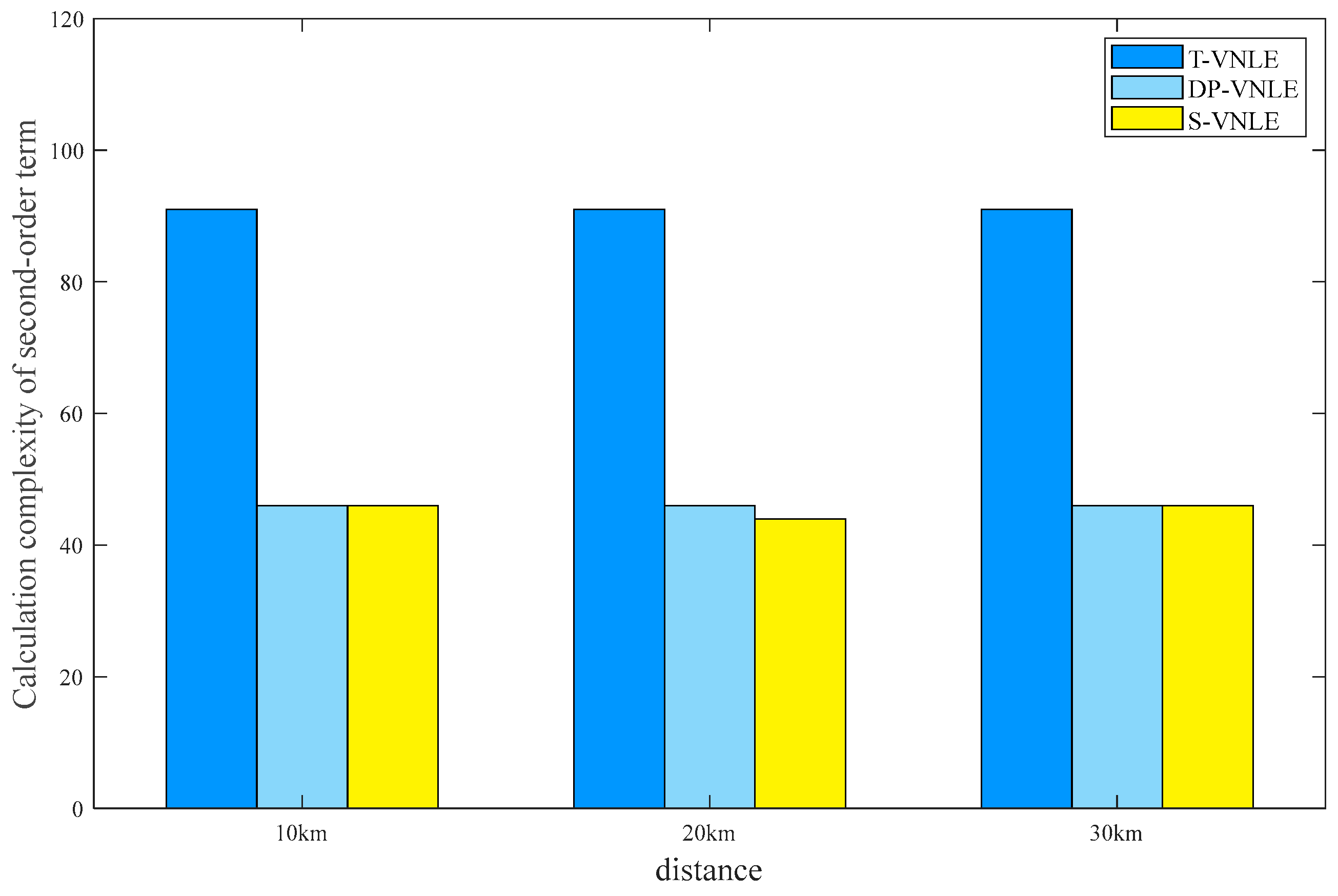
| Distance | T-VNLE | S-VNLE | 0.1S-VNLE | 10S-VNLE |
|---|---|---|---|---|
| 10 km | 91 | 46 | 43 | 58 |
| 20 km | 91 | 44 | 44 | 43 |
| 30 km | 91 | 46 | 46 | 35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Z.; Li, N.; Li, W.; He, P.; Luo, M.; Hu, Q.; Huang, L.; Jiang, Y. A Simplified Volterra Equalizer Based on System Characteristics for Direct Modulation Laser (DML)-Based Intensity Modulation and Direct Detection (IM/DD) Transmission Systems. Photonics 2023, 10, 1174. https://doi.org/10.3390/photonics10101174
Feng Z, Li N, Li W, He P, Luo M, Hu Q, Huang L, Jiang Y. A Simplified Volterra Equalizer Based on System Characteristics for Direct Modulation Laser (DML)-Based Intensity Modulation and Direct Detection (IM/DD) Transmission Systems. Photonics. 2023; 10(10):1174. https://doi.org/10.3390/photonics10101174
Chicago/Turabian StyleFeng, Zhongshuai, Na Li, Wei Li, Peili He, Ming Luo, Qianggao Hu, Liyan Huang, and Yi Jiang. 2023. "A Simplified Volterra Equalizer Based on System Characteristics for Direct Modulation Laser (DML)-Based Intensity Modulation and Direct Detection (IM/DD) Transmission Systems" Photonics 10, no. 10: 1174. https://doi.org/10.3390/photonics10101174
APA StyleFeng, Z., Li, N., Li, W., He, P., Luo, M., Hu, Q., Huang, L., & Jiang, Y. (2023). A Simplified Volterra Equalizer Based on System Characteristics for Direct Modulation Laser (DML)-Based Intensity Modulation and Direct Detection (IM/DD) Transmission Systems. Photonics, 10(10), 1174. https://doi.org/10.3390/photonics10101174





