Influence of High-Order Twisting Phases on Polarization States and Optical Angular Momentum of a Vector Light Field

Abstract

This study investigates the influence of high-order twisting phases on polarization states and optical angular momentum of a vector light field with locally linear polarization and a hybrid state of polarization (SoP). The twisted vector optical field (TVOF) is experimentally generated based on the orthogonal polarization bases with high-order twisting phases. The initial SoP of a TVOF modulated by the high-order twisting phase possesses various symmetric distributions. The propagation properties of a high-order TVOF with locally linear polarization and hybrid SoP are explored, including the intensity compression, expansion, and conversion between the linear and circular polarization components. In particular, orbital angular momentum (OAM) appears in a high-order TVOF during propagation where no OAM exists in the initial field. The variation of OAM distribution in cross-section becomes more frequent with the increase of the twisting phase order. In addition, a non-symmetric OAM distribution appears in a non-isotropic TVOF, leading to the rotation of the beam around the propagation axis during propagation. The optical energy flow distribution of a high-order TVOF provides a more profound understanding of the propagation dynamics of high-order TVOF. These results provide a new approach for optical field manipulation in a high-order TVOF.

1. Introduction

In recent years, vector optical fields have attracted significant attention due to their unique properties and wide-ranging applications in various areas, including optical communications [1], imaging [2], and beam manipulation. These vector fields can possess characteristics such as complex spatial structures, nonuniform polarization distribution [3], and novel phase distributions [4], providing a new way to precisely manipulate light [5]. The concept of phase modulation in vector optical fields originates from the study of wave optics and optical phase engineering. Early investigations focused on controlling the spatial phase distribution [6,7] of light waves, leading to the development of techniques such as spatial light modulators (SLMs) [8] and holography [9,10]. These methods allowed for the precise manipulation of phase profiles, enabling the generation of structured light beams with tailored phase distributions [11]. Building upon these foundational works, researchers began to explore the effect of spatial phase modulation on the scalar beam and the vector optical fields. Many novel properties have been demonstrated with the impact of different phase distributions on a vector optical field [12,13,14,15].

In 1993, Simon and Mukunda discovered an inseparable quadratic phase [16], termed the twist phase, while searching for rotationally invariant partially coherent light fields. This in turn led to the study of the effect of this phase on different light fields in different media [17,18,19]. This twist phase can induce beam rotation during transmission [20]. Research indicated that the twist phase can only exist in partially coherent light fields due to constraints imposed by non-negative-definiteness conditions [21]. In 2019, a new separable twisting phase was proposed [22], introducing the twist phase into fully coherent beams. This provided a new method for generating and measuring scalar vortex beams. In 2021, a high-order twisting phase (cross-phase) was introduced into Bessel–Gaussian beams [23], offering a novel approach to shaping perfect optical vortices. Recently, we introduced the twisting phase into vector beams, revealing that vector vortex beams can be dynamically manipulated using the twisting phase [24]. Nevertheless, to date, the investigation of the effect of high-order twisting phases on a vector light field still needs to be explored.

In this study, we investigated the properties of vector optical fields with high-order twisting phases. The twisted vector optical field (TVOF) is experimentally generated with high-order twisting phases. The effect of a high-order twisting phase on the initial polarization distribution of vector beams was analyzed. In particular, the evolution of polarization and orbital angular momentum in vector optical fields with high-order twisting phases during propagation is demonstrated. The optical energy flow distribution of a high-order TVOF provides a more profound understanding of the propagation dynamics of high-order TVOF. These results also contribute to the deeper understanding and utilization of twisted vector optical fields and shed light on the origin and development of the corresponding research area, such as optical trapping, high-capacity optical communications, and the generation of structured light for advanced imaging and manipulation techniques.

2. Experiment Generation of a High-Order TVOF

The form of the general twisting phase δ (x, y) in Cartesian coordinates (x, y) is

$$\delta \left(x,y\right)=u{x}^p{y}^q$$

(1)

where u is the twisted strength of the twisting phase. The exponents p and q are both positive integers. The sum p + q is referred to as the order of the twisted phase. When both exponents are equal to 1 (resulting in a sum of 2), it is termed a low-order twisting phase, as shown in Figure 1a. Conversely, when the sum is greater than 2 (i.e., p + q > 2), it is referred to as a high-order twisting phase, as shown in Figure 1b,c.

The TVOF at the source plane with a twisting phase can be expressed as follows:

$$E\left(x,y\right)=\exp \left(-x^2/{\sigma }_x^2\right)\exp \left(-y^2/{\sigma }_y^2\right)·\left[\exp \left(\mathrm{i}\delta \right)·{\mathit{e}}_1+\exp \left(-\mathrm{i}\delta \right)\cdot {\mathit{e}}_2\right]$$

(2)

where ${\sigma }_x$ and ${\sigma }_y$ are the waist radius of the beam in x- and y-directions, respectively. ${\mathit{e}}_1=\left({\mathit{e}}_{\mathit{x}}-\mathrm{e}\mathrm{x}\mathrm{p}(\mathrm{i}\Delta \theta ){\mathit{e}}_{\mathit{y}}\right),{\mathit{e}}_2=\left({\mathit{e}}_{\mathit{x}}+\mathrm{e}\mathrm{x}\mathrm{p}(\mathrm{i}\Delta \theta ){\mathit{e}}_{\mathit{y}}\right)$. ${\mathit{e}}_{\mathit{x}}$ and ${\mathit{e}}_{\mathit{y}}$ are the unit vectors in the x- and y-directions, respectively.

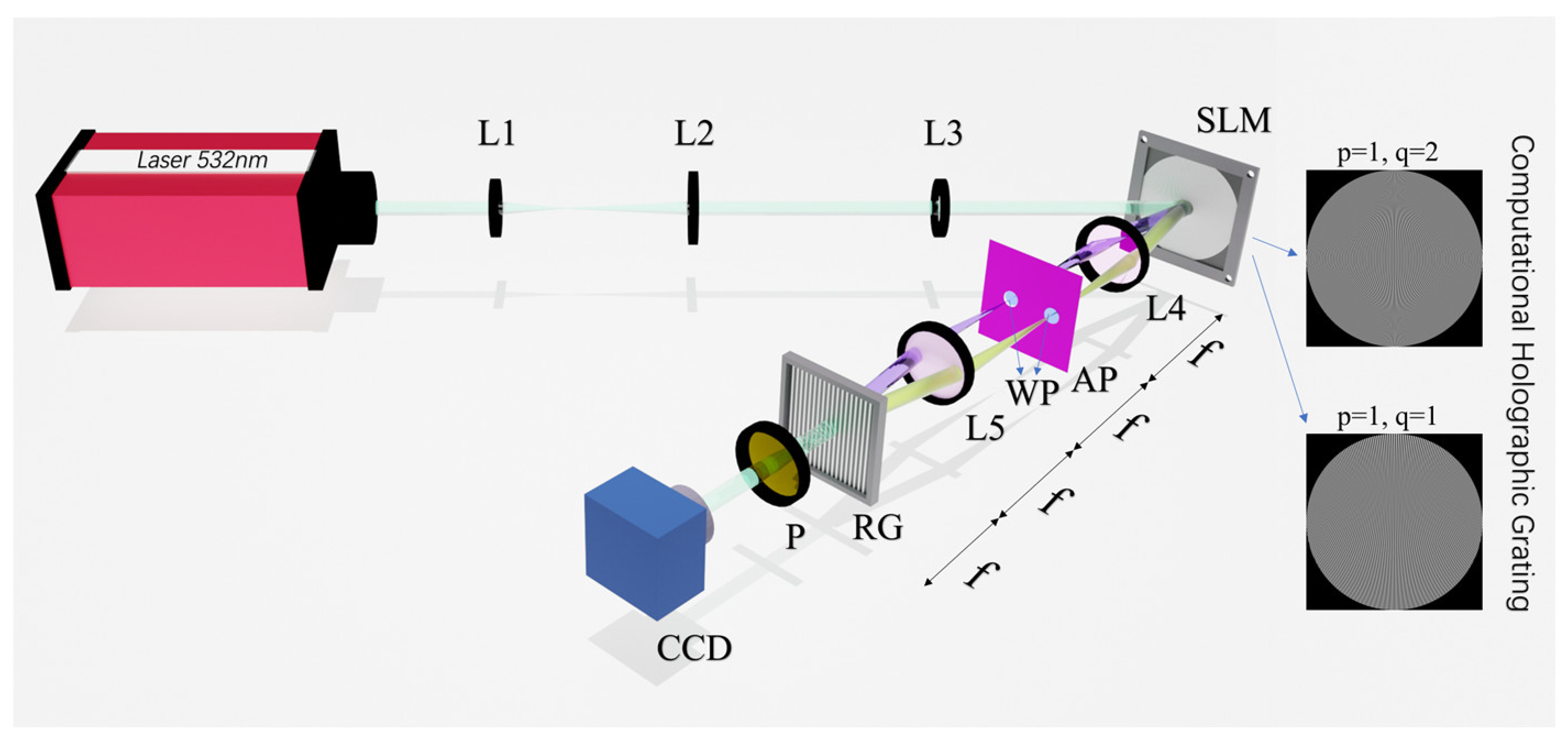
The experimental setup for generating a high-order TVOF is shown in Figure 2. The laser beam with a wavelength of 532 nm is expanded after passing through a telescope composed of two lenses (L1, L2), and then reflects off of a reflective spatial light modulator (SLM). The transmission function of the computational holographic grating (CHG) loaded into the SLM is defined as T (x₀, y₀) = 0.5 + γ [cos(2πf₀x₀ + δ)]/2, where γ represents the modulation depth, f₀ is the spatial frequency of the CHG, and δ represents the twisting phase distribution of the CHG. The first-order diffraction of the beam is selected using an aperture (AP) to avoid other stray light. The beams are then transformed into left and right circular polarizations (or orthogonal linear polarizations) using a λ/4 (or λ/2) waveplate (WP). The ±1 order diffraction beams’ spots are recombined at the focal plane of L5 using a Ronchi grating (RG) to generate the desired TVOF. The generated TVOF with p = 1, q = 1, u = 12 × 10⁶, and Δθ = π/2 and p = 1, q = 2, u = 12 × 10⁹, and Δθ = 0 are shown in Figure 3, represented by the Stokes parameters S₀ (total intensity), S₁ (the linear polarization components in the horizontal and vertical direction), S₂ (the linear polarization components of 45°and 135°), and S₃ (the left and right circular polarization components).

When $\Delta \theta =0$, different spatial positions on the cross-section exhibit various states of polarization (SoP), including linear, circular, and elliptical polarization. If Δθ = π/2, different polarization directions of locally linear polarization can be observed at different positions on the initial wavefront. The initial SoP for high-order twisted vector beams with locally linear polarization (Δθ =π/2) and hybrid polarization (Δθ = 0) are depicted in Figure 4. By comparing the differences in SoP between locally linear polarization (as shown in Figure 4a) and hybrid SoP (as shown in Figure 4b), it can be observed that their S₂ and S₃ parameters are mutually interchangeable, i.e., the S₂ (or S₃) of a high-order twisted vector beam with locally linear polarization is similar to the S₃ (or S₂) of the high-order twisted vector beam with locally linear polarization. The SoP distributions of the initial fields are modulated by the twisting phases, as shown in Figure 4. As recognized from Equation (1), E (x, y) = exp(−x²/σ_x²) exp(−y²/σ_y²) ∙ [exp(iδ) e₁ + exp(−iδ) e₂] = exp(−x²/σ_x²) exp(−y²/σ_y²) ∙ [cosδ·e_x + exp(i(Δθ + π/2))sinδ⋅e_y]. As the position approaches the origin (x and y values tend to be zero), the y-direction polarization component goes to zero to form an x-polarized linear polarization. With the increase of twisting phase orders, the region with x-linear polarization in the beam center becomes broader, as evident from the distribution of S₁ in Figure 4. If Δθ = π/2, when the order of twisting phase p (or q) is odd, it results in a symmetrical amplitude modulation to the SoP about the x-axis, but an antisymmetrical amplitude modulation about the y-axis. For Δθ = 0, the odd order of twisting phase p (or q) leads to a symmetrical phase modulation to the SoP about the x-axis, but an antisymmetrical phase modulation about the y-axis. However, if the order of twisting phase p (or q) is even, the modulations of the high-order twisting phase to the SoP in the initial cross-section are symmetrical about the x (or y)-axis at either Δ$\theta$= 0 or π/2, as shown in the first column in Figure 4.

For the twisted vector optical field with a high-order twisting phase, the distributions of SoP (represented by the Stokes parameters) exhibit the following properties. The distributions of S₀ and S₁ always appear symmetric about the x- or y-axis, denoting the symmetric distributions of total intensity, and x- or y-component intensity, as shown in Figure 4. In the case of locally linear polarized optical fields (see Figure 4a), when both p and q are odd, the S₂ distributions show symmetry about the origin but antisymmetry about the x- and y-axes, representing that the directions of polarization are symmetric about the origin but antisymmetric about x- and y-axes, as shown in the first column in Figure 4a for p = 1 and q = 1. If p (or q) is odd but q (or p) is even, the S₂ is symmetric about the y (or x) axis but antisymmetric about the x (or y) axis. This corresponds to the directions of polarization that are symmetric about the x (or y) axis but antisymmetric about the y (or x) axis, as shown in the second and fourth columns in Figure 4a for p = 1 and q = 2. For the hybrid SoP (p = 0), the variation in initial SoP distributions with the high-order twisting phase modulations is represented by S₃ (replaced with S₂ for locally linear polarization in Figure 4a), as shown in Figure 4b, denoting the polarization direction changes of circular polarizations resulting from the modulation of high-order twisting phases. It is seen that the fundamental physical properties resulting from the twisted phase are similar to that of the locally linear polarization described above. Nevertheless, the initial SoP modulated with a high-order twisting phase possesses a unique distribution, different from a lower-order TVOF or other phase modulation. In addition, the theoretical and experimental results are consistent by comparing Figure 3 and Figure 4. Therefore, subsequent analysis mainly focuses on the theoretical results.

3. Evolution of Polarization State in a High-Order Twisted Vector Optical Field

Under the paraxial approximation conditions, the vector-twisted optical beam propagating in free space can be expressed in the following form using the Rayleigh–Sommerfeld diffraction integral formula:

$$\begin{gathered} E_x\left(x,y,z\right)=-\frac{iz}{\lambda }\frac{e^{ikz}}{z^2}\underset{-\infty }{\overset{\infty }{\int }}\underset{-\infty }{\overset{\infty }{\int }}{E}_{x0}·\exp \left(-\frac{x^2}{{\sigma }_x^2}\right)\exp \left(-\frac{y^2}{{\sigma }_y^2}\right)\exp \left(ik\frac{x_0^2+y_0^2-2x{x}_0-2y{y}_0}{2z}\right)d{x}_{0}d{y}_{0,} \\ {E}_y\left(x,y,z\right)=-\frac{iz}{\lambda }\frac{e^{ikz}}{z^2}\underset{-\infty }{\overset{\infty }{\int }}\underset{-\infty }{\overset{\infty }{\int }}{E}_{y0}·\exp \left(-\frac{x^2}{{\sigma }_x^2}\right)\exp \left(-\frac{y^2}{{\sigma }_y^2}\right)\exp \left(ik\frac{x_0^2+y_0^2-2x{x}_0-2y{y}_0}{2z}\right)d{x}_{0}d{y}_0. \end{gathered}$$

(3)

Similar to scalar-twisted light fields [25,26], the vector light fields carrying a twisting phase experience gradual compression and expansion during propagation in free space. During propagation, conversations between linear and circular polarizations in a twisted vector light field occur. When the initial light field is locally linearly polarized, the conversion to circular polarization from linear polarization during propagation leads to S₃ no longer being entirely zero, as shown in Figure 5a. The 45° and 135° linear polarization components appear for the hybrid polarized twisted vector beam as the variation of S₂ values in Figure 5b. All polarization components and the whole field gradually compress and expand during propagation. For the non-isotropic beams with σ_x ≠ σ_y [22,23], the influence of the high-order twisting phase on the SoP is similar to that of isotropic beams with σ_x = σ_y. However, the intensity distribution of non-isotropic beams is elliptical, unlike the circular shape of isotropic beams. Moreover, the non-isotropic twisted vector beam experiences rotation during propagation, as depicted in Figure 5c. Therefore, the effect of a high-order twisting phase can provide a diversified manipulation in a structured optical field evolution and conversions between linear and circular polarization. In particular, to our best knowledge, asymmetric compression and expansion in a high-order TVOF reshape (p ≠ q, see Figure 5) during propagation has not been reported, providing a new approach to manipulate a complex structured optical field. Meanwhile, the conversions between linear and circular polarizations during propagation can be manipulated by various high-order twisting phases.

4. Effect of a High-Order Twisting Phase on the Optical Angular Momentum and Optical Energy Flow of TVOF

Polarization conversions between linear and circular, and the manipulation of optical angular momentum in structured light fields are essential topics in optical field manipulation, with significant fundamental research interest and practical applications. The spin angular momentum (SAM) relies on circular polarization [27,28,29] (referred to as the S₃ in Figure 4), while the OAM is related to the gradient phase distribution [30]. The SAM and OAM densities of structured beams in the focal region can be calculated as follows:

$$\begin{gathered} S\propto \mathrm{Im}[E^{\ast }\times E], \\ L\propto \mathrm{Im} [r\times (E^{\ast }\cdot (\nabla )E\left)\right], \end{gathered}$$

(4)

where Im [.] denotes the imaginary part, and the asterisk represents the complex conjugation. S and L describe the SAM and OAM densities, respectively. The linear/circular polarization conversion during propagation leads to the SAM appearance even if there is no SAM in the initial field for the locally linear twisted vector optical field, represented by S_3, as shown in Figure 5a. The evolutions of SAM in a twisted vector optical field (TVOF) and conversions between linear and circular polarizations for both locally linear polarized and hybrid SoP during propagation are sensitively dependent on the twisting phase orders p and q, as shown in Figure 5.

Distinct from the spin angular momentum associated with circular polarization, the OAM characteristics are related to the gradient phase distribution. There are no OAM distributions in the initial TVOF. However, different (positive and negative) OAM distributions in the cross-section will appear because of the twisting phase during propagation, as shown in Figure 6. The effect of a low-order twisting phase is similar to that of cylindrical lenses [17], leading to the generation of OAM [31]. With the increase of the twisting phase order, the variation of OAM distribution becomes more frequent, leading to more (positive or negative) extreme values of OAM distribution in the cross-section. In particular, a nonsymmetric OAM distribution appears due to the unequal field distributions in the x- and y-directions for a non-isotropic TVOF. This leads to the beam rotation during propagation, as shown in Figure 6c for 2σ_x = σ_y = 1.8 mm. These results offer a new approach to manipulating the SoP and OAM in a high-order TVOF. The introduction of high-order twisted phases induces non-uniform OAM distributions that can be manipulated by the high-order twisted phases.

The optical energy flow (the time-averaged Poynting vector) in the transverse plane to the propagation direction has attracted considerable research interest because of its potential applications in optical micro-manipulation [27,28,29,32]. The optical energy flow is given by $<\mathit{S}>=Re [\mathit{E}\times \mathit{H}]/2=Im [\mathit{E}\times (\nabla \times {\mathit{E}}^{\mathit{*}}\left)\right]/2{\mu }_0\omega$, where Re [.] and Im [.] denote the real and imaginary parts, respectively, and the asterisk corresponds to their complex conjugations. μ₀ and ω are the vacuum permeability and angular frequency, respectively. The optical energy flows of TVOF with various order twisting phases in different propagation distances are shown in Figure 7. The optical energy flow of a TVOF is closely related to the order of the twisting phase (p and q) and beam shape. When p = q, the directions of optical energy flow point to the diagonal and anti-diagonal in the initial propagation, and the beam intensity compresses along the diagonal and anti-diagonal directions. Then, the beam expands after the compression, as shown in the first and third rows in Figure 7a,b. If p ≠ q, the directions of the optical energy flow are not centrosymmetric, leading to the intensity compression deflected from the diagonal and anti-diagonal directions, as shown in the second rows in Figure 7a,b. For a non-isotropic TVOF (σ_x ≠ σ_y), the asymmetrical reshapes of the beam play a role in the directions of an optical energy flow, bringing about the rotation of the beam in cross-section during propagation [24], as shown in Figure 7c. The optical energy flow distributions of TVOF provide an intuitive understanding of the propagation dynamics and evolution of the OAM of TVOF.

5. Effect of a High-Order Twisting Phase on a Vector Beam

The TVOF analyzed above is based on the orthogonal polarization bases with high-order twisting phases. For a traditional vector beam, the effect of a low-order twisting phase on a vector beam has been reported [31]. Different from the low-order twisting phase, the effect of a high-order twisting phase on the vector beam will generate novel properties due to its unique phase distributions.

The vector optical field with a high-order twisting phase on the source plane can be represented as $E_2\left(x,y\right)=\exp \left(-x^2/{\sigma }_x^2\right)\exp \left(-y^2/{\sigma }_y^2\right)·\left[\exp \left(\mathrm{i}\delta +im\phi \right)\cdot {\mathit{e}}_1+\exp \left(-\mathrm{i}\delta -im\phi \right)\cdot {\mathit{e}}_2\right]$. Firstly, the initial SoP of the vector optical field modulated with various high-order twisting phases features unique distributions, as shown in the first column in Figure 8. During propagation, the evolution of beam shape closely depends on the orders of the twist phase, resulting in elliptical, triangular, and quadrilateral intensity distributions, respectively. Meanwhile, the conversion between linear and circular polarizations during propagation is sensitively dependent on different order twisting phases, as shown in the second and third columns in Figure 8. These results provide a more profound understanding of the manipulation of complex spatial optical fields, and it can find potential applications in micro-particle manipulation, optical information processing, and manipulation of complex optical fields.

6. Discussion

As a novel phase, the effect of a high-order twisting phase on TVOF with locally linear polarization and a hybrid SoP results in novel SoP distributions and propagation dynamics. Similar to the low-order twisting phase with p = 1 and q = 1, the TVOF with high-order twisting phases also performs the intensity compression and expansion, conversion between the linear and circular polarizations, and the appearance of OAM during propagation. However, these phenomena occur earlier with the order increase of the high-order twisting phase.

Unlike the effect of a low-order twisting phase [24], the vector effect of a high-order twisting phase generates novel properties due to its unique phase distributions. Firstly, the initial SoP of a TVOF modulated with various high-order twisting phases possesses unique distributions. During propagation, the evolution of beam shape, and the conversion between linear and circular polarizations are closely dependent on the orders of the twist phase. Asymmetric compression and expansion in a high-order TVOF reshape when p ≠ q (see Figure 5 for p = 1, q = 2) occur during propagation, providing a new approach to manipulate a complex structured optical field. In addition, the variation of OAM distribution becomes more frequent with the increasing orders of the twisting phase during propagation. Nonsymmetric OAM distributions appear in non-isotropic TVOF (${\sigma }_x\ne {\sigma }_y)$, which are closely related to the orders of twisting phases, leading to the rotation of the beam around the propagation axis. The optical energy flow distribution of a high-order TVOF provides a more profound understanding of the propagation dynamics of high-order TVOF and can find potential applications in corresponding fields such as micro-particle manipulation, optical information processing, and manipulation of complex optical fields.

The effect of a high-order twisting phase on the vector beams is also analyzed. The evolution of a vector optical field closely depends on the orders of the twist phase, resulting in elliptical, triangular, and quadrilateral intensity distributions, respectively. These results offer valuable insights into the properties and behavior of vector optical fields with modulation of a high-order twisting phase, providing a foundation for further advancements in optical field manipulation and potential applications in corresponding fields.

7. Conclusions

In summary, the TVOF is experimentally generated and analyzed based on the orthogonal polarization bases with high-order twisting phases. The influence of the high-order twisting phase on polarization states and the optical angular momentum of a vector light field is investigated in this work. The initial SoP of a TVOF is modulated by the high-order twisting phases, leading to novel SoP distributions with various symmetries. The propagation properties of high-order TVOF with locally linear polarization and hybrid SoP are explored, including the intensity compression and expansion, conversion between the linear and circular polarization components, and appearance of OAM during propagation. These phenomena occur earlier with the increasing order of the twisting phase. In addition, a nonsymmetric OAM distribution appears in a non-isotropic TVOF, leading to beam rotation around the propagation axis during propagation. The optical energy flow distribution of a high-order TVOF provides a more profound understanding of the propagation dynamics of high-order TVOF and can find potential applications in micro-particle manipulation, optical information processing, and manipulation of complex optical fields. The effect of a high-order twisting phase on the vector beams is also analyzed. These results offer a new approach to complex optical field manipulation and may find potential applications in the corresponding field.