Multivariable Analysis of Nonlinear Optical Loop Mirror Operating Parameters Using Jones Matrices and Three-Dimensional Renderings
Abstract
:1. Introduction
2. Numerical Development
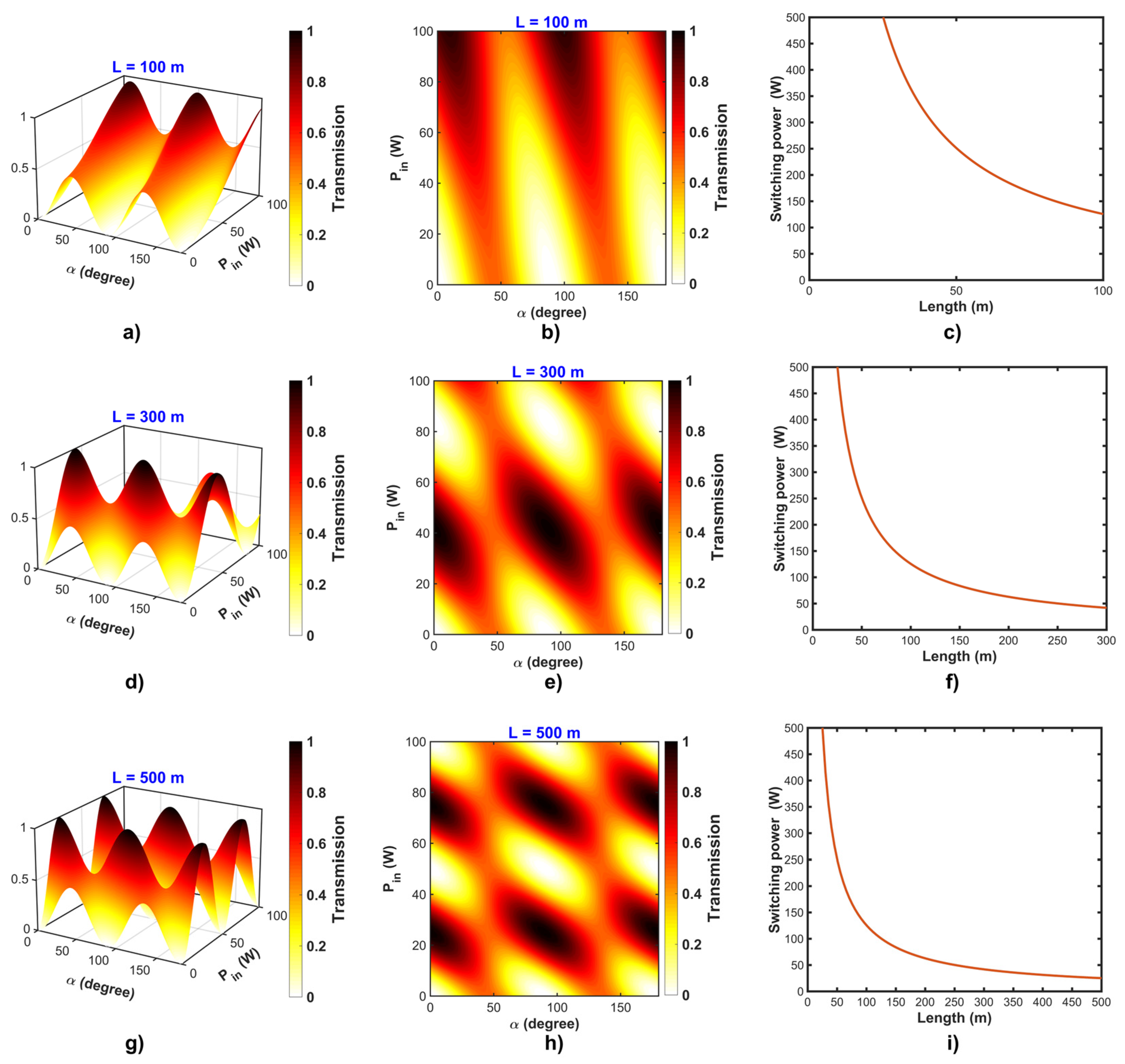
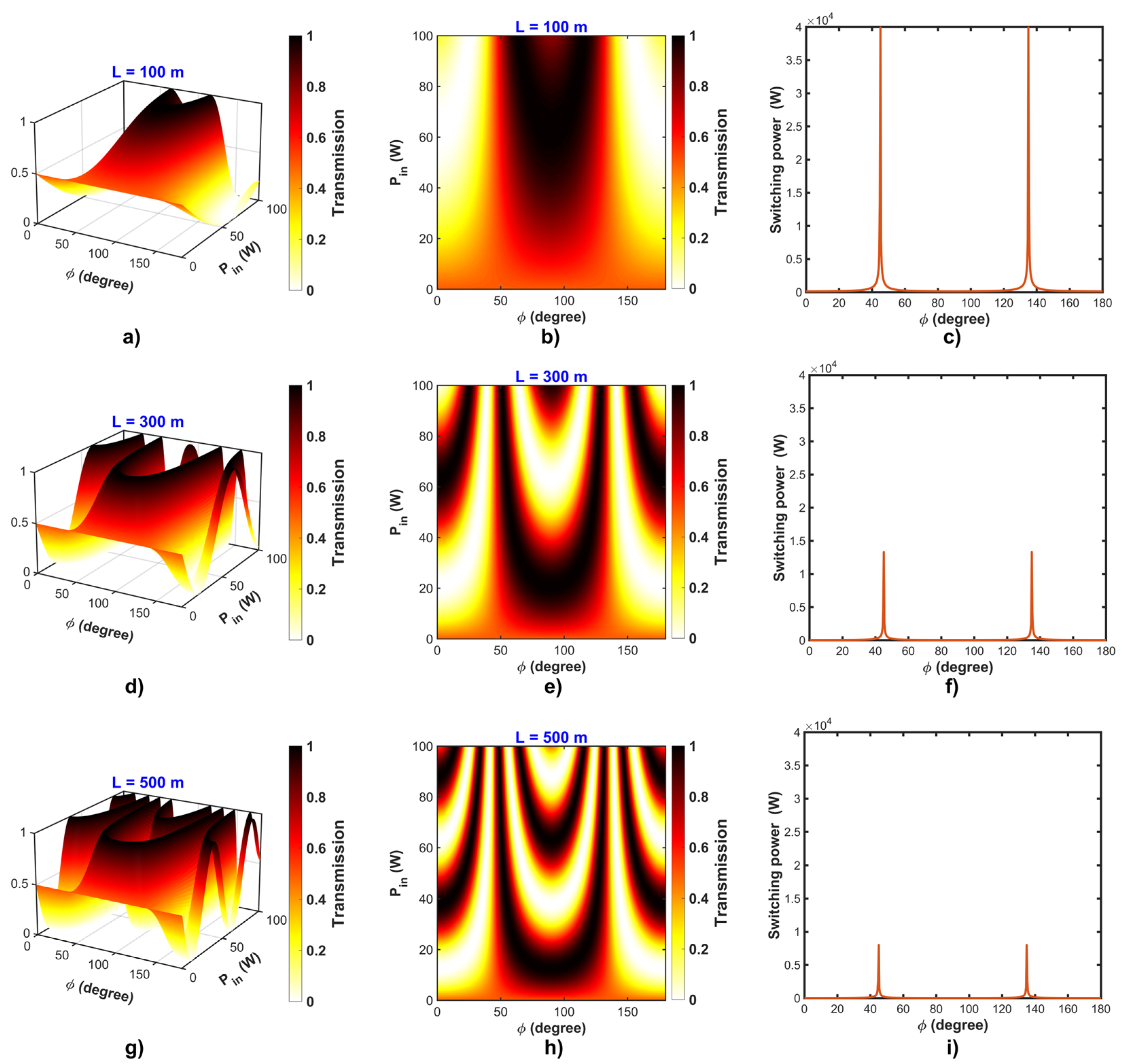
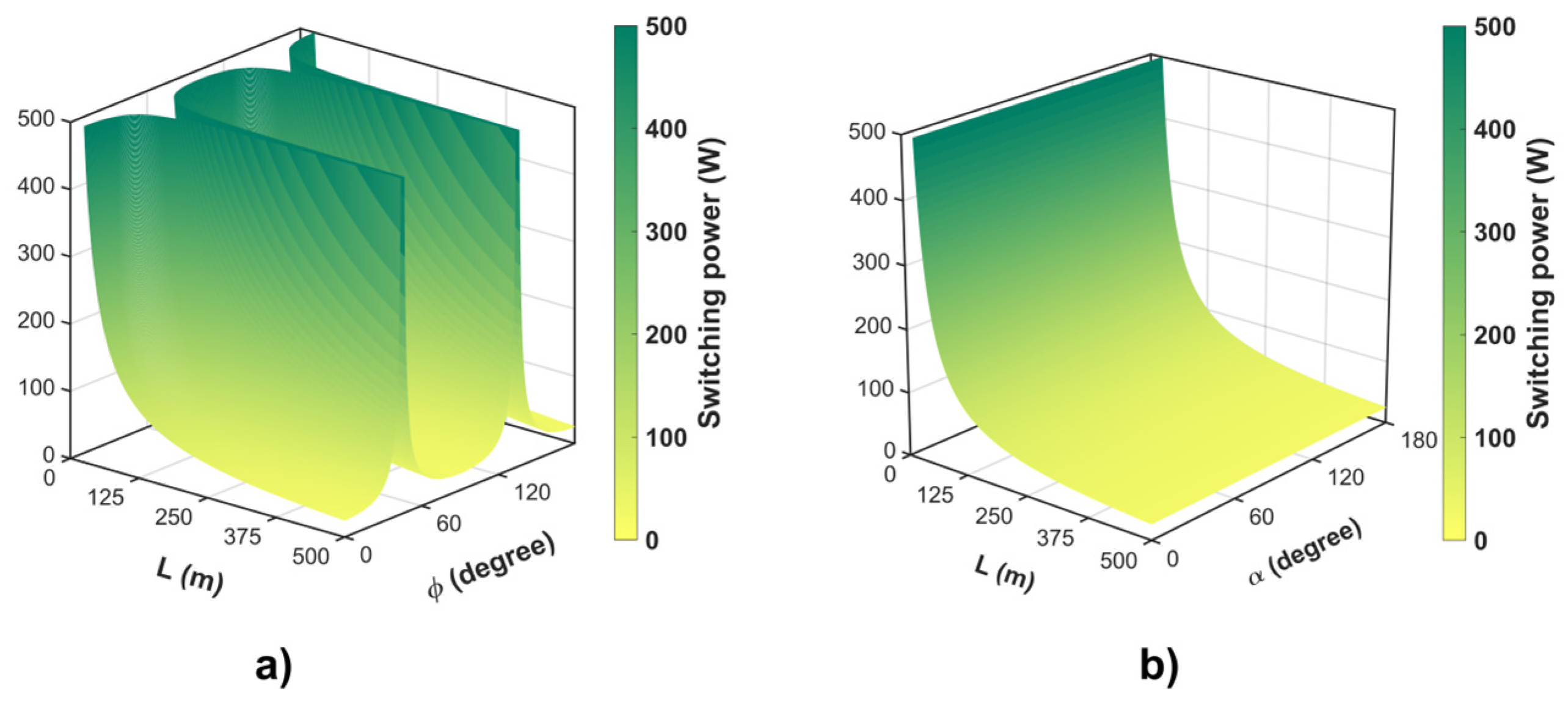
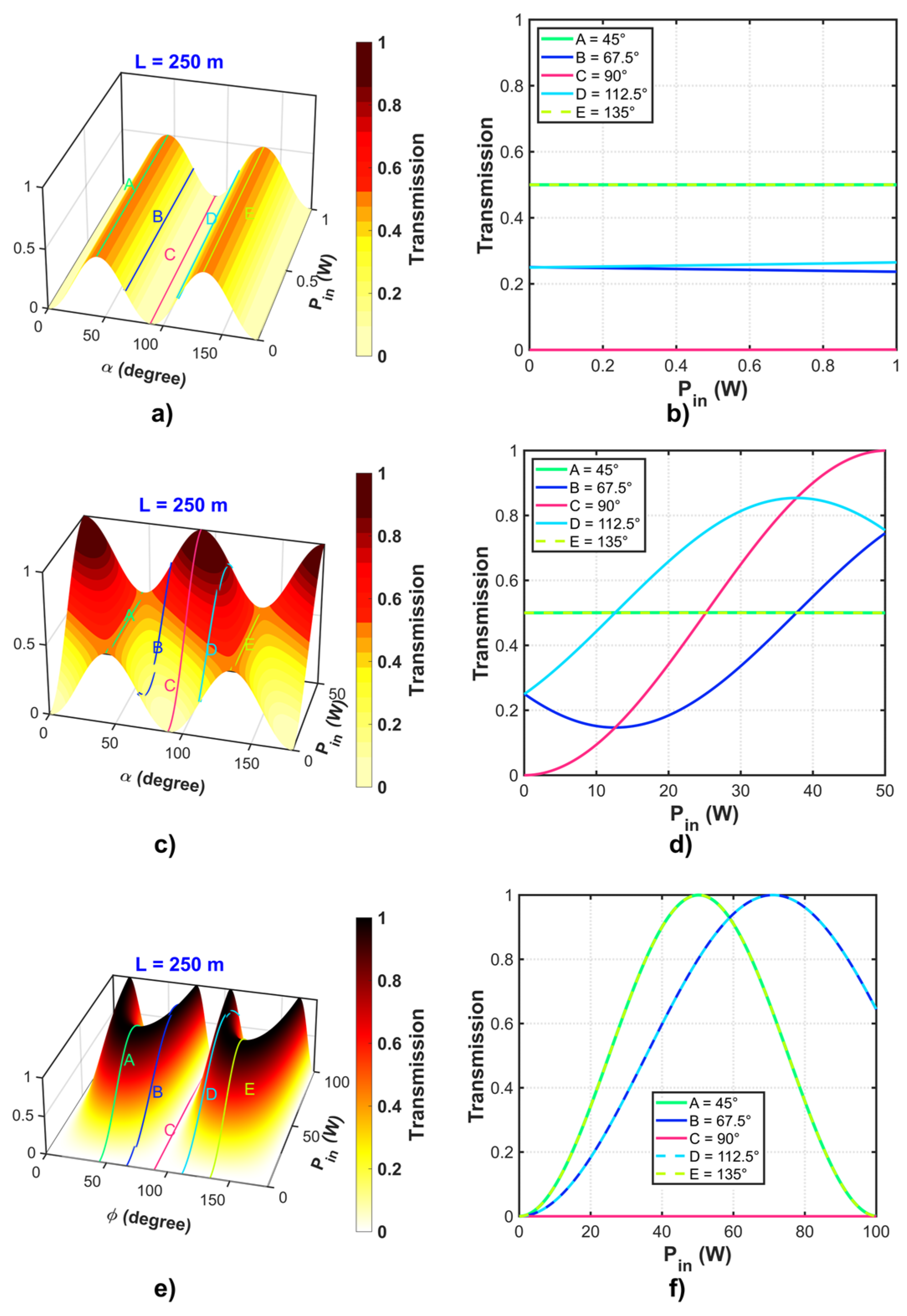
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hänsel, W.; Hoogland, H.; Giunta, M.; Schmid, S.; Steinmetz, T.; Doubek, R.; Mayer, P.; Dobner, S.; Cleff, C.; Fischer, M.; et al. All Polarization-Maintaining Fiber Laser Architecture for Robust Femtosecond Pulse Generation. In Exploring the World with the Laser: Dedicated to Theodor Hänsch on His 75th Birthday; Springer: Berlin/Heidelberg, Germany, 2018; pp. 331–340. ISBN 9783319643465. [Google Scholar]
- Wang, M.; Liu, M.; Chen, Y.; Ouyang, D.; Zhao, J.; Pei, J.; Ruan, S. Stable Noise-like Pulse Generation in All-PM Mode-Locked Tm-Doped Fiber Laser Based on NOLM. Chin. Opt. Lett. 2021, 19, 91402. [Google Scholar] [CrossRef]
- Han, Y.; Guo, Y.; Gao, B.; Ma, C.; Zhang, R.; Zhang, H. Generation, Optimization, and Application of Ultrashort Femtosecond Pulse in Mode-Locked Fiber Lasers. Prog. Quantum Electron. 2020, 71, 100264. [Google Scholar] [CrossRef]
- Yamamoto, T.; Yoshida, E.; Nakazawa, M. Ultrafast Nonlinear Optical Loop Mirror for Demultiplexing 640 Gbit/s TDM Signals. Electron. Lett. 1998, 34, 1013–1014. [Google Scholar] [CrossRef]
- Zhang, X.; Cao, T.; Dong, W. Engineering Nonlinear Effects of Quantum-Well Semiconductor Optical Amplifiers for Applications in Optical Signal Processing. IEEE J. Sel. Top. Quantum Electron. 2022, 29, 1–11. [Google Scholar] [CrossRef]
- Yang, Y.; Wen, F.; Zhao, T.; Yang, F.; Wu, B.; Qiu, K. Optical Reservoir-Based Noise Compensation in a Space Division Multiplexing Transmission System. In Proceedings of the Asia Communications and Photonics Conference, Shanghai, China, 24–27 October 2021; Optica Publishing Group: Washington, DC, USA, 2021; p. T4A-258. [Google Scholar]
- Prince, M.N.H.; Faisal, M.; Majumder, S.P. Performance Analysis of an Optical TDM Transmission Link Considering Fiber Dispersion and Demultiplexer Crosstalk. Optik (Stuttg.) 2022, 251, 168435. [Google Scholar] [CrossRef]
- Guo, B.; Wen, F.; Wu, B.; Qiu, K. Polarization Rotation Enhanced Nonlinear-Optical Loop Mirror (PR-NOLM) Multilevel Amplitude Regenerator. In Proceedings of the Optical Fiber Communication Conference, San Francisco, CA, USA, 6–10 June 2021; Optica Publishing Group: Washington, DC, USA, 2021; p. W6A-9. [Google Scholar]
- Ghazali, N.F.; Wahid, M.H.A.; Hambali, N.A.M.; Juhari, N.; Zahari, S.M.; Shahimin, M.M. Characterization of All-Optical Tofolli and Peres Gates Employing Optimized SOA-NOLM. In Proceedings of the AIP Conference Proceedings, Putrajaya, Malaysia, 22 August 2019; AIP Publishing: Melville, NY, USA, 2020; Volume 2203. [Google Scholar]
- Anagha, E.G.; Jeyachitra, R.K. Review on All-Optical Logic Gates: Design Techniques and Classifications–Heading toward High-Speed Optical Integrated Circuits. Opt. Eng. 2022, 61, 60902. [Google Scholar] [CrossRef]
- Semaan, G.; Braham, F.B.; Fourmont, J.; Salhi, M.; Bahloul, F.; Sanchez, F. 10 ΜJ Dissipative Soliton Resonance Square Pulse in a Dual Amplifier Figure-of-Eight Double-Clad Er:Yb Mode-Locked Fiber Laser. Opt. Lett. 2016, 41, 4767–4770. [Google Scholar] [CrossRef] [PubMed]
- Torres-Muñoz, O.S.; Pottiez, O.; Bracamontes-Rodriguez, Y.; Lauterio-Cruz, J.P.; Ibarra-Villalon, H.E.; Hernandez-Garcia, J.C.; Bello-Jimenez, M.; Kuzin, E.A. Simultaneous Temporal and Spectral Analysis of Noise-like Pulses in a Mode-Locked Figure-Eight Fiber Laser. Opt. Express 2019, 27, 17521–17538. [Google Scholar] [CrossRef]
- Hernández-Escobar, E.; Bello-Jiménez, M.; Pottiez, O.; Ibarra-Escamilla, B.; López-Estopier, R.; Duran-Sánchez, M.; García Ramírez, M.A.; Kuzin, E.A. Elimination of Continuous-Wave Component in a Figure-Eight Fiber Laser Based on a Polarization Asymmetrical NOLM. Laser Phys. 2017, 27, 075105. [Google Scholar] [CrossRef]
- Guo, Y.-X.; Li, X.-H.; Guo, P.; Zheng, H. Supercontinuum Generation in an Er-Doped Figure-Eight Passively Mode-Locked Fiber Laser. Opt. Express 2018, 26, 9893. [Google Scholar] [CrossRef]
- Braham, F.B.; Semaan, G.; Bahloul, F.; Salhi, M.; Sanchez, F. Experimental Optimization of Dissipative Soliton Resonance Square Pulses in All Anomalous Passively Mode-Locked Fiber Laser. J. Opt. 2017, 19, 105501. [Google Scholar] [CrossRef]
- Addanki, S.; Amiri, I.S.; Yupapin, P. Review of Optical Fibers-Introduction and Applications in Fiber Lasers. Results Phys. 2018, 10, 743–750. [Google Scholar] [CrossRef]
- Zazali, N.A.; Latif, A.A.; Lau, K.Y.; Mahdi, M.A.; Muhammad, F.D.; Yusoff, Z.; Abdul-Rashid, H.A.; Radzi, N.M.; Tamchek, N.; Abu Bakar, M.H. 860 Femtoseconds Mode-Locked Fiber Laser by Gallium Co-Doped Erbium Fiber (Ga-EDF). Results Phys. 2019, 15, 102644. [Google Scholar] [CrossRef]
- Zhang, T.; Pan, Y.; Yang, L.; Tian, Z.; Liu, W.; Miao, J.; Dong, Q. NOLM-Based Mode-Locked Yb-Doped Fiber Laser with Wide-Spectrum. J. Electron. Res. Appl. 2019, 3, 35–44. [Google Scholar] [CrossRef]
- Birks, T.A.; Morkel, P. Jones Calculus Analysis of Single-Mode Fiber Sagnac Reflector. Appl. Opt. 1988, 27, 3107. [Google Scholar] [CrossRef]
- Stępień, W.; Szczepanek, J.; Kardaś, T.; Nejbauer, M.; Radzewicz, C.; Stepanenko, Y. Study on Parameters of Fiber Loop Mirrors as Artificial Saturable Absorbers. In Proceedings of the Frontiers in Ultrafast Optics: Biomedical, Scientific, and Industrial Applications XVII, San Francisco, CA, USA, 29 January–2 February 2017. [Google Scholar]
- Ibarra-Escamilla, B.; Kuzin, E.A.; Álvarez-Tamayo, R.I.; Duran-Sanchez, M.; Pottiez, O.; Haus, J.W. Symmetric Nonlinear Optical Loop Using the Nonlinear Polarization Rotation. In Proceedings of the 2015 IEEE Summer Topicals Meeting Series (SUM), Nassau, Bahamas, 13–15 July 2015; pp. 205–206. [Google Scholar]
- Pottiez, O.; Kuzin, E.A.; Ibarra-Escamilla, B.; Méndez-Martínez, F. Theoretical Investigation of the NOLM with Highly Twisted Fibre and a λ/4 Birefringence Bias. Opt. Commun. 2005, 254, 152–167. [Google Scholar] [CrossRef]
- Pottiez, O.; Kuzin, E.A.; Ibarra-Escamilla, B.; Camas-Anzueto, J.T.; Gutierrez-Zainos, F. Easily Tunable Nonlinear Optical Loop Mirror Based on Polarization Asymmetry. Opt. Express 2004, 12, 3878–3887. [Google Scholar] [CrossRef]
- Hernandez-Garcia, J.C.; Estudillo-Ayala, J.M.; Pottiez, O.; Filoteo-Razo, J.D.; Lauterio-Cruz, J.P.; Sierra-Hernandez, J.M.; Rojas-Laguna, R. Flat Supercontinuum Generation by a F8L in High-Energy Harmonic Noise-like Pulsing Regime. Laser Phys. Lett. 2016, 13, 125104. [Google Scholar] [CrossRef]
- Lauterio-Cruz, J.P.; Hernandez-Garcia, J.C.; Pottiez, O.; Estudillo-Ayala, J.M.; Kuzin, E.A.; Rojas-Laguna, R.; Santiago-Hernandez, H.; Jauregui-Vazquez, D. High Energy Noise-like Pulsing in a Double-Clad Er/Yb Figure-of-Eight Fiber Laser. Opt. Express 2016, 24, 13778. [Google Scholar] [CrossRef] [PubMed]
- Pottiez, O.; Kuzin, E.A.; Ibarra-Escamilla, B.; Camas-Anzueto, J.T.; Gutiérrez-Zainos, F. Experimental Demonstration of NOLM Switching Based on Nonlinear Polarisation Rotation. Electron. Lett. 2004, 40, 1. [Google Scholar] [CrossRef]
- Doran, N.J.; Wood, D. Nonlinear-Optical Loop Mirror. Opt. Lett. 1988, 13, 56–58. [Google Scholar] [CrossRef]
- Feng, Z.; Rong, Q.; Qiao, X.; Shao, Z.; Su, D. Experimental Observation of Different Soliton Types in a Net-Normal Group-Dispersion Fiber Laser. Appl. Opt. 2014, 53, 6237–6242. [Google Scholar] [CrossRef] [PubMed]
- Bernabe, V.; Kuzin, E.A.; Ibarra-Escamilla, B.; Korneev, N.; Flores-Rosas, A. Efectos de Dispersión a Primer Orden y SRS Sobre Un Pulso Con Polarización Circular Dentro de Un NOLM Con Fibra Torcida En Lazo. Rev. Mex. Física 2013, 59, 419–425. [Google Scholar]
- Kuzin, E.A.; Korneev, N.; Haus, J.W.; Ibarra-Escamilla, B. Theory of Nonlinear Loop Mirrors with Twisted Low-Birefringence Fiber. J. Opt. Soc. Am. B 2001, 18, 919–925. [Google Scholar] [CrossRef]
- Pang, Y.; Ma, S.; Ji, Q.; Zhao, X.; Li, Y.; Qin, Z.; Liu, Z.; Xu, Y. Frequency Comb Generation Based on Brillouin Random Lasing Oscillation and Four-Wave Mixing Assisted with Nonlinear Optical Loop Mirror. In Proceedings of the Photonics; MDPI: Basel, Switzerland, 2023; Volume 10, p. 296. [Google Scholar]
- Guo, B.; Wen, F.; Wu, B.; Sun, F.; Qiu, K. All-Optical Multilevel Amplitude Regeneration Based on Polarization-Orthogonal Continuous-Wave-Light-Assisted Nonlinear-Optical Loop Mirror (PC-NOLM) Subsystem. IEEE Access 2019, 7, 149666–149671. [Google Scholar] [CrossRef]
- Guo, B.; Wu, B.; Wen, F.; Qiu, K. All-Optical OPC-NOLM Amplitude Regeneration for Intact Phase Preservation. Acta Opt. Sin. 2023, 43, 0306001. [Google Scholar]
- Kikuchi, K.; Tanemura, T. Circular-Birefringence Fiber for Nonlinear Optical Signal Processing. J. Light. Technol. 2006, 24, 4108–4119. [Google Scholar]
- Flores-Rosas, A.; Peralta-Hernandez, J.I.; Bracamontes-Rodríguez, Y.E.; Villagomez-Bernabe, B.A.; Beltrán-Pérez, G.; Pottiez, O.; Ibarra-Escamilla, B.; Rojas-Laguna, R.; Kuzin, E.A. Observation of a High Grade of Polarization of Solitons Generated in the Process of Pulse Breakup in a Twisted Fiber. JOSA B 2014, 31, 821–826. [Google Scholar] [CrossRef]
- Guo, L.; Gan, Z.; Liang, X. 27nJ, 114fs Pulses from an Environmentally Stable All-Normal All-PM Yb-Doped Fiber Laser Mode-Locked with a Nonlinear Amplifying Loop Mirror. IEEE Photonics J. 2022, 14, 1–6. [Google Scholar] [CrossRef]
- Kobtsev, S.M. Artificial Saturable Absorbers for Ultrafast Fibre Lasers. Opt. Fiber Technol. 2022, 68, 102764. [Google Scholar] [CrossRef]
- Bello-Jiménez, M.; Kuzin, E.A.; Pottiez, O.; Ibarra-Escamilla, B.; Flores-Rosas, A.; Durán-Sánchez, M. Soliton Extraction from a Bunch of Solitons Resulting from Pulse Breakup by Using a Nonlinear Optical Loop Mirror. JOSA B 2009, 26, 1456–1462. [Google Scholar] [CrossRef]
- Pottiez, O.; Escamilla, B.I.; Kuzin, E.A.; Haus, J.W. Nonlinear Switching in a Symmetrical Sagnac Interferometer Including a Quarter-Wave Plate. In Proceedings of the OSA Trends in Optics and Photonics Series; Optica Publishing Group; Bellingham, WA, USA, 2004. [Google Scholar]
- Pottiez, O.; Ibarra-Escamilla, B.; Kuzin, E.A. High-Quality Amplitude Jitter Reduction and Extinction Enhancement Using a Power-Symmetric NOLM and a Polarizer. Opt. Express 2007, 15, 2564–2572. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Wen, F.; Yang, F.; Qiu, K. Optical Dispersion Compensation through a Nonlinear-Optical Loop Mirror (NOLM)-Based Optical Reservoir. In Proceedings of the 2022 Photonics & Electromagnetics Research Symposium (PIERS), Hangzhou, China, 25–27 April 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 557–562. [Google Scholar]
- Saeedizadeh, R.; Sabouri, S.G.; Khorsandi, A. Engineering the Temporal Shape of a Chirped Pulse Compressed in a Pressure-Gradient-Based Cascaded Hollow-Core Photonic Crystal Fiber. Opt. Quantum Electron. 2023, 55, 515. [Google Scholar] [CrossRef]
- Pan, H.; Chen, Z.; Zhang, A.; Zhang, B.; Peng, Y.; Liu, Z.; Wang, Q.; Cui, N.; Zhou, J. Tunable and Switchable Low-Threshold Multi-Wavelength Erbium-Doped Fiber Pulsed Laser Based on Lyot Filter and NOLM. J. Russ. Laser Res. 2023, 44, 303–313. [Google Scholar] [CrossRef]
- Kaur, R.; Kaur, B.; Kaur, H. A Review on OTDM Transmission. Int. J. Eng. Res. Technol. 2023, 12. [Google Scholar]
- Tapia-Garcia, M.R.; Hernandez-Garcia, S.G.; Hernandez-García, J.C.; Razo-Medina, D.A.; Estudillo-Ayala, J.M.; Pottiez, O.; Filoteo-Razo, J.D.; Lauterio-Cruz, J.P.; Gomez-Rodriguez, F.A.; Rojas-Laguna, R. Experimental Study of a F8L Using an Automated Adjustment System Based in Polarization Control Plates. In Fiber Lasers XX: Technology and Systems; SPIE: Bellingham, WA, USA, 2023; Volume 12400, pp. 174–180. [Google Scholar]
- Avazpour, M.; Beltrán Pérez, G.; Kuzin, E. Suppression of Kelly Sidebands and Compression of Soliton Spectrum Using a Polarization Imbalance Nonlinear Loop Mirror. In Progress in Optomechatronic Technologies: Proceedings of International Symposium on Optomechatronic (2018); Springer: Berlin, Germany, 2019; pp. 147–152. [Google Scholar]

| Optical Element Description | Nomenclature | Jones Matrix |
|---|---|---|
| Quarter-wave plate with clockwise direction | ||
| Quarter-wave plate with counterclockwise direction | ||
| Twisted optical fiber with clockwise direction | ||
| Twisted optical fiber with counterclockwise direction |
| Optical Element Description | Nomenclature | Jones Matrix |
|---|---|---|
| Quarter-wave plate with clockwise direction | ||
| Quarter-wave plate with counterclockwise direction | ||
| Twisted optical fiber with clockwise direction | ||
| Twisted optical fiber with counterclockwise direction |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Filoteo-Razo, J.D.; Hernandez-Garcia, J.C.; Estudillo-Ayala, J.M.; Pottiez, O.; Martinez-Angulo, J.R.; Barron-Zambrano, J.H.; Elizondo-Leal, J.C.; Saldivar-Alonso, V.P.; Lauterio-Cruz, J.P.; Rojas-Laguna, R. Multivariable Analysis of Nonlinear Optical Loop Mirror Operating Parameters Using Jones Matrices and Three-Dimensional Renderings. Photonics 2023, 10, 1071. https://doi.org/10.3390/photonics10101071
Filoteo-Razo JD, Hernandez-Garcia JC, Estudillo-Ayala JM, Pottiez O, Martinez-Angulo JR, Barron-Zambrano JH, Elizondo-Leal JC, Saldivar-Alonso VP, Lauterio-Cruz JP, Rojas-Laguna R. Multivariable Analysis of Nonlinear Optical Loop Mirror Operating Parameters Using Jones Matrices and Three-Dimensional Renderings. Photonics. 2023; 10(10):1071. https://doi.org/10.3390/photonics10101071
Chicago/Turabian StyleFiloteo-Razo, Jose D., Juan C. Hernandez-Garcia, Julian M. Estudillo-Ayala, Olivier Pottiez, Jose R. Martinez-Angulo, Jose H. Barron-Zambrano, Juan C. Elizondo-Leal, Vicente P. Saldivar-Alonso, Jesus P. Lauterio-Cruz, and Roberto Rojas-Laguna. 2023. "Multivariable Analysis of Nonlinear Optical Loop Mirror Operating Parameters Using Jones Matrices and Three-Dimensional Renderings" Photonics 10, no. 10: 1071. https://doi.org/10.3390/photonics10101071
APA StyleFiloteo-Razo, J. D., Hernandez-Garcia, J. C., Estudillo-Ayala, J. M., Pottiez, O., Martinez-Angulo, J. R., Barron-Zambrano, J. H., Elizondo-Leal, J. C., Saldivar-Alonso, V. P., Lauterio-Cruz, J. P., & Rojas-Laguna, R. (2023). Multivariable Analysis of Nonlinear Optical Loop Mirror Operating Parameters Using Jones Matrices and Three-Dimensional Renderings. Photonics, 10(10), 1071. https://doi.org/10.3390/photonics10101071







