Integrating Emotion-Specific Factors into the Dynamics of Biosocial and Ecological Systems: Mathematical Modeling Approaches Accounting for Psychological Effects
Abstract
1. Introduction
2. Effects of Different Psychological Factors on Humans
2.1. Psychological Effects on Brain Networks
2.1.1. Large-Scale Brain Networks and Emotional Modulation
2.1.2. Metabolic Constraints and Generative Modeling
2.1.3. Emotion-Induced Collective Dynamics and Crowd Behavior
2.1.4. Emotion and Decision-Making: Drift-Diffusion Models (DDMs)
2.1.5. Advances in Psychophysics, Signal Processing, and Computational Emotion
2.1.6. Stochastic Modeling of Emotional Dynamics
2.2. Psychological Effects on Mental Illness
2.2.1. Stigma, Cognitive Appraisals, and Social Context
2.2.2. Illness Perceptions and Emotional Regulation
2.2.3. Physiological and Developmental Mechanisms
2.2.4. Mathematical and Computational Modeling of Psychopathology
2.2.5. Dialectical Behavior Therapy (DBT): Mathematical Representations
2.2.6. Emerging Therapies and Neurocomputational Developments
2.3. Psychological Factors in Chronic Physical Diseases (CPDs)
2.3.1. Bidirectional Links Between CPDs and Psychological Distress
2.3.2. Mathematical and Computational Perspectives on Emotional Regulation in CPDs
2.3.3. Cognitive Deficits and Pain Amplification Mechanisms
2.3.4. Developmental, Psychosocial, and Neurobiological Contributors
2.3.5. Role of AI and Emotional Computing in CPD Management
2.3.6. Psychological Interventions and Interdisciplinary Care
3. Similarities and Differences in Model Formulation: Human and Animal Psychology
3.1. Shared Mathematical Foundations
3.2. Animal Psychology Modeling
3.3. Human Psychology Modeling
3.4. Neurophysiological Integration
4. Psychological Effects in Ecological Modeling: From the Perspective of Predator–Prey Interactions
4.1. Fear Effect on Prey
4.2. Prey Refuge
- (i)
- Refuge proportional to the prey population:
- (ii)
- Constant refuge population:
- (iii)
- Refuge proportional to the predator population:
- (iv)
- Refuge proportional to both prey and predator population:
4.3. Inducible Defense
4.4. Cooperative Hunting
4.5. Herd Behavior
4.6. Anti-Predator Behavior
4.7. Group Defense
4.8. Population Dispersal/Migration
4.9. Prey Switching by Looking for Alternative Food Sources
5. Psychological Effects in Epidemiological Modeling
- Psychological inhibition and modified incidence rates: People generally respond to epidemic problems by making psychological changes that help them avoid contact with others and stop the spread of the disease [581,582,583]. These modifications, which range from social disengagement to improved hygiene, necessitate adjustments to the normal bilinear incidence rates, typically represented as in SIR/SEIR models [584,585,586,587,588,589]. Subsequently, epidemiological studies utilized a nonlinear incidence rate [590,591,592,593,594]. Capasso and Serio proposed a saturated incidence rate to reflect behavioral inhibition [595]:where k and are constants, measures the infection force, and reflects the reduction in contact due to psychological inhibition as infection prevalence increases [583,596]. This functional form is mostly phenomenological, despite its widespread use in classical epidemic modeling. Its empirical validation is largely derived from initial short-term outbreak findings, and its repeatability across diverse populations or long-term behavioral responses is still constrained. So, even if it does a good job of capturing monotonic behavioral inhibition, its generalizability is limited by how simple its assumptions are. This was further generalized to nonmonotonic forms, such as [597], capturing the ‘psychological effect’ in response to infection prevalence. Nonetheless, numerous extensions depend predominantly on simulation-based validation and are deficient in extensive empirical calibration. Consequently, the scope and duration of the inferred psychological effects exhibit significant variability across research, and their consistency across other disorders or temporal intervals are yet to be definitively determined. Subsequent research elucidates the impact of psychological inhibition on illness suppression by including information-induced behavioral alteration [598] and optimal control strategies, such as social distancing and heightened awareness [599]. These models have conceptual viability; nevertheless, as to previous formulations, their behavioral elements are predominantly substantiated through theoretical frameworks rather than replicated empirical datasets, hence constraining their resilience.
- Network topology, crowding effects, and behavioral feedback: Other types of studies have looked at how the structure of a network influences how people act and how information spreads [600,601,602,603,604]. Research on business and communication networks shows that topological features like connectivity and clustering affect how users operate and how viruses spread. In particular, crowding effects in point-to-group (P2G) network sharing might inhibit the transmission of viruses by causing delays and withdrawal behavior when people feel threatened [605]. It is important to note that many of these behavioral consequences are only replicated under certain or idealized network assumptions, which makes it unclear how well they apply to real-world systems that are not homogeneous [606]. Controlling a virus depends extensively on psychological factors, such as disconnecting from infected nodes [607]. Using a modified incidence rate, Yuan et al. created a nonlinear e-SEIR model including crowding and behavioral inhibition [608]:thereby integrating user connectivity to psychological feedback. Here, captures virus transmission influenced by user connectivity, and reflects psychological inhibition as infections rise. Behavioral inhibition increases with the number of infectives and is influenced by network-driven exposure patterns. This model’s behavioral modulation is closely linked to network structure, which makes its predictions very sensitive to assumptions about topology and how users interact with each other. This is different from the standard saturated incidence form. Its validation relies predominantly on simulations, and evidence supporting its replication outside of stylized networks is still scarce.Bellomo et al. proposed a multi-scale modeling framework for behavioral human crowds, underscoring the necessity of emotional states, varied strategic planning, and nonlinear social interactions [458]. Their incorporation of ‘activity’ as a dynamic behavioral variable facilitates a nuanced examination of group-level responses shaped by individual psychological traits, augmenting the understanding of crowd-mediated behavioral feedback during epidemics. Similarly, a fractional-order SIRS model incorporating memory-driven vaccination behavior captures nonlinear reactions to public health communications [609]. Network-level behavioral interactions and awareness of HIV preventive methods, such as PrEP, similarly influence epidemic patterns [610]. These differences reveal that both formulations in (28) and (29) represent psychological inhibition, but they are very different in terms of their assumptions, scope, and evidence. The standard saturated incidence is more ideal for uniform population-level behavioral responses, while the network-based formulation is preferable when connection and exposure structure predominate behavioral adaptations. This comparative framework helps make it clear when one model is right and also where further empirical reproducibility is needed.
- Emotional distress and public compliance: Public cooperation with health treatments is extensively shaped by emotional reactions during epidemics, including dread, worry, and depression. Growing empirical studies show an increase in psychological suffering during infectious outbreaks, disproportionately affecting those with low socioeconomic levels [611,612,613,614,615,616,617,618,619]. These emotional states might compromise public health policies, lead to avoidance behaviors, disseminate false information, or even result in panic-driven decision-making.Media coverage sometimes magnifies these dynamics by raising perceived threats, which could then enhance maladaptive behavior reactions. For instance, Taylor et al. discovered during Australia’s equine influenza epidemic that financial uncertainty was strongly correlated with emotional stress, therefore illustrating how structural vulnerabilities impact psychological effects [612]. Socioeconomic level also influences coping strategies like hope for recovery or faith in organizations. Studies by Zhou et al., Li et al., and Vázquez et al. validate that these emotional elements, especially optimism and trust, act as moderating variables that may either buffer psychological stress or magnify its impact under uncertainty [615,617,619].Carbonaro and Serra [121] presented a model reflecting the stochastic evolution of emotional states, including anxiety and reliability, over time-dependent interpersonal encounters, thereby capturing such dynamics quantitatively. The model characterizes the probability of a certain emotional state shared across persons i and j developing via the following equation:where and represent gain and loss terms influenced by both self-reflection and emotional contagion through social networks. This formulation corresponds with expansions of behavioral SIR models, in which emotional dynamics interact with epidemiological states to enable researchers to predict adaptive behavioral transitions such as risk denial, greater compliance, or panic-induced withdrawal. Including such emotion-specific processes into disease modeling algorithms helps one to better grasp how psychological elements affect epidemic paths, particularly in times of crisis that test public health infrastructure and collective emotional resilience.
- Behavioral adaptation and disease transmission: Essential to epidemic outcomes and influenced by psychological elements like anxiety, unpredictability, exhaustion, and compliance to social norms are behavioral reactions that include social distance, hand cleanliness, and restricted mobility [599,610,620,621,622,623,624,625,626,627,628,629,630,631,632,633,634,635,636,637,638,639,640,641,642,643,644,645,646,647,648,649,650,651,652,653]. Behavioral changes like panic purchasing, broad mask usage, remote working, and altered travel patterns were clearly seen during the COVID-19 epidemic. Though first successful, these adaptive activities often fade with time from habituation or tiredness [654,655,656,657,658,659,660,661,662,663,664,665,666,667,668,669]. Trust in authority and social conventions mediates these actions; tiredness may cause them to fade over time [670,671,672,673,674]. Using fractional derivatives [609], transitions between immune and non-immune susceptibles depending on past exposure [675], and time-dependent vaccination and distancing approaches [676], models including memory-driven alterations in vaccination attitudes describe behavioral adaptability. These strategies draw attention to how adaptive feedback shapes the course of an epidemic.
- Migration restrictions and their psychological effects: Recommended responses to epidemic challenges include migration controls like lockdowns, quarantines, and travel bans, but they also have major psychological effects. Public confidence and obedience may be undermined by fear, solitude, and financial stress linked with these regulations [227,677,678,679]. Several research studies show that a lack of accessibility and insufficient communication aggravate these consequences, hence lowering the effectiveness of mobility limitations. Mathematical models sometimes show such constraints as control variables controlling isolation or social distance. Researchers have worked on models, for example, that limit movement through the variables signaling remoteness and isolation rather than geographical restrictions [599,609,680,681]. These depictions help one understand how public perceptions and legislative stringency interact to affect results. Trust in authority and clear communication define public adherence most of all; contradictory communication reduces compliance [682,683,684,685].
- Advances in behaviorally informed modeling: Recent advances in epidemiological modeling have progressively recognized how closely disease dynamics are shaped by emotional contagion and behavioral feedback. Compartmental models are often lacking in reflecting these intricate psychological dynamics. Bedson et al. underline the shortcomings of traditional models by means of a thorough evaluation of approaches that include psychological aspects in epidemic models, therefore supporting more complex behavioral representations [686]. One important example of this kind of progress is the prevalence-elastic behavior model, which holds that people change their social distance or vaccine intake in response to imagined illness risks [687]. Building on this, Dutta et al. show how to simulate long-memory behavioral effects using fractional calculus, hence allowing the capturing of continuous individual responses throughout time [609]. In companion work, Dutta et al. and Saha et al. include immunological variability, optimum vaccination techniques, and dynamic feedback mechanisms, including adaptive social distance, therefore offering more realistic representations of behavioral development during epidemics [675,676].Coupled contagion models improve our knowledge substantially as they concurrently represent the transmission of transmissible diseases and anxiety. Studies by Funk et al. and Epstein et al. have demonstrated that these systems may produce intricate dynamics, including oscillating epidemic patterns [688,689]. Particularly, Agent_Zero, an agent-based model (ABM), shows a major advance in this respect. These models provide a detailed picture of behavioral variety by simulating diverse creatures whose decisions are shaped by cognitive, emotional, and social stimuli [690]. Further improving the relevance of these models is the growing availability of real-time behavioral data and qualitative insights from risk communication and community involvement (RCCE) approaches. Infection paths are much shaped by social and psychological elements, including individual vulnerability, patterns of social mixing, and public activity engagement. Emphasizing the part of behaviorally driven variation in epidemic dissemination, ABMs have revealed how psychosocial interactions dramatically affect asymptomatic transmission patterns in COVID-19 [691].Gigerenzer’s idea of psychological AI also brings heuristic-based methods that give human judgment under ambiguity top priority. His criticism of data-centric epidemic forecasting systems such as Google Flu Trends emphasizes the need for psychological heuristics, such as the recency effect, which, in some situations, can beat more intricate prediction algorithms [692]. These results highlight the need to include limited rationality and psychological realism into epidemic models to improve their predictive and explanatory capacity.
- Psychoneuroimmunological insights: A key assumption of psychoneuroimmunology (PNI) is that psychological moods and immunological function have a complicated, bidirectional interaction. Depression, anxiety, and chronic stress are among the mental health disorders most linked to aggravation of inflammatory diseases, including inflammatory bowel disease (IBD), via the gut–brain axis and vagal tone changes [693,694,695]. Results from animal models also confirm this link; for example, experimentally induced psychological discomfort has been found to disturb gut flora and decrease immune function, therefore highlighting physiologically ingrained routes by which emotions affect immunological resistance [696,697].These revelations are now included in models of epidemiology. Dutta et al. use fractional-order models, for instance, to capture memory-dependent behavioral reactions like vaccination reluctance, therefore illustrating how cognitive biases and belief systems directly affect immunological risk via behavioral paths [609]. Models of HIV control show a similar junction of psychological and immunological processes whereby cognitive assessment of risk and informational awareness shape the intake of pre-exposure prophylaxis (PrEP), therefore tying emotional states to population-level disease resistance [610]. Further extending this integration, Lv et al. suggest an enhanced SIRS framework including psychological variation among people. Under this approach, the population is split into level-headed and impatient groups to reflect differences in behavioral responsiveness during public crises [698]. Dynamic psychological interactions bridge ideas from personality psychology and conventional epidemiology to simulate emotional contagion, much as infectious disease transmission is modeled. This formulation offers a convincing structure for modeling panic spread and its influence on epidemic dynamics. These models, taken together, highlight the requirement of epidemiological methods that consider the interactions among psychological features, emotional reactions, and immunological results. Such integration improves the forecasting power of models under actual psychosocial settings and provides a more complete knowledge of population health.
6. Psychological Effects in Advanced Technology, AI, and Complex Systems
- (i)
- Facial attractiveness and visual psychology: Deep learning architectures like AlexNet and ResNet, trained on datasets like SCUT-FBP5500, have efficiently represented human impressions of face aesthetics molded by consistent psychological preferences across age, culture, and gender [725,726,727]. Combining local and global face characteristics with multi-task learning helps Vahdati et al. increase prediction accuracy [728]. Meta-learning techniques have been used to personalize elegance evaluation and dynamically adjust to user-specific aesthetic choices, hence addressing individual variance [729,730,731,732,733].
- (ii)
- Affective computing and emotion recognition: Originally put up by Picard, affective computing recognizes the importance of emotion in intelligent behavior from a viewpoint compatible with Simon’s claim that cognition is incomplete without affect [734,735]. Bechara et al. have shown that deficits in emotional-processing brain areas compromise decision-making even in cases with logical thinking intact [736]. Emotion identification systems depend more and more on multimodal data, including speech characteristics [737], facial action units (e.g., FACS) [738,739], and EEG signals [740,741]. Liu et al. suggested a spatio-temporal convolution attention neural network (3DCANN) leveraging dual attention processes to show better classification performance over many channels and time frames for EEG-based emotion identification [742]. In a similar vein, Cheng et al. presented MSDCGTNet, a new multi-scale CNN and gated transformer-based model that allows accurate and effective emotional state identification throughout several benchmark datasets [743]. Effective temporal emotional signals in speech-based systems are captured by deep learning models, including LSTM and the upgraded BLSTM-DSA architecture [744,745]. With depression diagnosis systems combining BP neural networks and Adaboost algorithms reaching over 81% accuracy, multimodal approaches integrating voice and facial expression have also demonstrated great efficacy in mental health diagnoses [746]. Hernández-Marcos and Ros suggested a self-learning emotional framework for AI agents based on reinforcement learning ideas, hence extending this trend [747]. Their approach shows congruence with natural emotional patterns and develops synthetic feelings by means of the temporal dynamics of reward-based variables.
- (iii)
- Music, emotion, and psychological regulation: An essentially emotional medium with great regulating power is music. AI-based music systems are now able to analyze and modify musical output in real time to reflect or impact a user’s emotive state are. Showing statistically substantial categorization accuracy of emotional states, Affective Brain-Computer Music Intervals (aBCMI) use EEG inputs to identify arousal and valence levels and change music accordingly [748,749]. Strong connections between auditory stimuli and emotional responses throughout cortical and limbic networks help EEG-based studies to support these systems [750]. Today, EEG-based functional connectivity during emotional experience has attracted significant attention. Moreover, as pointed out in [751] and references therein, EEG evidence consistently reveals shared neural mechanisms between affect and cognition, overlapping anatomical substrates, and coordinated temporal dynamics between emotional and cognitive processes. This underscores the need to develop unified mathematical models that preserve insights from specialized research while capturing the holistic nature of mental function. It is expected that such models will assist in areas ranging from clinical intervention to educational technology, and from brain–computer interfaces to artificial intelligence [751], with applications in developing new therapies for emotional rehabilitation programs, psychological trauma recovery, and other fields.
7. Psychological Effects in Finance, Business, Economics, and Other Areas of Social Sciences
- Cognitive and neural foundations of financial decisions: Frydman and Camerer examine how cognitive biases and brain processes influence financial behavior in a variety of areas, including household finance and business decision-making. They stress the role of overconfidence, overtrading, and insufficient financial literacy in driving unsatisfactory results. Neuroscientific research utilizing functional magnetic resonance imaging (fMRI) reinforces these behavioral trends by linking brain activity to risk perception and investment behavior [760].Frydman and Camerer [760], as well as Frydman et al. [761], use fMRI data to give empirical support for the “realization utility hypothesis”, which holds that investors derive utility at the moment of realizing profits or losses rather than from intertemporal wealth growth. This behavioral inclination can be represented as follows:where is the vector of realized returns over time, is the vector of corresponding purchase prices, and is a discount factor. The utility function u is determined not by total wealth but by the emotional enjoyment obtained from temporary gains or losses, particularly when selling assets.Taken together, these findings indicate that even at the most basic level of trading, emotional responses to realized gains and losses can systematically shape financial behavior.Kahneman and Tversky’s prospect theory provides a psychologically based alternative to anticipated utility theory by elucidating how humans really assess risk and uncertainty. The conventional model posits a linear utility function with rational agents maximizing predicted utility. In contrast, prospect theory provides a value function defined by gains and losses relative to a reference point, rather than eventual wealth levels [762]. This function is concave for gains and convex for losses, which means that it becomes less sensitive as the amount of money lost increases. It is also steeper for losses than for gains, which is in line with the idea of loss aversion, which says that losses are more important than gains of the same size. Mathematically, this is represented by a value function , which allocates a subjective value to each outcome x. In this case, x stands for the change in wealth compared to a reference point. Gains are positive and losses are negative. The function is defined as follows:where represents the degree of loss aversion, and captures diminishing sensitivity to gains and losses [763]. Empirical estimates often indicate , signifying that losses are often valued more than twice as much as corresponding benefits.Prospect theory includes a probability weighting function in addition to the value function. This function reflects the fact that people tend to put too much weight on tiny probabilities and not enough weight on moderate to high probabilities. This conduct diverges from the utilization of objective probability in anticipated utility theory. The Prelec weighting function that is most often used is as follows:where shows how the distortion works. When , the function becomes the identity line , which means that the perception is not skewed. For , it has the S-shape that is typical of it, with low probabilities getting too much weight and high probabilities getting too little weight. Both the value function and the probability weighting function are the two main parts of prospect theory. They explain a lot of strange things that happen when people make decisions under risk, like the certainty effect, the isolation effect, and preference reversals. This makes prospect theory very important in behavioral finance and economics.Frydman et al. provide additional evidence for the realized utility theory by demonstrating that brain responses, particularly in reward-related regions, correspond to the pleasure obtained from selling winning assets [761]. Recent emotional neuroscience research shows that brain signals from areas like the nucleus accumbens (NAcc) can predict market-level outcomes such as crowdfunding campaign success and collective investing decisions. These findings highlight how emotional and cognitive processes accessible by brain imaging help to better understand financial psychology and behavior [114].Having established these micro-level cognitive and neural mechanisms, we can now examine how similar psychological forces scale up to shape aggregate market behavior and asset prices.
- Market behavior, investor biases, and overconfidence: Shiller questions the efficient market theory, demonstrating that stock values are too volatile due to investor mood, over-reaction, and herd behavior [764,765]. He considers market prices to deviate from fundamentals owing to investor mood. A basic mispricing dynamic, using sentiment , may be represented as follows:where P signifies the observed price, F is the fundamental value, and weights the psychological sentiment. On the contrary, Odean and Barber show empirical proof of the overconfidence bias and disposition impact, proving that these kinds of actions lower portfolio returns [766,767]. Barber and Odean highlight even more personal investor prejudices, including overconfidence-driven excessive trading and the inclination to sell successes while keeping losses [768]. Greenwood and Shleifer study extrapolative expectations, in which investors wildly extrapolate historical returns into the future, hence creating asset bubbles [769].Beyond these market-wide anomalies, psychological limitations also manifest in how individuals construct portfolios and process basic financial information.
- Cognitive foundations and decision-making: Lusardi and Mitchell investigate the effects of inadequate financial literacy, stressing bad saving habits and credit mismanagement, often exacerbated by restricted attention and difficulties in grasping fundamental financial ideas such as compound interest [770]. Hedesström et al. and Benartzi and Thaler show that rather than addressing the mean-variance portfolio optimization issue, investors often depend on heuristics, including the naïve rule:where n is the number of available assets, is the vector of portfolio weights, is the vector of expected returns, is the covariance matrix of returns, and denotes the investor’s risk aversion. Heuristic-based decision-making of this kind sometimes results in ineffective diversification [771,772].Unlike the efficient market hypothesis, which Shiller challenges with data of too much stock price volatility resulting from investor mood and herd behavior [764,765], other research implies that market efficiency may still be maintained. For example, Akdeniz et al. and Lewis and Whiteman find that under strong decision-making models and general equilibrium theories, efficiency could show up [773,774].While these analyses focus on cross-sectional portfolio choice and market efficiency, psychological influences are equally pronounced in how people trade off consumption and saving over time.
- Financial literacy and temporal choice behavior: Detrimental financial conduct is mostly determined by low financial literacy. Lusardi and Mitchell demonstrate how poor knowledge of ideas like compound interest results in insufficient savings and credit misbehavior [770]. Benartzi and Thaler investigate the heuristic [772], in which investors forgo sophisticated research by simply diversifying blindly across choices. Hyperbolic discounting better captures time-inconsistent desires:where U is the total utility, is the instantaneous utility from consumption at time t, and reflects the degree of present bias. Berns et al. relate these kinds of behaviors to brain processes underpinning intertemporal decision, therefore relating impulsive expenditure to hyperbolic discounting [775]. Hershfield et al. show that seeing one’s future self lowers current bias and promotes saving [776]. Thaler’s theory of mental accounting helps one to understand how individuals divide their money, usually irrationally, which results in contradictory decisions in different situations [777].Beyond cognitive limits and present-biased preferences, affective states and lived experiences further color how individuals perceive and manage financial risks.
- Emotional and experiential influences: Financial decision-making is much shaped by emotions and prior experiences, therefore questioning presumptions of logical conduct. Kuhnen and Knutson emphasize the neurological underpinnings of economic decisions by demonstrating how directly emotional emotions mediated by neurotransmitters such as dopamine impact risk preferences [778]. Cameron and Shah also discover that stressful events, including natural disasters, can cause ongoing changes in risk-taking behavior [779]. Following trauma, they model ongoing risk-aversion changes. One may write a dynamic utility formulation including emotional state as follows:where captures traumatic or emotionally salient events, and is the decay rate of emotional impact. This highlights emotion–memory coupling in behavioral responses. Personal financial history is also very important. Malmendier and Nagel show that those who experienced significant inflation during formative years often choose more cautious investing approaches [780]. Hoelzl and Huber highlight the limits of experience foresight in financial planning, as borrowers can understate long-term repayment obligations, which results in over-indebtedness [781]. Beyond financial situations, subjective emotional states have great predictive power. Simple self-reported emotions, according to Kaiser and Oswald, can predict behavior like job changes and hospital visits better than conventional economic indicators [782]. Under uncertainty and adaptive dynamics specifically, these results highlight the need to include emotional and sensory aspects in models of economic and social behavior. Roberts et al.’s affect-informed decision paradigm also provides insightful analysis for economic psychology, as it shows that emotional valence may change perceived value under various contextual weightings, thereby changing economic choice behavior [151].These findings naturally connect to broader economic–psychological frameworks that formalize how subjective states mediate between objective environments and observable economic behavior.
- Economic psychology and mental models: Economic psychology focuses on the connection between mental processes and economic behavior. Examining how motivation, perspective, decision-making, and social factors impact financial decisions, Antonides offers an integrated picture of psychology and economics [783]. Based on psychological motives and resources, the book explores the Values and Lifestyles (VALS) model, which puts readers into categories including Survivors, Achievers, and Emulators. Structured as a causal chain, Figure 2 offers a fundamental economic psychology model: the external environment (e.g., money; employment) impacts mental processes (e.g., attitudes; expectations), which in turn define behavior (e.g., spending; saving). Rooted in behaviorist psychology, this S-O-R (Stimulus–Organism–Response) model shows how subjective interpretation moderates the effect of economic stimuli [784,785,786].By separating objective economic elements from subjective psychological processes, Figure 3 broadens this model and shows how mental representations, emotions, and societal standards shape financial conduct. This framework shows how closely economic conduct is ingrained in a larger framework of social influence, perspective, and motivation [783].At the level of strategic interaction, these psychological foundations become especially salient when individual incentives conflict with collective welfare.
- Strategic behavior and collective outcomes: The Prisoner’s Dilemma is a prime example of how individual rationality could produce collectively less than ideal results in economic settings. Using this approach, Antonides emphasizes the need for trust, justice, and social conventions in allowing collaboration and enhancing results beyond what simple self-interest suggests for financial decisions [783].Relatedly, when economic behavior is embedded in institutions such as taxation and public spending, psychological responses to fairness and norms can strongly influence contributions to public goods.
- Crowding-out effect and public goods: Economic psychology, to a great extent, investigates how psychological incentives influence public policy responses. It clarifies voluntary contribution decreases under taxes by means of the following equation:where signifies the individual contribution, is intrinsic motivation, denotes the perceived fairness loss due to taxation, and represents the effect of social norms. The crowding-out effect explains how higher government expenditure could lower public good voluntary donations. Apart from substitution effects, this phenomenon is driven by perceived justice, societal conventions, and personal beliefs that defy the conventional wisdom of only maximizing behavior [783].Psychological determinants of economic behavior are equally crucial when individuals and societies confront risks that are complex, low-probability, or difficult to interpret.
- Risk perception and societal decision-making: Slovic and associates investigate how people discern danger, depending more on emotions and heuristics than on probability [787,788,789,790,791,792,793]. These impressions help to form reactions to public hazards, financial risks, and legal rules. Slovic contends, in reality, that emotional heuristics define risk, and the expected value becomes [789]:where is the affective response associated with the outcome x, often diverging from statistical risk assessments. Garling et al. contend that financial crises are caused in part by psychological elements like capital delusion, framing effects, and crowd behavior. They support better financial education that seeks to reduce such prejudices [794].These insights have direct consequences for how markets are regulated and how policies are designed to protect consumers and maintain stability.
- Policy implications and regulation: Campbell et al. investigate how present and status quo bias among behavioral biases affect consumer saving and investment, therefore implying the requirement of customized treatments [795]. According to Akerlof and Shiller, sometimes systemic crises result from emotions, tales, and group dynamics over-riding logical conduct in financial markets [796]. Models of debt and savings guided by behavior combine limited rationality and status quo bias. For example, Bertrand et al. demonstrate that psychological frictions like complexity and framing affect consumer choices on credit intake in addition to interest rates [797]. These results draw attention to cognitive overload and status quo bias, which may be abstracted as a threshold-based behavioral paradigm whereby changes only occur if perceived value increases surpass a psychological cost. Mathematically, it can be modeled as follows:where is a threshold for inertia reflecting emotional or cognitive conflict, and status quo bias suggests that change is avoided until advantages exceed . Also, denotes the net utility gain from switching from the current (status quo) to a new state, and signifies the decision to accept or reject a credit offer. Bertrand et al. look at cognitive overload and framing in debt decisions; Lewis addresses psychological aspects of tax compliance [798]. Selective attention biases shown by Sicherman et al. help to explain overtrading and inadequate asset allocation [799].Debates over market volatility and efficiency further illustrate how far psychological considerations have reshaped the interpretation of financial dynamics.
- Alternative views on market volatility: Shill stresses elevated volatility in stock prices [764]; however, Akdeniz et al. and Lewis & Whiteman provide counterpoints demonstrating that markets may stay efficient or even under-respond to information when modeled under general equilibrium or strong decision frameworks [773,774]. This review shows the need for including psychological insights into financial and economic models. Behavioral finance offers a more realistic framework for analyzing policy design, market behavior, and decision-making by including cognitive limits, emotions, and biases.At the broadest level, these strands of research converge in explaining how psychological forces contribute to financial instability and large-scale economic crises.
- Broader implications and financial crises: Cognitive biases, including overconfidence, framing effects, and herd behavior, help to explain financial instability and crises, according to Garling et al. and Akerlof and Shiller [794,796]. Lewis and Bertrand et al. stress how behavioral biases also influence tax compliance and debt behavior [797,798]. Slovic’s research on risk perception emphasizes how different people misinterpret financial dangers depending on emotions and heuristics, therefore deviating from professional opinions [788,789,791].
8. Decision-Making with Psychological Effects
8.1. Visual Cognition and Cognitive Biases
8.2. Emotion, Sleep Deprivation, and Risk-Taking
8.3. Stochastic Dynamics Under Uncertainty
8.4. Psychological Feedback in AI Systems
8.5. Dynamic Decision Systems and Trait Modulation
8.6. Collective Decision-Making and Emergent Responsiveness
8.7. Applications to Biosocial and Ecological Systems
9. Nonequilibrium Phenomena, Nonlocality, and Complex Psychological Behavior
- t: time;
- : real-valued state variable representing the emotional intensity (e.g., affection or rejection);
- : probability density function (PDF) of individual A’s emotional state x at time t;
- : time-dependent inner evolution rate (velocity) of the emotional state x for individual A;
- : transport term capturing propagation of internal changes in emotional space;
- : external interaction term (gain-loss type) that models the stochastic effect of interactions between individuals A and B, which includes probabilistic changes in feelings due to actual encounters or communication, and depends on both individuals’ emotional state distributions and .
10. Conclusions and Future Directions
Funding
Acknowledgments
Conflicts of Interest
References
- El Zaatari, W.; Maalouf, I. How the Bronfenbrenner bio-ecological system theory explains the development of students’ sense of belonging to school? SAGE Open 2022, 12, 21582440221134089. [Google Scholar] [CrossRef]
- Cannon, W.B. The James-Lange theory of emotions: A critical examination and an alternative theory. Am. J. Psychol. 1927, 39, 106–124. [Google Scholar] [CrossRef]
- Schachter, S.; Singer, J. Cognitive, social, and physiological determinants of emotional state. Psychol. Rev. 1962, 69, 379–399. [Google Scholar] [CrossRef] [PubMed]
- Scherer, K.R.; Moors, A. The Emotion Process: Event Appraisal and Component Differentiation. Annu. Rev. Psychol. 2019, 70, 719–745. [Google Scholar] [CrossRef] [PubMed]
- Fry, C.M.; Ram, N.; Gatzke-Kopp, L.M. Integrating dynamic and developmental time scales: Emotion-specific autonomic coordination predicts baseline functioning over time. Int. J. Psychophysiol. 2022, 171, 29–37. [Google Scholar] [CrossRef] [PubMed]
- Tretter, F.; Löffler-Stastka, H. The human ecological perspective and biopsychosocial medicine. Int. J. Environ. Res. Public Health 2019, 16, 4230. [Google Scholar] [CrossRef]
- Loreau, M. Linking biodiversity and ecosystems: Towards a unifying ecological theory. Philos. Trans. R. Soc. B Biol. Sci. 2010, 365, 49–60. [Google Scholar] [CrossRef]
- Tadić, B.; Melnik, R. Self-Organised Critical Dynamics as a Key to Fundamental Features of Complexity in Physical, Biological, and Social Networks. Dynamics 2021, 1, 181–197. [Google Scholar] [CrossRef]
- Tadić, B.; Dankulov, M.M.; Melnik, R. Evolving cycles and self-organised criticality in social dynamics. Chaos Solitons Fractals 2023, 171, 113459. [Google Scholar] [CrossRef]
- Feldman, W.M. Biomathematics: Being the Principles of Mathematics for Students of Biological Science; C. Griffin & Company, Limited: Lichfield, UK, 1923. [Google Scholar]
- Rashevsky, N. Mathematical Biophysics and Psychology. Psychometrika 1936, 1, 1–26. [Google Scholar] [CrossRef]
- Rashevsky, N. Mathematical Biophysics; Dover Publictions: Garden City, NY, USA, 1938. [Google Scholar]
- Turing, A.M. The chemical basis of morphogenesis. Bull. Math. Biol. 1990, 52, 153–197. [Google Scholar] [CrossRef] [PubMed]
- Murray, J.D. Mathematical Biology I: An Introduction; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Edelstein-Keshet, L. Mathematical Models in Biology; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2005. [Google Scholar]
- Tomlin, C.J.; Axelrod, J.D. Biology by numbers: Mathematical modelling in developmental biology. Nat. Rev. Genet. 2007, 8, 331–340. [Google Scholar] [CrossRef] [PubMed]
- Mittelbach, G.G.; McGill, B.J. Chapter The Fundamentals of Predator–Prey Interactions. In Community Ecology, 2nd ed.; Oxford University Press: Oxford, UK, 2019; pp. 81–95. [Google Scholar]
- Vandermeer, J. How populations grow: The exponential and logistic equations. Nat. Educ. Knowl. 2010, 3, 15. [Google Scholar]
- Cappuccino, N.; Price, P.W. Population Dynamics: New Approaches and Synthesis; Elsevier: Amsterdam, The Netherlands, 1995. [Google Scholar]
- Pal, S.; Melnik, R. Nonlocal models in biology and life sciences: Sources, developments, and applications. Phys. Life Rev. 2025, 53, 24–75. [Google Scholar] [CrossRef]
- Azuaje, F. Computational discrete models of tissue growth and regeneration. Brief. Bioinform. 2011, 12, 64–77. [Google Scholar] [CrossRef]
- Azizi, T. Topological properties of periodic and chaotic attractors. In Novel Research Aspects in Mathematical and Computer Science; Wang, X., Ed.; B P International: Dordrecht, The Netherlands, 2022; Volume 7, pp. 90–105. [Google Scholar]
- Coppin, G.; Sander, D. Theoretical approaches to emotion and its measurement. In Emotion Measurement, 7th ed.; Meiselman, H.L., Ed.; Woodhead Publishing: Cambridge, UK, 2021; pp. 3–37. [Google Scholar]
- Stam, C.J.; Reijneveld, J.C. Graph theoretical analysis of complex networks in the brain. Nonlinear Biomed. Phys. 2007, 1, 3. [Google Scholar] [CrossRef]
- Bullmore, E.; Sporns, O. Complex brain networks: Graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 2009, 10, 186–198. [Google Scholar] [CrossRef]
- Sporns, O.; Tononi, G.; Kötter, R. The human connectome: A structural description of the human brain. PLoS Comput. Biol. 2005, 1, e42. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Meunier, D.; Lambiotte, R.; Bullmore, E.T. Modular and hierarchically modular organization of brain networks. Front. Neurosci. 2010, 4, 200. [Google Scholar] [CrossRef]
- Achard, S.; Salvador, R.; Whitcher, B.; Suckling, J.; Bullmore, E. A resilient, low-frequency, small-world human brain functional network with highly connected association cortical hubs. J. Neurosci. 2006, 26, 63–72. [Google Scholar] [CrossRef]
- Muldoon, S.F.; Bridgeford, E.W.; Bassett, D.S. Small-World Propensity and Weighted Brain Networks. Sci. Rep. 2016, 6, 22057. [Google Scholar] [CrossRef] [PubMed]
- Laughlin, S.B.; Sejnowski, T.J. Communication in neuronal networks. Science 2003, 301, 1870–1874. [Google Scholar] [CrossRef] [PubMed]
- Cherniak, C. Component placement optimization in the brain. J. Neurosci. 1994, 14, 2418–2427. [Google Scholar] [CrossRef] [PubMed]
- Klyachko, V.A.; Stevens, C.F. Connectivity optimization and the positioning of cortical areas. Proc. Natl. Acad. Sci. USA 2003, 100, 7937–7941. [Google Scholar] [CrossRef]
- Chklovskii, D.B.; Schikorski, T.; Stevens, C.F. Wiring optimization in cortical circuits. Neuron 2002, 34, 341–347. [Google Scholar] [CrossRef]
- Cherniak, C.; Mokhtarzada, Z.; Rodriguez-Esteban, R.; Changizi, K. Global optimization of cerebral cortex layout. Proc. Natl. Acad. Sci. USA 2004, 101, 1081–1086. [Google Scholar] [CrossRef]
- White, J.G.; Southgate, E.; Thomson, J.N.; Brenner, S. The structure of the nervous system of the nematode Caenorhabditis elegans. Phil. Trans. R. Soc. Lond B Biol. Sci. 1986, 314, 340. [Google Scholar]
- Niven, J.E.; Laughlin, S.B. Energy limitation as a selective pressure on the evolution of sensory systems. J. Exp. Biol. 2008, 211, 1792–1804. [Google Scholar] [CrossRef]
- Chklovskii, D.B. Exact Solution for the Optimal Neuronal Layout Problem. Neural Comput. 2004, 16, 2067–2078. [Google Scholar] [CrossRef]
- Salvador, R.; Suckling, J.; Coleman, M.R.; Pickard, J.D.; Menon, D.; Bullmore, E. Neurophysiological Architecture of Functional Magnetic Resonance Images of Human Brain. Cereb. Cortex 2005, 15, 1332–1342. [Google Scholar] [CrossRef] [PubMed]
- Kaiser, M.; Hilgetag, C.C. Spatial growth of real-world networks. Phys. Rev. E 2004, 69, 036103. [Google Scholar] [CrossRef] [PubMed]
- Kaiser, M.; Hilgetag, C.C. Modelling the development of cortical networks. Neurocomputing 2004, 58, 297–302. [Google Scholar] [CrossRef]
- Yook, S.H.; Jeong, H.; Barabási, A.L. Modeling the Internet’s large-scale topology. Proc. Natl. Acad. Sci. USA 2002, 99, 13382–13386. [Google Scholar] [CrossRef]
- Vértes, P.E.; Alexander-Bloch, A.F.; Gogtay, N.; Giedd, J.N.; Rapoport, J.L.; Bullmore, E.T. Simple models of human brain functional networks. Proc. Natl. Acad. Sci. USA 2012, 109, 5868–5873. [Google Scholar] [CrossRef]
- Tajima, Y.; Nagatani, T. Scaling behavior of crowd flow outside a hall. Phys. A Stat. Mech. Its Appl. 2001, 292, 545–554. [Google Scholar] [CrossRef]
- Helbing, D.; Isobe, M.; Nagatani, T.; Takimoto, K. Lattice gas simulation of experimentally studied evacuation dynamics. Phys. Rev. E 2003, 67, 067101. [Google Scholar] [CrossRef]
- Helbing, D.; Molnar, P. Social force model for pedestrian dynamics. Phys. Rev. E 1995, 51, 4282. [Google Scholar] [CrossRef]
- Helbing, D.; Farkas, I.; Vicsek, T. Simulating dynamical features of escape panic. Nature 2000, 407, 487–490. [Google Scholar] [CrossRef]
- Seyfried, A.; Steffen, B.; Lippert, T. Basics of modelling the pedestrian flow. Phys. A Stat. Mech. Its Appl. 2006, 368, 232–238. [Google Scholar] [CrossRef]
- Sticco, I.M.; Frank, G.A.; Cornes, F.E.; Dorso, C.O. A re-examination of the role of friction in the original Social Force Model. Saf. Sci. 2020, 121, 42–53. [Google Scholar] [CrossRef]
- Parisi, D.R.; Dorso, C.O. Microscopic dynamics of pedestrian evacuation. Phys. A Stat. Mech. Its Appl. 2005, 354, 606–618. [Google Scholar] [CrossRef]
- Parisi, D.R.; Dorso, C.O. Morphological and dynamical aspects of the room evacuation process. Phys. A Stat. Mech. Its Appl. 2007, 385, 343–355. [Google Scholar] [CrossRef]
- Zheng, M.; Kashimori, Y.; Kambara, T. A model describing collective behaviors of pedestrians with various personalities in danger situations. In Proceedings of the 9th International Conference on Neural Information Processing, 2002, ICONIP’02, Singapore, 18–22 November 2002; IEEE: New York, NY, USA, 2002; Volume 4, pp. 2083–2087. [Google Scholar]
- Guo, R.; Huang, H.J. A mobile lattice gas model for simulating pedestrian evacuation. Phys. A Stat. Mech. Its Appl. 2008, 387, 580–586. [Google Scholar] [CrossRef]
- Song, W.; Xu, X.; Wang, B.H.; Ni, S. Simulation of evacuation processes using a multi-grid model for pedestrian dynamics. Phys. A Stat. Mech. Its Appl. 2006, 363, 492–500. [Google Scholar] [CrossRef]
- Hughes, R.L. A continuum theory for the flow of pedestrians. Transp. Res. Part B Methodol. 2002, 36, 507–535. [Google Scholar] [CrossRef]
- Colombo, R.M.; Rosini, M.D. Pedestrian flows and non-classical shocks. Math. Methods Appl. Sci. 2005, 28, 1553–1567. [Google Scholar] [CrossRef]
- Goldstone, R.L.; Janssen, M.A. Computational models of collective behavior. Trends Cogn. Sci. 2005, 9, 424–430. [Google Scholar] [CrossRef]
- Lo, S.M.; Huang, H.C.; Wang, P.; Yuen, K. A game theory based exit selection model for evacuation. Fire Saf. J. 2006, 41, 364–369. [Google Scholar] [CrossRef]
- Daoliang, Z.; Lizhong, Y.; Jian, L. Exit dynamics of occupant evacuation in an emergency. Phys. A Stat. Mech. Its Appl. 2006, 363, 501–511. [Google Scholar] [CrossRef]
- Jian, L.; Lizhong, Y.; Daoliang, Z. Simulation of bi-direction pedestrian movement in corridor. Phys. A Stat. Mech. Its Appl. 2005, 354, 619–628. [Google Scholar] [CrossRef]
- Perez, G.J.; Tapang, G.; Lim, M.; Saloma, C. Streaming, disruptive interference and power-law behavior in the exit dynamics of confined pedestrians. Phys. A Stat. Mech. Its Appl. 2002, 312, 609–618. [Google Scholar] [CrossRef]
- Varas, A.; Cornejo, M.; Mainemer, D.; Toledo, B.; Rogan, J.; Munoz, V.; Valdivia, J. Cellular automaton model for evacuation process with obstacles. Phys. A Stat. Mech. Its Appl. 2007, 382, 631–642. [Google Scholar] [CrossRef]
- Yu, Y.; Song, W. Cellular automaton simulation of pedestrian counter flow considering the surrounding environment. Phys. Rev. E 2007, 75, 046112. [Google Scholar] [CrossRef]
- Hamagami, T.; Hirata, H. Method of crowd simulation by using multiagent on cellular automata. In Proceedings of the IEEE/WIC International Conference on Intelligent Agent Technology (IAT 2003), Halifax, NA, Canada, 13–17 October 2003; IEEE: New York, NY, USA, 2003; pp. 46–52. [Google Scholar]
- Kirchner, A.; Nishinari, K.; Schadschneider, A. Friction effects and clogging in a cellular automaton model for pedestrian dynamics. Phys. Rev. E 2003, 67, 056122. [Google Scholar] [CrossRef]
- Li, S.; Niu, H. Simulation of Bi-direction Pedestrian Movement in Corridor Based on Crowd Space. Procedia-Soc. Behav. Sci. 2014, 138, 323–331. [Google Scholar] [CrossRef]
- Weng, W.; Chen, T.; Yuan, H.; Fan, W. Cellular automaton simulation of pedestrian counter flow with different walk velocities. Phys. Rev. E 2006, 74, 036102. [Google Scholar] [CrossRef]
- Song, G.; Park, J. Discrete element method for emergency flow of pedestrian in S-type corridor. J. Nanosci. Nanotechnol. 2014, 14, 7469–7476. [Google Scholar] [CrossRef]
- Oh, H.; Park, J. Main factor causing “faster-is-slower” phenomenon during evacuation: Rodent experiment and simulation. Sci. Rep. 2017, 7, 13724. [Google Scholar] [CrossRef]
- Park, J.H.; Lee, D.; Kim, H.; Yang, Y. Development of evacuation model for human safety in maritime casualty. Ocean Eng. 2004, 31, 1537–1547. [Google Scholar] [CrossRef]
- Gotoh, H.; Harada, E.; Kubo, Y.; Sakai, T. Particle-system model of the behavior of crowd in tsunami flood refuge. Annu. J. Coast. Eng. JSCE 2004, 51, 1261–1265. [Google Scholar]
- Abustan, M.S.; Harada, E.; Gotoh, H. Numerical simulation for evacuation process against tsunami disaster at Teluk Batik in Malaysia by multi-agent DEM model. In Proceedings of the Coastal Engineering, JSCE, Nagoya, Japan, 5–7 September 2012; Volume 3, pp. 56–60. [Google Scholar]
- Tsuji, Y. Numerical Simulation of Pedestrian Flow at High Densities. Pedestr. Evacuation Dyn. 2003, 3, 27–38. [Google Scholar]
- Langston, P.A.; Masling, R.; Asmar, B.N. Crowd dynamics discrete element multi-circle model. Saf. Sci. 2006, 44, 395–417. [Google Scholar] [CrossRef]
- Gotoh, H.; Harada, E.; Andoh, E. Simulation of pedestrian contra-flow by multi-agent DEM model with self-evasive action model. Saf. Sci. 2012, 50, 326–332. [Google Scholar] [CrossRef]
- Zheng, X.; Zhong, T.; Liu, M. Modeling crowd evacuation of a building based on seven methodological approaches. Build. Environ. 2009, 44, 437–445. [Google Scholar] [CrossRef]
- Fudenberg, D.; Newey, W.; Strack, P.; Strzalecki, T. Testing the drift-diffusion model. Proc. Natl. Acad. Sci. USA 2020, 117, 33141–33148. [Google Scholar] [CrossRef]
- Vellmer, S.; Lindner, B. Decision-time statistics of nonlinear diffusion models: Characterizing long sequences of subsequent trials. J. Math. Psychol. 2020, 99, 102445. [Google Scholar] [CrossRef]
- Smith, P.L. The Poisson shot noise model of visual short-term memory and choice response time: Normalized coding by neural population size. J. Math. Psychol. 2015, 66, 41–52. [Google Scholar] [CrossRef]
- Mavrodiev, P.; Tessone, C.J.; Schweitzer, F. Quantifying the effects of social influence. Sci. Rep. 2013, 3, 1360. [Google Scholar] [CrossRef]
- Mavrodiev, P.; Schweitzer, F. The ambigous role of social influence on the wisdom of crowds: An analytic approach. Phys. A Stat. Mech. Its Appl. 2021, 567, 125624. [Google Scholar] [CrossRef]
- Haghani, M.; Sarvi, M. Imitative (herd) behaviour in direction decision-making hinders efficiency of crowd evacuation processes. Saf. Sci. 2019, 114, 49–60. [Google Scholar] [CrossRef]
- Gold, J.I.; Shadlen, M.N. The neural basis of decision making. Annu. Rev. Neurosci. 2007, 30, 535–574. [Google Scholar] [CrossRef] [PubMed]
- Bogacz, R.; Brown, E.; Moehlis, J.; Holmes, P.; Cohen, J.D. The physics of optimal decision making: A formal analysis of models of performance in two-alternative forced-choice tasks. Psychol. Rev. 2006, 113, 700. [Google Scholar] [CrossRef] [PubMed]
- Bitzer, S.; Park, H.; Blankenburg, F.; Kiebel, S.J. Perceptual decision making: Drift-diffusion model is equivalent to a Bayesian model. Front. Hum. Neurosci. 2014, 8, 102. [Google Scholar] [CrossRef]
- Fard, P.R.; Park, H.; Warkentin, A.; Kiebel, S.J.; Bitzer, S. A Bayesian reformulation of the extended drift-diffusion model in perceptual decision making. Front. Comput. Neurosci. 2017, 11, 29. [Google Scholar] [CrossRef]
- Diederich, A.; Colonius, H. A two-stage diffusion modeling approach to the compelled-response task. Psychol. Rev. 2021, 128, 787. [Google Scholar] [CrossRef]
- Fan, R.; Varol, O.; Varamesh, A.; Barron, A.; van de Leemput, I.A.; Scheffer, M.; Bollen, J. The minute-scale dynamics of online emotions reveal the effects of affect labeling. Nat. Hum. Behav. 2019, 3, 92–100. [Google Scholar] [CrossRef]
- Dokka, K.; Park, H.; Jansen, M.; DeAngelis, G.C.; Angelaki, D.E. Causal inference accounts for heading perception in the presence of object motion. Proc. Natl. Acad. Sci. USA 2019, 116, 9060–9065. [Google Scholar] [CrossRef]
- Dokka, K.; DeAngelis, G.C.; Angelaki, D.E. Multisensory integration of visual and vestibular signals improves heading discrimination in the presence of a moving object. J. Neurosci. 2015, 35, 13599–13607. [Google Scholar] [CrossRef]
- Noel, J.P.; Angelaki, D.E. Cognitive, systems, and computational neurosciences of the self in motion. Annu. Rev. Psychol. 2022, 73, 103–129. [Google Scholar] [CrossRef]
- Li, H.; Li, H.; Ma, L.; Polina, D. Revealing brain’s cognitive process deeply: A study of the consistent EEG patterns of audio-visual perceptual holistic. Front. Hum. Neurosci. 2024, 18, 1377233. [Google Scholar] [CrossRef] [PubMed]
- Thieu, T.; Melnik, R. Social human collective decision-making and its applications with brain network models. In Crowd Dynamics, Volume 4: Analytics and Human Factors in Crowd Modeling; Bellomo, N., Gibelli, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2023; pp. 103–141. [Google Scholar]
- Thieu, T.; Melnik, R. Modelling the behavior of human crowds as coupled active-passive dynamics of interacting particle systems. Methodol. Comput. Appl. Probab. 2025, 27, 15. [Google Scholar] [CrossRef]
- Burge, J.; Bonnen, K. Continuous psychophysics: Past, present, future. Trends Cogn. Sci. 2025, 29, 481–493. [Google Scholar] [CrossRef] [PubMed]
- Waskom, M.L.; Okazawa, G.; Kiani, R. Designing and Interpreting Psychophysical Investigations of Cognition. Neuron 2019, 104, 100–112. [Google Scholar] [CrossRef]
- Narayanan, S.; Georgiou, P.G. Behavioral Signal Processing: Deriving Human Behavioral Informatics From Speech and Language. Proc. IEEE 2013, 101, 1203–1233. [Google Scholar] [CrossRef]
- Hernández-Gutiérrez, D.; Sorrel, M.A.; Shanks, D.R.; Vadillo, M.A. The Conscious Side of ‘Subliminal’ Linguistic Priming: A Systematic Review with Meta-Analysis and Reliability Analysis of Visibility Measures. J. Cogn. 2025, 8, 13. [Google Scholar] [CrossRef]
- Ten Oever, S.; Titone, L.; Te Rietmolen, N.; Martin, A.E. Phase-dependent word perception emerges from region-specific sensitivity to the statistics of language. Proc. Natl. Acad. Sci. USA 2024, 121, e2320489121. [Google Scholar] [CrossRef]
- Ambrosio, B. Beyond the brain: Towards a mathematical modeling of emotions. In Proceedings of the 10th International Conference on Mathematical Modeling in Physical Sciences (IC-MSQUARE 2021), Virtual, 6–9 September 2021; Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2021; Volume 2090, p. 012119. [Google Scholar] [CrossRef]
- Mattek, A.M.; Wolford, G.L.; Whalen, P.J. A Mathematical Model Captures the Structure of Subjective Affect. Perspect. Psychol. Sci. 2017, 12, 508–526. [Google Scholar] [CrossRef]
- Asghar, N.; Kobyzev, I.; Hoey, J.; Poupart, P.; Sheikh, M.B. Generating Emotionally Aligned Responses in Dialogues using Affect Control Theory. arXiv 2020, arXiv:2003.03645. [Google Scholar] [CrossRef]
- Ojha, S.; Vitale, J.; Williams, M.A. EEGS: A transparent model of emotions. arXiv 2020, arXiv:2011.02573. [Google Scholar] [CrossRef]
- Zhang, J.E.; Hilpert, B.; Broekens, J.; Jokinen, J.P.P. Simulating Emotions with an Integrated Computational Model of Appraisal and Reinforcement Learning. In Proceedings of the 2024 CHI Conference on Human Factors in Computing Systems, New York, NY, USA, 11–16 May 2024; pp. 1–12. [Google Scholar]
- Yanagisawa, H. Free-Energy Model of Emotion Potential: Modeling Arousal Potential as Information Content Induced by Complexity and Novelty. Front. Comput. Neurosci. 2021, 15, 698252. [Google Scholar] [CrossRef] [PubMed]
- Yanagisawa, H.; Wu, X.; Ueda, K.; Kato, T. Free energy model of emotional valence in dual-process perceptions. Neural Netw. 2023, 157, 422–436. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Dang, T.; Sethu, V.; Ambikairajah, E. Dual-Constrained Dynamical Neural ODEs for Ambiguity-aware Continuous Emotion Prediction. In Proceedings of the Interspeech, Kos Island, Greece, 1–5 September 2024; pp. 3185–3189. [Google Scholar]
- Kervadec, C.; Vielzeuf, V.; Pateux, S.; Lechervy, A.; Jurie, F. CAKE: Compact and accurate K-dimensional representation of emotion. arXiv 2018, arXiv:1807.11215. [Google Scholar] [CrossRef]
- Dong, H.; Li, N.; Fan, L.; Wei, J.; Xu, J. Integrative interaction of emotional speech in audio-visual modality. Front. Neurosci. 2022, 16, 797277. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Huangfu, X.; Tong, D.; He, A. Regional gray matter volume mediates the relationship between neuroticism and depressed emotion. Front. Psychol. 2022, 13, 993694. [Google Scholar] [CrossRef]
- Kim, S.G. On the encoding of natural music in computational models and human brains. Front. Neurosci. 2022, 16, 928841. [Google Scholar] [CrossRef]
- Das, A.; Mock, J.; Irani, F.; Huang, Y.; Najafirad, P.; Golob, E. Multimodal explainable AI predicts upcoming speech behavior in adults who stutter. Front. Neurosci. 2022, 16, 912798. [Google Scholar] [CrossRef]
- Chen, J.; Min, C.; Wang, C.; Tang, Z.; Liu, Y.; Hu, X. Electroencephalograph-based emotion recognition using brain connectivity feature and domain adaptive residual convolution model. Front. Neurosci. 2022, 16, 878146. [Google Scholar] [CrossRef]
- Suomala, J.; Kauttonen, J. Human’s Intuitive Mental Models as a Source of Realistic Artificial Intelligence and Engineering. Front. Psychol. 2022, 13, 873289. [Google Scholar] [CrossRef]
- Neuroscience News. Detecting Hidden Brain States with Mathematical Models. Available online: https://neurosciencenews.com/math-models-brain-state-22789/ (accessed on 23 May 2025).
- Silverstein, S.M.; Wibral, M.; Phillips, W.A. Implications of information theory for computational modeling of schizophrenia. Comput. Psychiatry 2017, 1, 82–101. [Google Scholar] [CrossRef]
- Tian, Y.; Tan, Z.; Hou, H.; Li, G.; Cheng, A.; Qiu, Y.; Weng, K.; Chen, C.; Sun, P. Theoretical foundations of studying criticality in the brain. Netw. Neurosci. 2022, 6, 1148–1185. [Google Scholar] [CrossRef] [PubMed]
- Dankulov, M.M.; Melnik, R.; Tadić, B. The dynamics of meaningful social interactions and the emergence of collective knowledge. Sci. Rep. 2015, 5, 12197. [Google Scholar] [CrossRef] [PubMed]
- Tadić, B.; Dankulov, M.M.; Melnik, R. Mechanisms of self-organized criticality in social processes of knowledge creation. Phys. Rev. E 2017, 96, 032307. [Google Scholar] [CrossRef] [PubMed]
- Tadić, B.; Melnik, R. Fundamental interactions in self-organised critical dynamics on higher order networks. Eur. Phys. J. B 2024, 97, 68. [Google Scholar] [CrossRef]
- Carbonaro, B.; Serra, N. Towards Mathematical Models in Psychology: A Stochastic Description of Human Feelings. Math. Model. Methods Appl. Sci. 2002, 12, 1453–1490. [Google Scholar] [CrossRef]
- Cantor, C. Post-traumatic stress disorder: Evolutionary perspectives. Aust. N. Z. J. Psychiatry 2009, 43, 1038–1048. [Google Scholar] [CrossRef]
- Markowitz, F.E. The Effects of Stigma on the Psychological Well-Being and Life Satisfaction of Persons with Mental Illness. J. Health Soc. Behav. 1998, 39, 335–347. [Google Scholar] [CrossRef]
- Lam, D.C.; Salkovskis, P.M.; Warwick, H.M. An experimental investigation of the impact of biological versus psychological explanations of the cause of “mental illness”. J. Ment. Health 2005, 14, 453–464. [Google Scholar] [CrossRef]
- Holmes, A.M.; Deb, P. The Effect of Chronic Illness on the Psychological Health of Family Members. J. Ment. Health Policy Econ. 2003, 6, 13–22. [Google Scholar]
- Oyserman, D.; Bybee, D.; Mowbray, C. Influences of maternal mental illness on psychological outcomes for adolescent children. J. Adolesc. 2002, 25, 587–602. [Google Scholar] [CrossRef] [PubMed]
- Williams, K.; Frech, A.; Carlson, D.L. Marital Status and Mental Health. In A Handbook for the Study of Mental Health: Social Contexts, Theories, and Systems; Williams, K., Frech, A., Carlson, D.L., Eds.; Cambridge University Press: Cambridge, UK, 2009; pp. 306–320. [Google Scholar]
- Gilsbach, S.; Herpertz-Dahlmann, B.; Konrad, K. Psychological impact of the COVID-19 pandemic on children and adolescents with and without mental disorders. Front. Public Health 2021, 9, 679041. [Google Scholar] [CrossRef] [PubMed]
- Iasevoli, F.; Fornaro, M.; D’Urso, G.; Galletta, D.; Casella, C.; Paternoster, M.; Buccelli, C.; de Bartolomeis, A. the COVID-19 in Psychiatry Study Group. Psychological distress in patients with serious mental illness during the COVID-19 outbreak and one-month mass quarantine in Italy. Psychol. Med. 2021, 51, 1054–1056. [Google Scholar] [CrossRef] [PubMed]
- Lobban, F.; Barrowclough, C.; Jones, S. A review of the role of illness models in severe mental illness. Clin. Psychol. Rev. 2003, 23, 171–196. [Google Scholar] [CrossRef]
- Barrowclough, C.; Tarrier, N.; Johnston, M. Distress, Expressed Emotion, and Attributions in Relatives of Schizophrenia Patients. Schizophr. Bull. 1996, 22, 691–701. [Google Scholar] [CrossRef]
- Hinrichsen, G.; Lieberman, J. Family attributions and coping in the prediction of emotional adjustment in family members of patients with first-episode schizophrenia. Acta Psychiatr. Scand. 1999, 100, 359–366. [Google Scholar] [CrossRef]
- Chadwick, P.; Birchwood, M. The Omnipotence of Voices: A Cognitive Approach to Auditory Hallucinations. Br. J. Psychiatry 1994, 164, 190–201. [Google Scholar] [CrossRef]
- Birchwood, M.; Iqbal, Z.; Chadwick, P.; Trower, P. Cognitive approach to depression and suicidal thinking in psychosis: I. Ontogeny of post-psychotic depression. Br. J. Psychiatry 2000, 177, 516–521. [Google Scholar] [CrossRef]
- Chadwick, P.; Sambrooke, S.; Rasch, S.; Davies, E. Challenging the omnipotence of voices: Group cognitive behavior therapy for voices. Behav. Res. Ther. 2000, 38, 993–1003. [Google Scholar] [CrossRef]
- Barrowclough, C.; Lobban, F.; Hatton, C.; Quinn, J. An investigation of models of illness in carers of schizophrenia patients using the Illness Perception Questionnaire. Br. J. Clin. Psychol. 2001, 40, 371–385. [Google Scholar] [CrossRef]
- Östman, M.; Kjellin, L. Stigma by association: Psychological factors in relatives of people with mental illness. Br. J. Psychiatry 2002, 181, 494–498. [Google Scholar] [CrossRef] [PubMed]
- Birchwood, M.; Mason, R.; MacMillan, F.; Healy, J. Depression, demoralization and control over psychotic illness: A comparison of depressed and non-depressed patients with a chronic psychosis. Psychol. Med. 1993, 23, 387–395. [Google Scholar] [CrossRef] [PubMed]
- Morrison, A.P. A cognitive analysis of the maintenance of auditory hallucinations: Are voices to schizophrenia what bodily sensations are to panic? Behav. Cogn. Psychother. 1998, 26, 289–302. [Google Scholar] [CrossRef]
- Wahl, O.F. Mass media images of mental illness: A review of the literature. J. Community Psychol. 1992, 20, 343–352. [Google Scholar] [CrossRef]
- Wahl, O.F.; Roth, R. Television images of mental illness: Results of a metropolitan Washington media watch. J. Broadcast. Electron. Media 1982, 26, 599–605. [Google Scholar] [CrossRef]
- Domino, G. Impact of the film, One Flew Over the Cuckoo’s Nest, on attitudes towards mental illness. Psychol. Rep. 1983, 53, 179–182. [Google Scholar] [CrossRef]
- Wahl, O.F.; Lefkowits, J.Y. Impact of a Television Film on Attitudes Toward Mental Illness. Am. J. Community Psychol. 1989, 17, 521. [Google Scholar] [CrossRef]
- Lannes, A.; Bui, E.; Arnaud, C.; Raynaud, J.P.; Revet, A. Preventive interventions in offspring of parents with mental illness: A systematic review and meta-analysis of randomized controlled trials. Psychol. Med. 2021, 51, 2321–2336. [Google Scholar] [CrossRef]
- Garber, J.; Clarke, G.N.; Weersing, V.R.; Beardslee, W.R.; Brent, D.A.; Gladstone, T.R.; DeBar, L.L.; Lynch, F.L.; D’Angelo, E.; Hollon, S.D.; et al. Prevention of depression in at-risk adolescents: A randomized controlled trial. JAMA 2009, 301, 2215–2224. [Google Scholar] [CrossRef]
- Beardslee, W.R.; Brent, D.A.; Weersing, V.R.; Clarke, G.N.; Porta, G.; Hollon, S.D.; Gladstone, T.R.; Gallop, R.; Lynch, F.L.; Iyengar, S.; et al. Prevention of depression in at-risk adolescents: Longer-term effects. JAMA Psychiatry 2013, 70, 1161–1170. [Google Scholar] [CrossRef]
- Ginsburg, G.S.; Tein, J.Y.; Riddle, M.A. Preventing the Onset of Anxiety Disorders in Offspring of Anxious Parents: A Six-Year Follow-up. Child Psychiatry Hum. Dev. 2021, 52, 751–760. [Google Scholar] [CrossRef] [PubMed]
- Lam, W.K.; Fals-Stewart, W.; Kelley, M.L. Effects of parent skills training with behavioral couples therapy for alcoholism on children: A randomized clinical pilot trial. Addict. Behav. 2008, 33, 1076–1080. [Google Scholar] [CrossRef] [PubMed]
- Stanger, C.; Ryan, S.R.; Fu, H.; Budney, A.J. Parent training plus contingency management for substance abusing families: A complier average causal effects (CACE) analysis. Drug Alcohol Depend. 2011, 118, 119–126. [Google Scholar] [CrossRef] [PubMed]
- Stein, A.; Netsi, E.; Lawrence, P.J.; Granger, C.; Kempton, C.; Craske, M.G.; Nickless, A.; Mollison, J.; Stewart, D.A.; Rapa, E.; et al. Mitigating the impact of persistent postnatal depression on child outcomes: A randomised controlled trial of an intervention to treat depression and improve parenting. Lancet Psychiatry 2018, 5, 134–144. [Google Scholar] [CrossRef]
- Roberts, I.D.; HajiHosseini, A.; Hutcherson, C.A. How bad becomes good: A neurocomputational model of affect-informed choice. Emotion 2024, 24, 1737. [Google Scholar] [CrossRef]
- Chen, M.S.; Cai, Q.; Omari, D.; Sanghvi, D.E.; Lyu, S.; Bonanno, G.A. Emotion regulation and mental health across cultures: A systematic review and meta-analysis. Nat. Hum. Behav. 2025, 9, 1176–1200. [Google Scholar] [CrossRef]
- Chapman, A.L. Dialectical behavior therapy: Current indications and unique elements. Psychiatry 2006, 3, 62. [Google Scholar]
- Dimeff, L.; Linehan, M.M. Dialectical behavior therapy in a nutshell. Calif. Psychol. 2001, 34, 10–13. [Google Scholar]
- Bohlmeijer, E.; Westerhof, G. The Model for Sustainable Mental Health: Future Directions for Integrating Positive Psychology Into Mental Health Care. Front. Psychol. 2021, 12, 747999. [Google Scholar] [CrossRef]
- Harvey, A.G.; Callaway, C.A.; Zieve, G.G.; Gumport, N.B.; Armstrong, C.C. Applying the Science of Habit Formation to Evidence-Based Psychological Treatments for Mental Illness. Perspect. Psychol. Sci. 2022, 17, 572–589. [Google Scholar] [CrossRef]
- Huys, Q.J.; Maia, T.V.; Frank, M.J. Computational psychiatry as a bridge from neuroscience to clinical applications. Nat. Neurosci. 2016, 19, 404–413. [Google Scholar] [CrossRef] [PubMed]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; Adaptive Computation and Machine Learning; The MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Särkkä, S. Bayesian Filtering and Smoothing; Institute of Mathematical Statistics Textbooks; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Ritter, P.; Schirner, M.; McIntosh, A.R.; Jirsa, V.K. The Virtual Brain Integrates Computational Modeling and Multimodal Neuroimaging. Brain Connect. 2013, 3, 121–145. [Google Scholar] [CrossRef] [PubMed]
- Borsboom, D. A network theory of mental disorders. World Psychiatry 2017, 16, 5–13. [Google Scholar] [CrossRef] [PubMed]
- Bringmann, L.F.; Vissers, N.; Wichers, M.; Geschwind, N.; Kuppens, P.; Peeters, F.; Borsboom, D.; Tuerlinckx, F. A Network Approach to Psychopathology: New Insights into Clinical Longitudinal Data. PLoS ONE 2013, 8, e60188. [Google Scholar] [CrossRef]
- Rolls, E.T. Emotion and decision-making explained: A précis. Cortex 2014, 59, 185–193. [Google Scholar] [CrossRef]
- Montague, P.R.; Dolan, R.J.; Friston, K.J.; Dayan, P. Computational psychiatry. Trends Cogn. Sci. 2012, 16, 72–80. [Google Scholar] [CrossRef]
- Hamill, J.; Hallak, J.; Dursun, S.M.; Baker, G. Ayahuasca: Psychological and Physiologic Effects, Pharmacology and Potential Uses in Addiction and Mental Illness. Curr. Neuropharmacol. 2019, 17, 108–128. [Google Scholar] [CrossRef]
- Grob, C.S.; McKenna, D.J.; Callaway, J.C.; Brito, G.S.; Neves, E.S.; Oberlaender, G.; Saide, O.L.; Labigalini, E.; Tacla, C.; Miranda, C.T.; et al. Human psychopharmacology of hoasca, a plant hallucinogen used in ritual context in Brazil. J. Nerv. Ment. Dis. 1996, 184, 86–94. [Google Scholar] [CrossRef]
- Soler, J.; Elices, M.; Franquesa, A.; Barker, S.; Friedlander, P.; Feilding, A.; Pascual, J.C.; Riba, J. Exploring the therapeutic potential of Ayahuasca: Acute intake increases mindfulness-related capacities. Psychopharmacology 2016, 233, 823–829. [Google Scholar] [CrossRef]
- Barbosa, P.C.R.; Strassman, R.J.; Da Silveira, D.X.; Areco, K.; Hoy, R.; Pommy, J.; Thoma, R.; Bogenschutz, M. Psychological and neuropsychological assessment of regular hoasca users. Compr. Psychiatry 2016, 71, 95–105. [Google Scholar] [CrossRef]
- Bouso, J.C.; González, D.; Fondevila, S.; Cutchet, M.; Fernández, X.; Ribeiro Barbosa, P.C.; Alcázar-Córcoles, M.Á.; Araújo, W.S.; Barbanoj, M.J.; Fábregas, J.M.; et al. Personality, psychopathology, life attitudes and neuropsychological performance among ritual users of Ayahuasca: A longitudinal study. PLoS ONE 2012, 7, e42421. [Google Scholar] [CrossRef] [PubMed]
- Westerhof, G.J.; Keyes, C.L. Mental Illness and Mental Health: The Two Continua Model Across the Lifespan. J. Adult Dev. 2010, 17, 110–119. [Google Scholar] [CrossRef] [PubMed]
- Keyes, C.L.; Eisenberg, D.; Perry, G.S.; Dube, S.R.; Kroenke, K.; Dhingra, S.S. The Relationship of Level of Positive Mental Health with Current Mental Disorders in Predicting Suicidal Behavior and Academic Impairment in College Students. J. Am. Coll. Health 2012, 60, 126–133. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Wu, M.; Zhou, L.; Wang, X.; Jia, J. Cognitive psychology-based artificial intelligence review. Front. Neurosci. 2022, 16, 1024316. [Google Scholar] [CrossRef]
- Sprangers, M.A.; de Regt, E.B.; Andries, F.; van Agt, H.M.; Bijl, R.V.; de Boer, J.B.; Foets, M.; Hoeymans, N.; Jacobs, A.E.; Kempen, G.I.; et al. Which chronic conditions are associated with better or poorer quality of life? J. Clin. Epidemiol. 2000, 53, 895–907. [Google Scholar] [CrossRef]
- Vos, T.; Allen, C.; Arora, M.; Barber, R.M.; Bhutta, Z.A.; Brown, A.; Carter, A.; Casey, D.C.; Charlson, F.J.; Chen, A.Z.; et al. Global, regional, and national incidence, prevalence, and years lived with disability for 310 diseases and injuries, 1990–2015: A systematic analysis for the Global Burden of Disease Study 2015. Lancet 2016, 388, 1545–1602. [Google Scholar] [CrossRef]
- Daré, L.O.; Bruand, P.E.; Gérard, D.; Marin, B.; Lameyre, V.; Boumédiène, F.; Preux, P.M. Co-morbidities of mental disorders and chronic physical diseases in developing and emerging countries: A meta-analysis. BMC Public Health 2019, 19, 304. [Google Scholar] [CrossRef]
- Martino, G.; Catalano, A.; Bellone, F.; Russo, G.T.; Vicario, C.M.; Lasco, A.; Quattropani, M.C.; Morabito, N. As time goes by: Anxiety negatively affects the perceived quality of life in patients with type 2 diabetes of long duration. Front. Psychol. 2019, 10, 1779. [Google Scholar] [CrossRef]
- Rosa, V.; Tomai, M.; Lauriola, M.; Martino, G.; Di, T.M. Body mass index, personality traits, and body image in Italian pre-adolescents: An opportunity for overweight prevention. Psihologija 2019, 52, 379–393. [Google Scholar] [CrossRef]
- Marchini, F.; Caputo, A.; Napoli, A.; Balonan, J.T.; Martino, G.; Nannini, V.; Langher, V. Chronic illness as loss of good self: Underlying mechanisms affecting diabetes adaptation. Mediterr. J. Clin. Psychol. 2018, 6, 1–25. [Google Scholar]
- Miniati, M.; Fabrini, M.G.; Genovesi Ebert, F.; Mancino, M.; Maglio, A.; Massimetti, G.; Massimetti, E.; Marazziti, D. Quality of life, depression, and anxiety in patients with uveal melanoma: A review. J. Oncol. 2018, 2018, 5253109. [Google Scholar] [CrossRef] [PubMed]
- Catalano, A.; Martino, G.; Bellone, F.; Gaudio, A.; Lasco, C.; Langher, V.; Lasco, A.; Morabito, N. Anxiety levels predict fracture risk in postmenopausal women assessed for osteoporosis. Menopause 2018, 25, 1110–1115. [Google Scholar] [CrossRef] [PubMed]
- Martino, G.; Catalano, A.; Bellone, F.; Langher, V.; Lasco, C.; Penna, A.; Nicocia, G.; Morabito, N. Quality of life in postmenopausal women: Which role for vitamin D? Mediterr. J. Clin. Psychol. 2018, 6, 1–14. [Google Scholar]
- Martino, G.; Catalano, A.; Bellone, F.; Sardella, A.; Lasco, C.; Caprì, T.; Langher, V.; Caputo, A.; Fabio, R.A.; Morabito, N. Vitamin D status is associated with anxiety levels in postmenopausal women evaluated for osteoporosis. Mediterr. J. Clin. Psychol. 2018, 6, 1–16. [Google Scholar]
- Ciuluvica, C.; Fulcheri, M.; Amerio, P. Expressive suppression and negative affect, pathways of emotional dysregulation in psoriasis patients. Front. Psychol. 2019, 10, 1907. [Google Scholar] [CrossRef]
- Kelly, R.R.; McDonald, L.T.; Jensen, N.R.; Sidles, S.J.; LaRue, A.C. Impacts of psychological stress on osteoporosis: Clinical implications and treatment interactions. Front. Psychiatry 2019, 10, 443946. [Google Scholar] [CrossRef]
- Marchi, L.; Marzetti, F.; Orrù, G.; Lemmetti, S.; Miccoli, M.; Ciacchini, R.; Hitchcott, P.K.; Bazzicchi, L.; Gemignani, A.; Conversano, C. Alexithymia and psychological distress in patients with fibromyalgia and rheumatic disease. Front. Psychol. 2019, 10, 1735. [Google Scholar] [CrossRef]
- Martino, M.L.; Gargiulo, A.; Lemmo, D.; Dolce, P.; Barberio, D.; Abate, V.; Avino, F.; Tortoriello, R. Longitudinal effect of emotional processing on psychological symptoms in women under 50 with breast cancer. Health Psychol. Open 2019, 6, 2055102919844501. [Google Scholar] [CrossRef]
- Bernard, P.; Romain, A.J.; Caudroit, J.; Chevance, G.; Carayol, M.; Gourlan, M.; Needham Dancause, K.; Moullec, G. Cognitive behavior therapy combined with exercise for adults with chronic diseases: Systematic review and meta-analysis. Health Psychol. 2018, 37, 433–450. [Google Scholar] [CrossRef]
- McGilton, K.S.; Vellani, S.; Yeung, L.; Chishtie, J.; Commisso, E.; Ploeg, J.; Andrew, M.K.; Ayala, A.P.; Gray, M.; Morgan, D.; et al. Identifying and understanding the health and social care needs of older adults with multiple chronic conditions and their caregivers: A scoping review. BMC Geriatr. 2018, 18, 321. [Google Scholar] [CrossRef]
- Shao, J.; Yang, H.; Zhang, Q.; Du, W.; Lei, H. Commonalities and differences in psychological adjustment to chronic illnesses among older adults: A comparative study based on the stress and coping paradigm. Int. J. Behav. Med. 2019, 26, 143–153. [Google Scholar] [CrossRef]
- Carrero, G.; Makin, J.; Malinowski, P. A mathematical model for the dynamics of happiness. Math. Biosci. Eng. 2021, 19, 2002–2029. [Google Scholar] [CrossRef]
- Guicciardi, M.; Crisafulli, A.; Doneddu, A.; Fadda, D.; Lecis, R. Effects of metabolic syndrome on cognitive performance of adults during exercise. Front. Psychol. 2019, 10, 1845. [Google Scholar] [CrossRef] [PubMed]
- Sullivan, M.J.; Thorn, B.; Haythornthwaite, J.A.; Keefe, F.; Martin, M.; Bradley, L.A.; Lefebvre, J.C. Theoretical perspectives on the relation between catastrophizing and pain. Clin. J. Pain 2001, 17, 52–64. [Google Scholar] [CrossRef] [PubMed]
- Lauriola, M.; Tomai, M.; Palma, R.; La Spina, G.; Foglia, A.; Panetta, C.; Raniolo, M.; Pontone, S. Intolerance of uncertainty and anxiety-related dispositions predict pain during upper endoscopy. Front. Psychol. 2019, 10, 1112. [Google Scholar] [CrossRef] [PubMed]
- Stewart, S.T.; Zelinski, E.M.; Wallace, R.B. Age, medical conditions, and gender as interactive predictors of cognitive performance: The effects of selective survival. J. Gerontol. Ser. B Psychol. Sci. Soc. Sci. 2000, 55, P381–P383. [Google Scholar] [CrossRef][Green Version]
- Klein, M.; Silva, M.A.; Belizario, G.O.; Rocca, C.C.d.A.; Padua Serafim, A.D.; Louzã, M.R. Longitudinal neuropsychological assessment in two elderly adults with attention-deficit/hyperactivity disorder: Case report. Front. Psychol. 2019, 10, 1119. [Google Scholar] [CrossRef]
- Dell’Osso, L.; Stratta, P.; Conversano, C.; Massimetti, E.; Akiskal, K.K.; Akiskal, H.S.; Rossi, A.; Carmassi, C. Lifetime mania is related to post-traumatic stress symptoms in high school students exposed to the 2009 L’Aquila earthquake. Compr. Psychiatry 2014, 55, 357–362. [Google Scholar] [CrossRef]
- Settineri, S.; Frisone, F.; Merlo, E.M.; Geraci, D.; Martino, G. Compliance, adherence, concordance, empowerment, and self-management: Five words to manifest a relational maladjustment in diabetes. J. Multidiscip. Healthc. 2019, 12, 299–314. [Google Scholar] [CrossRef]
- Settineri, S.; Frisone, F.; Alibrandi, A.; Merlo, E.M. Emotional Suppression and Oneiric Expression in Psychosomatic Disorders: Early Manifestations in Emerging Adulthood and Young Patients. Front. Psychol. 2019, 10, 1897. [Google Scholar] [CrossRef]
- Schiavon, C.C.; Marchetti, E.; Gurgel, L.G.; Busnello, F.M.; Reppold, C.T. Optimism and hope in chronic disease: A systematic review. Front. Psychol. 2017, 7, 2022. [Google Scholar] [CrossRef] [PubMed]
- Gentili, C.; Rickardsson, J.; Zetterqvist, V.; Simons, L.E.; Lekander, M.; Wicksell, R.K. Psychological flexibility as a resilience factor in individuals with chronic pain. Front. Psychol. 2019, 10, 2016. [Google Scholar] [CrossRef] [PubMed]
- Naro, A.; Milardi, D.; Russo, M.; Terranova, C.; Rizzo, V.; Cacciola, A.; Marino, S.; Calabro, R.S.; Quartarone, A. Non-invasive brain stimulation, a tool to revert maladaptive plasticity in neuropathic pain. Front. Hum. Neurosci. 2016, 10, 376. [Google Scholar] [CrossRef] [PubMed]
- Callus, E.; Pravettoni, G. The role of clinical psychology and peer to peer support in the management of chronic medical conditions—A practical example with adults with congenital heart disease. Front. Psychol. 2018, 9, 731. [Google Scholar] [CrossRef]
- Conversano, C.; Poli, A.; Ciacchini, R.; Hitchcott, P.; Bazzichi, L.; Gemignani, A. A psychoeducational intervention is a treatment for fibromyalgia syndrome. Clin. Exp. Rheumatol. 2019, 37, S98–S104. [Google Scholar]
- Lotka, A.J. Elements of Physical Biology; Williams & Wilkins: Philadelphia, PA, USA, 1925. [Google Scholar]
- Volterra, V. Fluctuations in the abundance of a species considered mathematically. Nature 1926, 118, 558–560. [Google Scholar] [CrossRef]
- Fretwell, S.D.; Lucas, H.L. On territorial behavior and other factors influencing habitat distribution in birds. Acta Biotheor. 1969, 19, 16–36. [Google Scholar] [CrossRef]
- Hethcote, H.W. The mathematics of infectious diseases. SIAM Rev. 2000, 42, 599–653. [Google Scholar] [CrossRef]
- Allen, L.J. An Introduction to Stochastic Processes with Applications to Biology; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Wang, X.; Zanette, L.; Zou, X. Modelling the fear effect in predator–prey interactions. J. Math. Biol. 2016, 73, 1179–1204. [Google Scholar] [CrossRef]
- Stephens, D.W.; Krebs, J.R. Foraging Theory; Monographs in Behavior and Ecology; Princeton University Press: Princeton, NJ, USA, 2019. [Google Scholar]
- Smith, S.E.; Read, D.J. Mycorrhizal Symbiosis; Academic Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Lima, S.L.; Dill, L.M. Behavioral decisions made under the risk of predation: A review and prospectus. Can. J. Zool. 1990, 68, 619–640. [Google Scholar] [CrossRef]
- Sih, A.; Ferrari, M.C.; Harris, D.J. Evolution and behavioural responses to human-induced rapid environmental change. Evol. Appl. 2011, 4, 367–387. [Google Scholar] [CrossRef] [PubMed]
- Pyke, G.H.; Pulliam, H.R.; Charnov, E.L. Optimal Foraging: A Selective Review of Theory and Tests. Q. Rev. Biol. 1977, 52, 137–154. [Google Scholar] [CrossRef]
- Houston, A.I.; McNamara, J.M. Models of Adaptive Behaviour: An Approach Based on State; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Byrne, R.W.; Bates, L.A. Primate social cognition: Uniquely primate, uniquely social, or just unique? Neuron 2010, 65, 815–830. [Google Scholar] [CrossRef] [PubMed]
- Tomasello, M.; Call, J. Thirty years of great ape gestures. Anim. Cogn. 2019, 22, 461–469. [Google Scholar] [CrossRef]
- Emery, N.J.; Clayton, N.S. Comparing the complex cognition of birds and primates. In Comparative Vertebrate Cognition: Are Primates Superior to Nonprimates? Rogers, L., Kaplan, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 3–55. [Google Scholar]
- LeDoux, J.E. The Emotional Brain: The Mysterious Underpinnings of Emotional Life; Simon and Schuster: New York, NY, USA, 1998. [Google Scholar]
- Penn, D.C.; Holyoak, K.J.; Povinelli, D.J. Darwin’s mistake: Explaining the discontinuity between human and nonhuman minds. Behav. Brain Sci. 2008, 31, 109–130. [Google Scholar] [CrossRef]
- De Waal, F. Are We Smart Enough to Know How Smart Animals Are? WW Norton & Company: New York, NY, USA, 2016. [Google Scholar]
- Bekoff, M. Minding Animals: Awareness, Emotions, and Heart; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Panksepp, J. Affective Neuroscience: The Foundations of Human and Animal Emotions (Series in Affective Science); Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Kahneman, D. Thinking, Fast and Slow; Farrar, Straus and Giroux: New York, NY, USA, 2011. [Google Scholar]
- Loewenstein, G.F.; Weber, E.U.; Hsee, C.K.; Welch, N. Risk as feelings. Psychol. Bull. 2001, 127, 267. [Google Scholar] [CrossRef]
- Sun, R.; Naveh, I. Simulating organizational decision-making using a cognitively realistic agent model. J. Artif. Soc. Soc. Simul. 2004, 7, 3. [Google Scholar]
- Epstein, J.M.; Goedecke, D.M.; Yu, F.; Morris, R.J.; Wagener, D.K.; Bobashev, G.V. Controlling pandemic flu: The value of international air travel restrictions. PLoS ONE 2007, 2, e401. [Google Scholar] [CrossRef]
- Epstein, J.M. Generative Social Science: Studies in Agent-Based Computational Modeling; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Thagard, P.; Kunda, Z. Making sense of people: Coherence mechanisms 1. In Connectionist Models of Social Reasoning and Social Behavior; Read, S.J., Miller, L.C., Eds.; Psychology Press: Abingdon, UK, 2014; pp. 3–26. [Google Scholar]
- Schelling, T.C. Dynamic models of segregation. J. Math. Sociol. 1971, 1, 143–186. [Google Scholar] [CrossRef]
- Whiten, A.; Hinde, R.A.; Laland, K.N.; Stringer, C.B. Culture evolves. Philos. Trans. R. Soc. B Biol. Sci. 2011, 366, 938–948. [Google Scholar] [CrossRef]
- Laland, K.N.; Galef, B.G. The Question of Animal Culture; Harvard University Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Henrich, J.; Heine, S.J.; Norenzayan, A. The weirdest people in the world? Behav. Brain Sci. 2010, 33, 61–83. [Google Scholar] [CrossRef]
- Gallup, G.G., Jr. Chimpanzees: Self-recognition. Science 1970, 167, 86–87. [Google Scholar] [CrossRef] [PubMed]
- Povinelli, D. Folk Physics for Apes: The Chimpanzee’s Theory of How the World Works; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Suddendorf, T.; Corballis, M.C. The evolution of foresight: What is mental time travel, and is it unique to humans? Behav. Brain Sci. 2007, 30, 299–313. [Google Scholar] [CrossRef] [PubMed]
- Krupenye, C.; Kano, F.; Hirata, S.; Call, J.; Tomasello, M. Great apes anticipate that other individuals will act according to false beliefs. Science 2016, 354, 110–114. [Google Scholar] [CrossRef] [PubMed]
- Sapolsky, R. Social cultures among nonhuman primates. Curr. Anthropol. 2006, 47, 641–656. [Google Scholar] [CrossRef]
- Buckner, R.L.; Andrews-Hanna, J.R.; Schacter, D.L. The brain’s default network: Anatomy, function, and relevance to disease. Ann. N. Y. Acad. Sci. 2008, 1124, 1–38. [Google Scholar] [CrossRef]
- Lotka, A.J. Analytical note on certain rhythmic relations in organic systems. Proc. Natl. Acad. Sci. USA 1920, 6, 410–415. [Google Scholar] [CrossRef]
- Volterra, V. Variations and fluctuations of the number of individuals in animal species living together. J. Cons. 1928, 3, 3–51. [Google Scholar] [CrossRef]
- Panday, P.; Pal, N.; Samanta, S.; Chattopadhyay, J. Stability and bifurcation analysis of a three-species food chain model with fear. Int. J. Bifurc. Chaos 2018, 28, 1850009. [Google Scholar] [CrossRef]
- Sk, N.; Tiwari, P.K.; Kang, Y.; Pal, S. A nonautonomous model for the interactive effects of fear, refuge and additional food in a prey–predator system. J. Biol. Syst. 2021, 29, 107–145. [Google Scholar] [CrossRef]
- Sk, N.; Tiwari, P.K.; Pal, S. A delay nonautonomous model for the impacts of fear and refuge in a three species food chain model with hunting cooperation. Math. Comput. Simul. 2022, 192, 136–166. [Google Scholar] [CrossRef]
- Han, R.; Mandal, G.; Guin, L.N.; Chakravarty, S. Dynamical response of a reaction–diffusion predator–prey system with cooperative hunting and prey refuge. J. Stat. Mech. Theory Exp. 2022, 2022, 103502. [Google Scholar] [CrossRef]
- Kundu, S.; Maitra, S. Dynamical behaviour of a delayed three species predator–prey model with cooperation among the prey species. Nonlinear Dyn. 2018, 92, 627–643. [Google Scholar] [CrossRef]
- Pal, S.; Pal, N.; Samanta, S.; Chattopadhyay, J. Effect of hunting cooperation and fear in a predator-prey model. Ecol. Complex. 2019, 39, 100770. [Google Scholar] [CrossRef]
- Vishwakarma, K.; Sen, M. Role of Allee effect in prey and hunting cooperation in a generalist predator. Math. Comput. Simul. 2021, 190, 622–640. [Google Scholar] [CrossRef]
- Parshad, R.D.; Basheer, A.; Jana, D.; Tripathi, J.P. Do prey handling predators really matter: Subtle effects of a Crowley-Martin functional response. Chaos Solitons Fractals 2017, 103, 410–421. [Google Scholar] [CrossRef]
- Pettorelli, N.; Coulson, T.; Durant, S.M.; Gaillard, J.M. Predation, individual variability and vertebrate population dynamics. Oecologia 2011, 167, 305–314. [Google Scholar] [CrossRef]
- Skalski, G.T.; Gilliam, J.F. Functional responses with predator interference: Viable alternatives to the Holling type II model. Ecology 2001, 82, 3083–3092. [Google Scholar] [CrossRef]
- Preisser, E.L.; Bolnick, D.I. The many faces of fear: Comparing the pathways and impacts of nonconsumptive predator effects on prey populations. PLoS ONE 2008, 3, e2465. [Google Scholar] [CrossRef]
- Pangle, K.L.; Peacor, S.D.; Johannsson, O.E. Large nonlethal effects of an invasive invertebrate predator on zooplankton population growth rate. Ecology 2007, 88, 402–412. [Google Scholar] [CrossRef]
- Ripple, W.J.; Beschta, R.L. Wolves and the ecology of fear: Can predation risk structure ecosystems? BioScience 2004, 54, 755–766. [Google Scholar] [CrossRef]
- Wirsing, A.J.; Heithaus, M.R.; Dill, L.M. Living on the edge: Dugongs prefer to forage in microhabitats that allow escape from rather than avoidance of predators. Anim. Behav. 2007, 74, 93–101. [Google Scholar] [CrossRef]
- Sih, A. Optimal behavior: Can foragers balance two conflicting demands? Science 1980, 210, 1041–1043. [Google Scholar] [CrossRef] [PubMed]
- Wirsing, A.J.; Ripple, W.J. A comparison of shark and wolf research reveals similar behavioral responses by prey. Front. Ecol. Environ. 2011, 9, 335–341. [Google Scholar] [CrossRef]
- Suraci, J.P.; Clinchy, M.; Dill, L.M.; Roberts, D.; Zanette, L.Y. Fear of large carnivores causes a trophic cascade. Nat. Commun. 2016, 7, 10698. [Google Scholar] [CrossRef]
- Preisser, E.L.; Bolnick, D.I.; Benard, M.F. Scared to death? The effects of intimidation and consumption in predator–prey interactions. Ecology 2005, 86, 501–509. [Google Scholar] [CrossRef]
- Zanette, L.Y.; White, A.F.; Allen, M.C.; Clinchy, M. Perceived predation risk reduces the number of offspring songbirds produce per year. Science 2011, 334, 1398–1401. [Google Scholar] [CrossRef]
- Wang, X.; Zou, X. Modeling the fear effect in predator–prey interactions with adaptive avoidance of predators. Bull. Math. Biol. 2017, 79, 1325–1359. [Google Scholar] [CrossRef]
- Sarkar, K.; Khajanchi, S. Impact of fear effect on the growth of prey in a predator–prey interaction model. Ecol. Complex. 2020, 42, 100826. [Google Scholar] [CrossRef]
- Dong, Y.; Wu, D.; Shen, C.; Ye, L. Influence of fear effect and predator-taxis sensitivity on dynamical behavior of a predator–prey model. Z. Für Angew. Math. Und Phys. 2022, 73, 25. [Google Scholar] [CrossRef]
- Sahoo, D.; Samanta, G. Impact of fear effect in a two prey–one predator system with switching behaviour in predation. Differ. Equ. Dyn. Syst. 2024, 32, 377–399. [Google Scholar] [CrossRef]
- Hamdallah, S.A.; Arafa, A.A. Stability analysis of Filippov prey–predator model with fear effect and prey refuge. J. Appl. Math. Comput. 2024, 70, 73–102. [Google Scholar] [CrossRef]
- Liang, Z.; Meng, X. Stability and Hopf bifurcation of a multiple delayed predator–prey system with fear effect, prey refuge and Crowley–Martin function. Chaos Solitons Fractals 2023, 175, 113955. [Google Scholar] [CrossRef]
- Umrao, A.K.; Srivastava, P.K. Bifurcation analysis of a predator–prey model with Allee effect and fear effect in prey and hunting cooperation in predator. Differ. Equ. Dyn. Syst. 2023, 33, 1123–1149. [Google Scholar] [CrossRef]
- Thirthar, A.A.; Majeed, S.J.; Alqudah, M.A.; Panja, P.; Abdeljawad, T. Fear effect in a predator-prey model with additional food, prey refuge and harvesting on super predator. Chaos Solitons Fractals 2022, 159, 112091. [Google Scholar] [CrossRef]
- Debnath, S.; Majumdar, P.; Sarkar, S.; Ghosh, U. Memory effect on prey–predator dynamics: Exploring the role of fear effect, additional food and anti-predator behaviour of prey. J. Comput. Sci. 2023, 66, 101929. [Google Scholar] [CrossRef]
- Xie, B.; Zhang, Z. Impact of Allee and fear effects in a fractional order prey–predator system incorporating prey refuge. Chaos Interdiscip. J. Nonlinear Sci. 2023, 33, 013131. [Google Scholar] [CrossRef]
- Chauhan, R.; Singh, R.; Kumar, A.; Thakur, N.K. Role of prey refuge and fear level in fractional prey–predator model with anti-predator. J. Comput. Sci. 2024, 81, 102385. [Google Scholar] [CrossRef]
- Saha, S.; Samanta, G. Analysis of a tritrophic food chain model with fear effect incorporating prey refuge. Filomat 2021, 35, 4971–4999. [Google Scholar] [CrossRef]
- Das, A.; Samanta, G.P. Modeling the fear effect on a stochastic prey–predator system with additional food for the predator. J. Phys. A Math. Theor. 2018, 51, 465601. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, S. Dynamics of a stochastic delay predator-prey model with fear effect and diffusion for prey. J. Math. Anal. Appl. 2024, 537, 128267. [Google Scholar] [CrossRef]
- Rao, F.; Kang, Y. Dynamics of a stochastic prey–predator system with prey refuge, predation fear and its carry-over effects. Chaos Solitons Fractals 2023, 175, 113935. [Google Scholar] [CrossRef]
- Qi, H.; Meng, X. Threshold behavior of a stochastic predator–prey system with prey refuge and fear effect. Appl. Math. Lett. 2021, 113, 106846. [Google Scholar] [CrossRef]
- Panday, P.; Samanta, S.; Pal, N.; Chattopadhyay, J. Delay induced multiple stability switch and chaos in a predator–prey model with fear effect. Math. Comput. Simul. 2020, 172, 134–158. [Google Scholar] [CrossRef]
- Dubey, B.; Kumar, A. Stability switching and chaos in a multiple delayed prey–predator model with fear effect and anti-predator behavior. Math. Comput. Simul. 2021, 188, 164–192. [Google Scholar] [CrossRef]
- Debnath, S.; Majumdar, P.; Sarkar, S.; Ghosh, U. Complex dynamical behaviour of a delayed prey-predator model with square root functional response in presence of fear in the prey. Int. J. Model. Simul. 2023, 43, 612–637. [Google Scholar] [CrossRef]
- Li, Y.X.; Liu, H.; Wei, Y.M.; Ma, M.; Ma, G.; Ma, J.Y. Population dynamic study of prey–predator interactions with weak Allee effect, fear effect, and delay. J. Math. 2022, 2022, 8095080. [Google Scholar] [CrossRef]
- Wei, Z.; Chen, F. Dynamics of a delayed predator–prey model with prey refuge, Allee effect and fear effect. Int. J. Bifurc. Chaos 2023, 33, 2350036. [Google Scholar] [CrossRef]
- Cao, Q.; Chen, G.; Yang, W. The impact of fear effect on the dynamics of a delayed predator–prey model with stage structure. Int. J. Biomath. 2023, 16, 2250139. [Google Scholar] [CrossRef]
- Zhang, X.; An, Q.; Wang, L. Spatiotemporal dynamics of a delayed diffusive ratio-dependent predator–prey model with fear effect. Nonlinear Dyn. 2021, 105, 3775–3790. [Google Scholar] [CrossRef]
- Mishra, S.; Upadhyay, R.K. Spatial pattern formation and delay induced destabilization in predator–prey model with fear effect. Math. Methods Appl. Sci. 2022, 45, 6801–6823. [Google Scholar] [CrossRef]
- KP, R.; Kumar, A. Global Dynamics of a Stage Structure Prey–Predator Model with Fear, Group Defense, and Antipredator Behavior. Math. Methods Appl. Sci. 2025, 48, 9819–9839. [Google Scholar] [CrossRef]
- Mondal, S.; Samanta, G. Impact of fear on a predator–prey system with prey-dependent search rate in deterministic and stochastic environment. Nonlinear Dyn. 2021, 104, 2931–2959. [Google Scholar] [CrossRef]
- Ishaque, W.; Din, Q.; Khan, K.A.; Mabela, R.M. Dynamics of Predator–Prey Model Based on Fear Effect with Bifurcation Analysis and Chaos Control. Qual. Theory Dyn. Syst. 2024, 23, 26. [Google Scholar] [CrossRef]
- Sarkar, K.; Khajanchi, S. Spatiotemporal dynamics of a predator-prey system with fear effect. J. Frankl. Inst. 2023, 360, 7380–7414. [Google Scholar] [CrossRef]
- Ke, C.; Yi, M.; Guo, Y. Qualitative analysis of a spatiotemporal prey–predator model with additive Allee effect and fear effect. Complexity 2022, 2022, 5715922. [Google Scholar] [CrossRef]
- Bi, Z.; Liu, S.; Ouyang, M.; Wu, X. Pattern dynamics analysis of spatial fractional predator–prey system with fear factor and refuge. Nonlinear Dyn. 2023, 111, 10653–10676. [Google Scholar] [CrossRef]
- Liu, J.; Kang, Y. Spatiotemporal dynamics of a diffusive predator–prey model with fear effect. Nonlinear Anal. Model. Control 2022, 27, 841–862. [Google Scholar] [CrossRef]
- Souna, F.; Djilali, S.; Lakmeche, A. Spatiotemporal behavior in a predator–prey model with herd behavior and cross-diffusion and fear effect. Eur. Phys. J. Plus 2021, 136, 474. [Google Scholar] [CrossRef]
- Qi, H.; Meng, X.; Hayat, T.; Hobiny, A. Bifurcation dynamics of a reaction–diffusion predator–prey model with fear effect in a predator-poisoned environment. Math. Methods Appl. Sci. 2022, 45, 6217–6254. [Google Scholar] [CrossRef]
- Han, R.; Guin, L.N.; Dai, B. Cross-diffusion-driven pattern formation and selection in a modified Leslie–Gower predator–prey model with fear effect. J. Biol. Syst. 2020, 28, 27–64. [Google Scholar] [CrossRef]
- Pal, D.; Kesh, D.; Mukherjee, D. Cross-diffusion mediated spatiotemporal patterns in a predator–prey system with hunting cooperation and fear effect. Math. Comput. Simul. 2024, 220, 128–147. [Google Scholar] [CrossRef]
- Zhu, N.; Yuan, S. Spatial dynamics of a diffusive prey–predator model with stage structure and fear effect. J. Nonlinear Model. Anal. 2022, 4, 392–408. [Google Scholar]
- Zhang, X.; Zhu, H.; An, Q. Dynamics analysis of a diffusive predator-prey model with spatial memory and nonlocal fear effect. J. Math. Anal. Appl. 2023, 525, 127123. [Google Scholar] [CrossRef]
- Saha, S.; Pal, S.; Melnik, R. Analysis of the impact of fear in the presence of additional food and prey refuge with nonlocal predator–prey models. Ecol. Model. 2025, 505, 111103. [Google Scholar] [CrossRef]
- Dong, X.; Niu, B. On a diffusive predator–prey model with nonlocal fear effect. Appl. Math. Lett. 2022, 132, 108156. [Google Scholar] [CrossRef]
- Sun, X. Dynamics of a diffusive predator–prey model with nonlocal fear effect. Chaos Solitons Fractals 2023, 177, 114221. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, F.; Zhong, L. Stability analysis of a prey–predator model with Holling type III response function incorporating a prey refuge. Appl. Math. Comput. 2006, 182, 672–683. [Google Scholar] [CrossRef]
- Xiao, D.; Ruan, S. Global analysis in a predator–prey system with nonmonotonic functional response. SIAM J. Appl. Math. 2001, 61, 1445–1472. [Google Scholar] [CrossRef]
- Gause, G.F. Experimental analysis of Vito Volterra’s mathematical theory of the struggle for existence. Science 1934, 79, 16–17. [Google Scholar] [CrossRef]
- Ruxton, G.D. Short term refuge use and stability of predator–prey models. Theor. Popul. Biol. 1995, 47, 1–17. [Google Scholar] [CrossRef]
- Du, Y.; Shi, J. A diffusive predator–prey model with a protection zone. J. Differ. Equ. 2006, 229, 63–91. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J. Influence of prey refuge on predator–prey dynamics. Nonlinear Dyn. 2012, 67, 191–201. [Google Scholar] [CrossRef]
- Lv, Y.; Yuan, R.; Pei, Y. A prey-predator model with harvesting for fishery resource with reserve area. Appl. Math. Model. 2013, 37, 3048–3062. [Google Scholar] [CrossRef]
- Wang, J.; Cai, Y.; Fu, S.; Wang, W. The effect of the fear factor on the dynamics of a predator-prey model incorporating the prey refuge. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 083109. [Google Scholar] [CrossRef] [PubMed]
- García, C.C. Bifurcations in a Leslie–Gower model with constant and proportional prey refuge at high and low density. Nonlinear Anal. Real World Appl. 2023, 72, 103861. [Google Scholar] [CrossRef]
- García, C.C. Impact of prey refuge in a discontinuous Leslie-Gower model with harvesting and alternative food for predators and linear functional response. Math. Comput. Simul. 2023, 206, 147–165. [Google Scholar] [CrossRef]
- Maji, C. Impact of fear effect in a fractional-order predator–prey system incorporating constant prey refuge. Nonlinear Dyn. 2022, 107, 1329–1342. [Google Scholar] [CrossRef]
- Saha, S.; Samanta, G. Switching effect on a two prey–one predator system with strong Allee effect incorporating prey refuge. Int. J. Biomath. 2024, 17, 2350012. [Google Scholar] [CrossRef]
- Saha, S.; Maiti, A.; Samanta, G. Analysis of a prey–predator model with prey refuge in infected prey and strong Allee effect in susceptible prey population. Discontin. Nonlinearity Complex. 2022, 11, 671–703. [Google Scholar] [CrossRef]
- Liu, X.; Han, M. Chaos and Hopf bifurcation analysis for a two species predator–prey system with prey refuge and diffusion. Nonlinear Anal. Real World Appl. 2011, 12, 1047–1061. [Google Scholar] [CrossRef]
- Bairagi, N.; Roy, P.K.; Chattopadhyay, J. Role of infection on the stability of a predator–prey system with several response functions—A comparative study. J. Theor. Biol. 2007, 248, 10–25. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharyya, R.; Mukhopadhyay, B. On an eco-epidemiological model with prey harvesting and predator switching: Local and global perspectives. Nonlinear Anal. Real World Appl. 2010, 11, 3824–3833. [Google Scholar] [CrossRef]
- Kooi, B.W.; van Voorn, G.A.; Das, K.P. Stabilization and complex dynamics in a predator–prey model with predator suffering from an infectious disease. Ecol. Complex. 2011, 8, 113–122. [Google Scholar] [CrossRef]
- Kumar, A.; Dubey, B. Modeling the effect of fear in a prey–predator system with prey refuge and gestation delay. Int. J. Bifurc. Chaos 2019, 29, 1950195. [Google Scholar] [CrossRef]
- Kar, T.K. Stability analysis of a prey–predator model incorporating a prey refuge. Commun. Nonlinear Sci. Numer. Simul. 2005, 10, 681–691. [Google Scholar] [CrossRef]
- Kar, T.K. Modelling and analysis of a harvested prey–predator system incorporating a prey refuge. J. Comput. Appl. Math. 2006, 185, 19–33. [Google Scholar] [CrossRef]
- González-Olivares, E.; Ramos-Jiliberto, R. Dynamic consequences of prey refuges in a simple model system: More prey, fewer predators and enhanced stability. Ecol. Model. 2003, 166, 135–146. [Google Scholar] [CrossRef]
- Ma, Z.; Li, W.; Zhao, Y.; Wang, W.; Zhang, H.; Li, Z. Effects of prey refuges on a predator–prey model with a class of functional responses: The role of refuges. Math. Biosci. 2009, 218, 73–79. [Google Scholar] [CrossRef]
- Meijaard, E.; de Wijeyeratne, G.S. Aquatic escape behaviour in mouse-deer provides insight into tragulid evolution. Mamm. Biol. 2010, 75, 471–473. [Google Scholar] [CrossRef]
- Lambert, M.S. Control of Norway Rats in the Agricultural Environment: Alternatives to Rodenticide Use. Ph.D. Thesis, University of Leicester, Leicester, UK, 2003. [Google Scholar]
- Sih, A. Prey refuges and predator-prey stability. Theor. Popul. Biol. 1987, 31, 1–12. [Google Scholar] [CrossRef]
- Ricketts, E.F.; Calvin, J.; Hedgpeth, J.W.; Phillips, D.W. Between Pacific Tides; Stanford University Press: Redwood City, CA, USA, 1985. [Google Scholar]
- Rassweiler, A.; Costello, C.; Siegel, D.A. Marine protected areas and the value of spatially optimized fishery management. Proc. Natl. Acad. Sci. USA 2012, 109, 11884–11889. [Google Scholar] [CrossRef] [PubMed]
- Tolon, V.; Martin, J.; Dray, S.; Loison, A.; Fischer, C.; Baubet, E. Predator–prey spatial game as a tool to understand the effects of protected areas on harvester–wildlife interactions. Ecol. Appl. 2012, 22, 648–657. [Google Scholar] [CrossRef] [PubMed]
- Takyi, E.M.; Cooper, K.; Dreher, A.; McCrorey, C. Dynamics of a predator–prey system with wind effect and prey refuge. J. Appl. Nonlinear Dyn 2023, 12, 427–440. [Google Scholar] [CrossRef]
- Khan, A.; Alsulami, I.M. Complicate dynamical analysis of a discrete predator-prey model with a prey refuge. AIMS Math. 2023, 8, 15035–15057. [Google Scholar] [CrossRef]
- Manaf, Z.I.A.; Mohd, M.H. Dynamical system analysis of the prey–predator interactions involving prey refuge and herd behaviors in preys. Malays. J. Fundam. Appl. Sci. 2022, 18, 105–115. [Google Scholar] [CrossRef]
- Stephano, M.A.; Jung, I.H. Effects of refuge prey on stability of the prey–predator model subject to immigrants: A mathematical modelling approach. Tanzan. J. Sci. 2021, 47, 1376–1391. [Google Scholar] [CrossRef]
- Gangur, A.N.; Smout, M.; Liddell, M.J.; Seymour, J.E.; Wilson, D.; Northfield, T.D. Changes in predator exposure, but not in diet, induce phenotypic plasticity in scorpion venom. Proc. R. Soc. B Biol. Sci. 2017, 284, 20171364. [Google Scholar] [CrossRef]
- Baldwin, J.M. A new factor in evolution. Am. Nat. 1896, 30, 441–451. [Google Scholar] [CrossRef]
- Yamamichi, M.; Klauschies, T.; Miner, B.E.; van Velzen, E. Modelling inducible defences in predator–prey interactions: Assumptions and dynamical consequences of three distinct approaches. Ecol. Lett. 2019, 22, 390–404. [Google Scholar] [CrossRef]
- Schoener, T.W. The newest synthesis: Understanding the interplay of evolutionary and ecological dynamics. Science 2011, 331, 426–429. [Google Scholar] [CrossRef] [PubMed]
- Hammill, E.; Petchey, O.L.; Anholt, B.R. Predator functional response changed by induced defenses in prey. Am. Nat. 2010, 176, 723–731. [Google Scholar] [CrossRef] [PubMed]
- Riessen, H.P.; Trevett-Smith, J.B. Turning inducible defenses on and off: Adaptive responses of Daphnia to a gape-limited predator. Ecology 2009, 90, 3455–3469. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Brönmark, C.; Hansson, L.A. Predator ontogeny affects expression of inducible defense morphology in rotifers. Ecology 2017, 98, 2499–2505. [Google Scholar] [CrossRef]
- Gomez-Mestre, I.; Díaz-Paniagua, C. Invasive predatory crayfish do not trigger inducible defences in tadpoles. Proc. R. Soc. B Biol. Sci. 2011, 278, 3364–3370. [Google Scholar] [CrossRef]
- Takahara, T.; Kohmatsu, Y.; Maruyama, A.; Doi, H.; Yamanaka, H.; Yamaoka, R. Inducible defense behavior of an anuran tadpole: Cue-detection range and cue types used against predator. Behav. Ecol. 2012, 23, 863–868. [Google Scholar] [CrossRef]
- West, R.; Letnic, M.; Blumstein, D.T.; Moseby, K.E. Predator exposure improves anti-predator responses in a threatened mammal. J. Appl. Ecol. 2018, 55, 147–156. [Google Scholar] [CrossRef]
- Sun, X.; Li, Y.; Xiao, Y. A predator–prey model with prey population guided anti-predator behavior. Int. J. Bifurc. Chaos 2017, 27, 1750099. [Google Scholar] [CrossRef]
- Vos, M.; Kooi, B.W.; DeAngelis, D.L.; Mooij, W.M. Inducible defences and the paradox of enrichment. Oikos 2004, 105, 471–480. [Google Scholar] [CrossRef]
- Liu, X.; Liu, S. Dynamics of a predator–prey system with inducible defense and disease in the prey. Nonlinear Anal. Real World Appl. 2023, 71, 103802. [Google Scholar] [CrossRef]
- Ramos-Jiliberto, R.; Frodden, E.; Aranguiz-Acuna, A. Pre-encounter versus post-encounter inducible defenses in predator–prey model systems. Ecol. Model. 2007, 200, 99–108. [Google Scholar] [CrossRef]
- González-Olivares, E.; González-Yañez, B.; Becerra-Klix, R.; Ramos-Jiliberto, R. Multiple stable states in a model based on predator-induced defenses. Ecol. Complex. 2017, 32, 111–120. [Google Scholar] [CrossRef]
- Van Velzen, E.; Thieser, T.; Berendonk, T.; Weitere, M.; Gaedke, U. Inducible defense destabilizes predator–prey dynamics: The importance of multiple predators. Oikos 2018, 127, 1551–1562. [Google Scholar] [CrossRef]
- Boeing, W.J.; Ramcharan, C.W. Inducible defences are a stabilizing factor for predator and prey populations: A field experiment. Freshw. Biol. 2010, 55, 2332–2338. [Google Scholar] [CrossRef]
- Creel, S.; Macdonald, D. Sociality, Group Size, and Reproductive, Suppression among Carnivores. Adv. Study Behav. 1995, 24, 203–257. [Google Scholar]
- Stander, P.E. Cooperative hunting in lions: The role of the individual. Behav. Ecol. Sociobiol. 1992, 29, 445–454. [Google Scholar] [CrossRef]
- Scheel, D.; Packer, C. Group hunting behaviour of lions: A search for cooperation. Anim. Behav. 1991, 41, 697–709. [Google Scholar] [CrossRef]
- Uetz, G.W. Foraging strategies of spiders. Trends Ecol. Evol. 1992, 7, 155–159. [Google Scholar] [CrossRef]
- Boesch, C.; Boesch, H.; Vigilant, L. Cooperative hunting in chimpanzees: Kinship or mutualism? In Cooperation in Primates and Humans: Mechanisms and Evolution; Kappeler, P.M., Schaik, C.P., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 139–150. [Google Scholar]
- Dugatkin, L.A. Cooperation Among Animals: An Evolutionary Perspective; Oxford University Press: Cary, NC, USA, 1997. [Google Scholar]
- Packer, C.; Ruttan, L. The evolution of cooperative hunting. Am. Nat. 1988, 132, 159–198. [Google Scholar] [CrossRef]
- Cordes, E.E.; Arthur, M.A.; Shea, K.; Arvidson, R.S.; Fisher, C.R. Modeling the mutualistic interactions between tubeworms and microbial consortia. PLoS Biol. 2005, 3, e77. [Google Scholar] [CrossRef]
- Berec, L. Impacts of foraging facilitation among predators on predator–prey dynamics. Bull. Math. Biol. 2010, 72, 94–121. [Google Scholar] [CrossRef]
- Alves, M.T.; Hilker, F.M. Hunting cooperation and Allee effects in predators. J. Theor. Biol. 2017, 419, 13–22. [Google Scholar] [CrossRef]
- Chow, Y.; Jang, S.R.J.; Wang, H.M. Cooperative hunting in a discrete predator–prey system II. J. Biol. Dyn. 2019, 13, 247–264. [Google Scholar] [CrossRef] [PubMed]
- Boesch, C. Cooperative hunting in wild chimpanzees. Anim. Behav. 1994, 48, 653–667. [Google Scholar] [CrossRef]
- Boesch, C. Cooperative hunting roles among Tai chimpanzees. Hum. Nat. 2002, 13, 27–46. [Google Scholar] [CrossRef] [PubMed]
- Mills, M. Foraging behaviour of the Brown Hyaena (Hyaena brunnea Thunberg, 1820) in the Southern Kalahari. Z. Tierpsychol. 1978, 48, 113–141. [Google Scholar] [CrossRef]
- Cook, W.; Streams, F. Fish predation on Notonecta (Hemiptera): Relationship between prey risk and habitat utilization. Oecologia 1984, 64, 177–183. [Google Scholar] [CrossRef]
- Major, P.F. Predator-prey interactions in two schooling fishes, Caranx ignobilis and Stolephorus purpureus. Anim. Behav. 1978, 26, 760–777. [Google Scholar] [CrossRef]
- Dinets, V. Apparent coordination and collaboration in cooperatively hunting crocodilians. Ethol. Ecol. Evol. 2015, 27, 244–250. [Google Scholar] [CrossRef]
- Rypstra, A.L. Aggregations of Nephila clavipes (L.) (Araneae, Araneidae) in relation to prey availability. J. Arachnol. 1985, 13, 71–78. [Google Scholar]
- Ward, P.I.; Enders, M.M. Conflict and cooperation in the group feeding of the social spider Stegodyphus mimosarum. Behaviour 1985, 94, 167–182. [Google Scholar] [CrossRef]
- Nakasuji, F.; Dyck, V. Evaluation of the role of Microvelia Douglasi Atrolineata (Bergroth) (Heteroptera: Veliidae) Predat. Brown Planthopper Nilaparvata Lugens (Stål) (Homoptera: Delphacidae). Res. Popul. Ecol. 1984, 26, 134–149. [Google Scholar] [CrossRef]
- Pacher, K.; Krause, J.; Bartashevich, P.; Romanczuk, P.; Bideau, P.; Pham, D.; Burns, A.; Deffner, D.; Dhellemmes, F.; Binder, B.; et al. Evidence for a by-product mutualism in a group hunter depends on prey movement state. Funct. Ecol. 2024, 38, 2123–2138. [Google Scholar] [CrossRef]
- Porat, D.; Chadwick-Furman, N. Effects of anemonefish on giant sea anemones: Expansion behavior, growth, and survival. Hydrobiologia 2004, 530, 513–520. [Google Scholar] [CrossRef]
- Tambling, C.J.; Druce, D.J.; Hayward, M.W.; Castley, J.G.; Adendorff, J.; Kerley, G.I. Spatial and temporal changes in group dynamics and range use enable anti-predator responses in African buffalo. Ecology 2012, 93, 1297–1304. [Google Scholar] [CrossRef]
- Ghosh, S.; Al Basir, F.; Chowdhury, G.; Bhattacharya, S.; Ray, S. Is the primary helper always a key group for the dynamics of cooperative birds? A mathematical study on cooperative breeding birds. Ecol. Model. 2021, 459, 109728. [Google Scholar] [CrossRef]
- Creel, S.; Creel, N.M. Communal hunting and pack size in African wild dogs, Lycaon pictus. Anim. Behav. 1995, 50, 1325–1339. [Google Scholar] [CrossRef]
- Bednarz, J.C. Cooperative hunting Harris’ Hawks (Parabuteo unicinctus). Science 1988, 239, 1525–1527. [Google Scholar] [CrossRef]
- Pitcher, T.; Magurran, A.; Winfield, I. Fish in larger shoals find food faster. Behav. Ecol. Sociobiol. 1982, 10, 149–151. [Google Scholar] [CrossRef]
- Vucetich, J.A.; Peterson, R.O.; Waite, T.A. Raven scavenging favours group foraging in wolves. Anim. Behav. 2004, 67, 1117–1126. [Google Scholar] [CrossRef]
- Pati, N.; Layek, G.; Pal, N. Bifurcations and organized structures in a predator-prey model with hunting cooperation. Chaos Solitons Fractals 2020, 140, 110184. [Google Scholar] [CrossRef]
- Duarte, J.; Januário, C.; Martins, N.; Sardanyés, J. Chaos and crises in a model for cooperative hunting: A symbolic dynamics approach. Chaos Interdiscip. J. Nonlinear Sci. 2009, 19, 043102. [Google Scholar] [CrossRef] [PubMed]
- Kundu, S.; Maitra, S. Dynamics of a delayed predator-prey system with stage structure and cooperation for preys. Chaos Solitons Fractals 2018, 114, 453–460. [Google Scholar] [CrossRef]
- Pal, S.; Pal, N.; Chattopadhyay, J. Hunting cooperation in a discrete-time predator–prey system. Int. J. Bifurc. Chaos 2018, 28, 1850083. [Google Scholar] [CrossRef]
- Han, R.; Dey, S.; Banerjee, M. Spatio-temporal pattern selection in a prey–predator model with hunting cooperation and Allee effect in prey. Chaos Solitons Fractals 2023, 171, 113441. [Google Scholar] [CrossRef]
- Santra, N.; Saha, S.; Samanta, G. Exploring cooperative hunting dynamics and PRCC analysis: Insights from a spatio-temporal mathematical model. J. Phys. A Math. Theor. 2024, 57, 305601. [Google Scholar] [CrossRef]
- Creel, S.; Winnie, J., Jr.; Maxwell, B.; Hamlin, K.; Creel, M. Elk alter habitat selection as an antipredator response to wolves. Ecology 2005, 86, 3387–3397. [Google Scholar] [CrossRef]
- Creel, S.; Winnie, J.A., Jr. Responses of elk herd size to fine-scale spatial and temporal variation in the risk of predation by wolves. Anim. Behav. 2005, 69, 1181–1189. [Google Scholar] [CrossRef]
- Winnie, J.; Christianson, D.; Creel, S.; Maxwell, B. Elk decision-making rules are simplified in the presence of wolves. Behav. Ecol. Sociobiol. 2006, 61, 277–289. [Google Scholar] [CrossRef]
- Ripple, W.J.; Larsen, E.J. Historic aspen recruitment, elk, and wolves in northern Yellowstone National Park, USA. Biol. Conserv. 2000, 95, 361–370. [Google Scholar] [CrossRef]
- Valeix, M.; Loveridge, A.; Chamaillé-Jammes, S.; Davidson, Z.; Murindagomo, F.; Fritz, H.; Macdonald, D. Behavioral adjustments of African herbivores to predation risk by lions: Spatiotemporal variations influence habitat use. Ecology 2009, 90, 23–30. [Google Scholar] [CrossRef]
- Valeix, M.; Fritz, H.; Loveridge, A.J.; Davidson, Z.; Hunt, J.E.; Murindagomo, F.; Macdonald, D.W. Does the risk of encountering lions influence African herbivore behaviour at waterholes? Behav. Ecol. Sociobiol. 2009, 63, 1483–1494. [Google Scholar] [CrossRef]
- Courbin, N.; Loveridge, A.J.; Macdonald, D.W.; Fritz, H.; Valeix, M.; Makuwe, E.T.; Chamaillé-Jammes, S. Reactive responses of zebras to lion encounters shape their predator–prey space game at large scale. Oikos 2016, 125, 829–838. [Google Scholar] [CrossRef]
- Capone, F.; Carfora, M.F.; De Luca, R.; Torcicollo, I. Turing patterns in a reaction–diffusion system modeling hunting cooperation. Math. Comput. Simul. 2019, 165, 172–180. [Google Scholar] [CrossRef]
- Han, R.; Dey, S.; Huang, J.; Banerjee, M. Spatio-Temporal Steady-State Analysis in a Prey-Predator Model with Saturated Hunting Cooperation and Chemotaxis. Acta Appl. Math. 2024, 191, 10. [Google Scholar] [CrossRef]
- Pandey, S.; Ghosh, U.; Das, D.; Chakraborty, S.; Sarkar, A. Rich dynamics of a delay-induced stage-structure prey–predator model with cooperative behaviour in both species and the impact of prey refuge. Math. Comput. Simul. 2024, 216, 49–76. [Google Scholar] [CrossRef]
- Saha, S.; Pal, S.; Melnik, R. Nonlocal cooperative behavior, psychological effects, and collective decision-making: An exemplification with predator–prey models. Math. Methods Appl. Sci. 2025, 48, 12011–12037. [Google Scholar] [CrossRef]
- Tener, J.S. Muskoxen in Canada, a Biological and Taxonomic Review; Queen’s Printer: Ottawa, ON, USA, 1965. [Google Scholar]
- Raw, S.; Mishra, P.; Kumar, R.; Thakur, S. Complex behavior of prey-predator system exhibiting group defense: A mathematical modeling study. Chaos Solitons Fractals 2017, 100, 74–90. [Google Scholar] [CrossRef]
- Panday, P.; Pal, N.; Samanta, S.; Tryjanowski, P.; Chattopadhyay, J. Dynamics of a stage-structured predator-prey model: Cost and benefit of fear-induced group defense. J. Theor. Biol. 2021, 528, 110846. [Google Scholar] [CrossRef]
- Arditi, R.; Ginzburg, L.R. Coupling in predator-prey dynamics: Ratio-Dependence. J. Theor. Biol. 1989, 139, 311–326. [Google Scholar] [CrossRef]
- Ajraldi, V.; Pittavino, M.; Venturino, E. Modeling herd behavior in population systems. Nonlinear Anal. Real World Appl. 2011, 12, 2319–2338. [Google Scholar] [CrossRef]
- Braza, P.A. Predator–prey dynamics with square root functional responses. Nonlinear Anal. Real World Appl. 2012, 13, 1837–1843. [Google Scholar] [CrossRef]
- Singh, T.; Banerjee, S. Spatiotemporal Model of a Predator–Prey System with Herd Behavior and Quadratic Mortality. Int. J. Bifurc. Chaos 2019, 29, 1950049. [Google Scholar] [CrossRef]
- Biswas, S.; Pal, D.; Mahapatra, G.; Samanta, G. Dynamics of a prey–predator system with herd behaviour in both and strong Allee effect in prey. Biophysics 2020, 65, 826–835. [Google Scholar] [CrossRef]
- Angulo, E.; Rasmussen, G.S.A.; Macdonald, D.W.; Courchamp, F. Do social groups prevent Allee effect related extinctions? The case of wild dogs. Front. Zool. 2013, 10, 11. [Google Scholar] [CrossRef]
- Biswas, S.; Bhutia, L.T.; Kar, T.K. Impact of the herd harvesting on a temporal and spatiotemporal prey–predator model with certain prey herd behaviors and density-dependent cross-diffusion. Eur. Phys. J. Plus 2024, 139, 1101. [Google Scholar] [CrossRef]
- Ahmed, R.; Almatrafi, M. Complex Dynamics of a Predator-Prey System with Gompertz Growth and Herd Behavior. Int. J. Anal. Appl. 2023, 21, 100. [Google Scholar] [CrossRef]
- Alebraheem, J. Asymptotic stability of deterministic and stochastic prey-predator models with prey herd immigration. AIMS Math. 2025, 10, 4620–4640. [Google Scholar] [CrossRef]
- Javaid, Y.; Jawad, S.; Ahmed, R.; Ali, A.H.; Rashwani, B. Dynamic complexity of a discretized predator-prey system with Allee effect and herd behaviour. Appl. Math. Sci. Eng. 2024, 32, 2420953. [Google Scholar] [CrossRef]
- Akanksha; Shivam; Kumar, S.; Singh, T. Role of Allee effect, hunting cooperation, and dispersal to prey–predator model. Int. J. Bifurc. Chaos 2023, 33, 2350155. [Google Scholar] [CrossRef]
- Pareek, S.; Baghel, R.S. Modelling and Analysis of Prey-Predator Interaction on Spatio-temporal Dynamics: A Systematic Review. In Proceedings of the 4th International Conference On Emerging Trends in Multi-Disciplinary Research “ETMDR-2023”, Jaipur, India, 2–4 March 2023; pp. 77–85. [Google Scholar]
- Peng, M.; Lin, R.; Zhang, Z.; Huang, L. The dynamics of a delayed predator-prey model with square root functional response and stage structure. Electron. Res. Arch. 2024, 32, 3275–3298. [Google Scholar] [CrossRef]
- Peng, Y.; Li, Y. Stability and Hopf bifurcation of a delayed predator–prey system with nonlocal competition and herd behaviour. J. Appl. Anal. Comput. 2024, 14, 1932–1958. [Google Scholar] [CrossRef] [PubMed]
- Saha, S.; Samanta, G. Impact of fear in a prey-predator system with herd behaviour. Comput. Math. Biophys. 2021, 9, 175–197. [Google Scholar] [CrossRef]
- Chen, X.; Yang, W. Complex dynamical behaviors of a Leslie-Gower predator–prey model with herd behavior. J. Nonlinear Model. Anal. 2024, 6, 1064–1082. [Google Scholar]
- Bartashevich, P.; Herbert-Read, J.E.; Hansen, M.J.; Dhellemmes, F.; Domenici, P.; Krause, J.; Romanczuk, P. Collective anti-predator escape manoeuvres through optimal attack and avoidance strategies. Commun. Biol. 2024, 7, 1586. [Google Scholar] [CrossRef]
- Kiss, K.; Kovács, S. Qualitative behavior of n-dimensional ratio-dependent predator–prey systems. Appl. Math. Comput. 2008, 199, 535–546. [Google Scholar] [CrossRef]
- Zuo, W. Global stability and Hopf bifurcations of a Beddington–DeAngelis type predator–prey system with diffusion and delays. Appl. Math. Comput. 2013, 223, 423–435. [Google Scholar] [CrossRef]
- Deng, L.; Wang, X.; Peng, M. Hopf bifurcation analysis for a ratio-dependent predator–prey system with two delays and stage structure for the predator. Appl. Math. Comput. 2014, 231, 214–230. [Google Scholar] [CrossRef]
- Tang, S.; Liang, J. Global qualitative analysis of a non-smooth Gause predator–prey model with a refuge. Nonlinear Anal. Theory Methods Appl. 2013, 76, 165–180. [Google Scholar] [CrossRef]
- Perc, M.; Grigolini, P. Collective behavior and evolutionary games- An introduction. Chaos Solitons Fractals 2013, 56, 1–5. [Google Scholar] [CrossRef]
- Szolnoki, A.; Mobilia, M.; Jiang, L.L.; Szczesny, B.; Rucklidge, A.M.; Perc, M. Cyclic dominance in evolutionary games: A review. J. R. Soc. Interface 2014, 11, 20140735. [Google Scholar] [CrossRef]
- Ford, J.K.; Reeves, R.R. Fight or flight: Antipredator strategies of baleen whales. Mammal Rev. 2008, 38, 50–86. [Google Scholar] [CrossRef]
- Lingle, S.; Pellis, S. Fight or flight? Antipredator behavior and the escalation of coyote encounters with deer. Oecologia 2002, 131, 154–164. [Google Scholar] [CrossRef] [PubMed]
- Lai, C.H.; Smith, A.T. Keystone status of plateau pikas (Ochotona curzoniae): Effect of control on biodiversity of native birds. Biodivers. Conserv. 2003, 12, 1901–1912. [Google Scholar] [CrossRef]
- Smith, A.T.; Foggin, J.M. The plateau pika (Ochotona curzoniae) is a keystone species for biodiversity on the Tibetan plateau. Anim. Conserv. Forum 1999, 2, 235–240. [Google Scholar] [CrossRef]
- Wei, X.; Li, S.; Yang, P.; Cheng, H. Soil erosion and vegetation succession in alpine Kobresia steppe meadow caused by plateau pika—A case study of Nagqu County, Tibet. Chin. Geogr. Sci. 2007, 17, 75–81. [Google Scholar] [CrossRef]
- Yinzhu, S. On the influences of range land vegetation to the density of plateau pika (Ochotona curzoniae). Acta Theriol. Sin. 2011, 3, 181. [Google Scholar]
- McLellan, C.F.; Cuthill, I.C.; Montgomery, S.H. Pattern variation is linked to anti-predator coloration in butterfly larvae. Proc. R. Soc. B 2023, 290, 20230811. [Google Scholar] [CrossRef]
- Choh, Y.; Ignacio, M.; Sabelis, M.W.; Janssen, A. Predator-prey role reversals, juvenile experience and adult antipredator behaviour. Sci. Rep. 2012, 2, 728. [Google Scholar] [CrossRef]
- Janssen, A.; Faraji, F.; Van Der Hammen, T.; Magalhães, S.; Sabelis, M.W. Interspecific infanticide deters predators. Ecol. Lett. 2002, 5, 490–494. [Google Scholar] [CrossRef]
- Saitō, Y. Prey kills predator: Counter-attack success of a spider mite against its specific phytoseiid predator. Exp. Appl. Acarol. 1986, 2, 47–62. [Google Scholar] [CrossRef]
- Tian, Y.; Gao, Y.; Sun, K. A fishery predator-prey model with anti-predator behavior and complex dynamics induced by weighted fishing strategies. Math. Biosci. Eng 2023, 20, 1558–1579. [Google Scholar] [CrossRef]
- Zhang, W.; Jin, D.; Yang, R. Hopf Bifurcation in a Predator–Prey Model with Memory Effect in Predator and Anti-Predator Behaviour in Prey. Mathematics 2023, 11, 556. [Google Scholar] [CrossRef]
- Lima, S.L. Stress and Decision Making under the Risk of Predation: Recent Developments from Behavioral, Reproductive, and Ecological Perspectives. Adv. Study Behav. 1998, 27, 215–290. [Google Scholar]
- Pallini; Janssen; Sabelis. Predators induce interspecific herbivore competition for food in refuge space. Ecol. Lett. 1998, 1, 171–177. [Google Scholar] [CrossRef]
- Relyea, R.A. How prey respond to combined predators: A review and an empirical test. Ecology 2003, 84, 1827–1839. [Google Scholar] [CrossRef]
- Tollrian, R. Predator-induced morphological defenses: Costs, life history shifts, and maternal effects in Daphnia pulex. Ecology 1995, 76, 1691–1705. [Google Scholar] [CrossRef]
- Tan, M.; Zhang, S.; Stevens, M.; Li, D.; Tan, E.J. Antipredator defences in motion: Animals reduce predation risks by concealing or misleading motion signals. Biol. Rev. 2024, 99, 778–796. [Google Scholar] [CrossRef] [PubMed]
- Kikuchi, D.W.; Allen, W.L.; Arbuckle, K.; Aubier, T.G.; Briolat, E.S.; Burdfield-Steel, E.R.; Cheney, K.L.; Daňková, K.; Elias, M.; Hämäläinen, L.; et al. The evolution and ecology of multiple antipredator defences. J. Evol. Biol. 2023, 36, 975–991. [Google Scholar] [CrossRef]
- Ives, A.R.; Dobson, A.P. Antipredator Behavior and the Population Dynamics of Simple Predator-Prey Systems. Am. Nat. 1987, 130, 431–447. [Google Scholar] [CrossRef]
- Abrams, P.; Matsuda, H. Effects of adaptive predatory and anti-predator behaviour in a two-prey—one-predator system. Evol. Ecol. 1993, 7, 312–326. [Google Scholar] [CrossRef]
- Tang, B.; Xiao, Y. Bifurcation analysis of a predator–prey model with anti-predator behaviour. Chaos Solitons Fractals 2015, 70, 58–68. [Google Scholar] [CrossRef]
- Karthikeyan, S.; Ramesh, P.; Sambath, M. Stability analysis of fractional-order predator-prey model with anti-predator behaviour and prey refuge. J. Math. Model. 2023, 11, 527–546. [Google Scholar]
- Saha, S.; Santra, N.; Samanta, G. Role of multiple time delays on a stage-structured harvested predator–prey system with anti-predator behavior. Int. J. Dyn. Control 2024, 12, 696–724. [Google Scholar] [CrossRef]
- Klamser, P.P.; Romanczuk, P. Collective predator evasion: Putting the criticality hypothesis to the test. PLoS Comput. Biol. 2021, 17, e1008832. [Google Scholar] [CrossRef]
- Lima, S.L. Nonlethal effects in the ecology of predator–prey interactions. Bioscience 1998, 48, 25–34. [Google Scholar] [CrossRef]
- Maerz, J.C.; Panebianco, N.L.; Madison, D.M. Effects of predator chemical cues and behavioral biorhythms on foraging, activity of terrestrial salamanders. J. Chem. Ecol. 2001, 27, 1333–1344. [Google Scholar] [CrossRef]
- Sheriff, M.J.; Krebs, C.J.; Boonstra, R. The sensitive hare: Sublethal effects of predator stress on reproduction in snowshoe hares. J. Anim. Ecol. 2009, 78, 1249–1258. [Google Scholar] [CrossRef]
- Wirsing, A. Dynamic fine-tuning of anti-predator behaviour in snowshoe hares illustrates the context dependence of risk effects. J. Anim. Ecol. 2025, 94, 4–6. [Google Scholar] [CrossRef]
- Cresswell, W. Predation in bird populations. J. Ornithol. 2011, 152, 251–263. [Google Scholar] [CrossRef]
- Holling, C.S. The functional response of predators to prey density and its role in mimicry and population regulation. Mem. Entomol. Soc. Can. 1965, 97, 5–60. [Google Scholar] [CrossRef]
- Zhu, H.; Campbell, S.A.; Wolkowicz, G.S. Bifurcation analysis of a predator-prey system with nonmonotonic functional response. SIAM J. Appl. Math. 2003, 63, 636–682. [Google Scholar] [CrossRef]
- Mishra, P.; Tiwari, B. Drivers of pattern formation in a predator–prey model with defense in fearful prey. Nonlinear Dyn. 2021, 105, 2811–2838. [Google Scholar] [CrossRef]
- Chen, X.; Yang, W. Impact of fear-induced group defense in a Monod–Haldane type prey–predator model. J. Appl. Math. Comput. 2024, 70, 3331–3368. [Google Scholar] [CrossRef]
- Lent, P.C. Muskoxen and Their Hunters: A History; University of Oklahoma Press: Norman, OK, USA, 1999; Volume 5. [Google Scholar]
- Holmes, J.C.; Bethel, W.M. Modification of intermediate host behaviour by parasites. In Behavioural Aspects of Parasite Transmission; Canning, E., Wrighteditors, C., Eds.; Academic Press Inc.: London, UK; New York, NY, USA, 1972; pp. 123–149. [Google Scholar]
- Jiao, J.; Meng, X.; Chen, L. A stage-structured Holling mass defence predator–prey model with impulsive perturbations on predators. Appl. Math. Comput. 2007, 189, 1448–1458. [Google Scholar] [CrossRef]
- Liu, Z.; Tan, R. Impulsive harvesting and stocking in a Monod–Haldane functional response predator–prey system. Chaos Solitons Fractals 2007, 34, 454–464. [Google Scholar] [CrossRef]
- Bellomo, N.; Gibelli, L.; Quaini, A.; Reali, A. Towards a mathematical theory of behavioral human crowds. Math. Model. Methods Appl. Sci. 2022, 32, 321–358. [Google Scholar] [CrossRef]
- Dawidowicz, P. Can Daphnia prevent a blue-green algal bloom in hypertrophic lakes? A laboratory test. Limnologica 1988, 19, 21–26. [Google Scholar]
- Jang, S.J.; Baglama, J.; Rick, J. Nutrient-phytoplankton-zooplankton models with a toxin. Math. Comput. Model. 2006, 43, 105–118. [Google Scholar] [CrossRef]
- Mukhopadhyay, B.; Bhattacharyya, R. Modelling phytoplankton allelopathy in a nutrient-plankton model with spatial heterogeneity. Ecol. Model. 2006, 198, 163–173. [Google Scholar] [CrossRef]
- Andrews, J.F. A mathematical model for the continuous culture of microorganisms utilizing inhibitory substrates. Biotechnol. Bioeng. 1968, 10, 707–723. [Google Scholar] [CrossRef]
- Sugie, J.; Howell, J. Kinetics of phenol oxidation by washed cell. Biotechnol. Bioeng. 1980, 23, 2039–2049. [Google Scholar]
- Haldane, J.B.S. The molecular statistics of an enzyme action. Proc. R. Soc. Lond. Ser. B Contain. Pap. A Biol. Character 1931, 108, 559–567. [Google Scholar]
- Freedman, H.I.; Wolkowicz, G.S. Predator-prey systems with group defence: The paradox of enrichment revisited. Bull. Math. Biol. 1986, 48, 493–508. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Yuan, S.; Zhang, T. Global dynamics of a predator–prey model with defense mechanism for prey. Appl. Math. Lett. 2016, 62, 42–48. [Google Scholar] [CrossRef]
- Bulai, I.M.; Venturino, E. Shape effects on herd behavior in ecological interacting population models. Math. Comput. Simul. 2017, 141, 40–55. [Google Scholar] [CrossRef]
- Salman, S.; Yousef, A.; Elsadany, A. Stability, bifurcation analysis and chaos control of a discrete predator-prey system with square root functional response. Chaos Solitons Fractals 2016, 93, 20–31. [Google Scholar] [CrossRef]
- Bi, Z.; Liu, S.; Ouyang, M. Three-dimensional pattern dynamics of a fractional predator-prey model with cross-diffusion and herd behavior. Appl. Math. Comput. 2022, 421, 126955. [Google Scholar] [CrossRef]
- Yao, W.; Li, X. Complicate bifurcation behaviors of a discrete predator–prey model with group defense and nonlinear harvesting in prey. Appl. Anal. 2023, 102, 2567–2582. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, Y.; Xiao, Y. Canard phenomena for a slow-fast predator-prey system with group defense of the prey. J. Math. Anal. Appl. 2023, 527, 127418. [Google Scholar] [CrossRef]
- Suleman, A.; Ahmed, R.; Alshammari, F.S.; Shah, N.A. Dynamic complexity of a slow-fast predator-prey model with herd behavior. AIMS Math. 2023, 8, 24446–24472. [Google Scholar] [CrossRef]
- Ager, W.; Ager, A. The psychology of enforced mobility. In The Psychology of Global Mobility; Springer: New York, NY, USA, 2010; pp. 151–170. [Google Scholar]
- Virupaksha, H.; Kumar, A.; Nirmala, B.P. Migration and mental health: An interface. J. Nat. Sci. Biol. Med. 2014, 5, 233–239. [Google Scholar] [CrossRef] [PubMed]
- Murillo, F. Migrants and Rapid Urbanization: A New Agenda for Humanitarian and Development Urban Planning; United Nations Department of Economic and Social Affairs (UN-DESA): New York, NY, USA, 2017; p. 03. [Google Scholar]
- Castro, F.G.; Murray, K.E. Cultural adaptation and resilience: Controversies, issues, and emerging models. In Handbook of Adult Resilience; Reich, J.W., Zautra, A.J., Hall, J.S., Eds.; The Guilford Press: New York, NY, USA, 2010; pp. 375–403. [Google Scholar]
- Reed, H.E.; Ludwig, B.; Braslow, L. Forced migration. In International Handbook of Migration and Population Distribution; Springer: Dordrecht, The Netherlands, 2016; pp. 605–625. [Google Scholar]
- Adelman, H. From refugees to forced migration: The UNHCR and human security. Int. Migr. Rev. 2001, 35, 7–32. [Google Scholar] [CrossRef]
- Bhugra, D.; Becker, M.A. Migration, cultural bereavement and cultural identity. World Psychiatry 2005, 4, 18–24. [Google Scholar] [PubMed]
- James, D.C. Coping with a new society: The unique psychosocial problems of immigrant youth. J. Sch. Health 1997, 67, 98–102. [Google Scholar] [CrossRef]
- Fazel, M.; Wheeler, J.; Danesh, J. Prevalence of serious mental disorder in 7000 refugees resettled in western countries: A systematic review. Lancet 2005, 365, 1309–1314. [Google Scholar] [CrossRef]
- Sher, L. A model of suicidal behavior among depressed immigrants. Expert Rev. Neurother. 2010, 10, 5–7. [Google Scholar] [CrossRef][Green Version]
- James, P.; Iyer, A.; Webb, T.L. The impact of post-migration stressors on refugees’ emotional distress and health: A longitudinal analysis. Eur. J. Soc. Psychol. 2019, 49, 1359–1367. [Google Scholar] [CrossRef]
- Thomas, L.; Orme, E.; Kerrigan, F. Student loneliness: The role of social media through life transitions. Comput. Educ. 2020, 146, 103754. [Google Scholar] [CrossRef]
- Dick, S. Changing the equation: Refugees as valuable resources rather than helpless victims. Fletcher J. Int. Dev. 2003, 18, 19–30. [Google Scholar]
- Berry, J.W.; Phinney, J.S.; Sam, D.L.; Vedder, P. Immigrant Youth in Cultural Transition: Acculturation, Identity, and Adaptation Across National Contexts; Erlbaum: Mahwah, NJ, USA, 2006. [Google Scholar]
- Sampasa-Kanyinga, H.; Lewis, R.F. Frequent use of social networking sites is associated with poor psychological functioning among children and adolescents. Cyberpsychol. Behav. Soc. Netw. 2015, 18, 380–385. [Google Scholar] [CrossRef]
- Anderson, L.E. A new look at an old construct: Cross-cultural adaptation. Int. J. Intercult. Relat. 1994, 18, 293–328. [Google Scholar] [CrossRef]
- Demes, K.A.; Geeraert, N. The highs and lows of a cultural transition: A longitudinal analysis of sojourner stress and adaptation across 50 countries. J. Personal. Soc. Psychol. 2015, 109, 316–337. [Google Scholar] [CrossRef] [PubMed]
- Hwang, W.C. The psychotherapy adaptation and modification framework: Application to Asian Americans. Am. Psychol. 2006, 61, 702–715. [Google Scholar] [CrossRef] [PubMed]
- Eyber, C. FMO Thematic Guide: Psychosocial Issues. Available online: https://alnap.org/documents/5385/fmo004-forced-migration-online-series.pdf (accessed on 28 October 2025).
- Bolker, B.M.; Pacala, S.W. Spatial moment equations for plant competition: Understanding spatial strategies and the advantages of short dispersal. Am. Nat. 1999, 153, 575–602. [Google Scholar] [CrossRef]
- Levin, S.A. Dispersion and population interactions. Am. Nat. 1974, 108, 207–228. [Google Scholar] [CrossRef]
- Rees, M.; Grubb, P.J.; Kelly, D. Quantifying the impact of competition and spatial heterogeneity on the structure and dynamics of a four-species guild of winter annuals. Am. Nat. 1996, 147, 1–32. [Google Scholar] [CrossRef]
- Seabloom, E.W.; Bjørnstad, O.N.; Bolker, B.M.; Reichman, O.J. Spatial signature of environmental heterogeneity, dispersal, and competition in successional grasslands. Ecol. Monogr. 2005, 75, 199–214. [Google Scholar] [CrossRef]
- Shahak, Y.; Gal, E.; Offir, Y.; Ben-Yakir, D. Photoselective shade netting integrated with greenhouse technologies for improved performance of vegetable and ornamental crops. In Proceedings of the International Workshop on Greenhouse Environmental Control and Crop Production in Semi-Arid Regions 797, Tucson, AZ, USA, 20–24 October 2008; pp. 75–80. [Google Scholar]
- Rietkerk, M.; Van de Koppel, J. Regular pattern formation in real ecosystems. Trends Ecol. Evol. 2008, 23, 169–175. [Google Scholar] [CrossRef]
- Van de Koppel, J.; Gascoigne, J.C.; Theraulaz, G.; Rietkerk, M.; Mooij, W.M.; Herman, P.M. Experimental evidence for spatial self-organization and its emergent effects in mussel bed ecosystems. Science 2008, 322, 739–742. [Google Scholar] [CrossRef]
- Miller, T.F.; Mladenoff, D.J.; Clayton, M.K. Old-growth northern hardwood forests: Spatial autocorrelation and patterns of understory vegetation. Ecol. Monogr. 2002, 72, 487–503. [Google Scholar] [CrossRef]
- Aarssen, L.; Turkington, R. Biotic specialization between neighbouring genotypes in Lolium perenne and Trifolium repens from a permanent pasture. J. Ecol. 1985, 73, 605–614. [Google Scholar] [CrossRef]
- Kéfi, S.; Rietkerk, M.; van Baalen, M.; Loreau, M. Local facilitation, bistability and transitions in arid ecosystems. Theor. Popul. Biol. 2007, 71, 367–379. [Google Scholar] [CrossRef] [PubMed]
- Soro, A.; Sundberg, S.; Rydin, H. Species diversity, niche metrics and species associations in harvested and undisturbed bogs. J. Veg. Sci. 1999, 10, 549–560. [Google Scholar] [CrossRef]
- Hassell, M.; Southwood, T. Foraging strategies of insects. Annu. Rev. Ecol. Syst. 1978, 9, 75–98. [Google Scholar] [CrossRef]
- Kareiva, P.; Odell, G. Swarms of predators exhibit “preytaxis” if individual predators use area-restricted search. Am. Nat. 1987, 130, 233–270. [Google Scholar] [CrossRef]
- Gillies, M.; Wilkes, T. The range of attraction of single baits for some West African mosquitoes. Bull. Entomol. Res. 1970, 60, 225–235. [Google Scholar] [CrossRef]
- Gillies, M.; Wilkes, T. The range of attraction of animal baits and carbon dioxide for mosquitoes. Studies in a freshwater area of West Africa. Bull. Entomol. Res. 1972, 61, 389–404. [Google Scholar] [CrossRef]
- Gillies, M.; Wilkes, T. The range of attraction of birds as baits for some West African mosquitoes (Diptera, Culicidae). Bull. Entomol. Res. 1974, 63, 573–582. [Google Scholar] [CrossRef]
- Ford, J. The Role of the Trypanosomiases in African Ecology: A Study of the Tsetse Fly Problem; Oxford University Press: Oxford, UK, 1971. [Google Scholar]
- Hutson, V.; Schmitt, K. Permanence and the dynamics of biological systems. Math. Biosci. 1992, 111, 1–71. [Google Scholar] [CrossRef]
- Madden, J. Physiological reactions of Pinus radiata to attack by woodwasp, Sirex noctilio F. (Hymenoptera: Siricidae). Bull. Entomol. Res. 1977, 67, 405–426. [Google Scholar] [CrossRef]
- Carroll, C.R.; Janzen, D.H. Ecology of foraging by ants. Annu. Rev. Ecol. Syst. 1973, 4, 231–257. [Google Scholar] [CrossRef]
- Schoonhoven, L. Plant recognition by lepidopterous larvae. Symp. R. Entomol. Soc. Lond. 1973, 87–99. Available online: https://www.cabidigitallibrary.org/doi/full/10.5555/19730504578 (accessed on 28 October 2025).
- Schoonhoven, L. On the variability of chemosensory information. In The Host-Plant in Relation to Insect Behaviour and Reproduction; Jermy, T., Ed.; Springer: Berlin/Heidelberg, Germany, 1976; pp. 261–266. [Google Scholar]
- Kummel, M.; Brown, D.; Bruder, A. How the aphids got their spots: Predation drives self-organization of aphid colonies in a patchy habitat. Oikos 2013, 122, 896–906. [Google Scholar] [CrossRef]
- Loughrin, J.H.; Potter, D.A.; Hamilton-Kemp, T.R.; Byers, M.E. Role of feeding-induced plant volatiles in aggregative behavior of the Japanese beetle (Coleoptera: Scarabaeidae). Environ. Entomol. 1996, 25, 1188–1191. [Google Scholar] [CrossRef]
- MP, H. Spatial structure and chaos in insect population dynamics. Nature 1991, 353, 1133–1136. [Google Scholar] [CrossRef]
- Bascompte, J.; Solé, R.V. Spatially induced bifurcations in single-species population dynamics. J. Anim. Ecol. 1994, 63, 256–264. [Google Scholar] [CrossRef]
- Hassell, M.; Miramontes, O.; Rohani, P.; May, R. Appropriate formulations for dispersal in spatially structured models: Comments on Bascompte & Solé. J. Anim. Ecol. 1995, 64, 662–664. [Google Scholar] [CrossRef]
- Hastings, A. Can spatial variation alone lead to selection for dispersal? Theor. Popul. Biol. 1983, 24, 244–251. [Google Scholar] [CrossRef]
- Hastings, A. Complex interactions between dispersal and dynamics: Lessons from coupled logistic equations. Ecology 1993, 74, 1362–1372. [Google Scholar] [CrossRef]
- Kang, Y.; Armbruster, D. Dispersal effects on a discrete two-patch model for plant–insect interactions. J. Theor. Biol. 2011, 268, 84–97. [Google Scholar] [CrossRef] [PubMed]
- Kang, Y.; Castillo-Chavez, C. Multiscale analysis of compartment models with dispersal. J. Biol. Dyn. 2012, 6, 50–79. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Rohani, P.; Ruxton, G.D. Dispersal and stability in metapopulations. Math. Med. Biol. A J. IMA 1999, 16, 297–306. [Google Scholar] [CrossRef]
- Ruxton, G.D. Density-dependent migration and stability in a system of linked populations. Bull. Math. Biol. 1996, 58, 643–660. [Google Scholar] [CrossRef]
- Tilman, D.; Kareiva, P. Spatial Ecology: The Role of Space in Population Dynamics and Interspecific Interactions (MPB-30); Princeton University Press: Princeton, NJ, USA, 1997; Volume 30. [Google Scholar]
- Kareiva, P. Population dynamics in spatially complex environments: Theory and data. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 1990, 330, 175–190. [Google Scholar]
- Hauzy, C.; Gauduchon, M.; Hulot, F.D.; Loreau, M. Density-dependent dispersal and relative dispersal affect the stability of predator–prey metacommunities. J. Theor. Biol. 2010, 266, 458–469. [Google Scholar] [CrossRef][Green Version]
- Jansen, V.A. Regulation of predator-prey systems through spatial interactions: A possible solution to the paradox of enrichment. Oikos 1995, 74, 384–390. [Google Scholar] [CrossRef]
- Jansen, V.A. Theoretical Aspects of Metapopulation Dynamics. Ph.D. Thesis, Leiden University, Leiden, The Netherlands, 1994. [Google Scholar]
- Huang, Y.; Diekmann, O. Predator migration in response to prey density: What are the consequences? J. Math. Biol. 2001, 43, 561–581. [Google Scholar] [CrossRef]
- Murdoch, W.W.; Briggs, C.J.; Nisbet, R.M.; Gurney, W.S.; Stewart-Oaten, A. Aggregation and stability in metapopulation models. Am. Nat. 1992, 140, 41–58. [Google Scholar] [CrossRef]
- Hassell, M.P.; May, R. Aggregation of predators and insect parasites and its effect on stability. J. Anim. Ecol. 1974, 43, 567–594. [Google Scholar] [CrossRef]
- Chesson, P.L.; Murdoch, W.W. Aggregation of risk: Relationships among host-parasitoid models. Am. Nat. 1986, 127, 696–715. [Google Scholar] [CrossRef]
- Ghosh, S.; Bhattacharyya, S. A two-patch prey-predator model with food-gathering activity. J. Appl. Math. Comput. 2011, 37, 497–521. [Google Scholar] [CrossRef]
- Cressman, R.; Křivan, V. Two-patch population models with adaptive dispersal: The effects of varying dispersal speeds. J. Math. Biol. 2013, 67, 329–358. [Google Scholar] [CrossRef] [PubMed]
- Kang, Y.; Sasmal, S.K.; Messan, K. A two-patch prey-predator model with predator dispersal driven by the predation strength. Math. Biosci. Eng. 2017, 14, 843–880. [Google Scholar] [CrossRef]
- Bolter, C.J.; Dicke, M.; Van Loon, J.J.; Visser, J.; Posthumus, M.A. Attraction of Colorado potato beetle to herbivore-damaged plants during herbivory and after its termination. J. Chem. Ecol. 1997, 23, 1003–1023. [Google Scholar] [CrossRef]
- Xiao, S.; Wang, Y.; Wang, S. Effects of prey’s diffusion on predator–prey systems with two patches. Bull. Math. Biol. 2021, 83, 45. [Google Scholar] [CrossRef]
- Gao, M.; Chen, L.; Chen, F. Dynamical analysis of a discrete two-patch model with the Allee effect and nonlinear dispersal. Math. Biosci. Eng. 2024, 21, 5499–5520. [Google Scholar] [CrossRef]
- Lu, M.; Xiang, C.; Huang, J.; Ruan, S. Dynamics of the generalized Rosenzweig–MacArthur model in a changing and patchy environment. Phys. D Nonlinear Phenom. 2024, 465, 134197. [Google Scholar] [CrossRef]
- Yousif, M.A.; Al-Husseiny, H.F. Stability analysis of a diseased prey-predator-scavenger system incorporating migration and competition. Int. J. Nonlinear Anal. Appl. 2021, 12, 1827–1853. [Google Scholar]
- Sen, D.; Přibylová, L. Complex dynamics in prey-predator systems with cross-coupling: Exploring nonlinear interactions and population oscillations. Commun. Nonlinear Sci. Numer. Simul. 2024, 137, 108154. [Google Scholar] [CrossRef]
- Mondal, D.; Sen, M.; Sen, D. Exploring population oscillations: Cross-coupling and dispersal effects in prey–predator dynamics. Phys. D Nonlinear Phenom. 2025, 472, 134525. [Google Scholar] [CrossRef]
- Crespo-Miguel, R.; Jarillo, J.; Cao-García, F.J. Dispersal-induced resilience to stochastic environmental fluctuations in populations with Allee effect. Phys. Rev. E 2022, 105, 014413. [Google Scholar] [CrossRef] [PubMed]
- Das, A.; Sahoo, D.; Samanta, G.; Nieto, J.J. Deterministic and stochastic analysis of a two-prey–one-predator system with fear effect and switching behaviour in predation. Int. J. Dyn. Control 2023, 11, 1076–1101. [Google Scholar] [CrossRef]
- Murdoch, W.W. Switching in general predators: Experiments on predator specificity and stability of prey populations. Ecol. Monogr. 1969, 39, 335–354. [Google Scholar] [CrossRef]
- Murdoch, W.W.; Oaten, A. Predation and population stability. Adv. Ecol. Res. 1975, 9, 1–131. [Google Scholar]
- Tansky, M. Switching effect in prey-predator system. J. Theor. Biol. 1978, 70, 263–271. [Google Scholar] [CrossRef]
- Garrott, R.A.; Bruggeman, J.E.; Becker, M.S.; Kalinowski, S.T.; White, P.J. Evaluating prey switching in wolf–ungulate systems. Ecol. Appl. 2007, 17, 1588–1597. [Google Scholar] [CrossRef]
- Saha, S.; Samanta, G. Modelling of a two prey and one predator system with switching effect. Comput. Math. Biophys. 2021, 9, 90–113. [Google Scholar] [CrossRef]
- Saha, S.; Sahoo, D.; Samanta, G. Role of predation efficiency in prey–predator dynamics incorporating switching effect. Math. Comput. Simul. 2023, 209, 299–323. [Google Scholar] [CrossRef]
- Srinivasu, P.; Prasad, B.; Venkatesulu, M. Biological control through provision of additional food to predators: A theoretical study. Theor. Popul. Biol. 2007, 72, 111–120. [Google Scholar] [CrossRef]
- Sahoo, B.; Poria, S. Dynamics of a predator-prey system with seasonal effects on additional food. Int. J. Ecosyst. 2011, 1, 10–13. [Google Scholar] [CrossRef]
- Das, B.K.; Sahoo, D.; Samanta, G. Impact of fear in a delay-induced predator–prey system with intraspecific competition within predator species. Math. Comput. Simul. 2022, 191, 134–156. [Google Scholar] [CrossRef]
- Mattioli, L.; Capitani, C.; Gazzola, A.; Scandura, M.; Apollonio, M. Prey selection and dietary response by wolves in a high-density multi-species ungulate community. Eur. J. Wildl. Res. 2011, 57, 909–922. [Google Scholar] [CrossRef]
- Latham, A.D.M.; Latham, M.C.; Knopff, K.H.; Hebblewhite, M.; Boutin, S. Wolves, white-tailed deer, and beaver: Implications of seasonal prey switching for woodland caribou declines. Ecography 2013, 36, 1276–1290. [Google Scholar] [CrossRef]
- Prokopenko, C.M. Hungry Wolves and Dangerous Prey: A Tale of Prey Switching. Ph.D. Thesis, Memorial University of Newfoundland, St. John’s, NL, Canada, 2022. [Google Scholar]
- Sand, H.; Eklund, A.; Zimmermann, B.; Wikenros, C.; Wabakken, P. Prey selection of Scandinavian wolves: Single large or several small? PLoS ONE 2016, 11, e0168062. [Google Scholar] [CrossRef]
- Stickney, A. Seasonal patterns of prey availability and the foraging behavior of arctic foxes (Alopex lagopus) in a waterfowl nesting area. Can. J. Zool. 1991, 69, 2853–2859. [Google Scholar] [CrossRef]
- Giroux, M.A.; Berteaux, D.; Lecomte, N.; Gauthier, G.; Szor, G.; Bêty, J. Benefiting from a migratory prey: Spatio-temporal patterns in allochthonous subsidization of an arctic predator. J. Anim. Ecol. 2012, 81, 533–542. [Google Scholar] [CrossRef]
- Wells, B.K.; Santora, J.A.; Henderson, M.J.; Warzybok, P.; Jahncke, J.; Bradley, R.W.; Huff, D.D.; Schroeder, I.D.; Nelson, P.; Field, J.C.; et al. Environmental conditions and prey-switching by a seabird predator impact juvenile salmon survival. J. Mar. Syst. 2017, 174, 54–63. [Google Scholar] [CrossRef]
- Schwemmer, P.; Garthe, S. Regular habitat switch as an important feeding strategy of an opportunistic seabird species at the interface between land and sea. Estuar. Coast. Shelf Sci. 2008, 77, 12–22. [Google Scholar] [CrossRef]
- Suryan, R.M.; Irons, D.B.; Benson, J. Prey switching and variable foraging strategies of black-legged kittiwakes and the effect on reproductive success. Condor 2000, 102, 374–384. [Google Scholar] [CrossRef]
- Warzybok, P.; Santora, J.A.; Ainley, D.G.; Bradley, R.W.; Field, J.C.; Capitolo, P.J.; Carle, R.D.; Elliott, M.; Beck, J.N.; McChesney, G.J.; et al. Prey switching and consumption by seabirds in the central California Current upwelling ecosystem: Implications for forage fish management. J. Mar. Syst. 2018, 185, 25–39. [Google Scholar] [CrossRef]
- Kuepfer, A.; Votier, S.C.; Sherley, R.B.; Ventura, F.; Matias, R.; Anderson, O.; Brickle, P.; Arkhipkin, A.; Catry, P. Prey-switching to fishery discards does not compensate for poor natural foraging conditions in breeding albatross. ICES J. Mar. Sci. 2023, 80, 2414–2426. [Google Scholar] [CrossRef]
- Wade, P.R.; Burkanov, V.N.; Dahlheim, M.E.; Friday, N.A.; Fritz, L.W.; Loughlin, T.R.; Mizroch, S.A.; Muto, M.M.; Rice, D.W.; Barrett-Lennard, L.G.; et al. Killer whales and marine mammal trends in the North Pacific–A re-examination of evidence for sequential megafauna collapse and the prey-switching hypothesis. Mar. Mammal Sci. 2007, 23, 766–802. [Google Scholar] [CrossRef]
- Mizroch, S.A.; Rice, D.W. Have North Pacific killer whales switched prey species in response to depletion of the great whale populations? Mar. Ecol. Prog. Ser. 2006, 310, 235–246. [Google Scholar] [CrossRef]
- Vongraven, D.; Bisther, A. Prey switching by killer whales in the north-east Atlantic: Observational evidence and experimental insights. J. Mar. Biol. Assoc. UK 2014, 94, 1357–1365. [Google Scholar] [CrossRef]
- Kjellander, P.; Nordström, J. Cyclic voles, prey switching in red fox, and roe deer dynamics–a test of the alternative prey hypothesis. Oikos 2003, 101, 338–344. [Google Scholar] [CrossRef]
- Bergerud, A.T. Prey switching in a simple ecosystem. Sci. Am. 1983, 249, 130–141. [Google Scholar] [CrossRef]
- Vettorazzi, M.; Mogensen, N.; Kaelo, B.; Broekhuis, F. Understanding the effects of seasonal variation in prey availability on prey switching by large carnivores. J. Zool. 2022, 318, 218–227. [Google Scholar] [CrossRef]
- McCard, M.; South, J.; Cuthbert, R.N.; Dickey, J.W.; McCard, N.; Dick, J.T. Pushing the switch: Functional responses and prey switching by invasive lionfish may mediate their ecological impact. Biol. Invasions 2021, 23, 2019–2032. [Google Scholar] [CrossRef]
- Jaworski, C.C.; Bompard, A.; Genies, L.; Amiens-Desneux, E.; Desneux, N. Preference and prey switching in a generalist predator attacking local and invasive alien pests. PLoS ONE 2013, 8, e82231. [Google Scholar] [CrossRef]
- Kiørboe, T.; Saiz, E.; Viitasalo, M. Prey switching behaviour in the planktonic copepod Acartia tonsa. Mar. Ecol. Prog. Ser. 1996, 143, 65–75. [Google Scholar] [CrossRef]
- Prokopenko, C.M.; Avgar, T.; Ford, A.; Vander Wal, E. Optimal prey switching: Predator foraging costs provide a mechanism for functional responses in multi-prey systems. Ecology 2023, 104, e3928. [Google Scholar] [CrossRef] [PubMed]
- Idmbarek, A.; Achik, Y.; Agmour, I.; Nafia, H.; El Foutayeni, Y. Interrelationships between prey and predators and how predators choose their prey to maximize their utility functions. J. Appl. Math. 2021, 2021, 6619500. [Google Scholar] [CrossRef]
- Hoy, S.R.; MacNulty, D.R.; Metz, M.C.; Smith, D.W.; Stahler, D.R.; Peterson, R.O.; Vucetich, J.A. Negative frequency-dependent prey selection by wolves and its implications on predator–prey dynamics. Anim. Behav. 2021, 179, 247–265. [Google Scholar] [CrossRef]
- Van Baalen, M.; Křivan, V.; van Rijn, P.C.; Sabelis, M.W. Alternative food, switching predators, and the persistence of predator-prey systems. Am. Nat. 2001, 157, 512–524. [Google Scholar] [CrossRef]
- Wolf, C.; Ripple, W.J. Prey depletion as a threat to the world’s large carnivores. R. Soc. Open Sci. 2016, 3, 160252. [Google Scholar] [CrossRef]
- Bloom, D.E.; Cadarette, D. Infectious disease threats in the twenty-first century: Strengthening the global response. Front. Immunol. 2019, 10, 445106. [Google Scholar] [CrossRef]
- Sime, J.D. Crowd psychology and engineering. Saf. Sci. 1995, 21, 1–14. [Google Scholar] [CrossRef]
- Leung, G.M.; Lam, T.H.; Ho, L.M.; Ho, S.; Chan, B.; Wong, I.; Hedley, A.J. The impact of community psychological responses on outbreak control for severe acute respiratory syndrome in Hong Kong. J. Epidemiol. Community Health 2003, 57, 857–863. [Google Scholar] [CrossRef]
- Xiao, D.; Ruan, S. Global analysis of an epidemic model with nonmonotone incidence rate. Math. Biosci. 2007, 208, 419–429. [Google Scholar] [CrossRef]
- Kephart, J.O.; White, S.R. Measuring and modeling computer virus prevalence. In Proceedings of the 1993 IEEE Computer Society Symposium on Research in Security and Privacy, Oakland, CA, USA, 24–26 May 1993; IEEE: New York, NY, USA, 1993; pp. 2–15. [Google Scholar]
- Beretta, E.; Hara, T.; Ma, W.; Takeuchi, Y. Global asymptotic stability of an SIR epidemic model with distributed time delay. Nonlinear Anal. Theory Methods Appl. 2001, 47, 4107–4115. [Google Scholar] [CrossRef]
- Serazzi, G.; Zanero, S. Computer virus propagation models. In Proceedings of the International Workshop on Modeling, Analysis, and Simulation of Computer and Telecommunication Systems, Paris, France, 21–23 October 2003; Springer: Berlin/Heidelberg, Germany, 2003; pp. 26–50. [Google Scholar]
- Chen, L.C.; Carley, K.M. The impact of countermeasure propagation on the prevalence of computer viruses. IEEE Trans. Syst. Man, Cybern. Part B Cybern. 2004, 34, 823–833. [Google Scholar] [CrossRef] [PubMed]
- Mishra, B.K.; Saini, D.K. SEIRS epidemic model with delay for transmission of malicious objects in computer network. Appl. Math. Comput. 2007, 188, 1476–1482. [Google Scholar] [CrossRef]
- Teng, Z.; Liu, Y.; Zhang, L. Persistence and extinction of disease in non-autonomous SIRS epidemic models with disease-induced mortality. Nonlinear Anal. Theory Methods Appl. 2008, 69, 2599–2614. [Google Scholar] [CrossRef]
- Wang, X.; Tao, Y.; Song, X. Pulse vaccination on SEIR epidemic model with nonlinear incidence rate. Appl. Math. Comput. 2009, 210, 398–404. [Google Scholar] [CrossRef]
- Buonomo, B.; Rionero, S. On the Lyapunov stability for SIRS epidemic models with general nonlinear incidence rate. Appl. Math. Comput. 2010, 217, 4010–4016. [Google Scholar] [CrossRef]
- Sun, R.; Shi, J. Global stability of multigroup epidemic model with group mixing and nonlinear incidence rates. Appl. Math. Comput. 2011, 218, 280–286. [Google Scholar] [CrossRef]
- Enatsu, Y.; Messina, E.; Muroya, Y.; Nakata, Y.; Russo, E.; Vecchio, A. Stability analysis of delayed SIR epidemic models with a class of nonlinear incidence rates. Appl. Math. Comput. 2012, 218, 5327–5336. [Google Scholar] [CrossRef]
- Lahrouz, A.; Omari, L.; Kiouach, D.; Belmaâti, A. Complete global stability for an SIRS epidemic model with generalized non-linear incidence and vaccination. Appl. Math. Comput. 2012, 218, 6519–6525. [Google Scholar] [CrossRef]
- Capasso, V.; Serio, G. A generalization of the Kermack-McKendrick deterministic epidemic model. Math. Biosci. 1978, 42, 43–61. [Google Scholar] [CrossRef]
- Saha, S.; Samanta, G. Dynamics of an epidemic model with impact of toxins. Phys. A Stat. Mech. Its Appl. 2019, 527, 121152. [Google Scholar] [CrossRef]
- Liu, W.m.; Levin, S.A.; Iwasa, Y. Influence of nonlinear incidence rates upon the behavior of SIRS epidemiological models. J. Math. Biol. 1986, 23, 187–204. [Google Scholar] [CrossRef]
- Saha, S.; Samanta, G.; Nieto, J.J. Epidemic model of COVID-19 outbreak by inducing behavioural response in population. Nonlinear Dyn. 2020, 102, 455–487. [Google Scholar] [CrossRef] [PubMed]
- Saha, S.; Samanta, G. Modelling the role of optimal social distancing on disease prevalence of COVID-19 epidemic. Int. J. Dyn. Control 2021, 9, 1053–1077. [Google Scholar] [CrossRef] [PubMed]
- Kephart, J.O. How topology affects population dynamics. In Proceedings of the Artificial Life III: Studies in the Science of Complexity; Addison–Wesley Publishing Co.: Boston, MA, USA, 1994; Volume 17, pp. 447–463. [Google Scholar]
- May, R.M.; Lloyd, A.L. Infection dynamics on scale-free networks. Phys. Rev. E 2001, 64, 066112. [Google Scholar] [CrossRef] [PubMed]
- Lloyd, A.L.; May, R.M. How viruses spread among computers and people. Science 2001, 292, 1316–1317. [Google Scholar] [CrossRef]
- Pastor-Satorras, R.; Vespignani, A. Epidemic dynamics and endemic states in complex networks. Phys. Rev. E 2001, 63, 066117. [Google Scholar] [CrossRef]
- Baum, A.; Harpin, R.E.; Valins, S. The role of group phenomena in the experience of crowding. Environ. Behav. 1975, 7, 185–198. [Google Scholar] [CrossRef]
- Yuan, H.; Chen, G. Network virus-epidemic model with the point-to-group information propagation. Appl. Math. Comput. 2008, 206, 357–367. [Google Scholar] [CrossRef]
- Madar, N.; Kalisky, T.; Cohen, R.; Ben-avraham, D.; Havlin, S. Immunization and epidemic dynamics in complex networks. Eur. Phys. J. B 2004, 38, 269–276. [Google Scholar] [CrossRef]
- Garetto, M.; Gong, W.; Towsley, D. Modeling malware spreading dynamics. In Proceedings of the IEEE INFOCOM 2003. Twenty-Second Annual Joint Conference of the IEEE Computer and Communications Societies (IEEE Cat. No. 03CH37428); San Francisco, CA, USA, 30 March–3 April 2003, IEEE: New York, NY, USA, 2003; Volume 3, pp. 1869–1879. [Google Scholar]
- Yuan, H.; Liu, G.; Chen, G. On modeling the crowding and psychological effects in network-virus prevalence with nonlinear epidemic model. Appl. Math. Comput. 2012, 219, 2387–2397. [Google Scholar] [CrossRef]
- Dutta, P.; Santra, N.; Samanta, G.; De la Sen, M. Nonlinear SIRS fractional-order model: Analysing the impact of public attitudes towards vaccination, government actions, and social behavior on disease spread. Mathematics 2024, 12, 2232. [Google Scholar] [CrossRef]
- Saha, S.; Samanta, G. Modelling and optimal control of HIV/AIDS prevention through PrEP and limited treatment. Phys. A Stat. Mech. Its Appl. 2019, 516, 280–307. [Google Scholar] [CrossRef]
- Andrews, G.; Sanderson, K.; Corry, J.; Lapsley, H.M. Using epidemiological data to model efficiency in reducing the burden of depression. J. Ment. Health Policy Econ. 2000, 3, 175–186. [Google Scholar] [CrossRef] [PubMed]
- Taylor, M.R.; Agho, K.E.; Stevens, G.J.; Raphael, B. Factors influencing psychological distress during a disease epidemic: Data from Australia’s first outbreak of equine influenza. BMC Public Health 2008, 8, 347. [Google Scholar] [CrossRef]
- Zhou, B.; Jiang, D.; Dai, Y.; Hayat, T. Threshold dynamics and probability density function of a stochastic avian influenza epidemic model with nonlinear incidence rate and psychological effect. J. Nonlinear Sci. 2023, 33, 29. [Google Scholar] [CrossRef]
- Drapeau, A.; Marchand, A.; Beaulieu-Prévost, D. Epidemiology of Psychological Distress. In Mental Illnesses–Understanding, Prediction and Control; LAbate, L., Ed.; IntechOpen: Rijeka, Croatia, 2012; Chapter 5; pp. 105–134. [Google Scholar]
- Zhou, B.; Jiang, D.; Han, B.; Hayat, T. Threshold dynamics and density function of a stochastic epidemic model with media coverage and mean-reverting Ornstein–Uhlenbeck process. Math. Comput. Simul. 2022, 196, 15–44. [Google Scholar] [CrossRef]
- Duarte, F.; Jiménez-Molina, Á. Psychological distress during the COVID-19 epidemic in Chile: The role of economic uncertainty. PLoS ONE 2021, 16, e0251683. [Google Scholar] [CrossRef]
- Li, X.; Lyu, H. Epidemic risk perception, perceived stress, and mental health during COVID-19 pandemic: A moderated mediating model. Front. Psychol. 2021, 11, 563741. [Google Scholar] [CrossRef]
- Van Loo, H.M.; Beijers, L.; Wieling, M.; de Jong, T.R.; Schoevers, R.A.; Kendler, K.S. Prevalence of internalizing disorders, symptoms, and traits across age using advanced nonlinear models. Psychol. Med. 2023, 53, 78–87. [Google Scholar] [CrossRef]
- Vazquez, C.; Valiente, C.; García, F.E.; Contreras, A.; Peinado, V.; Trucharte, A.; Bentall, R.P. Post-traumatic growth and stress-related responses during the COVID-19 pandemic in a national representative sample: The role of positive core beliefs about the world and others. J. Happiness Stud. 2021, 22, 2915–2935. [Google Scholar] [CrossRef]
- Neuhouser, M.L. The importance of healthy dietary patterns in chronic disease prevention. Nutr. Res. 2019, 70, 3–6. [Google Scholar] [CrossRef] [PubMed]
- Cena, H.; Calder, P.C. Defining a healthy diet: Evidence for the role of contemporary dietary patterns in health and disease. Nutrients 2020, 12, 334. [Google Scholar] [CrossRef] [PubMed]
- Conlon, M.A.; Bird, A.R. The impact of diet and lifestyle on gut microbiota and human health. Nutrients 2014, 7, 17–44. [Google Scholar] [CrossRef] [PubMed]
- Calcaterra, V.; Regalbuto, C.; Porri, D.; Pelizzo, G.; Mazzon, E.; Vinci, F.; Zuccotti, G.; Fabiano, V.; Cena, H. Inflammation in obesity-related complications in children: The protective effect of diet and its potential role as a therapeutic agent. Biomolecules 2020, 10, 1324. [Google Scholar] [CrossRef]
- Pinckard, K.; Baskin, K.K.; Stanford, K.I. Effects of exercise to improve cardiovascular health. Front. Cardiovasc. Med. 2019, 6, 69. [Google Scholar] [CrossRef]
- Gaesser, G.A. Exercise for prevention and treatment of cardiovascular disease, type 2 diabetes, and metabolic syndrome. Curr. Diabetes Rep. 2007, 7, 14–19. [Google Scholar] [CrossRef]
- Hansen, D.; Dendale, P.; van Loon, L.J.; Meeusen, R. The impact of training modalities on the clinical benefits of exercise intervention in patients with cardiovascular disease risk or type 2 diabetes mellitus. Sport. Med. 2010, 40, 921–940. [Google Scholar] [CrossRef]
- Stewart, K.J. Exercise training and the cardiovascular consequences of type 2 diabetes and hypertension: Plausible mechanisms for improving cardiovascular health. JAMA 2002, 288, 1622–1631. [Google Scholar] [CrossRef]
- Bassuk, S.S.; Manson, J.E. Epidemiological evidence for the role of physical activity in reducing risk of type 2 diabetes and cardiovascular disease. J. Appl. Physiol. 2005, 99, 1193–1204. [Google Scholar] [CrossRef]
- Chudyk, A.; Petrella, R.J. Effects of exercise on cardiovascular risk factors in type 2 diabetes: A meta-analysis. Diabetes Care 2011, 34, 1228–1237. [Google Scholar] [CrossRef] [PubMed]
- Lambers, S.; Van Laethem, C.; Van Acker, K.; Calders, P. Influence of combined exercise training on indices of obesity, diabetes and cardiovascular risk in type 2 diabetes patients. Clin. Rehabil. 2008, 22, 483–492. [Google Scholar] [CrossRef] [PubMed]
- Woodyard, C. Exploring the therapeutic effects of yoga and its ability to increase quality of life. Int. J. Yoga 2011, 4, 49–54. [Google Scholar] [CrossRef] [PubMed]
- Carlson, L.E. Mindfulness-based interventions for physical conditions: A narrative review evaluating levels of evidence. Int. Sch. Res. Not. 2012, 2012, 651583. [Google Scholar] [CrossRef]
- Khalsa, S. Yoga as a therapeutic intervention. In Principles and Practice of Stress Management; Lehrer, P.M., Woolfolk, R.L., Sime, W.E., Eds.; Guilford: New York, NY, USA, 2007; pp. 449–462. [Google Scholar]
- Mineka, S.; Zinbarg, R. A contemporary learning theory perspective on the etiology of anxiety disorders: It’s not what you thought it was. Am. Psychol. 2006, 61, 10–26. [Google Scholar] [CrossRef]
- Miller, M.A.; Cappuccio, F.P. Inflammation, sleep, obesity and cardiovascular disease. Curr. Vasc. Pharmacol. 2007, 5, 93–102. [Google Scholar] [CrossRef]
- Besedovsky, L.; Lange, T.; Haack, M. The sleep-immune crosstalk in health and disease. Physiol. Rev. 2019, 99, 1325–1380. [Google Scholar] [CrossRef]
- Medic, G.; Wille, M.; Hemels, M.E. Short-and long-term health consequences of sleep disruption. Nat. Sci. Sleep 2017, 9, 151–161. [Google Scholar] [CrossRef]
- De Frel, D.L.; Atsma, D.E.; Pijl, H.; Seidell, J.C.; Leenen, P.J.; Dik, W.A.; Van Rossum, E.F. The impact of obesity and lifestyle on the immune system and susceptibility to infections such as COVID-19. Front. Nutr. 2020, 7, 597600. [Google Scholar] [CrossRef]
- Bloomfield, S.F.; Aiello, A.E.; Cookson, B.; O’Boyle, C.; Larson, E.L. The effectiveness of hand hygiene procedures in reducing the risks of infections in home and community settings including handwashing and alcohol-based hand sanitizers. Am. J. Infect. Control 2007, 35, S27–S64. [Google Scholar] [CrossRef]
- Aiello, A.E.; Larson, E.L. What is the evidence for a causal link between hygiene and infections? Lancet Infect. Dis. 2002, 2, 103–110. [Google Scholar] [CrossRef] [PubMed]
- Aiello, A.E.; Coulborn, R.M.; Perez, V.; Larson, E.L. Effect of hand hygiene on infectious disease risk in the community setting: A meta-analysis. Am. J. Public Health 2008, 98, 1372–1381. [Google Scholar] [CrossRef] [PubMed]
- Boone, S.A.; Gerba, C.P. Significance of fomites in the spread of respiratory and enteric viral disease. Appl. Environ. Microbiol. 2007, 73, 1687–1696. [Google Scholar] [CrossRef] [PubMed]
- Noronha, A.S.; Markowitz, L.E.; Dunne, E.F. Systematic review of human papillomavirus vaccine coadministration. Vaccine 2014, 32, 2670–2674. [Google Scholar] [CrossRef]
- Jansen, K.U.; Shaw, A.R. Human papillomavirus vaccines and prevention of cervical cancer. Annu. Rev. Med. 2004, 55, 319–331. [Google Scholar] [CrossRef]
- World Health Organization. Measles vaccines: WHO position paper, April 2017–recommendations. Vaccine 2019, 37, 219–222. [Google Scholar] [CrossRef]
- FitzSimons, D.; Hendrickx, G.; Lernout, T.; Badur, S.; Vorsters, A.; Van Damme, P. Incentives and barriers regarding immunization against influenza and hepatitis of health care workers. Vaccine 2014, 32, 4849–4854. [Google Scholar] [CrossRef]
- Kamb, M.L.; Fishbein, M.; Douglas, J.M., Jr.; Rhodes, F.; Rogers, J.; Bolan, G.; Zenilman, J.; Hoxworth, T.; Malotte, C.K.; Iatesta, M.; et al. Efficacy of risk-reduction counseling to prevent human immunodeficiency virus and sexually transmitted diseases: A randomized controlled trial. JAMA 1998, 280, 1161–1167. [Google Scholar] [CrossRef]
- Warner, L.; Stone, K.M.; Macaluso, M.; Buehler, J.W.; Austin, H.D. Condom use and risk of gonorrhea and Chlamydia: A systematic review of design and measurement factors assessed in epidemiologic studies. Sex. Transm. Dis. 2006, 33, 36–51. [Google Scholar] [CrossRef]
- Bernstein, K.T.; Marcus, J.L.; Nieri, G.; Philip, S.S.; Klausner, J.D. Rectal gonorrhea and chlamydia reinfection is associated with increased risk of HIV seroconversion. JAIDS J. Acquir. Immune Defic. Syndr. 2010, 53, 537–543. [Google Scholar] [CrossRef]
- Marrazzo, J.M.; Cates, W. Interventions to prevent sexually transmitted infections, including HIV infection. Clin. Infect. Dis. 2011, 53, S64–S78. [Google Scholar] [CrossRef] [PubMed]
- Narayanan, D.L.; Saladi, R.N.; Fox, J.L. Ultraviolet radiation and skin cancer. Int. J. Dermatol. 2010, 49, 978–986. [Google Scholar] [CrossRef] [PubMed]
- Mohania, D.; Chandel, S.; Kumar, P.; Verma, V.; Digvijay, K.; Tripathi, D.; Choudhury, K.; Mitten, S.K.; Shah, D. Ultraviolet radiations: Skin defense-damage mechanism. In Ultraviolet Light in Human Health, Diseases and Environment; Ahmad, S.I., Ed.; Springer: Berlin/Heidelberg, Germany, 2017; Volume 996, pp. 71–87. [Google Scholar]
- Elsner, P.; Hölzle, E.; Diepgen, T.; Grether-Beck, S.; Hönigsmann, H.; Krutmann, J.; Scharffetter-Kochanek, K.; Schwarz, T.; Luger, T. Recommendation: Daily sun protection in the prevention of chronic UV-induced skin damage. JDDG J. Der Dtsch. Dermatol. Ges. 2007, 5, 166–173. [Google Scholar] [CrossRef] [PubMed]
- Hillier, M.D. Using effective hand hygiene practice to prevent and control infection. Nurs. Stand. 2020, 35, 45–50. [Google Scholar] [CrossRef]
- Pessoa-Silva, C.L.; Hugonnet, S.; Pfister, R.; Touveneau, S.; Dharan, S.; Posfay-Barbe, K.; Pittet, D. Reduction of health care–associated infection risk in neonates by successful hand hygiene promotion. Pediatrics 2007, 120, e382–e390. [Google Scholar] [CrossRef]
- Beale, S.; Johnson, A.M.; Zambon, M.; Hayward, A.C.; Fragaszy, E.B.; Group, F.W. Hand hygiene practices and the risk of human coronavirus infections in a UK community cohort. Wellcome Open Res. 2020, 5, 98. [Google Scholar] [CrossRef]
- Rezaei, M.; Azarmi, M. Deepsocial: Social distancing monitoring and infection risk assessment in COVID-19 pandemic. Appl. Sci. 2020, 10, 7514. [Google Scholar] [CrossRef]
- Hatoun, J.; Correa, E.T.; Donahue, S.M.A.; Vernacchio, L. Social distancing for COVID-19 and diagnoses of other infectious diseases in children. Pediatrics 2020, 146, e2020006460. [Google Scholar] [CrossRef]
- Thunström, L.; Newbold, S.C.; Finnoff, D.; Ashworth, M.; Shogren, J.F. The benefits and costs of using social distancing to flatten the curve for COVID-19. J. Benefit-Cost Anal. 2020, 11, 179–195. [Google Scholar] [CrossRef]
- Matrajt, L.; Leung, T. Evaluating the effectiveness of social distancing interventions to delay or flatten the epidemic curve of coronavirus disease. Emerg. Infect. Dis. 2020, 26, 1740–1748. [Google Scholar] [CrossRef]
- Sommerstein, R.; Fux, C.A.; Vuichard-Gysin, D.; Abbas, M.; Marschall, J.; Balmelli, C.; Troillet, N.; Harbarth, S.; Schlegel, M.; Widmer, A.; et al. Risk of SARS-CoV-2 transmission by aerosols, the rational use of masks, and protection of healthcare workers from COVID-19. Antimicrob. Resist. Infect. Control 2020, 9, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Cheng, K.K.; Lam, T.H.; Leung, C.C. Wearing face masks in the community during the COVID-19 pandemic: Altruism and solidarity. Lancet 2022, 399, e39–e40. [Google Scholar] [CrossRef] [PubMed]
- Goh, Y.; Tan, B.Y.; Bhartendu, C.; Ong, J.J.; Sharma, V.K. The face mask: How a real protection becomes a psychological symbol during Covid-19? Brain Behav. Immun. 2020, 88, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Horton, R. The COVID-19 Catastrophe: What’s Gone Wrong and How to Stop It Happening Again; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Nicomedes, C.J.C.; Avila, R.M.A. An analysis on the panic during COVID-19 pandemic through an online form. J. Affect. Disord. 2020, 276, 14–22. [Google Scholar] [CrossRef]
- Boin, A.; Lodge, M.; Luesink, M. Learning from the COVID-19 crisis: An initial analysis of national responses. Policy Des. Pract. 2020, 3, 189–204. [Google Scholar] [CrossRef]
- Borkowski, P.; Jażdżewska-Gutta, M.; Szmelter-Jarosz, A. Lockdowned: Everyday mobility changes in response to COVID-19. J. Transp. Geogr. 2021, 90, 102906. [Google Scholar] [CrossRef]
- Nicola, M.; Alsafi, Z.; Sohrabi, C.; Kerwan, A.; Al-Jabir, A.; Iosifidis, C.; Agha, M.; Agha, R. The socio-economic implications of the coronavirus pandemic (COVID-19): A review. Int. J. Surg. 2020, 78, 185–193. [Google Scholar] [CrossRef]
- Anwari, N.; Ahmed, M.T.; Islam, M.R.; Hadiuzzaman, M.; Amin, S. Exploring the travel behavior changes caused by the COVID-19 crisis: A case study for a developing country. Transp. Res. Interdiscip. Perspect. 2021, 9, 100334. [Google Scholar] [CrossRef]
- Porcelli, P. Fear, anxiety and health-related consequences after the COVID-19 epidemic. Clin. Neuropsychiatry 2020, 17, 103–111. [Google Scholar]
- Pedrosa, A.L.; Simões e Silva, A.C. Emotional, behavioral, and psychological impact of the COVID-19 pandemic. Front. Psychol. 2020, 11, 566212. [Google Scholar] [CrossRef]
- Starcke, K.; Brand, M. Decision making under stress: A selective review. Neurosci. Biobehav. Rev. 2012, 36, 1228–1248. [Google Scholar] [CrossRef] [PubMed]
- Gilmore, B.; Ndejjo, R.; Tchetchia, A.; de Claro, V.; Mago, E.; Lopes, C.; Bhattacharyya, S. Community engagement for COVID-19 prevention and control: A rapid evidence synthesis. BMJ Glob. Health 2020, 5, e003188. [Google Scholar] [CrossRef] [PubMed]
- Tambo, E.; Djuikoue, I.C.; Tazemda, G.K.; Fotsing, M.F.; Zhou, X.N. Early stage risk communication and community engagement (RCCE) strategies and measures against the coronavirus disease 2019 (COVID-19) pandemic crisis. Glob. Health J. 2021, 5, 44–50. [Google Scholar] [CrossRef] [PubMed]
- Dutta, P.; Saha, S.; Samanta, G. Assessing the influence of public behavior and governmental action on disease dynamics: A PRCC analysis and optimal control approach. Eur. Phys. J. Plus 2024, 139, 527. [Google Scholar] [CrossRef]
- Saha, S.; Samanta, G.; Nieto, J.J. Impact of optimal vaccination and social distancing on COVID-19 pandemic. Math. Comput. Simul. 2022, 200, 285–314. [Google Scholar] [CrossRef]
- Chinazzi, M.; Davis, J.T.; Ajelli, M.; Gioannini, C.; Litvinova, M.; Merler, S.; Pastore y Piontti, A.; Mu, K.; Rossi, L.; Sun, K.; et al. The effect of travel restrictions on the spread of the 2019 novel coronavirus (COVID-19) outbreak. Science 2020, 368, 395–400. [Google Scholar] [CrossRef]
- Han, E.; Tan, M.M.J.; Turk, E.; Sridhar, D.; Leung, G.M.; Shibuya, K.; Asgari, N.; Oh, J.; García-Basteiro, A.L.; Hanefeld, J.; et al. Lessons learnt from easing COVID-19 restrictions: An analysis of countries and regions in Asia Pacific and Europe. Lancet 2020, 396, 1525–1534. [Google Scholar] [CrossRef]
- Bajardi, P.; Poletto, C.; Ramasco, J.J.; Tizzoni, M.; Colizza, V.; Vespignani, A. Human mobility networks, travel restrictions, and the global spread of 2009 H1N1 pandemic. PLoS ONE 2011, 6, e16591. [Google Scholar] [CrossRef]
- Seyfi, S.; Hall, C.M.; Shabani, B. COVID-19 and international travel restrictions: The geopolitics of health and tourism. Tour. Geogr. 2023, 25, 357–373. [Google Scholar] [CrossRef]
- Ullah, A.A.; Nawaz, F.; Chattoraj, D. Locked up under lockdown: The COVID-19 pandemic and the migrant population. Soc. Sci. Humanit. Open 2021, 3, 100126. [Google Scholar] [CrossRef]
- Al-Dmour, H.; Salman, A.; Abuhashesh, M.; Al-Dmour, R. Influence of social media platforms on public health protection against the COVID-19 pandemic via the mediating effects of public health awareness and behavioral changes: Integrated model. J. Med Internet Res. 2020, 22, e19996. [Google Scholar] [CrossRef] [PubMed]
- Mheidly, N.; Fares, J. Leveraging media and health communication strategies to overcome the COVID-19 infodemic. J. Public Health Policy 2020, 41, 410–420. [Google Scholar] [CrossRef] [PubMed]
- DeSalvo, K.B.; Wang, Y.C.; Harris, A.; Auerbach, J.; Koo, D.; O’Carroll, P. Public health 3.0: A call to action for public health to meet the challenges of the 21st century. Prev. Chronic Dis. 2017, 14, E78. [Google Scholar] [CrossRef] [PubMed]
- Bedford, J.; Farrar, J.; Ihekweazu, C.; Kang, G.; Koopmans, M.; Nkengasong, J. A new twenty-first century science for effective epidemic response. Nature 2019, 575, 130–136. [Google Scholar] [CrossRef]
- Bedson, J.; Skrip, L.A.; Pedi, D.; Abramowitz, S.; Carter, S.; Jalloh, M.F.; Funk, S.; Gobat, N.; Giles-Vernick, T.; Chowell, G.; et al. A review and agenda for integrated disease models including social and behavioural factors. Nat. Hum. Behav. 2021, 5, 834–846. [Google Scholar] [CrossRef]
- Philipson, T. Chapter 33 Economic epidemiology and infectious diseases. In Handbook of Health Economics; Culyer, A.J., Newhouse, J.P., Eds.; Elsevier: Amsterdam, The Netherlands, 2000; Volume 1B, pp. 1761–1799. [Google Scholar]
- Funk, S.; Salathé, M.; Jansen, V.A. Modelling the influence of human behaviour on the spread of infectious diseases: A review. J. R. Soc. Interface 2010, 7, 1247–1256. [Google Scholar] [CrossRef]
- Epstein, J.M. Modelling to contain pandemics. Nature 2009, 460, 687. [Google Scholar] [CrossRef]
- Epstein, J.M. Agent_Zero: Toward Neurocognitive Foundations for Generative Social Science; Princeton Studies in Complexity; Princeton University Press: Princeton, NJ, USA, 2014. [Google Scholar]
- Tadić, B.; Melnik, R. Microscopic dynamics modeling unravels the role of asymptomatic virus carriers in SARS-CoV-2 epidemics at the interplay between biological and social factors. Comput. Biol. Med. 2021, 133, 104422. [Google Scholar] [CrossRef]
- Gigerenzer, G. Psychological AI: Designing algorithms informed by human psychology. Perspect. Psychol. Sci. 2024, 19, 839–848. [Google Scholar] [CrossRef]
- Bisgaard, T.H.; Allin, K.H.; Keefer, L.; Ananthakrishnan, A.N.; Jess, T. Depression and anxiety in inflammatory bowel disease: Epidemiology, mechanisms and treatment. Nat. Rev. Gastroenterol. Hepatol. 2022, 19, 717–726. [Google Scholar] [CrossRef]
- Frolkis, A.D.; Vallerand, I.A.; Shaheen, A.A.; Lowerison, M.W.; Swain, M.G.; Barnabe, C.; Patten, S.B.; Kaplan, G.G. Depression increases the risk of inflammatory bowel disease, which may be mitigated by the use of antidepressants in the treatment of depression. Gut. 2019, 68, 1606–1612. [Google Scholar] [CrossRef] [PubMed]
- Bernstein, C.N.; Hitchon, C.A.; Walld, R.; Bolton, J.M.; Sareen, J.; Walker, J.R.; Graff, L.A.; Patten, S.B.; Singer, A.; Lix, L.M.; et al. Increased Burden of Psychiatric Disorders in Inflammatory Bowel Disease. Inflamm. Bowel Dis. 2019, 25, 360–368. [Google Scholar] [CrossRef] [PubMed]
- Ghia, J.E.; Blennerhassett, P.; Collins, S.M. Impaired parasympathetic function increases susceptibility to inflammatory bowel disease in a mouse model of depression. J. Clin. Investig. 2008, 118, 2209–2218. [Google Scholar] [CrossRef] [PubMed]
- Li, N.; Wang, Q.; Wang, Y.; Sun, A.; Lin, Y.; Jin, Y.; Li, X. Fecal microbiota transplantation from chronic unpredictable mild stress mice donors affects anxiety-like and depression-like behavior in recipient mice via the gut microbiota-inflammation-brain axis. Stress 2019, 22, 592–602. [Google Scholar] [CrossRef]
- Lv, R.; Li, H.; Sun, Q. Panic spreading model with different emotions under emergency. Mathematics 2021, 9, 3190. [Google Scholar] [CrossRef]
- Williams, G.Y.; Lim, S. Psychology of AI: How AI impacts the way people feel, think, and behave. Curr. Opin. Psychol. 2024, 58, 101835. [Google Scholar] [CrossRef]
- Tenenbaum, J.B.; Griffiths, T.L.; Kemp, C. Theory-based Bayesian models of inductive learning and reasoning. Trends Cogn. Sci. 2006, 10, 309–318. [Google Scholar] [CrossRef]
- Rouast, P.V.; Adam, M.T.; Chiong, R. Deep learning for human affect recognition: Insights and new developments. IEEE Trans. Affect. Comput. 2019, 12, 524–543. [Google Scholar] [CrossRef]
- Zheng, C.; Wu, W.; Chen, C.; Yang, T.; Zhu, S.; Shen, J.; Kehtarnavaz, N.; Shah, M. Deep learning-based human pose estimation: A survey. ACM Comput. Surv. 2023, 56, 1–37. [Google Scholar] [CrossRef]
- Conati, C. Probabilistic assessment of user’s emotions in educational games. Appl. Artif. Intell. 2002, 16, 555–575. [Google Scholar] [CrossRef]
- Conati, C.; Maclaren, H. Empirically building and evaluating a probabilistic model of user affect. User Model. User-Adapt. Interact. 2009, 19, 267–303. [Google Scholar] [CrossRef]
- Schröder, T.; Hoey, J.; Rogers, K.B. Modeling dynamic identities and uncertainty in social interactions: Bayesian affect control theory. Am. Sociol. Rev. 2016, 81, 828–855. [Google Scholar] [CrossRef]
- Kaplan, A.; Garner, J.K. A complex dynamic systems perspective on identity and its development: The dynamic systems model of role identity. Dev. Psychol. 2017, 53, 2036–2051. [Google Scholar] [CrossRef]
- Zhu, J.Q.; Peterson, J.C.; Enke, B.; Griffiths, T.L. Capturing the complexity of human strategic decision-making with machine learning. arXiv 2024, arXiv:2408.07865. [Google Scholar] [CrossRef]
- Hartford, J.; Wright, J.R.; Leyton-Brown, K. Deep learning for predicting human strategic behavior. In Proceedings of the 29th International Conference on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 2432–2440. [Google Scholar]
- Fintz, M.; Osadchy, M.; Hertz, U. Using deep learning to predict human decisions and using cognitive models to explain deep learning models. Sci. Rep. 2022, 12, 4736. [Google Scholar] [CrossRef] [PubMed]
- Jupalle, H.; Kouser, S.; Bhatia, A.B.; Alam, N.; Nadikattu, R.R.; Whig, P. Automation of human behaviors and its prediction using machine learning. Microsyst. Technol. 2022, 28, 1879–1887. [Google Scholar] [CrossRef]
- Zhou, X.; Liang, W.; Kevin, I.; Wang, K.; Wang, H.; Yang, L.T.; Jin, Q. Deep-learning-enhanced human activity recognition for internet of healthcare things. IEEE Internet Things J. 2020, 7, 6429–6438. [Google Scholar] [CrossRef]
- Raina, A.; McComb, C.; Cagan, J. Learning to design from humans: Imitating human designers through deep learning. J. Mech. Des. 2019, 141, 111102. [Google Scholar] [CrossRef]
- Zador, A.M. A critique of pure learning and what artificial neural networks can learn from animal brains. Nat. Commun. 2019, 10, 3770. [Google Scholar] [CrossRef]
- Shi, Y.; Li, C. Exploration of Computer Emotion Decision Based on Artificial Intelligence. In Proceedings of the 2018 International Conference on Virtual Reality and Intelligent Systems (ICVRIS), Hunan, China, 10–11 August 1028; IEEE: New York, NY, USA, 2018; pp. 293–295. [Google Scholar]
- Nadji-Tehrani, M.; Eslami, A. A brain-inspired framework for evolutionary artificial general intelligence. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 5257–5271. [Google Scholar] [CrossRef]
- Kriegeskorte, N.; Douglas, P.K. Cognitive computational neuroscience. Nat. Neurosci. 2018, 21, 1148–1160. [Google Scholar] [CrossRef] [PubMed]
- Pradhan, N.; Singh, A.S.; Singh, A. Cognitive computing: Architecture, technologies and intelligent applications. In Machine Learning and Cognitive Computing for Mobile Communications and Wireless Networks; Singh, K.K., Singh, A., Cengiz, K., Le, D.N., Eds.; Wiley Online Library: Hoboken, NJ, USA, 2020; pp. 25–50. [Google Scholar]
- Miller, T. Explanation in artificial intelligence: Insights from the social sciences. Artif. Intell. 2019, 267, 1–38. [Google Scholar] [CrossRef]
- Zhang, C.E.; Collins, K.M.; Weller, A.; Tenenbaum, J.B. AI for mathematics: A cognitive science perspective. arXiv 2023, arXiv:2310.13021. [Google Scholar] [CrossRef]
- Minsky, M. The Society of Mind; Simon and Schuster: New York, NY, USA, 1986. [Google Scholar]
- Auxier, R.E. The pluralist: An editorial statement. Pluralist 2006, 1, v–viii. [Google Scholar] [CrossRef]
- Rabinowitz, N.; Perbet, F.; Song, F.; Zhang, C.; Eslami, S.A.; Botvinick, M. Machine theory of mind. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; Volume 80, pp. 4218–4227. [Google Scholar]
- Ritter, S.; Barrett, D.G.; Santoro, A.; Botvinick, M.M. Cognitive psychology for deep neural networks: A shape bias case study. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 11–15 August 2017; Volume 70, pp. 2940–2949. [Google Scholar]
- Ali, S.; Wang, G.; Riaz, S. Aspect based sentiment analysis of ridesharing platform reviews for kansei engineering. IEEE Access 2020, 8, 173186–173196. [Google Scholar] [CrossRef]
- Han, S.; Liu, S.; Li, Y.; Li, W.; Wang, X.; Gan, Y.; Xu, Q.; Zhang, L. Why do you attract me but not others? Retrieval of person knowledge and its generalization bring diverse judgments of facial attractiveness. Soc. Neurosci. 2020, 15, 505–515. [Google Scholar] [CrossRef]
- Huang, C. Combining convolutional neural networks for emotion recognition. In Proceedings of the 2017 IEEE MIT Undergraduate Research Technology Conference (URTC), Cambridge, MA, USA, 3–5 November 2017; IEEE: New York, NY, USA, 2017; pp. 1–4. [Google Scholar]
- Liang, L.; Lin, L.; Jin, L.; Xie, D.; Li, M. SCUT-FBP5500: A diverse benchmark dataset for multi-paradigm facial beauty prediction. In Proceedings of the 2018 24th International Conference on Pattern Recognition (ICPR), Beijing, China, 20–24 August 2018; IEEE: New York, NY, USA, 2018; pp. 1598–1603. [Google Scholar]
- Vahdati, E.; Suen, C.Y. Facial beauty prediction from facial parts using multi-task and multi-stream convolutional neural networks. Int. J. Pattern Recognit. Artif. Intell. 2021, 35, 2160002. [Google Scholar] [CrossRef]
- Lebedeva, I.; Ying, F.; Guo, Y. Personalized facial beauty assessment: A meta-learning approach. Vis. Comput. 2023, 39, 1095–1107. [Google Scholar] [CrossRef]
- Zhao, J.; Cao, M.; Xie, X.; Zhang, M.; Wang, L. Data-driven facial attractiveness of Chinese male with epoch characteristics. IEEE Access 2019, 7, 10956–10966. [Google Scholar] [CrossRef]
- Zhao, J.; Deng, F.; Jia, J.; Wu, C.; Li, H.; Shi, Y.; Zhang, S. A new face feature point matrix based on geometric features and illumination models for facial attraction analysis. Discret. Contin. Dyn. Syst.-S 2019, 12, 1065–1072. [Google Scholar] [CrossRef]
- Zhao, J.; Su, W.; Jia, J.; Zhang, C.; Lu, T. Research on depression detection algorithm combine acoustic rhythm with sparse face recognition. Clust. Comput. 2019, 22, 7873–7884. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, M.; He, C.; Xie, X.; Li, J. A novel facial attractiveness evaluation system based on face shape, facial structure features and skin. Cogn. Neurodyn. 2020, 14, 643–656. [Google Scholar] [CrossRef] [PubMed]
- Picard, R.W. Affective computing: Challenges. Int. J. Hum.-Comput. Stud. 2003, 59, 55–64. [Google Scholar] [CrossRef]
- Simon, H.A. Making management decisions: The role of intuition and emotion. Acad. Manag. Perspect. 1987, 1, 57–64. [Google Scholar] [CrossRef]
- Bechara, A.; Damasio, H.; Damasio, A.R. Emotion, decision making and the orbitofrontal cortex. Cereb. Cortex 2000, 10, 295–307. [Google Scholar] [CrossRef]
- Albanie, S.; Nagrani, A.; Vedaldi, A.; Zisserman, A. Emotion recognition in speech using cross-modal transfer in the wild. In Proceedings of the 26th ACM International Conference on Multimedia, Seoul, Republic of Korea, 22–26 October 2018; Association for Computing Machinery: New York, NY, USA, 2018; MM ’18, pp. 292–301. [Google Scholar]
- Buhari, A.M.; Ooi, C.P.; Baskaran, V.M.; Phan, R.C.; Wong, K.; Tan, W.H. FACS-based graph features for real-time micro-expression recognition. J. Imaging 2020, 6, 130. [Google Scholar] [CrossRef]
- Zhao, K.; Chu, W.S.; Zhang, H. Deep Region and Multi-label Learning for Facial Action Unit Detection. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 3391–3399. [Google Scholar]
- Luo, Y.; Fu, Q.; Xie, J.; Qin, Y.; Wu, G.; Liu, J.; Jiang, F.; Cao, Y.; Ding, X. EEG-based emotion classification using spiking neural networks. IEEE Access 2020, 8, 46007–46016. [Google Scholar] [CrossRef]
- Khateeb, M.; Anwar, S.M.; Alnowami, M. Multi-domain feature fusion for emotion classification using DEAP dataset. IEEE Access 2021, 9, 12134–12142. [Google Scholar] [CrossRef]
- Liu, S.; Wang, X.; Zhao, L.; Li, B.; Hu, W.; Yu, J.; Zhang, Y.D. 3DCANN: A spatio-temporal convolution attention neural network for EEG emotion recognition. IEEE J. Biomed. Health Inform. 2021, 26, 5321–5331. [Google Scholar] [CrossRef]
- Cheng, Z.; Bu, X.; Wang, Q.; Yang, T.; Tu, J. EEG-based emotion recognition using multi-scale dynamic CNN and gated transformer. Sci. Rep. 2024, 14, 31319. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Li, D.; Liu, J.; Yang, Z.; Sun, L.; Wang, Z. Speech emotion recognition using recurrent neural networks with directional self-attention. Expert Syst. Appl. 2021, 173, 114683. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, M.; He, C.; Zuo, K. Data-driven research on the matching degree of eyes, eyebrows and face shapes. Front. Psychol. 2019, 10, 1466. [Google Scholar] [CrossRef] [PubMed]
- Hernández-Marcos, A.; Ros, E. A generic self-learning emotional framework for machines. Sci. Rep. 2024, 14, 25858. [Google Scholar] [CrossRef] [PubMed]
- Rahman, J.S.; Gedeon, T.; Caldwell, S.; Jones, R.; Jin, Z. Towards effective music therapy for mental health care using machine learning tools: Human affective reasoning and music genres. J. Artif. Intell. Soft Comput. Res. 2021, 11, 5–20. [Google Scholar] [CrossRef]
- Daly, I.; Williams, D.; Kirke, A.; Weaver, J.; Malik, A.; Hwang, F.; Miranda, E.; Nasuto, S.J. Affective brain–computer music interfacing. J. Neural Eng. 2016, 13, 046022. [Google Scholar] [CrossRef]
- Banerjee, A.; Sanyal, S.; Patranabis, A.; Banerjee, K.; Guhathakurta, T.; Sengupta, R.; Ghosh, D.; Ghose, P. Study on brain dynamics by non linear analysis of music induced EEG signals. Phys. A Stat. Mech. Its Appl. 2016, 444, 110–120. [Google Scholar] [CrossRef]
- Gkintoni, E.; Halkiopoulos, C. Mapping EEG Metrics to Human Affective and Cognitive Models: An Interdisciplinary Scoping Review from a Cognitive Neuroscience Perspective. Biomimetics 2025, 10, 730. [Google Scholar] [CrossRef]
- Leibo, J.Z.; d’Autume, C.d.M.; Zoran, D.; Amos, D.; Beattie, C.; Anderson, K.; Castañeda, A.G.; Sanchez, M.; Green, S.; Gruslys, A.; et al. Psychlab: A psychology laboratory for deep reinforcement learning agents. arXiv 2018, arXiv:1801.08116. [Google Scholar] [CrossRef]
- Taylor, J.E.T.; Taylor, G.W. Artificial cognition: How experimental psychology can help generate explainable artificial intelligence. Psychon. Bull. Rev. 2021, 28, 454–475. [Google Scholar] [CrossRef]
- Yang, G.Z.; Dario, P.; Kragic, D. Social robotics–Trust, learning, and social interaction. Sci. Robot. 2018, 3, eaau8839. [Google Scholar] [CrossRef] [PubMed]
- Branch, B. Artificial intelligence applications and psychology: An overview. Neuropsychopharmacol. Hung. 2019, 21, 119–126. [Google Scholar]
- Shiffrin, R.; Mitchell, M. Probing the psychology of AI models. Proc. Natl. Acad. Sci. USA 2023, 120, e2300963120. [Google Scholar] [CrossRef] [PubMed]
- Collins, K.M.; Jiang, A.Q.; Frieder, S.; Wong, L.; Zilka, M.; Bhatt, U.; Lukasiewicz, T.; Wu, Y.; Tenenbaum, J.B.; Hart, W.; et al. Evaluating language models for mathematics through interactions. Proc. Natl. Acad. Sci. USA 2024, 121, e2318124121. [Google Scholar] [CrossRef]
- Houlihan, S.D.; Kleiman-Weiner, M.; Hewitt, L.B.; Tenenbaum, J.B.; Saxe, R. Emotion prediction as computation over a generative theory of mind. Philos. Trans. R. Soc. A 2023, 381, 20220047. [Google Scholar] [CrossRef]
- Hartmann, K.; Siegert, I.; Glüge, S.; Wendemuth, A.; Kotzyba, M.; Deml, B. Describing Human Emotions Through Mathematical Modelling. IFAC Proc. Vol. 2012, 45, 463–468. [Google Scholar] [CrossRef]
- Frydman, C.; Camerer, C.F. The psychology and neuroscience of financial decision making. Trends Cogn. Sci. 2016, 20, 661–675. [Google Scholar] [CrossRef]
- Frydman, C.; Barberis, N.; Camerer, C.; Bossaerts, P.; Rangel, A. Using neural data to test a theory of investor behavior: An application to realization utility. J. Financ. 2014, 69, 907–946. [Google Scholar] [CrossRef]
- Kahneman, D.; Tversky, A. Prospect theory: An analysis of decision under risk. Econometrica 1979, 47, 263–292. [Google Scholar] [CrossRef]
- Tversky, A.; Kahneman, D. Advances in prospect theory: Cumulative representation of uncertainty. J. Risk Uncertain. 1992, 5, 297–323. [Google Scholar] [CrossRef]
- Shiller, R.J. Do Stock Prices Move Too Much to Be Justified by Subsequent Changes in Dividends? Technical Report; National Bureau of Economic Research: Cambridge, MA, USA, 1981. [Google Scholar]
- Shiller, R.J. Irrational Exuberance: Revised and Expanded, 3rd ed.; Princeton University Press: Princeton, NJ, USA, 2015. [Google Scholar]
- Odean, T. Are investors reluctant to realize their losses? J. Financ. 1998, 53, 1775–1798. [Google Scholar] [CrossRef]
- Odean, T. Do investors trade too much? Am. Econ. Rev. 1999, 89, 1279–1298. [Google Scholar] [CrossRef]
- Barber, B.M.; Odean, T. The behavior of individual investors. In Handbook of the Economics of Finance; Constantinides, G.M., Harris, M., Stulz, R.M., Eds.; Elsevier: Amsterdam, The Netherlands, 2013; Volume 2, pp. 1533–1570. [Google Scholar]
- Greenwood, R.; Shleifer, A. Expectations of returns and expected returns. Rev. Financ. Stud. 2014, 27, 714–746. [Google Scholar] [CrossRef]
- Lusardi, A.; Mitchell, O.S. The economic importance of financial literacy: Theory and Evidence. J. Econ. Lit. 2014, 52, 5–44. [Google Scholar] [CrossRef]
- Hedesström, T.M.; Svedsäter, H.; Gärling, T. Covariation neglect among novice investors. J. Exp. Psychol. Appl. 2006, 12, 155–165. [Google Scholar] [CrossRef]
- Benartzi, S.; Thaler, R.H. Naive diversification strategies in defined contribution saving plans. Am. Econ. Rev. 2001, 91, 79–98. [Google Scholar] [CrossRef]
- Akdeniz, L.; Salih, A.A.; Ok, S.T. Are stock prices too volatile to be justified by the dividend discount model? Phys. A Stat. Mech. Its Appl. 2007, 376, 433–444. [Google Scholar] [CrossRef]
- Lewis, K.F.; Whiteman, C.H. Robustifying Shiller: Do Stock Prices Move Enough to Be Justified by Subsequent Changes in Dividends? Technical Report; Mimeo: Memphis, TN, USA, 2006. [Google Scholar]
- Berns, G.S.; Laibson, D.; Loewenstein, G. Intertemporal choice–toward an integrative framework. Trends Cogn. Sci. 2007, 11, 482–488. [Google Scholar] [CrossRef]
- Hershfield, H.E.; Goldstein, D.G.; Sharpe, W.F.; Fox, J.; Yeykelis, L.; Carstensen, L.L.; Bailenson, J.N. Increasing saving behavior through age-progressed renderings of the future self. J. Mark. Res. 2011, 48, S23–S37. [Google Scholar] [CrossRef]
- Thaler, R. Mental Accounting and Consumer Choice. Mark. Sci. 1985, 4, 199–214. [Google Scholar] [CrossRef]
- Kuhnen, C.M.; Knutson, B. The influence of affect on beliefs, preferences, and financial decisions. J. Financ. Quant. Anal. 2011, 46, 605–626. [Google Scholar] [CrossRef]
- Cameron, L.; Shah, M. Risk-taking behavior in the wake of natural disasters. J. Hum. Resour. 2015, 50, 484–515. [Google Scholar] [CrossRef]
- Malmendier, U.; Nagel, S. Learning from inflation experiences. Q. J. Econ. 2016, 131, 53–87. [Google Scholar] [CrossRef]
- Hoelzl, E.; Pollai, M.; Kamleitner, B. Experience, prediction and recollection of loan burden. J. Econ. Psychol. 2009, 30, 446–454. [Google Scholar] [CrossRef]
- Kaiser, C.; Oswald, A.J. The scientific value of numerical measures of human feelings. Proc. Natl. Acad. Sci. USA 2022, 119, e2210412119. [Google Scholar] [CrossRef]
- Antonides, G. Psychology in Economics and Business: An Introduction to Economic Psychology; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Katona, G. Psychological Economics; Elsevier: Amsterdam, The Netherlands, 1975. [Google Scholar]
- Rossiter, J.R.; Percy, L. Advertising Communications & Promotion Management; McGraw-Hill Book Company: Columbus, OH, USA, 1987. [Google Scholar]
- Van Raaij, W.F. Economic psychology. J. Econ. Psychol. 1981, 1, 1–24. [Google Scholar] [CrossRef]
- Slovic, P.; Fischhoff, B.; Lichtenstein, S. Perceived risk: Psychological factors and social implications. Proc. R. Soc. Lond. A Math. Phys. Sci. 1981, 376, 17–34. [Google Scholar]
- Slovic, P.; Fischhoff, B.; Lichtenstein, S. Characterizing perceived risk. In Perilous Progress: Managing the Hazards of Technology; Kates, R.W., Hohenemser, C., Kasperson, J.X., Eds.; Avalon Publishing: Emeryville, CA, USA, 1985; pp. 91–125. [Google Scholar]
- Slovic, P. Perception of risk. Science 1987, 236, 280–285. [Google Scholar] [CrossRef]
- Slovic, P.; Fischhoff, B.; Lichtenstein, S. Facts and fears: Understanding perceived risk. In Societal Risk Assessment: How Safe Is Safe Enough? Schwing, R.C., Albers, W.A., Eds.; Springer: Boston, MA, USA, 1980; pp. 181–214. [Google Scholar]
- Slovic, P.; Fischhoff, B.; Lichtenstein, S. Behavioral decision theory perspectives on risk and safety. Acta Psychol. 1984, 56, 183–203. [Google Scholar] [CrossRef]
- Slovic, P. Informing and educating the public about risk. Risk Anal. 1986, 6, 403–415. [Google Scholar] [CrossRef]
- Slovic, P.; Lichtenstein, S.; Fischhoff, B. Modeling the societal impact of fatal accidents. Manag. Sci. 1984, 30, 464–474. [Google Scholar] [CrossRef]
- Gärling, T.; Kirchler, E.; Lewis, A.; Van Raaij, F. Psychology, financial decision making, and financial crises. Psychol. Sci. Public Interest 2009, 10, 1–47. [Google Scholar] [CrossRef] [PubMed]
- Campbell, J.Y. Restoring rational choice: The challenge of consumer financial regulation. Am. Econ. Rev. 2016, 106, 1–30. [Google Scholar] [CrossRef]
- Akerlof, G.A.; Shiller, R.J. Animal Spirits: Wie Wirtschaft Wirklich Funktioniert; Campus Verlag: Frankfurt am Main, Germany, 2009. [Google Scholar]
- Bertrand, M.; Karlan, D.; Mullainathan, S.; Shafir, E.; Zinman, J. What’s Psychology Worth? A Field Experiment in the Consumer Credit Market; Working Paper 11892; National Bureau of Economic Research: Cambridge, MA, USA, 2005. [Google Scholar]
- Lewis, A.; Carrera, S.; Cullis, J.; Jones, P. Individual, cognitive and cultural differences in tax compliance: UK and Italy compared. J. Econ. Psychol. 2009, 30, 431–445. [Google Scholar] [CrossRef]
- Sicherman, N.; Loewenstein, G.; Seppi, D.J.; Utkus, S.P. Financial attention. Rev. Financ. Stud. 2016, 29, 863–897. [Google Scholar] [CrossRef]
- Cippà, P.E.; Cugnata, F.; Ferrari, P.; Brombin, C.; Ruinelli, L.; Bianchi, G.; Beria, N.; Schulz, L.; Bernasconi, E.; Merlani, P.; et al. A data-driven approach to identify risk profiles and protective drugs in COVID-19. Proc. Natl. Acad. Sci. USA 2021, 118, e2016877118. [Google Scholar] [CrossRef]
- Nisioti, A.; Loukas, G.; Laszka, A.; Panaousis, E. Data-driven decision support for optimizing cyber forensic investigations. IEEE Trans. Inf. Forensics Secur. 2021, 16, 2397–2412. [Google Scholar] [CrossRef]
- Catelani, M.; Ciani, L.; Galar, D.; Patrizi, G. Optimizing maintenance policies for a yaw system using reliability-centered maintenance and data-driven condition monitoring. IEEE Trans. Instrum. Meas. 2020, 69, 6241–6249. [Google Scholar] [CrossRef]
- Liu, J.; Kong, X.; Zhou, X.; Wang, L.; Zhang, D.; Lee, I.; Xu, B.; Xia, F. Data Mining and Information Retrieval in the 21st century: A bibliographic review. Comput. Sci. Rev. 2019, 34, 100193. [Google Scholar] [CrossRef]
- Dolgin, E. The pandemic is prompting widespread use—and misuse—of real-world data. Proc. Natl. Acad. Sci. USA 2020, 117, 27754–27758. [Google Scholar] [CrossRef]
- Yu, S.; Qing, Q.; Zhang, C.; Shehzad, A.; Oatley, G.; Xia, F. Data-driven decision-making in COVID-19 response: A survey. IEEE Trans. Comput. Soc. Syst. 2021, 8, 1016–1029. [Google Scholar] [CrossRef]
- Konchak, C.W.; Krive, J.; Au, L.; Chertok, D.; Dugad, P.; Granchalek, G.; Livschiz, E.; Mandala, R.; McElvania, E.; Park, C.; et al. From testing to decision-making: A data-driven analytics COVID-19 response. Acad. Pathol. 2021, 8, 23742895211010257. [Google Scholar] [CrossRef] [PubMed]
- Ogungbe, O.; Commodore-Mensah, Y.; Himmelfarb, C.R.D.; Ferguson, C.; Martin, K.; Davidson, P.M. COVID-19: Lessons learned and a need for data driven decision making. Hear. Lung Circ. 2022, 31, 905–909. [Google Scholar] [CrossRef] [PubMed]
- Leung, C.K.; Chen, Y.; Shang, S.; Deng, D. Big data science on COVID-19 data. In Proceedings of the 2020 IEEE 14th International Conference on Big Data Science and Engineering (BigDataSE), Guangzhou, China, 29 December–1 January 2020; IEEE: New York, UY, USA, 2020; pp. 14–21. [Google Scholar]
- Van Gheluwe, C.; Lopez, A.J.; Semanjski, I.; Gautama, S. Repurposing existing traffic data sources for COVID-19 crisis management. In Proceedings of the 2020 IEEE International Smart Cities Conference (ISC2), Piscataway, NJ, USA, 28 September–1 October 2020; IEEE: New York, UY, USA, 2020; pp. 1–5. [Google Scholar]
- Ballard, A. Promoting performance information use through data visualization: Evidence from an experiment. Public Perform. Manag. Rev. 2020, 43, 109–128. [Google Scholar] [CrossRef]
- Kumar, N.; Susan, S. COVID-19 pandemic prediction using time series forecasting models. In Proceedings of the 2020 11th International Conference on Computing, Communication and Networking Technologies (ICCCNT), Kharagpur, India, 1–3 July 2020; IEEE: New York, UY, USA, 2020; pp. 1–7. [Google Scholar]
- Bradshaw, W.J.; Alley, E.C.; Huggins, J.H.; Lloyd, A.L.; Esvelt, K.M. Bidirectional contact tracing could dramatically improve COVID-19 control. Nat. Commun. 2021, 12, 232. [Google Scholar] [CrossRef]
- Duque, D.; Morton, D.P.; Singh, B.; Du, Z.; Pasco, R.; Meyers, L.A. Timing social distancing to avert unmanageable COVID-19 hospital surges. Proc. Natl. Acad. Sci. USA 2020, 117, 19873–19878. [Google Scholar] [CrossRef]
- Baldwin, R.E.; Tomiura, E. Thinking ahead about the trade impact of COVID-19. In Economics in the Time of COVID-19; Baldwin, R., Beatrice, W.d.M., Eds.; CEPR Press: Paris & London, 2020; pp. 59–71. [Google Scholar]
- Williams, C.C.; Kayaoglu, A. COVID-19 and undeclared work: Impacts and policy responses in Europe. Serv. Ind. J. 2020, 40, 914–931. [Google Scholar] [CrossRef]
- Duan, L.; Zhu, G. Psychological interventions for people affected by the COVID-19 epidemic. Lancet Psychiatry 2020, 7, 300–302. [Google Scholar] [CrossRef]
- Liu, J.; Kong, X.; Xia, F.; Bai, X.; Wang, L.; Qing, Q.; Lee, I. Artificial intelligence in the 21st century. IEEE Access 2018, 6, 34403–34421. [Google Scholar] [CrossRef]
- Hale, T.; Angrist, N.; Goldszmidt, R.; Kira, B.; Petherick, A.; Phillips, T.; Webster, S.; Cameron-Blake, E.; Hallas, L.; Majumdar, S.; et al. A global panel database of pandemic policies (Oxford COVID-19 Government Response Tracker). Nat. Hum. Behav. 2021, 5, 529–538. [Google Scholar] [CrossRef]
- Schwab, P.; Mehrjou, A.; Parbhoo, S.; Celi, L.A.; Hetzel, J.; Hofer, M.; Schölkopf, B.; Bauer, S. Real-time prediction of COVID-19 related mortality using electronic health records. Nat. Commun. 2021, 12, 1058. [Google Scholar] [CrossRef]
- Singh, R.; Adhikari, R. Age-structured impact of social distancing on the COVID-19 epidemic in India. arXiv 2020, arXiv:2003.12055. [Google Scholar] [CrossRef]
- Viner, R.M.; Russell, S.J.; Croker, H.; Packer, J.; Ward, J.; Stansfield, C.; Mytton, O.; Bonell, C.; Booy, R. School closure and management practices during coronavirus outbreaks including COVID-19: A rapid systematic review. Lancet Child Adolesc. Health 2020, 4, 397–404. [Google Scholar] [CrossRef]
- Del Rio-Chanona, R.M.; Mealy, P.; Pichler, A.; Lafond, F.; Farmer, J.D. Supply and demand shocks in the COVID-19 pandemic: An industry and occupation perspective. Oxf. Rev. Econ. Policy 2020, 36, S94–S137. [Google Scholar] [CrossRef] [PubMed]
- Padilla, L.M.; Hansen, G.; Ruginski, I.T.; Kramer, H.S.; Thompson, W.B.; Creem-Regehr, S.H. The influence of different graphical displays on nonexpert decision making under uncertainty. J. Exp. Psychol. Appl. 2015, 21, 37–46. [Google Scholar] [CrossRef] [PubMed]
- Okan, Y.; Garcia-Retamero, R.; Cokely, E.T.; Maldonado, A. Biasing and debiasing health decisions with bar graphs: Costs and benefits of graph literacy. Q. J. Exp. Psychol. 2018, 71, 2506–2519. [Google Scholar] [CrossRef]
- Wu, C.M.; Meder, B.; Filimon, F.; Nelson, J.D. Asking better questions: How presentation formats influence information search. J. Exp. Psychol. Learn. Mem. Cogn. 2017, 43, 1274. [Google Scholar] [CrossRef] [PubMed]
- Hellmann, A.; Yeow, C.; De Mello, L. The influence of textual presentation order and graphical presentation on the judgements of non-professional investors. Account. Bus. Res. 2017, 47, 455–470. [Google Scholar] [CrossRef]
- Sanfey, A.; Hastie, R. Does evidence presentation format affect judgment? An experimental evaluation of displays of data for judgments. Psychol. Sci. 1998, 9, 99–103. [Google Scholar] [CrossRef]
- Parrott, R.; Silk, K.; Dorgan, K.; Condit, C.; Harris, T. Risk comprehension and judgments of statistical evidentiary appeals: When a picture is not worth a thousand words. Hum. Commun. Res. 2005, 31, 423–452. [Google Scholar] [CrossRef]
- Beattie, V.; Jones, M.J. Measurement distortion of graphs in corporate reports: An experimental study. Account. Audit. Account. J. 2002, 15, 546–564. [Google Scholar] [CrossRef]
- Pennington, R.; Tuttle, B. Managing impressions using distorted graphs of income and earnings per share: The role of memory. Int. J. Account. Inf. Syst. 2009, 10, 25–45. [Google Scholar] [CrossRef]
- Radley, K.C.; Dart, E.H.; Wright, S.J. The effect of data points per x-to y-axis ratio on visual analysts evaluation of single-case graphs. Sch. Psychol. Q. 2018, 33, 314. [Google Scholar] [CrossRef]
- Lawrence, M.; O’Connor, M. Scale, variability, and the calibration of judgmental prediction intervals. Organ. Behav. Hum. Decis. Process. 1993, 56, 441–458. [Google Scholar] [CrossRef]
- Eberhard, K. The effects of visualization on judgment and decision-making: A systematic literature review. Manag. Rev. Q. 2023, 73, 167–214. [Google Scholar] [CrossRef]
- Padilla, L.M.; Creem-Regehr, S.H.; Hegarty, M.; Stefanucci, J.K. Decision making with visualizations: A cognitive framework across disciplines. Cogn. Res. Princ. Implic. 2018, 3, 29. [Google Scholar] [CrossRef] [PubMed]
- Perdana, A.; Robb, A.; Rohde, F. Does visualization matter? The role of interactive data visualization to make sense of information. Australas. J. Inf. Syst. 2018, 22, 1–35. [Google Scholar] [CrossRef]
- Falschlunger, L.M.; Eisl, C.; Losbichler, H.; Greil, A.M. Impression management in annual reports of the largest European companies: A longitudinal study on graphical representations. J. Appl. Account. Res. 2015, 16, 383–399. [Google Scholar] [CrossRef]
- McBride, M.; Caldara, M. The efficacy of tables versus graphs in disrupting dark networks: An experimental study. Soc. Netw. 2013, 35, 406–422. [Google Scholar] [CrossRef]
- Hirsch, B.; Seubert, A.; Sohn, M. Visualisation of data in management accounting reports: How supplementary graphs improve every-day management judgments. J. Appl. Account. Res. 2015, 16, 221–239. [Google Scholar] [CrossRef]
- Cardoso, R.L.; Leite, R.d.O.; Aquino, A.C.B.d. The effect of cognitive reflection on the efficacy of impression management: An experimental analysis with financial analysts. Account. Audit. Account. J. 2018, 31, 1668–1690. [Google Scholar] [CrossRef]
- Diacon, S.; Hasseldine, J. Framing effects and risk perception: The effect of prior performance presentation format on investment fund choice. J. Econ. Psychol. 2007, 28, 31–52. [Google Scholar] [CrossRef]
- Klockow-McClain, K.E.; McPherson, R.A.; Thomas, R.P. Cartographic design for improved decision making: Trade-offs in uncertainty visualization for tornado threats. Ann. Am. Assoc. Geogr. 2020, 110, 314–333. [Google Scholar] [CrossRef]
- Wesslen, R.; Santhanam, S.; Karduni, A.; Cho, I.; Shaikh, S.; Dou, W. Investigating Effects of Visual Anchors on Decision-Making about Misinformation. Comput. Graph. Forum 2019, 38, 161–171. [Google Scholar] [CrossRef]
- Wei, X.; Ma, J.; Liu, S.; Li, S.; Shi, S.; Guo, X.; Liu, Z. The effects of sleep deprivation on risky decision making. Psychon. Bull. Rev. 2025, 32, 80–96. [Google Scholar] [CrossRef]
- Maric, A.; Montvai, E.; Werth, E.; Storz, M.; Leemann, J.; Weissengruber, S.; Ruff, C.C.; Huber, R.; Poryazova, R.; Baumann, C.R. Insufficient sleep: Enhanced risk-seeking relates to low local sleep intensity. Ann. Neurol. 2017, 82, 409–418. [Google Scholar] [CrossRef]
- Wang, Y.; Dai, C.; Shao, Y.; Wang, C.; Zhou, Q. Changes in ventromedial prefrontal cortex functional connectivity are correlated with increased risk-taking after total sleep deprivation. Behav. Brain Res. 2022, 418, 113674. [Google Scholar] [CrossRef]
- Brunet, J.F.; McNeil, J.; Doucet, É.; Forest, G. The association between REM sleep and decision-making: Supporting evidences. Physiol. Behav. 2020, 225, 113109. [Google Scholar] [CrossRef]
- Sundelin, T.; Bayard, F.; Schwarz, J.; Cybulski, L.; Petrovic, P.; Axelsson, J. Framing effect, probability distortion, and gambling tendency without feedback are resistant to two nights of experimental sleep restriction. Sci. Rep. 2019, 9, 8554. [Google Scholar] [CrossRef]
- Nishimura, R.; Menrai, K.; Kajihara, M.; Asaoka, S. Is decision-making influenced by interactions between extended wakefulness and weak emotional stressors? An experimental study. Ind. Health 2022, 61, 92–101. [Google Scholar] [CrossRef]
- Mao, T.; Fang, Z.; Chai, Y.; Deng, Y.; Rao, J.; Quan, P.; Goel, N.; Basner, M.; Guo, B.; Dinges, D.F.; et al. Sleep deprivation attenuates neural responses to outcomes from risky decision-making. Psychophysiology 2024, 61, e14465. [Google Scholar] [CrossRef] [PubMed]
- Lim, J.Y.; Boardman, J.; Dyche, J.; Anderson, C.; Dickinson, D.L.; Drummond, S.P. Sex moderates the effects of total sleep deprivation and sleep restriction on risk preference. Sleep 2022, 45, zsac120. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Gong, X.; Wang, L.; Xu, M.; Zhong, X.; Peng, Z.; Song, T.; Xu, L.; Lian, J.; Shao, Y.; et al. Altered postcentral connectivity after sleep deprivation correlates to impaired risk perception: A resting-state functional magnetic resonance imaging study. Brain Sci. 2023, 13, 514. [Google Scholar] [CrossRef] [PubMed]
- Bedder, R.L.; Vaghi, M.M.; Dolan, R.J.; Rutledge, R.B. Risk taking for potential losses but not gains increases with time of day. Sci. Rep. 2023, 13, 5534. [Google Scholar] [CrossRef]
- Elliott, M.V.; Johnson, S.L.; Pearlstein, J.G.; Lopez, D.E.M.; Keren, H. Emotion-related impulsivity and risky decision-making: A systematic review and meta-regression. Clin. Psychol. Rev. 2023, 100, 102232. [Google Scholar] [CrossRef]
- Petter, J.; Mehta, A.; Petrova, K.; Kindt, M.; Sheppes, G.; Haslbeck, J.; Gross, J.J. Emotion regulation, fast or slow: A computational model of strategy choice. Emotion 2025, 25, 1273–1292. [Google Scholar] [CrossRef]
- Sperry, S.H.; Lynam, D.R.; Kwapil, T.R. The convergence and divergence of impulsivity facets in daily life. J. Personal. 2018, 86, 841–852. [Google Scholar] [CrossRef]
- Buelow, M.T.; Barnhart, W.R. Test–retest reliability of common behavioral decision making tasks. Arch. Clin. Neuropsychol. 2018, 33, 125–129. [Google Scholar] [CrossRef]
- Pearlstein, J.G.; Johnson, S.L.; Modavi, K.; Peckham, A.D.; Carver, C.S. Neurocognitive mechanisms of emotion-related impulsivity: The role of arousal. Psychophysiology 2019, 56, e13293. [Google Scholar] [CrossRef]
- Carrier Emond, F.; Gagnon, J.; Nolet, K.; Cyr, G.; Rouleau, J.L. What money can’t buy: Different patterns in decision making about sex and money predict past sexual coercion perpetration. Arch. Sex. Behav. 2018, 47, 429–441. [Google Scholar] [CrossRef]
- Dekker, M.R.; Johnson, S.L. Major depressive disorder and emotion-related impulsivity: Are both related to cognitive inhibition? Cogn. Ther. Res. 2018, 42, 398–407. [Google Scholar] [CrossRef]
- Herman, A.M.; Critchley, H.D.; Duka, T. The impact of Yohimbine-induced arousal on facets of behavioural impulsivity. Psychopharmacology 2019, 236, 1783–1795. [Google Scholar] [CrossRef] [PubMed]
- Smith, B.J.; Xue, F.; Droutman, V.; Barkley-Levenson, E.; Melrose, A.J.; Miller, L.C.; Monterosso, J.R.; Bechara, A.; Appleby, P.R.; Christensen, J.L.; et al. Virtually ‘in the heat of the moment’: Insula activation in safe sex negotiation among risky men. Soc. Cogn. Affect. Neurosci. 2018, 13, 80–91. [Google Scholar] [CrossRef] [PubMed]
- Xue, G.; Lu, Z.; Levin, I.P.; Bechara, A. The impact of prior risk experiences on subsequent risky decision-making: The role of the insula. Neuroimage 2010, 50, 709–716. [Google Scholar] [CrossRef]
- Owens, M.M.; Amlung, M.T.; Stojek, M.; MacKillop, J. Negative urgency moderates reactivity to laboratory stress inductions. J. Abnorm. Psychol. 2018, 127, 385–393. [Google Scholar] [CrossRef]
- Xiao, L.; Bechara, A.; Gong, Q.; Huang, X.; Li, X.; Xue, G.; Wong, S.; Lu, Z.L.; Palmer, P.; Wei, Y.; et al. Abnormal affective decision making revealed in adolescent binge drinkers using a functional magnetic resonance imaging study. Psychol. Addict. Behav. 2013, 27, 443–454. [Google Scholar] [CrossRef]
- Johnson, S.L.; Elliott, M.V.; Carver, C.S. Impulsive responses to positive and negative emotions: Parallel neurocognitive correlates and their implications. Biol. Psychiatry 2020, 87, 338–349. [Google Scholar] [CrossRef]
- Iinuma, K.; Kogiso, K. Emotion-involved human decision-making model. Math. Comput. Model. Dyn. Syst. 2021, 27, 543–561. [Google Scholar] [CrossRef]
- Shah, S.F.; Alshurideh, M.; Kurdi, B.A.; Salloum, S.A. The impact of the behavioral factors on investment decision-making: A systemic review on financial institutions. In Proceedings of the International Conference on Advanced Intelligent Systems and Informatics, Cairo, Egypt, 19–21 October 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 100–112. [Google Scholar]
- Vollrath, M.D.; Villegas, S.G. Avoiding digital marketing analytics myopia: Revisiting the customer decision journey as a strategic marketing framework. J. Mark. Anal. 2021, 10, 106–113. [Google Scholar] [CrossRef]
- Bouteska, A.; Regaieg, B. Psychology and behavioral finance: Anchoring bias by financial analysts on the Tunisian stock market. EuroMed J. Bus. 2020, 15, 39–64. [Google Scholar] [CrossRef]
- Shah, S.Z.A.; Ahmad, M.; Mahmood, F. Heuristic biases in investment decision-making and perceived market efficiency: A survey at the Pakistan stock exchange. Qual. Res. Financ. Mark. 2018, 10, 85–110. [Google Scholar] [CrossRef]
- Ifcher, J.; Zarghamee, H. Behavioral economic phenomena in decision-making for others. J. Econ. Psychol. 2020, 77, 102180. [Google Scholar] [CrossRef]
- Ellul, N.; Capocchi, L.; Santucci, J.F. Big data decision making based on predictive data analysis using DEVS simulations. In Proceedings of the 3rd ACM SIGSIM Conference on Principles of Advanced Discrete Simulation, London, UK, 10–12 June 2015; pp. 257–258. [Google Scholar]
- Clayton, W.S. Remediation Decision-Making and Behavioral Economics: Results of an Industry Survey. Groundw. Monit. Remediat. 2017, 37, 23–33. [Google Scholar] [CrossRef]
- Basu, R.; Lim, W.M.; Kumar, A.; Kumar, S. Marketing analytics: The bridge between customer psychology and marketing decision-making. Psychol. Mark. 2023, 40, 2588–2611. [Google Scholar] [CrossRef]
- Agarwal, R.; Dugas, M.; Gao, G.; Kannan, P. Emerging technologies and analytics for a new era of value-centered marketing in healthcare. J. Acad. Mark. Sci. 2020, 48, 9–23. [Google Scholar] [CrossRef]
- Behera, R.K.; Bala, P.K.; Rana, N.P. Creation of sustainable growth with explainable artificial intelligence: An empirical insight from consumer packaged goods retailers. J. Clean. Prod. 2023, 399, 136605. [Google Scholar] [CrossRef]
- Dwivedi, Y.K.; Hughes, L.; Wang, Y.; Alalwan, A.A.; Ahn, S.J.; Balakrishnan, J.; Barta, S.; Belk, R.; Buhalis, D.; Dutot, V.; et al. Metaverse marketing: How the metaverse will shape the future of consumer research and practice. Psychol. Mark. 2023, 40, 750–776. [Google Scholar] [CrossRef]
- Rahman, M.S.; Hossain, M.A.; Fattah, F.A.M.A. Does marketing analytics capability boost firms’ competitive marketing performance in data-rich business environment? J. Enterp. Inf. Manag. 2021, 35, 455–480. [Google Scholar] [CrossRef]
- Liang, X.; Li, G.; Zhang, H.; Nolan, E.; Chen, F. Firm performance and marketing analytics in the Chinese context: A contingency model. J. Bus. Res. 2022, 141, 589–599. [Google Scholar] [CrossRef]
- Akter, S.; Bandara, R.; Hani, U.; Wamba, S.F.; Foropon, C.; Papadopoulos, T. Analytics-based decision-making for service systems: A qualitative study and agenda for future research. Int. J. Inf. Manag. 2019, 48, 85–95. [Google Scholar] [CrossRef]
- Cao, G.; Duan, Y.; El Banna, A. A dynamic capability view of marketing analytics: Evidence from UK firms. Ind. Mark. Manag. 2019, 76, 72–83. [Google Scholar] [CrossRef]
- Hallikainen, H.; Savimäki, E.; Laukkanen, T. Fostering B2B sales with customer big data analytics. Ind. Mark. Manag. 2020, 86, 90–98. [Google Scholar] [CrossRef]
- Jeble, S.; Kumari, S.; Patil, Y. Role of big data in decision making. Oper. Supply Chain Manag. Int. J. 2017, 11, 36–44. [Google Scholar] [CrossRef]
- Miniard, P.W.; Bhatla, S.; Lord, K.R.; Dickson, P.R.; Unnava, H.R. Picture-based persuasion processes and the moderating role of involvement. J. Consum. Res. 1991, 18, 92–107. [Google Scholar] [CrossRef]
- Gkiouzepas, L.; Hogg, M.K. Articulating a new framework for visual metaphors in advertising. J. Advert. 2011, 40, 103–120. [Google Scholar] [CrossRef]
- Phillips, B.K.; Prybutok, V.R.; Peak, D.A. Decision Confidence, Information Usefulness, and Information Seeking Intention in the Presence of Disconfirming Information. Informing Sci. Int. J. Emerg. Transdiscipl. 2014, 17, 1–24. [Google Scholar] [CrossRef]
- Celik, E.; Gul, M.; Yucesan, M.; Mete, S. Stochastic multi-criteria decision-making: An overview to methods and applications. Beni-Suef Univ. J. Basic Appl. Sci. 2019, 8, 1–11. [Google Scholar] [CrossRef]
- Kalloniatis, A.C.; McLennan-Smith, T.A.; Roberts, D.O. Modelling distributed decision-making in command and control using stochastic network synchronisation. Eur. J. Oper. Res. 2020, 284, 588–603. [Google Scholar] [CrossRef]
- Pandey, S.; Medd, R.W. A stochastic dynamic programming framework for weed control decision making: An application to Avena fatua L. Agric. Econ. 1991, 6, 115–128. [Google Scholar]
- Kettunen, J. Applications of Stochastic Modeling for Investment Decision-Making Under Market Uncertainties. Ph.D. Thesis, Helsinki University of Technology, Espoo, Finland, 2009. [Google Scholar]
- Watling, D.P.; Cantarella, G.E. Model representation & decision-making in an ever-changing world: The role of stochastic process models of transportation systems. Netw. Spat. Econ. 2015, 15, 843–882. [Google Scholar]
- Goda, D.R.; Yerram, S.R.; Mallipeddi, S.R. Stochastic Optimization Models for Supply Chain Management: Integrating Uncertainty into Decision-Making Processes. Glob. Discl. Econ. Bus. 2018, 7, 123–136. [Google Scholar] [CrossRef]
- Sevinchan, Y.; Sarkanych, P.; Tenenbaum, A.; Holovatch, Y.; Romanczuk, P. Collective decision-making with heterogeneous biases: Role of network topology and susceptibility. Phys. Rev. Res. 2025, 7, 013286. [Google Scholar] [CrossRef]
- Langer, M.; Landers, R.N. The future of artificial intelligence at work: A review on effects of decision automation and augmentation on workers targeted by algorithms and third-party observers. Comput. Hum. Behav. 2021, 123, 106878. [Google Scholar] [CrossRef]
- Höddinghaus, M.; Sondern, D.; Hertel, G. The automation of leadership functions: Would people trust decision algorithms? Comput. Hum. Behav. 2021, 116, 106635. [Google Scholar] [CrossRef]
- Bigman, Y.E.; Wilson, D.; Arnestad, M.N.; Waytz, A.; Gray, K. Algorithmic discrimination causes less moral outrage than human discrimination. J. Exp. Psychol. Gen. 2023, 152, 4–27. [Google Scholar] [CrossRef]
- Longoni, C.; Bonezzi, A.; Morewedge, C.K. Resistance to medical artificial intelligence. J. Consum. Res. 2019, 46, 629–650. [Google Scholar] [CrossRef]
- Newman, D.T.; Fast, N.J.; Harmon, D.J. When eliminating bias isn’t fair: Algorithmic reductionism and procedural justice in human resource decisions. Organ. Behav. Hum. Decis. Process. 2020, 160, 149–167. [Google Scholar] [CrossRef]
- Marcinkowski, F.; Kieslich, K.; Starke, C.; Lünich, M. Implications of AI (un-) fairness in higher education admissions: The effects of perceived AI (un-) fairness on exit, voice and organizational reputation. In Proceedings of the 2020 Conference on Fairness, Accountability, and Transparency, Barcelona, Spain, 27–30 January 2020; Association for Computing Machinery: New York, NY, USA, 2020; pp. 122–130. [Google Scholar]
- Lee, M.K. Understanding perception of algorithmic decisions: Fairness, trust, and emotion in response to algorithmic management. Big Data Soc. 2018, 5, 2053951718756684. [Google Scholar] [CrossRef]
- Acikgoz, Y.; Davison, K.H.; Compagnone, M.; Laske, M. Justice perceptions of artificial intelligence in selection. Int. J. Sel. Assess. 2020, 28, 399–416. [Google Scholar] [CrossRef]
- Galière, S. When food-delivery platform workers consent to algorithmic management: A Foucauldian perspective. New Technol. Work Employ. 2020, 35, 357–370. [Google Scholar] [CrossRef]
- Möhlmann, M.; Zalmanson, L.; Henfridsson, O.; Gregory, R.W. Algorithmic management of work on online labor platforms: When matching meets control. Manag. Inf. Syst. Q. 2021, 45, 1999–2022. [Google Scholar] [CrossRef]
- Tobia, K.; Nielsen, A.; Stremitzer, A. When does physician use of AI increase liability? J. Nucl. Med. 2021, 62, 17–21. [Google Scholar] [CrossRef] [PubMed]
- Stai, B.; Heller, N.; McSweeney, S.; Rickman, J.; Blake, P.; Vasdev, R.; Edgerton, Z.; Tejpaul, R.; Peterson, M.; Rosenberg, J.; et al. Public perceptions of artificial intelligence and robotics in medicine. J. Endourol. 2020, 34, 1041–1048. [Google Scholar] [CrossRef] [PubMed]
- Valletta, J.J.; Torney, C.; Kings, M.; Thornton, A.; Madden, J. Applications of machine learning in animal behaviour studies. Anim. Behav. 2017, 124, 203–220. [Google Scholar] [CrossRef]
- Verschure, P.F.M.J. (Ed.) The Nature and Dynamics of Collaboration; MIT Press: Cambridge, CA, USA, 2025. [Google Scholar]
- Wu, B.; Huo, L. Studying the impact of individual emotional states on the co-evolution of information, behavior and disease in multiplex networks. Phys. A Stat. Mech. Appl. 2025, 665, 130480. [Google Scholar] [CrossRef]
- Ashby, W.R. Principles of Self-organization. In Proceedings of the Transactions of the University of Illinois Symposium; Foerster, H.V., Zopf, G.W.J., Eds.; Pergamon Press: London, UK, 1962; pp. 255–278. [Google Scholar]
- Lazarević, M.P. Elements of mathematical phenomenology of self-organization nonlinear dynamical systems: Synergetics and fractional calculus approach. Int. J. Non-Linear Mech. 2015, 73, 31–42. [Google Scholar] [CrossRef]
- Rylands, C.; Andrei, N. Nonequilibrium aspects of integrable models. Annu. Rev. Condens. Matter Phys. 2020, 11, 147–168. [Google Scholar] [CrossRef]
- Pal, S.; Melnik, R. Complex non-Markovian dynamics and the dual role of astrocytes in Alzheimer’s disease development and propagation. Quant. Biol. 2025, 13, e70001. [Google Scholar] [CrossRef]
- Cimmelli, V.A.; Sellitto, A.; Jou, D. Nonlocal effects and second sound in a nonequilibrium steady state. Phys. Rev. B 2009, 79, 014303. [Google Scholar] [CrossRef]
- Maes, C.; Safaverdi, S.; Visco, P.; Van Wijland, F. Fluctuation-response relations for nonequilibrium diffusions with memory. Phys. Rev. E 2013, 87, 022125. [Google Scholar] [CrossRef]
- Thieu, T.; Melnik, R. Human Biosocial Dynamics with Complex Psychological Behaviour: Hierarchy of Mathematical Models and Nonequilibrium Phenomena. In Proceedings of the XXVII Sitges Conference on Statistical Mechanics, Nonequilibrium Phenomena: From Quantum to Macroscopic Scales, Sitges, Spain, 29 May–2 June 2023; p. 77. [Google Scholar]
- Sengupta, A. Is nature quantum non-local, complex holistic, or what? II—Applications. Nonlinear Anal. Real World Appl. 2010, 11, 1201–1219. [Google Scholar] [CrossRef]
- Poznanski, R. The dynamic organicity theory of consciousness: How consciousness arises from the functionality of multiscale complexity in the material brain. J. Multiscale Neurosci. 2024, 3, 68–87. [Google Scholar] [CrossRef]
- Sanz Perl, Y.; Bocaccio, H.; Pallavicini, C.; Pérez-Ipiña, I.; Laureys, S.; Laufs, H.; Kringelbach, M.; Deco, G.; Tagliazucchi, E. Nonequilibrium brain dynamics as a signature of consciousness. Phys. Rev. E 2021, 104, 014411. [Google Scholar] [CrossRef] [PubMed]
- Tschacher, W.; Haken, H. Intentionality in non-equilibrium systems? The functional aspects of self-organized pattern formation. New Ideas Psychol. 2007, 25, 1–15. [Google Scholar] [CrossRef]
- Haken, H.; Tschacher, W. Theoretical model of intentionality. Mind Matter 2010, 8, 7–18. [Google Scholar]
- Freeman, W.J. Consciousness, intentionality and causality. J. Conscious. Stud. 1999, 6, 143–172. [Google Scholar]
- Eisbach, S.; Mai, O.; Hertel, G. Combining theoretical modelling and machine learning approaches: The case of teamwork effects on individual effort expenditure. New Ideas Psychol. 2024, 73, 101077. [Google Scholar] [CrossRef]
- Pribram, K.H. Brain and Perception: Holonomy and Structure in Figural Processing; Psychology Press: London, UK, 2013. [Google Scholar]
- Hameroff, S.; Penrose, R. Consciousness in the universe: A review of the ‘Orch OR’ theory. Phys. Life Rev. 2014, 11, 39–78. [Google Scholar] [CrossRef]
- Sargsyan, R.; Karamyan, G. Nonlocal Correlations in Macroscopic Systems: Living Objects, Mental Influence and Physical Processes. NeuroQuantology 2014, 12, 355–365. [Google Scholar] [CrossRef][Green Version]
- Pal, S.; Melnik, R. Coupled Spatio-Temporal Dynamics and Nonlocality in Advanced Mathematical Models for the Analysis of Complex Neurodegenerative Disease Pathologies. In Proceedings of the X International Conference on Computational Methods for Coupled Problems in Science and Engineering (COUPLED PROBLEMS 2023), Chania, Greece, 5–7 June 2023; pp. 1–12. [Google Scholar]
- Lutz, E. Fractional Langevin equation. Phys. Rev. E 2001, 64, 051106. [Google Scholar] [CrossRef]
- Burov, S.; Barkai, E. Fractional Langevin equation: Overdamped, underdamped, and critical behaviors. Phys. Rev. E 2008, 78, 031112. [Google Scholar] [CrossRef] [PubMed]
- Da Silva, M.A.A.; Cressoni, J.C.; Schütz, G.M.; Viswanathan, G.; Trimper, S. Non-Gaussian propagator for elephant random walks. Phys. Rev. E 2013, 88, 022115. [Google Scholar] [CrossRef] [PubMed]
- Reeves, C.C.; Zhu, Y.; Yang, C.; Vlček, V. Unimportance of memory for the time nonlocal components of the Kadanoff-Baym equations. Phys. Rev. B 2023, 108, 115152. [Google Scholar] [CrossRef]
- Balzer, K.; Bonitz, M.; Van Leeuwen, R.; Stan, A.; Dahlen, N. Nonequilibrium Green’s function approach to strongly correlated few-electron quantum dots. Phys. Rev. B 2009, 79, 245306. [Google Scholar] [CrossRef]
- Pal, S.; Melnik, R. Nonequilibrium landscape of amyloid-beta and calcium ions in application to Alzheimer’s disease. Phys. Rev. E 2025, 111, 014418. [Google Scholar] [CrossRef]
- Pal, S.; Banerjee, M.; Melnik, R. Nonequilibrium dynamics in a noise-induced predator–prey model. Chaos Solitons Fractals 2025, 191, 115884. [Google Scholar] [CrossRef]
- Khrennikov, A. Quantum-like model for unconscious–conscious interaction and emotional coloring of perceptions and other conscious experiences. Biosystems 2021, 208, 104471. [Google Scholar] [CrossRef]
- Kyriazos, T.; Poga, M. Quantum concepts in psychology: Exploring the interplay of physics and the human psyche. Biosystems 2024, 235, 105070. [Google Scholar] [CrossRef]
- Barrett, L.F.; Lewis, M.; Haviland-Jones, J.M. Handbook of Emotions; Guilford Publications: New York, NY, USA, 2016. [Google Scholar]
- Wang, P.; Huo, J.; Wang, X.M.; Wang, B.H. Diffusion and memory effect in a stochastic process and the correspondence to an information propagation in a social system. Phys. A Stat. Mech. Appl. 2022, 607, 128206. [Google Scholar] [CrossRef]
- Messori, C. Mind-Brain-Body system’s dynamics. Open Access Libr. J. 2020, 7, 1–49. [Google Scholar] [CrossRef]
- Ward, D.; Stapleton, M. Es are good: Cognition as enacted, embodied, embedded, affective and extended. In Consciousness in Interaction: The Role of the Natural and Social Context in Shaping Consciousness; Paglieri, F., Ed.; John Benjamins Publishing Company: Amsterdam, The Netherlands, 2012; pp. 89–104. [Google Scholar]
- Seif, A.; Hafezi, M.; Jarzynski, C. Machine learning the thermodynamic arrow of time. Nat. Phys. 2021, 17, 105–113. [Google Scholar] [CrossRef]
- Wood, A.; Coan, J.A. Beyond Nature Versus Nurture: The Emergence of Emotion. Affect. Sci. 2023, 4, 443–452. [Google Scholar] [CrossRef]
- Zanette, L.Y.; Hobbs, E.C.; Witterick, L.E.; MacDougall-Shackleton, S.A.; Clinchy, M. Predator-induced fear causes PTSD-like changes in the brains and behaviour of wild animals. Sci. Rep. 2019, 9, 11474. [Google Scholar] [CrossRef]
- Löw, A.; Lang, P.J.; Smith, J.C.; Bradley, M.M. Both predator and prey: Emotional arousal in threat and reward. Psychol. Sci. 2008, 19, 865–873. [Google Scholar] [CrossRef]
- Kigar, S.L.; Cuarenta, A.; Zuniga, C.L.; Chang, L.; Auger, A.P.; Bakshi, V.P. Brain, behavior, and physiological changes associated with predator stress—An animal model for trauma exposure in adult and neonatal rats. Front. Mol. Neurosci. 2024, 17, 1322273. [Google Scholar] [CrossRef]
- Batabyal, A. Predator–prey systems as models for integrative research in biology: The value of a non-consumptive effects framework. J. Exp. Biol. 2023, 226, jeb245851. [Google Scholar] [CrossRef]
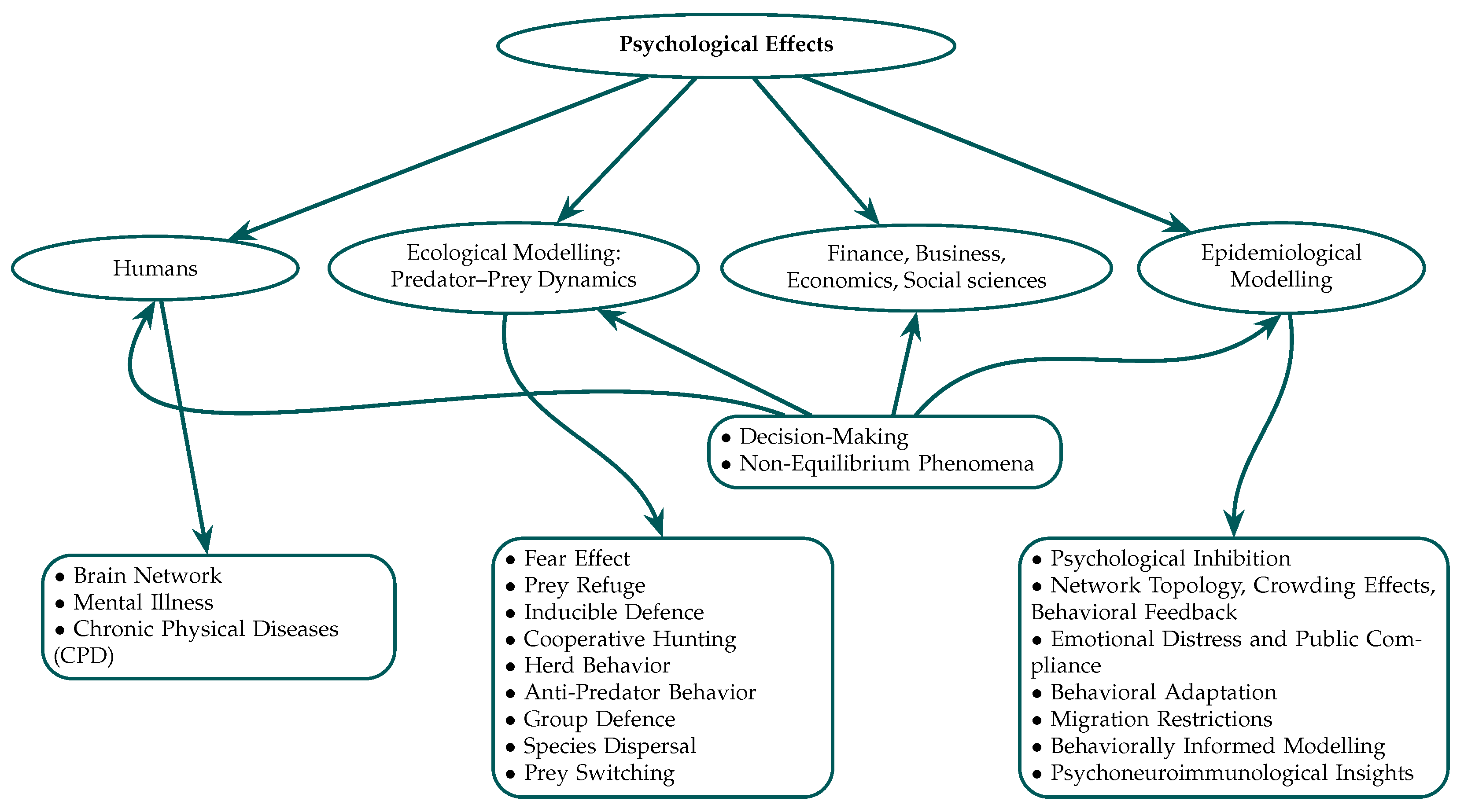

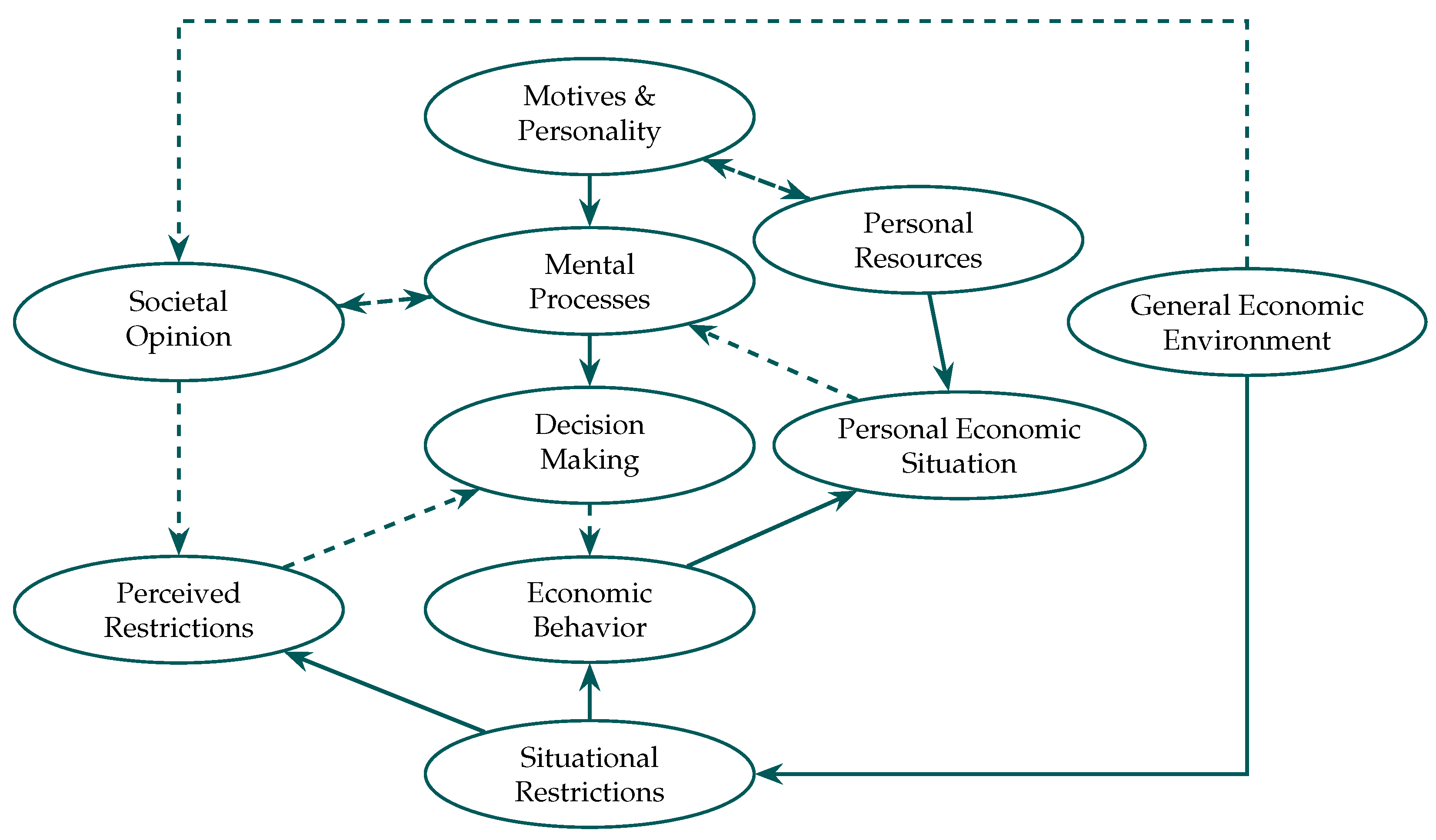
| Model Type | Mathematical Tool | Equation | DBT Influence |
|---|---|---|---|
| Dynamical Systems [163,164] | Differential Equations | stabilizes emotional trajectories via control input | |
| Reinforcement Learning [157,158] | MDP+Q-learning | reinforces skill acquisition through adaptive decision-making | |
| Stochastic Modeling [159,160] | Stochastic Diff. Equation | reduces mood volatility and increases emotional resilience | |
| Network Analysis [161,162] | Graph Theory | Network structure of symptoms and skills | weakens maladaptive links, strengthens adaptive psychological nodes |
| Modeling Dimension | Animal Psychology | Human Psychology |
|---|---|---|
| Focus of primary modeling | Adaptive behavior for survival and energy efficiency | Emotional regulation, cognitive processing, social conformity |
| Representative modeling approaches | Optimal foraging theory, predator–prey dynamics, signal detection models | Reinforcement learning, prospect theory, agent-based models, delay differential equations |
| Learning and adaptation mechanisms | Classical and operant conditioning, basic reinforcement learning | Meta-learning, Bayesian belief updating, affect-biased decision-making |
| Nature of feedback | immediate, environmentally contingent | Delayed, emotionally charged, and socially contextualized |
| Neural and cognitive representations | Implicit or species-constrained neural substrates | Explicit neural correlates (e.g., prefrontal cortex, limbic system, DMN) |
| Cognitive and systemic complexity | Low to moderate, domain-specific | High-level integration across cognitive, emotional, and sociocultural domains |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saha, S.; Melnik, R. Integrating Emotion-Specific Factors into the Dynamics of Biosocial and Ecological Systems: Mathematical Modeling Approaches Accounting for Psychological Effects. Math. Comput. Appl. 2025, 30, 136. https://doi.org/10.3390/mca30060136
Saha S, Melnik R. Integrating Emotion-Specific Factors into the Dynamics of Biosocial and Ecological Systems: Mathematical Modeling Approaches Accounting for Psychological Effects. Mathematical and Computational Applications. 2025; 30(6):136. https://doi.org/10.3390/mca30060136
Chicago/Turabian StyleSaha, Sangeeta, and Roderick Melnik. 2025. "Integrating Emotion-Specific Factors into the Dynamics of Biosocial and Ecological Systems: Mathematical Modeling Approaches Accounting for Psychological Effects" Mathematical and Computational Applications 30, no. 6: 136. https://doi.org/10.3390/mca30060136
APA StyleSaha, S., & Melnik, R. (2025). Integrating Emotion-Specific Factors into the Dynamics of Biosocial and Ecological Systems: Mathematical Modeling Approaches Accounting for Psychological Effects. Mathematical and Computational Applications, 30(6), 136. https://doi.org/10.3390/mca30060136






