A Fav-Jerry Distribution Under Joint Type-II Censoring: Quantifying Cross-Cultural Differences in Autism Knowledge

Abstract

The given paper proposes a new statistical framework based on the combination of the Fav-Jerry distribution (FJD) and a joint type-II censoring scheme (JT-II-CS) to examine heterogeneous and censored data. The FJD offers tractability in analysis by using its closed form of the quantile function, whereas with missing or incomplete data, the JT-II-CS offers multi-sample comparisons. Bayesian estimation is based on Markov chain Monte Carlo procedures, while the maximum likelihood estimation is obtained via a Newton–Raphson method. Both estimation strategies provide estimates of the parameters along with corresponding measures of uncertainty. The proposed methodology is also used on coded survey data on the knowledge of autism in both Hong Kong and Canada, which illustrates its potential in the measurement of cultural variance. In addition to this use, the framework highlights the potential for integrating more complex distributional modeling with censoring methods for general applications in engineering, natural sciences, and social sciences.

1. Introduction

Autism spectrum disorder (ASD) is a neurodevelopmental condition in which variations in social communication, behavior, and sensory perception are evident. This definition of ASD follows the internationally accepted clinical standard established by the Diagnostic and Statistical Manual of Mental Disorders, Fifth Edition (DSM-5) [1]. It is essential that autism perception is better understood by the general population and especially by education workers. Furthermore, it would help in creating inclusive schooling conditions and alleviating stigmas. For the future workforce in classrooms, pre-service teachers have a central role to play when supporting autistic students, and the knowledge and attitudes held by pre-service teachers directly affect the quality of educational experiences for learners. The cross-cultural comparison of autism knowledge is particularly significant since there are often significant differences across countries in the perceptions, attitudes, and possibilities to train. As an example, studies carried out recently have revealed that in certain instances, pre-service teachers can harbor more teacher misconceptions or have less correct information regarding autism compared with pre-service teachers in other regions.

Among these studies are the following recent works. As has been reported by Sanz-Cervera et al. [2], despite an average level of knowledge of pre-service teachers about autism being reported, there are still significant misconceptions, and the knowledge level of cohorts of pre-service teachers who have studied various cultural and educational contexts differs considerably. El-Setouhy et al. [3] discovered that there are strong regional and institutional variations in teacher preparedness and accuracy of autism knowledge, with respondents in certain areas showing higher misconception rates. Hernandez-Gonzalez et al. [4] revealed that the levels of awareness and misconceptions of Cuban teachers about autism were lower than those of teachers in other nations, which confirms the presence of cross-regional differences in the knowledge of teachers. All these studies prove the fact that the knowledge of pre-service teachers about autism is heterogeneous in different regions and that the lack of knowledge and the presence of misconceptions are problems at the international level. Unless addressed, such inequalities may lead to inequality in educational opportunities for people with autism across the globe.

Cross-cultural research on autism is of the utmost importance because the cultural context plays a critical role in its determination, recognition, and intervention. A recent study by Cheng et al. [5] demonstrated significant disparities in autism-related knowledge, clear stigma, and implicit biases in Hong Kong, the UK, and the US. Keating et al. [6] also proved that camouflaging, societal acceptance, and mental health outcomes differ significantly in cultural contexts, posing the urgent necessity to conduct culturally specific studies and interventions. Aside from that, a systematic review by Zhang and Chen [7] highlighted the multidimensional nature of the cultural and language-mediated individualities that influence the decision-making patterns of minority parents of children with ASD in terms of service seeking.

Because this is not sufficient to inform evidence-based policy and training interventions, it is not enough to note if there are differences. Such differences have to be measured in a manner that should be statistically solid as well as easily understandable for researchers, educators, and policymakers. Conventional inferential methods (e.g., mean comparison performed through t-tests or proportion comparison through chi-squared analyses) afford little explanation of the overall size of cross-cultural differences that cross-cultural research is attempting to examine and convey little about the practical implications of regional differences in the context of procedural form. In other words, although traditional tests may show the presence or absence of a statistically significant difference, they do not explicitly show the size of the difference or its distributional characteristics; that is, a p value is information saying that a group of people is different but not by how much or in what manner (e.g., how the whole distribution of responses differs and not only the mean). For more details, see Younes et al. [8].

Although there is an increasing awareness of these cultural processes, solid statistical models based on the survival and reliability literature are not being exploited in autism studies. A promising methodology that can help with cultural comparison effectively is the joint type-II censoring scheme (JT-II-CS), which is a long-established technique in lifetime studies, with many populations involved, as explained by Balakrishnan and Feng [9]. The JT-II-CS is modified in this study to evaluate autism perceptions within two communities $(k=2)$, and it is combined with the Fav-Jerry distribution (FJD), a flexible one-parameter model suggested by Ekemezie and Obulezi [10]. The FJD is both analytically tractable because of its close-form quantile operation and its being empirically robust in the modeling of heterogeneous cultural information.

This study fills the gap between statistical rigor and cultural understanding by coding qualitative responses to autism based on Appendix D (Lam et al. [11]) and modeling them as survey knowledge scores under the JT-II-CS. It enables an accurate comparison of FJD parameters, which serve as cultural indicators for both Hong Kong and Canada, using MLE and Bayesian estimation methods. This cross-pollination methodology not only enhances autism studies but also demonstrates how statistical inference methods can be used to clarify cultural heterogeneity in social perception.

The rest of this paper is arranged as follows. In Section 2, the main characteristics of the Fav-Jerry distribution are introduced, and the reason why it is an appropriate distribution to use when the data are not homogeneous and have censoring is given. Section 3 defines the model of the JT-II-CS and how it can be modified for cross-cultural research on autism. Section 4 presents the inferential procedures, which consist of both maximum likelihood estimation and Bayesian estimation. Section 5 uses the suggested methodology with real data from Hong Kong and Canada, whereas in Section 6, the quantitative findings are discussed in terms of extension and validation of the qualitative findings of Lam et al. [11]. Lastly, there is Section 7, which wraps up the paper with implications, limitations, and future research directions.

2. Fav-Jerry Distribution (FJD)

The FJD, suggested by Ekemezie and Obulezi [10], is a new addition to the Lindley family of distributions. It is derived from a mixture of exponential and gamma distributions and is unique in having a closed form of quantile function, which simplifies both analysis and simulations. Its main properties were defined by Ekemezie and Obulezi [10]. Estimation procedures without and with Bayesian inference were developed, and the efficiency of the model in light of real profiles of infant mortality and airplane system failure rates were shown. It was observed that the FJD was more fitting than the conventional distributions, including the Weibull, Chris-Jerry, and exponentiated inverted exponential distributions. The probability density function (PDF) of the FJD can be given as follows:

$$f\left(x\right)=\left({\displaystyle \frac{\psi }{{\psi }^2+2}}\right)\left(2+{\psi }^{3}x\right)e^{-\psi x},x>0,\psi >0,$$

Meanwhile, the cumulative distribution function (CDF) is given as follows:

$$F\left(x\right)=1-\left(1+{\displaystyle \frac{{\psi }^{3}x}{{\psi }^2+2}}\right)e^{-\psi x}.$$

Although the FJD was originally intended to address reliability problems, the method can be viewed as an appealing statistical framework for solving problems in other areas. We use the FJD in a common type-II censoring setting to analyze the cross-cultural difference in perceptions of autism. In particular, the qualitative aspect of the responses of two groups of people (Hong Kong and Canada) is converted into numerical profiles that are suitable to be modeled with the FJD. Here, we view each of the lifetimes as a coded response or score indicating our knowledge or perception of autism, with censoring being a logical consequence of missing or incomplete answers. Our main strengths in this work are that by using the FJD under joint censoring, we obtain two advantages. (1) The analytical tractability of the quantile function is given in a closed form, and inferences and simulations at the community level are efficient. (2) Empirical flexibility of the FJD is known to be analytically effective with heterogeneous lifetime data, as explained by Ekemezie and Obulezi [10]. Hence, it could be used to adequately measure the cross-cultural variation of autism knowledge and attitudes.

Therefore, aside from the status of a theoretically sound distributional choice, the FJD becomes a practical instrument allowing quantification of cultural dissimilarities within the context of autism, which further broadens the area of application of said instrument into the domains of social and health sciences.

3. Joint K Censored Samples

The JT-II-CS is a life test in which a fixed number of failures r have occurred. Several populations are observed concurrently until such a time is reached. First used in reliability analysis, Balakrishnan and Feng [9] gave a formal likelihood-based framework in which it is possible to perform exact Bayesian inferences. The JT-II-CS also allows for fast and efficient simultaneous comparison of populations as well as lowering the cost and data collection burden associated with the experiment. In this paper, we modify the JT-II-CS engineering reliability framework for cross-cultural autism studies. In this case, Hong Kong and Canada ($k=2$) are being compared with coded response informational measures of their observed knowledge on autism. By subtracting any non-informative responses and retaining only elements of correspondence between both groups, there can be no bias in a comparison. The answer to each question is considered a lifetime, with the censoring depicting incomplete and missing data. The JT-II-CS has a formal statistical model (i.e., the FJD; Section 2) of the individual response distributions, which can answer the cultural differences question decisively.

Assume k number of samples, where each one represents the responses collected from surveys distributed among different communities about a certain matter. These responses can be transformed into scores and represented as follows.

Suppose $X_{11},X_{12},\dots ,X_{1n_1}$ are the scores of $n_1$ participants from community $C_1$, and they are assumed to be independent and identically distributed (iid) variables from a community with a CDF $F_1\left(x\right)$ and PDF $f_1\left(x\right)$. Similarly, $X_{21},X_{22},\dots ,X_{2n_2}$ represent the scores of $n_2$ participants from community $C_2$, which is assumed to be a sample from $f_2\left(x\right)$ and a CDF $F_2\left(x\right)$. Similarly, $X_{k1},X_{k2},\dots ,X_{k{n}_k}$ denote the scores of $n_k$ participants from a community $C_k$, being iid variables from a PDF $f_k\left(x\right)$ and CDF $F_k\left(x\right)$. Moreover, let $N={\displaystyle \sum _{i=1}^k}$ $n_i$ denote the total sample size and r denote the total number of registered scores.

Let ${\varphi }_1\le {\varphi }_2\le \cdots \le {\varphi }_N$ denote the order statistics of the N random variables $\{X_{ij};1$ $\le i\le k,$ $1\le j\le n_i\}.$ Therefore, under the joint Type-II censoring scheme (JT-II-CS) for the k samples, the data consist of $\left(\delta ,\varphi \right),$ where $\varphi =({\varphi }_1,{\varphi }_2,\dots ,{\varphi }_r),$ ${\varphi }_i\in \{X_{h_{i}1},X_{h_{i}2},\dots ,X_{h_i{n}_i}\}$ for $1\le h_1\le h_2\le \cdots \le h_r\le k$, with r being a prefixed integer. Finally, in association with $(h_1,h_2,\dots ,h_r),$ $\delta$ can be defined as $\delta =\left({\delta }_1\left(h\right),{\delta }_2\left(h\right),\dots ,{\delta }_r\left(h\right)\right),$ where

$${\delta }_i\left(h\right)=\left\{\begin{array}{c}1,\hfill \\ 0,\hfill \end{array}\begin{array}{c}\mathrm{if}h=h_i\hfill \\ \multicolumn{1}{c}{\mathrm{elsewhere},}\end{array}\right.$$

(1)

with ${\sum }_{h=1}^k{\delta }_i\left(h\right)=1$ for $i=1,2,\dots ,r.$

According to the JT-II-CS, it is possible to assume that $r={\sum }_{h=1}^k{M}_r\left(h\right),h=1,2,\dots ,k,$ where $M_r\left(h\right)={\sum }_{i=1}^r{\delta }_i\left(h\right)$ represents the number of scores in $\varphi$, which belonging to sample h.

4. Statistical Inferences About k Parameters of FJD

For the JT-II-CS, it is possible to have situations where both failures are observed and censored items are included in the likelihood function, thus allowing a simultaneous estimation of parameters across the populations (Balakrishnan and Feng [9]). In a case where all the populations are also assumed to be FJDs, the PDF and CDF take on known forms, giving tractable maximum likelihood and Bayesian estimates.

Balakrishnan and Feng [9] introduced the likelihood function in a general form for k samples drawn from any PDF under the JT-II-CS as follows:

$$L({\psi }_1,{\psi }_2,\dots ,{\psi }_k,\delta ,\varphi )=D_r{\displaystyle \prod _{i=1}^r}{\displaystyle \prod _{h=1}^k}{\left(f_h\left({\varphi }_i\right)\right)}^{{\delta }_i\left(h\right)}\prod _{h=1}^k{\left({\overline{F}}_h\left({\varphi }_r\right)\right)}^{n_h-M_r\left(h\right)},$$

(2)

where $D_r={\displaystyle \frac{{\prod }_{h=1}^k{n}_h!}{{\prod }_{h=1}^k\left[n_h-M_r\left(h\right)\right]!}}$ and ${\overline{F}}_h\left({\varphi }_r\right)=1-F_h\left({\varphi }_r\right).$ When the k communities follow the FJD with a CDF $F_h\left(x\right)=1-\left(1+{\displaystyle \frac{{\psi }_h^{3}x}{{\psi }_h^2+2}}\right)e^{-{\psi }_{h}x}$ and a PDF $f_h\left(x\right)=\left({\displaystyle \frac{{\psi }_h}{{\psi }_h^2+2}}\right)\left(2+{\psi }_h^{3}x\right)e^{-{\psi }_{h}x},x>0,$ for $1\le h\le k,$ the likelihood function in Equation (2) becomes

$$\begin{array}{ccc}\hfill L({\psi }_1,{\psi }_2,\dots ,{\psi }_k,\delta ,\varphi )& =& D_r{e}^{-{\displaystyle \sum _{i=1}^r}{\displaystyle \sum _{h=1}^k}{\psi }_h{\delta }_i\left(h\right){\varphi }_i}{\displaystyle \prod _{i=1}^r}{\displaystyle \prod _{h=1}^k}{\left[\begin{array}{c}\left({\displaystyle \frac{{\psi }_h}{{\psi }_h^2+2}}\right)\left(2+{\psi }_h^3{\varphi }_i\right)\end{array}\right]}^{{\delta }_i\left(h\right)}\hfill \\ & & e^{-{\varphi }_r{\displaystyle \sum _{h=1}^k}{\psi }_h[n_h-M_r\left(h\right)]}{\displaystyle \prod _{h=1}^k}{\left[\begin{array}{c}1+{\displaystyle \frac{{\psi }_h^3{\varphi }_r}{{\psi }_h^2+2}}\end{array}\right]}^{n_h-M_r\left(h\right)},\hfill \end{array}$$

(3)

Another benefit of the JT-II-CS framework is that it is practical and efficient in terms of statistics when comparing two or more groups at the same time. Its strength and flexibility have been affirmed by recent research. For example, Kumar et al. [12] used Bayesian and classical inference on two inverted Chen populations with the JT-II-CS and showed that the approach produces correct and reliable estimators and can effectively address censoring, which further supports the adaptability of the method in various lifetime models. Likewise, Bargoshadi and Bevrani [13] demonstrated that the shrinkage estimation models applied to the JT-II censored data of two Burr-XII populations increased the estimation precision and predictive performance of the models, particularly for small sample sizes. Taken together, these contributions demonstrate that the JT-II-CS not only minimizes the cost of data collection and the duration of an experiment but also facilitates both frequentist and Bayesian estimation with proven high performance. This, in the current study, provides a good reason to use the JT-II-CS in a cross-cultural autism context. The framework allows noninformative or missing responses to be accommodated without preferential treatment, whereas statistically rigorous comparisons of cultural distributions are possible.

4.1. Classical Inferences Based on MLEs

We estimate the Fav-Jerry distribution parameters under a standard JT-II-CS in this subsection to obtain the maximum likelihood estimates (MLEs). The MLE method is statistically powerful because it is consistent and asymptotically efficient, and a likelihood-based interpretation is possible (Casella and Berger [14]). Recent research by Ding and Gui [15] showed that the JT-II-CS allows useful estimation and inference of lifetime models, e.g., gamma distributions, with both MLE and Bayesian approaches. These developments affirm that the JT-II-CS is amenable to statistically sound inference under a wide range of models and the appropriateness of the JT-II-CS for the Fav-Jerry framework. Based on this evidence, we develop the log-likelihood for the Fav-Jerry model under the JT-II-CS for both frequentist and Bayesian approaches.

The log-likelihood function may then be written as

$$\begin{array}{ccc}\hfill lnL({\psi }_1,{\psi }_2,\dots ,{\psi }_k,\delta ,\varphi )& =& ln\left|D\right|-\sum _{i=1}^r\sum _{h=1}^k\left[\begin{array}{c}{\psi }_h{\delta }_i\left(h\right){\varphi }_i\end{array}\right]+\sum _{i=1}^r\sum _{h=1}^k{\delta }_i\left(h\right)\left[\begin{array}{c}ln\left[{\displaystyle \frac{{\psi }_h}{{\psi }_h^2+2}}\right]+ln\left[\begin{array}{c}2+{\psi }_h^3{\varphi }_i\end{array}\right]\end{array}\right]+\hfill \\ & & -{\varphi }_r\sum _{h=1}^k{\psi }_h[n_h-M_r\left(h\right)]+\sum _{h=1}^k\left[\begin{array}{c}\left(\begin{array}{c}{n}_h-M_r\left(h\right)\end{array}\right)ln\left[\begin{array}{c}1+{\displaystyle \frac{{\psi }_h^3{\varphi }_r}{{\psi }_h^2+2}}\end{array}\right]\end{array}\right].\hfill \end{array}$$

(4)

The partial derivatives of the log-likelihood function with respect to the parameters ${\psi }_h$, $h=1,2,\dots ,k$ can be derived as follows:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial lnL}{\partial {\psi }_h}}& =& -\sum _{i=1}^r\sum _{h=1}^k\left[\begin{array}{c}{\delta }_i\left(h\right){\varphi }_i\end{array}\right]+\sum _{i=1}^r\sum _{h=1}^k{\delta }_i\left(h\right)\left[\begin{array}{c}{\displaystyle \frac{1}{{\psi }_h}}-{\displaystyle \frac{2{\psi }_h}{{\psi }_h^2+2}}+{\displaystyle \frac{3{\psi }_h^2{\varphi }_i}{2+{\psi }_h^3{\varphi }_i}}\end{array}\right]+\hfill \\ & & -{\varphi }_r\sum _{h=1}^k[n_h-M_r\left(h\right)]+\sum _{h=1}^k\left[\begin{array}{c}\left(\begin{array}{c}{n}_h-M_r\left(h\right)\end{array}\right)\left({\displaystyle \frac{{\psi }_h^2{\varphi }_i({\psi }_h^2+6)}{\left({\psi }_h^2+2\right)\left({\psi }_h^3{\varphi }_i+{\psi }_h^2+2\right)}}\right)\end{array}\right],\hfill \end{array}$$

(5)

and

$$\begin{array}{ccc}\hfill {\displaystyle \frac{{\partial }^{2}lnL}{\partial {\psi }_h^2}}& =& \sum _{i=1}^r\sum _{h=1}^k{\delta }_i\left(h\right)\left[\begin{array}{c}-{\displaystyle \frac{1}{{\psi }_h^2}}+{\displaystyle \frac{2\left({\psi }_h^2-2\right)}{{\left({\psi }_h^2+2\right)}^2}}-{\displaystyle \frac{3{\psi }_h{\varphi }_i\left({\psi }_h^3{\varphi }_i-4\right)}{{\left(2+{\psi }_h^3{\varphi }_i\right)}^2}}\end{array}\right]\hfill \\ & & -\sum _{h=1}^k\left[\begin{array}{c}{\psi }_h{\varphi }_i\left(\begin{array}{c}{n}_h-M_r\left(h\right)\end{array}\right)\left({\displaystyle \frac{{\psi }_h^2({\psi }_h^5{\varphi }_i+16{\psi }_h^2{\varphi }_i+4{\psi }_h^2+12{\psi }_h{\varphi }_i-16)-48}{{\left({\psi }_h^2+2\right)}^2{\left({\psi }_h^3{\varphi }_i+{\psi }_h^2+2\right)}^2}}\right)\end{array}\right],\hfill \end{array}$$

(6)

Equation (5) shows nonlinear simultaneous equations for k unknown variables ${\psi }_h$ for $h=1,2,\dots ,k$. It is obvious that an exact solution is not easy to obtain. Therefore, a numerical method such as Newton–Raphson can be used to find an approximate solution. The algorithm has been implemented using the following steps:

(1)

Use the method of moments or some other proper estimates of the parameters as initial points of iteration, denoting the initials as ${\psi }_h\left(0\right)$ for the parameters ${\psi }_h$ and setting $j=0.$

(2)

Calculate ${{\displaystyle \frac{\partial lnL}{\partial {\psi }_h}}}_{{\psi }_h\left(j\right)}$ and the observed asymptotic inverse Fisher information matrix $I^{-1}\left({\psi }_h\right)$.

(3)

Update ${\psi }_h$ as

$$\begin{array}{ccc}\hfill {\psi }_h(j+1)& =& {\psi }_h\left(j\right)-{{\displaystyle \frac{\partial lnL}{\partial {\psi }_h}}}_{{\psi }_h\left(j\right)}\times I^{-1}\left({\psi }_h\right).\hfill \\ & \end{array}$$

(4)

Set $j=j+1$, and then return to step $2.$

(5)

Continue the consecutive steps until

$$\left|{\psi }_h(j+1)-{\psi }_h\left(j\right)\right|\le ϵ\to 0.$$

For more details about the Newton–Raphson algorithm, see Burden and Faires [16]. The final estimates of ${\psi }_h$ are the MLEs of the parameters, denoted as ${\widehat{\psi }}_h$ for $h=1,2,\dots ,k.$

The $\left(1-\zeta \right)100\%$ approximate confidence intervals (ACIs) for the parameters ${\psi }_h$, $h=1,2,\dots ,k$ can be written as

$$({\widehat{\psi }}_{hL},{\widehat{\psi }}_{hU})={\widehat{\psi }}_h\pm z_{1-{\displaystyle \frac{\zeta }{2}}}\sqrt{var\left({\widehat{\psi }}_h\right)},$$

where $z_{1-{\displaystyle \frac{\zeta }{2}}}$ is the percentile of the standard normal distribution with a left-tail probability $1-{\displaystyle \frac{\zeta }{2}}$ and $var\left({\widehat{\psi }}_h\right)$ represents the asymptotic variances in the maximum likelihood estimate, which can be calculated using the inverse of the Fisher information matrix. The asymptotic variance–covariance matrix for the maximum likelihood estimates can be formulated as follows:

$$I^{-1}={\left[-\left({\displaystyle \frac{{\partial }^{2}lnL}{\partial {\psi }_i\partial {\psi }_j}}\right)\right]}_{\downarrow \left({\widehat{\psi }}_i,{\widehat{\psi }}_j\right)}^{-1},i,j\in \{1,2,\dots ,k\}.$$

(7)

for more details, see Cohen [17].

The estimation of the FJD under joint Type-II censoring with the maximum likelihood is directly related to Bayesian approaches, which permit the calculation of credible intervals and sophisticated inference. This framework has the benefit of having strong statistics underpinning the subsequent empirical uses of the presented material and cross-cultural comparisons.

4.2. Bayesian Estimation

In this subsection, we further develop our inferential model by applying the Bayesian method to the estimation of the Fav-Jerry parameters in joint Type-II censoring. Bayesian techniques have a number of benefits, such as the ability to use prior information and complete quantification of uncertainty through the posterior distribution. Nevertheless, the posteriors are usually not computationally amenable to the derivation of closed-form expressions because of the complexity of the Fav-Jerry likelihood when censoring is considered. As a result, Markov chain Monte Carlo (MCMC) techniques, based on the Metropolis-Hastings algorithm within the Gibbs sampling approach, will be indispensable for sampling the posterior distribution and allowing inference. For more details, see Robert and Casella [18]. More recent methodological changes attest to the effectiveness of MCMC techniques in complex survival models. MCMC-driven Bayesian methods can be especially effective in survival analysis in the case of complex censoring (see Devashish et al. [19]). There is also, alternatively, integrated nested Laplace approximation (INLA), which is a faster Bayesian inference alternative used in similar contexts and an effective replacement of MCMC techniques (see Rustand et al. [20]).

Let the prior knowledge of the parameters ${\psi }_h$ be described by the following Gamma prior distributions:

$${\pi }_h\left({\psi }_h\right)\propto {\displaystyle \prod _{h=1}^k}\left[\begin{array}{c}{\psi }_h^{a_h-1}\end{array}\right]e^{-{\displaystyle \sum _{h=1}^k}{b}_h{\psi }_h},{\psi }_h>0,\mathrm{where}{a}_h,b_h>0,$$

(8)

The joint posterior density function of ${\psi }_h,$ denoted by ${\pi }^{*}\left({\psi }_h\right|\delta ,\varphi ),$ for $1\le h\le k$ can be written as follows:

$$\begin{array}{ccc}\hfill {\pi }^{*}\left({\psi }_h\right|\delta ,\varphi )& \propto & e^{-{\displaystyle \sum _{i=1}^r}{\displaystyle \sum _{h=1}^k}\left[\begin{array}{c}{\psi }_h{\delta }_i\left(h\right){\varphi }_i\end{array}\right]}{\displaystyle \prod _{i=1}^r}{\displaystyle \prod _{h=1}^k}{\left[\begin{array}{c}\left({\displaystyle \frac{{\psi }_h}{{\psi }_h^2+2}}\right)\left(2+{\psi }_h^3{\varphi }_i\right)\end{array}\right]}^{{\delta }_i\left(h\right)}\hfill \\ & & e^{-{\displaystyle \sum _{h=1}^k}\left[\begin{array}{c}{b}_h{\psi }_h+{\varphi }_r{\psi }_h\left(n_h-M_r\left(h\right)\right)\end{array}\right]}\prod _{h=1}^k\left[\begin{array}{c}\begin{array}{c}{\psi }_h^{a_h-1}\end{array}{\left[\begin{array}{c}1+{\displaystyle \frac{{\psi }_h^3{\varphi }_r}{{\psi }_h^2+2}}\end{array}\right]}^{n_h-M_r\left(h\right)}\end{array}\right].\hfill \end{array}$$

(9)

Through the use of MCMC techniques, we can have a complete probabilistic description of the uncertainty of enabling methodologically sound comparisons of cultural response distributions. In contrast to point estimators, Bayesian inference provides credible intervals that allow measurement of the estimation accuracy and strength during censoring. The effectiveness of MCMC techniques as a numerical method is solid evidence of their use in the present case. For more details about the MCMC algorithm, see Hasaballah et al. [21]. These posterior results merged well with the MLE framework (Section 4.1), and they preempt further analysis and interpretation within the results (Section 5) and discussion (Section 6) sections.

5. Real Data Application: Autism Knowledge in Hong Kong and Canada

In the present research, we use the framework with $k=2$ communities (Hong Kong and Canada). Autism-coded responses are treated as lifetime data, or as we call it the knowledge score, and we applied lifetime analysis tools to these scores as if they were lifetime data, with non-informative values discarded and the common responses only being retained. The parameters ${\psi }_1$ and ${\psi }_2$ estimate together the cultural distributions, which are censored. The differences between the two estimates provide a statistically rigorous measure of cross-cultural variation in autism knowledge. To demonstrate the effectiveness of the suggested methodology, we will use the data provided in Appendix D of Lam et al. [11], who analyzed the responses of pre-service teachers in Hong Kong and Canada in terms of how well they understood autism. The types of responses fell under three categories: (1) autism definitions, (2) views toward autistic children, and (3) treatment of the families of autistic children.

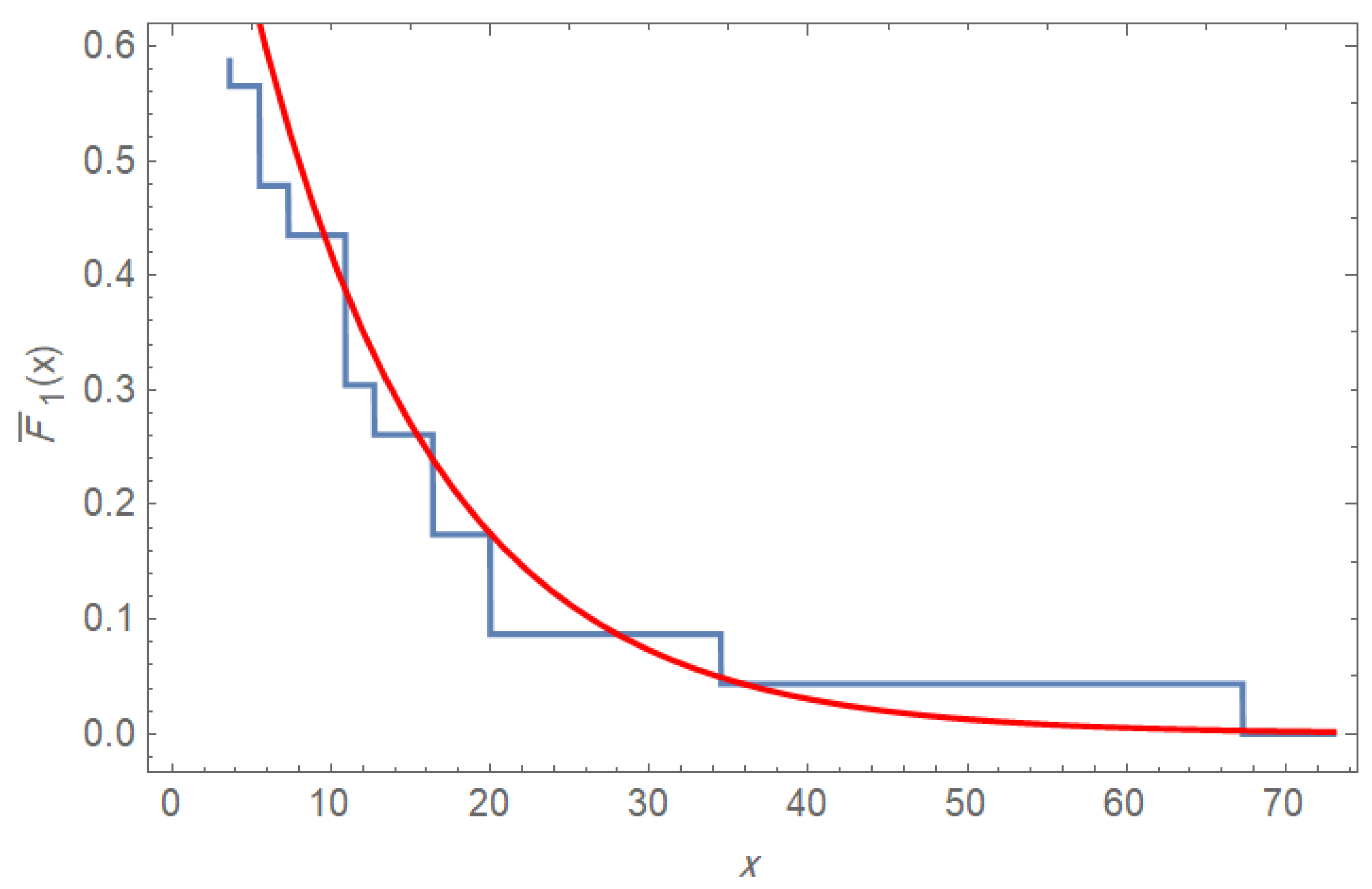
Now, assume the evaluated responses of the Canadian participants are represented by

$$f_1\left(x\right)=\left({\displaystyle \frac{{\psi }_1}{{\psi }_1^2+2}}\right)\left(2+{\psi }_1^{3}x\right)e^{-{\psi }_{1}x},x>0,$$

as shown in Figure 1, and the evaluated responses of Hong Kong participants are fitted by

$$f_2\left(x\right)=\left({\displaystyle \frac{{\psi }_2}{{\psi }_2^2+2}}\right)\left(2+{\psi }_2^{3}x\right)e^{-{\psi }_{2}x},$$

as illustrated in Figure 2.

Figure 1. Canadian coded responses.

Figure 2. Hong Kong coded responses.

• Data Preparation

The qualitative answers were coded into similar categories that reflect important cultural motives (e.g., the approach of examining autism in a medical sense or a social sense, the perspective on autism as a disability or an advantage, and inclusive or exclusionary views). To make a comparison between the two communities impartially, the zeros (non-informative responses or missing answers) were omitted. Only common categories noted in both populations were not dropped. This produced two balanced data sets against the two populations: Hong Kong (${\psi }_2$) opinions that responded to culturally East Asian views and Canada (${\psi }_1$): responses that relate to Western cultural attitudes.

Coded Responses for the Canadian Participants								Coded Responses for the Hong Kong Participants
$67.3$	$10.9$	$3.6$	$3.6$	$20.0$	$16.4$	$5.5$	$1.8$	$63.2$	$15.8$	$3.5$	$19.3$	$38.6$	$10.5$	$19.3$	$12.3$
$10.9$	$1.8$	$1.8$	$16.4$	$7.3$	$34.5$	$20.0$	$3.6$	$10.5$	$1.8$	$1.8$	$5.3$	$3.5$	$3.5$	$15.8$	$8.8$
$12.7$	$1.8$	$1.8$	$5.5$	$3.6$	$1.8$	$10.9$		$7.0$	$1.8$	$3.5$	$47.4$	$28.1$	$10.5$	$29.8$	$7.0$

Figure 1 and Figure 2 show how varied and interpretable the Fav-Jerry distribution can be, with varying parameter values. The distributions can reproduce skewed and dispersed curves, as demonstrated by Figure 1, and the cumulative nature of the curves can be emphasized by Figure 2. Combined, the values support the idea that the Fav-Jerry model can fit heterogeneous cultural response data, where the flatter curves and heavier tails correspond to the increased variability in the Canadian responses and the steep curves correspond to the more homogeneous, deficit-focused responses in Hong Kong.

Table 1 presents the classical goodness-of-fit values between the Fav-Jerry model and log-logistic Burr-XII, exponential, and Weibull distributions. Canadian data were better fitted by the Fav-Jerry model because of the lower measures of discrepancy used.

Table 1. Goodness-of-fit criteria for Canadian data.

Model	AIC	BIC	HQIC
FJD	$160.17$	$161.31$	$160.46$
Log-Logistic	$161.11$	$164.52$	$161.97$
Burr-XII	$160.50$	$165.04$	$161.64$
Exponential	$162.17$	$164.44$	$163.02$
Weibull	$164.04$	$167.45$	$165.29$

In Table 2, the goodness-of-fit measures of the Fav-Jerry distribution are reported against the inverse Gaussian, log-normal, exponential, and log-logistic distributions. The Fav-Jerry distribution consistently gave the most appropriate fit to both cultural groups using the means of posterior predictive checks and information criteria. These findings, reported in Table 1 and Table 2, establish the validity and appropriateness of the Fav-Jerry model in explaining cross-cultural differences in knowledge of autism.

Ordered Joint Type-II Censored Sample
$3.5$	$3.5$	$3.5$	$3.5$	$3.6$	$3.6$	$3.6$	$3.6$	$5.3$	$5.5$
$5.5$	$7.0$	$7.0$	$7.3$	$8.8$	$10.5$	$10.5$	$10.5$	$10.9$	$10.9$
$10.9$	$12.3$	$12.7$	$15.8$	$15.8$	$16.4$	$16.4$	$19.3$	$19.3$	$20.0$
$20.0$	$28.1$	$29.8$	$34.5$	$38.6$	$47.4$	$63.2$	$67.3$

Table 2. Goodness-of-fit criteria to Hong Kong data.

Model	AIC	BIC	HQIC
FJD	$181.12$	$182.30$	$181.43$
Inv. Gauss	$182.14$	$185.67$	$183.08$
Log-Normal	$182.95$	$186.49$	$183.89$
Exponential	$183.12$	$185.48$	$183.74$
Log-Logistic	$184.61$	$188.14$	$185.54$

• JT-II-CS under Model Fitting

All the data sets were fit through the Fav-Jerry distribution (FJD) within the joint Type-II censoring scheme (JT-II-CS). Model fitting was assessed in terms of log-likelihood, AIC, BIC, HQIC, and goodness-of-fit measures that included the Anderson–Darling (AD) and Cramer–von Mises (CVM) tests. Graphical representations of the goodness of fit between the fitted and empirical distribution provided additional corroboration to the model’s validation.

• Results and Interpretation

As presented in Table 3, the fitted Fav-Jerry models under the joint Type-II censoring scheme provided clear evidence of cross-cultural differences between the Canadian and Hong Kong participants. The Canadian parameter estimate $({\widehat{\psi }}_1=0.034)$ with a tail probability $P(X>70)=0.162$ indicates a greater diversity of responses and higher likelihood of extreme views, suggesting that the Canadian participants conceptualized autism in broader and more heterogeneous ways. In contrast, the Hong Kong estimate $({\widehat{\psi }}_2=0.044)$ with a lower tail probability of $P(X>70)=0.073$ reflects more concentrated perspectives and fewer outlier responses, consistent with more uniform cultural framings of autism. The asymptotic confidence intervals were wide, reflecting some sampling variability, yet the Bayesian credible intervals were narrower and more stable, underscoring the reliability of the Bayesian inference approach.

Table 3. Extrapolated results from the joint censored data.

	Canadian Side				Hong Kong Side
	MLE	SEL	ACI	CRI	MLE	SEL	ACI	CRI
Parameter	$0.034$	$0.031$	$0.014,0.038$	$0.025,0.027$	$0.044$	$0.043$	$0.021,0.053$	$0.036,0.039$
$P(X>70)$	$0.162$	$0.164$	$0.019,0.301$	$0.148,0.178$	$0.073$	$0.071$	$-0.013,0.153$	$0.064,0.081$

Computations of the MCMC algorithm were conducted in Wolfram Mathematica version 12, which provides effective symbolic and numerical computation of any customizable sampling routine. This process involved 10,000 iterations, and the first 4000 iterations were discarded to provide a burn-in period to verify that the posterior samples sampled corresponded to the stationary phase. The chosen hyperparameters for the gamma priors were as follows: $a_1=a_2=b_1=b_2=0.01$.

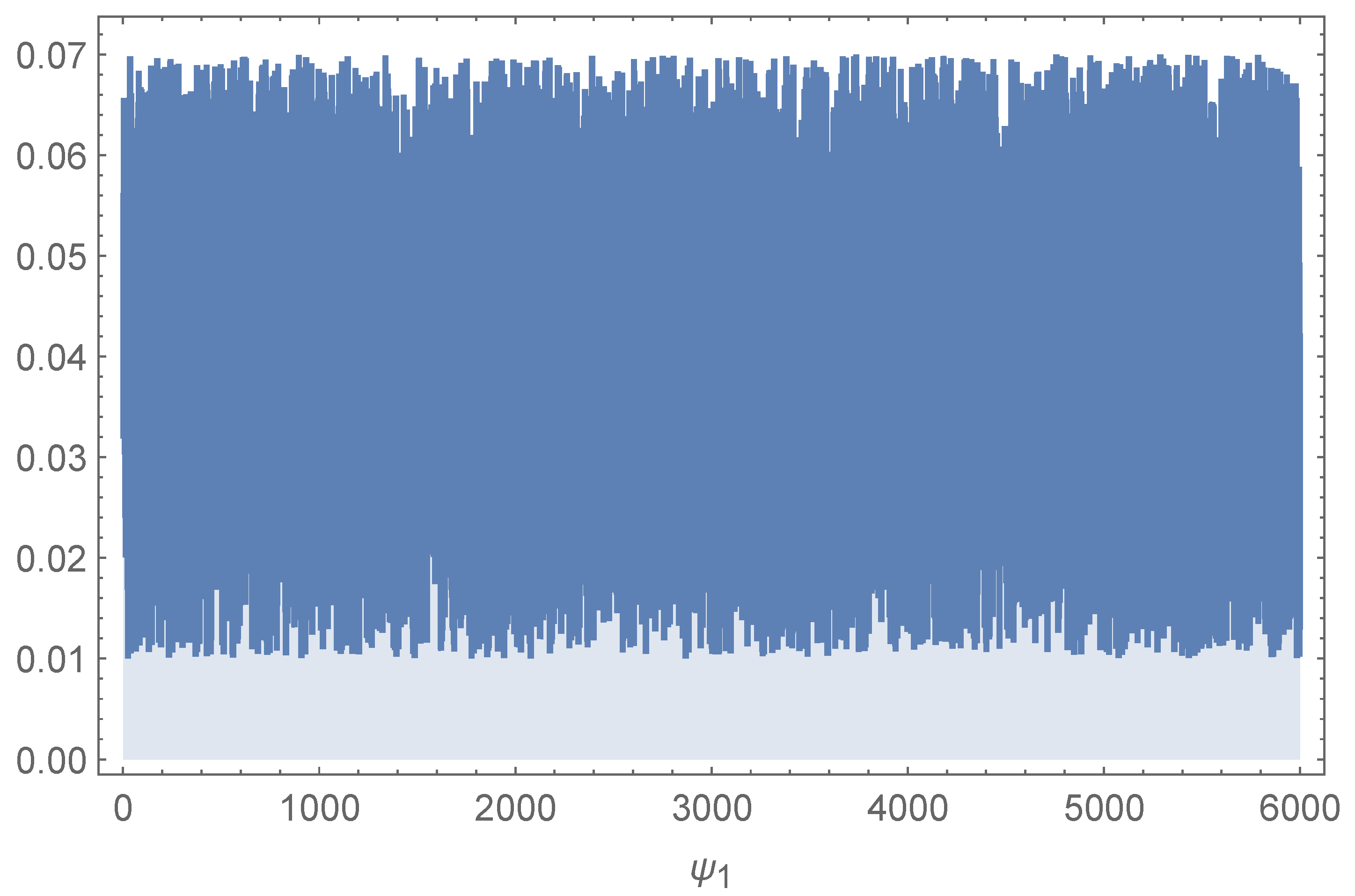
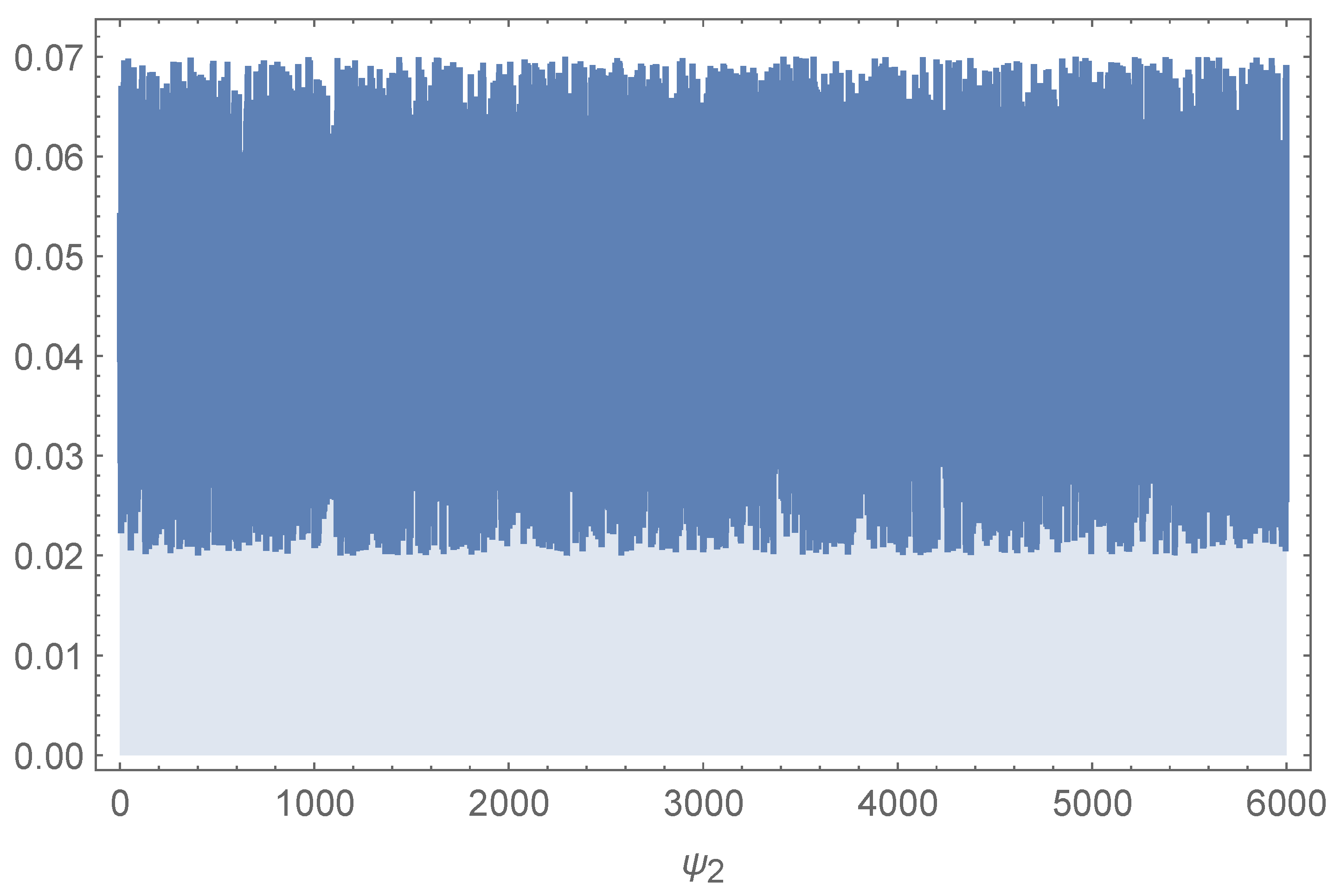
The convergence was measured by the visual analysis of trace plots, indicating that there were stable and well-mixed chains with no trend or drift observed between runs. To demonstrate this, Figure 3 and Figure 4 show two sample trace plots for the parameters ${\psi }_1$ and ${\psi }_2$, indicating the convergence behavior of the model parameters. In order to evaluate the sensitivity of the analysis, we reran the analysis with a different, equally diffuse prior structure. There were no significant changes in the posterior estimates, indicating the robustness of the results for the prior specifications. Since this analysis obtained similar posteriors and credible intervals, we have no doubt that the prior sensitivity did not have a significant impact on our findings. Together, these results validate the efficiency of the Fav-Jerry distribution for modeling such data and highlight meaningful cross-cultural contrasts in autism knowledge.

Figure 3. MCMC tracing plot for ${\psi }_1$.

Figure 4. MCMC tracing plot for ${\psi }_2$.

6. Bridging the Gap Between Qualitative Narratives and Quantitative Evidence

These quantitative results are a natural continuation and expansion of the previous qualitative results of Lam et al. [11]. Their article found that Canadian pre-service teachers tended to take a broader or even strength-based approach to autism, whereas the Hong Kong respondents took a more deficit- and medically oriented viewpoint. Our modeling system conducted a statistically rigorous test of these observations. The increased dispersion of the Canadian responses, as reflected by the smaller parameter estimate as well as the larger tail probability, indicates increased heterogeneity and inclusivity of the conceptualizations of autism. On the other hand, the closer distribution of the Hong Kong answers is related to the existence of more homogenous cultural narratives.

The difference between this work and the original study, aside from the confirmation of the mentioned cultural tendencies, lies in the introduction of distributional quantification. Compared with conventional t-tests or chi-squared tests, which focus only on group means or proportions, our approach captures the shape of whole distributions of responses and allow for more complex comparisons. Joint censoring diminishes bias due to non-informative or missing responses, and the Fav-Jerry model is tractable and flexible in estimation. In this way, our findings overcome the gap between the qualitative and quantitative rigor, presenting a more comprehensive understanding of cultural variations in autism knowledge. Thus, our study confirms the results of Lam et al. [11] but augments them, with formal statistical inference, to indicate that the qualitative differences in culture they identified and described also translate into quantitative differences in distribution when studied identically.

7. Conclusions and Implications

This study presented a new use of the Fav-Jerry distribution in a joint Type-II censoring model to compare cultural variations in autism knowledge between Hong Kong and Canadian pre-service teachers. The results aligned and broadened those of Lam et al. [11]; the teachers in Canada had more diverse and more inclusive opinions about autism, which were both strength-based and medical in nature. They responded in different and varied ways, indicating that they were exposed to various cultural discourses which promote inclusivity and pluralism. In comparison, the answers of the Hong Kong teachers were more homogeneous and deficit-focused and relied primarily on medicalized discourses. This created a more homogeneous distribution of perceptions, and there was not much of a sign of alternative or inclusive framing. A key methodological contribution is the quantification of cultural variation in a distributional way. In contrast to conventional approaches, which tend to focus on averages or proportions of groups, this one provides the full shape of the response distributions, giving a more detailed insight into cultural differences. In practical terms, the findings may indicate that teacher education in Hong Kong might be enhanced by diversifying medicalized perceptions to more inclusive ones, whereas Canadian programs might aim at directing various perceptions to coherent, inclusive practice. In a broader sense, this paper shows the importance of integrating quantitative rigor and cultural understanding, which bridges qualitative narratives and statistical inference. This provides an opportunity to use the same framework for other related studies of comparison across different cultures or health-related issues in which missing data and heterogeneity are typical.