Application of the Kurganov–Tadmor Scheme in Curvilinear Coordinates for Supersonic Flow
Abstract
1. Introduction
2. Numerical Method
2.1. Fundamental Equations
2.2. Kurganov–Tadmor Scheme
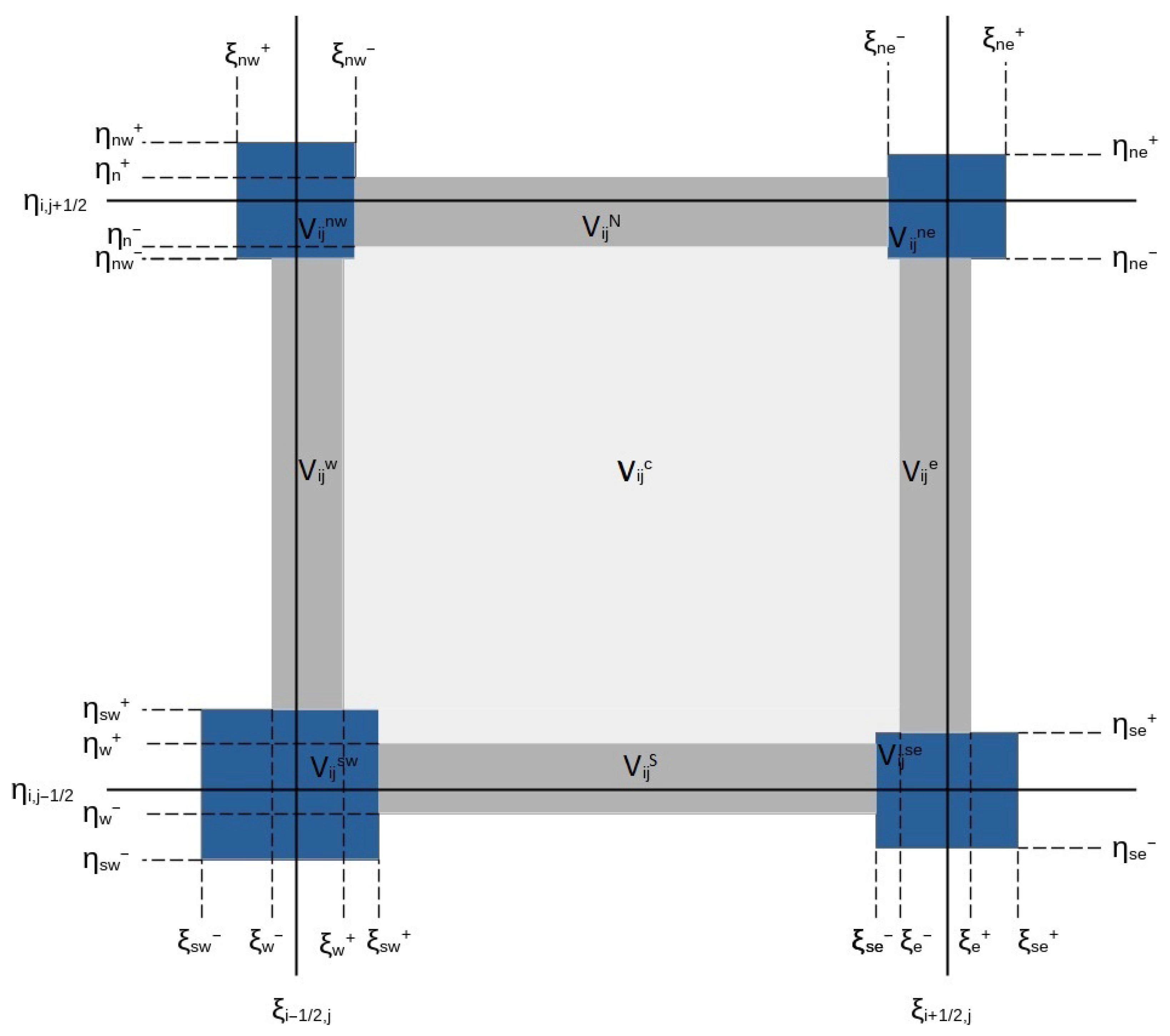
2.2.1. Domain
2.2.2. Domain
2.2.3. Domain
2.2.4. Final Formulation
- In this research, we considered that terms greater than in Equation (21) did not contribute, as the limit applied in the final step of results in a null value.
- From the outset of the analysis, we worked with scale factors affected by the limit of while executing integrals, as it yields simpler expressions without affecting the development.
- The conservative variables at the interface after the limit is applied result asThe numerical derivatives will be obtained through the limiter minmod with
- The analysis in this section applies to domains where all cells are of uniform size.
- If a rectangular coordinate system is used with unitary metrics, the two-dimensional Kurganov–Tadmor scheme is obtained.
2.3. Time Integration
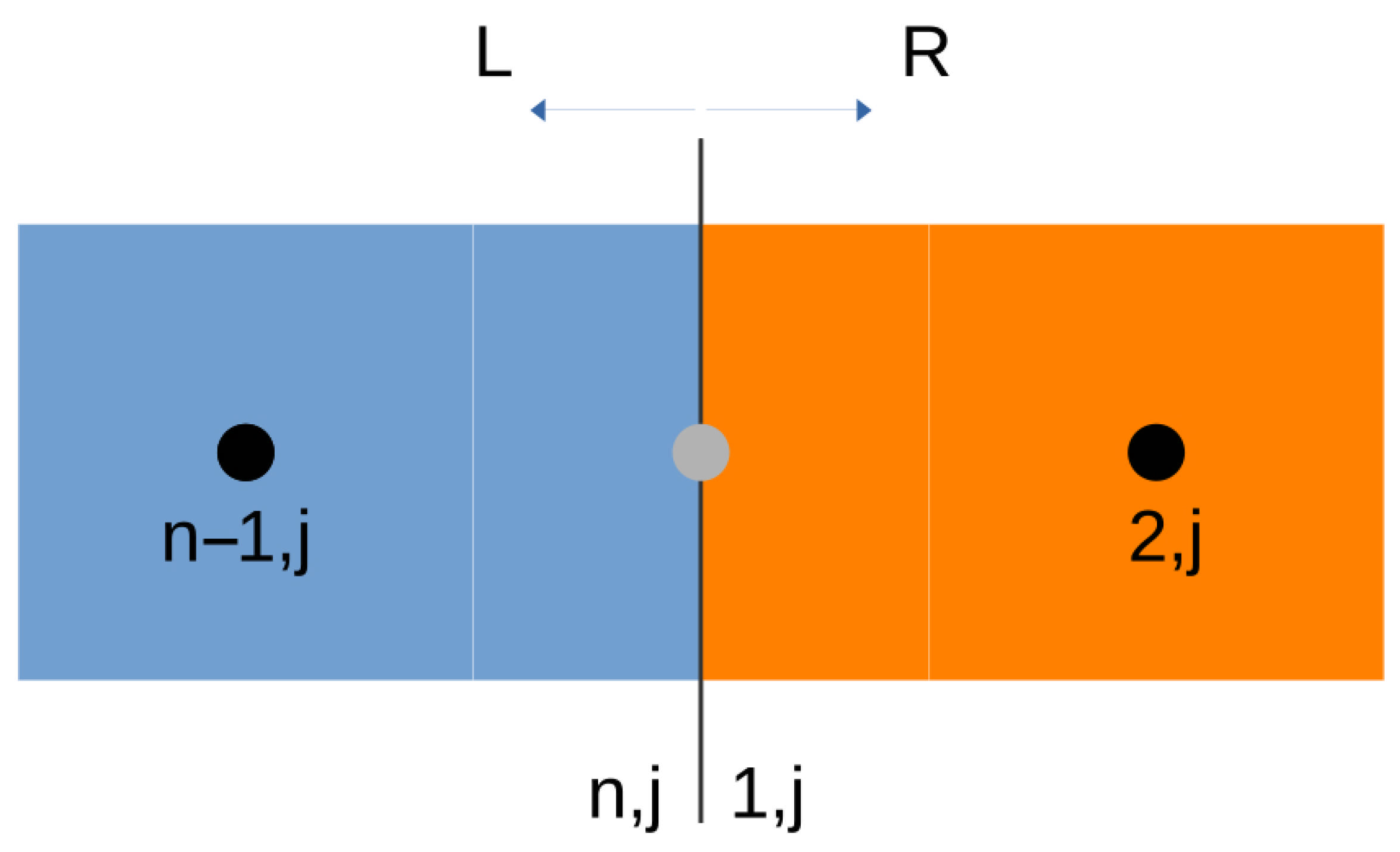
2.4. Interface Treatment
3. Numerical Tests
3.1. Flow over a Cylinder
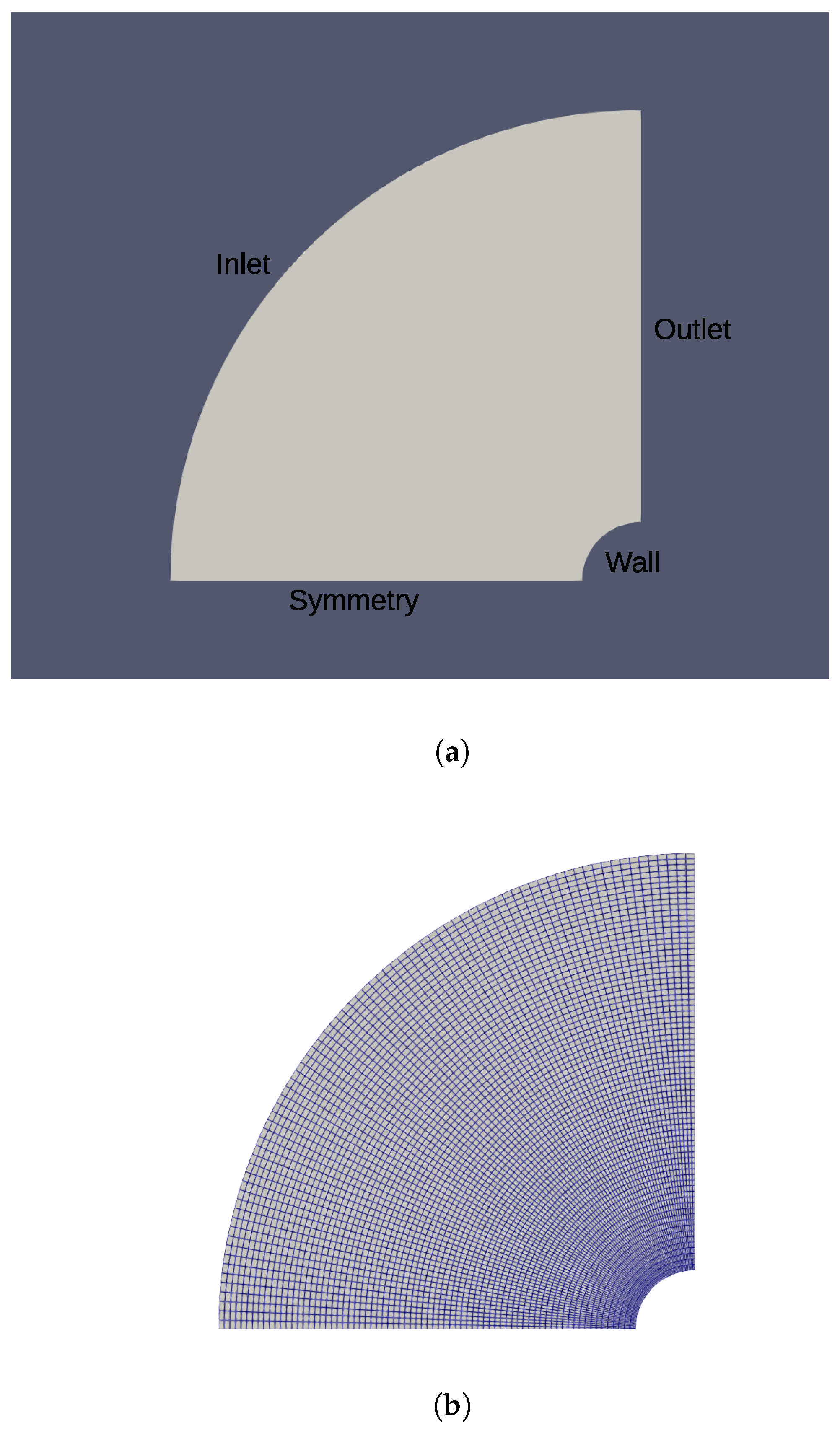
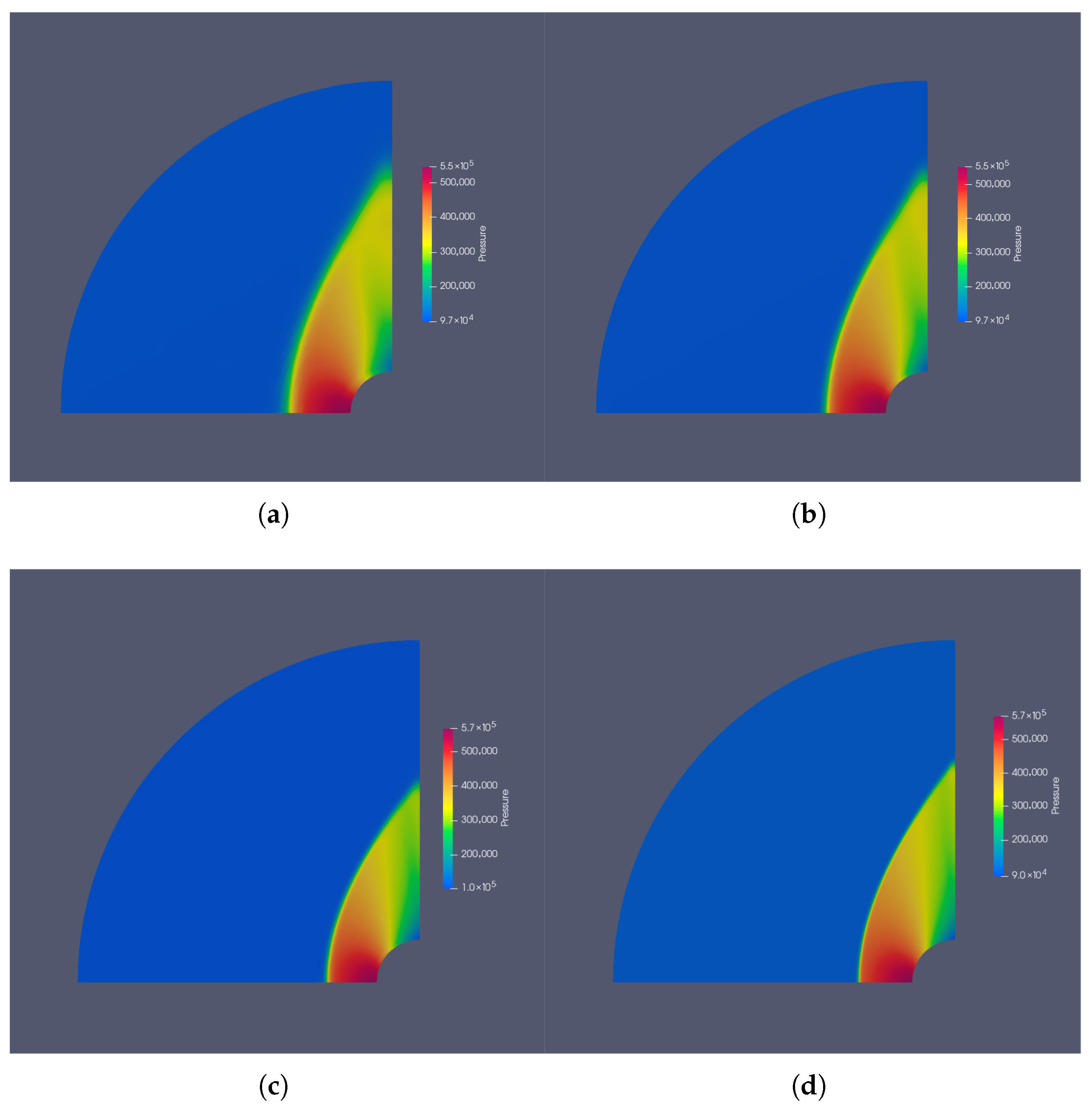
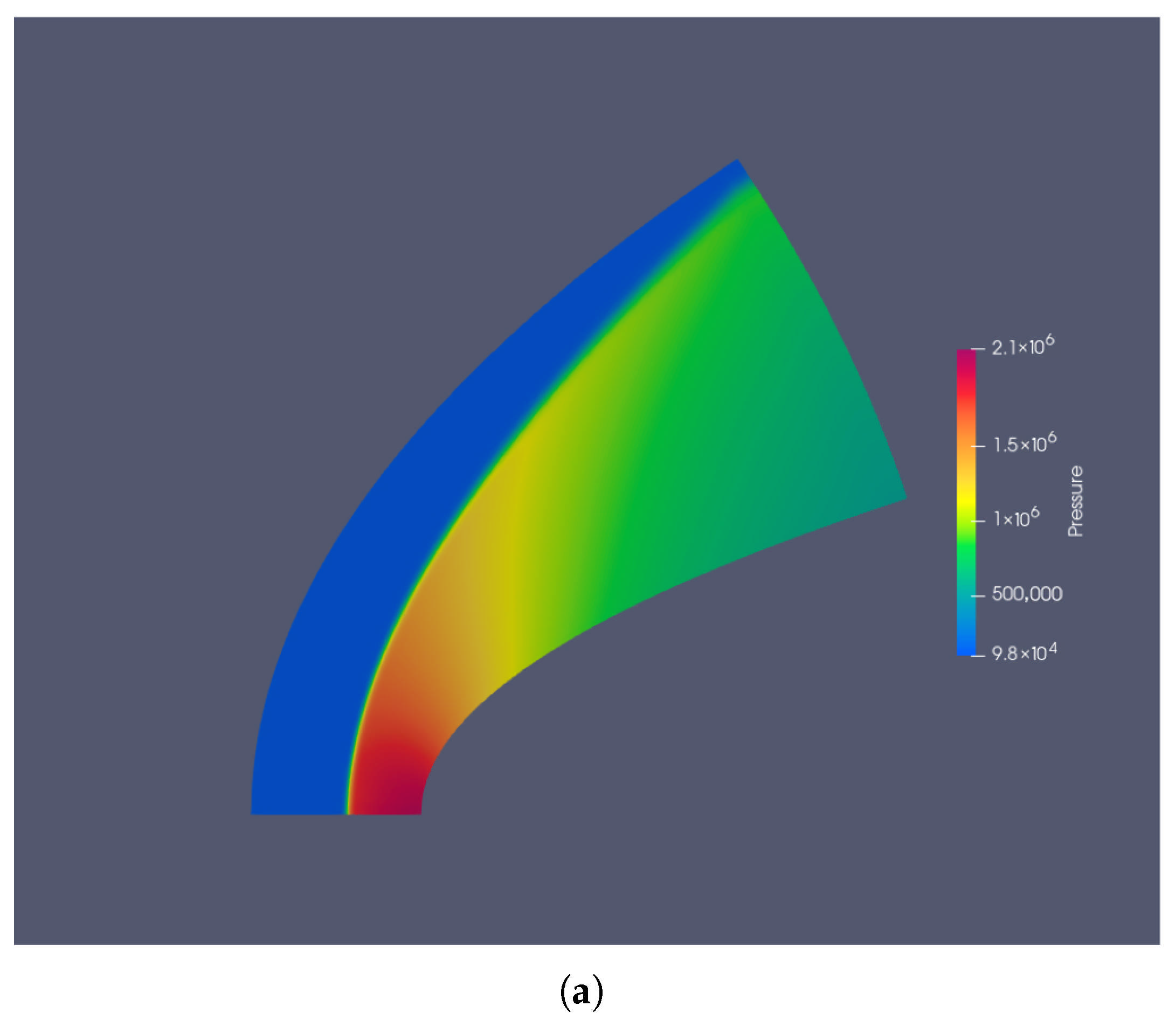
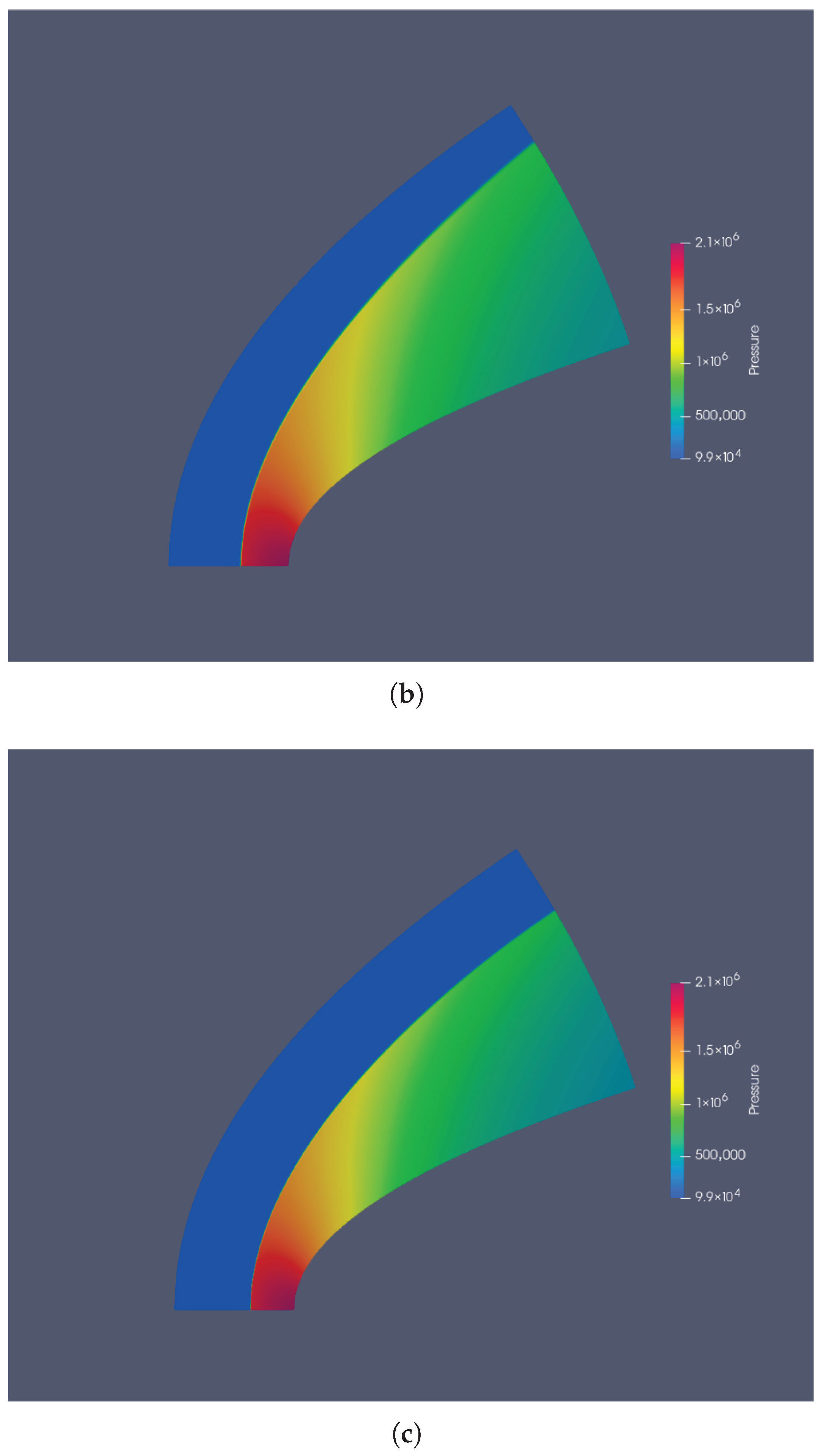
3.2. Flow over a Blunt Body
3.3. Flow over a Wedge
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Anderson, J. Hypersonic and High Temperature Gas Dynamics; McGraw-Hill: Boston, MA, USA, 1989. [Google Scholar]
- Anderson, J. Modern Compressible Flow: With Historical Perspective, 3rd ed.; McGraw-Hill: Boston, MA, USA, 2003. [Google Scholar]
- LeVeque, R. Finite Volume Methods for Hyperbolic Problems, 1st ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Bakhtiyarov, S.; Adanur, S. Airflow over Wavy Yarn in Air-Jet Filling Insertion. Math. Comput. Appl. 1999, 4, 1–7. [Google Scholar] [CrossRef]
- Wang, B.; Garg, N. Third-order numerical scheme for Euler equations of gas dynamics using Jordan canonical based splitting flux. Comput. Fluids 2024, 281, 106370. [Google Scholar] [CrossRef]
- Trojak, W.; Dzanic, T. Positivity-preserving discontinuous spectral element methods for compressible multispecies flows. Comput. Fluids 2024, 280, 106343. [Google Scholar] [CrossRef]
- Tamagno, J.; Elaskar, S.; Ríos, G. Numerical simulation of time-dependent reacting flows in pulse facilities. Appl. Numer. Math. 2003, 47, 515–530. [Google Scholar] [CrossRef]
- Falcinelli, O.; Elaskar, S.; Tamagno, J. Reducing the numerical viscosity in non-structured three-dimensional finite volumes computations. J. Spacecr. Rocket AIAA 2008, 45, 406–408. [Google Scholar] [CrossRef]
- Toro, E. Riemann Solvers and Numerical Methods for Fluid Dynamics, 3rd ed.; Springer: Berlin, Germany, 2009. [Google Scholar]
- EsfandAbadi, M.; Mohammadi, A.; Djavareshkian, M. Design and analysis of supersonic inlet for ramjet engines: Aerodynamic considerations and performance optimization. J. Aerosp. Sci. Technol. 2024, 17, 47–59. [Google Scholar]
- Araya, G. Unsteady subsonic/supersonic flow simulations in 3D unstructured grids over an acoustic cavity. Fluids 2024, 9, 92. [Google Scholar] [CrossRef]
- Kurganov, A.; Noelle, S.; Petrova, G. Semidiscrete central-upwind schemes for hyperbolic conservation laws and hamilton-jacobi equations. J. Sci. Comput. 2001, 23, 707–740. [Google Scholar] [CrossRef]
- Kurganov, A.; Tadmor, E. New high-resolution central schemes for nonlinear conservation laws and convection–diffusion equations. J. Comput. Phys. 2000, 160, 241–282. [Google Scholar] [CrossRef]
- Illenseer, T.; Duschl, W. Two-dimensional central-upwind schemes for curvilinear grids and application to gas dynamics with angular momentum. Comput. Phys. Commun. 2009, 180, 2283–2302. [Google Scholar] [CrossRef]
- Greenshields, C.; Weller, H.; Gasparini, L.; Reese, J. Implementation of semi-discrete, non-staggered central schemes in a colocated, polyhedral, finite volume framework, for high-speed viscous flows. Int. J. Numer. Math. Fluids 2010, 63, 1–21. [Google Scholar] [CrossRef]
- Gutiérrez Marcantoni, L.; Tamagno, J.; Elaskar, S. rhocentralrffoam: An openfoam solver for high speed chemically active flows—Simulation of planar detonations. Comput. Phys. Commun. 2017, 219, 209–222. [Google Scholar] [CrossRef]
- Gutiérrez Marcantoni, L.; Tamagno, J.; Elaskar, S. Numerical study on the impact of chemical modeling on simulating methane-air detonations. Fuel 2019, 240, 289–298. [Google Scholar] [CrossRef]
- Weng, Z.; Mével, R. Implementation of an openfoam solver for shock and detonation simulation at high pressure. Comput. Fluids 2023, 265, 10601. [Google Scholar] [CrossRef]
- Kreiss, H.; Ortiz, O. Introduction to Numerical Methods for Time Dependent Differential Equations; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Landau, L.; Lifshitz, E. Mecánica de Fluidos, Vol, 6, Colección de Física Teórica; Reverté: Barcelona, Spain, 1986. [Google Scholar]
- Whitham, G. Linear and Nonlinear Waves; John Wiley & Sons: New York, NY, USA, 1974. [Google Scholar]
- Aris, R. Vectors, Tensors, and the Basic Equations of Fluid Mechanics; Dover Publications: Mineola, NY, USA, 1989. [Google Scholar]
- Tannehill, J.; Anderson, D.; Pletcher, R. Computational Fluid Mechanics and Heat Transfer, 2nd ed.; Taylor & Francis: Washington, DC, USA, 1997. [Google Scholar]
- Chapra, S.; Canale, R. Numerical Methods for Engineers, 7th ed.; McGraw-Hill Education: New York, NY, USA, 2015. [Google Scholar]
- Montes, P.; Reula, O. New numerical interface scheme for the Kurganov-Tadmor second-order method. arXiv 2021, arXiv:2105.03452. [Google Scholar]
- Roache, P. Verification and Validation in Computational Science and Engineering; Hermosa: Albuquerque, NM, USA, 1998. [Google Scholar]
- Oberkampf, W.; Trucano, T. Verification and validation in computational fluid dynamics. Prog. Aerosp. Sci. 2002, 38, 209–272. [Google Scholar] [CrossRef]
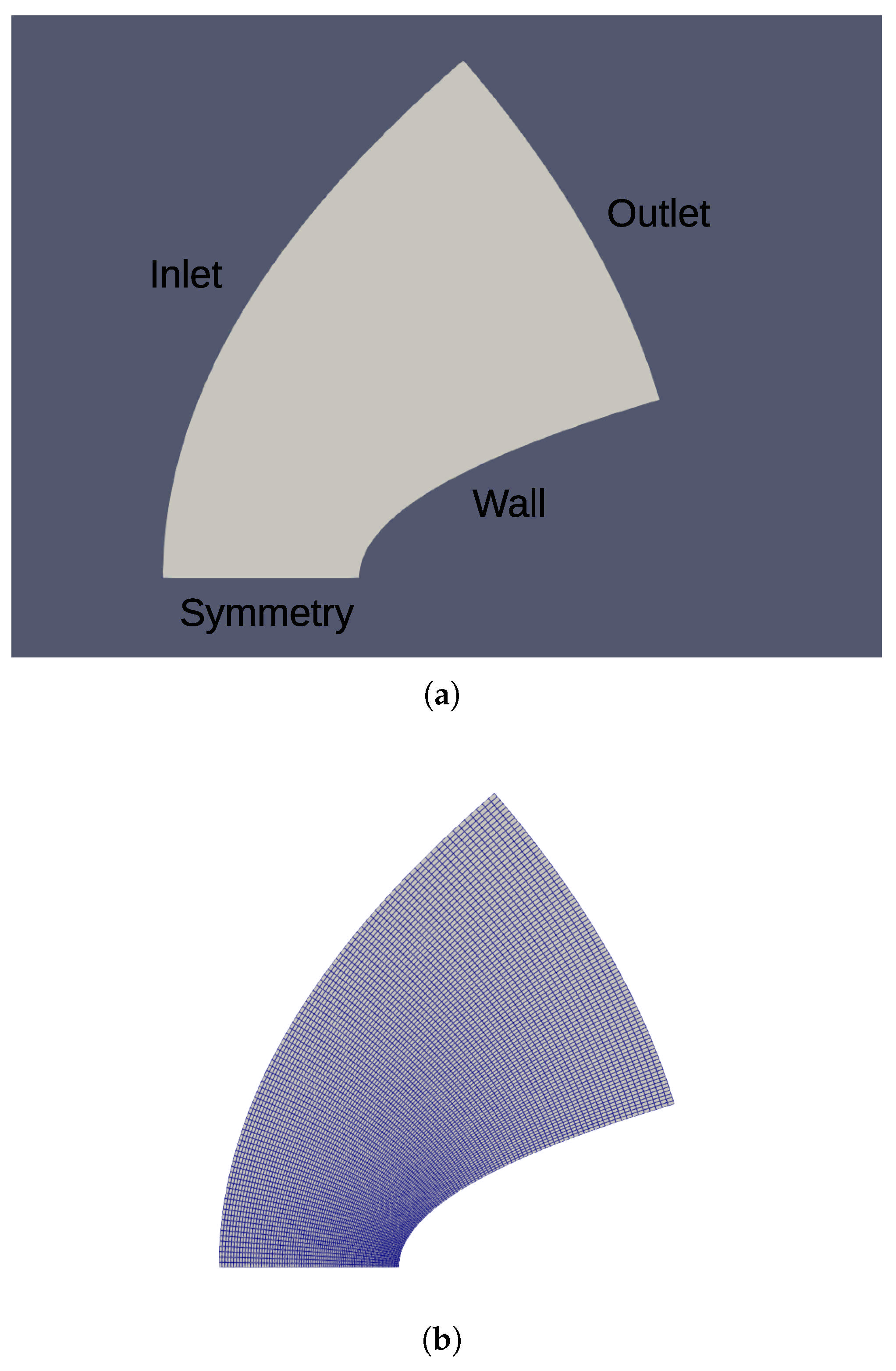


| u | v | p | T | |
| Inlet | Dirichlet | Dirichlet | Dirichlet | Dirichlet |
| Outlet | Dirichlet | Neumann | Neumann | Neumann |
| Symmetry | Neumann | Dirichlet | Neumann | Neumann |
| Wall | Dirichlet | Neumann | Neumann | Neumann |
| Number of Cells | % Error | |
|---|---|---|
| 2700 | 5.3924 | 4.39 |
| 6000 | 5.4345 | 3.65 |
| 14,400 | 5.5805–5.4903 | 1.06–2.659 |
| 40,000 | 5.5953 | 0.79 |
| u | v | p | T | |
| Inlet | Dirichlet | Dirichlet | Dirichlet | Dirichlet |
| Outlet | Neumann | Neumann | Neumann | Neumann |
| Symmetry | Dirichlet | Neumann | Neumann | Neumann |
| Wall | Neumann | Dirichlet | Neumann | Neumann |
| Numbers of Elements | % Error | |
|---|---|---|
| 8100 | 20.2456 | 3.912 |
| 44,100 | 20.5666 | 2.38 |
| 102,000 | 20.9445 | 0.595 |
| Subdomain 1 | ||||
|---|---|---|---|---|
| u | v | p | T | |
| Inlet | Dirichlet | Dirichlet | Dirichlet | Dirichlet |
| Outlet | interface | interface | interface | interface |
| Symmetry | Neumann | Dirichlet | Neumann | Neumann |
| Point | Neumann | Neumann | Neumann | Neumann |
| Subdomain 2 | ||||
| u | v | p | T | |
| Left | interface | interface | interface | interface |
| Right | interface | interface | interface | interface |
| Top | Neumann | Neumann | Neumann | Neumann |
| Wall | Neumann | Dirichlet | Neumann | Neumann |
| Subdomain 3 | ||||
| u | v | p | T | |
| Inlet | interface | interface | interface | interface |
| Outlet | Neumann | Neumann | Neumann | Neumann |
| Top | Neumann | Neumann | Neumann | Neumann |
| Point | Neumann | Neumann | Neumann | Neumann |
| Mesh | Number of Cells | Shock Wave Angle | % Error |
|---|---|---|---|
| 1 | 3750 | 2.39 | |
| 2 | 10,400 | 1.7 | |
| 3 | 13,000 | 1.05 | |
| 4 | 26,400 | 0.62 | |
| 5 | 30,000 | 0.52 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bertolo, S.; Elaskar, S.; Gutiérrez Marcantoni, L. Application of the Kurganov–Tadmor Scheme in Curvilinear Coordinates for Supersonic Flow. Math. Comput. Appl. 2025, 30, 92. https://doi.org/10.3390/mca30050092
Bertolo S, Elaskar S, Gutiérrez Marcantoni L. Application of the Kurganov–Tadmor Scheme in Curvilinear Coordinates for Supersonic Flow. Mathematical and Computational Applications. 2025; 30(5):92. https://doi.org/10.3390/mca30050092
Chicago/Turabian StyleBertolo, Sebastián, Sergio Elaskar, and Luis Gutiérrez Marcantoni. 2025. "Application of the Kurganov–Tadmor Scheme in Curvilinear Coordinates for Supersonic Flow" Mathematical and Computational Applications 30, no. 5: 92. https://doi.org/10.3390/mca30050092
APA StyleBertolo, S., Elaskar, S., & Gutiérrez Marcantoni, L. (2025). Application of the Kurganov–Tadmor Scheme in Curvilinear Coordinates for Supersonic Flow. Mathematical and Computational Applications, 30(5), 92. https://doi.org/10.3390/mca30050092






