Thrinax radiata Seed Germplasm Dynamics Analysis Assisted by Chaos Theory

Abstract

This study examines the contrast in the nonlinear dynamics of Thrinax radiata Lodd. ex Schult. & Schult. f. Seed germplasm explored by optical and electrical signals. By integrating chaotic attractors for the modulation of the optical and electrical measurements, the research ensures high sensitivity monitoring of seed germplasm dynamics. Reflectance measurements and electrical responses were analyzed across different laser pulse energies using Newton–Leipnik and Rössler chaotic attractors for signal characterization. The optical attractor captured laser-induced changes in reflectance, highlighting nonlinear thermal effects, while the electrical attractor, through a custom-designed circuit, revealed electromagnetic interactions within the seed. Results showed that increasing laser energy amplified voltage magnitudes in both systems, demonstrating their sensitivity to energy inputs and distinct energy-dependent chaotic patterns. Fractional calculus, specifically the Caputo fractional derivative, was applied for modeling temperature distribution within the seeds during irradiation. Simulations revealed heat transfer about 1 °C in central regions, closely correlating with observed changes in chaotic attractor morphology. This interdisciplinary approach emphasizes the unique strengths of each method: optical attractors effectively analyze photoinduced thermal effects, while electrical attractors offer complementary insights into bioelectrical properties. Together, these techniques provide a realistic framework for studying seed germplasm dynamics, advancing knowledge of their responses to external perturbations. The findings pave the way for future applications and highlight the potential of chaos theory for early detection of structural and bioelectrical changes induced by external energy inputs, thereby contributing to sample protection. Our results provide quantitative dynamical descriptors of laser-evoked seed responses that establish a tractable framework for future studies linking these metrics to physiological outcomes.

1. Introduction

Germplasm is any tissue or plant material that can be used for the reproduction of a new plant. DNA is the hereditary molecule within cells, whereas germplasm refers to living genetic resources (e.g., seeds, tissues, or propagules) that preserve and transmit genetic variation. It is the basis of plant reproduction and genetic diversity, present in seeds, tissues, and other vegetative organs [1]. Plant reproduction generates and maintains genetic variation; germplasm denotes the living genetic resources that conserve and make that variation available for breeding, research, and conservation. It plays a crucial role in agriculture and horticulture, as it is the basis of critical plant genetic information passed down from one generation to the next. Seeds house the embryo and its genome as living genetic resources (germplasm); however, developmental outcomes also depend on epigenetic states, maternal effects, and environmental conditions [2]. Biological studies are essential, as they enable the development of strategies to improve seed viability, optimize germination rates, and contribute to sustainable agricultural practices. Therefore, understanding the complex dynamics of seed germplasm under divergent environmental and experimental regimes is crucial [3]. Seed germination has a long tradition of population-based threshold models (thermal/hydro/hydrothermal time) in which germination rate increases approximately linearly with temperature or water potential within sub-optimal ranges [4]. In parallel, differential-equation and nonlinear statistical frameworks are widely used [5].

Consistent with processual perspectives that treat time as constitutive of plant function, we adopt a time-aware dynamical framing of seed germplasm behavior rather than static endpoints [6].

Thrinax radiata Lodd. ex Schult. & Schult. f., known as the chit palm in the Yucatán Peninsula, is an ecologically and culturally significant species whose conservation is a priority. This palm is endemic to the Caribbean region, southern Florida, and certain parts of Mexico, where it has been traditionally used for construction, handicrafts, and thatching [7]. Additionally, medicinal uses have been reported in Maya communities, where its leaves are applied as poultices to stop bleeding, and its roots are infused to treat kidney stones and nervous disorders. Despite its ethnobotanical value, Thrinax radiata has been classified as a threatened species in Mexico [8], primarily due to habitat destruction caused by human activities such as tourism, agriculture, and cattle ranching, as well as unregulated exploitation [9].

Seed studies, including morphological characterization, provide an insight towards viability assessment and a study of factors affecting germination and survival and the conservation of Thrinax radiata germplasm is crucial to ensure the persistence of this species in its natural ecosystem and its sustainable use. In this context, the establishment of germplasm banks and the development of advanced methodologies for its analysis and preservation become critically important. Specifically, the application of analytical models based on chaos theory and laser technology offers an innovative strategy for exploring the germplasm dynamics of this palm.

Chaos theory enables the characterization of the complex response of seeds to external stimuli, providing mathematical tools such as the Newton–Leipnik and Rössler attractors to model these dynamic processes. Additionally, irradiation with a 532 nm Nd:YVO₄ pulsed laser, combined with optical and electrical measurements, facilitates the early detection of structural and bioelectrical changes in seeds, allowing for the evaluation of their viability and resistance to adverse environmental factors, ensuring minimal disruption and maximizing sample preservation [10]. Seed germination can be predicted with useful accuracy within sub-optimal ranges using population-based threshold fitted to appropriate measurements; predictive performance typically declines near supra-optimal conditions or under heterogeneous stress. Chaos theory defines the ground rules of nonlinear, deterministic systems that show and possess the attribute of being unpredictable. Some chaotic attractors like that of Rössler and Newton–Leipnik are now being used as efficient tools for modeling such dynamic biological processes [11]. As indicators of internal sensitivity towards external stimuli, these attractors describe the response patterns along with the variability of seed responses [12]. At the same time, laser ablation enables the localized assessment of thermal effects on seed germplasm [13]. The effects of different energy levels on the actions of seeds, both at the macroscopic and microscopic levels, can be understood by changing the energy of the laser pulse [14]. Moreover, the use of fractional calculus, particularly the Caputo fractional derivative, allows for the simulation of temperature distribution induced by laser irradiation, providing insights into thermal effects and dynamics on seed internal structures [15]. By considering the fractional derivatives within the analysis of temperature distributions during laser irradiation, it renders possible the influence of memory effects and anomalous diffusion processes which classical integer-order models would not account for [16].

By memory effects we mean history-dependent signal behavior, whereby identical instantaneous conditions can elicit different responses depending on prior inputs. Operationally, this manifests as long-range temporal correlations and non-exponential relaxations; in our modeling, we represent it with a fractional-order term $0<\alpha <1$.

Optical reflectance variations supplement such a study as they furnish in-the-moment optical science data for changes in seed surface properties. These reflectance measurements can also capture structural and compositional changes induced by laser ablation and thus provide a profile on how seeds would interact with different thermal conditions in light [17]. The combination of optical reflectance and thermal simulations shall provide a comprehensive view into the responses of seed germplasm while linking microscale physical phenomena to macroscale biological behaviors [18]. Further, electrical potentials in seeds that were subjected to laser irradiation act as an indication of the alterations in their underlying biophysical states. Change in electrical conductivity and impedance indicates the effect of localized heating, the redistribution of moisture content, and possible structural changes [19]. When combining these electrical measurements with the dynamic models which arise from chaotic attractors, it becomes quite feasible to analyze and quantify the relationship between both thermal effects and germplasm dynamics as fully as possible [20].

This research explores the potential of chaos theory for the assistance of laser technology and fractional calculus in analyzing Thrinax radiata seeds dynamics. The integration of these techniques does not only contribute to a better understanding of the biological processes underlying seed conservation but also offers innovative tools for monitoring and protecting endangered species. Accordingly, we present a dynamical analysis framework for non-destructive, time-resolved characterization of seed responses under controlled irradiation, without inferring biological outcomes such as viability or conservation efficacy. The findings may open new avenues in seed science, species conservation, and crop improvement, highlighting the potential of interdisciplinary approaches in plant germplasm research.

2. Materials and Methods

2.1. Description of the Biological Material Studied, Image Acquisition and Processing

Thrinax radiata Lodd. ex Schult. & Schult. f. (Arecaceae), commonly called Chit. is a monocot palm that can grow up to 8 m tall, it grows in coastal areas from Florida to Nicaragua. However, the Mexican Official Standard classifies it as an endangered species and its conservation in Botanical Gardens has been promoted for years. The fruits are fleshy drupes of white color that contain one brown spherical seed (5 mm of diameter) with linear under-development embryo of 1–2 mm length. The Thrinax radiata seeds are tolerant to desiccation but lose viability if preserved at low temperatures. Due to its morpho-physiological traits and storage behavior, are considered as intermediate or recalcitrant seeds for its conservation in traditional seed banks [21]. Mature fruits and seeds were collected in field collections at the Regional Laboratory for the Study and Conservation of Germplasm (GermoLab-CICY, 21°07′48.12″ N, 89°46′45.93″ W; 5 m a.s.l.). Initial moisture content of seeds was 15.13%, with 100% of viability (in tetrazolium test) and 93.3% of germination under controlled laboratory conditions (25–32 °C, and photoperiod of 12/12 h light/darkness). Seeds provenance are individuals planted outside their habitat in the GermoLab-CICY field collections. The seeds for this study were collected in November 2022, air-dried in a laminar flow chamber and stored at room temperature (25 °C) in an airtight glass jar until its use. Details of the methods used to evaluate viability, germination, and storage behavior of the Thrinax radiata seed samples studied has been previously reported in detail [21].

High-resolution digital images of Thrinax radiata were acquired under controlled lighting conditions and against a neutral, non-reflective background, ensuring consistency across all samples. Seeds were arranged in well-defined subsets to facilitate individualized morphological analysis. The implemented pipeline yielded accurate segmentation in over 95% of the processed images. A total of N = 3 seeds were evaluated and the experiments repeated by triplicate; each processed independently under the same irradiation protocol. Photographic images of Thrinax radiata seeds were captured using a triple digital camera (50 MP/12 MP/5 MP, Samsung Galaxy A54, Nueva Delhi, India) equipped with optical image stabilization, under controlled lighting conditions to ensure consistency across shots. The seeds were arranged in subsets on a neutral background to facilitate image segmentation. The acquired images were processed using the Python (version 3.12.7) programming language, employing the OpenCV library for preprocessing tasks such as grayscale conversion, filtering, and segmentation through thresholding techniques. Subsequently, the scikit-image library was used to extract relevant morphological and textural features, including area, shape, convexity, and contrast. The effectiveness of this image preparation approach for seed analysis is supported by Nucci et al. [22], who employed computer vision to segment images of Guavira seeds for classification into viable and non-viable categories.

2.2. Chaotic Attractors Generation

For modulating monitoring signals, we generated two chaotic systems exhibiting just one attractor: the Rössler and the Newton–Leipnik attractors. These dynamic systems were selected for their simplicity in their coefficients in the differential equations.

The Rössler attractor is a three-dimensional system of ordinary differential equations introduced by Otto Rössler in 1976 [23]. It was designed to show chaotic behavior in a simpler form compared to the Lorenz system.

The Rössler system was defined mathematically as:

$${\displaystyle \frac{dx}{dt}}=-y-z,$$

(1)

$${\displaystyle \frac{dy}{dt}}=x+ay,$$

(2)

$${\displaystyle \frac{dz}{dt}}=b+z\left(x-c\right),$$

(3)

where $a$, $b$, and $c$ are parameters that influence the system dynamics. The used chaotic parameters were $a=0.2$, $b=0.2$, $c=5.7$. The system exhibits a single scroll attractor when it is in the chaotic regime and x, y and z represent the state variables of the system theoretically assumed.

The Newton–Leipnik system was defined as [24]:

$${\displaystyle \frac{dx}{dt}}=-0.4x+y+10yz,$$

(4)

$${\displaystyle \frac{dy}{dt}}=-x-0.4y+5xz,$$

(5)

$${\displaystyle \frac{dz}{dt}}=-\alpha z-5xy,$$

(6)

where $\alpha$ acts as a damping and control parameter that influences the attractor dynamic behavior. $\alpha =0.4$ for this case as a typical chaotic parameter. The Newton–Leipnik system features both scroll-like and spiral shapes.

2.3. Optical Monitoring of Seed Reflectance via Chaotic Attractors

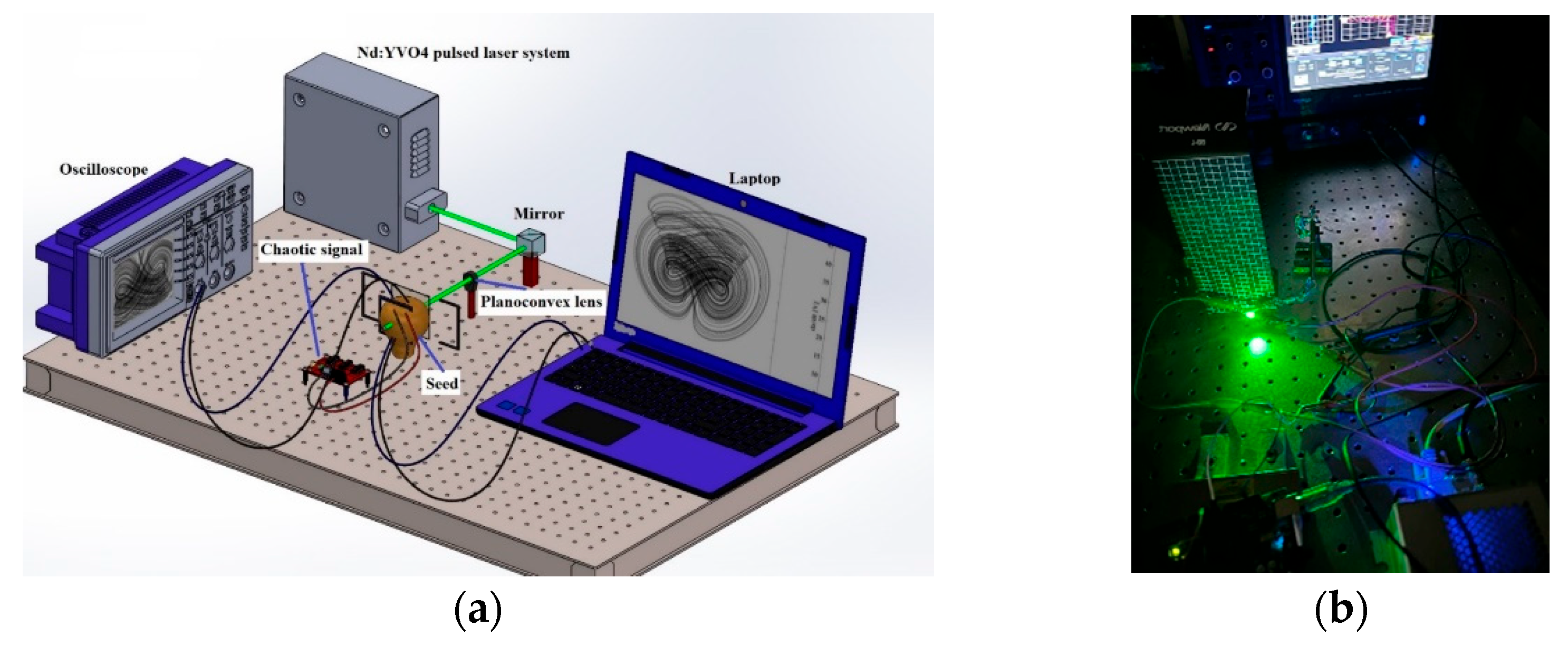
In order to monitor the optical behavior of Thrinax radiata seeds under pulsed laser excitation, a system was designed to capture real-time reflectance changes associated with photoinduced thermal and structural modifications. A Nd:YVO₄ pulsed laser (Spectra-Physics Explorer^® One™ XP, Santa Clara, CA, USA) at 532 nm was used to irradiate the seed, while a chaotic signal, modeled using the Rössler attractor, was employed to interpret the reflectance variations as a function of energy input.

The optical monitoring setup included a focus-tunable lens (Optotune EL-10–30-TC Series, Dietikon, Switzerland) with a focal range from +40 mm to +900 mm, which was controlled by a chaotic signal generated by an Arduino Uno. Two plano-convex lenses (focal lengths 10 cm and 12 cm) directed the laser beam onto the sample, ensuring consistent beam profile and spot size.

Optical reflectance was recorded using a fiber optic spectrometer (Ocean Optics USB2000, Orlando, FL, USA) and a calibrated PIN photodetector (Model: 818-BB-21, Newport, Irvine, CA, USA). These measurements allowed us to detect subtle surface alterations in reflectivity in real time. The morphology of the chaotic attractor varied with laser pulse energy, revealing thermal sensitivity and seed surface reactivity to external perturbation.

In order to determine the photoinduced temperature in the biological probe, generated by the Nd:YVO₄ pulsed laser system, we combined the experimental data and the fractional Newton cooling equation.

Figure 1 shows the representation of experimental setup used for optical monitoring of reflectance in Thrinax radiata seeds irradiated with a Nd:YVO₄ pulsed laser operating at 532 nm. This method enables real-time detection of laser-induced structural changes using chaos theory to interpret variations in the seed’s optical properties.

The laser beam is first directed through a focus-tunable lens, whose focal range is modulated by a chaotic signal generated electronically. The beam then passes through a planoconvex lens, which focuses it precisely onto the surface of the seed. This optical path allows for controlled energy delivery and facilitates the evaluation of photoinduced thermal effects.

The reflected light from the seed is captured by a fiber-optic spectrometer, which analyzes spectral variations in reflectance at different laser energy levels. Spectral data are transmitted in real time to a laptop, where the optical response is recorded and visualized as chaotic attractor trajectories, derived from the reflectance signal modulated by the light–seed interaction.

2.4. Electrical Monitoring of Seed Bioelectrical Response

Thrinax radiata seeds were irradiated using a Nd:YVO₄ pulsed laser at 532 nm. Some energy levels were tested (1 µJ to 6 µJ, 10 ns pulse duration, 10 Hz repetition rate) with irradiation times between 30–120 s and a fixed spot size of 1 mm. These parameters were selected to evaluate both low and high energy regimes and their influence on seed ablation and thermal response.

In parallel with the optical approach, an electrical monitoring system was established to evaluate the bioelectrical response of Thrinax radiata seeds during laser irradiation. This method involved generating a chaotic electrical signal based on the Newton–Leipnik attractor, propagated through an experimental circuit into which the seed was directly integrated.

The Arduino Uno microcontroller (Arduino, Scarmagno, Italy) was used to simulate the chaotic system, while a Tektronix TDS014B oscilloscope (Tektronix, Beaverton, OR, USA) displayed evolving attractor patterns, enabling real-time tracking of the seed electrical behavior.

A DC power supply ensured stability throughout the procedure, and all data acquisition was managed by a high-performance computing system (Omen by HP, Intel i7-9750H, 2.60 GHz).

Figure 2 provides a visual representation of the experimental setups used to study the effects of laser irradiation on Thrinax radiata seeds. Figure 2a is a schematic illustration of the experimental setup: It outlines the overall configuration, showcasing the key components used to irradiate the seed with a laser beam and monitor its response. Whereas Figure 2b expresses the experimental setup for a nonfocused laser beam: Here, the laser beam is directed at the seed without the use of focusing optics, allowing for a broader distribution of energy across the seed surface. A Nd:YVO₄ pulsed laser system is carefully calibrated to ensure precise energy delivery, minimizing excessive thermal load while maximizing sensitivity to seed germplasm changes.

The beam passes through a planoconvex lens to focus it and is reflected by a mirror before hitting the sample. The chaotic attractor was generated using an Arduino board, which was connected directly to the irradiated seed and later it was connected to an oscilloscope displaying the attractor waveform. A laptop (Omen by HP, 15” Intel© Core™ i7-9750H CPU, 2.60 GHz, Windows 10) was also part of the setup, used to control and monitor the experiment.

3. Results

3.1. Morphological Characterization of Thrinax radiata Seeds

Analyses were conducted on three seeds, unless stated otherwise, figures show one representative seed with consistent trends across specimens. The extracted parameters enabled clear differentiation between seeds with regular morphology and those exhibiting surface or structural irregularities. Figure 3 presents a representative subset of Thrinax radiata seeds used in this study. The visual consistency achieved across samples can support the suitability for phenotypic characterization, seed quality assessment (see Materials and Methods Section 2.1), and long-term germplasm optical monitoring.

3.2. Chaotic Attractor-Based Simulation for Monitoring Seed Morphodynamics

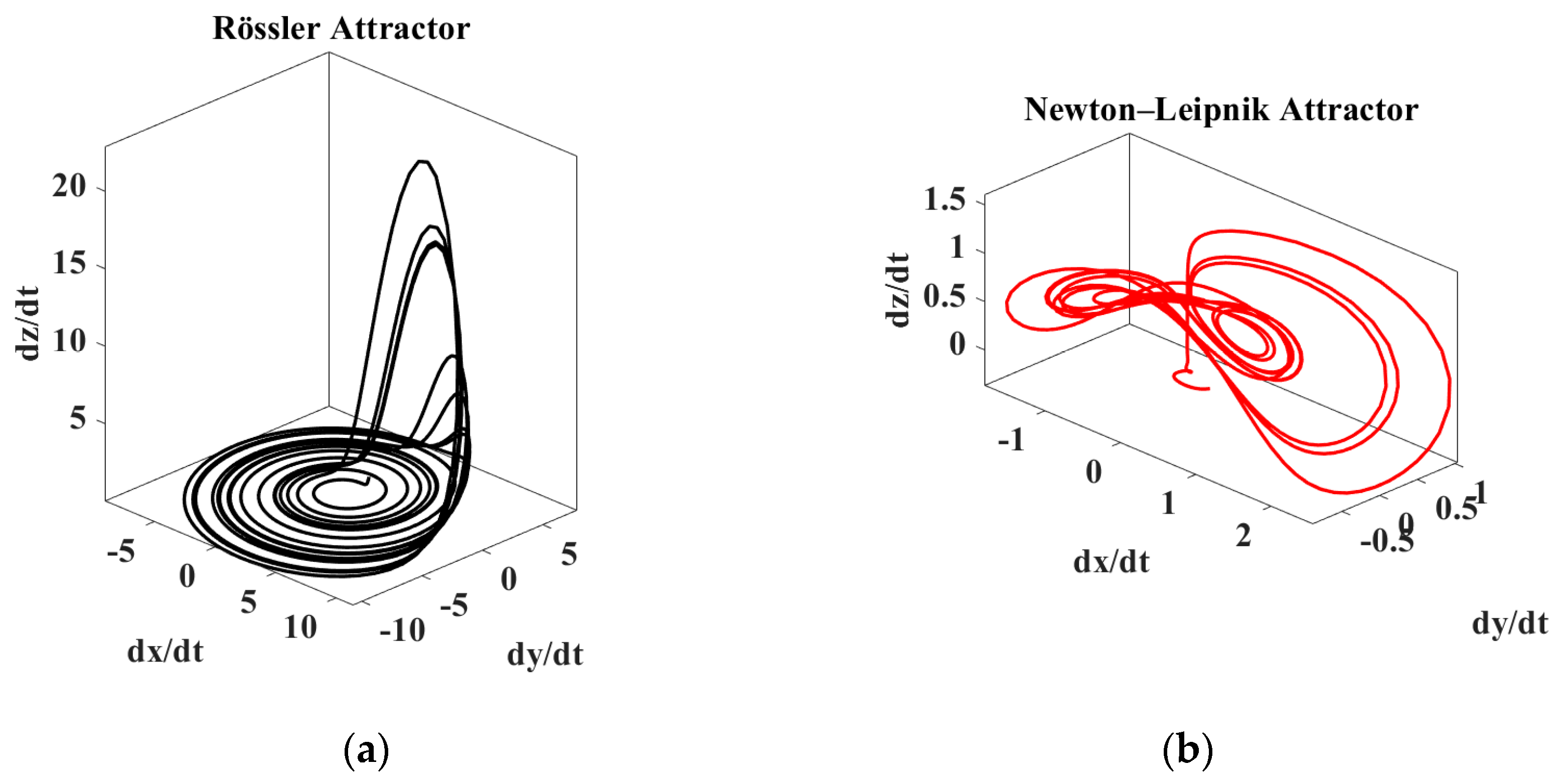
In order to simulate and monitor potential nonlinear biological changes in Thrinax radiata seeds, two chaotic attractors were numerically implemented and analyzed: the Rössler and Newton–Leipnik systems. Both attractors were selected for their ability to exhibit bounded yet complex trajectories in three-dimensional phase space; biological instability can be identified as a modification in the signals that provide feedback in the chaotic system.

Using Equations (1)–(3) for simulating the stable attractors and using a = 0.2, b = 0.2 and c = 5.7 for Rössler system, it exhibits a single-scroll chaotic attractor. In the simulated Rössler dynamics used in the manuscript the largest Lyapunov exponent is ≈0.071 per model time unit, indicating sustained but weak chaos. The correlation fractal dimension is ≈2.0, consistent with a low-dimensional attractor. Under a single positive exponent, the Kolmogorov–Sinai entropy is bounded below by λ₁ and thus ≈0.071 per unit time, reflecting a moderate rate of information production. The attractor remains bounded and structurally stable, ensuring reproducibility and sensitivity to initial conditions without diverging trajectories. It can be observed in Figure 4a. Whereas, for simulating the Newton–Leipnik attractor we utilized $\alpha =0.17$ parameters in Equations (4)–(6) generated a complex spiral–scroll hybrid attractor, sensitive to external perturbations yet remaining within a topologically invariant domain. By nonlinear environmental perturbations we mean stimuli whose effects are non-proportional and history-dependent, for example: pulsed irradiance showing thresholds, leading to non-proportional changes in the measured signals. Figure 4 illustrates the numerical simulation results of two classical chaotic systems. Figure 4a shows the Rössler attractor, exhibiting a smooth, spiral-like trajectory indicative of low-dimensional chaos. Figure 4b presents the Newton–Leipnik attractor, which features a more intricate and folded geometry typical of higher-dimensional chaotic dynamics. Both attractors demonstrate the sensitive dependence on initial conditions and nonlinear coupling that define chaotic behavior, providing valuable insights for applications in nonlinear system monitoring and control.

3.3. Optical Response of Seed Germplasm

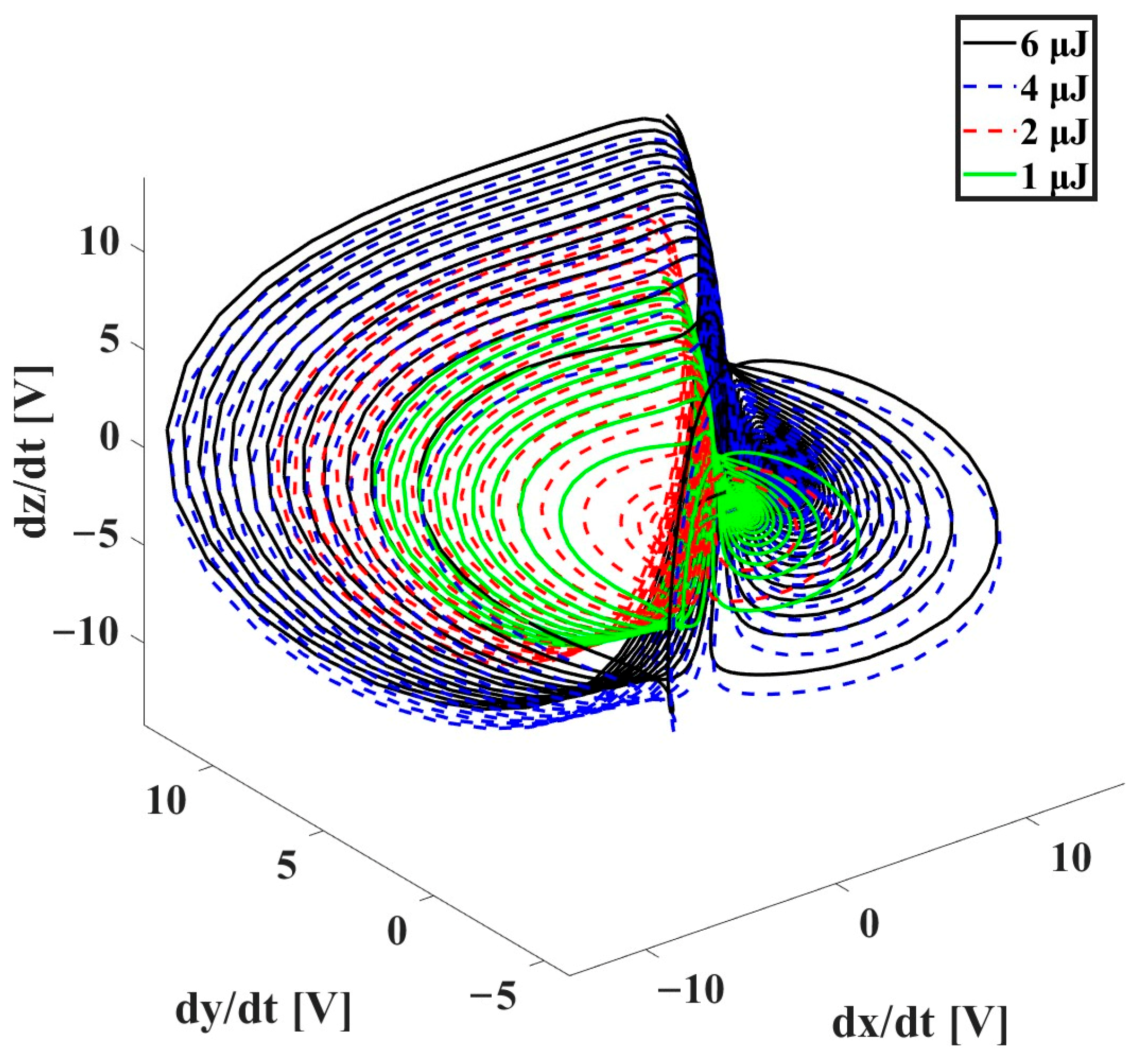
Figure 5 illustrates the experimental results associated with the Newton–Leipnik attractor. The figure captures the attractor evolution under different laser power settings, which ranged from 1 µJ to 6 µJ. The variations in the shape and trajectory of the attractor are directly influenced by the incremental adjustments in laser power. As the laser power increases, the attractor exhibits more pronounced and complex trajectories, reflecting the system nonlinear response to higher energy inputs. These morphological changes in the attractor are closely tied to reflectance measurements taken from the irradiated seeds. Reflectance serves as an indicator of the surface properties and thermal effects induced by the laser. As the seed’s optical properties are altered by varying laser energy, corresponding shifts in the attractor structure can be observed.

Figure 6 illustrates the reflectance measurements of the seed under laser irradiation, with the laser power varying between 2 µJ and 6 µJ. The data clearly show that the reflectance behavior depends significantly on the laser power, and the wavelength corresponding to the highest irradiance is centered at 532 nm, matching the wavelength of the laser used in the experiment. At a laser energy of 6 µJ, the reflectance reached its maximum value of 19%, as indicated by the red points. This peak demonstrates the strong optical interaction between the laser and the seed surface at this energy level. For a laser energy of 4 µJ, the reflectance decreased slightly to 17%, represented by the black points. This reduction suggests less optical coupling or surface modification at this lower energy. At the lowest laser power of 2 µJ, the reflectance was observed to be 14%, as indicated by the blue points. This reflects the minimal photothermal effect and optical response of the seed at this energy level. The laser beam was focused on the seed using a plano-convex lens with a focal length of 10 cm. This lens configuration ensured precise and concentrated energy delivery to the target area, which is crucial for achieving the observed reflectance variations.

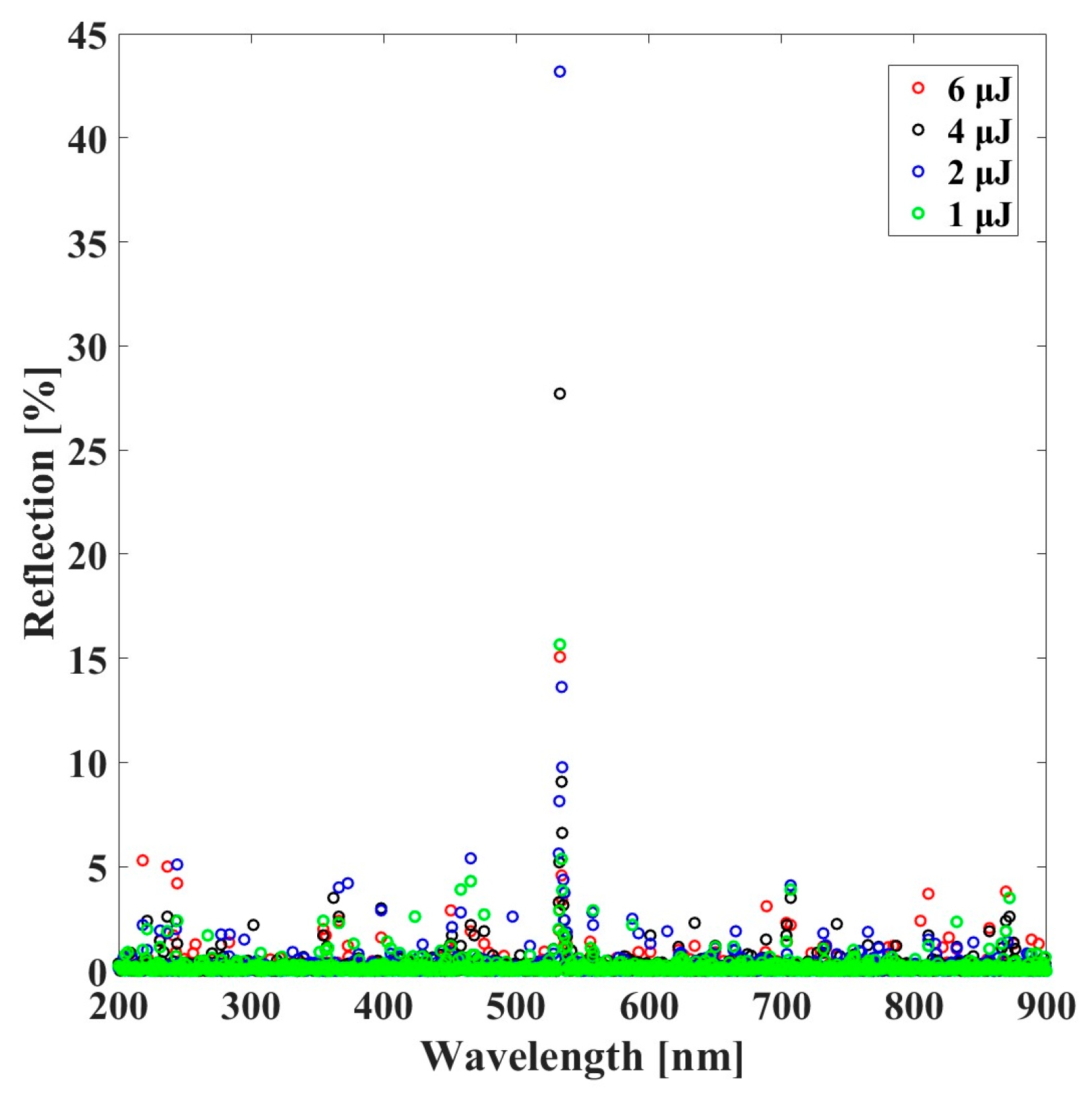
Figure 7 presents the reflectance measurements of the seed under laser irradiation with laser energy ranging from 1 µJ to 6 µJ. At the highest laser energy of 6 µJ, the reflectance reached 15%, indicating the minimal surface reflectivity at this energy level due to potential thermal or optical modifications. For a laser power of 4 µJ, the reflectance was measured at 30%, significantly higher than at 6 µJ, suggesting intermediate laser-material interaction. At a laser energy of 2 µJ, the reflectance peaked at 45%, representing the maximum reflectance among all measurements. This high value indicates minimal surface alteration at lower laser energies. At the lowest energy level of 1 µJ, the reflectance was measured at 16%, suggesting moderate surface reflectance with minimal laser-induced effects.

The measurements shown in Figure 6 and Figure 7 correspond to different laser beam configurations. Specifically, Figure 6 presents data obtained using a focused laser beam, allowing localized energy delivery and enhanced interaction with the seed surface. In contrast, Figure 7 displays results acquired under a non-focused beam configuration, which distributes energy more broadly across the seed, resulting in distinct reflectance behaviors.

We measured the sensor’s output voltage at ten fixed light levels and averaged repeated readings. A straight-line fit $V=a+bl$ was applied; $r\approx 0.9998, R^2\approx 0.9996$, it was used in Figure 8.

Figure 8 illustrates the calibration curve for the optical attractor, where reflectance values are plotted against the stability of the chaotic optical pattern. The optical system exhibits an estimated error margin of ±2.5%, highlighting its sensitivity to laser-induced perturbations. These calibration curves are essential for validating the accuracy and repeatability of the chaotic monitoring techniques, ensuring that the observed structural or bioelectrical changes in the seed germplasm are not due to instrumental fluctuations.

As shown in

Table 1. Stability of optical chaotic attractors.

Variable	Stable Attractor	Loss of Stability
Reflectance (%)	10–20%	>20% chaotic
Induced Temperature (°C)	Low (attractor shape preserved)	High (attractor deformation)
Attractor Morphology	Symmetrical	Asymmetrical and erratic
Optical Spectrum Dispersion	Low	High

, stable optical attractors are characterized by moderate reflectance values (10–20%), preservation of attractor morphology under low induced temperature, symmetrical shapes, and low spectral dispersion. When stability is lost, reflectance exceeds 20%, the attractor structure becomes asymmetrical and erratic, and optical spectrum dispersion increases significantly. Integrating both electrical and optical attractor analyses enables a more accurate and rapid assessment of seed germplasm dynamics compared to conventional germination methods. The calculated error margins for the optical and electrical measurements were ±2.5% and ±2.0%, respectively.

3.4. Electrical Chaotic Attractor Response

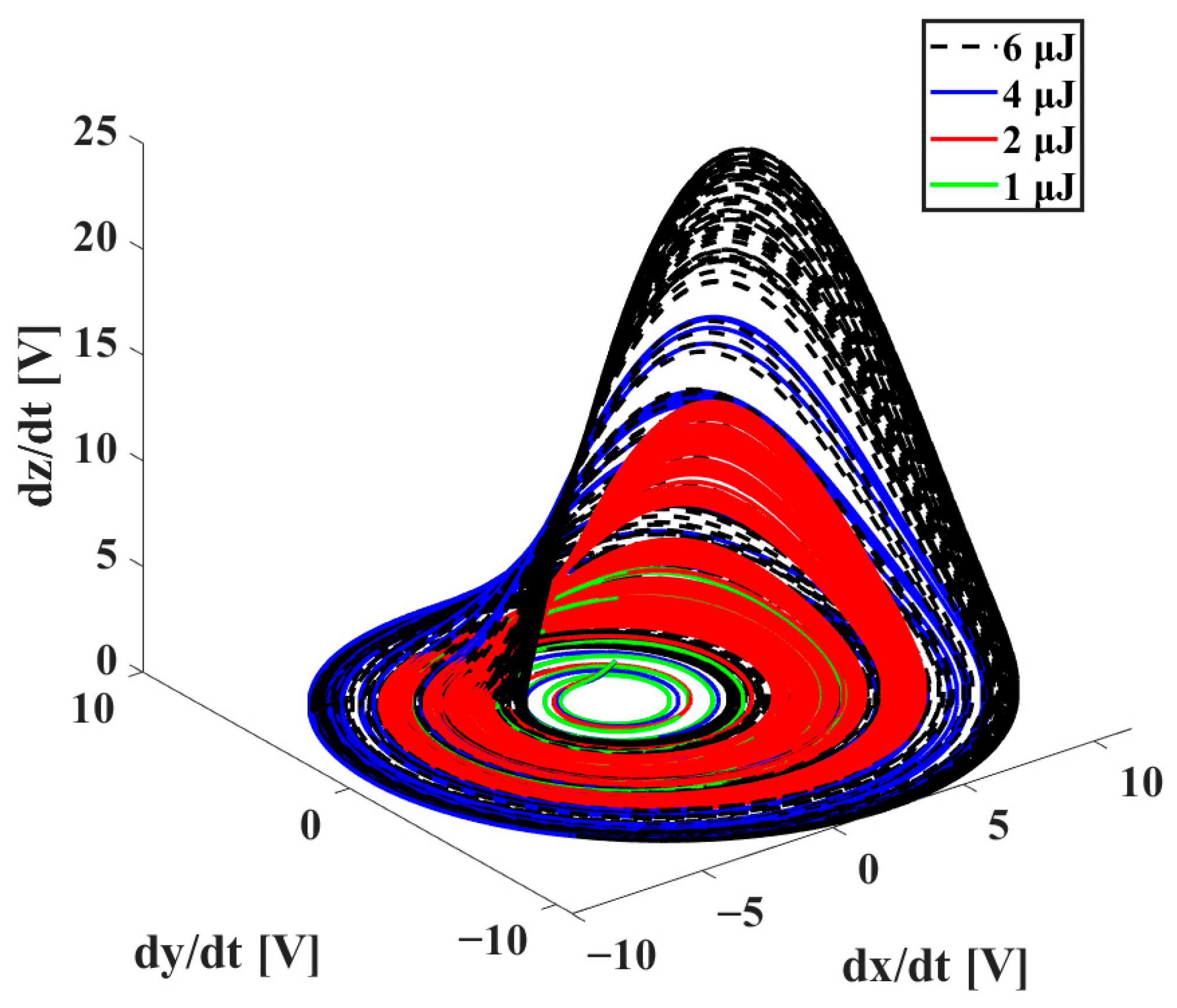
In order to evaluate the bioelectromagnetic behavior of the seed under pulsed laser excitation, the chaotic electrical attractor based on the Newton–Leipnik system was recorded using an oscilloscope. The seed was subjected to different laser pulse energies: 2 µJ, 3 µJ, 4 µJ, 5 µJ, and 6 µJ. As the laser energy increased, the electrical response exhibited increasingly complex attractor trajectories, reflecting the seed’s enhanced nonlinear electrical activity.

At lower energy (2 µJ), the attractor showed compact and symmetric shapes, indicating a stable and low-response regime. At 3 µJ and 4 µJ, the attractor began to stretch and oscillate with greater amplitude, suggesting early activation of bioelectrical dynamics. At 5 µJ and especially 6 µJ, the attractor became asymmetric and highly irregular, with dense loops and extended lobes, indicating strong chaotic activity induced by thermal and structural changes in the seed tissue. These changes in attractor morphology reflect variations in induced voltage and impedance. Specifically, at 6 µJ, the peak voltage reached up to 3.2 V and impedance showed nonlinear shifts, supporting the sensitivity of this method to detect early-stage bioelectrical transformations.

Upon irradiating the seed with varying pulse energies, we observed significant changes in the shape of the chaotic attractor. Figure 9 illustrates these variations, showing distinct Rössler attractor shapes corresponding to different energy levels. These variations indicate that the energy of the laser pulses directly influences the dynamical state of the seed germplasm. The correlation between pulse energy and attractor morphology suggests a sensitive dependence on initial conditions, a hallmark of chaotic systems.

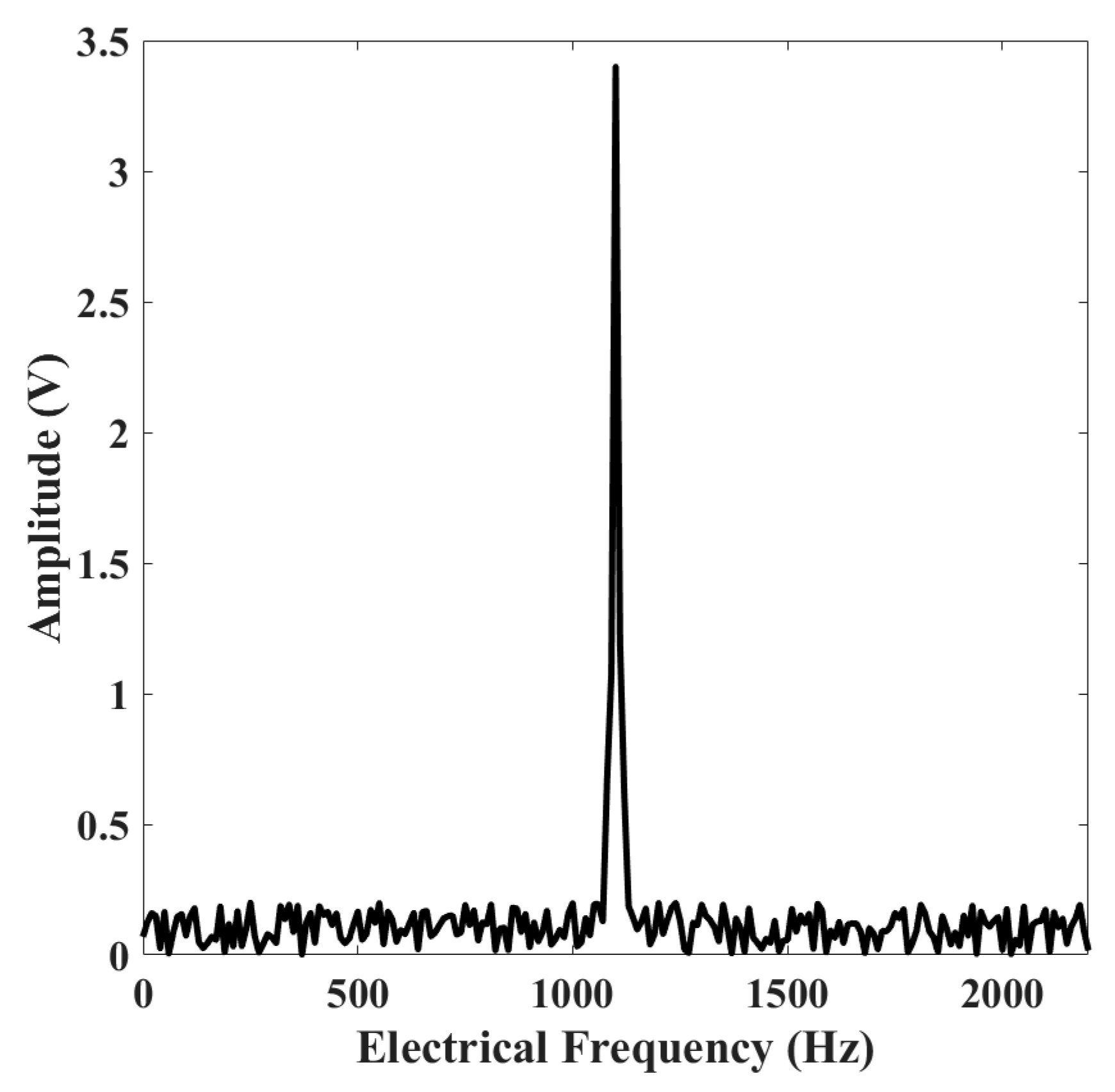
Figure 10 shows the Fast Fourier Transform (FFT) spectrum corresponding to the electrical chaotic attractor response of Thrinax radiata seeds under laser excitation. The figure provides a frequency-domain representation of the system’s nonlinear dynamics, where the stability of the attractor is assessed based on the distribution and sharpness of frequency components.

A dominant peak is clearly observed at approximately 1100 Hz, indicating a strong periodic or quasi-periodic component within the electrical signal. The surrounding frequency range displays a relatively low amplitude baseline, suggesting that the attractor maintains a coherent oscillatory structure with minimal spectral dispersion.

This concentration of energy in a narrow frequency band is characteristic of a stable chaotic attractor, as it implies that the system dynamic behavior is constrained within well-defined limits, without exhibiting broadband, irregular frequency components typical of fully developed chaos. Such spectral profiles validate the reliability of the chaotic electrical attractor as a sensitive yet stable tool for bioelectromagnetic monitoring.

The presence of a high-amplitude peak combined with a sharp spectral boundary confirms that the system is in a low-entropy, structured dynamical regime, enabling precise detection of seed responses to laser perturbation. The FFT analysis thereby reinforces the calibration findings and supports the ±2.0% error margin previously established for the electrical monitoring system.

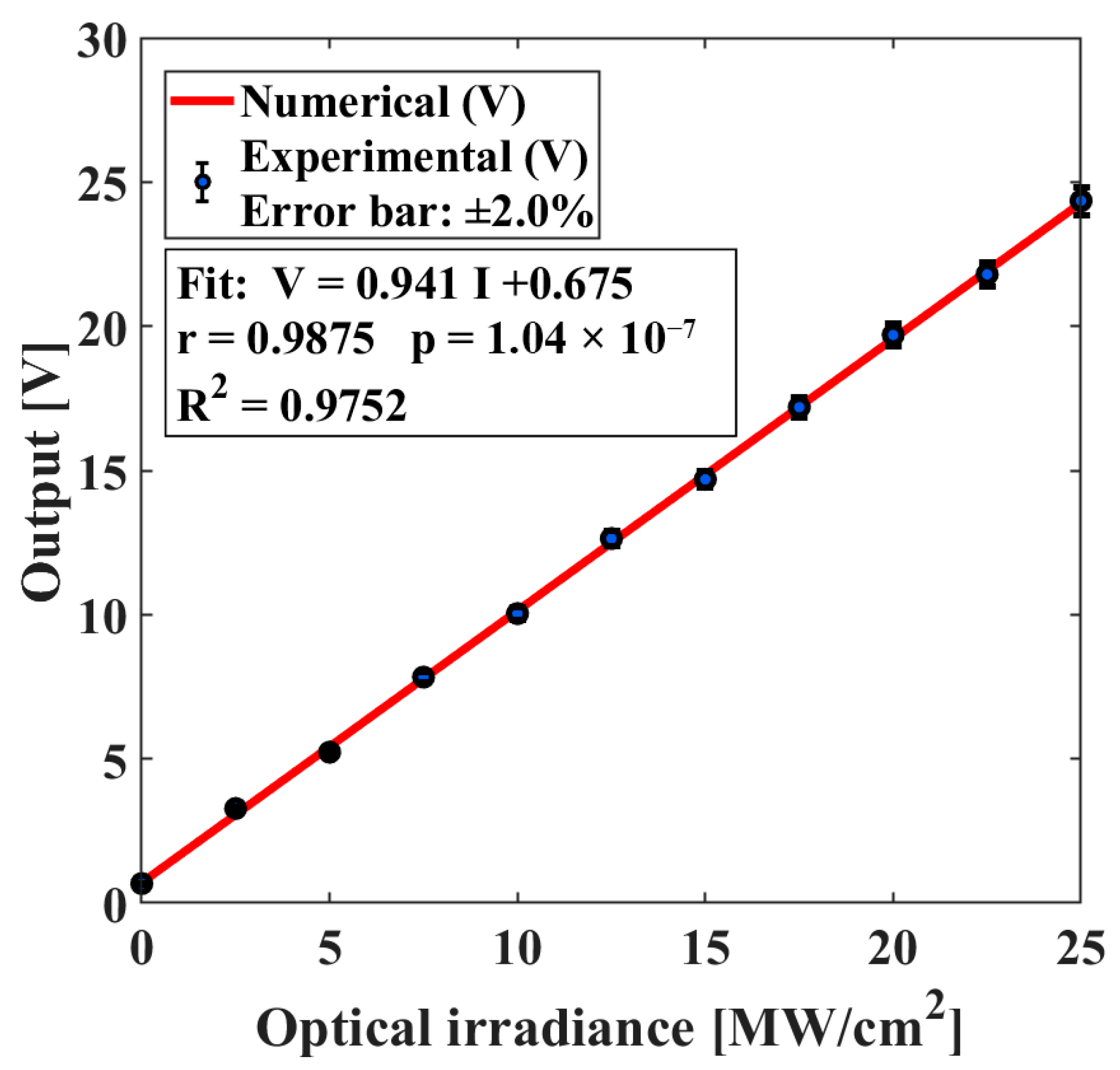
Figure 11 displays the calibration curve used to determine the error margin associated with the electrical chaotic attractor. This curve was constructed by systematically varying the laser pulse energy and recording the corresponding voltage responses from the seed sample using a digital oscilloscope. As the energy increased, the attractor exhibited broader and more irregular loops, which translated into voltage fluctuations with higher standard deviations. The result yielded an average uncertainty of ±2.0% for the electrical measurements across the tested energy range (1–6 µJ).

Table 2. Stability of electrical chaotic attractors.

Variable	Stable Attractor	Loss of Stability
Induced Voltage (V)	<2.5 V (stable)	<2.5 V (chaotic)
Impedance (Ω)	Low (attractor shape preserved)	High (attractor deformation)
Electromagnetic Response	Uniform	Abrupt fluctuations
Oscillation Frequency (Hz)	0–100 Hz (narrow peak in FT)	0–600 Hz (broad and asymmetric FT spectrum)

summarizes the stability criteria for electrical chaotic attractors. Stable attractors are associated with induced voltages below 2.5 V, low impedance, uniform electromagnetic responses, and a narrow frequency range (0–100 Hz) with a sharp peak in the Fourier transform (FT) spectrum. In contrast, loss of stability is indicated by chaotic behavior even below 2.5 V, increased impedance, abrupt electromagnetic fluctuations, and a broad, asymmetric FT spectrum spanning up to 600 Hz.

4. Discussion

Short-term, non-destructive signal dynamics of seeds under controlled laser irradiation; this study does not evaluate long-term germplasm stability or shelf life. Viability was guaranteed in the samples explored before their analysis (see Materials and Methods Section 2.1). This study seeks to put together chaos theory with laser technology to study plant seed germplasm quality and to contrast the light-based or electrical chaotic attractors. Nd:YVO₄ pulsed laser operating at 532 nm was used for seed irradiation and then analyzed the resulting seed germination responses by optically and electrically dual modalities. The optical approach utilized a Rössler chaotic attractor to study the changes in laser-induced reflectance, which included thermal effects supposedly resulted from irradiation, whilst on the other hand, a custom-designed electrical chaotic attractor system connected directly with the seeds captured the electromagnetic response of the seeds even to external stimulation [25]. Reflectance measurements, which are meant to study the dynamic results of thermal energy induced by laser, were performed at different laser pulse energies of 2, 3, 4, 5, 6, and 7 µJ [26]. Meanwhile, electric signals from seeds, subjected to the same conditions, were monitored using the chaotic electrical circuit. The results showed that the voltage magnitudes in optical and electrical attractor systems were increased by laser energy input [27,28]. Therefore, they are highly sensitive to energy input. The optical attractor proved to have nonlinear thermal dynamics that captured how laser energy interferes with reflectance, as in the electrical attractor capturing electromagnetic interactions among some seeds, quite different for looking into their bioelectrical properties [29,30]. For the better comprehension of laser irradiation thermal effects, fractional calculus based on the Caputo fractional derivative was employed [31,32]. This sophisticated mathematical modeling was further able to depict the heat transfer process inside the seeds since it had memory-dependent and non-local characteristics. Through such simulations, the inner regions of the seeds offered simulated temperatures above 1 °C which closely corresponded to changes being observed in the morphology of shapes attractors. Such observations were indicative of the significant contribution that fractional modeling made towards more refined insights into transient thermal phenomena in biological systems.

The relationship between laser ablation and chaotic dynamics was further clarified. Controlled variations in laser energy and irradiation time act as perturbations in the fractional-order model, leading to measurable modifications in attractor morphology. Numerical simulations confirm that these parameter changes induce shifts in the trajectories, consistent with experimental observations. This suggests that laser ablation can serve as a precise tool to adjust chaotic behavior in seed systems, reinforcing the advantages of the fractional modeling approach [33,34,35]. Additional details are provided in the Supplementary Material.

The main advantages of adopting a fractional-order approach over the classical integer-order models are evident. First, fractional derivatives incorporate memory effects, allowing the present thermal response to depend on past states, which matches the delayed relaxation observed experimentally. Second, the fractional formulation provides a closer agreement with experimental data, capturing non-exponential cooling and anomalous diffusion that the classical model cannot reproduce. Finally, the approach generalizes the traditional Newton’s law of cooling, reducing to the integer case, while extending the analysis to nonlinear, history-dependent regimes relevant to irradiated biological systems.

The comparative analysis between light-based and electrical chaotic attractors showed the specific applications and merits. The optical attractor had proved quite effective in analyzing photoinduced thermal dynamics; it can give a direct relationship between laser energy and seed reflectance behavior. On the other hand, the electrical attractor gave some electromagnetic responses of the seeds, capturing bioelectrical signals not visible through optical techniques. By this, the complementary approaches would provide a comprehensive resolution for seed germplasm studies combining thermal and electromagnetic perspectives [36,37].

Optical and electrical detection methods each provide unique advantages and limitations in the study of seed germplasm dynamics. Optical detection, based on reflectance measurements and chaotic attractors, offers high sensitivity to surface modifications and thermal effects induced by laser irradiation [38,39]. This method allows non-contact, high-resolution monitoring of structural and compositional changes, making it particularly useful for detecting subtle alterations in surface properties [40]. However, optical techniques can be affected by scattering, absorption variations, and surface irregularities, which may limit their accuracy in heterogeneous biological samples [41,42].

In contrast, electrical detection methods, such as the chaotic circuit employed in this study, provide direct insight into the bioelectromagnetic properties of seeds [43]. These techniques can reveal information about the internal physiological state, electrical conductivity, and impedance changes induced by laser energy [44,45]. Electrical monitoring is less influenced by surface roughness and can detect responses from deeper regions of the seed, offering complementary data to optical measurements [46,47]. However, electrical methods require direct contact with the sample, which may introduce artifacts due to electrode placement or seed heterogeneity [48]. Additionally, the interpretation of bioelectrical signals can be complex, as it involves multiple interacting variables that influence conductivity and impedance [49,50].

By integrating both techniques, it is possible to obtain a more comprehensive understanding of seed germplasm dynamics. Optical methods excel in detecting surface modifications and laser-induced heating effects, while electrical techniques provide deeper insights into bioelectromagnetic responses [51]. This multimodal approach enhances the robustness of the analysis, reducing the limitations associated with each individual technique.

This interdisciplinary study explores seed germplasm dynamics by integrating chaos theory, laser technology, and fractional calculus. Laser ablation significantly alters the optical and thermal properties of seeds, affecting their reflectance and the morphology of chaotic attractors. Variations in laser energy enable precise tuning of seed responses, suggesting applications in conservation and crop enhancement. Additionally, reflectance changes indicate key thermal and structural effects, with potential applications in optical diagnostics and laser-based treatments. This study did not measure germination rate, viability, or long-term storage performance; therefore, biological implications cannot be established from the present data. Future work will integrate our dynamical descriptors with standardized germination/viability assays across storage conditions to assess relevance for seed conservation.

In this work, we present two highly sensitive measurements as a concept test to explore potential physical differences exhibited by plant/seed stability. This can be a base for a study with an experimental design where the optical technique explores the surface of the sample and the electrical measurement analyzes its interior, considering the complexity of the dynamics.

5. Conclusions

We conclude that chaotic–dynamical descriptors can be robustly extracted from non-destructive measurements of laser-evoked seed responses, providing a methodological basis for subsequent studies that explicitly test links to physiological outcomes. This study analyzes the contrast in the advantages and limitations of optical and electrical monitoring of the nonlinear thermal dynamics exhibited by Thrinax radiata seed germplasm. The sensing performance was assisted by modulation related to chaotic attractors. Using both optical and electrical chaotic attractors, the research highlights the complementary insights provided by each method. The optical attractor captured nonlinear thermal effects with high sensitivity, while the electrical attractor provided early-stage detection of bioelectromagnetic changes, ensuring proactive monitoring to prevent potential structural damage in the seeds.

Fractional calculus simulations, employing the Caputo derivative, effectively modeled temperature distributions, emphasizing memory-dependent thermal transfer processes. Central regions of the seeds reached temperatures 1 °C, correlating with changes in attractor morphology. These findings establish a robust framework for linking theoretical chaos dynamics with experimental photothermal responses.

These results highlight the advantages of fractional calculus, particularly its ability to model memory-dependent thermal transport and anomalous diffusion, offering a more accurate description than classical integer-order models.

This study demonstrates that integrating chaos theory, laser technology, and fractional modeling enables high-sensitivity detection of seed germplasm changes, ensuring effective monitoring and protection of biological samples against excessive thermal and structural modifications, with implications for agricultural diagnostics, seed treatment, and conservation. This approach paves the way for innovative applications in biology, materials science, and precision agriculture.