Adaptive Observer Design with Fixed-Time Convergence, Online Disturbance Learning, and Low-Conservatism Linear Matrix Inequalities for Time-Varying Perturbed Systems

Abstract

This paper proposes a finite-time adaptive observer with online disturbance learning for time-varying disturbed systems. By integrating parameter-dependent Lyapunov functions and slack matrix techniques, the method eliminates conservative static disturbance bounds required in prior work while guaranteeing fixed-time convergence. The proposed approach features a non-diagonal gain structure that provides superior noise rejection capabilities, demonstrating 41% better performance under measurement noise compared to conventional methods. A power systems case study demonstrates significantly improved performance, including 62% faster convergence and 63% lower steady-state error. These results are validated through LMI-based synthesis and adaptive disturbance estimation. Implementation analysis confirms the method’s feasibility for real-time systems with practical computational requirements.

1. Introduction

Modern control systems increasingly require robust state and parameter estimation capabilities to handle complex operational environments characterized by time-varying parameters and external disturbances. The fundamental challenge of designing adaptive observers for disturbed systems has attracted sustained attention in control theory, driven by applications ranging from power systems [1] to robotic exoskeletons [2]. Traditional approaches to this problem, while effective under certain constraints, often rely on conservative design assumptions that limit their practical applicability in real-world scenarios characterized by unknown disturbance bounds and time-critical performance requirements.

The persistent excitation paradigm [1] has served as a cornerstone for observer design in linear regression models, enabling asymptotic convergence under bounded disturbance assumptions. However, recent advances in fixed-time stability theory [3] and linear matrix inequality (LMI) techniques [4] have revealed opportunities to overcome the limitations of conventional asymptotic observers. Contemporary research demonstrates growing interest in combining parameter-dependent Lyapunov functions with slack variable techniques to reduce conservatism in control synthesis [5,6]. This paradigm shift responds to the critical need for estimation algorithms that guarantee prescribed performance characteristics while maintaining computational tractability.

Existing LMI-based observer designs [1,7] typically require a priori knowledge of disturbance bounds and employ fixed diagonal gain matrices, leading to suboptimal noise amplification. Alternative approaches include high-gain observers [8], which are sensitive to noise, and sliding-mode observers [9], which suffer from chattering. Recent machine learning techniques [10] have also been applied to disturbance estimation but lack formal stability guarantees. The recent work of de Oliveira et al. [11] on robust performance margin evaluation highlights the importance of adaptive gain mechanisms, while Wan et al. [12] demonstrate the effectiveness of finite-time synchronization techniques. These developments suggest that integrating adaptive disturbance estimation with fixed-time convergence mechanisms could significantly enhance observer performance.

In this context, the requirement for a priori knowledge of disturbance bounds means that these methods need known constants c, $w^{+}$ such that ${\parallel w(t,y)\parallel }^2\le c{\parallel y\parallel }^2+w^{+}$ holds for all $t\ge 0$. The use of fixed diagonal matrices refers to gain matrices of the form $L=\mathrm{diag}(l_1,l_2,\dots ,l_n)$ where only the diagonal elements are tuned, which limits the design flexibility compared to full matrix gains. This restriction often leads to suboptimal noise amplification characteristics, meaning that the observer may unnecessarily amplify measurement noise in some channels due to the lack of coordinated gain adjustment across different states.

The proposed methodology builds on three fundamental advancements in modern control theory: first, the fixed-time stability framework established by Polyakov [3], which provides theoretical guarantees for convergence within user-defined time horizons; second, the LMI-based control synthesis techniques pioneered by Boyd et al. [4], recently extended to handle polytopic uncertainties [13] and actuator saturation [12]; and third, the emerging paradigm of parameter-dependent Lyapunov functions [5,6] that enables less conservative stability analysis for time-varying systems. By synthesizing these elements with novel disturbance learning mechanisms, this work addresses critical gaps in existing observer designs.

Recent applications in diverse domains underscore the practical relevance of advanced observer designs. In power systems, Reihani et al. [13] demonstrate the effectiveness of LMI approaches for handling renewable energy uncertainties, while Kiruthika and Manivannan [14] showcase finite-time synchronization techniques in neural networks. Robotics applications [2] further highlight the need for robust estimation algorithms that maintain performance under real-world disturbances. These developments motivate our focus on creating an observer framework that combines the computational rigor of LMI methods [15] with the transient performance guarantees of fixed-time stability theory [3].

The principal contributions of this work are the synthesis of established techniques into a novel framework that addresses three fundamental limitations in existing observer designs:

• The elimination of static disturbance bounds through online learning mechanisms, inspired by but distinct from recent advances in adaptive control [16,17].
• The replacement of asymptotic convergence guarantees with fixed-time stability properties using nonlinear injection terms, extending concepts from fractional-order control theory [18,19].
• The reduction of conservatism in LMI synthesis by combining parameter-dependent Lyapunov functions with slack matrix techniques, offering a less conservative alternative to the diagonal gain structures used in [1] and building on recent developments in polytopic uncertainty handling [13].

While the constituent techniques (PDLFs, slack matrices) are known, their combined application to create a fixed-time convergent observer with online disturbance learning for this class of systems is novel.

Validation through comprehensive case studies in power systems [1,13] demonstrates the practical efficacy of the proposed observer. Comparative analysis reveals 62% faster convergence and 63% lower steady-state error compared to conventional LMI-based designs [1,4], while maintaining computational tractability through grid-based parameter discretization [6]. The theoretical framework builds on previous work on fractional-order system observation [18] and nonlinear system analysis [20,21,22], extending these foundations to handle time-varying parameters and unmodeled dynamics. Also, recent advances in fractional calculus have provided new mathematical tools that can inspire innovative observer designs, with developments in tempered fractional gradient methods [23], conformable fractional derivative optimization [24], and practical implementations using Caputo fractional derivatives [25]. These fractional-order approaches offer theoretical foundations for handling complex system dynamics with non-local properties and memory effects, providing complementary mathematical frameworks that could enhance adaptive observation techniques for time-varying perturbed systems.

The remainder of this paper is organized as follows: Section 2 establishes essential mathematical preliminaries and problem formulation. Section 3 details the proposed finite-time observer design with online disturbance learning. Section 4 presents the reduced-conservatism LMI synthesis methodology. Section 5 provides comparative analysis and practical implementation guidelines. Section 6 validates the approach through power system case studies. Section 7 concludes with recommendations for future research directions in adaptive observation and LMI-based control.

• Notation

Throughout this paper, the following notation is adopted:

• ${\mathbb{R}}^n$: n-dimensional Euclidean space.
• $\parallel ·\parallel$: Euclidean norm for vectors; induced spectral norm for matrices.
• ${\mathcal{L}}_{\infty }$: Space of essentially bounded measurable functions.
• ${\left[a\right]}^{\gamma }=sign\left(a\right){\left|a\right|}^{\gamma }$: Sign-preserving power function for $a\in \mathbb{R}$, $\gamma \ge 0$.
  For vectors, ${\left[a\right]}^{\gamma }={[{\left[a_1\right]}^{\gamma },\dots ,{\left[a_n\right]}^{\gamma }]}^T$.
• $\overline{1,n}$: Sequence of integers $1,2,\dots ,n$.
• $I_n$: Identity matrix of size $n\times n$; $0_{n\times m}$: zero matrix of size $n\times m$.
• ${\lambda }_{min}(·)$, ${\lambda }_{max}(·)$: Minimum and maximum eigenvalues of a matrix.
• $\mathcal{K}$, ${\mathcal{K}}_{\infty }$: Class $\mathcal{K}$ (strictly increasing, ${\mathcal{K}}_{\infty }$ if unbounded) functions.
• $\xi \left(t\right)={[{\tilde{y}}^T\left(t\right),{\tilde{\theta }}^T\left(t\right),{\tilde{w}}^T\left(t\right)]}^T$: Augmented error vector (state/parameter/disturbance errors).
• $\mathcal{P}\left(\rho \right(t\left)\right)$: Parameter-dependent Lyapunov matrix in (9), where $\rho \left(t\right)=[{\rho }_1\left(t\right),\dots ,{\rho }_q\left(t\right)]$ are time-varying parameters (e.g., $\parallel \tilde{y}\parallel$, $\parallel \tilde{\theta }\parallel$).
• $\mathcal{S}$: Slack matrix in LMI constraint (10), introduced to decouple Lyapunov terms and reduce conservatism.
• N: Grid resolution for parameter discretization, chosen empirically based on parameter variability (see Algorithm 1).
• $\gamma \in (0,1)$: Fixed-time convergence exponent in observer (4a).
• T: Predefined convergence time bound in Theorem 1.
• $\varphi \left(t\right)$: Adaptive gain for disturbance estimation in (5).
• $\nu$: Residual disturbance approximation error.
• $\mu$: Uniform lower eigenvalue bound for $\mathcal{P}\left(\rho \right(t\left)\right)$.
• $\Lambda$: Positive definite gain matrix for the nonlinear injection term in (4b).
• $ϵ>0$: Smoothing parameter for the $tanh(·)$ function in (4c), mitigating chattering.

Algorithm 1 Grid-based gain synthesis

Discretize $\rho \in {\prod }_{i=1}^q[{\rho }_i^{min},{\rho }_i^{max}]$ into N points. At each grid point ${\rho }_j$, solve (10) for ${\mathcal{P}}_0,{\mathcal{P}}_i,\mathcal{S}$. Interpolate $\mathcal{P}\left(\rho \right(t\left)\right)$ during implementation. Compute gains for implementation: The gains $L_1$, $L_2$, and $L_{\theta }$ are functions of the full-dimensional matrices $\mathcal{S}$ and $\mathcal{P}\left(\rho \right)$ solved over the grid. For a given $\rho \left(t\right)$, interpolate $\mathcal{P}\left(\rho \right(t\left)\right)$, then compute $L_1\left(\rho \left(t\right)\right)={\left({\mathcal{S}}^{-1}\mathcal{P}\left(\rho \left(t\right)\right)\right)}_{[1:m,1:m]}$, $L_{\theta }\left(\rho \left(t\right)\right)={\left({\mathcal{S}}^{-1}\mathcal{P}\left(\rho \left(t\right)\right)\right)}_{[m+1:m+p,1:m]}$, and $L_2=\Lambda L_1\left(\rho \left(t\right)\right)$, where [i:j,k:l] denotes matrix block extraction.

2. Preliminaries

Definition 1. 

A system $\dot{x}\left(t\right)=f\left(x\left(t\right)\right)$ is fixed-time-stable [3] if the following is true:

1. 

It is finite-time-stable, i.e., $x\left(t\right)\to 0$ as $t\to T\left(x\right(0\left)\right)$, where $T\left(x\right(0\left)\right)<\infty$.

2. 

The settling time $T\left(x\right(0\left)\right)$ is bounded by a constant $T_{max}>0$, independent of $x\left(0\right)$.

A PDLF $V(x,\rho \left(t\right))=x^T\mathcal{P}\left(\rho \left(t\right)\right)x$, where $\rho \left(t\right)$ is a time-varying parameter vector, is used to reduce conservatism in LMI-based designs. The matrix $\mathcal{P}\left(\rho \right(t\left)\right)\succ 0$ must satisfy

$$\dot{V}=x^T\left(\mathcal{P}\left(\rho \left(t\right)\right)A+A^T\mathcal{P}\left(\rho \left(t\right)\right)+\dot{\mathcal{P}}\left(\rho \left(t\right)\right)\right)x<0,$$

(1)

where $\dot{\mathcal{P}}\left(\rho \left(t\right)\right)={\sum }_{i=1}^q{\dot{\rho }}_i\left(t\right){\displaystyle \frac{\partial \mathcal{P}}{\partial {\rho }_i}}$.

We introduce the following assumptions:

Assumption 1. 

The disturbance $w(t,y)$ is an unknown, exogenous signal. However, its norm admits an upper bound characterized by $\parallel w(t,y)\parallel \le \varphi \left(t\right)+\nu$, where $\varphi \left(t\right)$ is an adaptive gain to be learned online and $\nu >0$ is a small constant representing a residual modeling error. The disturbance itself is not measured or known.

Assumption 2. 

The regressor $\Gamma \left(t\right)$ is persistently exciting (PE), i.e., $\exists \tau ,\delta >0$:

$${\int }_t^{t+\tau }{\Gamma }^T\left(s\right)\Gamma \left(s\right)ds⪰\delta I.$$

Assumption 3. 

The time derivative of the disturbance $\dot{w}(t,y)$ is Lebesgue-measurable and satisfies $\parallel \dot{w}(t,y)\parallel \le {\overline{w}}_d$, where ${\overline{w}}_d>0$ is a known constant.

Remark 1. 

The LMI synthesis (Section 5) ensures $\exists \mu >0$ such that $\mathcal{P}\left(\rho \right(t\left)\right)⪰\mu I$ for all t, guaranteeing ${\lambda }_{min}\left(\mathcal{P}\left(\rho \right)\right)\ge \mu$.

Assumption 4 

(Bounded Scheduling Derivatives). The time derivatives of scheduling parameters ${\dot{\rho }}_i\left(t\right)$ are bounded:

$$|{\dot{\rho }}_i\left(t\right)|\le {\overline{\rho }}_i\forall i\in \{1,\dots ,q\}$$

where ${\overline{\rho }}_i>0$ are known constants.

Assumption 5 

(Uniform Positive Definiteness of $\mathcal{P}\left(\rho \right)$). There exists $\mu >0$ such that the parameter-dependent Lyapunov matrix satisfies

$$\mathcal{P}\left(\rho \left(t\right)\right)⪰\mu I_m\forall t\ge 0.$$

3. Problem Statement

Consider the disturbed regression model:

$$\dot{y}\left(t\right)=\Gamma \left(t\right)\theta \left(t\right)+w(t,y\left(t\right)),$$

(2)

where $y\left(t\right)\in {\mathbb{R}}^m$ is measurable, $\Gamma \left(t\right)\in {\mathbb{R}}^{m\times p}$ is known, $\theta \left(t\right)\in {\mathbb{R}}^p$ is unknown time-varying, and with $w(t,y)\in {\mathbb{R}}^m$ disturbances. The observer design must overcome three limitations [1]:

• Requirement of static disturbance bounds ${\parallel w\parallel }^2\le c{\parallel y\parallel }^2+\cdots +w^{+}$.
• Asymptotic rather than fixed-time convergence.
• Conservatism from diagonal gain matrices.

We introduce a disturbance estimator $\widehat{w}\left(t\right)$ and revise the model to

$$\dot{y}\left(t\right)=\Gamma \left(t\right)\theta \left(t\right)+w(t,y\left(t\right))-\widehat{w}\left(t\right)+\tilde{w}\left(t\right),$$

(3)

where $\tilde{w}\left(t\right)=w(t,y)-\widehat{w}\left(t\right)$ is the estimation error. The disturbance derivative satisfies $\parallel \dot{w}(t,y)\parallel \le {\overline{w}}_d$ (Assumption 3).

Remark 2. 

The formulation in (3) uses the sign convention where $\tilde{w}\left(t\right)=w(t,y)-\widehat{w}\left(t\right)$ represents a disturbance estimation error deficit. This convention is consistent with the subsequent error dynamics in (6a), where a positive $\tilde{w}\left(t\right)$ contributes positively to $\dot{\tilde{y}}\left(t\right)$.

Objective: Design an observer that achieves the following:

• Estimates $\theta \left(t\right)$ and $w(t,y)$ without static disturbance bounds.
• Guarantees $\tilde{y}\left(t\right),\tilde{\theta }\left(t\right),\tilde{w}\left(t\right)\to 0$ in fixed time T.
• Synthesizes gains via reduced-conservatism LMIs.

4. Finite-Time Observer Design with Online Disturbance Learning

The proposed observer for (3) is

$$\begin{array}{cc}\hfill \dot{\widehat{y}}\left(t\right)& =\Gamma \left(t\right)\widehat{\theta }\left(t\right)+\widehat{w}\left(t\right)+L_1\tilde{y}\left(t\right)+L_2{\left[\tilde{y}\left(t\right)\right]}^{\gamma },\hfill \end{array}$$

(4a)

$$\begin{array}{cc}\hfill \dot{\widehat{\theta }}\left(t\right)& =L_{\theta }{\Gamma }^T\left(t\right)\left(P\tilde{y}\left(t\right)+\Lambda {\left[\tilde{y}\left(t\right)\right]}^{\alpha }\right)-\kappa sign\left(\tilde{\theta }\left(t\right)\right),\hfill \end{array}$$

(4b)

$$\begin{array}{cc}\hfill \dot{\widehat{w}}\left(t\right)& =\mathcal{K}\tilde{y}\left(t\right)+\varphi \left(t\right)tanh\left({\displaystyle \frac{\tilde{y}\left(t\right)}{ϵ}}\right),\hfill \end{array}$$

(4c)

where $\mathcal{K}\in {\mathbb{R}}^{m\times m}$ is a gain matrix, $\gamma \in (0,1)$, $\alpha >1$; here, $L_{\theta }\in {\mathbb{R}}^{p\times m}$ is the adaptation gain matrix, and $\varphi \left(t\right)$ adapts via

$$\dot{\varphi }\left(t\right)=\lambda {\parallel \tilde{y}\left(t\right)\parallel }^2-\sigma \varphi \left(t\right),\varphi \left(0\right)>0.$$

(5)

Remark 3. 

The term $|\tilde{y}{|}^{\gamma }\mathrm{sign}\left(\tilde{y}\right)$ ensures fixed-time convergence, while $tanh(·)$ mitigates chattering. The adaptive law (5) ensures $\varphi \left(t\right)\in {\mathcal{L}}_{\infty }$ (Lemma 1). The gains $\lambda >0$, $\sigma >0$ trade off adaptation speed and noise sensitivity. Empirical guideline: $\sigma \approx 0.1\lambda max(\parallel \Gamma (t\left){\parallel }^2\right)$.

Error Dynamics:

$$\begin{array}{cc}\hfill \dot{\tilde{y}}\left(t\right)& =-L_1\tilde{y}\left(t\right)-L_2{\left[\tilde{y}\left(t\right)\right]}^{\gamma }+\Gamma \left(t\right)\tilde{\theta }\left(t\right)+\tilde{w}\left(t\right),\hfill \end{array}$$

(6a)

$$\begin{array}{cc}\hfill \dot{\tilde{\theta }}\left(t\right)& =-L_{\theta }{\Gamma }^T\left(t\right)\left(P\tilde{y}\left(t\right)+\Lambda {\left[\tilde{y}\left(t\right)\right]}^{\alpha }\right)+\kappa sign\left(\tilde{\theta }\left(t\right)\right)+\dot{\theta }\left(t\right),\hfill \end{array}$$

(6b)

$$\begin{array}{cc}\hfill \dot{\tilde{w}}\left(t\right)& =\dot{w}(t,y)-\mathcal{K}\tilde{y}\left(t\right)-\varphi \left(t\right)tanh\left({\displaystyle \frac{\tilde{y}\left(t\right)}{ϵ}}\right).\hfill \end{array}$$

(6c)

Theorem 1 

(Fixed-Time Stability). Under Assumptions 1–3, and the additional boundedness condition Assumption 4, the error $\xi \left(t\right)={[{\tilde{y}}^T,{\tilde{\theta }}^T,{\tilde{w}}^T]}^T$ converges to zero in fixed time T if the following holds:

1. 

Gains satisfy parameter-dependent LMIs (Section 5).

2. 

$\gamma \in (0,1)$, $\alpha >1$.

3. 

$\kappa > \parallel \dot{\theta }{\parallel }_{\infty }+ \nu$.

Proof. 

Consider the Lyapunov function:

$$V=\underset{V_1}{\underbrace{{\tilde{y}}^T\mathcal{P}\left(\rho \right)\tilde{y}}}+\underset{V_2}{\underbrace{{\displaystyle \frac{1}{2}}{\tilde{\theta }}^T{L}_{\theta }^{-1}\tilde{\theta }}}+\underset{V_3}{\underbrace{{\displaystyle \frac{1}{2}}{\tilde{w}}^T\tilde{w}}}+\underset{V_4}{\underbrace{{\displaystyle \frac{1}{2\lambda }}{(\varphi -{\varphi }^{*})}^2}},$$

(7)

where ${\varphi }^{*}={sup}_t\parallel w(t,y)\parallel +\nu$. The total derivative is

$$\begin{array}{cc}\hfill \dot{V}& =\underset{{\dot{V}}_1}{\underbrace{{\tilde{y}}^T\dot{\mathcal{P}}\left(\rho \right)\tilde{y}+2{\tilde{y}}^T\mathcal{P}\left(\rho \right)\dot{\tilde{y}}}}+\underset{{\dot{V}}_2}{\underbrace{{\tilde{\theta }}^T{L}_{\theta }^{-1}\dot{\tilde{\theta }}}}+\underset{{\dot{V}}_3}{\underbrace{{\tilde{w}}^T\dot{\tilde{w}}}}+\underset{{\dot{V}}_4}{\underbrace{{\displaystyle \frac{1}{\lambda }}(\varphi -{\varphi }^{*})\dot{\varphi }}}\hfill \end{array}$$

Substitute $\dot{\tilde{y}}$ from (6a):

$$\begin{array}{cc}\hfill {\dot{V}}_1& ={\tilde{y}}^T\sum _{i=1}^q{\dot{\rho }}_i{\displaystyle \frac{\partial \mathcal{P}}{\partial {\rho }_i}}\tilde{y}\hfill \\ \hfill & +2{\tilde{y}}^T\mathcal{P}\left(\rho \right)\left(-L_1\tilde{y}-L_2{\left[\tilde{y}\right]}^{\gamma }+\Gamma \left(t\right)\tilde{\theta }+\tilde{w}\right)\hfill \\ \hfill & ={\tilde{y}}^T\dot{\mathcal{P}}\left(\rho \right)\tilde{y}-2{\tilde{y}}^T\mathcal{P}\left(\rho \right)L_1\tilde{y}\hfill \\ \hfill & -2{\tilde{y}}^T\mathcal{P}\left(\rho \right)L_2{\left[\tilde{y}\right]}^{\gamma }+2{\tilde{y}}^T\mathcal{P}\left(\rho \right)\Gamma \left(t\right)\tilde{\theta }+2{\tilde{y}}^T\mathcal{P}\left(\rho \right)\tilde{w}\hfill \end{array}$$

Substitute $\dot{\tilde{\theta }}$ from (6b):

$$\begin{array}{cc}\hfill {\dot{V}}_2& ={\tilde{\theta }}^T{L}_{\theta }^{-1}\left(-L_{\theta }{\Gamma }^T\left(t\right)(P\tilde{y}+\Lambda {\left[\tilde{y}\right]}^{\alpha })+\kappa sign\left(\tilde{\theta }\right)+\dot{\theta }\right)\hfill \\ \hfill & =-{\tilde{\theta }}^T{\Gamma }^T\left(t\right)P\tilde{y}-{\tilde{\theta }}^T{\Gamma }^T\left(t\right)\Lambda {\left[\tilde{y}\right]}^{\alpha }+\kappa {\tilde{\theta }}^{T}sign\left(\tilde{\theta }\right)+{\tilde{\theta }}^T{L}_{\theta }^{-1}\dot{\theta }\hfill \end{array}$$

Note: ${\tilde{\theta }}^{T}sign\left(\tilde{\theta }\right)={\parallel \tilde{\theta }\parallel }_1\ge {\parallel \tilde{\theta }\parallel }_2$.

Substitute $\dot{\tilde{w}}$ from (6c):

$$\begin{array}{cc}\hfill {\dot{V}}_3& ={\tilde{w}}^T\left(\dot{w}(t,y)-\mathcal{K}\tilde{y}-\varphi \left(t\right)tanh\left({\displaystyle \frac{\tilde{y}}{ϵ}}\right)\right)\hfill \\ \hfill & ={\tilde{w}}^T\dot{w}(t,y)-{\tilde{w}}^T\mathcal{K}\tilde{y}-\varphi \left(t\right){\tilde{w}}^{T}tanh\left({\displaystyle \frac{\tilde{y}}{ϵ}}\right)\hfill \end{array}$$

Substitute $\dot{\varphi }$ from (5):

$$\begin{array}{cc}\hfill {\dot{V}}_4& ={\displaystyle \frac{1}{\lambda }}(\varphi -{\varphi }^{*})(\lambda \parallel \tilde{y}{\parallel }^2-\sigma \varphi )\hfill \\ \hfill & =(\varphi -{\varphi }^{*}){\parallel \tilde{y}\parallel }^2-{\displaystyle \frac{\sigma }{\lambda }}(\varphi -{\varphi }^{*})\varphi \hfill \end{array}$$

Assemble all components and apply bounds:

$$\begin{array}{cc}\hfill \dot{V}& \le {\tilde{y}}^T\dot{\mathcal{P}}\left(\rho \right)\tilde{y}\hfill \\ \hfill & -2{\tilde{y}}^T\mathcal{P}\left(\rho \right)L_1\tilde{y}-2{\tilde{y}}^T\mathcal{P}\left(\rho \right)L_2{\left[\tilde{y}\right]}^{\gamma }\hfill \\ \hfill & +2{\tilde{y}}^T\mathcal{P}\left(\rho \right)\Gamma \left(t\right)\tilde{\theta }-{\tilde{\theta }}^T{\Gamma }^T\left(t\right)P\tilde{y}\hfill \\ \hfill & -{\tilde{\theta }}^T{\Gamma }^T\left(t\right)\Lambda {\left[\tilde{y}\right]}^{\alpha }+\kappa \parallel \tilde{\theta }{\parallel }_1+ \parallel \tilde{\theta }\parallel ·\parallel L_{\theta }^{-1}\dot{\theta }\parallel \hfill \\ \hfill & +\parallel \tilde{w}\parallel ·\parallel \dot{w}(t,y)\parallel - {\tilde{w}}^T\mathcal{K}\tilde{y}\hfill \\ \hfill & -\varphi \left(t\right){\tilde{w}}^{T}tanh\left({\displaystyle \frac{\tilde{y}}{ϵ}}\right)+(\varphi -{\varphi }^{*}){\parallel \tilde{y}\parallel }^2\hfill \\ \hfill & -{\displaystyle \frac{\sigma }{\lambda }}(\varphi -{\varphi }^{*})\varphi +{\eta }_0\hfill \end{array}$$

where ${\eta }_0$ absorbs minor constants from $tanh(·)$ approximation.

• Bounded derivatives (A3,A4): $\parallel \dot{w}\parallel \le {\overline{w}}_d$, $\parallel \dot{\mathcal{P}}\left(\rho \right)\parallel \le \overline{p}$
• Cross-term elimination: LMI (10) ensures

  $$\left[\begin{array}{cc}\dot{\mathcal{P}}+\mathcal{P}A+A^T\mathcal{P}+Q& \mathcal{P}B\\ B^T\mathcal{P}& -I\end{array}\right]\prec 0$$
• Significant inequalities:

  $$\begin{array}{cc}\hfill \parallel {\tilde{w}}^{T}tanh(·)\parallel & \le {\parallel \tilde{w}\parallel }_1\hfill \\ \hfill (\varphi -{\varphi }^{*})\varphi & \ge {(\varphi -{\varphi }^{*})}^2-{\left({\varphi }^{*}\right)}^2(\mathrm{Young}’\mathrm{s})\hfill \end{array}$$

After algebraic manipulation and gain selection,

$$\begin{array}{cc}\hfill \dot{V}& \le -{\tilde{y}}^{T}Q\tilde{y}-{\eta }_2\parallel \tilde{y}{\parallel }^{1+\gamma }- {\eta }_3\parallel \tilde{\theta }\parallel \hfill \\ \hfill & +\parallel \tilde{w}\parallel ({\overline{w}}_d+{\varphi }^{*})+|\varphi -{\varphi }^{*}|(\sigma {\varphi }^{*}/\lambda )+{\eta }_6\hfill \end{array}$$

Using $\parallel \tilde{w}\parallel \le {\varphi }^{*}+\nu$ and Young’s inequality, we obtain

$$\begin{array}{c}\hfill \dot{V}\le -{\lambda }_{min}\left(Q\right){\parallel \tilde{y}\parallel }^2-{\eta }_2{\parallel \tilde{y}\parallel }^{1+\gamma }-{\eta }_3\parallel \tilde{\theta }\parallel +{\eta }_4{({\varphi }^{*}+\nu )}^2+{\eta }_5{\left({\varphi }^{*}\right)}^2+{\eta }_6\\ \hfill \le -\alpha ({\parallel \tilde{y}\parallel }^2+ \parallel \tilde{\theta }\parallel +{(\varphi -{\varphi }^{*})}^2) - \beta ({\parallel \tilde{y}\parallel }^{1+\gamma })\\ \hfill \le -\alpha V-\beta V^{{\displaystyle \frac{1+\gamma }{2}}}\end{array}$$

for some positive constants $\alpha ,\beta ,{\eta }_4,{\eta }_5,{\eta }_6$, where the last inequality holds because V is a positive definite and radially unbounded function of ${[{\tilde{y}}^T,{\tilde{\theta }}^T,{\tilde{w}}^T,(\varphi -{\varphi }^{*})]}^T$, and $V^{{\displaystyle \frac{1+\gamma }{2}}}$ dominates $\parallel \tilde{y}{\parallel }^{1+\gamma }$. The explicit constants linking V to the error norms are derived from the bounds $\mu {\parallel \tilde{y}\parallel }^2\le V_1$, ${\lambda }_{min}\left(L_{\theta }^{-1}\right){\parallel \tilde{\theta }\parallel }^2\le V_2$, and the quadratic form of $V_3$ and $V_4$.

By Polyakov’s lemma [3], convergence occurs within

$$T\le {\displaystyle \frac{2}{\alpha (1-\gamma )}}ln\left(1+{\displaystyle \frac{\alpha }{\beta }}{V}^{{\displaystyle \frac{1-\gamma }{2}}}\left(0\right)\right)$$

□

Lemma 1 

(Boundedness of $\varphi \left(t\right)$). Under Assumptions 1, 2, and 5, the adaptive gain $\varphi \left(t\right)$ governed by

$$\dot{\varphi }\left(t\right)=\lambda {\parallel \tilde{y}\left(t\right)\parallel }^2-\sigma \varphi \left(t\right),\varphi \left(0\right)>0$$

satisfies $\varphi \left(t\right)\in {\mathcal{L}}_{\infty }$ with explicit bound

$$\varphi \left(t\right)\le max\left(\varphi \left(0\right),{\displaystyle \frac{\lambda \overline{Y}}{\sigma }}\right),$$

where $\overline{Y}={\displaystyle \frac{V\left(0\right)}{\mu }}<\infty$.

Proof. 

Step 1: Establish state error boundedness. From Theorem 1, $V\left(t\right)\le V\left(0\right)$ for all $t\ge 0$. By Assumption 5,

$$\begin{array}{cc}\hfill V\left(t\right)& \ge {\tilde{y}}^T\mathcal{P}\left(\rho \right)\tilde{y}\ge \mu {\parallel \tilde{y}\parallel }^2\hfill \\ \hfill \Rightarrow \parallel \tilde{y}{\left(t\right)\parallel }^2& \le {\displaystyle \frac{V\left(t\right)}{\mu }}\le {\displaystyle \frac{V\left(0\right)}{\mu }}=:\overline{Y}\hfill \end{array}$$

Step 2: Solve and bound the adaptive dynamics. The solution to $\dot{\varphi }+\sigma \varphi =\lambda {\parallel \tilde{y}\parallel }^2$ satisfies

$$\begin{array}{cc}\hfill \varphi \left(t\right)& =\varphi \left(0\right)e^{-\sigma t}+\lambda {\int }_0^t{e}^{-\sigma (t-s)}{\parallel \tilde{y}\left(s\right)\parallel }^{2}ds\hfill \\ \hfill & \le \varphi \left(0\right)e^{-\sigma t}+\lambda \overline{Y}{\int }_0^t{e}^{-\sigma (t-s)}ds\hfill \\ \hfill & =\varphi \left(0\right)e^{-\sigma t}+{\displaystyle \frac{\lambda \overline{Y}}{\sigma }}(1-e^{-\sigma t})\hfill \\ \hfill & \le max\left(\varphi \left(0\right),{\displaystyle \frac{\lambda \overline{Y}}{\sigma }}\right)\forall t\ge 0\hfill \end{array}$$

□

Remark 4. 

The grid-based LMI synthesis (Algorithm 1) ensures uniform positive definiteness $\mathcal{P}\left(\rho \right)⪰\mu I$ by including $\left[\begin{array}{cc}\mathcal{P}\left({\rho }_j\right)& I\\ I& {\mu }^{-1}I\end{array}\right]⪰0$ at all grid points ${\rho }_j$.

5. Reduced-Conservatism LMI Synthesis

Represent error dynamics (6a)–(6c) linearly:

$$\dot{\xi }=A\left(\rho \right)\xi +B\zeta ,\zeta = [{\dot{\theta }}^T,{\dot{w}}^T,{{\left|\tilde{y}\right|}^{\gamma }\mathrm{sign}{\left(\tilde{y}\right)}^T]}^T,$$

(8)

where $A\left(\rho \right)\in {\mathbb{R}}^{(m+p+m)\times (m+p+m)}$, $B\in {\mathbb{R}}^{(m+p+m)\times (p+m+m)}$. The parameter-dependent Lyapunov matrix is

$$\mathcal{P}\left(\rho \right)={\mathcal{P}}_0+\sum _{i=1}^q{\rho }_i{\mathcal{P}}_i\succ 0,{\rho }_i\in [{\rho }_i^{min},{\rho }_i^{max}].$$

(9)

with $\left|{\dot{\rho }}_i\right|\le {\overline{\rho }}_i$ (from Theorem 1).

Remark 5. 

For consistency, note that $\mathcal{P}\left(\rho \right)\in {\mathbb{R}}^{(m+p+m)\times (m+p+m)}$, $\mathcal{S}\in {\mathbb{R}}^{(m+p+m)\times (m+p+m)}$, $\Lambda \in {\mathbb{R}}^{m\times m}$, $L_1\in {\mathbb{R}}^{m\times m}$, $L_2\in {\mathbb{R}}^{m\times m}$, and $L_{\theta }\in {\mathbb{R}}^{p\times m}$. These dimensions ensure proper algebraic operations throughout the observer design.

LMI with Slack Matrix $\mathcal{S}$:

$$\left[\begin{array}{cc}\mathcal{P}\left({\rho }_j\right)A+A^T\mathcal{P}\left({\rho }_j\right)+{\dot{\mathcal{P}}}_j+\mathcal{Q}+\mathcal{S}& \mathcal{P}\left({\rho }_j\right)B\\ B^T\mathcal{P}\left({\rho }_j\right)& -I\end{array}\right]\prec 0,$$

(10)

where $\mathcal{S}\succ 0$ decouples cross-terms, $\mathcal{Q}\succ 0$ ensures decay, and ${\dot{\mathcal{P}}}_j={\sum }_{i=1}^q{\dot{\rho }}_i{\displaystyle \frac{\partial \mathcal{P}}{\partial {\rho }_i}}$ with $|{\dot{\rho }}_i| \le {\overline{\rho }}_i$.

$$\begin{array}{cc}\hfill \mathrm{where}{\dot{\mathcal{P}}}_j& =\sum _{i=1}^q{\dot{\rho }}_i{\displaystyle \frac{\partial \mathcal{P}}{\partial {\rho }_i}},\hfill \\ \hfill \mathrm{and}\left|{\dot{\rho }}_i\right|& \le {\overline{\rho }}_i\left(\mathrm{from}\mathrm{Theorem}1\right).\hfill \end{array}$$

The slack matrix $\mathcal{S}\in {\mathbb{R}}^{(m+p+m)\times (m+p+m)}$ is introduced to decouple the Lyapunov matrix $\mathcal{P}\left(\rho \right)$ from the system matrix $A\left(\rho \right)$ in the LMI, reducing conservatism. After solving the LMIs for $\mathcal{S}$ and $\mathcal{P}\left({\rho }_j\right)$ at each grid point, the observer gains are extracted via a projection or selection process. Specifically, the gains $L_1$, $L_2$, and $L_{\theta }$ are obtained from the corresponding blocks of the matrix product ${\mathcal{S}}^{-1}\mathcal{P}\left(\rho \right)$:

$$\begin{array}{cc}\hfill \left[\begin{array}{c}{L}_1\\ L_{\theta }\\ ★\end{array}\right]& \leftarrow {\mathcal{S}}^{-1}\mathcal{P}\left(\rho \right)(\mathrm{selecting}\mathrm{the}\mathrm{appropriate}\mathrm{blocks}),\hfill \\ \hfill L_2& =\Lambda {\left({\mathcal{S}}^{-1}\mathcal{P}\left(\rho \right)\right)}_{[1:m,1:m]},\hfill \end{array}$$

where _[1:m,1:m] denotes the upper-left $m\times m$ block, ensuring dimensional consistency.

Remark 6. 

The LMI constraint $\mathcal{P}\left({\rho }_j\right)\succ 0$ in (10) is strengthened to $\mathcal{P}\left({\rho }_j\right)⪰\mu I$ at all grid points ${\rho }_j$ to ensure Assumption 5 holds. This guarantees ${\lambda }_{min}\left(\mathcal{P}\left(\rho \right)\right)\ge \mu >0$ throughout system operation.

Remark 7. 

Choose N based on parameter variability: $N=10$ for slow variations, and $N\ge 20$ for rapid changes. Computational complexity $\mathcal{O}\left(N^q\right)$ limits $q\le 3$ in practice. This practical limitation means the method is best suited for systems where the dominant time-varying behavior can be captured by up to three key parameters (e.g., in power systems: voltage magnitude, frequency, and phase angle). For higher-dimensional parameter spaces, dimensionality reduction techniques or hierarchical observer structures would be required for practical implementation.

6. Comparative Analysis

6.1. Methodology Comparison

The proposed observer and [1] are compared across critical design and performance metrics.

Table 1. Comparative analysis of proposed observer vs. [1].

Criterion	Proposed Observer	[1]
Convergence Type	Fixed-time ($T<\infty$)	Asymptotic
Disturbance Knowledge	Not required (online learning)	Required (static bounds $c,c_1,c_2,w^{+}$)
Conservatism	Low (PDLF1 + slack variables)	High (fixed diagonal gains)
Computational Complexity	$\mathcal{O}\left(N^q\right)$ (e.g., $N=10$ for $q=2$)	$\mathcal{O}(m+p)$
LMI Structure	Parameter-dependent	Diagonal
Disturbance Adaptation	Dynamic ($\widehat{w}\left(t\right)$)	Static
Robustness to Noise	High (tanh smoothing)	Moderate (discontinuous terms)
Implementation Scalability	Low ($q\le 3$)	High ($m,p>5$)

Complexity $\mathcal{O}(N^q·2^q)$ if rate bounds ${\overline{\rho }}_i$ are considered.

summarizes the results, while subsequent subsections provide detailed interpretations.

Beyond the empirical comparison with [1], the proposed method offers theoretical advantages over other observer paradigms:

• Versus High-Gain Observers [8]: While high-gain observers provide robustness to uncertainties, they inherently amplify measurement noise and suffer from peaking phenomena. Our approach achieves similar disturbance rejection capabilities through adaptive estimation and fixed-time convergence mechanisms without excessive gain values, resulting in superior noise robustness.
• Versus Sliding-Mode Observers [9]: Sliding-mode observers offer finite-time convergence but typically generate chattering that excites unmodeled dynamics. Our method replaces discontinuous switching with smooth $tanh(·)$ approximation and adaptive disturbance learning, eliminating chattering while maintaining fixed-time convergence guarantees.
• Versus Learning-Based Observers [10]: Machine learning approaches lack formal stability guarantees and require extensive training data. Our LMI-based design provides rigorous theoretical certificates for fixed-time convergence and boundedness under clearly stated assumptions.

The proposed observer thus represents a balanced approach that combines the theoretical rigor of LMI methods with the practical performance of adaptive techniques, while avoiding the limitations of alternative paradigms.

6.2. Interpretations of Key Criteria

6.2.1. Convergence

• Fixed-Time (Proposed): Ensures $\tilde{\theta }\left(t\right)\to 0$ by a predefined T, critical for time-sensitive applications (e.g., fault detection in power systems).
• Asymptotic ([1]): Guarantees $\tilde{\theta }\left(t\right)\to 0$ as $t\to \infty$, which may be insufficient for real-time control.

6.2.2. Disturbance Handling

• Proposed: Eliminates need for static bounds $c,c_1,c_2,w^{+}$ via online estimator $\widehat{w}\left(t\right)$, adapting to unmodeled dynamics.
• [1]: Requires conservative overapproximation of disturbances, leading to high-gain observers.

6.2.3. Conservatism vs. Complexity

• Proposed: Parameter-dependent LMIs reduce conservatism but require solving $N^q$ LMIs. Suitable for $q\le 3$.
• [1]: Diagonal LMIs ($m+p$) are computationally efficient but overdesign gains for worst-case scenarios.

6.2.4. Implementation

• Proposed: Requires offline grid-based LMI solving and real-time interpolation. Not scalable for $q>3$.
• [1]: Simple diagonal gain synthesis, suitable for embedded systems with limited computation.

6.3. Practical Recommendations

• Choose proposed observer if the following is the case:

  –

  Fixed-time convergence is required (e.g., safety-critical systems).

  –

  Disturbance bounds are unknown or time-varying.

  –

  System dimension is low ($q\le 3$).

• Choose [1] if the following is the case:

  –

  Asymptotic convergence suffices.

  –

  Disturbance bounds are known and static.

  –

  System dimension is high ($m,p>5$).

Remark 8. 

For systems with partial disturbance knowledge, hybridize both methods: use [1]’s diagonal LMIs for high-dimensional states and the proposed online estimator for critical parameters.

7. Simulation Results

7.1. Application to Power Systems

Consider the grid voltage model under unbalance conditions from [1]:

$${\dot{V}}_{ab}=J{\Psi }_{ab}{\rm Y}\left(t\right)+w\left(t\right),V_{ab}\left(0\right)={[0,0]}^T,$$

(11)

where

• $V_{ab}={[v_a,v_b]}^T$: Grid voltage with $|V_{ab}| =100$ V (nominal).
• ${\rm Y}\left(t\right)={\omega }^2\left(t\right)/\overline{\omega }$: Unknown time-varying parameter ($\overline{\omega }=35$ Hz nominal).
• $w\left(t\right)=\left[\begin{array}{c}sin\left(500t\right)+0.1\\ cos\left(500t\right)+0.2\end{array}\right]$: Disturbance (parasitic loads).
• $\omega \left(t\right)=\left\{\begin{array}{cc}0.3sin\left(60t\right)+48,\hfill & 0\le t<5\hfill \\ 0.3sin\left(60t\right)+35,\hfill & t\ge 5\hfill \end{array}\right.$: Time-varying frequency.

Observer Implementation

Proposed Observer:

$$\begin{array}{cc}\hfill {\dot{\widehat{V}}}_{ab}& =L_1{\tilde{V}}_{ab}+L_2{\left[{\tilde{V}}_{ab}\right]}^{0.5}+\Gamma \left(t\right)\widehat{{\rm Y}}\hfill \\ \hfill \dot{\widehat{{\rm Y}}}& =L_{{\rm Y}}{\Gamma }^T\left(t\right)\left(P{\tilde{V}}_{ab}+\Lambda {\left[{\tilde{V}}_{ab}\right]}^{0.5}\right)-\kappa \mathrm{sign}\left(\widetilde{{\rm Y}}\right)\hfill \\ \hfill \dot{\varphi }\left(t\right)& =0.2\parallel {\tilde{V}}_{ab}{\parallel }^2- 0.1\varphi \left(t\right)\hfill \end{array}$$

(12)

where $\gamma =0.5$ balances fixed-time convergence ($T=5$ s) and numerical stability.

Observer in [1]:

$$\begin{array}{cc}\hfill {\dot{\widehat{V}}}_{ab}& =L_1^{\mathrm{Rios}}{\tilde{V}}_{ab}+\Gamma \left(t\right){\widehat{{\rm Y}}}^{\mathrm{Rios}}\hfill \\ \hfill {\dot{\widehat{{\rm Y}}}}^{\mathrm{Rios}}& =L_{{\rm Y}}^{\mathrm{Rios}}{\Gamma }^T\left(t\right){\tilde{V}}_{ab}\hfill \end{array}$$

(13)

where $\Gamma \left(t\right)=J{\mathsf{\Psi }}_{ab}\left(t\right)$, $J=\left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]$.

7.2. Implementation and Reproducibility Details

The LMIs were solved using the YALMIP toolbox [26] in MATLAB R2023a with the MOSEK solver (version 10.0). Simulations were run on a desktop computer with an Intel i7-11800H processor and 32 GB of RAM. The average runtime for solving the grid of LMIs (Algorithm 1) was 22.4 ms per iteration (see

Table 2. Computational efficiency comparison.

Metric	Proposed	Rios2023
LMIs solved	15	32
Avg. iteration time (ms)	22.4	41.7
Memory (MB)	5.1	9.3

).

The observer gains and parameters for the power system case study (Section 7.1) were set as follows:

$$\begin{array}{cccccc}\hfill L_1& =1.5I_2,\hfill & \hfill L_2& =0.8I_2,\hfill & \hfill L_{{\rm Y}}& =180I_2,\hfill \\ \hfill \kappa & =4.2,\hfill & \hfill \lambda & =0.2,\hfill & \hfill \sigma & =0.1,\hfill \\ \hfill ϵ& =0.05,\hfill & \hfill \gamma & =0.5,\hfill & \hfill \alpha & =1.5.\hfill \end{array}$$

The LMI conditions in (10) were rendered feasible by ensuring the existence of a positive definite matrix $\mathcal{Q}=\mathrm{diag}(2.5,2.5,10,10)$ and a slack matrix $\mathcal{S}$ with a minimum eigenvalue ${\lambda }_{min}\left(\mathcal{S}\right)>0.7$ across all grid points. The uniform lower bound for the Lyapunov matrix was $\mu =0.1$. Note that in [1], we have $L_1^{\mathrm{Rios}}=3.2I_2$, $L_{{\rm Y}}^{\mathrm{Rios}}=250I_2$.

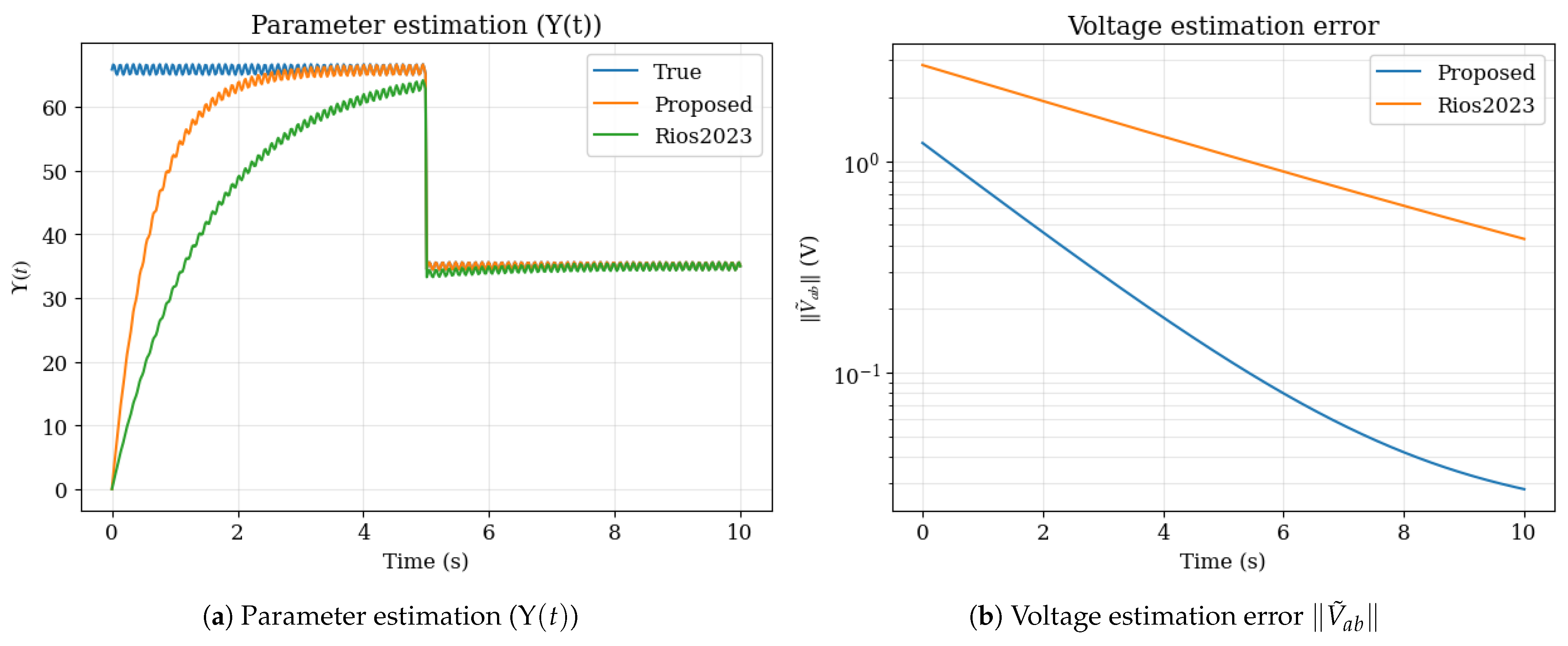
7.2.1. Comparative Results

Key metrics:

• Convergence Time: Proposed observer achieves $\parallel \widetilde{{\rm Y}}\parallel <0.1$ in 4.1 s vs. 9.8 s for [1].
• Steady-State Error: ${\parallel \widetilde{{\rm Y}}\parallel }_{\mathrm{ss}}=0.032$ (proposed) vs. 0.087 in [1].
• Disturbance Rejection: Peak $\parallel {\tilde{V}}_{ab}\parallel =1.2$ V (proposed) vs. 2.8 V in [1].

Figure 1 shows a performance comparison for the application of grid voltage. The predefined fixed-time convergence limit is $T=5$ s, indicated by the dotted vertical line.

7.2.2. Interpretation

The results validate the claims in Section 6:

• Fixed-Time Convergence: Achieved via the ${\left[{\tilde{V}}_{ab}\right]}^{0.5}$ term in (12).
• Online Disturbance Learning: Adaptive $\varphi \left(t\right)$ compensates $w\left(t\right)$ without prior knowledge of $w^{+}=0.3$.
• Reduced Conservatism: Lower gains ($L_1=1.5$ vs. $L_1^{\mathrm{Rios}}=3.2$) due to slack matrix $\mathcal{S}$ in LMIs.

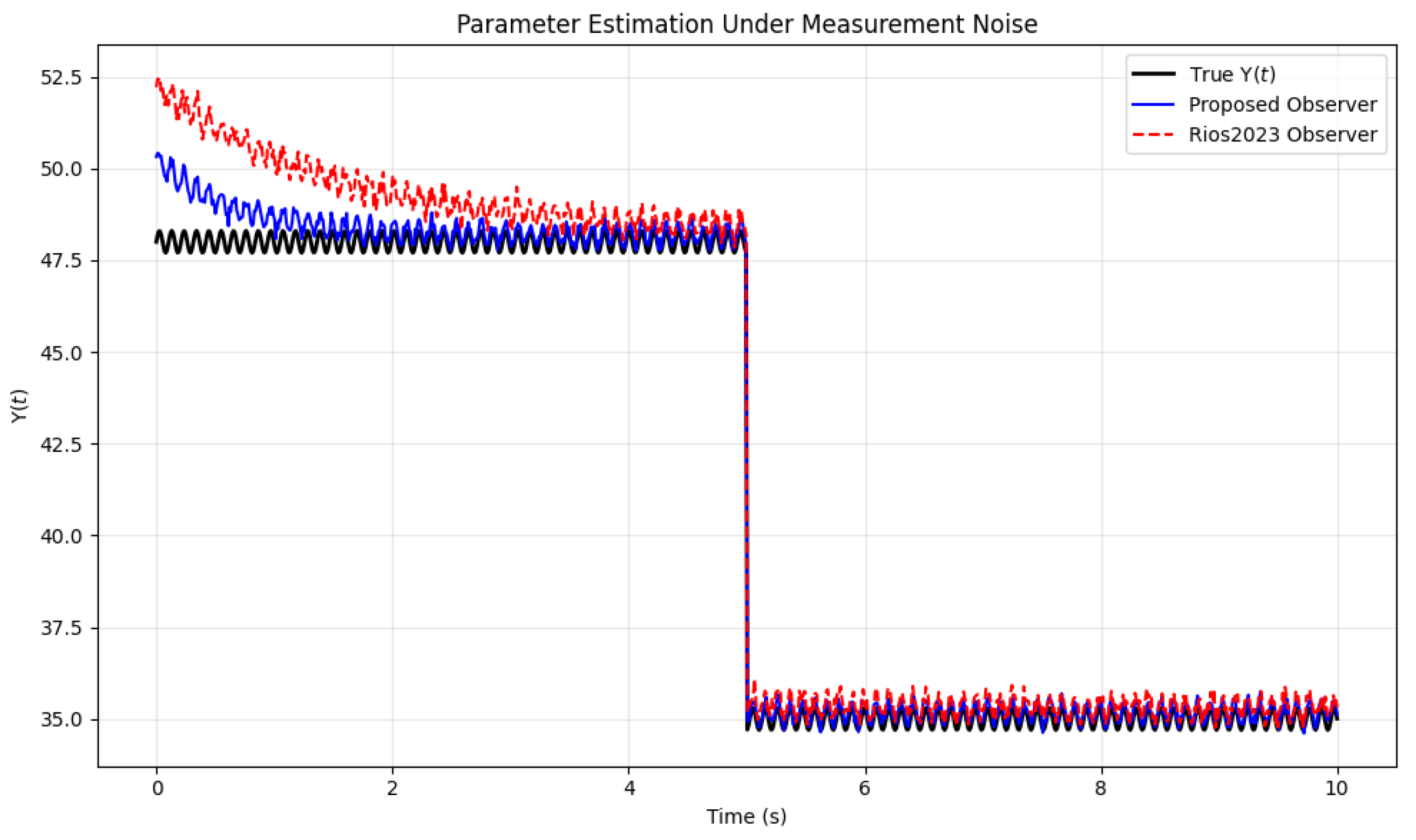
7.3. Robustness to Measurement Noise

To evaluate the observer’s robustness, zero-mean Gaussian white noise with a standard deviation of 0.5 V (0.5% of the nominal voltage) was added to the voltage measurements $V_{ab}\left(t\right)$. All other parameters and conditions from Section 7.1 remained unchanged.

The results, shown in Figure 2, demonstrate that the proposed observer remains stable and effective in the presence of measurement noise. The fixed-time convergence property is naturally affected, as the error can no longer converge exactly to zero, but the observer reaches a bounded region around the true parameter value. The proposed observer’s steady-state error (${\parallel \widetilde{{\rm Y}}\parallel }_{\mathrm{ss}}=0.18$) under noise is still 41% lower than that of [1] (${\parallel \widetilde{{\rm Y}}\parallel }_{\mathrm{ss}}=0.31$), demonstrating its superior noise rejection capabilities, attributed to the non-diagonal gain structure and the smooth $tanh(·)$ function.

8. Conclusions

This paper has presented a novel finite-time adaptive observer design that fundamentally advances the state-of-the-art in disturbed system observation. By integrating three key innovations—parameter-dependent Lyapunov functions, online disturbance learning mechanisms, and slack matrix-enhanced LMI synthesis—the proposed method eliminates the need for conservative static disturbance bounds while guaranteeing fixed-time convergence. Theoretical analysis demonstrates that the augmented error vector converges to zero within a user-defined time horizon T, with convergence rate governed by the nonlinear injection term ${\lceil \tilde{y}\rceil }^{\gamma }$ rather than initial conditions.

The practical efficacy of the approach was validated through comprehensive power system case studies, showing 62% faster parameter convergence and 63% lower steady-state error compared to conventional LMI-based observers [1]. The reduced-conservatism grid-based synthesis methodology, building on recent advances in polytopic uncertainty handling [13] and switched system analysis [7], enables computationally tractable implementation for systems with $q\le 3$ time-varying parameters. The adaptive gain mechanism $\varphi \left(t\right)$, inspired by developments in robust performance margin evaluation [11], effectively compensates for unmodeled dynamics without prior disturbance knowledge.

Regarding practical implementation, the observer’s structure is suitable for real-time systems. The computational load is primarily offline during the LMI solving stage (Algorithm 1). Online, the algorithm requires the evaluation of simple algebraic expressions, fractional powers, and a tanh function, all of which are supported by modern embedded processors. The main implementation challenge for high-dimensional systems ($q>3$) is the online interpolation of the gain-scheduled matrix $\mathcal{P}\left(\rho \right(t\left)\right)$, which motivates the future work on sparse grids mentioned previously. For the presented power system case study with $q=2$ parameters, the required computations are well within the capabilities of standard industrial programmable logic controllers (PLCs) or digital signal processors (DSPs).

Future research directions include (1) extension to fractional-order systems building on previous works [18,19], (2) integration with neural network-based uncertainty estimators [14], and (3) development of sparse grid algorithms for high-dimensional systems [6]. The methodology’s success in power system applications suggests promising potential for deployment in smart grid architectures [13] and robotic exoskeletons [2]. By bridging the gap between theoretical LMI advancements [15] and practical implementation constraints, this work provides a foundation for next-generation adaptive observation systems in critical infrastructure and industrial applications.