Permeability Prediction Using Vision Transformers
Abstract
1. Introduction
2. Related Literature
3. Operational Aspects of Special Core Analysis (SCAL) and Digital Rock Physics
4. Methodology
5. Model Development
5.1. Dataset Description
5.2. Data Preprocessing
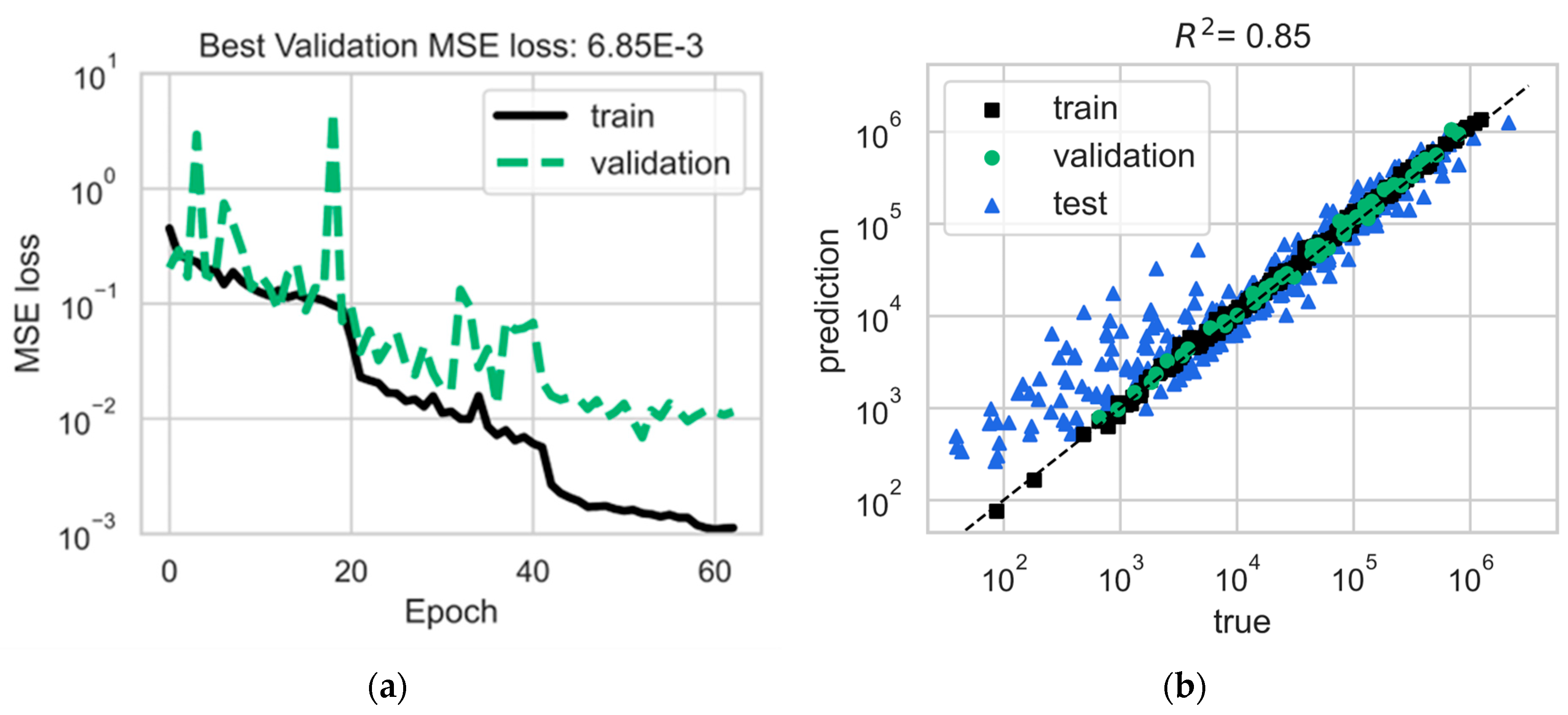
6. Results
Model Structure and Training
7. Discussion
7.1. Ablation Analysis
7.2. The Influence of Pressure Tokens
7.3. The Role of Characteristics in Enhancing Outcomes
7.4. Model’s Limitations in Low-Permeability Regimes and Proposed Improvements
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Da Wang, Y.; Blunt, M.J.; Armstrong, R.T.; Mostaghimi, P. Deep learning in pore scale imaging and modeling. Earth-Sci. Rev. 2021, 215, 103555. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Santos, J.E.; Chang, B.; Gigliotti, A.; Yin, Y.; Song, W.; Prodanović, M.; Kang, Q.; Lubbers, N.; Viswanathan, H. A Dataset of 3D Structural and Simulated Transport Properties of Complex Porous Media. Sci. Data 2022, 9, 579. [Google Scholar] [CrossRef] [PubMed]
- Rahmanifard, H.; Plaksina, T. Application of artificial intelligence techniques in the petroleum industry: A review. Artif. Intell. Rev. 2019, 52, 2295–2318. [Google Scholar] [CrossRef]
- Kuang, L.; Liu, H.; Ren, Y.; Luo, k.; Shi, M.; Su, J.; Li, X. Application and development trend of artificial intelligence in petroleum exploration and development. Pet. Explor. Dev. 2021, 48, 1–14. [Google Scholar] [CrossRef]
- Ng, C.S.W.; Amar, M.N.; Ghahfarokhi, A.J.; Imsland, L.S. A survey on the application of machine learning and metaheuristic algorithms for intelligent proxy modeling in reservoir simulation. Comput. Chem. Eng. 2023, 170, 108107. [Google Scholar] [CrossRef]
- Muther, T.; Syed, F.I.; Dahaghi, A.K.; Negahban, S. Socio-inspired multi-cohort intelligence and teaching-learning-based optimization for hydraulic fracturing parameters design in tight formations. J. Energy Resour. Technol. 2022, 144, 073201. [Google Scholar] [CrossRef]
- Zhang, D.; Lin, J.; Peng, Q.; Wang, D.; Yang, T.; Sorooshian, S.; Liu, X.; Zhuang, J. Modeling and simulating of reservoir operation using the artificial neural network, support vector regression, deep learning algorithm. J. Hydrol. 2018, 565, 720–736. [Google Scholar] [CrossRef]
- Kubeyev, A. Enhancing multi-physics modelling with deep learning: Predicting permeability through structural discontinuities. Eng. Appl. Artif. Intell. 2023, 124, 106562. [Google Scholar] [CrossRef]
- Yang, L.; Fomel, S.; Wang, S.; Chen, X.; Chen, W.; Saad, O.M.; Chen, Y. Porosity and permeability prediction using a transformer and periodic long short-term network. Geophysics 2023, 88, WA293–WA308. [Google Scholar] [CrossRef]
- Meng, Y.; Jiang, J.; Wu, J.; Wang, D. Transformer-based deep learning models for predicting permeability of porous media. Adv. Water Resour. 2023, 179, 104520. [Google Scholar] [CrossRef]
- Zhang, D.; Li, H. Efficient Surrogate Modeling Based on Improved Vision Transformer Neural Network for History Matching. SPE J. 2023, 28, 3046–3062. [Google Scholar] [CrossRef]
- Liu, L.; Santos, J.E.; Prodanović, M.; Pyrcz, M.J. Mitigation of spatial nonstationarity with vision transformers. Comput. Geosci. 2023, 178, 105412. [Google Scholar] [CrossRef]
- Lubbers, N.; Agarwal, A.; Chen, Y.; Son, S.; Mehana, M.; Kang, Q.; Karra, S.; Junghans, C.; Germann, T.C.; Viswanathan, H.S. Modeling and scale-bridging using machine learning: Nanoconfinement effects in porous media. Sci. Rep. 2020, 10, 13312. [Google Scholar] [CrossRef]
- Liu, M.; Kwon, B.; Kang, P.K. Machine learning to predict effective reaction rates in 3D porous media from pore structural features. Sci. Rep. 2022, 12, 5486. [Google Scholar] [CrossRef]
- Eberhard, U.; Seybold, H.J.; Secchi, E.; Jimenez-Martinez, J.; Rühs, P.A.; Ofner, A.; Andrade, J.S., Jr.; Holzner, M. Mapping the local viscosity of non-Newtonian fluids flowing through disordered porous structures. Sci. Rep. 2020, 10, 11733. [Google Scholar] [CrossRef]
- Kamrava, S.; Sahimi, M.; Tahmasebi, P. Simulating fluid flow in complex porous materials by integrating the governing equations with deep-layered machines. npj Comput. Mater. 2021, 7, 127. [Google Scholar] [CrossRef]
- Graczyk, K.M.; Strzelczyk, D.; Matyka, M. Deep learning for diffusion in porous media. Sci. Rep. 2023, 13, 9769. [Google Scholar] [CrossRef]
- Andrew, M. Permeability prediction using multivariant structural regression. E3S Web Conf. 2020, 146, 04001. [Google Scholar] [CrossRef]
- Abbasi, N. Evaluation of Digital Rock Physics for Routine and Special Core Analysis. In Proceedings of the 76th EAGE Conference and Exhibition 2014, Amsterdam, The Netherlands, 16–19 June 2014; European Association of Geoscientists & Engineers: Utrecht, The Netherlands, 2014; pp. 1–5. [Google Scholar]
- Mahmoud, A.; Gajbhiye, R.; Li, J.; Dvorkin, J.; Hussaini, S.R.; AlMukainah, H.S. Digital rock physics (DRP) workflow to assess reservoir flow characteristics. Arab. J. Geosci. 2023, 16, 248. [Google Scholar] [CrossRef]
- Sadeghnejad, S.; Enzmann, F.; Kersten, M. Digital rock physics, chemistry, and biology: Challenges and prospects of pore-scale modelling approach. Appl. Geochem. 2021, 131, 105028. [Google Scholar] [CrossRef]
- Dash, S.; Shakyawar, S.K.; Sharma, M.; Kaushik, S. Big data in healthcare: Management, analysis and future prospects. J. Big data 2019, 6, 54. [Google Scholar] [CrossRef]
- Guo, Y.; Yang, Z.; Feng, S.; Hu, J. Complex power system status monitoring and evaluation using big data platform and machine learning algorithms: A review and a case study. Complexity 2018, 2018, 8496187. [Google Scholar] [CrossRef]
- Karimpouli, S.; Tahmasebi, P. Segmentation of digital rock images using deep convolutional autoencoder networks. Comput. Geosci. 2019, 126, 142–150. [Google Scholar] [CrossRef]
- Tariq, Z.; Aljawad, M.S.; Hasan, A.; Murtaza, M.; Mohammed, E.; El-Husseiny, A.; Alarifi, S.A.; Mahmoud, M.; Abdulraheem, A. A systematic review of data science and machine learning applications to the oil and gas industry. J. Pet. Explor. Prod. Technol. 2021, 11, 4339–4374. [Google Scholar] [CrossRef]
- Alouffi, B.; Hasnain, M.; Alharbi, A.; Alosaimi, W.; Alyami, H.; Ayaz, M. A systematic literature review on cloud computing security: Threats and mitigation strategies. IEEE Access 2021, 9, 57792–57807. [Google Scholar] [CrossRef]
- Omar, I.A.; Jayaraman, R.; Salah, K.; Simsekler, M.C.E.; Yaqoob, I.; Ellahham, S. Ensuring protocol compliance and data transparency in clinical trials using Blockchain smart contracts. BMC Med. Res. Methodol. 2020, 20, 224. [Google Scholar] [CrossRef]
- Pande, P.K.; Clark, M.B.; Blasingame, T.A.; Doublet, L. Data Acquisition Design and Implementation: Opportunities and Challenges for Effective Programs in Mature Reservoirs. In Proceedings of the SPE Improved Oil Recovery Symposium, Tulsa, OK, USA, 17–20 April 1994; p. SPE-27760. [Google Scholar]
- Temizel, C.; Nabizadeh, M.; Kadkhodaei, N.; Ranjith, R.; Suhag, A.; Balaji, K.; Dhannoon, D. Data-driven optimization of injection/production in waterflood operations. In Proceedings of the SPE Middle East Intelligent Oil and Gas Symposium 2017, Manama, Bahrain, 6–9 March 2017; p. SPE-187468. [Google Scholar]
- Guiltinan, E.; Estrada Santos, J.; Kang, Q.; Cardenas, B.; Espinoza, D.N. Fractures with Variable Roughness and Wettability. Available online: https://digitalporousmedia.org/published-datasets/tapis/projects/drp.project.published/drp.project.published.DRP-314 (accessed on 4 March 2025).
- Xu, R.; Prodanović, M.; Landry, C. Pore-Scale Study of Water Adsorption and Subsequent Methane Transport in Clay in the Presence of Wettability Heterogeneity. Water Resour. Res. 2020, 56, e2020WR027568. [Google Scholar] [CrossRef]
- Daigle, H.; Cook, A.; Fang, Y.; Bihani, A.; Song, W.; Flemings, P.B. Gas-driven tensile fracturing in shallow marine sediments. J. Geophys. Res. Solid Earth 2020, 125, e2020JB020835. [Google Scholar] [CrossRef]
- Gostick, J.T.; Fowler, M.W.; Pritzker, M.D.; Ioannidis, M.A.; Behra, L.M. In-plane and through-plane gas permeability of carbon fiber electrode backing layers. J. Power Sources 2006, 162, 228–238. [Google Scholar] [CrossRef]
- Wark, D.A.; Watson, E.B. Grain-scale permeabilities of texturally equilibrated, monomineralic rocks. Earth Planet. Sci. Lett. 1998, 164, 591–605. [Google Scholar] [CrossRef]
- Blunt, M.J. Multiphase Flow in Permeable Media: A Pore-Scale Perspective; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Ehrenberg, S.N.; Nadeau, P.H. Sandstone vs. carbonate petroleum reservoirs: A global perspective on porosity-depth and porosity-permeability relationships. AAPG Bull. 2005, 89, 435–445. [Google Scholar] [CrossRef]
- Wildenschild, D.; Sheppard, A.P. X-ray imaging and analysis techniques for quantifying pore-scale structure and processes in subsurface porous medium systems. Adv. Water Resour. 2013, 51, 217–246. [Google Scholar] [CrossRef]
- Worthington, P.F. The uses and abuses of the Archie equations, 1: The formation factor-porosity relationship. J. Appl. Geophys. 1993, 30, 215–228. [Google Scholar] [CrossRef]
- Santos, J.E.; Xu, D.; Jo, H.; Landry, C.J.; Prodanović, M.; Pyrcz, M.J. PoreFlow-Net: A 3D convolutional neural network to predict fluid flow through porous media. Adv. Water Resour. 2020, 138, 103539. [Google Scholar] [CrossRef]
- Wang, Y.D.; Chung, T.; Armstrong, R.T.; Mostaghimi, P. ML-LBM: Predicting and accelerating steady state flow simulation in porous media with convolutional neural networks. Transp. Porous Media 2021, 138, 49–75. [Google Scholar] [CrossRef]
- Santos, J.E.; Yin, Y.; Jo, H.; Pan, W.; Kang, Q.; Viswanathan, H.S.; Prodanović, M.; Pyrcz, M.J.; Lubbers, N. Computationally efficient multiscale neural networks applied to fluid flow in complex 3D porous media. Transp. Porous Media 2021, 140, 241–272. [Google Scholar] [CrossRef]
- Röding, M.; Ma, Z.; Torquato, S. Predicting permeability via statistical learning on higher-order microstructural information. Sci. Rep. 2020, 10, 15239. [Google Scholar] [CrossRef]
- Fu, J.; Wang, M.; Chen, B.; Wang, J.; Xiao, D.; Luo, M.; Evans, B. A data-driven framework for permeability prediction of natural porous rocks via microstructural characterization and pore-scale simulation. Eng. Comput. 2023, 39, 3895–3926. [Google Scholar] [CrossRef]
- Karimpouli, S.; Kadyrov, R.; Siegert, M.; Saenger, E.H. Applicability of 2D algorithms for 3D characterization in digital rocks physics: An example of a machine learning-based super resolution image generation. Acta Geophys. 2024, 72, 861–874. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 11–17 October 2021; pp. 10012–10022. [Google Scholar]
- Cao, H.; Wang, Y.; Chen, J.; Jiang, D.; Zhang, X.; Tian, Q.; Wang, M. Swin-unet: Unet-like pure transformer for medical image segmentation. In European Conference on Computer Vision; Springer Nature: Cham, Switzerland, 2022; pp. 205–218. [Google Scholar]
- Hatamizadeh, A.; Tang, Y.; Nath, V.; Yang, D.; Myronenko, A.; Landman, B.; Roth, H.R.; Xu, D. Unetr: Transformers for 3D medical image segmentation. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2022; pp. 574–584. [Google Scholar]
- Tang, Y.; Yang, D.; Li, W.; Roth, H.R.; Landman, B.; Xu, D.; Nath, V.; Hatamizadeh, A. Self-supervised pre-training of swin transformers for 3D medical image analysis. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 20730–20740. [Google Scholar]

| Step | Description |
|---|---|
| Start | Data Collection: DRP 372 Dataset |
| - 217 samples from 125 projects | |
| - Lithologies include subsurface rocks, soils, biofilms, and more | |
| Data Processing | Filtering Data |
| - Select key petrophysical features: single-phase mean free path (MFP), electrical properties (elecuz), maximal inscribed spheres (MIS3D), and others | |
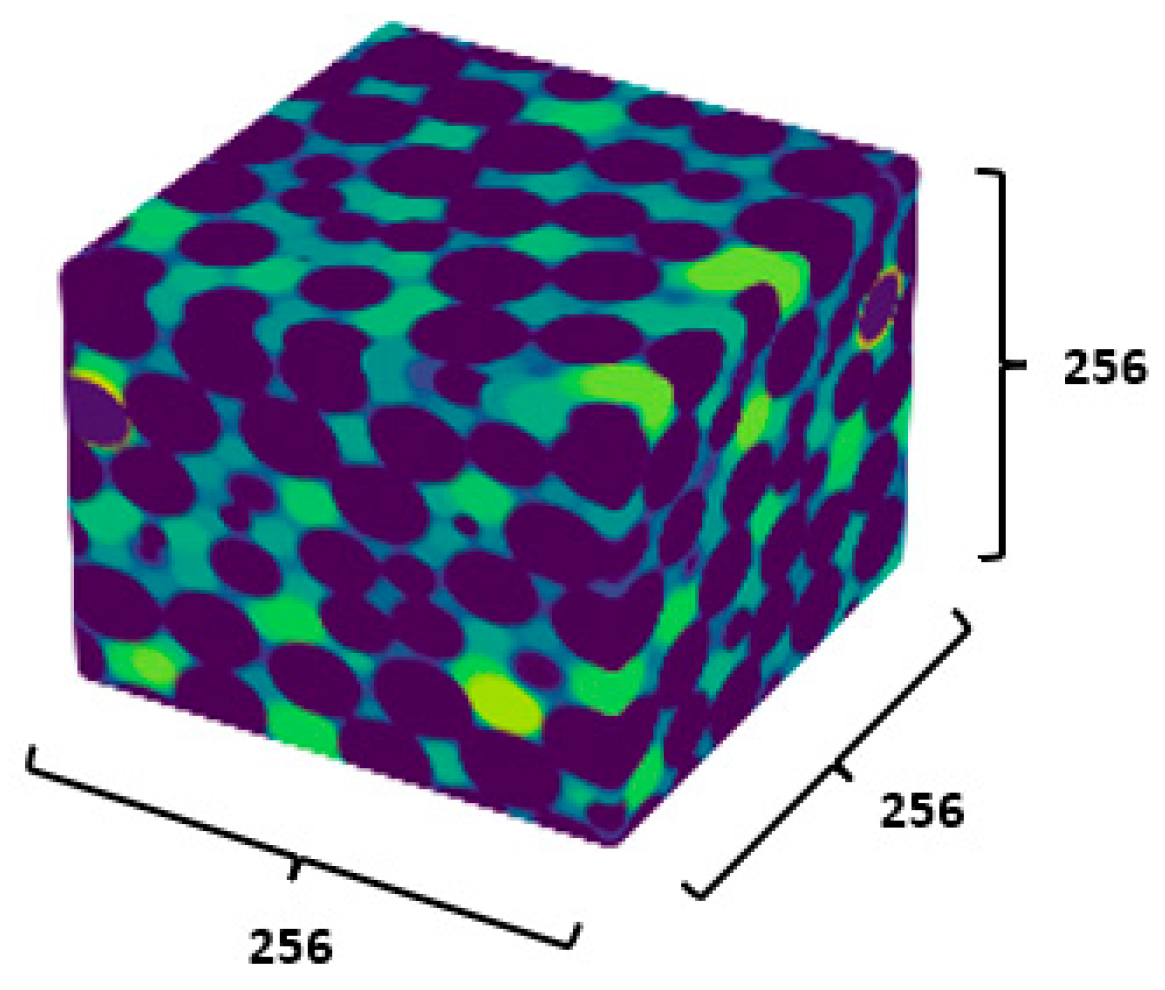
| Feature Extraction | Construct 6-channel 3D Cube |
| - Each feature becomes a 256 × 256 × 256 3D cube, forming input data | |
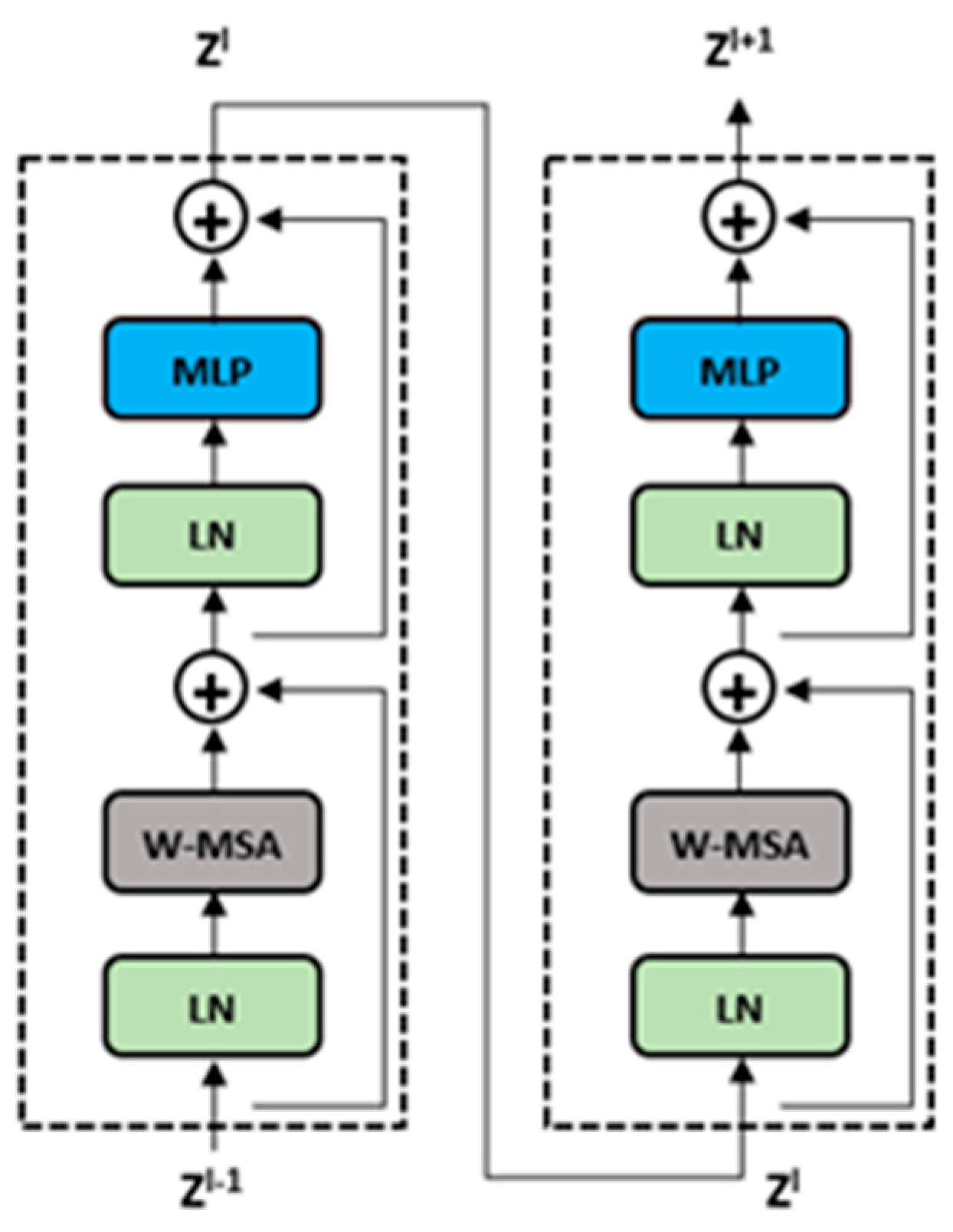
| Model Development | CNN-Transformer Hybrid Architecture |
| - Combine CNN for spatial feature extraction and Transformers for capturing complex dependencies | |
| Model Training & Validation | Training & Validation Sets |
| - 374 samples used for training and validation | |
| Model Testing | Testing Set |
| - Model tested on 193 samples for performance evaluation |
| Category | Examples |
|---|---|
| Sandstone | Leopard, Berea, Bentheimer, Belgian, Fontainebleau |
| Carbonate | Estaillades, Savonnières, Massangis Jaune |
| Shale | Platelets, Kerogen, Vaca Muerta |
| Spherepacks | Soils, Spherepacks, Bidispersed Fractures |
| Process based | Catalyst Layers, Salt, Planetesimals, Vuggy Cores |
| Others | Three-dimensional prints, Meteorites, Biofilms |
| Step | Action | Details |
|---|---|---|
| 1. Feature Pool | Start with all possible features. | The complete set of features available for selection. |
| 2. Trial Feature Set | Sequentially add one feature to the trial set. | Assess each feature’s contribution by adding it to the set. |
| 3. All Features Assessed? | Check if all features have been assessed. | Determine if the current round of feature assessment is complete. |
| 4. No: Return to Trial Feature Set | If all features have not been assessed, loop back and add the next feature to the trial set. | Continue the feature addition process. |
| 5. Yes: Keep the Best Feature | If all features have been assessed, keep the feature that yields the best predictive model. | Select the most significant feature from this round. |
| 6. Prediction Performance | Evaluate the predictive model’s performance using R2 or MSE. | Measure the effectiveness of the current model. |
| 7. Predictive Model | Construct the final predictive model using the optimized set of features. | Build the model with the selected features. |
| 8. Model Assessment Feedback | Assess the model and loop back to start the process again if necessary for further optimization. | Continuously refine the model by reassessing features. |
| MSE | R-Square | |
|---|---|---|
| Current Structure | 6.85 × 10−3 | 0.85 |
| Without Pressure Token | 3.07 × 10−2 | 0.69 |
| Without Additional Features | 8.46 × 10−3 | 0.75 |
| Without Data Augmentation | 9.71 × 10−3 | 0.72 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Temizel, C.; Odi, U.; Li, K.; Liu, L.; Tutun, S.; Santos, J. Permeability Prediction Using Vision Transformers. Math. Comput. Appl. 2025, 30, 71. https://doi.org/10.3390/mca30040071
Temizel C, Odi U, Li K, Liu L, Tutun S, Santos J. Permeability Prediction Using Vision Transformers. Mathematical and Computational Applications. 2025; 30(4):71. https://doi.org/10.3390/mca30040071
Chicago/Turabian StyleTemizel, Cenk, Uchenna Odi, Kehao Li, Lei Liu, Salih Tutun, and Javier Santos. 2025. "Permeability Prediction Using Vision Transformers" Mathematical and Computational Applications 30, no. 4: 71. https://doi.org/10.3390/mca30040071
APA StyleTemizel, C., Odi, U., Li, K., Liu, L., Tutun, S., & Santos, J. (2025). Permeability Prediction Using Vision Transformers. Mathematical and Computational Applications, 30(4), 71. https://doi.org/10.3390/mca30040071







