A PDE-ODE Coupled Model for Biofilm Growth in Porous Media That Accounts for Longitudinal Diffusion and Its Effect on Substrate Degradation

Abstract

We derive a one-dimensional macroscopic model for biofilm formation in a porous medium reactor to investigate the role of longitudinal diffusion of substrate and suspended bacteria on reactor performance. By comparing an existing base model—one without longitudinal diffusion, which was the point of departure for our work, to the new model—we noticed significant changes in system dynamics. Our results suggest that neglecting it can lead to underestimation of quenching length and biofilm accumulation downstream, even in the advection-dominated regime. The effects of attachment and detachment of suspended bacteria on biofilm formation and substrate degradation were also examined. In the one-dimensional model, it was found that attachment has a stronger influence on substrate depletion, which becomes more pronounced as diffusion in the pore space increases.

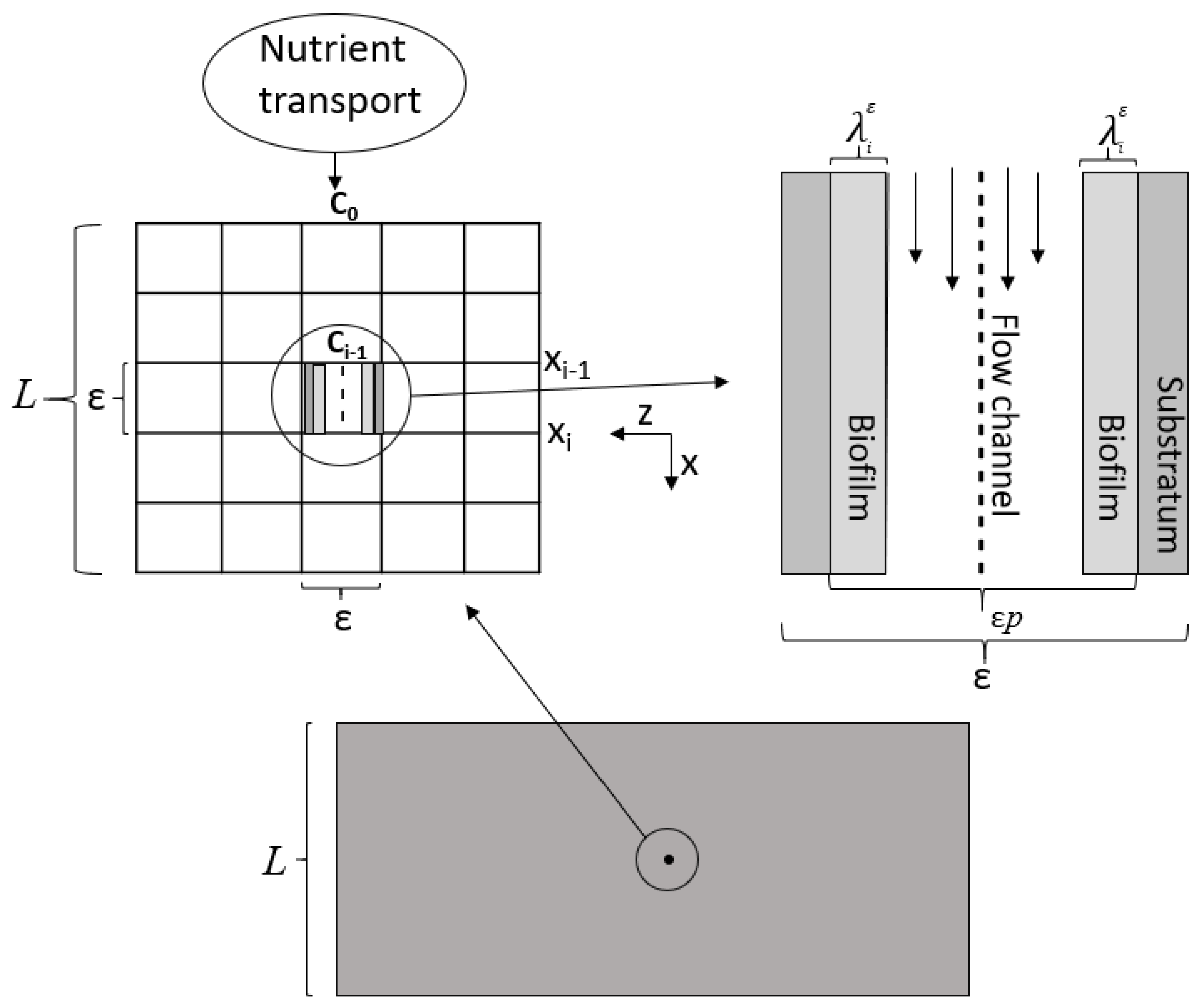
1. Introduction

Bacterial biofilms are a collection of bacteria attached to an immersed surface (also known as substratum). After the initial attachment, they begin producing an extracellular polymeric substance (EPS) in which they are embedded. The EPS provides bacteria protection against mechanical washout and antimicrobials [1].

In a medical context, biofilms are mostly detrimental, e.g., related to dental hygiene and bacterial infections. In environmental engineering they are used in wastewater treatment, soil remediation, and the protection of groundwater [2,3]. They play an important role in bioconversion processes in porous media. This prompts the development of mathematical and computational biofilm growth and accumulation models for such environments. In biofilm systems, growth-limiting nutrients are transported in the domain, which are utilized by bacteria for growth. As the biofilm forms, it interacts with and affects its environment. One such instance are reactive sub-surface bio-barriers: for example, aerobic biofilms have been used to degrade the oxygen in the environment in order to prevent subsequent oxygen dependent reactions that lead to the production and release of harmful contaminants, e.g., sulfuric acids that stem from an oxygen—iron sulfide reaction [4]. In some applications of biofilms in porous media, bioclogging might become relevant, i.e., the phenomenon that pore space is filled by the biofilm, which affects flow conditions and might locally alter subsurface flow paths [5].

Biofilms are naturally multi-scale structures, where the individual bacteria form the microscale (∼1 micron), biofilm colonies form the mesoscale (∼10–1000 microns), and the macroscale (>1 cm) is the scale of biofilm reactors and of natural or engineered systems. Similarly, timescales vary over several orders of magnitude, with biofilm growth on a timescale of days down to reactions in the biofilm in the order of minutes and mass transport and hydrodynamic effects in the order of seconds or less [6].

Several modelling approaches have been used over the years to describe biofilm growth and several review articles have been published on the topic [7,8,9]; we do not attempt a complete overview but restrict ourselves to making the direct connection from the early beginnings of biofilm modeling to the model that is the point of departure for the work that we present. In [10], authors demonstrated that the steady-state biofilm kinetics model is essential in linking substrate flux to the thickness a biofilm can achieve under specific substrate concentrations. The model is a two-point boundary value problem for a 1D steady-state diffusion–reaction equation for the growth-limiting substrate with Monod uptake kinetics. This model still forms one of the foundations of 1D biofilm models, and, extended to an elliptic diffusion–reaction equation, also of many 2D- or 3D spatio-temporal mesoscopic biofilm formation models.

In 1986, Wanner and Gujer presented a 1D multispecies biofilm model [11]. It established as a versatile platform to investigate microbial interactions in fixed biomass universally. The biofilm model contains nonlocal quasilinear hyperbolic balance equations for particulate system components coupled to an ordinary two-point moving boundary value problem for dissolved substrates. This model framework is nowadays routinely used in the engineering literature to study questions in biofilm-based environmental technology. It has been expanded by many authors to include additional biofilm processes. In [11], the biofilm model is coupled with a mass balance for the biofilm reactor and an ad hoc model for detachment, i.e., the transfer of biomass from the biofilm into the aqueous phase. A recent open source implementation of this model framework is the Julia package biofilm.jl [12].

Alternative, mathematically simpler formulations for biofilm reactors with sessile bacteria are the Freter Model, Platte’s 0D biofilm model, and chemostat models with wall attachment, all of which are systems of ordinary differential equations. The Freter model for biofilm formation was originally presented in [13]. In [14], the authors explored the formation of a bacterial community in both Continuous Stirred Tank Reactor (CSTR) and Plug Flow Reactor (PFR) environments. The model assumes an extremely thin biofilm (essentially a monolayer in which substrate gradients can be neglected). The newly introduced attachment process is modeled as competition for space, i.e., there is an upper limit on the amount of biomass that can accumulate per unit attachment surface area. The CSTR and PFR outcomes are quite similar, allowing a general overview of the model’s behavior, independent of the bioreactor type. The model indicates two steady-state scenarios: washout or colonization, where colonization depends on bacterial growth balancing losses from flushing, sloughing, and cell death. The survival threshold for bacteria is typically set by flushing, as genetic control over sloughing is limited. Despite its simplicity, the Freter model serves as a useful reference for biofilm reactor studies, providing a starting point for other modeling approaches. Similar 0D biofilm descriptions (i.e., models without substrate diffusion in the bacterial layer) are assumed in Platte-style 0D biofilm models that do not explicitly resolve the spatial processes in the biofilm, cf. [15,16,17], or in simple models of chemostats with wall attachment that can be found throughout the Mathematical Biology literature, e.g., [18]. These models differ in the algebraic formulation of attachment and detachment terms and whether the model has a complexity that permits insightful analytical treatment or whether it is entirely designed as a simulation tool.

In [19], authors compared Freter’s model for a single substrate and single species, with a model in which wall attached bacteria are described by a dynamically evolving 1D biofilm layer in which substrate diffusion is considered, as well as attachment and detachment. In essence, this is a single species version of the Wanner–Gujer model. This model is a hybrid model, in which an ordinary initial value problem for the reactor mass balance is coupled to a two-point moving boundary value problem for the substrate in the biofilm. Formally, this is still an ODE, the evaluation of the right hand side of which, however, requires the solution of a boundary value problem. Nevertheless, it permits with limitations the application of ODE methods. Despite the added biological, physical, and mathematical complexity, the model dynamics do not significantly change. Stability conditions for washout or persistence resemble, but are not identical to, those for Freter’s model, leading to a non-trivial equilibrium with both suspended and biofilm biomass. Biofilm growth is favored, especially at high flow rates where suspended biomass is prone to washout and substrate supply to the reactor is high. Increasing surface area boosts reactor performance up to a threshold. The research emphasizes the value of simplified models for initial qualitative insights, but calls also for more detailed computational studies. A multi-species reactor model for nitrification with Wanner–Gujer-like biofilm descriptions and attachment and detachment was presented by the same authors in [20]. This study investigates the role of suspended biomass in a biofilm reactor, finding its higher contribution to nutrient removal at low dilution rates. Increased dilution rates and colonisable surface area influence steady-state values, affecting the nitrification process. The study recommends a detailed model if the focus is on specific microbial processes, but suggests a simpler biofilm-only model to study general reactor performance. Despite detachment’s impact on reactor performance, establishing simple correlations remains challenging due to model complexity.

The basis of our research comes from the findings and developments in [21], where the authors simulated biofilm growth in porous media. This is an application and extension of the model in [11]. It involves dividing the overall reactor into a relatively small finite number of compartments (namely 10; the authors noted that there is no visible change when split into 12 compartments), each of which is described by a Wanner–Gujer-like biofilm reactor with well-mixed bulk fluid but not considering suspended biomass and attachment. The outflow of one such compartment is the inflow into the subsequent downstream neighbor, similar to gradostat models. In [22], Gaebler and Eberl took this spatially compartmentalized model of biofilm formation in porous media and extended the idea by transforming a discrete system of individual segments of size $ϵ$ into a continuous system by taking the continuous limit as $ϵ\to 0$ and thus deriving a PDE model in the macroscopic model.

Unlike the 0D Platte-type models, and unlike chemostat models with wall attachment, the models in [21], as well as [22] that is derived from it, consider diffusion into the biofilm, i.e., molecular diffusion perpendicular to the substratum. This is what we refer to here as normal diffusion. In our study, we specifically investigate what we define to be longitudinal diffusion in the main flow direction. Although the authors in [21] discussed such longitudinal diffusion, the diffusion-like behavior they observed resulted from a coarse spatial discretization in the flow direction. This is the well-understood effect of artificial numerical diffusion, an error associated with finite difference approximations of advection terms that arose in their model naturally when describing transport out of one and into the next compartment. The authors explained that if the number of biofilm reactor compartments is increased, mass transport in the reactor becomes purely advective, i.e., the artificial diffusion effect vanishes. As a result, they asserted that their model lacks the capability to effectively simulate longitudinal diffusion in the bulk fluid.

In recent years, probably due to the availability of increasingly powerful desktop computing, it has become an increasingly common practice in biofilm reactor modeling to account for the exchange from biomass between the fixed film and the aquatic phase and to consider also suspended bacteria, both in models that are based on 1D Wanner–Gujer-like biofilm models [19,20,23,24] and also in [12] (which, however, does not account for re-attachment), but also in simpler Platte-style 0D biofilm models that do not explicitly resolve the spatial processes in the biofilm, cf. [15,16,17].

(Re-)Attachment of cells to the biofilm is commonly modeled as a first-order process, proportional to the concentration of bacteria in the aqueous phase. Detachment models for 1D biofilms have been in the literature since at least Wanner and Gujer’s seminal paper [11]. Frequently, a second-order detachment formulation is used, although other descriptions have been proposed for just as long [25,26,27,28,29]. Primarily, these are models of mechanical or passive detachment, caused by external forces. There are relatively few models of chemical or active detachment, say due to nutrient limitations or internally controlled by quorum sensing, as in [24]. The second-order loss term for detachment essentially introduces a logistic nonlinearity and enforces an asymptotically stable steady state. Despite its widespread use over four decades, no convincing physical justification seems to be known, although authors of [25] suggest that second-order detachment can be interpreted in the sense of Poiseuille like bulk flow induced shear forces, whereas first-order is more appropriate for Couette-like bulk flow. Only for very few and very specific experimental systems quantitative relationships between the detachment rate parameter and the reactor and reactor operating condition have been experimentally proposed, e.g., in [30,31]. For porous medium applications, it was shown previously in [22] that their upscaling procedure from the biofilm to the reactor scale, which we also use, maintains first-order detachment, but that second-order mesoscale detachment does not have any effect in the macroscale description that is attained, but this has not been explored further.

In the present study, we extend the earlier advection–reaction model for substrate concentration and suspended and sessile bacteria in a porous medium to a diffusion–advection–reaction model. As a secondary objective of this study, we take a closer look at the role of attachment and detachment in the porous medium biofilm reactor model. This work builds on [21,22].

2. Mathematical Model

2.1. Model Assumptions

We derive a macroscopic mathematical model for biofilm accumulation in a porous medium under the following mesoscale assumptions:

(A1)

We consider a biofilm in a porous medium with a primary flow direction. The flow rate is assumed to be constant throughout.

(A2)

We define the porous medium by parallel non-communicating flow channels of outer width $ϵ$$\left[L\right]$ and inner width $ϵp$, $0<p\le 1$. In flow direction, each channel is compartmentalized into segments of length $ϵ$$\left[L\right]$. That is, these mesoscopic compartments are described as $ϵ\times ϵ$ in size. The porous material is assumed to be homogeneous, thus the size of each compartment is the same.

(A3)

Biofilm can form at the inner walls in each channel segment. We assume this to be symmetric, i.e., the biofilm thickness on both sides is the same, but it may vary along the channel in main flow direction.

(A4)

In each segment of length $ϵ$, the biofilm is assumed to be of homogeneous thickness, but biofilm thickness can vary between segments.

(A5)

The flow rate in each channel, and therefore in each compartment, is the same and remains constant. As the biofilm grows, the flow path becomes narrower, which in turn leads to a faster mean flow velocity.

(A6)

Each compartment is treated as a completely mixed biofilm reactor with attached (sessile) biomass that is not washed out from the reactor, as well as unattached (suspended) biomass and a growth-limiting dissolved substrate.

(A7)

Growth-limiting substrate and suspended biomass are transported by advection throughout the flow channels, i.e., they are moved from one compartment to the next (in the flow direction) at a rate determined by compartment size and flow rate.

(A8)

Growth-limiting substrate and suspended biomass are also transported by diffusion throughout the flow channels. There is exchange between each compartment and its upstream and downstream neighbors at a rate proportional to the difference in concentration.

(A9)

Biomass growth, for both attached and unattached bacteria, is controlled by Monod kinetics based on the availability of substrate. If substrate is available in abundance, biofilm growth proceeds at approximately a constant rate (zeroth-order kinetics limit), whereas if substrate becomes limited, biofilm growth is approximately proportional to the substrate concentration (first-order kinetics limit).

(A10)

Uptake of substrate by bacteria is proportional to bacterial growth rate.

(A11)

Substrate diffuses in the biofilm, normal to the main flow direction.

(A12)

There is exchange of biomass between the sessile and the suspended subpopulations by detachment and attachment. Bacteria detached from the biofilm are assumed to join the suspended subpopulation and suspended bacteria attaching to the biofilm become sessile.

(A13)

Attachment of biomass to the substratum and attachment of biomass to an existing biofilm colony are considered the same process.

Most assumptions here are taken from [22,32], the compartmentalization in the main-flow direction and treatment of each compartment as a biofilm reactor is also from [21]. Newly added here is Assumption (A8), which is the point of departure of our study and the main focus point. Below we formulate the mesoscopic compartment model and then obtain the macroscopic model by shrinking the compartment size $ϵ$ to 0, i.e., we shrink each compartment to a point; see also Figure 1.

2.2. Governing Equations

Substrate Flux Between the Aqueous Phase and the Biofilm

Inside the biofilm the substrate is transported by Fickian diffusion normal to the main flow direction. It is consumed by bacteria for growth. Invoking the usual time-scale argument in biofilm modeling, we assume that substrate diffusion and utilization are significantly faster than biofilm growth, enabling a quasi-steady-state assumption for the substrate [6]. We let ${\lambda }^{ϵ}$$\left[L\right]$ represent the thickness of the biofilm, then the substrate concentration $c\left(z\right)$$[M·L^{-2}]$ in the biofilm is given by the solution of

$$\underset{\left(\mathrm{A}11\right) \mathrm{normal} \mathrm{diffusion}}{\underbrace{D_m{\displaystyle \frac{d^{2}c}{d{z}^2}}}}=\underset{\left(\mathrm{A}10\right) \mathrm{substrate} \mathrm{uptake}}{\underbrace{{\displaystyle \frac{X_{\infty }}{Y_{\lambda }}}f\left(c\right)}},0<z<{\lambda }^{ϵ},{\displaystyle \frac{dc}{dz}}\left(0\right)=0,c\left({\lambda }^{ϵ}\right)=C,$$

(1)

where C$[M·L^{-2}]$ is the substrate concentration in the completely mixed aqueous phase, $D_m$$[L^2·T^{-1}]$ is the diffusion coefficient of substrate in the biofilm, $X_{\infty }$$[M·L^{-2}]$ is the biomass density in the biofilm, $Y_{\lambda }$ [-] is the yield coefficient that indicates the amount of biomass produced from a mass unit of substrate, and $f\left(c\right)$$\left[T^{-1}\right]$ is the growth rate of the bacteria. Following Assumption (A9), we have

$$f\left(c\right)={\displaystyle \frac{{\mu }_{\lambda }c}{{\kappa }_{\lambda }+c}},$$

(2)

where ${\mu }_{\lambda }$$\left[T^{-1}\right]$ is the maximum specific growth rate, ${\kappa }_{\lambda }$$[M·L^{-2}]$ is the half-saturation concentration.

The substrate flux into the biofilm from the aqueous phase, $J^{ϵ}$$[M·L^{-1}·T^{-1}]$, is thus computed from $c\left(z\right)$ as

$$J^{ϵ}(C,{\lambda }^{ϵ})=D_m{\displaystyle \frac{dc}{dz}}\left({\lambda }^{ϵ}\right)={\displaystyle \frac{X_{\infty }}{Y_{\lambda }}}\underset{0}{\overset{{\lambda }^{ϵ}}{\int }}f\left(c\left(z\right)\right)dz.$$

(3)

2.3. Mesoscopic Biofilm Model in the Pore Space

The biofilm thickness in the ith compartment is determined from a mass balance, accounting for inflow, outflow, biofilm growth, detachment and (re-)attachment of bacteria. We let ${\lambda }_i^{ϵ}$$\left[L\right]$, $C_i$$[M·L^{-2}]$, $U_i$$[M·L^{-2}]$ be the biofilm thickness, the substrate concentration in the aqueous phase, and the concentration of suspended bacteria in the ith compartment, respectively. The function $c_i\left(z\right),0<z<{\lambda }_i^{ϵ}$, denotes the substrate concentration in the biofilm in the ith compartment.

Biofilm thickness in the ith compartment is then given by

$$ϵX_{\infty }{\displaystyle \frac{d{\lambda }_i^{ϵ}}{dt}}=ϵX_{\infty }\underset{\left(\mathrm{A}9\right) \mathrm{biofilm} \mathrm{growth}}{\underbrace{\underset{0}{\overset{{\lambda }_i^{ϵ}}{\int }}f\left(c_i\left(z\right)\right)dz}}-\underset{\left(\mathrm{A}12\right) \mathrm{detachment}, \mathrm{attachment}}{\underbrace{ϵX_{\infty }\widehat{d}{\lambda }_i^{ϵ}+\widehat{a}{V}_i{U}_i}}.$$

(4)

Using (3), this is rewritten as

$${\displaystyle \frac{d{\lambda }_i^{ϵ}}{dt}}=\eta J^{ϵ}(C_i,{\lambda }_i^{ϵ})+\widehat{d}{\lambda }_i^{ϵ}+{\displaystyle \frac{\widehat{a}}{ϵX_{\infty }}}{V}_i{U}_i,$$

(5)

where $\eta ={\displaystyle \frac{Y_{\lambda }}{X_{\infty }}}$, and $\widehat{d}$$\left[T^{-1}\right]$ and $\widehat{a}$$\left[T^{-1}\right]$ represent the detachment and attachment rates, respectively.

In the above, $V_i$$\left[L^2\right]$ is the volume of the aqueous phase, i.e., the pore spaces without the biofilm

$$V_i=ϵ(ϵp-2{\lambda }_i^{ϵ}).$$

(6)

We then have the mass balance for the substrate in the aqueous phase of the ith compartment given by

$$\begin{array}{cc}\hfill {\displaystyle \frac{d\left(V_i{C}_i\right)}{dt}}& =\underset{\left(\mathrm{A}7\right) \mathrm{advection}}{\underbrace{ϵQ{C}_{i-1}-ϵQ{C}_i}}+\underset{\left(\mathrm{A}8\right) \mathrm{longitudinal} \mathrm{diffusion}}{\underbrace{D_c{C}_{i+1}+D_c{C}_{i-1}-2D_c{C}_i}}\hfill \\ \hfill & \underset{\left(\mathrm{A}10\right) \mathrm{uptake} \mathrm{by} \mathrm{biofilm} \mathrm{and} \mathrm{suspended} \mathrm{bacteria}}{\underbrace{-2ϵJ_i^{ϵ}(C_i,{\lambda }_i^{ϵ})-{\displaystyle \frac{1}{Y_u}}g\left(C_i\right)U_i{V}_i}}\hfill \end{array}$$

(7)

where $ϵQ$$[L^2·T^{-1}]$ is the flow rate in a channel of thickness $ϵ$. Here, we again model the bacterial growth as in Assumption (A9) using Monod kinetics, i.e.,

$$g\left(C\right)={\displaystyle \frac{{\mu }_{u}C}{{\kappa }_u+C}},$$

(8)

where ${\mu }_u$$\left[T^{-1}\right]$ is the maximum specific growth rate of suspended bacteria and ${\kappa }_u$$[M·L^{-2}]$ is their half-saturation concentration.

To complete the mesoscopic model for the ith compartment, we construct the corresponding mass balance for the suspended bacteria,

$$\begin{array}{c}\hfill {\displaystyle \frac{d\left(V_i{U}_i\right)}{dt}}=\underset{\left(\mathrm{A}7\right) \mathrm{advection}}{\underbrace{ϵQ{U}_{i-1}-ϵQ{U}_i}}+\underset{\left(\mathrm{A}8\right) \mathrm{longitudinal} \mathrm{diffusion}}{\underbrace{D_u{U}_{i+1}+D_u{U}_{i-1}-2D_u{U}_i}}\\ \hfill +\underset{\left(\mathrm{A}12\right) \mathrm{attachment}, \mathrm{detachment}}{\underbrace{2ϵX_{\infty }\widehat{d}{\lambda }_i^{ϵ}-2\widehat{a}{V}_i{U}_i}}+\underset{\left(\mathrm{A}9\right) \mathrm{growth}}{\underbrace{g\left(C_i\right)U_i{V}_i}}.\end{array}$$

(9)

Using (6) we obtain, from (7) and (9),

$$\begin{array}{c}\hfill {\displaystyle \frac{d\left(ϵ[ϵp-2{\lambda }_i^{ϵ}]C_i\right)}{dt}}=ϵQ{C}_{i-1}-ϵQ{C}_i+D_c{C}_{i+1}+D_c{C}_{i-1}\\ \hfill -2D_c{C}_i-2ϵJ_i^{ϵ}(C_i,{\lambda }_i^{ϵ})-{\displaystyle \frac{1}{Y_u}}g\left(C_i\right)U_iϵ[ϵp-2{\lambda }_i^{ϵ}],\end{array}$$

(10)

$$\begin{array}{c}\hfill {\displaystyle \frac{d\left(ϵ[ϵp-2{\lambda }_i^{ϵ}]U_i\right)}{dt}}=ϵQ{U}_{i-1}-ϵQ{U}_i+D_u{U}_{i+1}+D_u{U}_{i-1}\\ \hfill -2D_u{U}_i+2ϵX_{\infty }\widehat{d}{\lambda }_i^{ϵ}-2\widehat{a}ϵ[ϵp-2{\lambda }_i^{ϵ}]U_i+g\left(C_i\right)U_iϵ[ϵp-2{\lambda }_i^{ϵ}].\end{array}$$

(11)

Scaling the biofilm thickness ${\lambda }_i^{ϵ}$ relative to the compartment size $ϵ$, we introduce

$${\lambda }_i:={\displaystyle \frac{{\lambda }_i^{ϵ}}{ϵ}},0\le {\lambda }_i<{\displaystyle \frac{p}{2}}.$$

(12)

If the second inequality is violated, the flow channel is clogged and the model breaks down.

Substituting (12) into (4), (10), and (11), and then dividing by $ϵ$, the system becomes

$$\begin{array}{cc}\hfill {\displaystyle \frac{d\left([p-2{\lambda }_i]C_i\right)}{dt}}=& {\displaystyle \frac{Q{C}_{i-1}-Q{C}_i}{ϵ}}+{\displaystyle \frac{D_c{C}_{i+1}+D_c{C}_{i-1}-2D_c{C}_i}{{ϵ}^2}}\hfill \\ \hfill & -2{\displaystyle \frac{J_i^{ϵ}(C_i,{\lambda }_i^{ϵ})}{ϵ}}-{\displaystyle \frac{1}{Y_u}}g\left(C_i\right)U_i[p-2{\lambda }_i],\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill {\displaystyle \frac{d\left([p-2{\lambda }_i]U_i\right)}{dt}}=& {\displaystyle \frac{Q{U}_{i-1}-Q{U}_i}{ϵ}}+{\displaystyle \frac{D_c{C}_{i+1}+D_c{C}_{i-1}-2D_c{C}_i}{{ϵ}^2}}\hfill \\ & +2X_{\infty }\widehat{d}{\lambda }_i-2\widehat{a}[p-2{\lambda }_i]U_i+g\left(C_i\right)U_i[p-2{\lambda }_i],\hfill \end{array}$$

(14)

$${\displaystyle \frac{d{\lambda }_i}{dt}}=\eta {\displaystyle \frac{J_i^{ϵ}(C_i,{\lambda }_i^{ϵ})}{ϵ}}-\widehat{d}{\lambda }_i+{\displaystyle \frac{\widehat{a}}{X_{\infty }}}[p-2{\lambda }_i]U_i.$$

(15)

2.4. Macroscopic Biofilm Model

The macroscopic model is derived from the mesoscopic model by taking the continuous limit as $ϵ\to 0$ in (13)–(15), shrinking each compartment to a point. As in [22], for the upscaling of the mesoscopic model to the macroscale, the behavior of the detachment and attachment rates $\widehat{d}$ and $\widehat{a}$ as $ϵ\to 0$ is important. We recall the following result from [32], which is proved by a simple application of a comparison Theorem for semilinear two-point boundary value problems.

Lemma 1. 

For Monod kinetics, $J^{ϵ}(C,{\lambda }^{ϵ})=\mathcal{O}\left(ϵ\right)$.

Proposition 1. 

We consider (14), (15) with generic attachment rate $\widehat{a}=\mathcal{O}\left({ϵ}^{n_1}\right)$ and detachment rate $\widehat{d}=\mathcal{O}\left({ϵ}^{n_2}\right)$ with $n_1,n_2\ge 0$. By passing $ϵ\to 0$ to the continuous limit, the macroscopic model becomes

$${\displaystyle \frac{\partial }{\partial t}}\left(\begin{array}{c}(p-2\lambda )C\\ (p-2\lambda )U\\ \lambda \end{array}\right)+{\displaystyle \frac{\partial }{\partial x}}\left(\begin{array}{c}QC-D_c{\displaystyle \frac{\partial C}{\partial x}}\\ QU-D_u{\displaystyle \frac{\partial U}{\partial x}}\\ 0\end{array}\right)=\left(\begin{array}{c}-2J(C,\lambda )-{\displaystyle \frac{[p-2\lambda ]}{Y_u}}g\left(C\right)U\\ 2X_{\infty }d\lambda -2a[p-2\lambda ]U+g\left(C\right)[p-2\lambda ]U\\ \eta J(C,\lambda )-d\lambda +{\displaystyle \frac{a}{X_{\infty }}}[p-2\lambda ]U\end{array}\right),$$

(16)

where $J(C,\lambda ):={lim}_{ϵ\to 0}{\displaystyle \frac{J^{ϵ}(C,{\lambda }^{ϵ})}{ϵ}}$, $a:={lim}_{ϵ\to 0}\widehat{a}$, $d:={lim}_{ϵ\to 0}\widehat{d}$.

Proof. 

For the convective term in (13), we have

$$\underset{ϵ\to 0}{lim}{\displaystyle \frac{C_i-C_{i-1}}{ϵ}}={\displaystyle \frac{\partial C}{\partial x}},$$

and similarly, for the diffusion term,

$$\begin{array}{cc}\hfill \underset{ϵ\to 0}{lim}{\displaystyle \frac{-2D_c{C}_i+D_c{C}_{i+1}+D_c{C}_{i-1}}{{ϵ}^2}}& =\underset{ϵ\to 0}{lim}({\displaystyle \frac{D_c{C}_{i+1}-D_c{C}_i}{ϵ}}-{\displaystyle \frac{D_c{C}_i-D_c{C}_{i-1}}{ϵ}}){\displaystyle \frac{1}{ϵ}}\hfill \\ \hfill & =\underset{ϵ\to 0}{lim}(D_c{\displaystyle \frac{\partial C}{\partial x}}-D_c{\displaystyle \frac{\partial C}{\partial x}}){\displaystyle \frac{1}{ϵ}}\hfill \\ \hfill & =D_c{\displaystyle \frac{\partial C^2}{{\partial }^{2}x}}.\hfill \end{array}$$

The arguments for $U_i$ in (14) are the same.

The flux of substrate into the biofilm is such that

$$J^{ϵ}(C,{\lambda }^{ϵ})=D_c{\displaystyle \frac{dc}{dz}}\left({\lambda }^{ϵ}\right)=\mathcal{O}\left(ϵ\right),$$

per Lemma 1.    □

Remark 1. 

In [32], it was shown for a more involved multi-species/multi-substrate system of which our setting is a simpler special case that the limit of the flux of substrate into the biofilm can be represented by Monod kinetics as

$$J(C,\lambda )={\displaystyle \frac{X_{\infty }}{Y_{\lambda }}}{\displaystyle \frac{{\mu }_{\lambda }C\lambda }{{\kappa }_{\lambda }+C}}.$$

This relationship was also derived as an approximation for the mesoscopic flux under additional conditions with different mathematical arguments in [33,34].

Remark 2. 

Various detachment rates have been explored in different studies, as summarized in [25]. For example, shear-dependent detachment modeled as proposed in [35] behaves similarly to a constant rate. From this, we assume that detachment is linked to the biofilm thickness, so we express it as ${\widehat{d}}_i=d_i$, where $d_i$ is the detachment rate for biofilm species i.

Remark 3. 

Much less is known about attachment rates. So, we take a pragmatic approach and assume that the attachment of suspended biomass is proportional to the amount of suspended biomass in the bulk liquid, given as ${\widehat{a}}_i=a_i$, where $a_i$ is the attachment rate for suspended bacterial species i. Such a first-order attachment model was also used in [19,22,23,24].

To complete the macroscopic model, we specify the initial conditions for C, U, and $\lambda$ as

$$C(0,x)=C_0\left(x\right),U(0,x)=U_0\left(x\right),\lambda (0,x)={\lambda }_0\left(x\right),$$

as well as the boundary conditions for C and U,

$$C(t,0)=C_L\left(t\right),U(t,0)=U_L\left(t\right),{\displaystyle \frac{\partial }{\partial x}}C(t,L)=0,{\displaystyle \frac{\partial }{\partial x}}U(t,L)=0,$$

i.e., Dirichlet conditions upstream and standard outflow conditions downstream, i.e., mass washing out of the domain downstream is assumed to be due to advection only. Certainly, other choices of boundary conditions, such as Danckwerts conditions, would have been possible, depending on the circumstances and the specific model application. Ours mimic, for example, a bioaugmentation application of our model, in which suspended bacteria are added on inflow to establish a microbial community in the reactor, and the substrate supplied might be oxygen which the bacteria require as a growth-limiting oxygen acceptor. In a sandfilter application of our simplified model, the inflow to the reactor contains both a pollutant to be degraded and bacteria that are indigenous to the wastewater to be treated. In both cases the reactor is fed by pumping from a completely mixed reservoir upstream with a constant flow rate.

3. Numerical Simulations

3.1. Implementation

To simulate the stiff PDE-ODE coupled system (16), we used R 4.2.3 [36] and its ReacTran library (version 1.4.3.1) [37]. This required us to re-write (16) in the standard form

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial }{\partial t}}\left(\begin{array}{c}C\\ U\\ \lambda \end{array}\right)& ={\displaystyle \frac{1}{p-2\lambda }}\left({\displaystyle \frac{\partial }{\partial x}}\left(\begin{array}{c}-QC+D_c{\displaystyle \frac{\partial C}{\partial x}}\\ -QU+D_u{\displaystyle \frac{\partial U}{\partial x}}\\ 0\end{array}\right)+\right.\hfill \\ \hfill & \left.\left(\begin{array}{c}-{\zeta }_{\lambda }{\displaystyle \frac{C\lambda }{{\kappa }_{\lambda }+C}}-[p-2\lambda ]{\zeta }_u{\displaystyle \frac{CU}{{\kappa }_u+C}}+2C{\displaystyle \frac{\partial \lambda }{\partial t}}\\ {\mu }_u{\displaystyle \frac{CU}{{\kappa }_u+C}}[p-2\lambda ]+2d{X}_{\infty }\lambda -2aU[p-2\lambda ]+2U{\displaystyle \frac{\partial \lambda }{\partial t}}\\ {\mu }_{\lambda }{\displaystyle \frac{C\lambda }{{\kappa }_{\lambda }+C}}-d\lambda +{\displaystyle \frac{a}{X_{\infty }}}[p-2\lambda ]U\end{array}\right)\right),\hfill \end{array}$$

(17)

by applying the product rule to the term on the left hand side and rearranging, where we define the new parameters,

$${\zeta }_{\lambda }:=2{\displaystyle \frac{X_{\infty }{\mu }_{\lambda }}{Y_{\lambda }}},{\zeta }_u:={\displaystyle \frac{{\mu }_u}{Y_u}}$$

(18)

to simplify notation.

The simulations reported here were executed on a Lenovo P620 workstation under Ubuntu 20.04. All plots were generated in R 4.2.3.

Biofilm process parameter values in

Table 1. Model parameter and their values used in simulations.

Parameter	Symbol	Value	Unit 1
Substrate inflow concentration	$C_0$	1.0	gm−2
Suspended bacteria inflow concentration	$U_0$	0.001	gm−2
Relative biofilm thickness at inflow	${\lambda }_0$	0.0	[-] 2
Biomass density	$X_{\infty }$	104	gm−2
Biofilm uptake rate	${\zeta }_{\lambda }$	105	gm−2d−1
Biofilm half-saturation constant	${\kappa }_{\lambda }$	0.2	gm−2
Biofilm growth rate	${\mu }_{\lambda }$	0.6	d−1
Suspended bacteria uptake rate	${\zeta }_u$	10	d−1
Suspended bacteria half-saturation constant	${\kappa }_u$	0.2	gm−2
Suspended bacteria growth rate	${\mu }_u$	6.0	d−1
Void fraction	p	0.5	[-] 2
Detachment coefficient	d	Varied	d−1
Attachment coefficient	a	Varied	d−1
Flow velocity	Q	Varied	md−1
Substrate diffusion coefficient	$D_c$	Varied	m2d−1
Suspended bacteria diffusion coefficient	$D_u$	Varied	m2d−1
Reactor length	L	Varied	m

¹ [g] is grams, [m] meters, [d] days; ² [-] this parameter is dimensionless.

are assumed with reference to [6]. While parameters in [6] consider [M · L⁻³], our approach follows [M · L⁻²], expressing specific densities with respect to one unit length in the third dimension. Moreover, ref.  [6] does not consider suspended bacteria, only biofilms. We made here the assumption that the corresponding growth rates are comparable, similar to [19]. We set the half-saturation concentrations to be one-fifth of the substrate inflow concentration. This implies that close to the inlet substrate is close to zeroth-order regime (substrate available in abundance), but that further downstream substrate might be limited (i.e., first-order regime). That is, in this setting, neither a zeroth-order nor a first-order growth model throughout is appropriate. The void fraction value is as in [22]. We assume here throughout that the specific growth rate for suspended bacteria is an order of magnitude larger than that of the sessile bacteria to reflect that biofilm bacteria utilize some of their resources for defense mechanisms, which planktonic bacteria do not have to that extent, e.g., for EPS production. The substrate concentration, the concentration of suspended bacteria at inflow, as well as the flow rate are operating conditions.

3.2. Base Case Simulations

To illustrate model behavior, we set out two basic simulations. In the first one, longitudinal diffusion is neglected. This provides the base line for comparison with Model (17) in the focus of our study.

The setting we consider is a clean bed simulation, i.e., a scenario where initially no biofilm is present in the pore space. Biofilm accumulation originates from attachment of suspended bacteria that are added to the system on inflow and subsequent growth. The initial conditions are $C(x,0)=C_0$ [gm⁻²], $U(x,0)=U_0$ [gm⁻²], $\lambda (x,0)=0.0$ [-].

3.2.1. Simulations Without Diffusion

In these simulations, the upstream boundary conditions are $C(t,0)=1.0$ [gm⁻²], $U(t,0)=0.001$ [gm⁻²]. For $D_c=D_u=0$, this is a first-order problem, and no downstream boundary conditions are to be specified. The macroscopic attachment is set to $2.0$ [d⁻¹] and the macroscopic detachment rate is $0.3$ [d⁻¹]. The reactor length is set to $L=1.0$ [m].

An illustrative simulation is documented in Figure 2. Notably, the substrate concentration experiences rapid depletion near the inflow region of the reactor, which is indicative of intense microbial activity occurring within that region where nutrients are plentiful. After 10 time units, which is the time to replace the reactor volume once, with the exception of the first approximately 10% of the reactor length, nutrients are depleted everywhere. Prior to this time point, the substrate concentration declines in the upstream region and then increases downstream, where the substrate initially present has not yet been washed out or consumed. Attachment of suspended bacteria and biofilm formation in the pore space begins immediately in the upstream region. Both biomass fractions grow as they degrade substrate and attain the maximum in the interior of the reactor. As time progresses, the maximum is attained further downstream.

Notably, there is a correspondence between the biofilm thickness and the suspended bacteria concentration profiles. The biofilm exhibits maximal growth within the first half of the reactor before gradually diminishing. This decline can be attributed to the reduced substrate concentrations within the aqueous phase, which results in diminished substrate fluxes into the biofilm. This decline may also be due to the reduced suspended bacteria concentration in the downstream section of the reactor, which allows lesser biomass attachment and thus a smaller biofilm density. In earlier values of t, $t=3.5$ and 4 [d], we see that there is a second growth bump later in the reactor between 0.6 and 0.8 [m]. This is likely due to the fact that once we reach limitation of the substrate for the first time ($t=3.5$ and 4 [d]), the growth of suspended bacteria is limited since there is no more substrate to consume. Further downstream where initially the substrate concentration is not yet limited (signified by the steep substrate gradient), the suspended bacteria are able to grow due to the still better growth conditions.

3.2.2. Simulations with Diffusion

We compare this simulation against one in which a small amount of longitudinal diffusion is added, with $D_c=0.001$ [m²d⁻¹] and $D_u=0.001$ [m²d⁻¹]. The choice $D_c=D_u$ is primarily motivated by the effort to keep the number of degrees of freedom manageable in the absence of additional information. This is still in the heavily advection-dominated regime with a Peclet number of $Pe=QL/D_c=100$. Therefore, the results depicted in Figure 3 are qualitatively rather similar to those in Figure 2, yet there are already some notable quantitative differences that show the effect of even small longitudinal diffusion.

Without diffusion, the initial biofilm growth near the reactor inlet (spanning 0–0.05 [m]), is followed by a slight dip and subsequent biofilm presence downstream that results in a maximum peak around $0.3$ [m]. In contrast, in the simulation with diffusion, the initial growth near the inlet shows slightly greater density nearing that of the following peak. Notably, the biofilm achieves larger densities at earlier times with the presence of diffusion. This indicates a more accelerated growth leading up to $t=10.0$ [d].

The transient substrate trough before the volume is replaced, i.e., while $t<10$, is wider, i.e., the substrate is lower initially in the downstream region before it is depleted and washed out. These effects are a consequence of the slightly increased transport of substrate and bacteria in the flow direction, and may partially also be attributable to the averaging and smoothing effects induced by diffusion. This suggests that as the diffusion coefficient increases, this smoothing effect might become more pronounced.

With diffusion in the system, the suspended bacteria and biofilm density have larger magnitudes at outflow ($L=1.0$ [m]). This outlines the hold that substrate depletion has on the suspended biomass and biofilm growth. Downstream in the reactor, the growth conditions improve and allow for more suspended biomass and biofilm formation as compared to the simulation without diffusion. Biofilm density reflects the concentration of suspended bacteria. This means that a consistent profile in suspended bacteria promotes the ability for consistent attachment of biomass to the biofilm or substratum throughout. Overall, this simulation emphasizes how important a role diffusion can play in biofilm formation and substrate utilization within the reactor, even at small Peclet numbers.

To validate the impact of diffusion further, we conduct another simulation, shown in Figure 4. Here, we increase the diffusion coefficient to $D_c=0.01$ [m²d⁻¹] and $D_u=0.01$ [mm²d⁻¹]. The system is still advection dominated, but less so, as we have $Pe=10$. Again, we observe a shift in the substrate concentration curves as they become more levelled off and flattened compared to the simulations in Figure 2 and Figure 3. This trend is also reflected in the suspended bacteria and biofilm density.

While there is still a dip in the substrate concentration, which indicates a limitation, it becomes much more flattened out compared to the previous simulations. At $t=3.5$ [d], we observe the substrate approaching depletion and yet never completely reaching it. The levelling off of the substrate concentration sag allows greater consistency in growth conditions for the suspended bacteria and biofilm growth.

In this simulation, the initial growth in biofilm density is much larger compared to the previous simulations. This initial growth bump marks the peak density of the simulation. In prior simulations, the biofilm exhibited an initial peak near the reactor inlet, followed by a larger growth bump in which it reached its maximum. Here, the biofilm density peaks near the inlet, it then drops slightly and remains relatively constant throughout the reactor with a minor decrease. This pattern agrees with the behavior of the suspended bacteria, which reaches its maximum and remains relatively constant thereafter.

The suspended bacteria and biofilm density follow from the substrate concentration profile. Although the maximum concentrations of suspended bacteria and biofilm density approximate those of the previous simulations, here, they become much more constant once reaching these maxima. With a higher diffusion coefficient, both the suspended bacteria and the biofilm density maintain relatively constant levels with only a slight drop; in previous simulations, the fluctuations were much more pronounced. This levelling off effect, which is induced by diffusion, provides a more consistent growth profile for the suspended bacteria as well as the biofilm density.

In summary, the inclusion of even very little diffusion ($Pe=100$) in our simulations led to several observations that were not present in the purely convective case. Firstly, as we introduced diffusion, the substrate concentration curves tended to level off and become more consistent, with corresponding trends in the suspended bacteria and biofilm density. This was reinforced when we increased the diffusion coefficient tenfold, still remaining in the advection-dominated regime ($Pe=10$), which might suggest that as the system becomes diffusion dominated, concentration profiles exhibit greater consistency and levelling off. These observations stress the overall impact of diffusion on the model. As the system leans towards a diffusion-dominated regime, it alters the substrate utilization and biofilm formation and changes the overall system behavior.

We next examined the quenching length, i.e., the first location, $x^{*}$, at which substrate becomes depleted, which can be an important design parameter for remediation applications. We investigated how this output parameter depends on the diffusion rate. The results are shown in Figure 5, where we varied the Peclet number within the range $0<Pe<10$. Here, $0<Pe<1$ indicates that transport is diffusion dominated and $1<Pe<10$ that it is advection dominated. We have, again, $Q=0.01$, $L=1.0$, and vary $D_c$ and $D_u$. As we increased the diffusion coefficients, we noticed a significant shift in the substrate limitation point marked by $x^{*}$, towards the deeper regions of the reactor, suggesting that longitudinal diffusion even at high Peclet numbers carries a sufficient amount of substrate downstream to main bacterial activity. Lower diffusion rates correlate with earlier substrate depletion.

3.3. Role of Attachment and Detachment with Diffusion

Whereas, as discussed above, several mesoscopic detachment rate expressions have been proposed in the literature, modeling of attachment is rather underdeveloped. In both cases the question arises as to which extent these mesoscopic processes affect macroscopic performance.

Once again, we maintain the same initial and boundary conditions as before. The reactor length remains constant across all simulations at $L=3.0$ [m].

We vary longitudinal diffusion for substrate and suspended bacteria within the range of 0.003–0.3 [m²d⁻¹]. At first, we set $a=1.0$ [d⁻¹] and vary d between $0.0$ and $0.6$. For larger d, detachment is guaranteed to dominate growth and biomass is washed out quicker than it is produced. Subsequently, with $d=0.3$ [d⁻¹], we adjust a within the range of $0.0$ to $1.0$. The individual results of the one-at-a-time sensitivity analysis of attachment and detachment are visualized in Figure 6a and Figure 6b, respectively, where we focus the first location $x^{*}$ in the reactor, at which substrate is depleted, as defined above.

In Figure 6a, it seems that in all cases the graphs show similar behavior: For $D_c=D_u=0.003$ [m²d⁻¹], $x^{*}$ has a small variance within the range of 0.06–0.14 [m], which is a $57.1\%$ change. When $D_c=D_u=0.03$ [m²d⁻¹], the change in $x^{*}$ is again $57.1\%$. This suggests that as we increase the diffusion coefficients, the change in $x^{*}$ [m] may also increase, though the percent change may not. With the highest values of $D_c=D_u=0.3$ [m²d⁻¹], $x^{*}$ fluctuates between 0.4 and 1.2 [m], which is a $66.7\%$ change.

Figure 6a suggests that the depletion of substrate with attachment is influenced by the diffusion coefficient. If we focus solely on the first simulation where $D_c=D_u=0.003$, we may conclude that diffusion does not impact substrate depletion relative to attachment. However, after conducting other simulations with increasing diffusion coefficient rates, we discover that there is in fact an effect from diffusion on substrate depletion. We conjecture then that the attachment rate, perhaps, does not operate independently of diffusion.

While analyzing detachment in Figure 6b, we observe minimal variation in the shape of the graphs across all three simulations. In the scenario where diffusion is minimal (i.e., $D_c=D_u=0.003$ [m²d⁻¹]), the graph exhibits a change of $0.25$ [m], a $38.5\%$ change. For $D_c=D_u=0.03$ [m²d⁻¹], the change is more pronounced, between 0.04 and 0.18 [m], a $78\%$ change. With $D_c=D_u=0.3$ [m²d⁻¹], the largest variation is between 0.0 and 0.5 [m], a $100\%$ change.

Figure 6 suggests that both detachment and attachment may influence substrate depletion. Increased detachment results in more suspended bacteria being washed out, while increased attachment holds more bacteria in the system by attaching to either the existing biofilm or substratum. With a higher attachment rate, there is more potential for biofilm growth at the inlet where the substrate is originally plentiful. This then results in a faster substrate depletion. Considering that detachment and attachment have opposing effects, the increase in the location of substrate depletion $x^{*}$ in Figure 6b aligns with the decrease in the location of substrate depletion that was observed for attachment in Figure 6a.

For the smallest longitudinal diffusion coefficients in Figure 6, we observe discrete changes in $x^{*}$. Since $x^{*}$ is defined as the smallest grid location at which the substrate concentration drops below the critical value, it attains one of a finite number of values. For larger diffusion coefficients, this phenomenon is the same but not noteworthy as much in the graphs since the quenching length is much larger.

To conclude this question about the role of detachment and attachment in combination with longitudinal diffusion, we briefly show results of a simulation experiment where both a and d are changed at the same time; see Figure 7. These simulations suggest that attachment influences substrate depletion regardless of the detachment rate. At the lowest attachment rate, the graphs all show a yellow hue, indicating depletion that occurs deeper in the reactor. As we increase the attachment rate, the depletion moves closer to the reactor inlet. When the diffusion rate increases, the impact of attachment on substrate depletion seems to remain relatively consistent, although the heat maps begin to stratify.

The simulations also suggest there is no significant correlation between the diffusion coefficient and the detachment rate. However, in the advection-dominated simulation where $D_c=D_u=0.003$, the detachment rate variability shows the most change in depletion as compared to the other simulations. We note that when the diffusion rate is at its maximum and the system is diffusion dominated (i.e., $Pe=0.1$), the heatmap suggests that the detachment rate has minimal impact on substrate depletion.

The attachment rate has an influence on substrate depletion regardless of the detachment rate. However, the converse is not necessarily true. Detachment does not significantly affect the results regardless of the attachment rate. This could stem from the fact that the effects of attachment may outweigh those of detachment.

4. Discussion

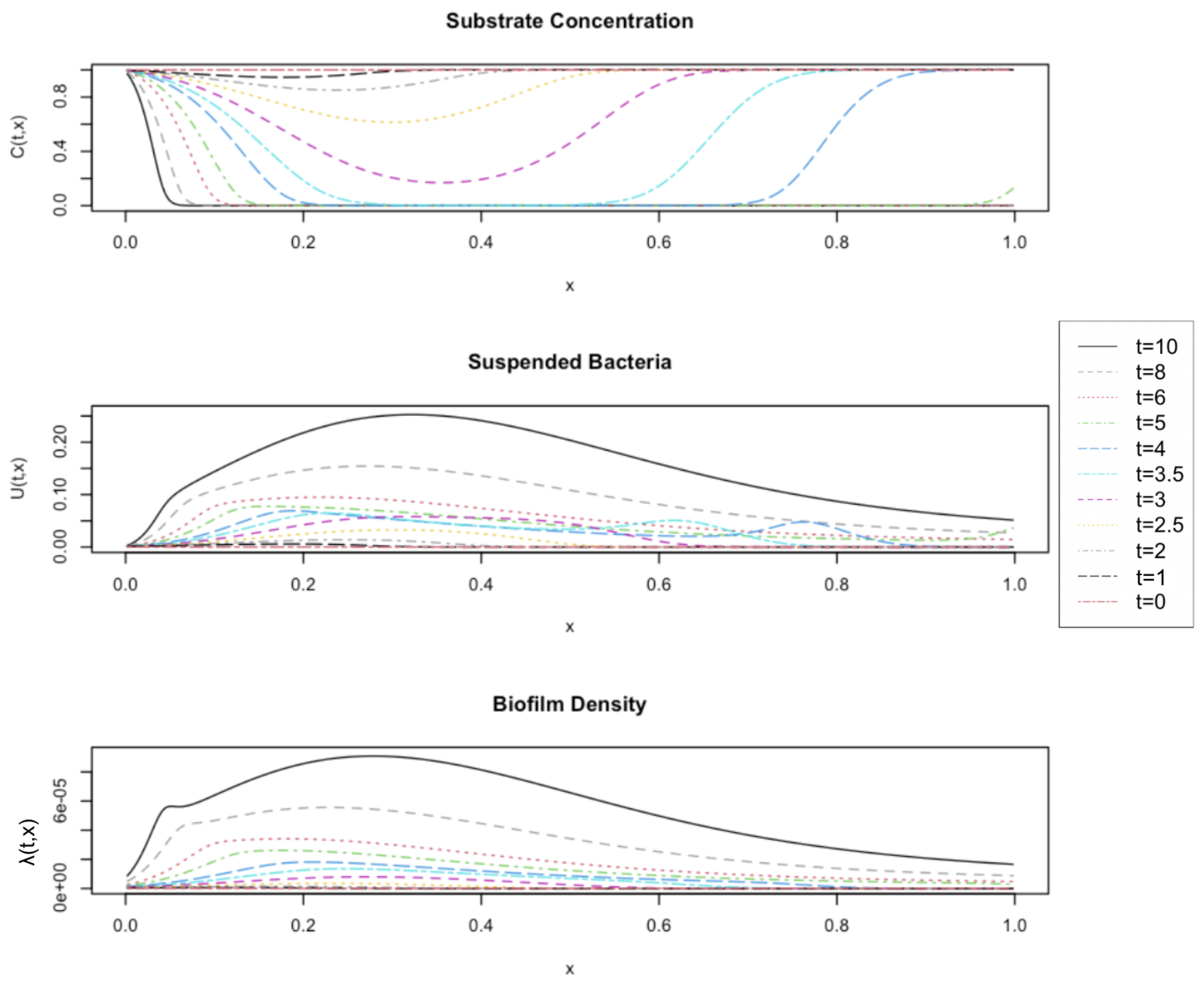
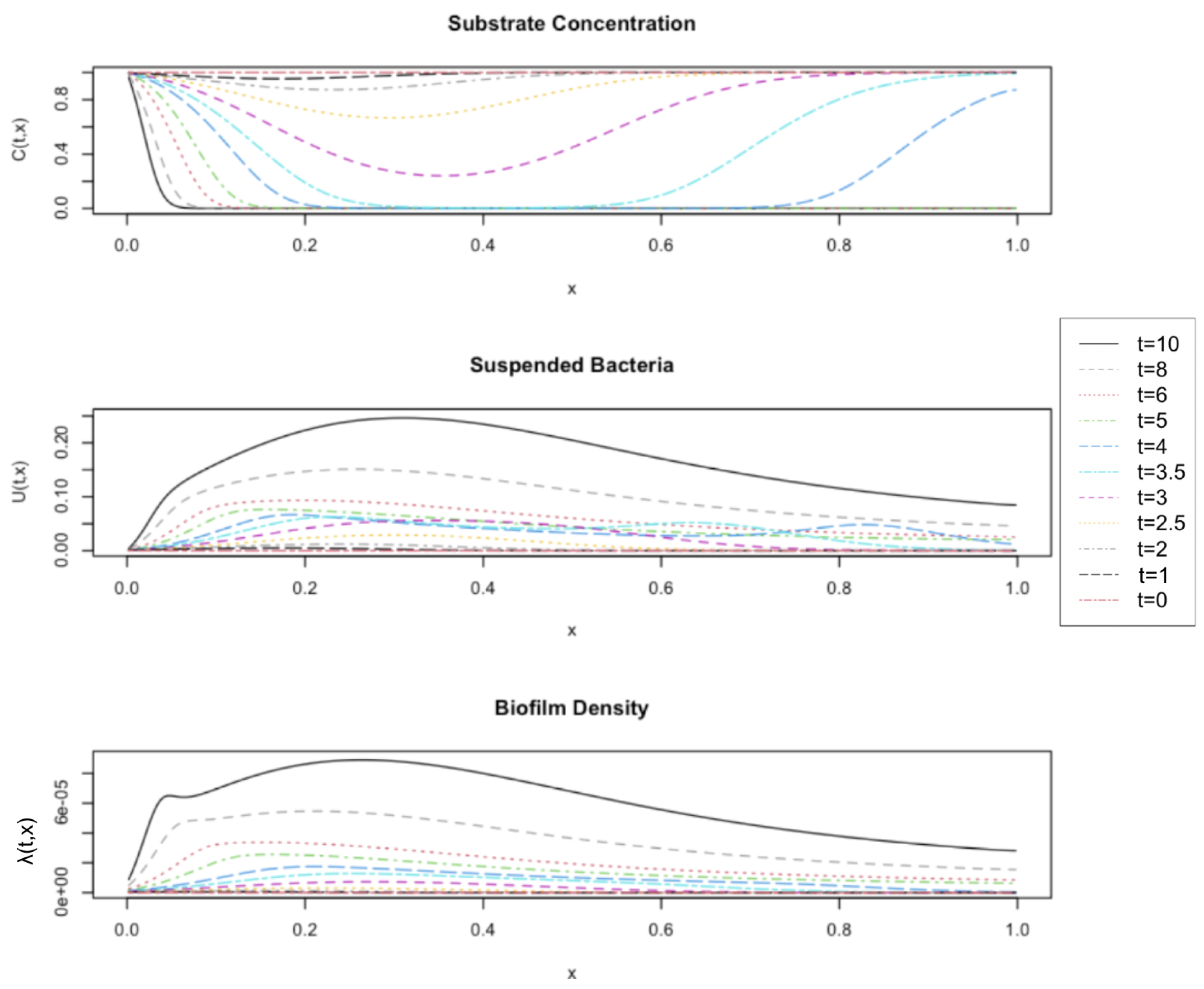
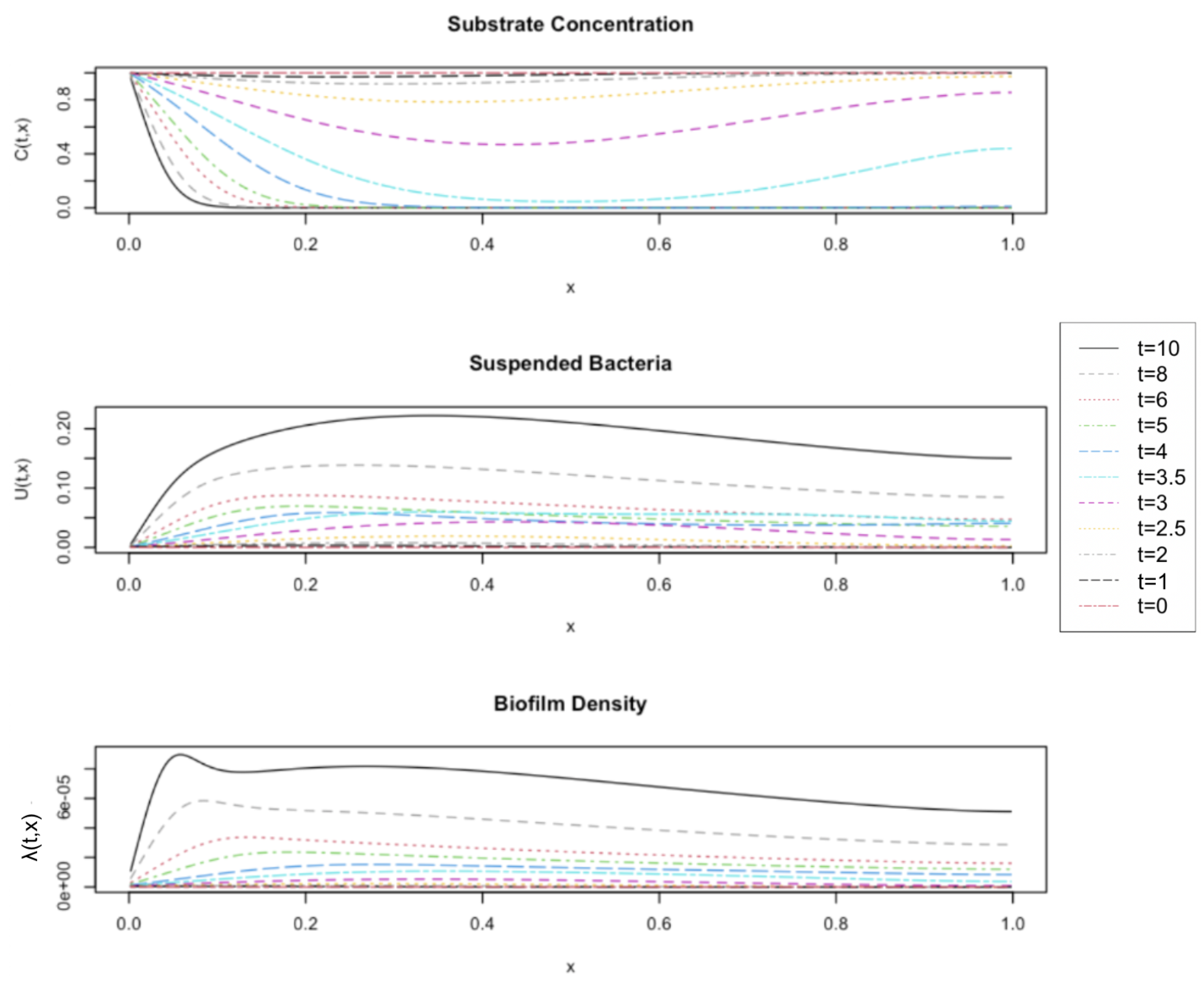
The results in this paper express the importance of longitudinal diffusion in the model formation, even under circumstances where the diffusive contribution is very small compared to the advective one. While comparing a base model without diffusion to the new model with diffusion, we identified the changes in system dynamics as the Peclet number was decreased, hence the model becoming more diffusion dominated. This observation was further validated by examining the effect that diffusion had on the substrate depletion.

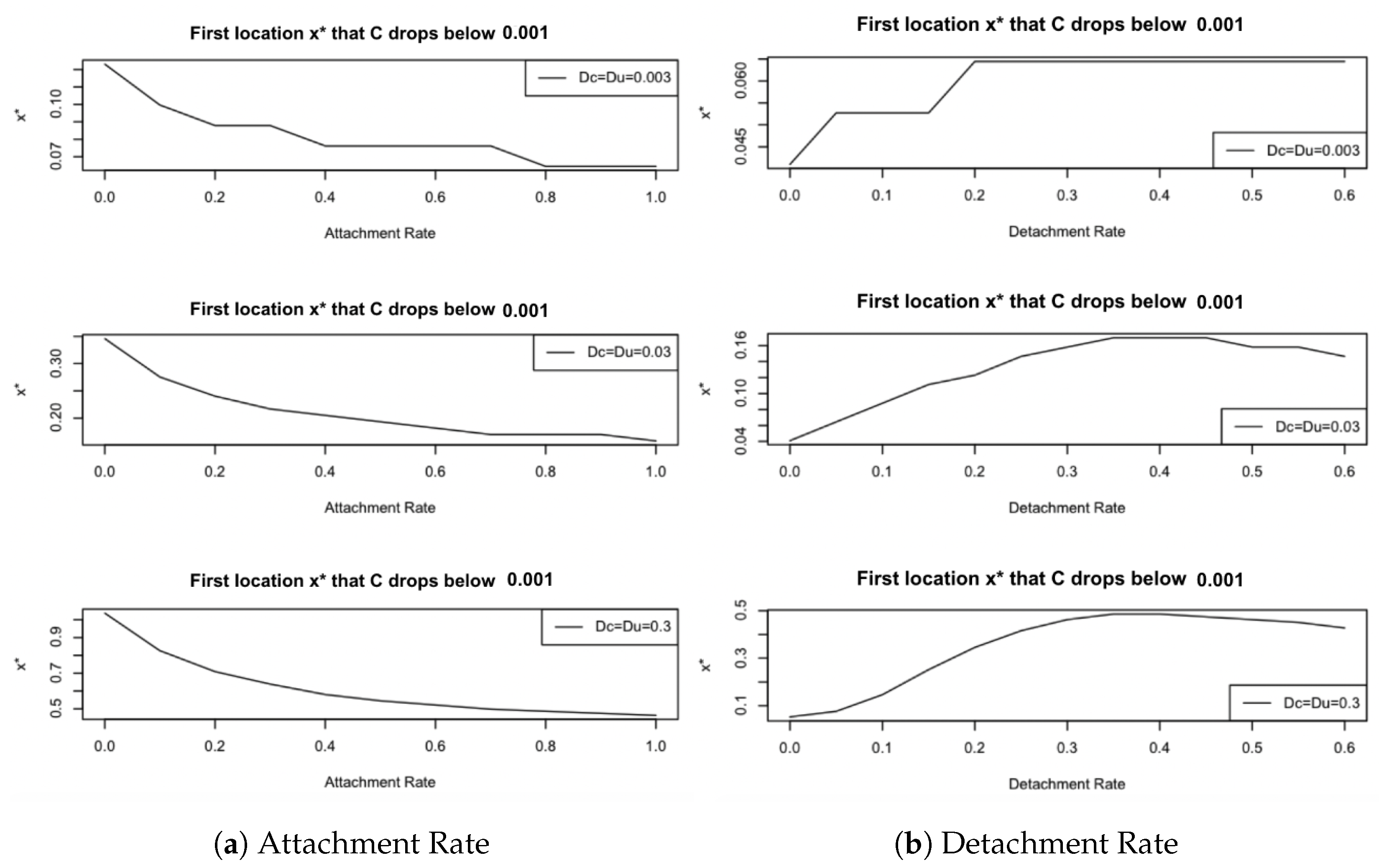
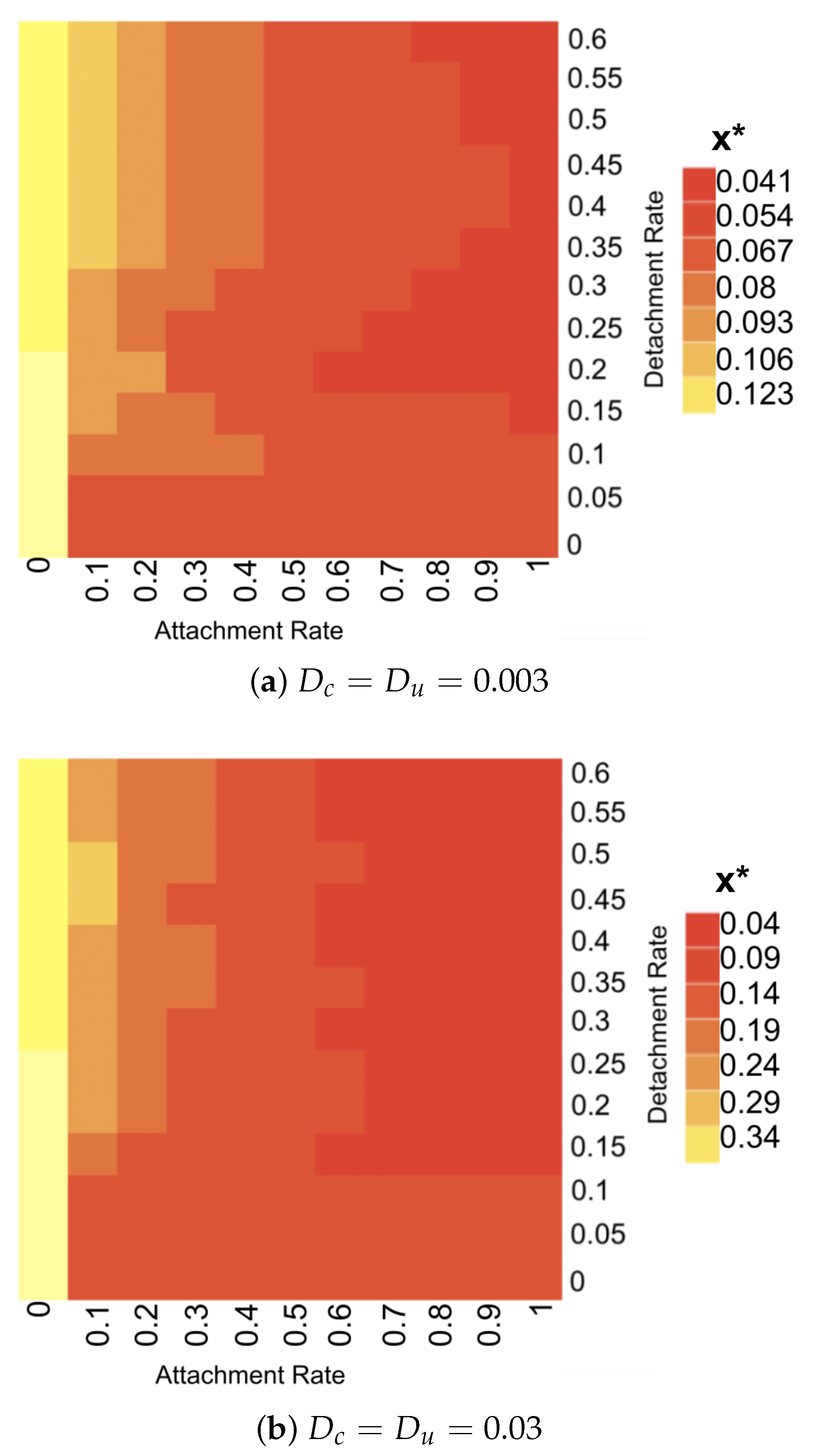
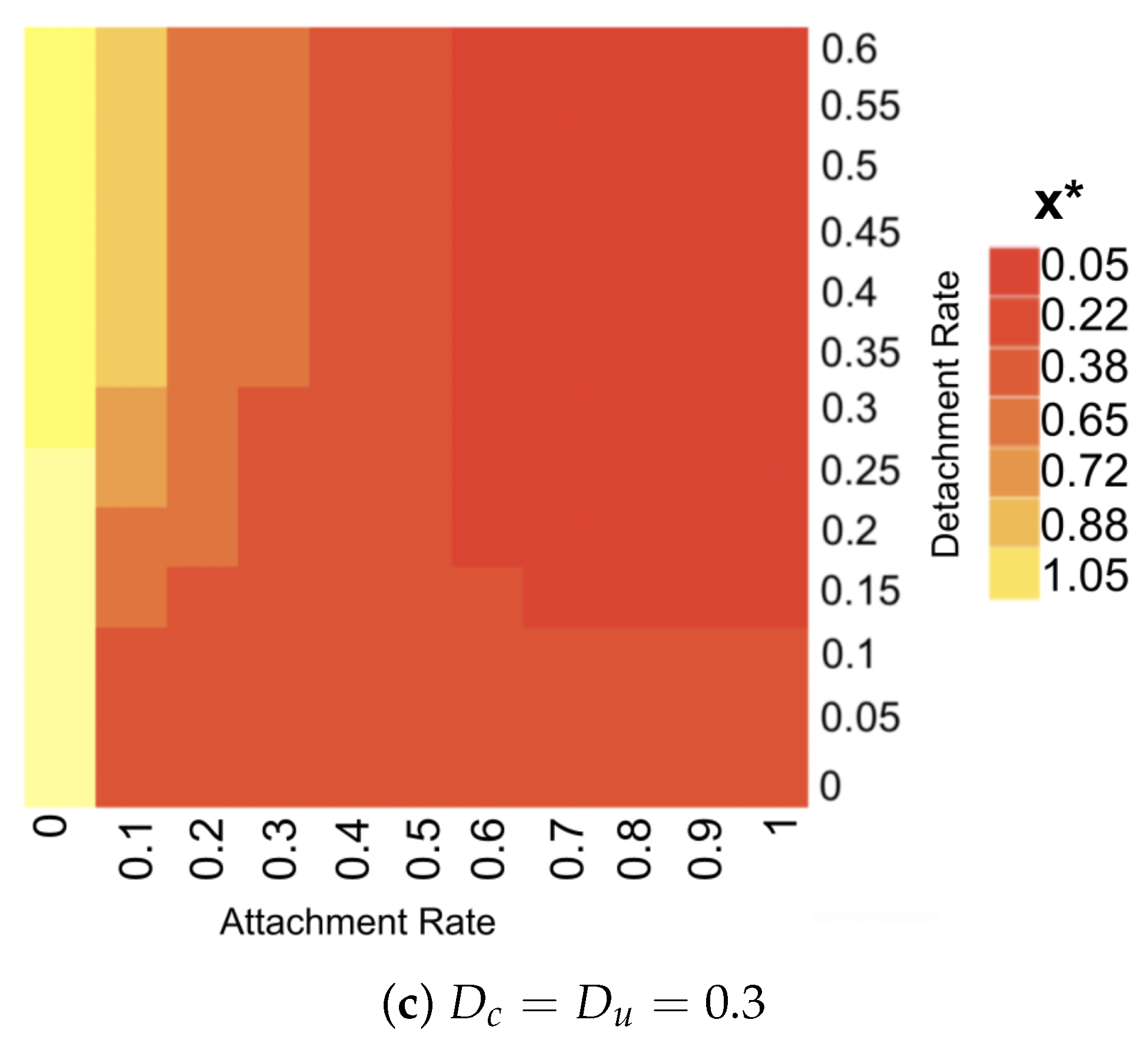
The role of attachment and detachment with diffusion was then studied, where, at least in the parameter range that we probed, attachment had more of an impact on substrate limitation than detachment. This becomes more pronounced as the diffusion coefficient is increased.

4.1. Multiscale Modeling of Biofilm Growth in Porous Media

Bacterial biofilms growing in porous media have an important ecological function in natural systems like soils as well as in engineered systems such as reactive biobarriers in ground water protection, in soil remediation processes, and in microbial sand filters, which find applications both in drinking water and in wastewater treatment [38,39].

In [21], it was proposed to model biofilm accumulation in porous media by dividing the 1D domain into several compartments and to consider a series of 1D biofilm reactors, similar in approach to a gradostat model. This is also the point of departure for our model development. Like [22], but unlike [21], we included suspended bacteria in the pore space. Whereas in [21], biofilm accumulation is simulated by using a relatively small finite number of such compartments, we follow [22] and shrink such compartments each to a point, obtaining a nonlinear PDE-ODE coupled system on the macroscale. This system consists of quasilinear diffusion–advection–reaction equations for dissolved substrates and suspended biomass and an ODE in each point of the domain for the biofilm. The growth kinetics of the biofilm in the macroscale model that is obtained with this upscaling procedure is the same as the one used ad hoc and per assumption in Platte’s 0D biofilm reactor models, for example [15,16,17], for environmental biotechnology applications in CSTRs. As such, our multiscaling approach also provides additional justification and support for that modeling framework.

In contrast to [21,22], we also consider in our model development longitudinal diffusion of substrate and suspended bacteria, i.e., diffusion in the main flow direction, in addition to the normal diffusion of substrate into the biofilm. In our simulation experiments that focus on de novo biofilm formation in clean beds, we observe that accounting for diffusion indeed has substantial effect: our results suggest that neglecting the contribution of diffusion tangential to the biofilm, in the main flow direction, may lead to underestimating quenching length, i.e., the distance over which the substrate is degraded, as well as biofilm accumulation downstream from the inlet. As expected, this is the more pronounced the smaller the reactor Peclet number is, i.e., the larger the contribution of diffusion to mass transport relative to the contribution of advection. Nevertheless, even in the strongly advection dominated case $Pe=100$, the effects of longitudinal diffusion are discernible.

A similar observation can be made about reactive biobarrier scenarios, in which, for example, bacteria are infused into the subsurface to deplete oxygen in an effort to prevent certain chemical reactions to happen that have environmental contaminants as a product [4]. In systems in which several species interact and in which several dissolved substrates are transported and undergo reactions, as in the Uranium bio-reduction setting of [32], it is difficult to predict in general whether neglecting diffusion overestimates or underestimates process efficiency, as this depends on the specifics of the system at hand. Our study shines some light on this question qualitatively.

4.2. Attachment and Detachment Modeling

Exchange of biomass between the biofilm phase and the aqueous phase is an important process in many natural or engineered biofilm systems. Since our main simulation focus is on clean bed simulation and hence de novo biofilm formation in porous media, including the attachment process is paramount, although it has mostly been neglected in modeling studies so far. Moreover, by neglecting suspended bacteria and how they attach, one neglects the contribution of unattached biomass to substrate degradation.

Attachment of bacteria from the aqueous phase to the substratum or to an already established biofilm is often neglected in biofilm modeling studies; for example, it is not considered by default in the probably most recent biofilm simulation software biofilm.jl [12], although a simple first-order attachment model was already proposed in [40] and later reprised in [19,20]. The assumption there is that suspended bacteria attach directly to the biofilm surface or if no biofilm is present to the substratum. This model process is what we used in our mesoscale description and, under the upscaling procedure, also appears in the macroscopic model as a first-order term.

Alternatively, in a 2D model in [41], suspended bacteria were assumed to be diffusing into and in the biofilm matrix. This idea was also implemented for Wanner–Gujer-style biofilm models in [42] and several subsequent papers such as [43]. We have not explored how this more involved mesoscopic model would behave in the upscaling process. This would require to perform in detail the limit process on the flux of biomass from the aqueous phase into the biofilm.

By contrast, including detachment is fairly routine in one-dimensional biofilm modeling. Usually, this considers passive detachment, i.e., detachment as a response of the biofilm to external factors. Only very few models of active detachment can be found, i.e., models in which detachment is the consequence of internal biofilm processes; for an example, see [24], where for a single species, single substrate biofilm (the situation with which we are also concerned) models of quorum-sensing-induced detachment and of starvation-induced detachment are proposed and studied.

Passive detachment is commonly thought to be induced by external forces to the biofilm, mostly shear forces exerted by bulk flow [44]. In many instances, bacterial biofilms form in heterogeneous structures, and the response of the biofilm to the fluid flow around it is a complicated fluid–structure interaction problem that depends on local shear forces which in turn depend strongly on local biofilm structure. In one-dimensional biofilm models in which the biofilm is described locally as a homogeneous slab, this can obviously only be described inadequately, and the possibility for a physics-based motivation and justification for such detachment model therefore is severely limited.

The most commonly used detachment formulation for 1D biofilm models, for which however, such a physics-based rationale appears to be lacking, is second-order detachment, where biomass loss is proportional to the square of the biofilm thickness. It was already shown in [22,32] that using this second-order model in the mesoscopic model leads to a substantial underestimation of detachment on the macroscale under our upscaling approach. As a model for passive detachment, the detachment coefficients should be relatable to the physical conditions in the biofilm reactor. Specifically, there is sufficient evidence for the role that the hydrodynamics in the aqueous phase plays in the detachment process, e.g., [44] (but there are many more studies that could be cited here). Despite the widespread use of this second-order detachment model, this relationship between detachment coefficient and bulk hydrodynamics is a surprisingly little studied question, with [30,31] being noteworthy exceptions, both, however, focusing on particular reactor settings rather than a general theory.

In [25], several mesoscopic detachment rate functions (as phenomenological constitutive relationships) for 1D biofilm models were studied from a long-term behavior analysis perspective, including some in which biomass loss is qualitatively (not quantitatively) related directly to reactor scale (i.e., global, not local) hydrodynamic conditions. In [22], it was pointed out that under our upscaling procedure, these models, far from clogging—which is also the situation we encounter—behave either like the second-order model or like the first-order model that we use here. In particular, a shear-dependent detachment model that was developed based on empirical observations in [35] several decades ago was found to behave like the first-order detachment model. A further argument for us to use this first-order detachment model is that it can be considered a linearization of any more involved nonlinear relationship about the washout equilibrium. In the case of the second-order detachment model, however, such a linearisation would yield a detachment coefficient $\delta =0$. This is the situation we also observe in our upscaling procedure for this model (cf. [22,32]). To better illustrate the difference between mesoscopic second-order and first-order detachment models, we consider first a situation in which the substrate does not become limited, such that $\mu C/({\kappa }_{\lambda }+C)\approx \mu$; then, the single species biofilm model with second-order detachment is well approximated by the logistic equation

$$\dot{\lambda }=\mu \lambda -\delta {\lambda }^2$$

(19)

where $\mu$ is the maximum specific growth rate. Here, the second-order detachment function enforces an asymptotically stable equilibrium ${\lambda }^{*}=\mu /\delta$. On the other hand, under such nutrient-rich conditions, the first-order detachment model leads to

$$\dot{\lambda }=(\mu -\delta )\lambda$$

(20)

which predicts unbounded growth for $\mu >\delta$ and washout for $\delta >\mu$, in which case the biofilm does not attain a positive steady state. In this situation, obviously, a first-order detachment model is insufficient. In our setting, and in most realistic biofilm scenarios, the situation is different: substrate is not perpetually unlimited throughout the biofilm. As the biofilm grows, substrate becomes depleted. To illustrate this, for simplicity, we make the ansatz that the biofilm growth rate $g\left(\lambda \right)$ decreases as the biofilm grows. This situation is more adequately described by a differential equation,

$$\dot{\lambda }=(g\left(\lambda \right)-\delta \left(\lambda \right))\lambda =:f\left(\lambda \right).$$

(21)

Here $\delta \left(\lambda \right)$ is the biofilm-thickness-dependent detachment rate. At a nontrivial steady state ${\lambda }^{*}>0$, we have $g\left({\lambda }^{*}\right)=\delta \left({\lambda }^{*}\right)$. Since g is monotonically decreasing and $\delta$ is monotonically non-decreasing (for example, it is constant for first-order detachment, increasing for second-order detachment), we find that $f^{\prime }\left({\lambda }^{*}\right)<0$. Hence, ${\lambda }^{*}$ is an asymptotically stable equilibrium, even for first-order detachment, and the logistic nonlinearity is not required to bound biofilm growth.

These uncertainties about how to adequately include attachment and detachment processes in mesoscopic 1D biofilm models require an investigation into the sensitivity of model outcomes with respect to the parameters that describe biomass exchange between the aqueous and the biofilm phase. In our simulation experiments, it appears that the model shows less sensitivity to the detachment rates than to the attachment rates.

4.3. Potential Breakdown of the Model and Possibilities of Future Model Extensions

A potential breakdown situation of our modelling is that the important condition $\lambda <p/2$ to keep open the flow channel is not necessarily guaranteed. If this happens, the pore space clogs, which in the physical system leads to flow being completely obstructed. This phenomenon can also occur in engineered systems, for example, in soil remediation, where whether or not such a breakdown happens depends, among other things, to a major extent on the soil properties and the bacterial growth conditions. For example, if the biofilm is able to clog the aqueous phase in bioventing, then this is not a suitable technology for the treatment of this soils, and similarly, our model would not be applicable. In analogy to these practical aspects, one might argue that our model framework is not suitable for situations where this occurs and needs to be appropriately extended. For example, depending on the mechanism that drives the flow (we assumed here constant flow rate), narrowing of the pore gap might lead to increased shear forces at the biofilm/water interface, i.e., requiring a solution-adaptive adjustment of the detachment rate; see also our discussion above. This poses the question of whether a detachment model that depends on these interfacial shear stresses might also prevent such model breakdown due to clogging. It might introduce a singularity in the detachment terms and as such considerably increase the complexity of the model. In this study, we remain firmly in the setting of the work from which we started, but it is important to pursue this question further.

Although our model is only formulated for a 1D setting, its extension to 2D or 3D scenarios seems relatively straightforward. Similarly, as demonstrated in [32] for the model that considers only advective transport in the aqueous phase, an extension from the single substrate, single-species setting to multi-species systems is possible.

4.4. Choice of Upstream Bounday Conditions

In our simulation experiments, we fixed the upstream boundary condition to Dirichlet conditions which we think is a proper choice for some applications, e.g., in remediation settings like the ones we discussed above in Section 2.4. In other applications, Danckwerts boundary conditions might be a better choice. These are of the type of Robin boundary conditions and reduce to Dirichlet boundary conditions for advection–reaction models, i.e., when the diffusion coefficient vanishes. That is, under such Danckwerts conditions, the advection–reaction model has the same solution as under Dirichlet conditions, but the advection–diffusion–reaction model does not. Specifically, both the inflow substrate concentration and the inflow concentration of suspended biomass differ from the values they attain in the advection–reaction model (i.e., the specified inflow concentration). This immediately leads to the conjecture that in systems with Danckwerts conditions, longitudinal diffusion should also not be neglected. The same rationale is applied to the generalized boundary condition proposed in [45] for advection–diffusion–reaction equations, which are essentially a weighted average of Dirichlet and Danckwerts boundary conditions.

4.5. Limitations

The model that we derived and simulated here has many constant model parameters and coefficient functions that depend on the dependent variables $\lambda ,C,U$. Our simulation results and observations are only valid for the choices that we made here. We limited ourselves to investigate a select few key parameters, namely diffusion coefficients, detachment rate, and attachment rate. This choice was prompted by the fact that these are the three processes where our model differs most from the work that was our point of departure, namely [21,32]. This is not to say that relationships between other parameters or different choices of coefficient functions would be less interesting. For example, our assumption $D_c=D_u$ throughout was somewhat arbitrary. It indeed would be very interesting to give up this restriction. We reserve this for future work, together with a major model extension that addresses the possible breakdown/clogging situation described above.

As discussed above, there is also much uncertainty about the detachment process in the biofilm literature (both modeling and experimental), which warrants a more specific investigation into this aspect.

5. Conclusions

In this paper, we studied a mathematical model for biofilm formation inside a porous media reactor. We extended the model from [22,32] by including longitudinal diffusion, in the main flow direction, which leads to a nonlinear PDE-ODE coupled system consisting of two diffusion–advection–reaction equations of suspended biomass and dissolved substrate and an ordinary differential equation in each point of the domain for biofilm thickness.

Our simulations of de novo biofilm formation in clean beds, such as sand filters, showed that neglecting diffusion in the aqueous phase can lead to underestimation of quenching length, i.e., the distance required for the substrate to be degraded. This effect is already noticeable for very little diffusion, i.e., when the system is still in the advection-dominated regime, which calls into doubt the practice of neglecting longitudinal diffusion.

We also saw that exchange of biomass between the biofilm and the aqueous phase plays an important role in this process and that model predictions are specifically sensitive to attachment rates. Biofilm attachment and detachment are three-dimensional phenomena and difficult to describe in 1D mesoscopic biofilm models. These uncertainties carry over into the macroscopic model formulation in the upscaling procedure.