A Conservative and Compact Finite Difference Scheme for the Sixth-Order Boussinesq Equation with Surface Tension

Abstract

In this study, we propose a conservative and compact finite difference scheme designed to preserve both the mass change rate and energy for solving the sixth-order Boussinesq equation with surface tension. Theoretical analysis confirms that the proposed scheme achieves second-order accuracy in temporal discretization and fourth-order accuracy in spatial discretization. The solvability, convergence, and stability of the difference scheme are rigorously established through the application of the discrete energy method. Additionally, a series of numerical experiments are conducted to illustrate the effectiveness and reliability of the conservative scheme for long-time simulations.

1. Introduction

The numerical solution of partial differential equations (PDEs) is a fundamental component in numerous scientific and engineering applications. In recent years, there has been a growing emphasis on developing high-order finite difference methods to improve both the accuracy and efficiency of solutions for a wide range of PDEs. A particular area of interest is the Boussinesq equation, which was first introduced by Joseph Boussinesq in 1872 to model nonlinear wave propagation in dispersive media [1]. Consequently, this equation has been extensively applied across multiple domains, including the investigation of ion sound waves in plasma, solitary waves in vascular systems, tsunami waves in oceanography and coastal sciences, as well as pressure waves in liquid–gas bubble mixtures, among others [2,3].

This article investigates the sixth-order Boussinesq equation, taking into account the effects of surface tension, as outlined in the following [4]:

$$\begin{array}{cc}\hfill & u_{tt}-k^2{u}_{xx}+a_1{u}_{xxxx}-a_2{u}_{xxtt}-b_1{u}_{xxxxxx}+b_2{u}_{xxxxtt}+c{\left(u^{2p}\right)}_{xx}=0,\hfill \end{array}$$

(1)

with the specified initial conditions

$$\begin{array}{cc}\hfill & u(x,0)=\phi \left(x\right),u_t(x,0)=\psi \left(x\right),\hfill \end{array}$$

(2)

where the parameters $a_1\ge 0$, $a_2\ge 0$, $b_1\ge 0$, and $b_2\ge 0$ are non-negative, while k and c are constants. Furthermore, $p\ge 1$ is a positive integer, and $\phi \left(x\right)$ and $\psi \left(x\right)$ are two provided smooth functions.

Solitary waves have attracted considerable interest in various fields of physics and engineering. Biswas [5] successfully derived an exact solitary wave solution for the Korteweg–de Vries equation, which is characterized by power law nonlinearity and time-varying coefficients. The singular solitary wave solution for the Rosenau–KdV equation is presented in [6], while a specific 1-soliton solution for the Rosenau–KdV RLW equation is detailed in [7]. Equation (1) is frequently encountered in numerous mathematical models concerning solitary wave propagation, as emphasized by Lu and Helal [8,9]. Furthermore, Biswas et al. [4] provided a variety of solitary wave, shock wave, and singular solitary wave solutions for the Boussinesq Equation (1), incorporating the effects of surface tension. Under the assumption of solitary wave behavior, it is observed that the solution to the sixth-order Boussinesq equation (1) and its derivatives approaches zero as $\left|x\right|\to \infty$, as noted by Burde and Yimnet et al. [10,11]

$$\begin{array}{cc}\hfill & \underset{x\to \pm \infty }{lim}u=0,\underset{x\to \pm \infty }{lim}{\displaystyle \frac{{\partial }^{n}u}{\partial x^n}}=0,n\ge 1.\hfill \end{array}$$

Thus, Equation (1) is linked to the following global conservation law:

$$\begin{array}{cc}\hfill & {\displaystyle \frac{d}{dt}}{\int }_{-\infty }^{+\infty }u(x,t)dx=C.\hfill \end{array}$$

This research focuses on the solitary wave solution and aims to develop a conservative linear finite difference scheme for the sixth-order Boussinesq Equation (1). To implement the numerical method effectively, we analyze a sufficiently large yet finite spatial domain, denoted as $[x_l,x_r]$, instead of the unbounded interval $(-\infty ,+\infty )$. This ensures that the solution remains sufficiently small at the domain boundaries. Consequently, we consider the following boundary conditions:

$$\begin{array}{cc}\hfill & u(x_l,t)=u(x_r,t)=0,u_x(x_l,t)=u_x(x_r,t)=0,u_{xx}(x_l,t)=u_{xx}(x_r,t)=0,\hfill \end{array}$$

(3)

where $0\le t\le T$. Considering the requirement for continuity, we further assume $\phi \left(x_l\right)=\phi \left(x_r\right)=0$.

The Boussinesq equation and its variants have been extensively studied through both theoretical and numerical methods. Esfahani and Farah [12] investigated the following nonlinear sixth-order Boussinesq equation in the theoretical context:

$$\begin{array}{cc}\hfill & u_{tt}-u_{xx}\pm u_{xxxx}-u_{xxxxxx}+{\left(u^2\right)}_{xx}=0,x\in R,t\ge 0.\hfill \end{array}$$

(4)

The authors established the local well-posedness of Equation (4) within the framework of non-homogeneous Sobolev spaces $H^s\left(\mathbb{R}\right)$, where $s<0$ and $s\in \mathbb{R}$. Subsequently, Wang and Esfahani [13] conducted an investigation into the sixth-order Boussinesq equation as follows:

$$\begin{array}{cc}\hfill & u_{tt}-u_{xx}\pm u_{xxxx}-u_{xxxxxx}-{\left(\right|u|}^2{u)}_{xx}=0,x\in R,t\ge 0.\hfill \end{array}$$

(5)

They demonstrated that the problem described by Equation (5) is globally well-posed within the Sobolev space $H^s\left(\mathbb{R}\right)$, where $3/2<s<2$ and $s\in \mathbb{R}$.

In a numerical context, Feng et al. [14] proposed a symmetric three-level implicit difference scheme that exhibits second-order accuracy for the following sixth-order Boussinesq equation

$$\begin{array}{cc}\hfill & u_{tt}-u_{xx}-u_{xxxx}-0.4u_{xxxxxx}-6{\left(u^2\right)}_{xx}=0.\hfill \end{array}$$

(6)

A linearized stability analysis indicates that the difference scheme, which incorporates a free parameter denoted as $\theta$, exhibits stability for values of $\theta$ that are equal to or greater than 1/4. In 2017, Kolkovska and Vucheva [15] introduced a nonlinear second-order difference scheme aimed at addressing the sixth-order Boussinesq problem, as detailed below:

$$\begin{array}{cc}\hfill & \left\{\begin{array}{c}{u}_{tt}-u_{xx}-{\beta }_1{u}_{xxtt}+{\beta }_2{u}_{xxxx}-{\beta }_3{u}_{xxxxxx}+\alpha {\left(u^2\right)}_{xx}=0,\hfill \\ u(x,0)=\phi \left(x\right),u_t(0,x)=\psi \left(x\right),\hfill \\ u\to 0,u_{xx}\to 0,u_{xxxx}\to 0,\left|x\right|\to \infty .\hfill \end{array}\right.\hfill \end{array}$$

(7)

However, the scheme presented in [15] demonstrates conditional stability, which is dependent on a strict limitation on the subsequent ratio

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\tau }{h^2}}<{\displaystyle \frac{3\sqrt{{\beta }_1}}{2\sqrt{1+4{\beta }_2+16{\beta }_3}}},{\beta }_1\ge 0,{\beta }_2\ge 0,{\beta }_3\ge 0.\hfill \end{array}$$

Moreover, there is a significant lack of theoretical analysis regarding the solvability and convergence properties of the scheme proposed by Kolkovska [15]. Recently, Arslan [16] introduced a novel methodology combining the differential transform method with the finite difference technique to approximate solutions for singularly perturbed ill-posed problems and sixth-order Boussinesq equations. In another study, Zhang et al. [17] introduced a meshless numerical technique called the generalized finite difference method, which has proven effective for solving enhanced Boussinesq-type equations, especially for simulating wave propagation over irregular bottom topographies.

In numerical simulations, compact difference schemes generally require fewer stencils than standard finite difference methods while providing better resolution and maintaining the same order of accuracy. Hou et al. [18] introduced an energy-preserving, high-order compact finite difference scheme specifically designed for two-dimensional nonlinear wave equations. Mohanty et al. [19,20,21,22] developed highly accurate compact difference schemes for several equations, including the coupled viscous Burgers equations, the good Boussinesq equation, the time-dependent viscous Burgers–Huxley equation, and a generalized version of fourth-order parabolic partial differential equations.

On the other hand, the principle of conservation of mass and energy is crucial in physics. A numerical scheme that fails to uphold local conservation may produce non-physical outcomes [23]. Therefore, preserving mass and energy is fundamental in the development of numerical schemes for solving PDEs. Significant research has been conducted on conservative finite difference schemes for various nonlinear wave equations. For instance, Deng et al. [24] proposed energy-preserving finite difference methods for two-dimensional nonlinear wave equations. Bayarassou et al. [25] investigated a high-order conservative linearized finite difference scheme for the regularized long wave (RLW) Korteweg–de Vries equation. Additionally, Nanta et al. [26] presented a wave model integrating the classical Camassa–Holm equation with the BBM–KdV equation, incorporating dual-power law nonlinearities while ensuring energy conservation.

This article aims to present a conservative difference scheme for solving the sixth-order Boussinesq problem as defined in Equations (1)–(3). Additional, it will examine the solvability, convergence, and stability of the proposed scheme.

Theorem 1. 

Consider u as the solution to the sixth-order Boussinesq problem defined by Equations (1)–(3). Let us denote $u_t=v_{xx}$ and assume that the supplementary boundary conditions are provided by $v_x(x_l,t)=v_x(x_r,t)=0$ and $v_{xx}(x_l,t)=v_{xx}(x_r,t)=0$. Under these conditions, it can be concluded that $E\left(t\right)=E\left(0\right)$ for all $t\in [0,T]$, where

$$\begin{array}{cc}\hfill & E\left(t\right)=k^2{\parallel u\parallel }_{L^2}^2+a_1\parallel u_x{\parallel }_{L^2}^2+a_2\parallel u_t{\parallel }_{L^2}^2+b_1\parallel u_{xx}{\parallel }_{L^2}^2+b_2\parallel u_{xt}{\parallel }_{L^2}^2+{\parallel v_x\parallel }_{L^2}^2\hfill \\ \hfill & -{\displaystyle \frac{2c}{2p+1}}{\int }_{x_l}^{x_r}{u}^{2p+1}dx.\hfill \end{array}$$

Proof. 

Let $u_t=v_{xx}$. We substitute this expression into Equation (1) and subsequently take the antiderivative twice. This process results in the following equation:

$$\begin{array}{cc}\hfill & v_t=k^{2}u-a_1{u}_{xx}+a_2{u}_{tt}+b_1{u}_{xxxx}-b_2{v}_{xxtt}-c{u}^{2p},\hfill \end{array}$$

we the obtain

$$\begin{array}{cc}\hfill & {\displaystyle \frac{dE}{dt}}=2{\int }_{x_l}^{x_r}\left(k^{2}u{u}_t+a_1{u}_x{u}_{xt}+a_2{u}_t{u}_{tt}+b_1{u}_{xx}{u}_{xxt}+b_2{u}_{xt}{u}_{xtt}+v_x{v}_{xt}-c{u}^{2p}{u}_t\right)dx\hfill \\ \hfill & =2{\int }_{x_l}^{x_r}\left[u_t\left(k^{2}u+a_2{u}_{tt}-c{u}^{2p}\right)+\left(a_1{u}_x{u}_{xt}+b_1{u}_{xx}{u}_{xxt}+b_2{u}_{xt}{u}_{xtt}+v_x{v}_{xt}\right)\right]dx\hfill \\ \hfill & =2{\int }_{x_l}^{x_r}[u_t\left(v_t+a_1{u}_{xx}-b_1{u}_{xxxx}+b_2{u}_{xxtt}\right)\hfill \\ \hfill & +\left(a_1{u}_x{u}_{xt}+b_1{u}_{xx}{u}_{xxt}+b_2{u}_{xt}{u}_{xtt}+v_x{v}_{xt}\right)]dx\hfill \\ \hfill & =2{\int }_{x_l}^{x_r}(u_t{v}_t+v_x{v}_{xt})dx+2a_1{\int }_{x_l}^{x_r}(u_t{u}_{xx}+u_x{u}_{xt})dx\hfill \\ \hfill & +2b_2{\int }_{x_l}^{x_r}(u_t{u}_{xxtt}+u_{xt}{u}_{xtt})dx-2b_1{\int }_{x_l}^{x_r}(u_t{u}_{xxxx}-u_{xx}{u}_{xxt})dx\hfill \\ \hfill & \equiv 2(l_1+a_1{l}_2+b_2{l}_3-b_1{l}_4).\hfill \end{array}$$

(8)

Utilizing the boundary conditions delineated in Equation (3) along with the additional assumptions, we derive the following results

$$\begin{array}{cc}\hfill & l_1={\int }_{x_l}^{x_r}(u_t{v}_t+v_x{v}_{xt})dx={\int }_{x_l}^{x_r}(v_{xx}{v}_t+v_x{v}_{xt})dx=v_t{v}_x{|}_{x_l}^{x_r}=0,\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill & l_2={\int }_{x_l}^{x_r}(u_t{u}_{xx}+u_x{u}_{xt})dx=u_t{u}_x{|}_{x_l}^{x_r}=0,\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill & l_3={\int }_{x_l}^{x_r}(u_t{u}_{xxtt}+u_{xt}{u}_{xtt})dx=u_t{u}_{xtt}{{|}_{x_l}^{x_r}=v_{xx}{u}_{xtt}|}_{x_l}^{x_r}=0.\hfill \end{array}$$

(11)

Since

$$\begin{array}{cc}\hfill & {\int }_{x_l}^{x_r}{u}_{xx}{u}_{xxt}dx={\int }_{x_l}^{x_r}{u}_{xx}d\left(u_{xt}\right)=u_{xt}{u}_{xx}{|}_{x_l}^{x_r}-{\int }_{x_l}^{x_r}{u}_{xt}{u}_{xxx}dx\hfill \\ \hfill & =-{\int }_{x_l}^{x_r}{u}_{xt}{u}_{xxx}dx=-{\int }_{x_l}^{x_r}{u}_{xxx}d\left(u_t\right)=-u_t{u}_{xxx}{|}_{x_l}^{x_r}+{\int }_{x_l}^{x_r}{u}_t{u}_{xxxx}dx\hfill \\ \hfill & =-v_{xx}{u}_{xxx}{|}_{x_l}^{x_r}+{\int }_{x_l}^{x_r}{u}_t{u}_{xxxx}dx={\int }_{x_l}^{x_r}{u}_t{u}_{xxxx}dx,\hfill \end{array}$$

which yields

$$\begin{array}{cc}\hfill & l_4={\int }_{x_l}^{x_r}(u_t{u}_{xxxx}-u_{xx}{u}_{xxt})dx={\int }_{x_l}^{x_r}{u}_t{u}_{xxxx}dx-{\int }_{x_l}^{x_r}{u}_{xx}{u}_{xxt}dx=0.\hfill \end{array}$$

(12)

Consequently, from Equations (8)–(12), we deduce that $dE/dt=0$, which indicates that $E\left(t\right)=E\left(0\right)$ for $t\in [0,T]$. This completes the proof.  □

It is essential to emphasize that, if parameters $a_1$, $a_2$, $b_1$, $b_2$, k, and c and the initial conditions $\phi \left(x\right)$ and $\psi \left(x\right)$ satisfy $E\left(0\right)\ge 0$, then $E\left(t\right)$ can be defined as the energy, and the solution to Equations (1)–(3) complies with the principle of energy conservation, where

$$\begin{array}{cc}\hfill & E\left(0\right)=k^2{\parallel \phi \parallel }_{L^2}^2+a_1\parallel {\phi }_x{\parallel }_{L^2}^2+a_2{\parallel \psi \parallel }_{L^2}^2+b_1\parallel {\phi }_{xx}{\parallel }_{L^2}^2+b_2\parallel {\psi }_x{\parallel }_{L^2}^2+{\parallel v_x(x,0)\parallel }_{L^2}^2\hfill \\ \hfill & -{\displaystyle \frac{2c}{2p+1}}{\int }_{x_l}^{x_r}{\phi }^{2p+1}dx.\hfill \end{array}$$

The remainder of this article is organized as follows. Section 2 introduces a compact finite difference scheme for solving the sixth-order Boussinesq Equations (1)–(3). Section 3 rigorously establishes the discrete conservation properties of mass change rate and energy. A comprehensive theoretical analysis addressing the scheme’s solvability, convergence, and stability is presented in Section 4. Numerical experiments validating the theoretical results are included in Section 5. Finally, Section 6 provides a concise summary of the findings.

2. Compact Difference Scheme

In this section, we present a compact and conservative difference scheme to solve the sixth-order Boussinesq problem as delineated in Equations (1)–(3). For two positive integers J and N, we define the spatial and temporal discretization parameters as $h=(x_r-x_l)/J$ and $\tau =T/N$, respectively. The uniform grid points are established as $x_j=x_l+jh$ and $t^n=n\tau$, where $j=0,1,\dots ,J$ and $n=0,1,\dots ,N$. We denote $U_j^n\approx u(x_j,t^n)$ as the approximation of the function u at the point $(x_j,t^n)$ and

$$\begin{array}{cc}\hfill & Z_h^0=\{U=\left(U_j\right)|U_{-2}=U_{-1}=U_0=U_1=U_2=U_{J-2}=U_{J-1}=U_J=U_{J+1}=U_{J+2}=0\},\hfill \end{array}$$

where $-2\le j\le J+2$. The Sobolev space is defined as described in [27]:

$$\begin{array}{cc}\hfill & H_0^k(\Omega )=\left\{u\left(x\right)\in H^k(\Omega ):{\displaystyle \frac{{\partial }^{i}u}{\partial x^i}}{|}_{\partial \Omega }=0,i=0,1,2,\dots ,k-1\right\}.\hfill \end{array}$$

For any two mesh functions $U^n,V^n\in Z_h^0$, we define the following difference operators, inner product and norms:

$$\begin{array}{cc}\hfill & {\left(U_j^n\right)}_{\tilde{x}}={\displaystyle \frac{1}{h}}(U_{j+1}^n-U_j^n),{\left(U_j^n\right)}_{\overline{x}}={\displaystyle \frac{1}{h}}(U_j^n-U_{j-1}^n),{\left(U_j^n\right)}_{\widehat{x}}={\displaystyle \frac{1}{2h}}(U_{j+1}^n-U_{j-1}^n),\hfill \\ \hfill & {\left(U_j^n\right)}_{\tilde{t}}={\displaystyle \frac{1}{\tau }}(U_j^{n+1}-U_j^n),{\left(U_j^n\right)}_{\overline{t}}={\displaystyle \frac{1}{\tau }}(U_j^n-U_j^{n-1}),{\left(U_j^n\right)}_{\widehat{t}}={\displaystyle \frac{1}{2\tau }}(U_j^{n+1}-U_j^{n-1}),\hfill \\ \hfill & {\overline{U}}_j^n=\frac{1}{2}(U_j^{n+1}+U_j^{n-1}),U_j^{n+{\displaystyle \frac{1}{2}}}=\frac{1}{2}(U_j^{n+1}+U_j^n),\hfill \\ \hfill & \langle U^n,V^n\rangle =h\sum _{j=1}^{J-1}{U}_j^n{V}_j^n,\parallel U^n{\parallel }^2=\langle U^n,U^n\rangle ,\parallel U^n{\parallel }_{\infty }=\underset{1\le j\le J-1}{max}\left|U_j^n\right|.\hfill \end{array}$$

By setting

$$\begin{array}{cc}\hfill & w=k^2{u}_{xx}-a_1{u}_{xxxx}+a_2{u}_{xxtt}+b_1{u}_{xxxxxx}-b_2{u}_{xxxxtt}-c{\left(u^{2p}\right)}_{xx},\hfill \end{array}$$

(13)

then Equation (1) can be expressed as $w=u_{tt}$. By utilizing the Taylor expansion for the variable x, we obtain

$$\begin{array}{cc}\hfill & w_j^n=k^2\left[{\left(U_j^n\right)}_{\tilde{x}\overline{x}}-{\displaystyle \frac{h^2}{12}}{\left({\partial }_x^{4}u\right)}_j^n\right]-a_1\left[{\left(U_j^n\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}}-{\displaystyle \frac{h^2}{6}}{\left({\partial }_x^{6}u\right)}_j^n\right]+a_2\left[{\left(U_j^n\right)}_{\tilde{x}\overline{x}\tilde{t}\overline{t}}-{\displaystyle \frac{h^2}{12}}{\left({\partial }_x^4{\partial }_t^{2}u\right)}_j^n\right]\hfill \\ \hfill & +b_1\left[{\left(U_j^n\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}}-{\displaystyle \frac{h^2}{4}}{\left({\partial }_x^{8}u\right)}_j^n\right]-b_2\left[{\left(U_j^n\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{t}\overline{t}}-{\displaystyle \frac{h^2}{6}}{\left({\partial }_x^6{\partial }_t^{2}u\right)}_j^n\right]\hfill \\ \hfill & -c\left\{{\left[{\left(U_j^n\right)}^{2p}\right]}_{\tilde{x}\overline{x}}-{\displaystyle \frac{h^2}{12}}{\left({\partial }_x^4{u}^{2p}\right)}_j^n\right\}+O({\tau }^2+h^4).\hfill \end{array}$$

(14)

Furthermore, Equation (2) is associated with

$$\begin{array}{cc}\hfill & b_1{\left({\partial }_x^{8}u\right)}_j^n=-k^2{\left({\partial }_x^{4}u\right)}_j^n+a_1{\left({\partial }_x^{6}u\right)}_j^n+a_2{\left({\partial }_x^4{\partial }_t^{2}u\right)}_j^n+b_2{\left({\partial }_x^6{\partial }_t^{2}u\right)}_j^n\hfill \\ \hfill & +c{\left({\partial }_x^4{u}^{2p}\right)}_j^n+{\left({\partial }_x^{2}w\right)}_j^n.\hfill \end{array}$$

(15)

Substituting Equation (15) into Equation (14) yields

$$\begin{array}{cc}\hfill & w_j^n=k^2{\left(U_j^n\right)}_{\tilde{x}\overline{x}}-a_1{\left(U_j^n\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}}+a_2{\left(U_j^n\right)}_{\tilde{x}\overline{x}\tilde{t}\overline{t}}+b_1{\left(U_j^n\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}}-b_2{\left(U_j^n\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{t}\overline{t}}\hfill \\ \hfill & -c{\left[{\left(U_j^n\right)}^{2p}\right]}_{\tilde{x}\overline{x}}+{\displaystyle \frac{k^2{h}^2}{6}}{\left({\partial }_x^{4}u\right)}_j^n-{\displaystyle \frac{a_1{h}^2}{12}}{\left({\partial }_x^{6}u\right)}_j^n+{\displaystyle \frac{a_2{h}^2}{6}}{\left({\partial }_x^4{\partial }_t^{2}u\right)}_j^n\hfill \\ \hfill & -{\displaystyle \frac{b_2{h}^2}{12}}{\left({\partial }_x^6{\partial }_t^{2}u\right)}_j^n-{\displaystyle \frac{c{h}^2}{6}}{\left({\partial }_x^4{u}^{2p}\right)}_j^n-{\displaystyle \frac{h^2}{4}}{\left({\partial }_x^{2}w\right)}_j^n.\hfill \end{array}$$

By applying second-order accuracy in our approximations, we achieve

$$\begin{array}{cc}\hfill & U_j^n={\overline{U}}_j^n+O\left({\tau }^2\right),w_j^n={\left({\partial }_t^{2}u\right)}_j^n={\left(U_j^n\right)}_{\tilde{t}\overline{t}}+O\left({\tau }^2\right),\hfill \\ \hfill & {\left({\partial }_x^{4}u\right)}_j^n={\left(U_j^n\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}}+O\left(h^2\right),{\left({\partial }_x^{6}u\right)}_j^n={\left(U_j^n\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}}+O\left(h^2\right),\hfill \\ \hfill & {\left({\partial }_x^2{\partial }_t^{2}u\right)}_j^n={\left(U_j^n\right)}_{\tilde{x}\overline{x}\tilde{t}\overline{t}}+O({\tau }^2+h^2),{\left({\partial }_x^4{\partial }_t^{2}u\right)}_j^n={\left(U_j^n\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{t}\overline{t}}+O({\tau }^2+h^2),\hfill \\ \hfill & {\left({\partial }_x^6{\partial }_t^{2}u\right)}_j^n={\left(U_j^n\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{t}\overline{t}}+O({\tau }^2+h^2),{\left({\partial }_x^4{u}^{2p}\right)}_j^n={\left[{\left(U_j^n\right)}^{2p}\right]}_{\tilde{x}\overline{x}\tilde{x}\overline{x}}+O\left(h^2\right).\hfill \end{array}$$

Consequently, the proposed compact finite difference scheme can be expressed as follows:

$$\begin{array}{cc}\hfill & {\left(U_j^n\right)}_{\tilde{t}\overline{t}}-k^2{\left({\overline{U}}_j^n\right)}_{\tilde{x}\overline{x}}+\left(a_1-{\displaystyle \frac{k^2{h}^2}{6}}\right){\left({\overline{U}}_j^n\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}}-\left(a_2-{\displaystyle \frac{h^2}{4}}\right){\left(U_j^n\right)}_{\tilde{x}\overline{x}\tilde{t}\overline{t}}-\left(b_1-{\displaystyle \frac{a_1{h}^2}{12}}\right){\left({\overline{U}}_j^n\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}}\hfill \end{array}$$

$$\begin{array}{cc}\hfill & +\left(b_2-{\displaystyle \frac{a_2{h}^2}{6}}\right){\left(U_j^n\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{t}\overline{t}}+{\displaystyle \frac{b_2{h}^2}{12}}{\left(U_j^n\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{t}\overline{t}}+c{\left[{\left(U_j^n\right)}^{2p}\right]}_{\tilde{x}\overline{x}}+{\displaystyle \frac{c{h}^2}{6}}{\left[{\left(U_j^n\right)}^{2p}\right]}_{\tilde{x}\overline{x}\tilde{x}\overline{x}}=0,\hfill \end{array}$$

(16)

$$U_j^0=\phi \left(x_j\right),{\left(U_j^0\right)}_{\widehat{t}}=\psi \left(x_j\right),0\le j\le J,$$

(17)

$$\begin{array}{cc}\hfill & U_0^n=0,{\displaystyle \frac{4}{3}}{\left(U_0^n\right)}_{\widehat{x}}-{\displaystyle \frac{1}{3}}{\left(U_0^n\right)}_{\ddot{x}}=0,{\displaystyle \frac{4}{3}}{\left(U_0^n\right)}_{\tilde{x}\overline{x}}-{\displaystyle \frac{1}{3}}{\left(U_0^n\right)}_{\widehat{x}\widehat{x}}=0,\hfill \\ \hfill & U_J^n=0,{\displaystyle \frac{4}{3}}{\left(U_J^n\right)}_{\widehat{x}}-{\displaystyle \frac{1}{3}}{\left(U_J^n\right)}_{\ddot{x}}=0,{\displaystyle \frac{4}{3}}{\left(U_J^n\right)}_{\tilde{x}\overline{x}}-{\displaystyle \frac{1}{3}}{\left(U_J^n\right)}_{\widehat{x}\widehat{x}}=0,0\le n\le N.\hfill \end{array}$$

(18)

It is essential to recognize that, since $U_0^n=0$, ${\displaystyle \frac{4}{3}{\left(U_0^n\right)}_{\widehat{x}}-\frac{1}{3}{\left(U_0^n\right)}_{\ddot{x}}=0}$, and ${\displaystyle \frac{4}{3}{\left(U_0^n\right)}_{\tilde{x}\overline{x}}-\frac{1}{3}{\left(U_0^n\right)}_{\widehat{x}\widehat{x}}=0}$ hold based on Equation (18), we may proceed with the assumption that $U_{-2}^n=U_{-1}^n=U_1^n=U_2^n=0$ for the sake of simplicity. Similarly, we can also assume that $U_{J-2}^n=U_{J-1}^n=U_{J+1}^n=U_{J+2}^n=0$, where $j=-2,-1,J+1$, and $J+2$ denote ghost points under the condition $1\le n\le N$. Consequently, it can be concluded that $U^n\in Z_h^0$.

In this context, we employ the following methodology to derive $U^1$:

$$\begin{array}{cc}\hfill & {\left(U_j^0\right)}_{\tilde{t}\overline{t}}-k^2{\left({\overline{U}}_j^0\right)}_{\tilde{x}\overline{x}}+\left(a_1-{\displaystyle \frac{k^2{h}^2}{6}}\right){\left({\overline{U}}_j^0\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}}-\left(a_2-{\displaystyle \frac{h^2}{4}}\right){\left(U_j^0\right)}_{\tilde{x}\overline{x}\tilde{t}\overline{t}}-\left(b_1-{\displaystyle \frac{a_1{h}^2}{12}}\right){\left({\overline{U}}_j^0\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}}\hfill \\ \hfill & +\left(b_2-{\displaystyle \frac{a_2{h}^2}{6}}\right){\left(U_j^0\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{t}\overline{t}}+{\displaystyle \frac{b_2{h}^2}{12}}{\left(U_j^0\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{t}\overline{t}}+c{\left[{\left(U_j^0\right)}^{2p}\right]}_{\tilde{x}\overline{x}}+{\displaystyle \frac{c{h}^2}{6}}{\left[{\left(U_j^0\right)}^{2p}\right]}_{\tilde{x}\overline{x}\tilde{x}\overline{x}}=0.\hfill \end{array}$$

(19)

From Equation (17), we obtain

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2\tau }}(U_j^1-U_j^{-1})={\left(U_j^0\right)}_{\widehat{t}}=\psi \left(x_j\right)+O\left({\tau }^2\right),0\le j\le J;\hfill \end{array}$$

that is,

$$\begin{array}{cc}\hfill & U_j^{-1}=U_j^1-2\tau \psi \left(x_j\right)+O\left({\tau }^3\right),0\le j\le J,\hfill \end{array}$$

(20)

which yields

$$\begin{array}{cc}\hfill & {\left(U_j^0\right)}_{\tilde{t}\overline{t}}={\displaystyle \frac{1}{{\tau }^2}}(U_j^1-2U_j^0+U_j^{-1})\hfill \\ \hfill & ={\displaystyle \frac{2}{{\tau }^2}}\left[U_j^1-U_j^0-\tau \psi \left(x_j\right)\right]={\displaystyle \frac{2}{{\tau }^2}}\left[U_j^1-\phi \left(x_j\right)-\tau \psi \left(x_j\right)\right]+O\left(\tau \right),\hfill \end{array}$$

where $0\le j\le J$.

3. Discrete Conservative Laws

In this section, we demonstrate that the proposed methodology, as outlined in Equations (16)–(18), maintains both the rate of mass change and energy conservation.

We will now present a modified version of the previously discussed scheme and define an auxiliary variable $V^n\in Z_h^0$ that fulfills the following conditions:

$$\begin{array}{cc}\hfill & {\left(V_j^{n+1/2}\right)}_{\tilde{x}\overline{x}}={\left(U_j^n\right)}_{\tilde{t}},j=0,1,\dots ,J,n=0,1,\dots ,N-1.\hfill \end{array}$$

(21)

Lemma 1 

([28,29,30]). For any two discrete functions $U,V\in Z_h^0$, it follows that

$$\begin{array}{cc}\hfill & \langle U_{\tilde{x}\overline{x}},U\rangle =-\langle U_{\tilde{x}},U_{\tilde{x}}\rangle =-{\parallel U_{\tilde{x}}\parallel }^2,\hfill \\ \hfill & \langle U_{\tilde{x}\overline{x}},V\rangle =-\langle U_{\tilde{x}},V_{\tilde{x}}\rangle =\langle U,V_{\tilde{x}\overline{x}}\rangle .\hfill \end{array}$$

Furthermore, we have

$$\begin{array}{cc}\hfill & \langle U_{\tilde{x}\tilde{x}\overline{x}\overline{x}},U\rangle ={\parallel U_{\tilde{x}\overline{x}}\parallel }^2.\hfill \end{array}$$

Lemma 2. 

For any discrete function $U\in Z_h^0$, it follows that

$$\begin{array}{cc}\hfill & \langle U_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}},U\rangle =-\langle U_{\tilde{x}\overline{x}\tilde{x}},U_{\tilde{x}\overline{x}\tilde{x}}\rangle =-{\parallel U_{\tilde{x}\overline{x}\tilde{x}}\parallel }^2.\hfill \end{array}$$

Proof. 

According to Lemma 1, it can be concluded that

$$\begin{array}{cc}\hfill & \langle U_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}},U\rangle =\langle {\left(U_{\tilde{x}\overline{x}\tilde{x}\overline{x}}\right)}_{\tilde{x}\overline{x}},U\rangle =\langle U_{\tilde{x}\overline{x}\tilde{x}\overline{x}},U_{\tilde{x}\overline{x}}\rangle \hfill \\ \hfill & =\langle {\left(U_{\tilde{x}\overline{x}}\right)}_{\tilde{x}\overline{x}},U_{\tilde{x}\overline{x}}\rangle =-\langle {\left(U_{\tilde{x}\overline{x}}\right)}_{\tilde{x}},{\left(U_{\tilde{x}\overline{x}}\right)}_{\tilde{x}}\rangle =-{\parallel U_{\tilde{x}\overline{x}\tilde{x}}\parallel }^2.\hfill \end{array}$$

This completes the proof.  □

Lemma 3 

([11,30]). For any discrete function $U^n\in Z_h^0$, it follows that

$$\begin{array}{cc}\hfill & \parallel U^n\parallel \le C\parallel U_{\tilde{x}}^n\parallel ,\parallel U^n{\parallel }_{\infty }\le C\parallel U_{\tilde{x}}^n\parallel .\hfill \end{array}$$

Lemma 4 

([11,31]). For any discrete function $U^n\in Z_h^0$, it follows that

$$\begin{array}{cc}\hfill & \parallel U_{\tilde{x}}^n\parallel \le {\displaystyle \frac{4}{h^2}}\parallel U^n\parallel .\hfill \end{array}$$

Theorem 2. 

Let $U^n\in Z_h^0$ denote the solution to Equations (16)–(18). We define the discrete mass as ${\displaystyle M^n=h\sum _{j=1}^{J-1}{U}_j^n}$. Consequently, the rate of change regarding discrete mass is described by the following equation:

$$\begin{array}{cc}\hfill & R^n\equiv {\displaystyle \frac{h}{\tau }}\sum _{j=1}^{J-1}(U_j^{n+1}-U_j^n)=R^{n-1}=···=R^0=h\sum _{j=1}^{J-1}\psi \left(x_j\right)+O\left({\tau }^{2}h\right),\hfill \end{array}$$

where $0\le n\le N-1$.

Proof. 

By multiplying Equation (16) by h and subsequently summing over j from 1 to J, we obtain the following result:

$$\begin{array}{cc}\hfill & h\sum _{j=1}^{J-1}{\left(U_j^n\right)}_{\tilde{t}\overline{t}}-k^{2}h\sum _{j=1}^{J-1}{\left({\overline{U}}_j^n\right)}_{\tilde{x}\overline{x}}+\left(a_1-{\displaystyle \frac{k^2{h}^2}{6}}\right)h\sum _{j=1}^{J-1}{\left({\overline{U}}_j^n\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}}-\left(a_2-{\displaystyle \frac{h^2}{4}}\right)h\sum _{j=1}^{J-1}{\left(U_j^n\right)}_{\tilde{x}\overline{x}\tilde{t}\overline{t}}\hfill \\ \hfill & -\left(b_1-{\displaystyle \frac{a_1{h}^2}{12}}\right)h\sum _{j=1}^{J-1}{\left({\overline{U}}_j^n\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}}+\left(b_2-{\displaystyle \frac{a_2{h}^2}{6}}\right)h\sum _{j=1}^{J-1}{\left(U_j^n\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{t}\overline{t}}+{\displaystyle \frac{b_2{h}^3}{12}}\sum _{j=1}^{J-1}{\left(U_j^n\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{t}\overline{t}}\hfill \\ \hfill & +ch\sum _{j=1}^{J-1}{\left[{\left(U_j^n\right)}^{2p}\right]}_{\tilde{x}\overline{x}}+{\displaystyle \frac{c{h}^3}{6}}\sum _{j=1}^{J-1}{\left[{\left(U_j^n\right)}^{2p}\right]}_{\tilde{x}\overline{x}\tilde{x}\overline{x}}=0.\hfill \end{array}$$

(22)

Noting that $U^n\in Z_h^0$, we can deduce

$$p_1=h\sum _{j=1}^{J-1}{\left(U_j^n\right)}_{\tilde{t}\overline{t}}={\displaystyle \frac{h}{{\tau }^2}}\sum _{j=1}^{J-1}(U_j^{n+1}-2U_j^n+U_j^{n-1}),$$

(23)

$$\begin{array}{cc}\hfill & p_2=h\sum _{j=1}^{J-1}{\left({\overline{U}}_j^n\right)}_{\tilde{x}\overline{x}}={\displaystyle \frac{1}{h}}\sum _{j=1}^{J-1}({\overline{U}}_{j+1}^n-2{\overline{U}}_j^n+{\overline{U}}_{j-1}^n)={\displaystyle \frac{1}{h}}\sum _{j=1}^{J-1}\left[({\overline{U}}_{j+1}^n-{\overline{U}}_j^n)-({\overline{U}}_j^n-{\overline{U}}_{j-1}^n)\right]\hfill \\ \hfill & ={\displaystyle \frac{1}{h}}\sum _{j=1}^{J-1}({\overline{U}}_{j+1}^n-{\overline{U}}_j^n)-{\displaystyle \frac{1}{h}}\sum _{j=1}^{J-1}({\overline{U}}_j^n-{\overline{U}}_{j-1}^n)={\displaystyle \frac{1}{h}}\left[({\overline{U}}_{J+1}^n-{\overline{U}}_J^n)-({\overline{U}}_1^n-{\overline{U}}_0^n)\right]=0,\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill & p_3=h\sum _{j=1}^{J-1}{\left({\overline{U}}_j^n\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}}={\displaystyle \frac{1}{h^3}}\sum _{j=1}^{J-1}({\overline{U}}_{j+2}^n-4{\overline{U}}_{j+1}^n+6{\overline{U}}_j^n-4{\overline{U}}_{j-1}^n+{\overline{U}}_{j-2}^n)\hfill \\ \hfill & ={\displaystyle \frac{1}{h^3}}\sum _{j=1}^{J-1}\left[({\overline{U}}_{j+2}^n-{\overline{U}}_{j+1}^n)-3({\overline{U}}_{j+1}^n-{\overline{U}}_j^n)+3({\overline{U}}_j^n-{\overline{U}}_{j-1}^n)-({\overline{U}}_{j-1}^n-{\overline{U}}_{j-2}^n)\right]\hfill \\ \hfill & ={\displaystyle \frac{1}{h^3}}\left[({\overline{U}}_{J+1}^n-{\overline{U}}_2^n)-3({\overline{U}}_J^n-{\overline{U}}_1^n)+3({\overline{U}}_{J-1}^n-{\overline{U}}_0^n)-({\overline{U}}_{J-2}^n-{\overline{U}}_{-1}^n)\right]=0,\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill & p_4=h\sum _{j=1}^{J-1}{\left({\overline{U}}_j^n\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}}={\displaystyle \frac{1}{h^5}}\sum _{j=1}^{J-1}({\overline{U}}_{j+3}^n-6{\overline{U}}_{j+2}^n+15{\overline{U}}_{j+1}^n-20{\overline{U}}_j^n+15{\overline{U}}_{j-1}^n-6{\overline{U}}_{j-2}^n+{\overline{U}}_{j-3}^n)\hfill \\ \hfill & ={\displaystyle \frac{1}{h^5}}[({\overline{U}}_{J+2}^n-{\overline{U}}_3^n)-5({\overline{U}}_{J+1}^n-{\overline{U}}_2^n)+10({\overline{U}}_J^n-{\overline{U}}_1^n)-10({\overline{U}}_{J-1}^n-{\overline{U}}_0^n)\hfill \\ \hfill & +5({\overline{U}}_{J-2}^n-{\overline{U}}_{-1}^n)-({\overline{U}}_{J-3}^n-{\overline{U}}_{-2}^n)]=0,\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill & p_5=h\sum _{j=1}^{J-1}{\left(U_j^n\right)}_{\tilde{x}\overline{x}\tilde{t}\overline{t}}={\displaystyle \frac{1}{h}}\sum _{j=1}^{J-1}\left[{(U_{j+1}^n-2U_j^n+U_{j-1}^n)}_{\tilde{t}\overline{t}}\right]\hfill \\ \hfill & ={\displaystyle \frac{1}{h}}\sum _{j=1}^{J-1}{(U_{j+1}^n-U_j^n)}_{\tilde{t}\overline{t}}-{\displaystyle \frac{1}{h}}\sum _{j=1}^{J-1}{(U_j^n-U_{j-1}^n)}_{\tilde{t}\overline{t}}\hfill \\ \hfill & ={\displaystyle \frac{1}{h}}{\left[(U_{J+1}^n-U_J^n)-(U_1^n-U_0^n)\right]}_{\tilde{t}\overline{t}}=0.\hfill \end{array}$$

(27)

Similarly, we obtain

$$\begin{array}{cc}\hfill & p_6=h\sum _{j=1}^{J-1}{\left[{\left(U_j^n\right)}^{2p}\right]}_{\tilde{x}\overline{x}}=0,p_7=h\sum _{j=1}^{J-1}{\left[{\left(U_j^n\right)}^{2p}\right]}_{\tilde{x}\overline{x}\tilde{x}\overline{x}}=0,\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill & p_8=h\sum _{j=1}^{J-1}{\left(U_j^n\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{t}\overline{t}}=0,p_9=h\sum _{j=1}^{J-1}{\left(U_j^n\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{t}\overline{t}}=0.\hfill \end{array}$$

(29)

Substituting Equations (23)–(29) into Equation (22), we obtain

$$\begin{array}{cc}\hfill & h\sum _{j=1}^{J-1}{\left(U_j^n\right)}_{\tilde{t}\overline{t}}={\displaystyle \frac{h}{{\tau }^2}}\sum _{j=1}^{J-1}(U_j^{n+1}-2U_j^n+U_j^{n-1})=0;\hfill \end{array}$$

that is,

$$\begin{array}{cc}\hfill & {\displaystyle \frac{h}{\tau }}\sum _{j=1}^{J-1}(U_j^{n+1}-U_j^n)={\displaystyle \frac{h}{\tau }}\sum _{j=1}^{J-1}(U_j^n-U_j^{n-1}),\hfill \end{array}$$

which yields $R^n=R^{n-1}=···=R^0$.

Additionally, as indicated by Equation (20), we obtain

$$\begin{array}{cc}\hfill & R^0={\displaystyle \frac{h}{\tau }}\sum _{j=1}^{J-1}(U_j^1-U_j^0)={\displaystyle \frac{h}{\tau }}\sum _{j=1}^{J-1}(U_j^0-U_j^{-1})\hfill \\ \hfill & ={\displaystyle \frac{h}{\tau }}\sum _{j=1}^{J-1}[U_j^0-U_j^1+2\tau \psi \left(x_j\right)+O\left({\tau }^3\right)]\hfill \\ \hfill & =-R^0+2h\sum _{j=1}^{J-1}\psi \left(x_j\right)+O\left({\tau }^{2}h\right),\hfill \end{array}$$

which yields ${\displaystyle R^0=h\sum _{j=1}^{J-1}\psi \left(x_j\right)+O\left({\tau }^{2}h\right)}$. This completes the proof.  □

Theorem 3. 

Let $U^n\in Z_h^0$ represent the solution to Equations (16)–(18) and let $V^n\in Z_h^0$ denote the solution to Equation (21). It can be inferred that the discrete energy is conserved, such that $E^n=E^{n-1}=\cdots =E^0$, where

$$\begin{array}{cc}\hfill & E^n\equiv {\parallel V_{\tilde{x}}^{n+\frac{1}{2}}\parallel }^2+{\displaystyle \frac{k^2}{2}}\left(\parallel U^{n+1}{\parallel }^2+{\parallel U^n\parallel }^2\right)+{\displaystyle \frac{1}{2}}\left(a_1-{\displaystyle \frac{k^2{h}^2}{6}}\right)\left(\parallel U_{\tilde{x}}^{n+1}{\parallel }^2+{\parallel U_{\tilde{x}}^n\parallel }^2\right)\hfill \\ \hfill & +\left(a_2-{\displaystyle \frac{h^2}{4}}\right){\parallel U_{\overline{t}}^{n+1}\parallel }^2+{\displaystyle \frac{1}{2}}\left(b_1-{\displaystyle \frac{a_1{h}^2}{12}}\right)\left(\parallel U_{\tilde{x}\overline{x}}^{n+1}{\parallel }^2+{\parallel U_{\tilde{x}\overline{x}}^n\parallel }^2\right)\hfill \\ \hfill & +\left(b_2-{\displaystyle \frac{a_2{h}^2}{6}}\right)\parallel U_{\tilde{x}\overline{t}}^{n+1}{\parallel }^2-{\displaystyle \frac{b_2{h}^2}{12}}{\parallel U_{\tilde{t}\overline{t}}^{n+1}\parallel }^2\hfill \\ \hfill & -{\displaystyle \frac{ch\tau }{6}}\sum _{k=0}^n\left\{\sum _{j=1}^{J-1}\left[{\left(U_{j+1}^k\right)}^{2p}+4{\left(U_j^k\right)}^{2p}+{\left(U_{j-1}^k\right)}^{2p}\right]{(U_j^{k+1}+U_j^k)}_{\overline{t}}\right\},\hfill \end{array}$$

where $0\le n\le N-1$.

Proof. 

By computing the inner product of Equation (16) with $V^{n+\frac{1}{2}}+V^{n-\frac{1}{2}}$, we obtain

$$\begin{array}{cc}\hfill & \langle U_{\tilde{t}\overline{t}}^n,V^{n+\frac{1}{2}}+V^{n-\frac{1}{2}}\rangle -k^2\langle {\overline{U}}_{\tilde{x}\overline{x}}^n,V^{n+\frac{1}{2}}+V^{n-\frac{1}{2}}\rangle +\left(a_1-{\displaystyle \frac{k^2{h}^2}{6}}\right)\langle {\overline{U}}_{\tilde{x}\overline{x}\tilde{x}\overline{x}}^n,V^{n+\frac{1}{2}}+V^{n-\frac{1}{2}}\rangle \hfill \\ \hfill & -\left(a_2-{\displaystyle \frac{h^2}{4}}\right)\langle U_{\tilde{x}\overline{x}\tilde{t}\overline{t}}^n,V^{n+\frac{1}{2}}+V^{n-\frac{1}{2}}\rangle -\left(b_1-{\displaystyle \frac{a_1{h}^2}{12}}\right)\langle {\overline{U}}_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}}^n,V^{n+\frac{1}{2}}+V^{n-\frac{1}{2}}\rangle \hfill \\ \hfill & +\left(b_2-{\displaystyle \frac{a_2{h}^2}{6}}\right)\langle U_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{t}\overline{t}}^n,V^{n+\frac{1}{2}}+V^{n-\frac{1}{2}}\rangle +{\displaystyle \frac{b_2{h}^2}{12}}\langle U_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{t}\overline{t}}^n,V^{n+\frac{1}{2}}+V^{n-\frac{1}{2}}\rangle \hfill \\ \hfill & +c\langle {\left(U^n\right)}_{\tilde{x}\overline{x}}^{2p},V^{n+\frac{1}{2}}+V^{n-\frac{1}{2}}\rangle +{\displaystyle \frac{c{h}^2}{6}}\langle {\left(U^n\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}}^{2p},V^{n+\frac{1}{2}}+V^{n-\frac{1}{2}}\rangle =0.\hfill \end{array}$$

(30)

Utilizing Lemmas 1 and 2, along with Equation (21), a simple computation yields

$$\begin{array}{cc}\hfill & q_1=\langle U_{\tilde{t}\overline{t}}^n,V^{n+\frac{1}{2}}+V^{n-\frac{1}{2}}\rangle =\langle {(V_{\tilde{x}\overline{x}}^{n+{\displaystyle \frac{1}{2}}})}_{\overline{t}},V^{n+\frac{1}{2}}+V^{n-\frac{1}{2}}\rangle \hfill \\ \hfill & ={\displaystyle \frac{1}{\tau }}\langle V_{\tilde{x}\overline{x}}^{n+\frac{1}{2}}-V_{\tilde{x}\overline{x}}^{n-\frac{1}{2}},V^{n+\frac{1}{2}}+V^{n-\frac{1}{2}}\rangle =-{\displaystyle \frac{1}{\tau }}(\parallel V_{\tilde{x}}^{n+\frac{1}{2}}{\parallel }^2-\parallel V_{\tilde{x}}^{n-\frac{1}{2}}{\parallel }^2),\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill & q_2=\langle {\overline{U}}_{\tilde{x}\overline{x}}^n,V^{n+\frac{1}{2}}+V^{n-\frac{1}{2}}\rangle ={\displaystyle \frac{1}{2}}\langle U^{n+1}+U^{n-1},{(V^{n+{\displaystyle \frac{1}{2}}}+V^{n-{\displaystyle \frac{1}{2}}})}_{\tilde{x}\overline{x}}\rangle \hfill \\ \hfill & ={\displaystyle \frac{1}{2}}\langle U^{n+1}+U^{n-1},{(U^n+U^{n-1})}_{\tilde{t}}\rangle ={\displaystyle \frac{1}{2\tau }}\langle U^{n+1}+U^{n-1},U^{n+1}-U^{n-1}\rangle \hfill \\ \hfill & ={\displaystyle \frac{1}{2\tau }}(\parallel U^{n+1}{\parallel }^2-\parallel U^{n-1}{\parallel }^2),\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill & q_3=\langle {\overline{U}}_{\tilde{x}\overline{x}\tilde{x}\overline{x}}^n,V^{n+\frac{1}{2}}+V^{n-\frac{1}{2}}\rangle ={\displaystyle \frac{1}{2}}\langle {(U^{n+1}+U^{n-1})}_{\tilde{x}\overline{x}},{(V^{n+{\displaystyle \frac{1}{2}}}+V^{n-{\displaystyle \frac{1}{2}}})}_{\tilde{x}\overline{x}}\rangle \hfill \\ \hfill & ={\displaystyle \frac{1}{2}}\langle {(U^{n+1}+U^{n-1})}_{\tilde{x}\overline{x}},{(U^n+U^{n-1})}_{\tilde{t}}\rangle ={\displaystyle \frac{1}{2\tau }}\langle {(U^{n+1}+U^{n-1})}_{\tilde{x}\overline{x}},U^{n+1}-U^{n-1}\rangle \hfill \\ \hfill & =-{\displaystyle \frac{1}{2\tau }}(\parallel U_{\tilde{x}}^{n+1}{\parallel }^2-\parallel U_{\tilde{x}}^{n-1}{\parallel }^2),\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill & q_4=\langle U_{\tilde{x}\overline{x}\tilde{t}\overline{t}}^n,V^{n+\frac{1}{2}}+V^{n-\frac{1}{2}}\rangle =\langle {(V_{\tilde{x}\overline{x}}^{n+{\displaystyle \frac{1}{2}}})}_{\tilde{x}\overline{x}\overline{t}},V^{n+\frac{1}{2}}+V^{n-\frac{1}{2}}\rangle \hfill \\ \hfill & ={\displaystyle \frac{1}{\tau }}\langle V_{\tilde{x}\overline{x}\tilde{x}\overline{x}}^{n+\frac{1}{2}}-V_{\tilde{x}\overline{x}\tilde{x}\overline{x}}^{n-\frac{1}{2}},V^{n+\frac{1}{2}}+V^{n-\frac{1}{2}}\rangle ={\displaystyle \frac{1}{\tau }}(\parallel V_{\tilde{x}\overline{x}}^{n+\frac{1}{2}}{\parallel }^2-\parallel V_{\tilde{x}\overline{x}}^{n-\frac{1}{2}}{\parallel }^2)\hfill \\ \hfill & ={\displaystyle \frac{1}{\tau }}(\parallel U_{\tilde{t}}^n{\parallel }^2-\parallel U_{\tilde{t}}^{n-1}{\parallel }^2)={\displaystyle \frac{1}{\tau }}(\parallel U_{\overline{t}}^{n+1}{\parallel }^2-\parallel U_{\overline{t}}^n{\parallel }^2),\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill & q_5=\langle {\overline{U}}_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}}^n,V^{n+\frac{1}{2}}+V^{n-\frac{1}{2}}\rangle ={\displaystyle \frac{1}{2}}\langle {(U^{n+1}+U^{n-1})}_{\tilde{x}\overline{x}\tilde{x}\overline{x}},{(V^{n+{\displaystyle \frac{1}{2}}}+V^{n-{\displaystyle \frac{1}{2}}})}_{\tilde{x}\overline{x}}\rangle \hfill \\ \hfill & ={\displaystyle \frac{1}{2}}\langle {(U^{n+1}+U^{n-1})}_{\tilde{x}\overline{x}\tilde{x}\overline{x}},{(U^n+U^{n-1})}_{\tilde{t}}\rangle ={\displaystyle \frac{1}{2\tau }}\langle {(U^{n+1}+U^{n-1})}_{\tilde{x}\overline{x}\tilde{x}\overline{x}},U^{n+1}-U^{n-1}\rangle \hfill \\ \hfill & ={\displaystyle \frac{1}{2\tau }}(\parallel U_{\tilde{x}\overline{x}}^{n+1}{\parallel }^2-\parallel U_{\tilde{x}\overline{x}}^{n-1}{\parallel }^2),\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill & q_6=\langle U_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{t}\overline{t}}^n,V^{n+\frac{1}{2}}+V^{n-\frac{1}{2}}\rangle =\langle {(V_{\tilde{x}\overline{x}}^{n+{\displaystyle \frac{1}{2}}})}_{\tilde{x}\overline{x}\tilde{x}\overline{x}\overline{t}},V^{n+\frac{1}{2}}+V^{n-\frac{1}{2}}\rangle \hfill \\ \hfill & ={\displaystyle \frac{1}{\tau }}\langle V_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}}^{n+\frac{1}{2}}-V_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}}^{n-\frac{1}{2}},V^{n+\frac{1}{2}}+V^{n-\frac{1}{2}}\rangle =-{\displaystyle \frac{1}{\tau }}(\parallel V_{\tilde{x}\overline{x}\tilde{x}}^{n+\frac{1}{2}}{\parallel }^2-\parallel V_{\tilde{x}\overline{x}\tilde{x}}^{n-\frac{1}{2}}{\parallel }^2)\hfill \\ \hfill & =-{\displaystyle \frac{1}{\tau }}(\parallel U_{\tilde{x}\tilde{t}}^n{\parallel }^2-\parallel U_{\tilde{x}\tilde{t}}^{n-1}{\parallel }^2)=-{\displaystyle \frac{1}{\tau }}(\parallel U_{\tilde{x}\overline{t}}^{n+1}{\parallel }^2-\parallel U_{\tilde{x}\overline{t}}^n{\parallel }^2),\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill & q_7=\langle U_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{t}\overline{t}}^n,V^{n+\frac{1}{2}}+V^{n-\frac{1}{2}}\rangle =\langle {(V_{\tilde{x}\overline{x}}^{n+{\displaystyle \frac{1}{2}}})}_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}\overline{t}},V^{n+\frac{1}{2}}+V^{n-\frac{1}{2}}\rangle \hfill \\ \hfill & ={\displaystyle \frac{1}{\tau }}\langle V_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}}^{n+\frac{1}{2}}-V_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}}^{n-\frac{1}{2}},V^{n+\frac{1}{2}}+V^{n-\frac{1}{2}}\rangle ={\displaystyle \frac{1}{\tau }}(\parallel V_{\tilde{x}\overline{x}\tilde{x}\overline{x}}^{n+\frac{1}{2}}{\parallel }^2-\parallel V_{\tilde{x}\overline{x}\tilde{x}\overline{x}}^{n-\frac{1}{2}}{\parallel }^2)\hfill \\ \hfill & ={\displaystyle \frac{1}{\tau }}(\parallel U_{\tilde{t}\tilde{t}}^n{\parallel }^2-\parallel U_{\tilde{t}\tilde{t}}^{n-1}{\parallel }^2)={\displaystyle \frac{1}{\tau }}(\parallel U_{\tilde{t}\overline{t}}^{n+1}{\parallel }^2-\parallel U_{\tilde{t}\overline{t}}^n{\parallel }^2),\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill & q_8=\langle {(U^n)}_{\tilde{x}\overline{x}}^{2p},V^{n+\frac{1}{2}}+V^{n-\frac{1}{2}}\rangle =\langle {(U^n)}^{2p},{(V^{n+{\displaystyle \frac{1}{2}}}+V^{n-{\displaystyle \frac{1}{2}}})}_{\tilde{x}\overline{x}}\rangle \hfill \\ \hfill & =\langle {(U^n)}^{2p},{(U^n+U^{n-1})}_{\tilde{t}}\rangle =\langle {(U^n)}^{2p},{(U^{n+1}+U^n)}_{\overline{t}}\rangle =h\sum _{j=1}^{J-1}\left[{(U_j^n)}^{2p}{(U_j^{n+1}+U_j^n)}_{\overline{t}}\right]\hfill \\ \hfill & =h\sum _{k=0}^n\left\{\sum _{j=1}^{J-1}\left[{(U_j^k)}^{2p}{(U_j^{k+1}+U_j^k)}_{\overline{t}}\right]\right\}-h\sum _{k=0}^{n-1}\left\{\sum _{j=1}^{J-1}\left[{(U_j^k)}^{2p}{(U_j^{k+1}+U_j^k)}_{\overline{t}}\right]\right\},\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill & q_9=\langle {(U^n)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}}^{2p},V^{n+\frac{1}{2}}+V^{n-\frac{1}{2}}\rangle =\langle {(U^n)}_{\tilde{x}\overline{x}}^{2p},{(V^{n+{\displaystyle \frac{1}{2}}}+V^{n-{\displaystyle \frac{1}{2}}})}_{\tilde{x}\overline{x}}\rangle \hfill \\ \hfill & =\langle {(U^n)}_{\tilde{x}\overline{x}}^{2p},{(U^n+U^{n-1})}_{\tilde{t}}\rangle =\langle {(U^n)}_{\tilde{x}\overline{x}}^{2p},{(U^{n+1}+U^n)}_{\overline{t}}\rangle =h\sum _{j=1}^{J-1}\left[{(U_j^n)}_{\tilde{x}\overline{x}}^{2p}{(U_j^{n+1}+U_j^n)}_{\overline{t}}\right]\hfill \\ \hfill & =h\sum _{k=0}^n\left\{\sum _{j=1}^{J-1}\left[{\left(U_j^k\right)}_{\tilde{x}\overline{x}}^{2p}{(U_j^{k+1}+U_j^k)}_{\overline{t}}\right]\right\}-h\sum _{k=0}^{n-1}\left\{\sum _{j=1}^{J-1}\left[{\left(U_j^k\right)}_{\tilde{x}\overline{x}}^{2p}{(U_j^{k+1}+U_j^k)}_{\overline{t}}\right]\right\}.\hfill \end{array}$$

(39)

As a result, following Equations (38) and (39), we arrive at the following conclusions

$$\begin{array}{cc}\hfill & c\langle {\left(U^n\right)}_{\tilde{x}\overline{x}}^{2p},V^{n+\frac{1}{2}}+V^{n-\frac{1}{2}}\rangle +{\displaystyle \frac{c{h}^2}{6}}\langle {\left(U^n\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}}^{2p},V^{n+\frac{1}{2}}+V^{n-\frac{1}{2}}\rangle \hfill \\ \hfill & =ch\sum _{k=0}^n\left\{\sum _{j=1}^{J-1}\left[{\left(U_j^k\right)}^{2p}{(U_j^{k+1}+U_j^k)}_{\overline{t}}\right]\right\}+{\displaystyle \frac{c{h}^3}{6}}\sum _{k=0}^n\left\{\sum _{j=1}^{J-1}\left[{\left(U_j^k\right)}_{\tilde{x}\overline{x}}^{2p}{(U_j^{k+1}+U_j^k)}_{\overline{t}}\right]\right\}\hfill \\ \hfill & -ch\sum _{k=0}^{n-1}\left\{\sum _{j=1}^{J-1}\left[{\left(U_j^k\right)}^{2p}{(U_j^{k+1}+U_j^k)}_{\overline{t}}\right]\right\}-{\displaystyle \frac{c{h}^3}{6}}\sum _{k=0}^{n-1}\left\{\sum _{j=1}^{J-1}\left[{\left(U_j^k\right)}_{\tilde{x}\overline{x}}^{2p}{(U_j^{k+1}+U_j^k)}_{\overline{t}}\right]\right\}\hfill \\ \hfill & ={\displaystyle \frac{ch}{6}}\sum _{k=0}^n\left\{\sum _{j=1}^{J-1}\left[{\left(U_{j+1}^k\right)}^{2p}+4{\left(U_j^k\right)}^{2p}+{\left(U_{j-1}^k\right)}^{2p}\right]{(U_j^{k+1}+U_j^k)}_{\overline{t}}\right\}\hfill \\ \hfill & ={\displaystyle \frac{ch}{6}}\sum _{k=0}^{n-1}\left\{\sum _{j=1}^{J-1}\left[{\left(U_{j+1}^k\right)}^{2p}+4{\left(U_j^k\right)}^{2p}+{\left(U_{j-1}^k\right)}^{2p}\right]{(U_j^{k+1}+U_j^k)}_{\overline{t}}\right\}.\hfill \end{array}$$

(40)

By substituting Equations (31)–(37) and (40) into Equation (30), we obtain

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{\tau }}\parallel V_{\tilde{x}}^{n+\frac{1}{2}}{\parallel }^2+{\displaystyle \frac{k^2}{2\tau }}\parallel U^{n+1}{\parallel }^2+{\displaystyle \frac{1}{2\tau }}\left(a_1-{\displaystyle \frac{k^2{h}^2}{6}}\right)\parallel U_{\tilde{x}}^{n+1}{\parallel }^2+{\displaystyle \frac{1}{\tau }}\left(a_2-{\displaystyle \frac{h^2}{4}}\right){\parallel U_{\overline{t}}^{n+1}\parallel }^2\hfill \\ \hfill & +{\displaystyle \frac{1}{2\tau }}\left(b_1-{\displaystyle \frac{a_1{h}^2}{12}}\right)\parallel U_{\tilde{x}\overline{x}}^{n+1}{\parallel }^2+{\displaystyle \frac{1}{\tau }}\left(b_2-{\displaystyle \frac{a_2{h}^2}{6}}\right)\parallel U_{\tilde{x}\overline{t}}^{n+1}{\parallel }^2-{\displaystyle \frac{b_2{h}^2}{12\tau }}{\parallel U_{\tilde{t}\overline{t}}^{n+1}\parallel }^2\hfill \\ \hfill & -{\displaystyle \frac{ch}{6}}\sum _{k=0}^n\left\{\sum _{j=1}^{J-1}\left[{\left(U_{j+1}^k\right)}^{2p}+4{\left(U_j^k\right)}^{2p}+{\left(U_{j-1}^k\right)}^{2p}\right]{(U_j^{k+1}+U_j^k)}_{\overline{t}}\right\}\hfill \\ \hfill & ={\displaystyle \frac{1}{\tau }}\parallel V_{\tilde{x}}^{n-\frac{1}{2}}{\parallel }^2+{\displaystyle \frac{k^2}{2\tau }}\parallel U^{n-1}{\parallel }^2+{\displaystyle \frac{1}{2\tau }}\left(a_1-{\displaystyle \frac{k^2{h}^2}{6}}\right)\parallel U_{\tilde{x}}^{n-1}{\parallel }^2+{\displaystyle \frac{1}{\tau }}\left(a_2-{\displaystyle \frac{h^2}{4}}\right){\parallel U_{\overline{t}}^n\parallel }^2\hfill \\ \hfill & +{\displaystyle \frac{1}{2\tau }}\left(b_1-{\displaystyle \frac{a_1{h}^2}{12}}\right)\parallel U_{\tilde{x}\overline{x}}^{n-1}{\parallel }^2+{\displaystyle \frac{1}{\tau }}\left(b_2-{\displaystyle \frac{a_2{h}^2}{6}}\right)\parallel U_{\tilde{x}\overline{t}}^n{\parallel }^2-{\displaystyle \frac{b_2{h}^2}{12\tau }}{\parallel U_{\tilde{t}\overline{t}}^n\parallel }^2\hfill \\ \hfill & -{\displaystyle \frac{ch}{6}}\sum _{k=0}^{n-1}\left\{\sum _{j=1}^{J-1}\left[{\left(U_{j+1}^k\right)}^{2p}+4{\left(U_j^k\right)}^{2p}+{\left(U_{j-1}^k\right)}^{2p}\right]{(U_j^{k+1}+U_j^k)}_{\overline{t}}\right\}.\hfill \end{array}$$

(41)

Multiplying Equation (41) by $\tau$, and subsequently adding the formula

$$\begin{array}{cc}\hfill & {\displaystyle \frac{k^2}{2}}\parallel U^n{\parallel }^2+{\displaystyle \frac{1}{2}}\left(a_1-{\displaystyle \frac{k^2{h}^2}{6}}\right)\parallel U_{\tilde{x}}^n{\parallel }^2+{\displaystyle \frac{1}{2}}\left(b_1-{\displaystyle \frac{a_1{h}^2}{12}}\right){\parallel U_{\tilde{x}\overline{x}}^n\parallel }^2\hfill \end{array}$$

to both sides, we obtain

$$\begin{array}{cc}\hfill & \parallel V_{\tilde{x}}^{n+\frac{1}{2}}{\parallel }^2+{\displaystyle \frac{k^2}{2}}\left(\parallel U^{n+1}{\parallel }^2+{\parallel U^n\parallel }^2\right)+{\displaystyle \frac{1}{2}}\left(a_1-{\displaystyle \frac{k^2{h}^2}{6}}\right)\left(\parallel U_{\tilde{x}}^{n+1}{\parallel }^2+{\parallel U_{\tilde{x}}^n\parallel }^2\right)\hfill \\ \hfill & +\left(a_2-{\displaystyle \frac{h^2}{4}}\right)\parallel U_{\overline{t}}^{n+1}{\parallel }^2+{\displaystyle \frac{1}{2}}\left(b_1-{\displaystyle \frac{a_1{h}^2}{12}}\right)\left(\parallel U_{\tilde{x}\overline{x}}^{n+1}{\parallel }^2+{\parallel U_{\tilde{x}\overline{x}}^n\parallel }^2\right)+\left(b_2-{\displaystyle \frac{a_2{h}^2}{6}}\right){\parallel U_{\tilde{x}\overline{t}}^{n+1}\parallel }^2\hfill \\ \hfill & -{\displaystyle \frac{b_2{h}^2}{12}}{\parallel U_{\tilde{t}\overline{t}}^{n+1}\parallel }^2-{\displaystyle \frac{ch\tau }{6}}\sum _{k=0}^n\left\{\sum _{j=1}^{J-1}\left[{\left(U_{j+1}^k\right)}^{2p}+4{\left(U_j^k\right)}^{2p}+{\left(U_{j-1}^k\right)}^{2p}\right]{(U_j^{k+1}+U_j^k)}_{\overline{t}}\right\}\hfill \\ \hfill & =\parallel V_{\tilde{x}}^{n-\frac{1}{2}}{\parallel }^2+{\displaystyle \frac{k^2}{2}}\left(\parallel U^n{\parallel }^2+{\parallel U^{n-1}\parallel }^2\right)+{\displaystyle \frac{1}{2}}\left(a_1-{\displaystyle \frac{k^2{h}^2}{6}}\right)\left(\parallel U_{\tilde{x}}^n{\parallel }^2+{\parallel U_{\tilde{x}}^{n-1}\parallel }^2\right)\hfill \\ \hfill & +\left(a_2-{\displaystyle \frac{h^2}{4}}\right)\parallel U_{\overline{t}}^n{\parallel }^2+{\displaystyle \frac{1}{2}}\left(b_1-{\displaystyle \frac{a_1{h}^2}{12}}\right)\left(\parallel U_{\tilde{x}\overline{x}}^n{\parallel }^2+{\parallel U_{\tilde{x}\overline{x}}^{n-1}\parallel }^2\right)+\left(b_2-{\displaystyle \frac{a_2{h}^2}{6}}\right){\parallel U_{\tilde{x}\overline{t}}^n\parallel }^2\hfill \\ \hfill & -{\displaystyle \frac{b_2{h}^2}{12}}{\parallel U_{\tilde{t}\overline{t}}^n\parallel }^2-{\displaystyle \frac{ch\tau }{6}}\sum _{k=0}^{n-1}\left\{\sum _{j=1}^{J-1}\left[{\left(U_{j+1}^k\right)}^{2p}+4{\left(U_j^k\right)}^{2p}+{\left(U_{j-1}^k\right)}^{2p}\right]{(U_j^{k+1}+U_j^k)}_{\overline{t}}\right\};\hfill \end{array}$$

(42)

that is, $E^n=E^{n-1}=···=E^0$.

In a similar manner, by computing the inner product of Equation (19) with $V^{{\displaystyle \frac{1}{2}}}+V^{-\frac{1}{2}}$, we obtain

$$\begin{array}{cc}\hfill & E^0=\parallel V_{\tilde{x}}^{{\displaystyle \frac{1}{2}}}{\parallel }^2+{\displaystyle \frac{k^2}{2}}\left(\parallel U^1{\parallel }^2+{\parallel U^0\parallel }^2\right)+{\displaystyle \frac{1}{2}}\left(a_1-{\displaystyle \frac{k^2{h}^2}{6}}\right)\left(\parallel U_{\tilde{x}}^1{\parallel }^2+{\parallel U_{\tilde{x}}^0\parallel }^2\right)+\left(a_2-{\displaystyle \frac{h^2}{4}}\right){\parallel U_{\overline{t}}^1\parallel }^2\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\left(b_1-{\displaystyle \frac{a_1{h}^2}{12}}\right)\left(\parallel U_{\tilde{x}\overline{x}}^1{\parallel }^2+{\parallel U_{\tilde{x}\overline{x}}^0\parallel }^2\right)+\left(b_2-{\displaystyle \frac{a_2{h}^2}{6}}\right)\parallel U_{\tilde{x}\overline{t}}^1{\parallel }^2-{\displaystyle \frac{b_2{h}^2}{12}}{\parallel U_{\tilde{t}\overline{t}}^1\parallel }^2\hfill \\ \hfill & -{\displaystyle \frac{ch\tau }{6}}\sum _{j=1}^{J-1}\left\{\left[{\left(U_{j+1}^0\right)}^{2p}+4{\left(U_j^0\right)}^{2p}+{\left(U_{j-1}^0\right)}^{2p}\right]{(U_j^1+U_j^0)}_{\overline{t}}\right\}\hfill \\ \hfill & =\parallel V_{\tilde{x}}^{-\frac{1}{2}}{\parallel }^2+{\displaystyle \frac{k^2}{2}}\left(\parallel U^0{\parallel }^2+{\parallel U^{-1}\parallel }^2\right)+{\displaystyle \frac{1}{2}}\left(a_1-{\displaystyle \frac{k^2{h}^2}{6}}\right)\left(\parallel U_{\tilde{x}}^0{\parallel }^2+{\parallel U_{\tilde{x}}^{-1}\parallel }^2\right)\hfill \\ \hfill & +\left(a_2-{\displaystyle \frac{h^2}{4}}\right){\parallel U_{\overline{t}}^0\parallel }^2+{\displaystyle \frac{1}{2}}\left(b_1-{\displaystyle \frac{a_1{h}^2}{12}}\right)\left(\parallel U_{\tilde{x}\overline{x}}^0{\parallel }^2+{\parallel U_{\tilde{x}\overline{x}}^{-1}\parallel }^2\right)\hfill \\ \hfill & +\left(b_2-{\displaystyle \frac{a_2{h}^2}{6}}\right)\parallel U_{\tilde{x}\overline{t}}^0{\parallel }^2-{\displaystyle \frac{b_2{h}^2}{12}}{\parallel U_{\tilde{t}\overline{t}}^0\parallel }^2,\hfill \end{array}$$

(43)

where $U_j^{-1}=U_j^1-2\tau \psi \left(x_j\right)$, $0\le j\le J$. This completes the proof.  □

Note 1. In Theorem 1, setting

$$\begin{array}{cc}\hfill & \eta \left(t\right)={\displaystyle \frac{2c}{2p+1}}{\int }_{x_l}^{x_r}{u}^{2p+1}dx,\hfill \end{array}$$

we have

$$\begin{array}{cc}\hfill & {\eta }^{\prime }\left(t\right)=2c{\int }_{x_l}^{x_r}{u}^{2p}{u}_{t}dx.\hfill \end{array}$$

By using Simpson’s formula, one obtains

$$\begin{array}{cc}\hfill & {\eta }^{\prime }\left(t^k\right)\approx {\displaystyle \frac{2ch}{6}}\sum _{j=1}^{J-1}\left[{\left(U_{j+1}^k\right)}^{2p}+4{\left(U_j^k\right)}^{2p}+{\left(U_{j-1}^k\right)}^{2p}\right]u_t(x_j,t^k)\hfill \\ \hfill & \approx {\displaystyle \frac{2ch}{6}}\sum _{j=1}^{J-1}\left[{\left(U_{j+1}^k\right)}^{2p}+4{\left(U_j^k\right)}^{2p}+{\left(U_{j-1}^k\right)}^{2p}\right]\left[{\displaystyle \frac{1}{2}}{(U_j^{k+1}+U_j^k)}_{\overline{t}}\right]\hfill \\ \hfill & \approx {\displaystyle \frac{ch}{6}}\sum _{j=1}^{J-1}\left[{\left(U_{j+1}^k\right)}^{2p}+4{\left(U_j^k\right)}^{2p}+{\left(U_{j-1}^k\right)}^{2p}\right]{(U_j^{k+1}+U_j^k)}_{\overline{t}}.\hfill \end{array}$$

We further obtain

$$\begin{array}{cc}\hfill & \eta \left(t\right)\approx {\int }_0^T{\eta }^{\prime }\left(t^k\right)d{t}^k={\displaystyle \frac{ch}{6}}{\int }_0^T\sum _{j=1}^{J-1}\left[{\left(U_{j+1}^k\right)}^{2p}+4{\left(U_j^k\right)}^{2p}+{\left(U_{j-1}^k\right)}^{2p}\right]{(U_j^{k+1}+U_j^k)}_{\overline{t}}d{t}^k\hfill \\ \hfill & \approx {\displaystyle \frac{ch\tau }{6}}\sum _{k=0}^n\left\{\sum _{j=1}^{J-1}\left[{\left(U_{j+1}^k\right)}^{2p}+4{\left(U_j^k\right)}^{2p}+{\left(U_{j-1}^k\right)}^{2p}\right]{(U_j^{k+1}+U_j^k)}_{\overline{t}}\right\},\hfill \end{array}$$

which is an approximation of the continuous term ${\displaystyle \frac{2c}{2p+1}{\int }_{x_l}^{x_r}{u}^{2p+1}dx}$ in Theorem 1.

Theorem 4. 

Let $\phi \left(x\right),\psi \left(x\right)\in H_0^2(\Omega )$; then, it follows that the solution $U^n$ to Equations (16)–(18) satisfies

$$\begin{array}{cc}\hfill & \parallel U^n\parallel \le C,\parallel U_{\tilde{x}}^n\parallel \le C,\parallel U^n{\parallel }_{\infty }\le C,0\le n\le N.\hfill \end{array}$$

Proof. 

We employ mathematical induction to derive the estimate. From Equation (17), it can be deduced that $\parallel U^0\parallel \le C$ and $\parallel U_{\tilde{x}}^0\parallel \le C$. From Lemma 3, we obtain $\parallel U^0{\parallel }_{\infty }\le C$. We will proceed with the assumption that

$$\begin{array}{cc}\hfill & \parallel U^m\parallel \le C,\parallel U_{\tilde{x}}^m\parallel \le C,\parallel U^m{\parallel }_{\infty }\le C,\hfill \end{array}$$

where $m=1,2,···,n$. By taking the inner product of Equation (16) with $U_{\widehat{t}}^n$, we can express the components of the inner product as follows:

$$\begin{array}{cc}\hfill & \langle U_{\tilde{t}\overline{t}}^n,U_{\widehat{t}}^n\rangle -k^2\langle {\overline{U}}_{\tilde{x}\overline{x}}^n,U_{\widehat{t}}^n\rangle +\left(a_1-{\displaystyle \frac{k^2{h}^2}{6}}\right)\langle {\overline{U}}_{\tilde{x}\overline{x}\tilde{x}\overline{x}}^n,U_{\widehat{t}}^n\rangle -\left(a_2-{\displaystyle \frac{h^2}{4}}\right)\langle U_{\tilde{x}\overline{x}\tilde{t}\overline{t}}^n,U_{\widehat{t}}^n\rangle \hfill \\ \hfill & -\left(b_1-{\displaystyle \frac{a_1{h}^2}{12}}\right)\langle {\overline{U}}_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}}^n,U_{\widehat{t}}^n\rangle +\left(b_2-{\displaystyle \frac{a_2{h}^2}{6}}\right)\langle U_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{t}\overline{t}}^n,U_{\widehat{t}}^n\rangle +{\displaystyle \frac{b_2{h}^2}{12}}\langle U_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{t}\overline{t}}^n,U_{\widehat{t}}^n\rangle \hfill \\ \hfill & =-c\langle {\left(U^n\right)}_{\tilde{x}\overline{x}}^{2p},U_{\widehat{t}}^n\rangle -{\displaystyle \frac{c{h}^2}{6}}\langle {\left(U^n\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}}^{2p},U_{\widehat{t}}^n\rangle .\hfill \end{array}$$

(44)

By utilizing Lemmas 1 and 2 in conjunction with the Cauchy–Schwarz inequality [28,32], a simple calculation yields

$$\begin{array}{cc}\hfill & s_1=\langle U_{\tilde{t}\overline{t}}^n,U_{\widehat{t}}^n\rangle ={\displaystyle \frac{1}{2\tau }}\langle U_{\overline{t}}^{n+1}-U_{\overline{t}}^n,U_{\overline{t}}^{n+1}+U_{\overline{t}}^n\rangle ={\displaystyle \frac{1}{2\tau }}(\parallel U_{\overline{t}}^{n+1}{\parallel }^2-\parallel U_{\overline{t}}^n{\parallel }^2),\hfill \end{array}$$

(45)

$$\begin{array}{cc}\hfill & s_2=\langle {\overline{U}}_{\tilde{x}\overline{x}}^n,U_{\widehat{t}}^n\rangle ={\displaystyle \frac{1}{4\tau }}\langle U_{\tilde{x}\overline{x}}^{n+1}+U_{\tilde{x}\overline{x}}^{n-1},U^{n+1}-U^{n-1}\rangle =-{\displaystyle \frac{1}{4\tau }}(\parallel U_{\tilde{x}}^{n+1}{\parallel }^2-\parallel U_{\tilde{x}}^{n-1}{\parallel }^2),\hfill \end{array}$$

(46)

$$\begin{array}{cc}\hfill & s_3=\langle {\overline{U}}_{\tilde{x}\overline{x}\tilde{x}\overline{x}}^n,U_{\widehat{t}}^n\rangle ={\displaystyle \frac{1}{4\tau }}\langle U_{\tilde{x}\overline{x}\tilde{x}\overline{x}}^{n+1}+U_{\tilde{x}\overline{x}\tilde{x}\overline{x}}^{n-1},U^{n+1}-U^{n-1}\rangle ={\displaystyle \frac{1}{4\tau }}(\parallel U_{\tilde{x}\overline{x}}^{n+1}{\parallel }^2-\parallel U_{\tilde{x}\overline{x}}^{n-1}{\parallel }^2),\hfill \end{array}$$

(47)

$$s_4=\langle U_{\tilde{x}\overline{x}\tilde{t}\overline{t}}^n,U_{\widehat{t}}^n\rangle =-\langle {\left(U_{\tilde{x}}^n\right)}_{\tilde{t}\overline{t}},{\left(U_{\tilde{x}}^n\right)}_{\widehat{t}}\rangle =-{\displaystyle \frac{1}{2\tau }}(\parallel U_{\tilde{x}\overline{t}}^{n+1}{\parallel }^2-\parallel U_{\tilde{x}\overline{t}}^n{\parallel }^2),$$

(48)

$$\begin{array}{cc}\hfill & s_5=\langle {\overline{U}}_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}}^n,U_{\widehat{t}}^n\rangle ={\displaystyle \frac{1}{4\tau }}\langle U_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}}^{n+1}+U_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}}^{n-1},U^{n+1}-U^{n-1}\rangle \hfill \\ \hfill & =-{\displaystyle \frac{1}{4\tau }}(\parallel U_{\tilde{x}\overline{x}\tilde{x}}^{n+1}{\parallel }^2-\parallel U_{\tilde{x}\overline{x}\tilde{x}}^{n-1}{\parallel }^2),\hfill \end{array}$$

(49)

$$\begin{array}{cc}\hfill & s_6=\langle U_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{t}\overline{t}}^n,U_{\widehat{t}}^n\rangle =\langle {\left(U_{\tilde{x}\overline{x}}^n\right)}_{\tilde{t}\overline{t}},{\left(U_{\tilde{x}\overline{x}}^n\right)}_{\widehat{t}}\rangle ={\displaystyle \frac{1}{2\tau }}(\parallel U_{\tilde{x}\overline{x}\overline{t}}^{n+1}{\parallel }^2-\parallel U_{\tilde{x}\overline{x}\overline{t}}^n{\parallel }^2),\hfill \end{array}$$

(50)

$$s_7=\langle U_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{t}\overline{t}}^n,U_{\widehat{t}}^n\rangle =-\langle {\left(U_{\tilde{x}\overline{x}\tilde{x}}^n\right)}_{\tilde{t}\overline{t}},{\left(U_{\tilde{x}\overline{x}\tilde{x}}^n\right)}_{\widehat{t}}\rangle =-{\displaystyle \frac{1}{2\tau }}(\parallel U_{\tilde{x}\overline{x}\tilde{x}\overline{t}}^{n+1}{\parallel }^2-\parallel U_{\tilde{x}\overline{x}\tilde{x}\overline{t}}^n{\parallel }^2),$$

(51)

$$\begin{array}{cc}\hfill & s_8=\langle {\left(U^n\right)}_{\tilde{x}\overline{x}}^{2p},U_{\widehat{t}}^n\rangle =-\langle {\left(U^n\right)}_{\tilde{x}}^{2p},U_{\tilde{x}\widehat{t}}^n\rangle =-h\sum _{j=1}^{J-1}\left[{\left(U_j^n\right)}_{\tilde{x}}^{2p}{\left(U_j^n\right)}_{\tilde{x}\widehat{t}}\right]\hfill \\ \hfill & =-h\sum _{j=1}^{J-1}\left[{\left(U_j^n\right)}_{\tilde{x}}^{2p-1}{U}_{j+1}^n+{\left(U_j^n\right)}^{2p-1}{\left(U_j^n\right)}_{\tilde{x}}\right]{\left(U_j^n\right)}_{\tilde{x}\widehat{t}}\hfill \\ \hfill & \le h\parallel U_{\tilde{x}}^n{\parallel }_{\infty }^{2p-1}\sum _{j=1}^{J-1}\left[|U_{j+1}^n|·|{\left(U_j^n\right)}_{\tilde{x}\widehat{t}}|\right]+h{\parallel U^n\parallel }_{\infty }^{2p-1}\sum _{j=1}^{J-1}\left[|{\left(U_j^n\right)}_{\tilde{x}}|·|{\left(U_j^n\right)}_{\tilde{x}\widehat{t}}|\right]\hfill \\ \hfill & \le C(\parallel U^n{\parallel }^2+\parallel U_{\tilde{x}}^n{\parallel }^2+\parallel U_{\tilde{x}\widehat{t}}^n{\parallel }^2).\hfill \end{array}$$

Since

$$\begin{array}{cc}\hfill & U_{\tilde{x}\widehat{t}}^n={\displaystyle \frac{1}{2}}(U_{\tilde{x}\overline{t}}^n+U_{\tilde{x}\overline{t}}^{n+1}),\parallel U^n\parallel \le C\parallel U_{\tilde{x}}^n\parallel ,\hfill \end{array}$$

then we finally have

$$\begin{array}{cc}\hfill & s_8=\langle {\left(U^n\right)}_{\tilde{x}\overline{x}}^{2p},U_{\widehat{t}}^n\rangle \le C(\parallel U_{\tilde{x}}^n{\parallel }^2+\parallel U_{\tilde{x}\overline{t}}^n{\parallel }^2+\parallel U_{\tilde{x}\overline{t}}^{n+1}{\parallel }^2).\hfill \end{array}$$

(52)

Similarly, we have

$$\begin{array}{cc}\hfill & s_9=h^2\langle {\left(U^n\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}}^{2p},U_{\widehat{t}}^n\rangle =h^2\langle {\left(U^n\right)}_{\tilde{x}\overline{x}}^{2p},U_{\tilde{x}\overline{x}\widehat{t}}^n\rangle =h^3\sum _{j=1}^{J-1}\left[{\left(U_j^n\right)}_{\tilde{x}\overline{x}}^{2p}{\left(U_j^n\right)}_{\tilde{x}\overline{x}\widehat{t}}\right]\hfill \\ \hfill & =h\sum _{j=1}^{J-1}\left[{\left(U_{j+1}^n\right)}^{2p}-2{\left(U_j^n\right)}^{2p}+{\left(U_{j-1}^n\right)}^{2p}\right]{\left(U_j^n\right)}_{\tilde{x}\overline{x}\widehat{t}}\le C(\parallel U^n{\parallel }^2+\parallel U_{\tilde{x}\overline{x}\widehat{t}}^n{\parallel }^2)\hfill \\ \hfill & \le C(\parallel U_{\tilde{x}}^n{\parallel }^2+\parallel U_{\tilde{x}\overline{x}\overline{t}}^n{\parallel }^2+\parallel U_{\tilde{x}\overline{x}\overline{t}}^{n+1}{\parallel }^2).\hfill \end{array}$$

(53)

By substituting Equations (45)–(53) into Equation (44), we obtain

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2}}(\parallel U_{\overline{t}}^{n+1}{\parallel }^2-\parallel U_{\overline{t}}^n{\parallel }^2)+{\displaystyle \frac{k^2}{4}}(\parallel U_{\tilde{x}}^{n+1}{\parallel }^2-\parallel U_{\tilde{x}}^{n-1}{\parallel }^2)+{\displaystyle \frac{1}{4}}\left(a_1-{\displaystyle \frac{k^2{h}^2}{6}}\right)(\parallel U_{\tilde{x}\overline{x}}^{n+1}{\parallel }^2-\parallel U_{\tilde{x}\overline{x}}^{n-1}{\parallel }^2)\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\left(a_2-{\displaystyle \frac{h^2}{4}}\right)(\parallel U_{\tilde{x}\overline{t}}^{n+1}{\parallel }^2-\parallel U_{\tilde{x}\overline{t}}^n{\parallel }^2)+{\displaystyle \frac{1}{4}}\left(b_1-{\displaystyle \frac{a_1{h}^2}{12}}\right)(\parallel U_{\tilde{x}\overline{x}\tilde{x}}^{n+1}{\parallel }^2-\parallel U_{\tilde{x}\overline{x}\tilde{x}}^{n-1}{\parallel }^2)\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\left(b_2-{\displaystyle \frac{a_2{h}^2}{6}}\right)(\parallel U_{\tilde{x}\overline{x}\overline{t}}^{n+1}{\parallel }^2-\parallel U_{\tilde{x}\overline{x}\overline{t}}^n{\parallel }^2)-{\displaystyle \frac{b_2{h}^2}{24}}(\parallel U_{\tilde{x}\overline{x}\tilde{x}\overline{t}}^{n+1}{\parallel }^2-\parallel U_{\tilde{x}\overline{x}\tilde{x}\overline{t}}^n{\parallel }^2)\hfill \\ \hfill & \le C\tau (\parallel U_{\tilde{x}}^n{\parallel }^2+\parallel U_{\tilde{x}\overline{t}}^n{\parallel }^2+\parallel U_{\tilde{x}\overline{t}}^{n+1}{\parallel }^2+\parallel U_{\tilde{x}\overline{x}\overline{t}}^n{\parallel }^2+\parallel U_{\tilde{x}\overline{x}\overline{t}}^{n+1}{\parallel }^2).\hfill \end{array}$$

(54)

Defining

$$\begin{array}{cc}\hfill & B^n={\displaystyle \frac{1}{2}}\parallel U_{\overline{t}}^{n+1}{\parallel }^2+{\displaystyle \frac{k^2}{4}}(\parallel U_{\tilde{x}}^{n+1}{\parallel }^2+\parallel U_{\tilde{x}}^n{\parallel }^2)+{\displaystyle \frac{1}{4}}\left(a_1-{\displaystyle \frac{k^2{h}^2}{6}}\right)(\parallel U_{\tilde{x}\overline{x}}^{n+1}{\parallel }^2+\parallel U_{\tilde{x}\overline{x}}^n{\parallel }^2)\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\left(a_2-{\displaystyle \frac{h^2}{4}}\right)\parallel U_{\tilde{x}\overline{t}}^{n+1}{\parallel }^2+{\displaystyle \frac{1}{4}}\left(b_1-{\displaystyle \frac{a_1{h}^2}{12}}\right)(\parallel U_{\tilde{x}\overline{x}\tilde{x}}^{n+1}{\parallel }^2+\parallel U_{\tilde{x}\overline{x}\tilde{x}}^n{\parallel }^2)\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\left(b_2-{\displaystyle \frac{a_2{h}^2}{6}}\right)\parallel U_{\tilde{x}\overline{x}\overline{t}}^{n+1}{\parallel }^2-{\displaystyle \frac{b_2{h}^2}{24}}{\parallel U_{\tilde{x}\overline{x}\tilde{x}\overline{t}}^{n+1}\parallel }^2,\hfill \end{array}$$

then, based on Lemma 4, we can conclude that

$$\begin{array}{cc}\hfill & B^n\ge {\displaystyle \frac{1}{2}}\parallel U_{\overline{t}}^{n+1}{\parallel }^2+{\displaystyle \frac{k^2}{4}}(\parallel U_{\tilde{x}}^{n+1}{\parallel }^2+\parallel U_{\tilde{x}}^n{\parallel }^2)+{\displaystyle \frac{a_1}{4}}(\parallel U_{\tilde{x}\overline{x}}^{n+1}{\parallel }^2+\parallel U_{\tilde{x}\overline{x}}^n{\parallel }^2)+{\displaystyle \frac{a_2}{2}}{\parallel U_{\tilde{x}\overline{t}}^{n+1}\parallel }^2\hfill \\ \hfill & +{\displaystyle \frac{b_1}{4}}(\parallel U_{\tilde{x}\overline{x}\tilde{x}}^{n+1}{\parallel }^2+\parallel U_{\tilde{x}\overline{x}\tilde{x}}^n{\parallel }^2)+{\displaystyle \frac{b_2}{2}}\parallel U_{\tilde{x}\overline{x}\overline{t}}^{n+1}{\parallel }^2-{\displaystyle \frac{k^2}{6}}(\parallel U_{\tilde{x}}^{n+1}{\parallel }^2+\parallel U_{\tilde{x}}^n{\parallel }^2)-{\displaystyle \frac{1}{2}}{\parallel U_{\overline{t}}^{n+1}\parallel }^2\hfill \\ \hfill & -{\displaystyle \frac{a_1}{12}}(\parallel U_{\tilde{x}\overline{x}}^{n+1}{\parallel }^2+\parallel U_{\tilde{x}\overline{x}}^n{\parallel }^2)-{\displaystyle \frac{a_2}{3}}\parallel U_{\tilde{x}\overline{t}}^{n+1}{\parallel }^2-{\displaystyle \frac{b_2}{6}}{\parallel U_{\tilde{x}\overline{x}\overline{t}}^{n+1}\parallel }^2\hfill \\ \hfill & ={\displaystyle \frac{k^2}{12}}(\parallel U_{\tilde{x}}^{n+1}{\parallel }^2+\parallel U_{\tilde{x}}^n{\parallel }^2)+{\displaystyle \frac{a_1}{6}}(\parallel U_{\tilde{x}\overline{x}}^{n+1}{\parallel }^2+\parallel U_{\tilde{x}\overline{x}}^n{\parallel }^2)+{\displaystyle \frac{a_2}{6}}{\parallel U_{\tilde{x}\overline{t}}^{n+1}\parallel }^2\hfill \\ \hfill & +{\displaystyle \frac{b_1}{4}}(\parallel U_{\tilde{x}\overline{x}\tilde{x}}^{n+1}{\parallel }^2+\parallel U_{\tilde{x}\overline{x}\tilde{x}}^n{\parallel }^2)+{\displaystyle \frac{b_2}{3}}{\parallel U_{\tilde{x}\overline{x}\overline{t}}^{n+1}\parallel }^2.\hfill \end{array}$$

(55)

Consequently, Equation (54) can be reformulated as follows

$$\begin{array}{cc}\hfill & B^n-B^{n-1}\le C\tau (B^n+B^{n-1}),1\le n\le N-1.\hfill \end{array}$$

Assuming that $\tau$ is sufficiently small, specifically $\tau \le {\displaystyle \frac{k_0-2}{k_{0}C}}$ with $k_0\ge 2$, we further obtain

$$\begin{array}{cc}\hfill & B^n\le \left({\displaystyle \frac{1+\tau C}{1-\tau C}}\right)B^{n-1}\le (1+\tau k_{0}C)B^{n-1}\le exp\left(k_{0}TC\right)B^0.\hfill \end{array}$$

This indicates that $B^n$ is bounded, which leads to the conclusions that $\parallel U_{\tilde{x}}^{n+1}\parallel \le C$ as derived from Equation (55). By applying Lemma 3, we further establish that $\parallel U^{n+1}\parallel \le C$, and $\parallel U^{n+1}{\parallel }_{\infty }\le C$. This completes the proof.  □

4. Solvability, Convergence, and Stability

In this section, we examine the solvability, convergence, and stability of the previously discussed scheme.

Theorem 5. 

The difference scheme outlined in Equations (16)–(18) exhibits a unique solution.

Proof. 

From Equation (17), we know that $U^0$ has a unique solution. To demonstrate the unique solvability of $U^1$, we will analyze the homogeneous version of Equation (19) as detailed below:

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{{\tau }^2}}{U}^1-{\displaystyle \frac{k^2}{2}}{U}_{\tilde{x}\overline{x}}^1+{\displaystyle \frac{1}{2}}\left(a_1-{\displaystyle \frac{k^2{h}^2}{6}}\right)U_{\tilde{x}\overline{x}\tilde{x}\overline{x}}^1-{\displaystyle \frac{1}{{\tau }^2}}\left(a_2-{\displaystyle \frac{h^2}{4}}\right)U_{\tilde{x}\overline{x}}^1-{\displaystyle \frac{1}{2}}\left(b_1-{\displaystyle \frac{a_1{h}^2}{12}}\right)U_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}}^1\hfill \\ \hfill & +{\displaystyle \frac{1}{{\tau }^2}}\left(b_2-{\displaystyle \frac{a_2{h}^2}{6}}\right)U_{\tilde{x}\overline{x}\tilde{x}\overline{x}}^1+{\displaystyle \frac{b_2{h}^2}{12{\tau }^2}}{U}_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}}^1=0.\hfill \end{array}$$

(56)

By computing the inner product of Equation (56) with $U^1$, we obtain

$$\begin{array}{cc}\hfill & \parallel U^1{\parallel }^2+\left({\displaystyle \frac{{\tau }^2{k}^2}{2}}+a_2-{\displaystyle \frac{h^2}{4}}\right)\parallel U_{\tilde{x}}^1{\parallel }^2+\left[{\displaystyle \frac{{\tau }^2}{2}}\left(a_1-{\displaystyle \frac{k^2{h}^2}{6}}\right)+\left(b_2-{\displaystyle \frac{a_2{h}^2}{6}}\right)\right]{\parallel U_{\tilde{x}\overline{x}}^1\parallel }^2\hfill \\ \hfill & +\left[{\displaystyle \frac{{\tau }^2}{2}}\left(b_1-{\displaystyle \frac{a_1{h}^2}{12}}\right)-{\displaystyle \frac{b_2{h}^2}{12}}\right]{\parallel U_{\tilde{x}\overline{x}\tilde{x}}^1\parallel }^2=0.\hfill \end{array}$$

(57)

Furthermore, from Lemma 4, one obtains

$$\begin{array}{cc}\hfill & \parallel U^1{\parallel }^2+\left({\displaystyle \frac{{\tau }^2{k}^2}{2}}+a_2\right)\parallel U_{\tilde{x}}^1{\parallel }^2+\left({\displaystyle \frac{{\tau }^2}{2}}{a}_1+b_2\right)\parallel U_{\tilde{x}\overline{x}}^1{\parallel }^2+{\displaystyle \frac{{\tau }^2{b}_1}{2}}{\parallel U_{\tilde{x}\overline{x}\tilde{x}}^1\parallel }^2\hfill \\ \hfill & ={\displaystyle \frac{h^2}{4}}\parallel U_{\tilde{x}}^1{\parallel }^2+\left({\displaystyle \frac{{\tau }^2{k}^2{h}^2}{12}}+{\displaystyle \frac{a_2{h}^2}{6}}\right)\parallel U_{\tilde{x}\overline{x}}^1{\parallel }^2+\left({\displaystyle \frac{a_1{\tau }^2{h}^2}{24}}+{\displaystyle \frac{b_2{h}^2}{12}}\right){\parallel U_{\tilde{x}\overline{x}\tilde{x}}^1\parallel }^2\hfill \\ \hfill & \le \parallel U^1{\parallel }^2+\left({\displaystyle \frac{{\tau }^2{k}^2}{3}}+{\displaystyle \frac{2a_2}{3}}\right)\parallel U_{\tilde{x}}^1{\parallel }^2+\left({\displaystyle \frac{a_1{\tau }^2}{6}}+{\displaystyle \frac{b_2}{3}}\right){\parallel U_{\tilde{x}\overline{x}}^1\parallel }^2,\hfill \end{array}$$

which yields

$$\begin{array}{cc}\hfill & \left({\displaystyle \frac{{\tau }^2{k}^2}{6}}+{\displaystyle \frac{a_2}{3}}\right)\parallel U_{\tilde{x}}^1{\parallel }^2+\left({\displaystyle \frac{a_1{\tau }^2}{3}}+{\displaystyle \frac{2b_2}{3}}\right)\parallel U_{\tilde{x}\overline{x}}^1{\parallel }^2+{\displaystyle \frac{{\tau }^2{b}_1}{2}}{\parallel U_{\tilde{x}\overline{x}\tilde{x}}^1\parallel }^2\le 0.\hfill \end{array}$$

(58)

Considering the parameters $a_1\ge 0$, $a_2\ge 0$, $b_1\ge 0$, and $b_2\ge 0$, we then obtain $\parallel U_{\tilde{x}}^1\parallel =0$, $\parallel U_{\tilde{x}\overline{x}}^1\parallel =0$, $\parallel U_{\tilde{x}\overline{x}\tilde{x}}^1\parallel =0$. We further obtain from Equation (57) that $\parallel U^1\parallel =0$. Consequently, Equation (19) admits only the trivial solution, indicating that $U^1$ is uniquely determined.

We then assume that $U^0$, $U^1$, $U^2$,…,$U^n$ are uniquely determined, where $n\le N-1$. By examining the homogeneous version of Equation (16) for $U^{n+1}$, we obtain

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{{\tau }^2}}{U}^{n+1}-{\displaystyle \frac{k^2}{2}}{U}_{\tilde{x}\overline{x}}^{n+1}+{\displaystyle \frac{1}{2}}\left(a_1-{\displaystyle \frac{k^2{h}^2}{6}}\right)U_{\tilde{x}\overline{x}\tilde{x}\overline{x}}^{n+1}-{\displaystyle \frac{1}{{\tau }^2}}\left(a_2-{\displaystyle \frac{h^2}{4}}\right)U_{\tilde{x}\overline{x}}^{n+1}-{\displaystyle \frac{1}{2}}\left(b_1-{\displaystyle \frac{a_1{h}^2}{12}}\right)U_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}}^{n+1}\hfill \\ \hfill & +{\displaystyle \frac{1}{{\tau }^2}}\left(b_2-{\displaystyle \frac{a_2{h}^2}{6}}\right)U_{\tilde{x}\overline{x}\tilde{x}\overline{x}}^{n+1}+{\displaystyle \frac{b_2{h}^2}{12{\tau }^2}}{U}_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}}^{n+1}=0.\hfill \end{array}$$

(59)

Similarly, by computing the inner product of Equation (59) with $U^{n+1}$, we obtain

$$\begin{array}{cc}\hfill & \parallel U^{n+1}{\parallel }^2+\left({\displaystyle \frac{{\tau }^2{k}^2}{2}}+a_2-{\displaystyle \frac{h^2}{4}}\right)\parallel U_{\tilde{x}}^{n+1}{\parallel }^2+\left[{\displaystyle \frac{{\tau }^2}{2}}\left(a_1-{\displaystyle \frac{k^2{h}^2}{6}}\right)+\left(b_2-{\displaystyle \frac{a_2{h}^2}{6}}\right)\right]{\parallel U_{\tilde{x}\overline{x}}^{n+1}\parallel }^2\hfill \\ \hfill & +\left[{\displaystyle \frac{{\tau }^2}{2}}\left(b_1-{\displaystyle \frac{a_1{h}^2}{12}}\right)-{\displaystyle \frac{b_2{h}^2}{12}}\right]{\parallel U_{\tilde{x}\overline{x}\tilde{x}}^{n+1}\parallel }^2=0,\hfill \end{array}$$

(60)

which yields $\parallel U^{n+1}\parallel =0$, $\parallel U_{\tilde{x}}^{n+1}\parallel =0$, $\parallel U_{\tilde{x}\overline{x}}^{n+1}\parallel =0$, $\parallel U_{\tilde{x}\overline{x}\tilde{x}}^{n+1}\parallel =0$. The difference scheme (16)–(18) is demonstrated to possess a unique solution through the application of the method of induction. This completes the proof.  □

Theorem 6. 

Assuming that $\phi \left(x\right),\psi \left(x\right)\in H_0^2(\Omega )$ and $u\in C_{x,t}^{10,4}([x_l,x_r]\times (0,T])$, it can be concluded that the solution $U^n$ to Equations (16)–(18) converges to the solution $u^n$ of the problem defined by Equations (1)–(3). Furthermore, the rate of convergence is characterized by $O({\tau }^2+h^4)$ in both the $\parallel ·\parallel$ and ${\parallel ·\parallel }_{\infty }$ norms. Specifically, this implies that

$$\begin{array}{cc}\hfill & \parallel u^n-U^n\parallel \le O({\tau }^2+h^4),{\parallel u^n-U^n\parallel }_{\infty }\le O({\tau }^2+h^4).\hfill \end{array}$$

Proof. 

The truncation errors associated with Equations (16)–(18) can be expressed as follows:

$$\begin{array}{cc}\hfill & {\left(u_j^n\right)}_{\tilde{t}\overline{t}}-k^2{\left({\overline{u}}_j^n\right)}_{\tilde{x}\overline{x}}+\left(a_1-{\displaystyle \frac{k^2{h}^2}{6}}\right){\left({\overline{u}}_j^n\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}}-\left(a_2-{\displaystyle \frac{h^2}{4}}\right){\left(u_j^n\right)}_{\tilde{x}\overline{x}\tilde{t}\overline{t}}-\left(b_1-{\displaystyle \frac{a_1{h}^2}{12}}\right){\left({\overline{u}}_j^n\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}}\hfill \end{array}$$

$$\begin{array}{cc}\hfill & +\left(b_2-{\displaystyle \frac{a_2{h}^2}{6}}\right){\left(u_j^n\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{t}\overline{t}}+{\displaystyle \frac{b_2{h}^2}{12}}{\left(u_j^n\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{t}\overline{t}}+c{\left[{\left(u_j^n\right)}^{2p}\right]}_{\tilde{x}\overline{x}}+{\displaystyle \frac{c{h}^2}{6}}{\left[{\left(u_j^n\right)}^{2p}\right]}_{\tilde{x}\overline{x}\tilde{x}\overline{x}}=r_j^n,\hfill \end{array}$$

(61)

$$u_j^0=\phi \left(x_j\right),{\left(u_j^0\right)}_{\widehat{t}}=\psi \left(x_j\right),0\le j\le J,$$

(62)

$$\begin{array}{cc}\hfill & u_0^n=0,{\displaystyle \frac{4}{3}}{\left(u_0^n\right)}_{\widehat{x}}-{\displaystyle \frac{1}{3}}{\left(u_0^n\right)}_{\ddot{x}}=0,{\displaystyle \frac{4}{3}}{\left(u_0^n\right)}_{\tilde{x}\overline{x}}-{\displaystyle \frac{1}{3}}{\left(u_0^n\right)}_{\widehat{x}\widehat{x}}=0,\hfill \\ \hfill & u_J^n=0,{\displaystyle \frac{4}{3}}{\left(u_J^n\right)}_{\widehat{x}}-{\displaystyle \frac{1}{3}}{\left(u_J^n\right)}_{\ddot{x}}=0,{\displaystyle \frac{4}{3}}{\left(u_J^n\right)}_{\tilde{x}\overline{x}}-{\displaystyle \frac{1}{3}}{\left(u_J^n\right)}_{\widehat{x}\widehat{x}}=0,0\le n\le N.\hfill \end{array}$$

(63)

Through the application of the Taylor expansion, it can be demonstrated that the inequality $|r_j^n|\le O({\tau }^2+h^4)$ is valid as both $\tau$ and h approach zero for $n\ge 0$. Letting $e_j^n=u_j^n-U_j^n$ and subtracting Equations (16)–(18) from Equations (61)–(63), we obtain

$$\begin{array}{cc}\hfill & r_j^n={\left(e_j^n\right)}_{\tilde{t}\overline{t}}-k^2{\left({\overline{e}}_j^n\right)}_{\tilde{x}\overline{x}}+\left(a_1-{\displaystyle \frac{k^2{h}^2}{6}}\right){\left({\overline{e}}_j^n\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}}-\left(a_2-{\displaystyle \frac{h^2}{4}}\right){\left(e_j^n\right)}_{\tilde{x}\overline{x}\tilde{t}\overline{t}}-\left(b_1-{\displaystyle \frac{a_1{h}^2}{12}}\right){\left({\overline{e}}_j^n\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}}\hfill \\ \hfill & +\left(b_2-{\displaystyle \frac{a_2{h}^2}{6}}\right){\left(e_j^n\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{t}\overline{t}}+{\displaystyle \frac{b_2{h}^2}{12}}{\left(u_j^e\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{x}\overline{x}\tilde{t}\overline{t}}+c{[{\left(u_j^n\right)}^{2p}-{\left(U_j^n\right)}^{2p}]}_{\tilde{x}\overline{x}}\hfill \\ \hfill & +{\displaystyle \frac{c{h}^2}{6}}{[{\left(u_j^n\right)}^{2p}-{\left(U_j^n\right)}^{2p}]}_{\tilde{x}\overline{x}\tilde{x}\overline{x}},\hfill \end{array}$$

(64)

$$e_j^0=0,{\left(e_j^0\right)}_{\widehat{t}}=0,0\le j\le J,$$

(65)

$$\begin{array}{cc}\hfill & e_0^n=0,{\displaystyle \frac{4}{3}}{\left(e_0^n\right)}_{\widehat{x}}-{\displaystyle \frac{1}{3}}{\left(e_0^n\right)}_{\ddot{x}}=0,{\displaystyle \frac{4}{3}}{\left(e_0^n\right)}_{\tilde{x}\overline{x}}-{\displaystyle \frac{1}{3}}{\left(e_0^n\right)}_{\widehat{x}\widehat{x}}=0,\hfill \\ \hfill & e_J^n=0,{\displaystyle \frac{4}{3}}{\left(e_J^n\right)}_{\widehat{x}}-{\displaystyle \frac{1}{3}}{\left(e_J^n\right)}_{\ddot{x}}=0,{\displaystyle \frac{4}{3}}{\left(e_J^n\right)}_{\tilde{x}\overline{x}}-{\displaystyle \frac{1}{3}}{\left(e_J^n\right)}_{\widehat{x}\widehat{x}}=0,0\le n\le N.\hfill \end{array}$$

(66)

By computing the inner product of Equation (64) with ${\left(e_j^n\right)}_{\widehat{t}}$, one obtains

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2}}(\parallel e_{\overline{t}}^{n+1}{\parallel }^2-\parallel e_{\overline{t}}^n{\parallel }^2)+{\displaystyle \frac{k^2}{4}}(\parallel e_{\tilde{x}}^{n+1}{\parallel }^2-\parallel e_{\tilde{x}}^{n-1}{\parallel }^2)+{\displaystyle \frac{1}{4}}\left(a_1-{\displaystyle \frac{k^2{h}^2}{6}}\right)(\parallel e_{\tilde{x}\overline{x}}^{n+1}{\parallel }^2-\parallel e_{\tilde{x}\overline{x}}^{n-1}{\parallel }^2)\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\left(a_2-{\displaystyle \frac{h^2}{4}}\right)(\parallel e_{\tilde{x}\overline{t}}^{n+1}{\parallel }^2-\parallel e_{\tilde{x}\overline{t}}^n{\parallel }^2)+{\displaystyle \frac{1}{4}}\left(b_1-{\displaystyle \frac{a_1{h}^2}{12}}\right)(\parallel e_{\tilde{x}\overline{x}\tilde{x}}^{n+1}{\parallel }^2-\parallel e_{\tilde{x}\overline{x}\tilde{x}}^{n-1}{\parallel }^2)\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\left(b_2-{\displaystyle \frac{a_2{h}^2}{6}}\right)(\parallel e_{\tilde{x}\overline{x}\overline{t}}^{n+1}{\parallel }^2-\parallel e_{\tilde{x}\overline{x}\overline{t}}^n{\parallel }^2)-{\displaystyle \frac{b_2{h}^2}{24}}(\parallel e_{\tilde{x}\overline{x}\tilde{x}\overline{t}}^{n+1}{\parallel }^2-\parallel e_{\tilde{x}\overline{x}\tilde{x}\overline{t}}^n{\parallel }^2)\hfill \\ \hfill & =\tau \langle r^n,e_{\widehat{t}}^n\rangle -c\tau \langle {[{\left(u^n\right)}^{2p}-{\left(U^n\right)}^{2p}]}_{\tilde{x}\overline{x}},e_{\widehat{t}}^n\rangle -{\displaystyle \frac{c\tau h^2}{6}}\langle {[{\left(u^n\right)}^{2p}-{\left(U^n\right)}^{2p}]}_{\tilde{x}\overline{x}\tilde{x}\overline{x}},e_{\widehat{t}}^n\rangle .\hfill \end{array}$$

(67)

According to Lemma 1 and the Cauchy–Schwarz inequality [28,32], it can be concluded that

$$\begin{array}{cc}\hfill & \langle |{[{\left(u^n\right)}^{2p}-{\left(U^n\right)}^{2p}]}_{\tilde{x}\overline{x}},e_{\widehat{t}}^n\rangle |=\langle {\left(u^n\right)}^{2p}-{\left(U^n\right)}^{2p},e_{\tilde{x}\overline{x}\widehat{t}}^n\rangle \hfill \\ \hfill & =h\sum _{j=1}^{J-1}[{\left(u_j^n\right)}^{2p}-{\left(U_j^n\right)}^{2p}]{\left(e_j^n\right)}_{\tilde{x}\overline{x}\widehat{t}}=h\sum _{j=1}^{J-1}\left\{e_j^n\left[\sum _{k=0}^{2p-1}{\left(u_j^n\right)}^{2p-1-k}{\left(U_j^n\right)}^k\right]{\left(e_j^n\right)}_{\tilde{x}\overline{x}\widehat{t}}\right\}\hfill \\ \hfill & \le C(\parallel e_{\tilde{x}}^n{\parallel }^2+\parallel e_{\tilde{x}\overline{x}\overline{t}}^{n+1}{\parallel }^2+\parallel e_{\tilde{x}\overline{x}\overline{t}}^n{\parallel }^2).\hfill \end{array}$$

(68)

Similarly, we have

$$\begin{array}{cc}\hfill & h^2\langle {[{\left(u^n\right)}^{2p}-{\left(U^n\right)}^{2p}]}_{\tilde{x}\overline{x}\tilde{x}\overline{x}},e_{\widehat{t}}^n\rangle =h^2\langle {[{\left(u^n\right)}^{2p}-{\left(U^n\right)}^{2p}]}_{\tilde{x}\overline{x}},e_{\tilde{x}\overline{x}\widehat{t}}^n\rangle \hfill \\ \hfill & =h\sum _{j=1}^{J-1}\left\{\left[{\left(u_{j+1}^n\right)}^{2p}-{\left(U_{j+1}^n\right)}^{2p}\right]-2\left[{\left(u_j^n\right)}^{2p}-{\left(U_j^n\right)}^{2p}\right]+\left[{\left(u_{j-1}^n\right)}^{2p}-{\left(U_{j-1}^n\right)}^{2p}\right]\right\}{\left(U_j^n\right)}_{\tilde{x}\overline{x}\widehat{t}}\hfill \\ \hfill & \le C(\parallel e_{\tilde{x}}^n{\parallel }^2+\parallel e_{\tilde{x}\overline{x}\overline{t}}^n{\parallel }^2+\parallel e_{\tilde{x}\overline{x}\overline{t}}^{n+1}{\parallel }^2).\hfill \end{array}$$

(69)

Furthermore, we obtain

$$\begin{array}{cc}\hfill & \langle r^n,e_{\widehat{t}}^n\rangle =\langle r^n,{\displaystyle \frac{1}{2}}(e_{\overline{t}}^{n+1}+e_{\overline{t}}^n)\rangle \le {\displaystyle \frac{1}{2}}\parallel r^n{\parallel }^2+{\displaystyle \frac{1}{4}}(\parallel e_{\overline{t}}^{n+1}{\parallel }^2+\parallel e_{\overline{t}}^n{\parallel }^2).\hfill \end{array}$$

(70)

Substituting Equations (68)–(70) into Equation (67), we obtain

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2}}(\parallel e_{\overline{t}}^{n+1}{\parallel }^2-\parallel e_{\overline{t}}^n{\parallel }^2)+{\displaystyle \frac{k^2}{4}}(\parallel e_{\tilde{x}}^{n+1}{\parallel }^2-\parallel e_{\tilde{x}}^{n-1}{\parallel }^2)+{\displaystyle \frac{1}{4}}\left(a_1-{\displaystyle \frac{k^2{h}^2}{6}}\right)(\parallel e_{\tilde{x}\overline{x}}^{n+1}{\parallel }^2-\parallel e_{\tilde{x}\overline{x}}^{n-1}{\parallel }^2)\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\left(a_2-{\displaystyle \frac{h^2}{4}}\right)(\parallel e_{\tilde{x}\overline{t}}^{n+1}{\parallel }^2-\parallel e_{\tilde{x}\overline{t}}^n{\parallel }^2)+{\displaystyle \frac{1}{4}}\left(b_1-{\displaystyle \frac{a_1{h}^2}{12}}\right)(\parallel e_{\tilde{x}\overline{x}\tilde{x}}^{n+1}{\parallel }^2-\parallel e_{\tilde{x}\overline{x}\tilde{x}}^{n-1}{\parallel }^2)\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\left(b_2-{\displaystyle \frac{a_2{h}^2}{6}}\right)(\parallel e_{\tilde{x}\overline{x}\overline{t}}^{n+1}{\parallel }^2-\parallel e_{\tilde{x}\overline{x}\overline{t}}^n{\parallel }^2)-{\displaystyle \frac{b_2{h}^2}{24}}(\parallel e_{\tilde{x}\overline{x}\tilde{x}\overline{t}}^{n+1}{\parallel }^2-\parallel e_{\tilde{x}\overline{x}\tilde{x}\overline{t}}^n{\parallel }^2)\hfill \\ \hfill & \le {\displaystyle \frac{\tau }{2}}\parallel r^n{\parallel }^2+C\tau (\parallel e_{\tilde{x}}^n{\parallel }^2+\parallel e_{\tilde{x}\overline{x}\overline{t}}^{n+1}{\parallel }^2+\parallel e_{\tilde{x}\overline{x}\overline{t}}^n{\parallel }^2+\parallel e_{\overline{t}}^{n+1}{\parallel }^2+\parallel e_{\overline{t}}^n{\parallel }^2).\hfill \end{array}$$

(71)

Setting

$$\begin{array}{cc}\hfill & D^n={\displaystyle \frac{1}{2}}\parallel e_{\overline{t}}^{n+1}{\parallel }^2+{\displaystyle \frac{k^2}{4}}(\parallel e_{\tilde{x}}^{n+1}{\parallel }^2+\parallel e_{\tilde{x}}^n{\parallel }^2)+{\displaystyle \frac{1}{4}}\left(a_1-{\displaystyle \frac{k^2{h}^2}{6}}\right)(\parallel e_{\tilde{x}\overline{x}}^{n+1}{\parallel }^2+\parallel e_{\tilde{x}\overline{x}}^n{\parallel }^2)\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\left(a_2-{\displaystyle \frac{h^2}{4}}\right)\parallel e_{\tilde{x}\overline{t}}^{n+1}{\parallel }^2+{\displaystyle \frac{1}{4}}\left(b_1-{\displaystyle \frac{a_1{h}^2}{12}}\right)(\parallel e_{\tilde{x}\overline{x}\tilde{x}}^{n+1}{\parallel }^2+\parallel e_{\tilde{x}\overline{x}\tilde{x}}^n{\parallel }^2)\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\left(b_2-{\displaystyle \frac{a_2{h}^2}{6}}\right)\parallel e_{\tilde{x}\overline{x}\overline{t}}^{n+1}{\parallel }^2-{\displaystyle \frac{b_2{h}^2}{24}}{\parallel e_{\tilde{x}\overline{x}\tilde{x}\overline{t}}^{n+1}\parallel }^2,\hfill \end{array}$$

(72)

then, from Lemma 4, we have

$$\begin{array}{cc}\hfill & D^n\ge {\displaystyle \frac{1}{2}}\parallel e_{\overline{t}}^{n+1}{\parallel }^2+{\displaystyle \frac{k^2}{4}}(\parallel e_{\tilde{x}}^{n+1}{\parallel }^2+\parallel e_{\tilde{x}}^n{\parallel }^2)+{\displaystyle \frac{a_1}{4}}(\parallel e_{\tilde{x}\overline{x}}^{n+1}{\parallel }^2+\parallel e_{\tilde{x}\overline{x}}^n{\parallel }^2)+{\displaystyle \frac{a_2}{2}}{\parallel e_{\tilde{x}\overline{t}}^{n+1}\parallel }^2\hfill \\ \hfill & +{\displaystyle \frac{b_1}{4}}(\parallel e_{\tilde{x}\overline{x}\tilde{x}}^{n+1}{\parallel }^2+\parallel e_{\tilde{x}\overline{x}\tilde{x}}^n{\parallel }^2)+{\displaystyle \frac{b_2}{2}}\parallel e_{\tilde{x}\overline{x}\overline{t}}^{n+1}{\parallel }^2-{\displaystyle \frac{k^2}{6}}(\parallel e_{\tilde{x}}^{n+1}{\parallel }^2+\parallel e_{\tilde{x}}^n{\parallel }^2)-{\displaystyle \frac{1}{2}}{\parallel e_{\overline{t}}^{n+1}\parallel }^2\hfill \\ \hfill & -{\displaystyle \frac{a_1}{12}}(\parallel e_{\tilde{x}\overline{x}}^{n+1}{\parallel }^2+\parallel e_{\tilde{x}\overline{x}}^n{\parallel }^2)-{\displaystyle \frac{a_2}{3}}\parallel e_{\tilde{x}\overline{t}}^{n+1}{\parallel }^2-{\displaystyle \frac{b_2}{6}}{\parallel e_{\tilde{x}\overline{x}\overline{t}}^{n+1}\parallel }^2\hfill \\ \hfill & ={\displaystyle \frac{k^2}{12}}(\parallel e_{\tilde{x}}^{n+1}{\parallel }^2+\parallel e_{\tilde{x}}^n{\parallel }^2)+{\displaystyle \frac{a_1}{6}}(\parallel e_{\tilde{x}\overline{x}}^{n+1}{\parallel }^2+\parallel e_{\tilde{x}\overline{x}}^n{\parallel }^2)+{\displaystyle \frac{a_2}{6}}{\parallel e_{\tilde{x}\overline{t}}^{n+1}\parallel }^2\hfill \\ \hfill & +{\displaystyle \frac{b_1}{4}}(\parallel e_{\tilde{x}\overline{x}\tilde{x}}^{n+1}{\parallel }^2+\parallel e_{\tilde{x}\overline{x}\tilde{x}}^n{\parallel }^2)+{\displaystyle \frac{b_2}{3}}{\parallel e_{\tilde{x}\overline{x}\overline{t}}^{n+1}\parallel }^2.\hfill \end{array}$$

(73)

Consequently, from Equations (71) and (72), we obtain

$$\begin{array}{cc}\hfill & D^n-D^{n-1}\le {\displaystyle \frac{\tau }{2}}{\parallel r^n\parallel }^2+C\tau (D^n+D^{n-1}).\hfill \end{array}$$

That is

$$\begin{array}{cc}\hfill & (1-C\tau )(D^n-D^{n-1})\le {\displaystyle \frac{\tau }{2}}{\parallel r^n\parallel }^2+2C\tau D^{n-1}.\hfill \end{array}$$

Therefore, if $\tau$ is sufficiently small such that $1-C\tau =1/c_0>0$, then

$$\begin{array}{cc}\hfill & D^n-D^{n-1}\le {\displaystyle \frac{c_0}{2}}\tau {\parallel r^n\parallel }^2+2C{c}_0\tau D^{n-1}.\hfill \end{array}$$

(74)

By summing Equation (74) from 1 to n, we obtain

$$\begin{array}{cc}\hfill & D^n\le D^0+{\displaystyle \frac{c_0}{2}}\tau \sum _{l=1}^n{\parallel r^l\parallel }^2+2C{c}_0\tau \sum _{l=1}^n{D}^{l-1}.\hfill \end{array}$$

It is essential to note that

$$\begin{array}{cc}\hfill & \tau \sum _{l=1}^n\parallel r^l{\parallel }^2\le n\tau \underset{1\le l\le n}{max}{\parallel r^l\parallel }^2\le T·O{({\tau }^2+h^4)}^2,D^0\le O{({\tau }^2+h^4)}^2.\hfill \end{array}$$

We then obtain from the Discrete Gronwall’s inequality [33,34] that $D^n\le O{({\tau }^2+h^4)}^2$. This leads to the conclusion that $\parallel e_x^n\parallel \le O({\tau }^2+h^4)$ and $\parallel e_{\tilde{x}}^n\parallel \le O({\tau }^2+h^4)$. Ultimately, we utilize Lemma 3 to demonstrate that $\parallel e^n\parallel \le O({\tau }^2+h^4)$ and $\parallel e^n{\parallel }_{\infty }\le O({\tau }^2+h^4)$. This completes the proof.  □

We subsequently obtain the following theorem.

Theorem 7. 

Under the conditions specified in Theorem 6, the solution $U^n$ of the Equations (16)–(18) exhibits stability. The analysis is conducted with respect to both the $\parallel ·\parallel$ norm and the ${\parallel ·\parallel }_{\infty }$ norm.

5. Numerical Experiments

In this section, we conduct a series of numerical experiments aimed at assessing the efficacy and accuracy of the theoretical analysis presented in the preceding sections. Following this, we will quantify the corresponding errors utilizing the designated error norms [31,33,35]:

$$\begin{array}{cc}\hfill & \parallel e^n\parallel ={\left[h\sum _{j=1}^{J-1}{|u_j^n-U_j^n|}^2\right]}^{{\displaystyle \frac{1}{2}}},\parallel e^n{\parallel }_{\infty }=\underset{1\le j\le J-1}{max}|u_j^n-U_j^n|.\hfill \end{array}$$

Example 1. 

Consider the parameters

$$\begin{array}{cc}\hfill & k=1,a_1=0,a_2=1,b_1=0,b_2=0,c=-1,p=1,\hfill \end{array}$$

which is the following improved Boussinesq equation [2,31]

$$\begin{array}{cc}\hfill & u_{tt}-u_{xx}-u_{xxtt}-{\left(u^2\right)}_{xx}=0,\hfill \end{array}$$

(75)

and the solitary wave solution is expressed as follows

$$\begin{array}{cc}\hfill & u(x,t)=A{sech}^2\left[{\displaystyle \frac{1}{c_0}}\sqrt{{\displaystyle \frac{A}{6}}}\left(x-x_0-c_{0}t\right)\right],c_0=\pm \sqrt{1+{\displaystyle \frac{2}{3}}A},\hfill \end{array}$$

(76)

where A, $x_0$, and $c_0$ are provided constants. The initial conditions may be established by evaluating Equation (76) and its derivative for t at the point $t=0$:

$$\begin{array}{cc}\hfill & \phi \left(x\right)=A{sech}^2\left[{\displaystyle \frac{1}{c_0}}\sqrt{{\displaystyle \frac{A}{6}}}\left(x-x_0\right)\right],\hfill \end{array}$$

(77)

$$\begin{array}{cc}\hfill & \psi \left(x\right)=2A\sqrt{{\displaystyle \frac{A}{6}}}{sech}^2\left[{\displaystyle \frac{1}{c_0}}\sqrt{{\displaystyle \frac{A}{6}}}\left(x-x_0\right)\right]tanh\left[{\displaystyle \frac{1}{c_0}}\sqrt{{\displaystyle \frac{A}{6}}}\left(x-x_0\right)\right].\hfill \end{array}$$

(78)

First, we choose the following parameters:

$$\begin{array}{cc}\hfill & x_0=0,A=0.5,c_0=\sqrt{1+2A/3},x_l=-60,x_r=100,t\in [0,1],\hfill \end{array}$$

and compare our findings with the numerical results presented in [2]. The computational accuracy for both temporal and spatial variables is evaluated at $T=1$ and is detailed in

Table 1. Comparative analysis of spatial errors and convergence rates for Example 1.

h	$\parallel {\mathit{e}}^{\mathit{n}}\parallel$ [2]	Rate	$\parallel {\mathit{e}}^{\mathit{n}}\parallel$	Rate	$\parallel {\mathit{e}}^{\mathit{n}}{\parallel }_{\mathit{\infty }}$ [2]	Rate	$\parallel {\mathit{e}}^{\mathit{n}}{\parallel }_{\mathit{\infty }}$	Rate
0.4	9.05$\times {10}^{-4}$	−	5.44$\times {10}^{-5}$	−	4.50$\times {10}^{-4}$	−	3.15$\times {10}^{-5}$	−
0.2	2.25$\times {10}^{-4}$	2.01	3.21$\times {10}^{-6}$	4.08	1.13$\times {10}^{-4}$	1.99	2.05$\times {10}^{-6}$	3.94
0.1	5.62$\times {10}^{-5}$	2.00	1.90$\times {10}^{-7}$	4.07	2.81$\times {10}^{-5}$	2.00	1.19$\times {10}^{-7}$	4.09

and

Table 2. Comparison of the temporal errors and convergence rates for Example 1.

h	$\parallel {\mathit{e}}^{\mathit{n}}\parallel$ [2]	Rate	$\parallel {\mathit{e}}^{\mathit{n}}\parallel$	Rate	$\parallel {\mathit{e}}^{\mathit{n}}{\parallel }_{\mathit{\infty }}$ [2]	Rate	$\parallel {\mathit{e}}^{\mathit{n}}{\parallel }_{\mathit{\infty }}$	Rate
0.04	8.69$\times {10}^{-4}$	−	2.76$\times {10}^{-5}$	−	4.32$\times {10}^{-4}$	−	1.51$\times {10}^{-5}$	−
0.02	2.19$\times {10}^{-4}$	1.98	6.58$\times {10}^{-6}$	2.06	1.10$\times {10}^{-4}$	1.97	3.63$\times {10}^{-6}$	2.05
0.01	5.53$\times {10}^{-5}$	1.99	1.59$\times {10}^{-6}$	2.04	2.78$\times {10}^{-5}$	1.99	9.04$\times {10}^{-7}$	2.00

, where $\tau =0.001$ in Table 1 and $\tau /h=0.1$ in Table 2. The data in Table 1 and Table 2 indicate that the current difference scheme (16)–(18) significantly outperforms the finite volume element scheme described in [2].

On the other hand, to further demonstrate the computational efficiency of the proposed compact difference scheme (16)–(18), we compare the numerical errors with the previous studies [3,36,37]. The results are detailed in

Table 3. Comparison of the computational errors between the present scheme and the other methods for Example 1.

h	$\mathit{\tau }$	(16)–(18)	Error [3]	Error [36]	Error [37]
0.4	0.04	2.29716$\times {10}^{-5}$	2.19$\times {10}^{-3}$	2.07164$\times {10}^{-4}$	1.22$\times {10}^{-5}$
0.2	0.02	5.96777$\times {10}^{-6}$	5.33$\times {10}^{-4}$	5.27850$\times {10}^{-5}$	8.41$\times {10}^{-6}$
0.1	0.01	1.50726$\times {10}^{-6}$	1.33$\times {10}^{-4}$	1.33205$\times {10}^{-5}$	8.11$\times {10}^{-6}$

, where the error is defined as follows

$$\begin{array}{cc}\hfill & Error=\parallel e^n\parallel /\parallel u_{exact}^n\parallel .\hfill \end{array}$$

It is evident that, under the same conditions, the computational errors of the proposed difference scheme (16)–(18) are smaller than those reported in other studies.

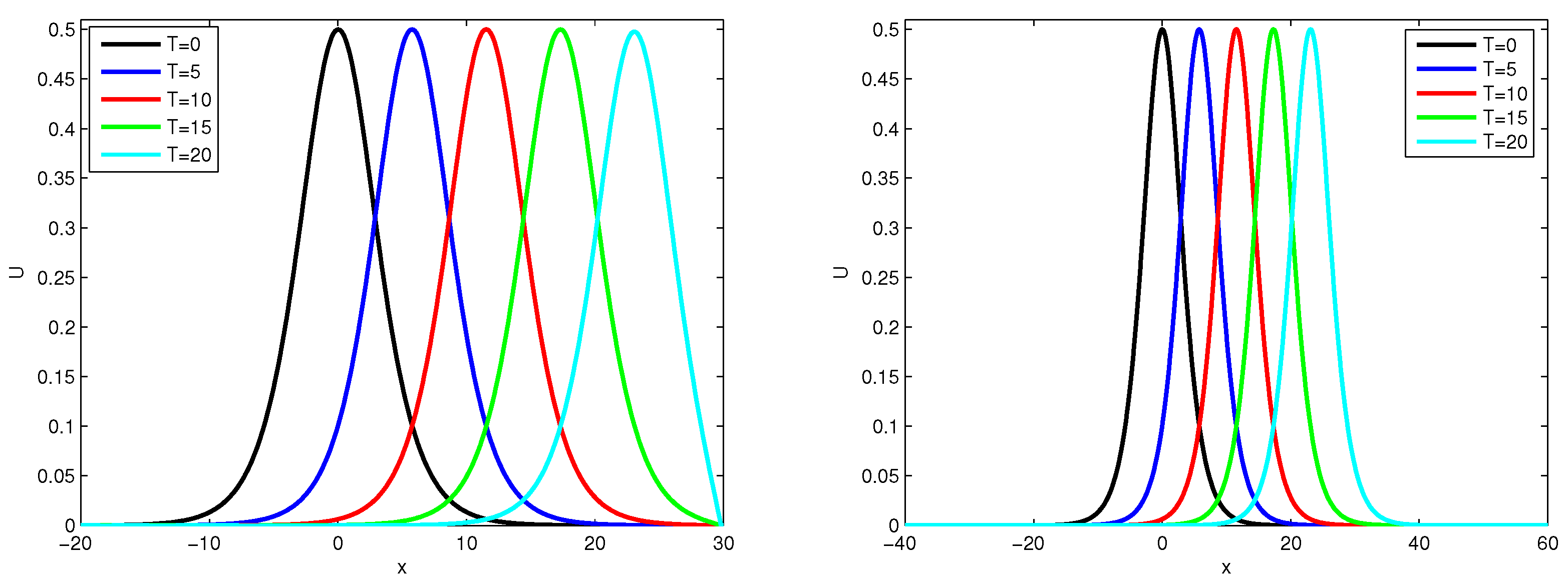
The present analysis investigates the solitary wave and its corresponding numerical solutions, as illustrated in Figure 1. The spatial domain is defined as $x\in [-20,30]$ and $[-40,60]$, with parameters set at $h=0.1$ and $\tau =h^2$ at the time instances $T=0,5,10,15,20$. Figure 1 indicates that the patterns generated by the current scheme (16)–(18), demonstrate a significant degree of agreement with the solitary wave solutions.

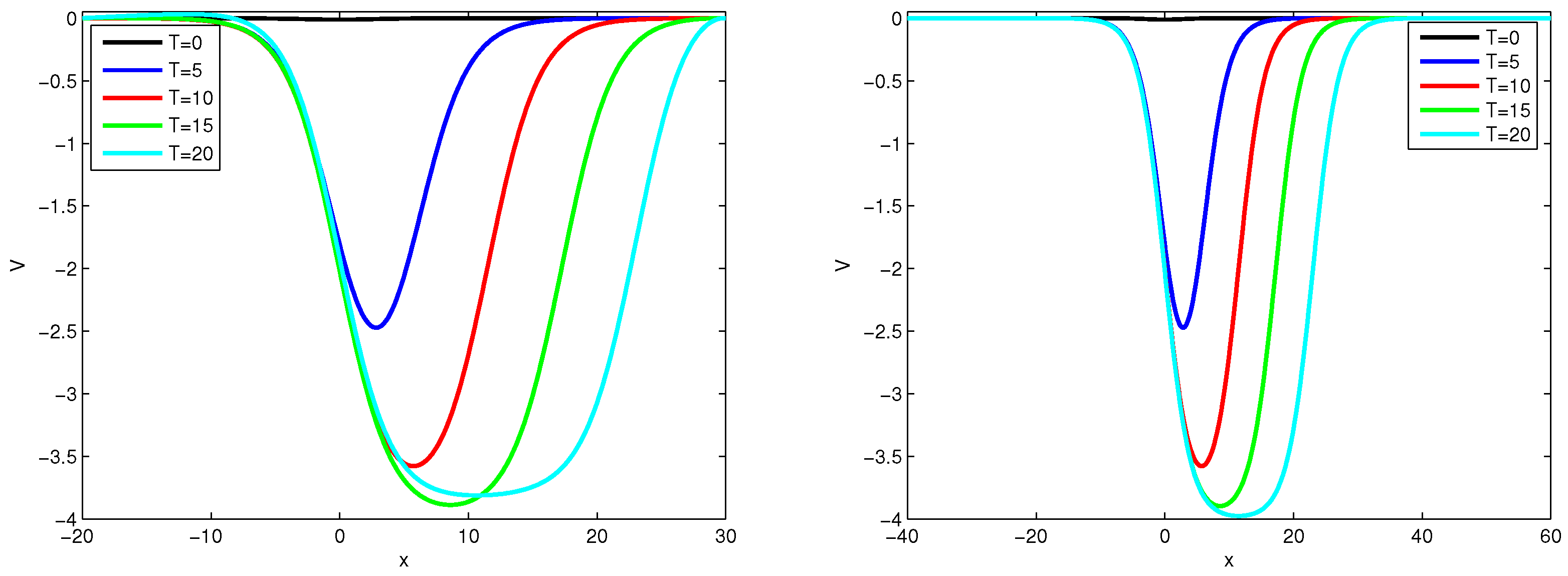
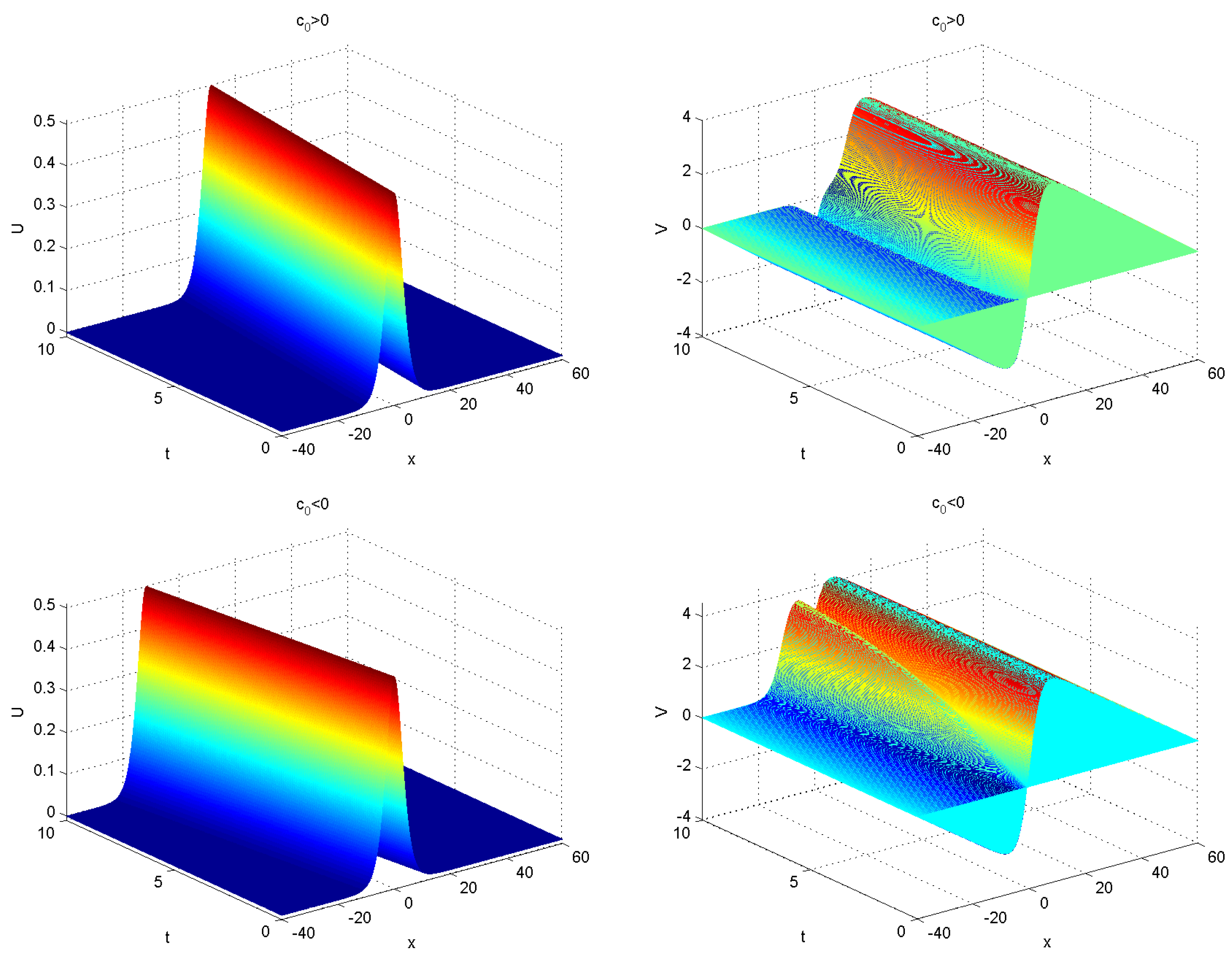
Furthermore, the numerical solutions for the auxiliary variable $V^n$, as estimated by Equation (21), are visually represented in Figure 2. The graphs displaying the approximate solutions $U^n$ and $V^n$, obtained from the difference scheme (16)–(18) with the parameters $x\in [-40,60]$, $h=0.1$, $\tau =h^2$, $c_0=\pm \sqrt{1+2A/3}$, $T=10$ are shown in Figure 3. It is observed that, when $c_0>0$, the solitary wave propagates to the right, while, for $c_0<0$, the solitary wave propagates to the left. These results are consistent with those reported in [31].

Finally, we present the discrete mass $M^n$, the discrete rate of mass change $R^n$, and the discrete energy $E^n$ at various time intervals, as detailed in

Table 4. Discrete mass $M^n$, discrete rate of mass change $R^n$, and discrete energy $E^n$ at various time intervals for Example 1.

T	${\mathit{M}}^{\mathit{n}}$	${\mathit{R}}^{\mathit{n}}$	${\mathit{E}}^{\mathit{n}}$
0	3.99999998662202	0.00000000770792	2.59519634357874
5	3.99999998684879	0.00000000748522	2.59519634801190
10	3.99999998721201	0.00000000711875	2.59519636602745
15	3.99999998755727	0.00000000676334	2.59519639725431
20	3.99999998788500	0.00000000641617	2.59519644155837

. The parameters are defined with $c_0>0$, $x\in [-40,60]$, $h=0.1$, and $\tau =h^2$. Analysis of Table 4 indicates that the discrete rate of mass change $R^n$ associated with soliton wave propagation is minimal, indicating that the mass change $R^n$ is conservative. Additionally, it is noted that the energy $E^n$ also exhibits conservative properties.

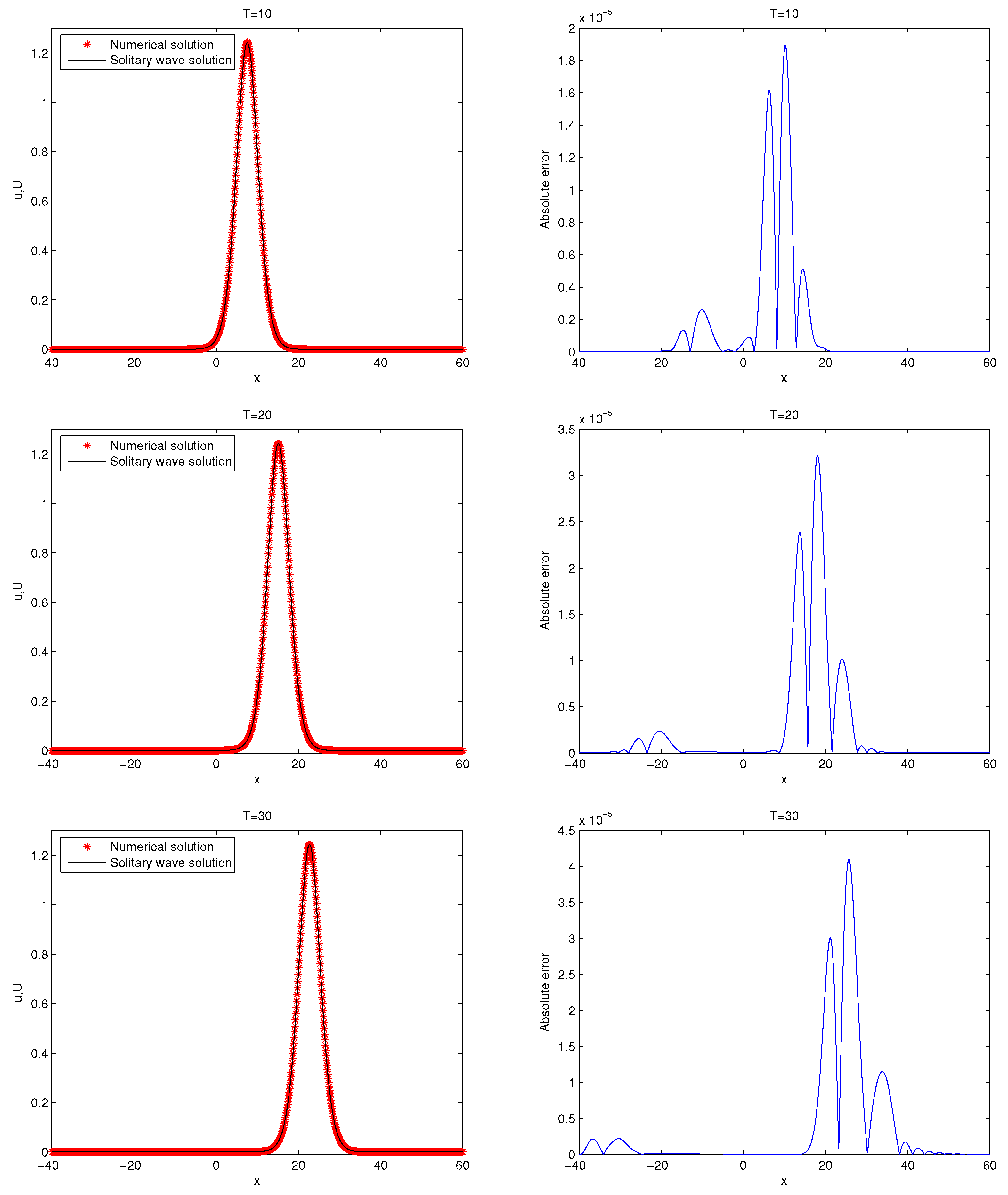
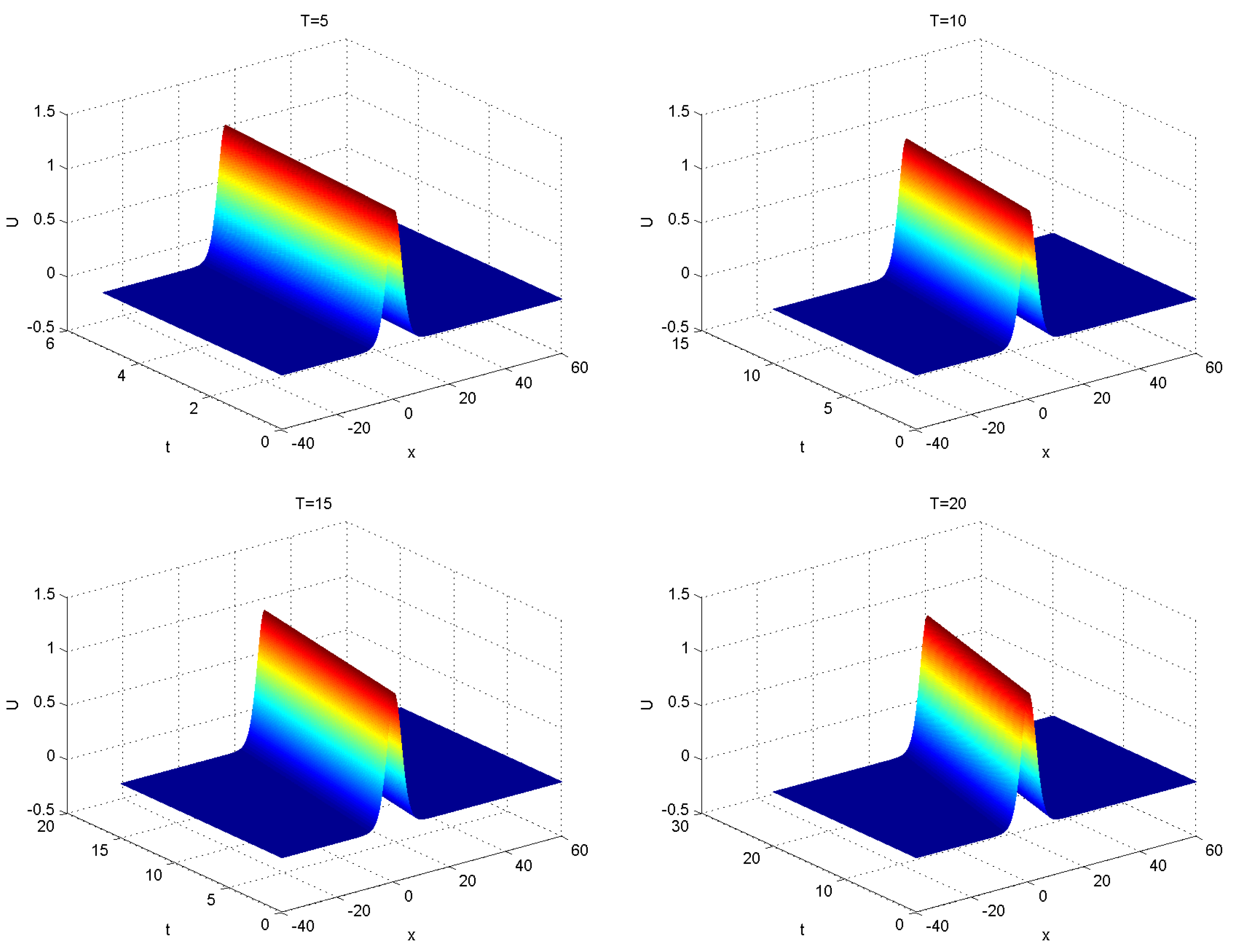
Example 2. 

Consider the parameters

$$\begin{array}{cc}\hfill & k=1,a_1={\displaystyle \frac{363}{169}},a_2=2,b_1={\displaystyle \frac{1}{2}},b_2=0,c={\displaystyle \frac{1}{2}},p=1,\hfill \end{array}$$

which is the sixth-order Boussinesq equation [15]

$$\begin{array}{cc}\hfill & u_{tt}-u_{xx}-2u_{xxtt}+{\displaystyle \frac{363}{169}}{u}_{xxxx}-{\displaystyle \frac{1}{2}}{u}_{xxxxxx}+{\displaystyle \frac{1}{2}}{\left(u^2\right)}_{xx}=0,\hfill \end{array}$$

(79)

and the solitary wave solution is provided by

$$\begin{array}{cc}\hfill & u(x,t)={\displaystyle \frac{210}{169}}{sech}^4\left({\displaystyle \frac{x}{\sqrt{26}}}-\sqrt{{\displaystyle \frac{97}{4394}}}t\right).\hfill \end{array}$$

(80)

The initial data are

$$\begin{array}{cc}\hfill & \phi \left(x\right)={\displaystyle \frac{210}{169}}{sech}^4\left({\displaystyle \frac{x}{\sqrt{26}}}\right),\hfill \end{array}$$

(81)

$$\begin{array}{cc}\hfill & \psi \left(x\right)={\displaystyle \frac{420}{\mathrm{28,561}}}\sqrt{2522}{sech}^4\left({\displaystyle \frac{x}{\sqrt{26}}}\right)tanh\left({\displaystyle \frac{x}{\sqrt{26}}}\right).\hfill \end{array}$$

(82)

In this example, we first calculate the solution over the spatial domain defined by $[-40,60]\times [0,40]$ with a grid size of $h=0.1$ and a time step $\tau =h^2$. The comparison between the solitary wave and the numerical solutions at the time instances $T=10$, 20, and 30 is presented in Figure 4. The results indicate that the errors across all grid points remain below $4.5\times {10}^{-5}$.

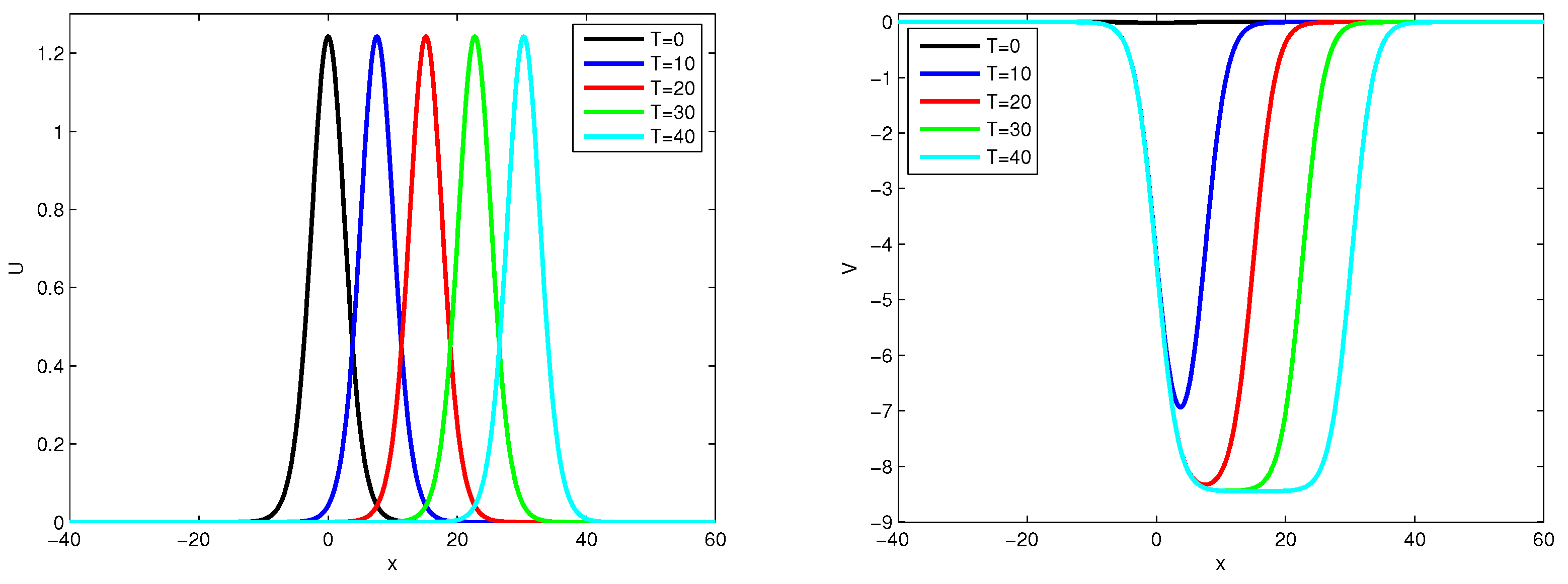
Figure 5 illustrates the numerical solutions at various time intervals, specifically $T=0$, 10, 20, 30, and 40. A detailed analysis of Figure 5 indicates that the wave heights at these specified time points are nearly indistinguishable. Figure 6 presents the graphs of the approximate solutions $U^n$ obtained from the current scheme described by Equations (16)–(18) at times $T=5$, 10, 15, and 20, with the parameters set to $h=0.1$, $\tau =h^2$, $x_l=-40$, and $x_r=60$.

Additionally,

Table 5. Discrete mass $M^n$, discrete rate of mass change $R^n$, and discrete energy $E^n$ with $h=0.1$ and $\tau =h^2$ at various time intervals for Example 2.

T	${\mathit{M}}^{\mathit{n}}$	${\mathit{R}}^{\mathit{n}}$	${\mathit{E}}^{\mathit{n}}$
0	8.44807966748734	1.88271050488737	15.35813895730075
5	8.44807966747724	1.88289006817254	15.35813896808486
10	8.44807966744347	1.88285678675310	15.35813901287684
15	8.44807966738941	1.88269314441971	15.35813909109440
20	8.44807966731402	1.88292585889068	15.35813920256866

presents a summary of the discrete mass $M^n$, the discrete rate of mass change $R^n$, and the discrete energy $E^n$ at various time points $T=0$, 5, 10, 15, and 20. The findings suggest that both the discrete rate of mass change $R^n$ and the discrete energy $E^n$ exhibit conservative behavior in the discrete sense.

Example 3. 

Consider the following sixth-order Boussinesq equation with the effects of surface tension

$$\begin{array}{cc}\hfill & u_{tt}-k^2{u}_{xx}+a_1{u}_{xxxx}-a_2{u}_{xxtt}-b_1{u}_{xxxxxx}+b_2{u}_{xxxxtt}+c{\left(u^{2p}\right)}_{xx}=0,\hfill \end{array}$$

(83)

where $a_1\ge 0$, $a_2\ge 0$, $b_1\ge 0$, $b_2\ge 0$, and $p\ge 1$. In their research, Biswas et al. [4] examined the solitary wave solution corresponding to Equation (83); that is,

$$\begin{array}{cc}\hfill & u(x,t)=A{sech}^{{\displaystyle \frac{2}{2p-1}}}\left[B(x-\nu t)\right],\hfill \end{array}$$

(84)

where

$$\begin{array}{cc}\hfill & A={\left[{\displaystyle \frac{(2p+1)(b_2{k}^2-b_1)}{2c{b}_2}}\right]}^{{\displaystyle \frac{1}{2p-1}}},B={\displaystyle \frac{|2p-1|}{2}}\sqrt{{\displaystyle \frac{b_2{k}^2-b_1}{a_1{b}_2-a_2{b}_1}}},\nu =\sqrt{{\displaystyle \frac{b_1}{b_2}}}.\hfill \end{array}$$

To perform numerical simulations, the initial conditions can be determined by evaluating Equation (84) and its derivative at the time point $t=0$; that is,

$$\begin{array}{cc}\hfill & \phi \left(x\right)=A{sech}^{{\displaystyle \frac{2}{2p-1}}}\left(Bx\right),\hfill \end{array}$$

(85)

$$\begin{array}{cc}\hfill & \psi \left(x\right)={\displaystyle \frac{2}{2p-1}}AB\nu {sech}^{{\displaystyle \frac{2}{2p-1}}}\left(Bx\right)tanh\left(Bx\right).\hfill \end{array}$$

(86)

To demonstrate the efficacy of the present difference scheme, we provide numerical results that pertain to the errors and rates of convergence. The parameters are configured with $h=0.4$ and $\tau =h^2$ at time $T=10$, as illustrated in

Table 6. Errors and convergence rates of the current scheme when $h=0.4$ and $\tau =h^2$ at $T=10$ for Example 3.

p		$\mathit{h},\mathit{\tau }$	$\mathit{h}/2,\mathit{\tau }/4$	$\mathit{h}/4,\mathit{\tau }/16$
	$\parallel e\parallel$	1.530067340$\times {10}^{-2}$	9.709362247$\times {10}^{-4}$	5.777896747$\times {10}^{-5}$
$p=1$	rate	−	3.9780748	4.07076021
	${\parallel e\parallel }_{\infty }$	1.015003674$\times {10}^{-2}$	6.556924437$\times {10}^{-4}$	4.127486212$\times {10}^{-5}$
	rate	−	3.9523219	3.9896839
	$\parallel e\parallel$	7.862155174$\times {10}^{-2}$	4.719448787$\times {10}^{-3}$	3.012389794$\times {10}^{-4}$
$p=2$	rate	−	4.0582346	3.9696380
	${\parallel e\parallel }_{\infty }$	7.973541804$\times {10}^{-2}$	4.682164328$\times {10}^{-3}$	3.018001249$\times {10}^{-4}$
	rate	−	4.0899732	3.9555103

, where $x_l=-40$ and $x_r=60$. From Table 6, it is evident that the convergence rate achieved by the current finite difference scheme is approximately 4.0, which is consistent with the theoretical order of convergence specified in Theorem 6.

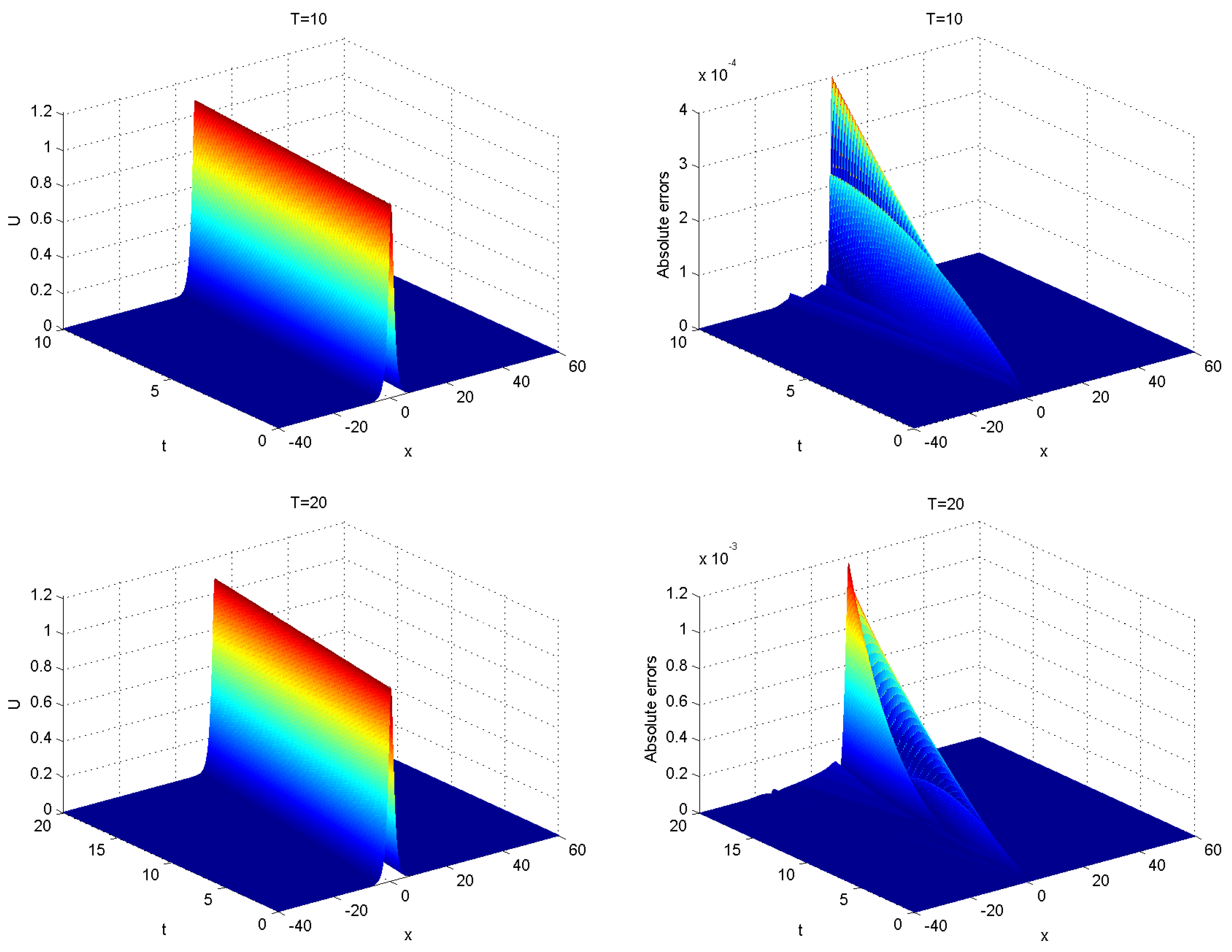
Figure 7 depicts the numerical solutions and absolute errors at times $T=10$ and 20 with $h=0.1$, $\tau =h^2$, $x_l=-40$, $x_r=60$, and $p=2$. Furthermore,

Table 7. Discrete mass $M^n$, discrete rate of mass change $R^n$, and discrete energy $E^n$ with $h=0.1$, $\tau =h^2$, and $P=2$ at various time intervals for Example 3.

T	${\mathit{M}}^{\mathit{n}}$	${\mathit{R}}^{\mathit{n}}$	${\mathit{E}}^{\mathit{n}}$
0	3.02090976925920	1.52260617289068	8.70669460321910
5	3.02090976827031	1.52400439056038	8.70669481288416
10	3.02090976455933	1.52404485849716	8.70669563361528
15	3.02090975829348	1.52179604152168	8.70669698162941
20	3.02090974941932	1.52420689642572	8.70669874989782
25	3.02090973801432	1.52375610223547	8.70670081739405
30	3.02090972410221	1.52240106874032	8.70670306135933

presents additional information regarding the discrete mass $M^n$, the discrete rate of mass change $R^n$, and the discrete energy $E^n$ at various time intervals $T=0$, $T=5$, $T=10$, $T=15$, $T=20$, $T=25$, and $T=30$. It is clear that both the rate of mass change $R^n$ and the energy $E^n$ exhibit conservative behavior in the discrete sense.

Furthermore, for $p=1$, Equation (83) exhibits two conserved quantities [4]:

$$\begin{array}{cc}\hfill & I_1={\displaystyle \frac{\nu }{10}}{\int }_{-\infty }^{\infty }\left(7b_2{u}_{xxx}^2-10a_2{u}_{xx}^2+10u_x^2\right)dx,\hfill \end{array}$$

(87)

$$\begin{array}{cc}\hfill & I_2={\displaystyle \frac{1}{30}}{\int }_{-\infty }^{\infty }\left\{-\left(15b_1+2b_2{\nu }^2\right)u_{xxx}^2-15a_2{\nu }^2{u}_{xx}^2+15\left(c^2-{\nu }^2-k^2\right)u_x^2\right\}dx.\hfill \end{array}$$

(88)

Furthermore, for any arbitrary $p>1$, Equation (83) possesses two conserved quantities [4]:

$$\begin{array}{cc}\hfill & I_3={\int }_{-\infty }^{\infty }\left(-{\displaystyle \frac{1}{3}}{b}_2{u}_{xxxxt}+{\displaystyle \frac{1}{2}}{a}_2{u}_{xxt}-u_t\right)dx,\hfill \end{array}$$

(89)

$$\begin{array}{cc}\hfill & I_4={\int }_{-\infty }^{\infty }\left(-{\displaystyle \frac{1}{3}}{b}_{2}t{u}_{xxxxt}+{\displaystyle \frac{1}{15}}{b}_2{u}_{xxx}+{\displaystyle \frac{1}{2}}{a}_{2}t{u}_{xxt}-{\displaystyle \frac{1}{6}}{a}_2{u}_{xx}-t{u}_t+u\right)dx.\hfill \end{array}$$

(90)

We will evaluate our numerical method by employing these invariants and selecting the approximate values as follows:

$$\begin{array}{cc}\hfill & \widetilde{I_1^n}={\displaystyle \frac{\nu h}{10}}\sum _{j=1}^{J-1}\left\{{\displaystyle \frac{7b_2}{2}}{[3{\left(U_j^n\right)}_{\tilde{x}\overline{x}\widehat{x}}-{\left(U_j^n\right)}_{\tilde{x}\overline{x}\ddot{x}}]}^2-{\displaystyle \frac{10a_2}{3}}{[4{\left(U_j^n\right)}_{\tilde{x}\overline{x}}-{\left(U_j^n\right)}_{\widehat{x}\widehat{x}}]}^2+{\displaystyle \frac{10}{3}}{[4{\left(U_j^n\right)}_{\widehat{x}}-{\left(U_j^n\right)}_{\ddot{x}}]}^2\right\},\hfill \\ \hfill & \widetilde{I_2^n}={\displaystyle \frac{h}{30}}\sum _{j=1}^{J-1}\{-\frac{1}{2}(15b_1+2b_2{\nu }^2){[3{\left(U_j^n\right)}_{\tilde{x}\overline{x}\widehat{x}}-{\left(U_j^n\right)}_{\tilde{x}\overline{x}\ddot{x}}]}^2-5a_2{\nu }^2{[4{\left(U_j^n\right)}_{\tilde{x}\overline{x}}-{\left(U_j^n\right)}_{\widehat{x}\widehat{x}}]}^2\hfill \\ \hfill & +5(c^2-{\nu }^2-k^2){[4{\left(U_j^n\right)}_{\widehat{x}}-{\left(U_j^n\right)}_{\ddot{x}}]}^2\},\hfill \\ \hfill & \widetilde{I_3^n}=h\sum _{j=1}^{J-1}\left\{-\frac{b_2}{9}{\left[5{\left(U_j^n\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}}-2{\left(U_j^n\right)}_{\tilde{x}\overline{x}\widehat{x}\widehat{x}}\right]}_{\widehat{t}}+\frac{a_2}{6}{\left[4{\left(U_j^n\right)}_{\tilde{x}\overline{x}}-{\left(U_j^n\right)}_{\widehat{x}\widehat{x}}\right]}_{\widehat{t}}-{\left(U_j^n\right)}_{\widehat{t}}\right\},\hfill \\ \hfill & \widetilde{I_4^n}=h\sum _{j=1}^{J-1}\{-\frac{b_2{t}^n}{9}{\left[5{\left(U_j^n\right)}_{\tilde{x}\overline{x}\tilde{x}\overline{x}}-2{\left(U_j^n\right)}_{\tilde{x}\overline{x}\widehat{x}\widehat{x}}\right]}_{\widehat{t}}+\frac{b_2}{30}[3{\left(U_j^n\right)}_{\tilde{x}\overline{x}\widehat{x}}-{\left(U_j^n\right)}_{\tilde{x}\overline{x}\ddot{x}}]\hfill \\ \hfill & +\frac{a_2{t}^n}{6}{\left[4{\left(U_j^n\right)}_{\tilde{x}\overline{x}}-{\left(U_j^n\right)}_{\widehat{x}\widehat{x}}\right]}_{\widehat{t}}-\frac{a_2}{18}\left[4{\left(U_j^n\right)}_{\tilde{x}\overline{x}}-{\left(U_j^n\right)}_{\widehat{x}\widehat{x}}\right]-t^n{\left(U_j^n\right)}_{\widehat{t}}+U_j^n\}.\hfill \end{array}$$

To demonstrate the conservative properties of the current difference scheme represented by Equations (16)–(18), we have compiled the invariants ${\tilde{I}}_1^n$, ${\overline{I}}_2^n$, ${\overline{I}}_3^n$, ${\overline{I}}_4^n$, $M^n$, $R^n$, and $E^n$ at various temporal intervals, as presented in

Table 8. Conservative quantities ${\tilde{I}}_1^n$ and ${\tilde{I}}_2^n$ and discrete quantities $M^n$, $R^n$, and $E^n$ with $h=0.1$, $\tau =h^2$, and $p=1$ at various time intervals for Example 3.

T	${\tilde{\mathit{I}}}_1^{\mathit{n}}$	${\tilde{\mathit{I}}}_2^{\mathit{n}}$	${\mathit{M}}^{\mathit{n}}$	${\mathit{R}}^{\mathit{n}}$	${\mathit{E}}^{\mathit{n}}$
0	0.77574398822	0.72568182168	2.99999999979	1.06047283470	3.78558199462
5	0.77574415451	0.72568197184	2.99999999869	1.06079683168	3.78558200635
10	0.77574474392	0.72568250450	2.99999999479	1.06080624484	3.78558205484
15	0.77574571092	0.72568337974	2.99999998836	1.06028637400	3.78558213956
20	0.77574703291	0.72568457913	2.99999997943	1.06084514881	3.78558226063
25	0.77574867931	0.72568607763	2.99999996804	1.06074072374	3.78558241692
30	0.77575061250	0.72568784435	2.99999995426	1.06042851618	3.78558260687

and

Table 9. Conservative quantities ${\tilde{I}}_3^n$ and ${\tilde{I}}_4^n$ and discrete quantities $M^n$, $R^n$, and $E^n$ with $h=0.1$, $\tau =h^2$, and $p=2$ at various time intervals for Example 3.

T	${\tilde{\mathit{I}}}_1^{\mathit{n}}$	${\tilde{\mathit{I}}}_2^{\mathit{n}}$	${\mathit{M}}^{\mathit{n}}$	${\mathit{R}}^{\mathit{n}}$	${\mathit{E}}^{\mathit{n}}$
0	0.00000000879	3.02090976945	3.02090976927	1.52260617358	8.70669460355
5	0.00000001689	3.02090976957	3.02090976906	1.52318643159	8.70669464967
10	0.00000002587	3.02090976979	3.02090976876	1.52365257478	8.70669471985
15	0.00000003535	3.02090977012	3.02090976836	1.52400439292	8.70669481421
20	0.00000004386	3.02090977051	3.02090976788	1.52424172749	8.70669493260
25	0.00000005221	3.02090977097	3.02090976732	1.52436447198	8.70669507504
30	0.00000006009	3.02090977148	3.02090976668	1.52437256971	8.70669524020

. The data illustrated in these tables indicate that the conservative quantities ${\tilde{I}}_j^n$$(j=1,2,3,4)$ and $R^n$ and $E^n$ remain approximately constant over a time frame of up to 30 units. Consequently, the compact scheme proposed, as outlined by Equations (16)–(18), demonstrates both efficiency and reliability for simulations conducted over long periods.

6. Conclusions

A conservative and compact fourth-order accurate difference scheme has been formulated for solving the sixth-order Boussinesq equation. A comprehensive analysis of solvability, convergence, and stability has been conducted. Numerical results show that the numerical solution effectively preserves the discrete rates of mass change $R^n$ and energy $E^n$.