Optimizing Power Flow and Stability in Hybrid AC/DC Microgrids: AC, DC, and Combined Analysis
Abstract
1. Introduction
- System efficiency is high because fewer conversion stages are necessary to connect electronic and nonlinear loads.
- More cost-effective energy storage and DG units based on DC, such as solar and fuel cells.
- More appropriate and efficient methods for DC loads, like LED lighting and electric vehicles (EVs).
- Small connecting interface with AC grids because of no synchronization and also has a more flexible energy paradigm for future expansion.
- The study includes an extensive review of existing research on power flow investigations and short-circuit analysis approaches for different architectures of microgrids (MGs).
- The paper addresses the importance of solving power flow and control issues using the droop control techniques of DGs.
- Mathematical modeling of the various components used in AC, DC, and hybrid AC/DC MGs is incorporated for both islanded and grid-connected modes of operation.
- The investigation addresses a thorough analysis of short-circuit situations in both AC and DC MG systems, taking into consideration different types of faults.
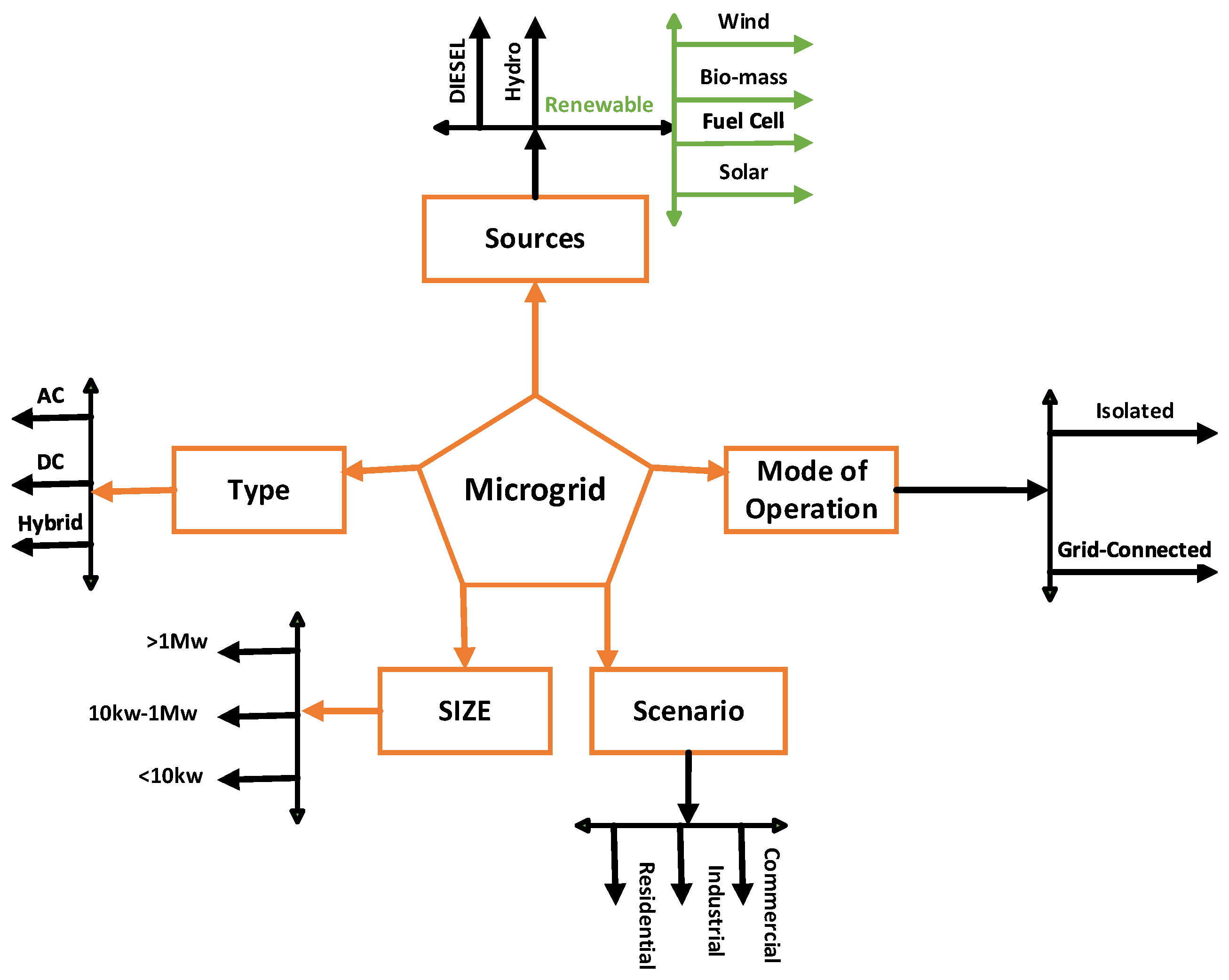
2. Different Architectures of Microgrids
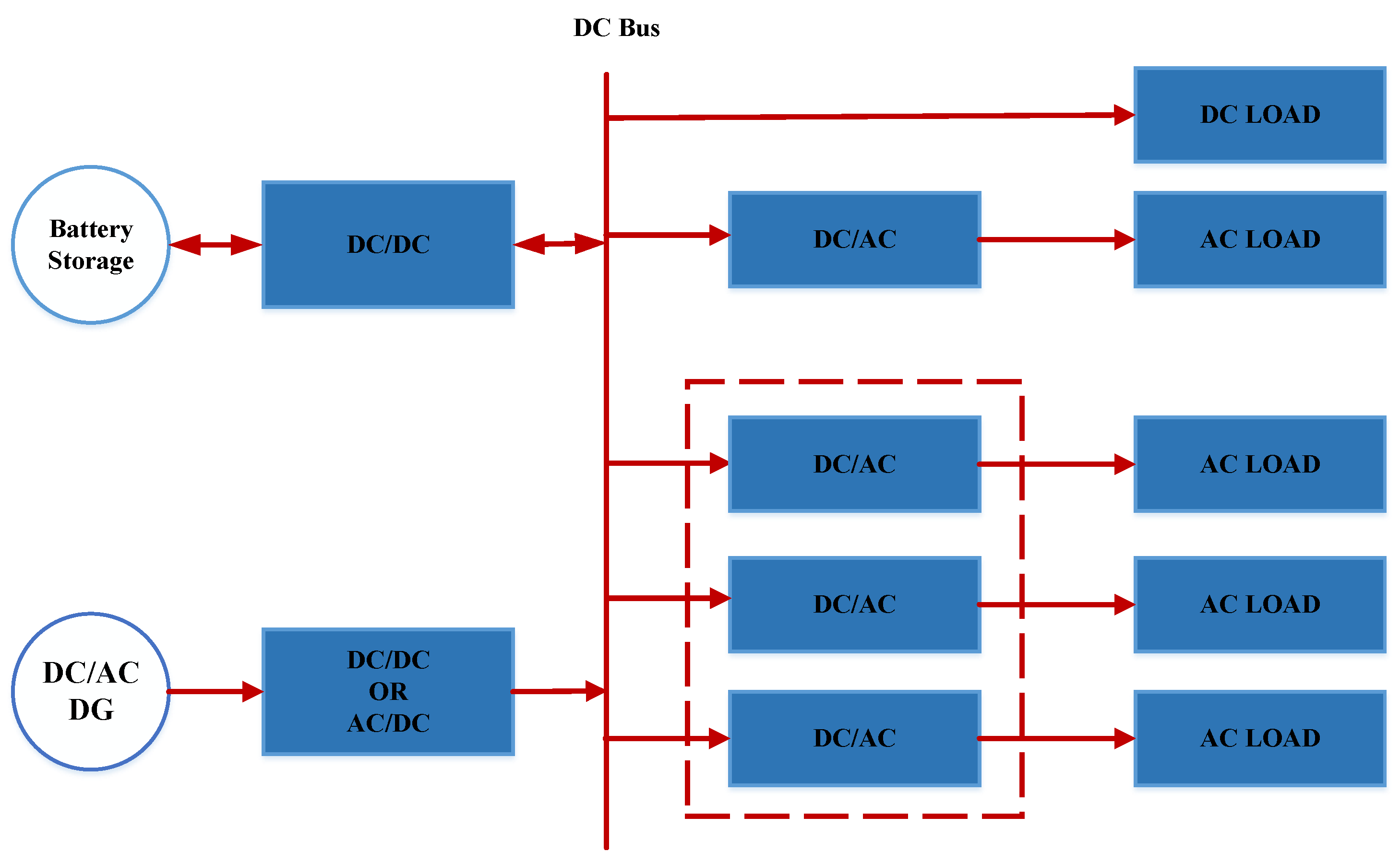
2.1. DC Microgrid
2.2. AC Microgrid
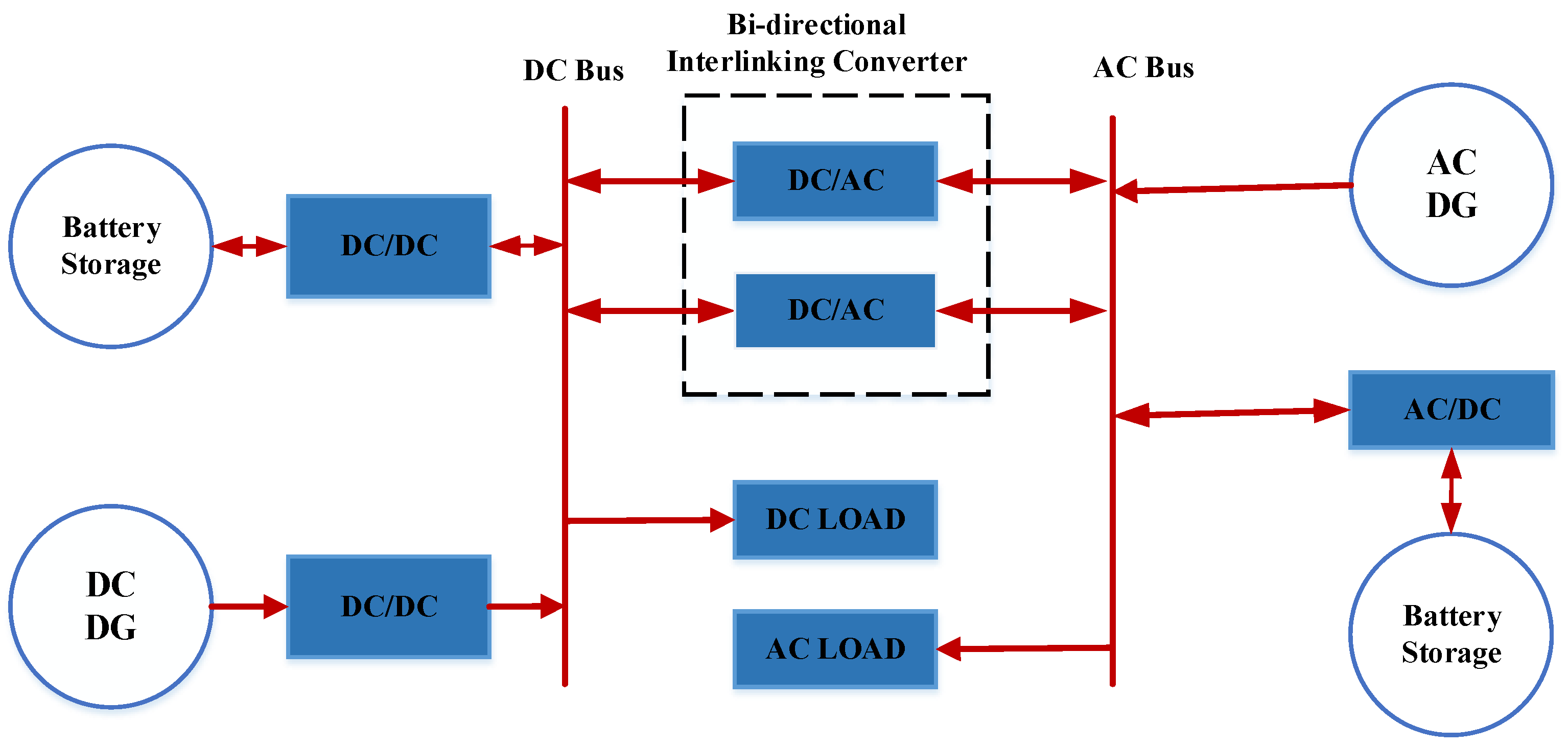
2.3. Hybrid AC/DC Coupled Microgrid
3. Modeling of Hybrid AC/DC Microgrid
3.1. Modeling of AC DERs
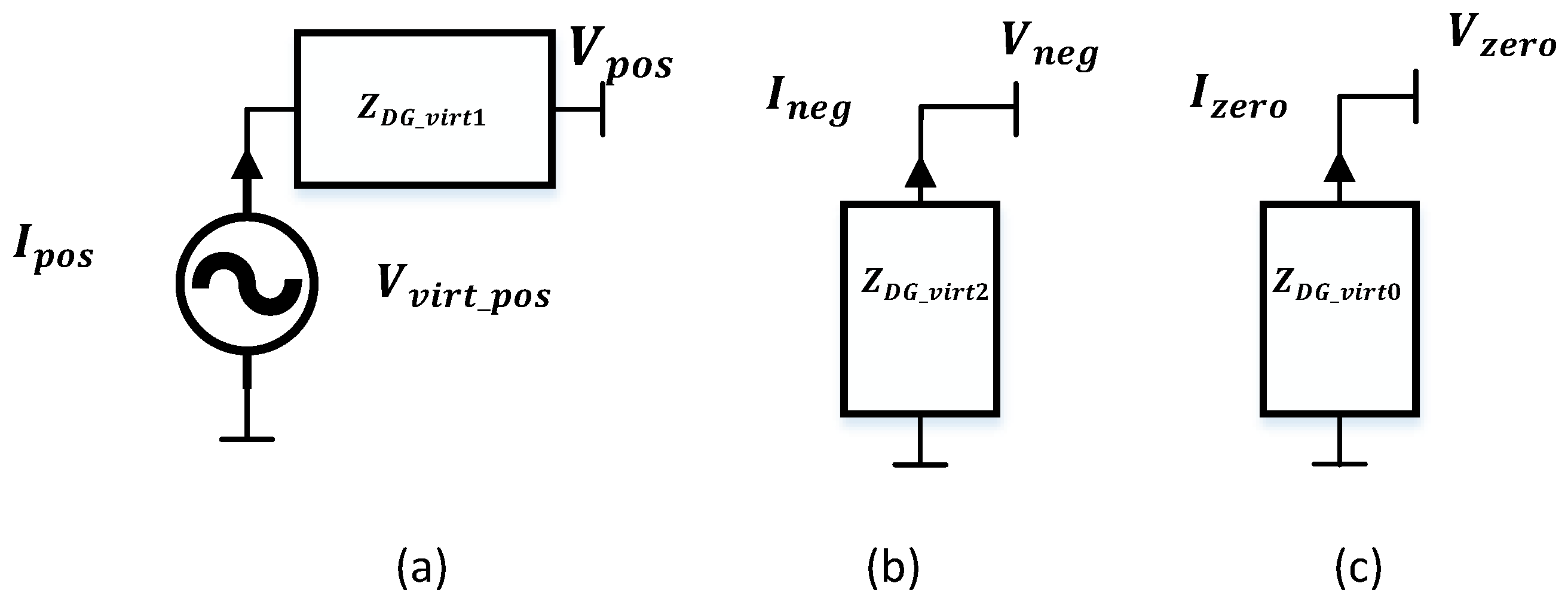
3.2. Modeling of IBDGs
3.3. Modeling of DC DERs
3.4. AC Line Modeling
3.5. DC Line Modeling
3.6. AC Load Modeling
3.7. DC Load Modeling
3.8. EV Loads
3.9. Interlinking Converter Modeling
4. Literature Review
4.1. Power Flow Analysis
4.2. Short-Circuit Analysis
- A short circuit is defined as an electrical circuit in which the flow of current goes through an unintentional channel with very low impedance.
- When a wire’s insulation cracks or another conducting substance is introduced, the charge might flow down an alternative route than it was intended to.
- Current in a short-circuit analysis is limited only by the resistance of the rest of the circuit, and it can cause severe harm, such as fire and tiny explosions. The probability of fault occurrence due to short circuits may be in between a phase and ground, a phase and neutral, or two phases.
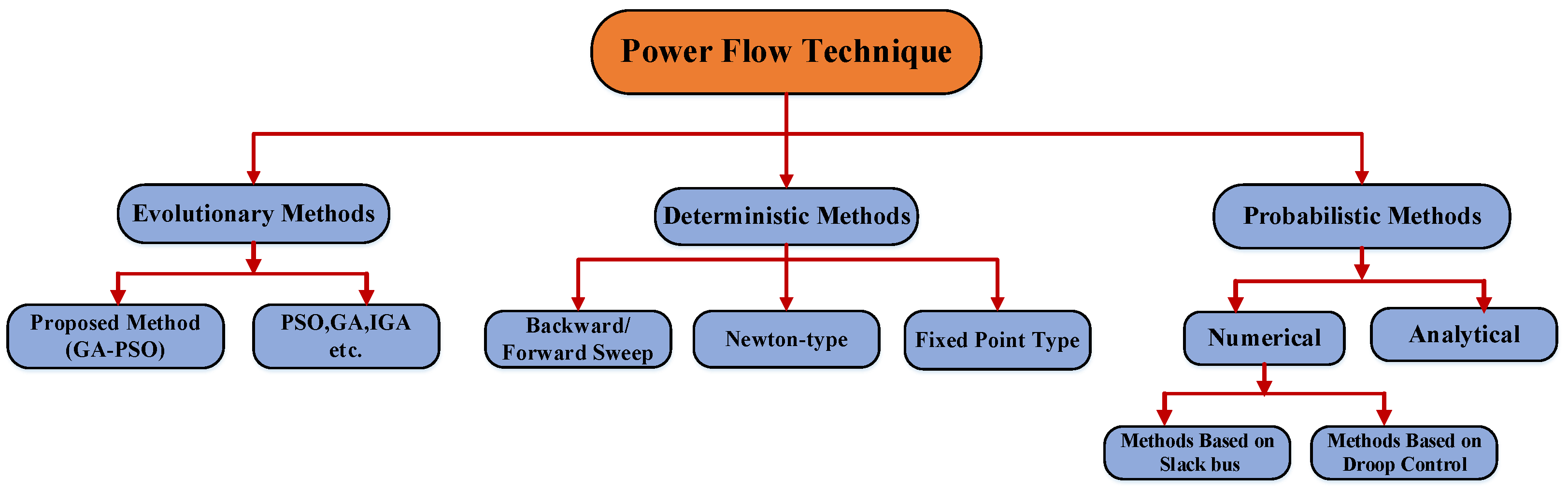
5. Methodology
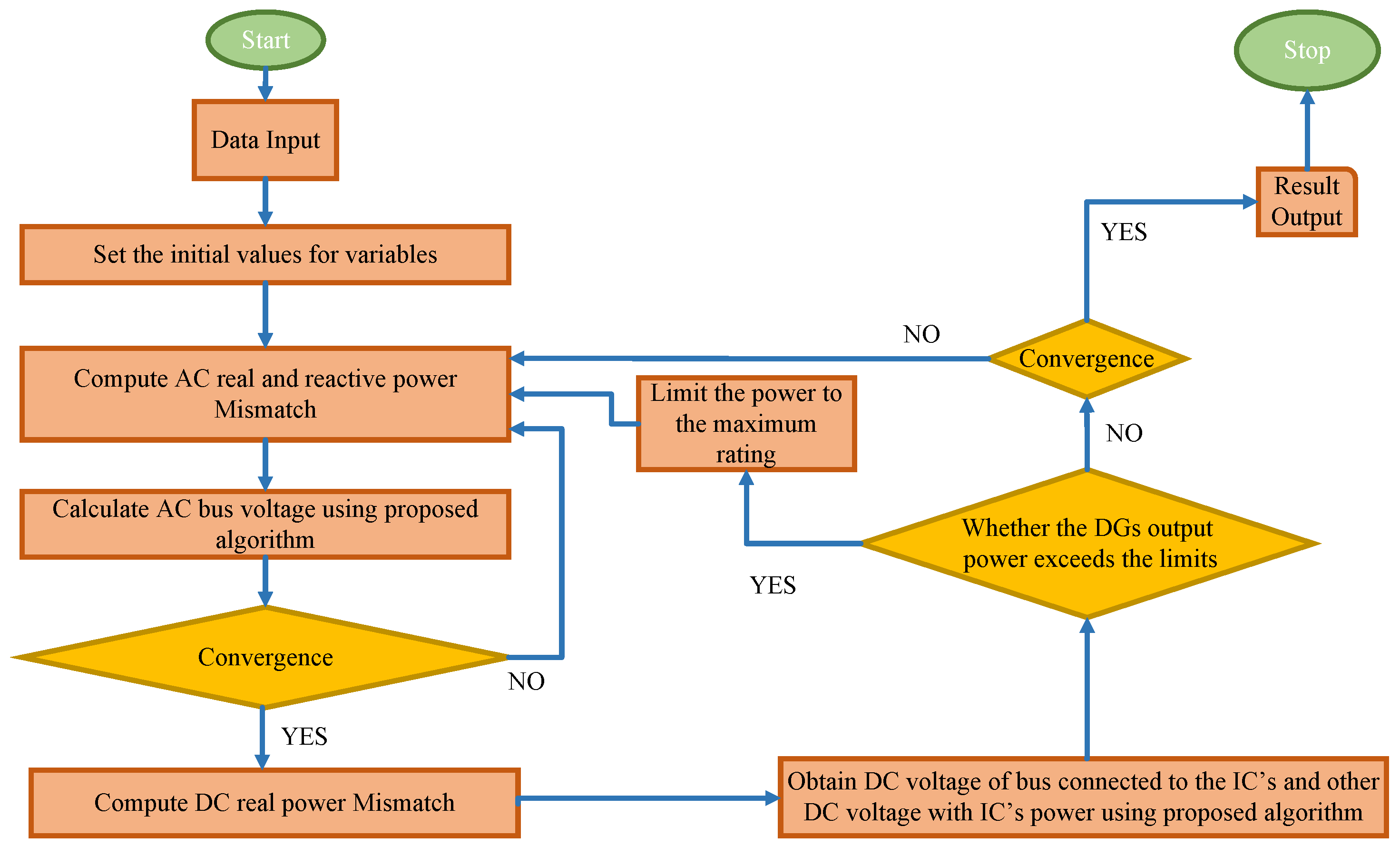
5.1. Power Flow Analysis
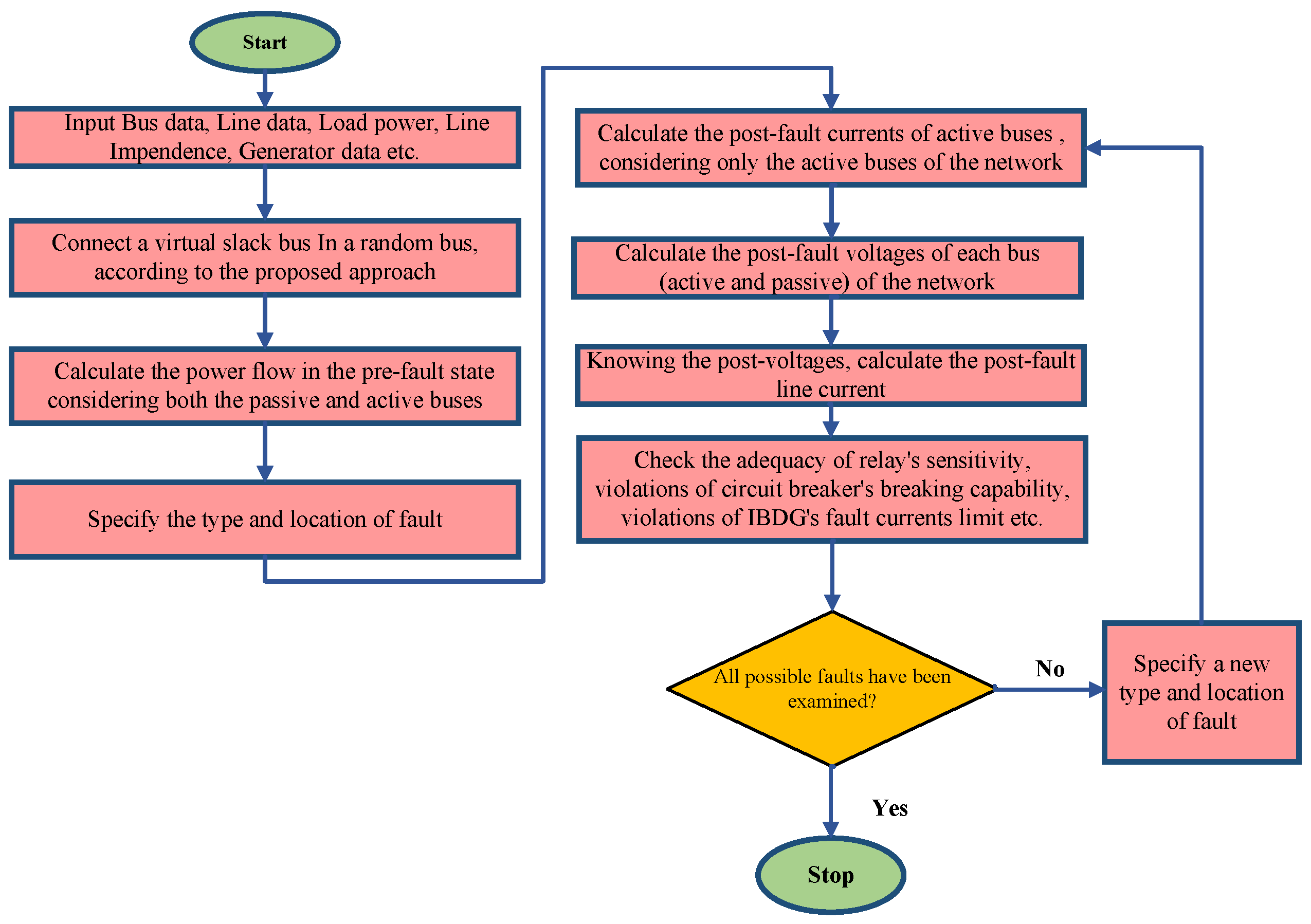
5.2. Short-Circuit Analysis
6. Promising Areas of Scientific Research
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sheykhi, N.; Salami, A.; Guerrero, J.M.; Agundis-Tinajero, G.D.; Faghihi, T. A comprehensive review on telecommunication challenges of microgrids secondary control. Int. J. Electr. Power Energy Syst. 2022, 140, 108081. [Google Scholar] [CrossRef]
- Zolfaghari, M.; Gharehpetian, G.B.; Shafie-khah, M.; Catalão, J.P. Comprehensive review on the strategies for controlling the interconnection of AC and DC microgrids. Int. J. Electr. Power Energy Syst. 2022, 136, 107742. [Google Scholar] [CrossRef]
- Green, T.C.; Prodanović, M. Control of inverter-based micro-grids. Electr. Power Syst. Res. 2007, 77, 1204–1213. [Google Scholar] [CrossRef]
- Gao, F.; Iravani, M.R. A control strategy for a distributed generation unit in grid-connected and autonomous modes of operation. IEEE Trans. Power Deliv. 2008, 23, 850–859. [Google Scholar]
- Vandoorn, T.L.; Meersman, B.; De Kooning, J.D.; Vandevelde, L. Analogy between conventional grid control and islanded microgrid control based on a global DC-link voltage droop. IEEE Trans. Power Deliv. 2012, 27, 1405–1414. [Google Scholar] [CrossRef]
- Yoldaş, Y.; Önen, A.; Muyeen, S.; Vasilakos, A.V.; Alan, I. Enhancing smart grid with microgrids: Challenges and opportunities. Renew. Sustain. Energy Rev. 2017, 72, 205–214. [Google Scholar] [CrossRef]
- Moradi, M.H.; Foroutan, V.B.; Abedini, M. Power flow analysis in islanded Micro-Grids via modeling different operational modes of DGs: A review and a new approach. Renew. Sustain. Energy Rev. 2017, 69, 248–262. [Google Scholar] [CrossRef]
- Hirsch, A.; Parag, Y.; Guerrero, J. Microgrids: A review of technologies, key drivers, and outstanding issues. Renew. Sustain. Energy Rev. 2018, 90, 402–411. [Google Scholar] [CrossRef]
- Bolgouras, V.; Ntantogian, C.; Panaousis, E.; Xenakis, C. Distributed key management in microgrids. IEEE Trans. Ind. Inform. 2019, 16, 2125–2133. [Google Scholar] [CrossRef]
- Cagnano, A.; De Tuglie, E.; Mancarella, P. Microgrids: Overview and guidelines for practical implementations and operation. Appl. Energy 2020, 258, 114039. [Google Scholar] [CrossRef]
- Azeem, O.; Ali, M.; Abbas, G.; Uzair, M.; Qahmash, A.; Algarni, A.; Hussain, M.R. A comprehensive review on integration challenges, optimization techniques and control strategies of hybrid AC/DC Microgrid. Appl. Sci. 2021, 11, 6242. [Google Scholar] [CrossRef]
- Jain, D.; Saxena, D. Comprehensive review on control schemes and stability investigation of hybrid AC-DC microgrid. Electr. Power Syst. Res. 2023, 218, 109182. [Google Scholar] [CrossRef]
- Pompodakis, E.E.; Kryonidis, G.C.; Demoulias, C.; Alexiadis, M.C. A generic power flow algorithm for unbalanced islanded hybrid AC/DC microgrids. IEEE Trans. Power Syst. 2020, 36, 1107–1120. [Google Scholar] [CrossRef]
- Surendra, K.; Das, B.; Pant, V. Static state estimation of islanded AC/DC Hybrid microgrids. Int. J. Electr. Power Energy Syst. 2024, 155, 109612. [Google Scholar] [CrossRef]
- Tinajero, G.D.A.; Nasir, M.; Vasquez, J.C.; Guerrero, J.M. Comprehensive power flow modelling of hierarchically controlled AC/DC hybrid islanded microgrids. Int. J. Electr. Power Energy Syst. 2021, 127, 106629. [Google Scholar] [CrossRef]
- Kamh, M.Z.; Iravani, R. Unbalanced model and power-flow analysis of microgrids and active distribution systems. IEEE Trans. Power Deliv. 2010, 25, 2851–2858. [Google Scholar] [CrossRef]
- Mathur, A.; Pant, V.; Das, B. Unsymmetrical short-circuit analysis for distribution system considering loads. Int. J. Electr. Power Energy Syst. 2015, 70, 27–38. [Google Scholar] [CrossRef]
- Meena, G.; Singh, V.P.; Sundariyal, N.; Mathur, A. Component Model of AC Microgrid for Short-Circuit Analysis. In Proceedings of the 2024 1st International Conference on Innovative Sustainable Technologies for Energy, Mechatronics, and Smart Systems (ISTEMS), Dehradun, India, 26–27 April 2024; pp. 1–6. [Google Scholar]
- Strezoski, L.; Prica, M.; Loparo, K.A. Generalized Δ-circuit concept for integration of distributed generators in online short-circuit calculations. IEEE Trans. Power Syst. 2016, 32, 3237–3245. [Google Scholar] [CrossRef]
- Pompodakis, E.E.; Strezoski, L.; Simic, N.; Paspatis, A.G.; Alexiadis, M.C.; Tsikalakis, A.G.; Katsigiannis, Y.A.; Karapidakis, E.S. Short-circuit calculation of droop-controlled islanded AC microgrids with virtual impedance current limiters. Electr. Power Syst. Res. 2023, 218, 109184. [Google Scholar] [CrossRef]
- Jabr, R.A.; Džafić, I. A Fortescue approach for real-time short circuit computation in multiphase distribution networks. IEEE Trans. Power Syst. 2014, 30, 3276–3285. [Google Scholar] [CrossRef]
- Abdelmalek, S.; Azar, A.T.; Dib, D. A novel actuator fault-tolerant control strategy of DFIG-based wind turbines using Takagi-Sugeno multiple models. Int. J. Control. Autom. Syst. 2018, 16, 1415–1424. [Google Scholar] [CrossRef]
- Varshney, T.; Waghmare, A.; Meena, V.; Singh, V.; Ramprabhakar, J.; Khan, B.; Singh, S. FOPDT model and CHR method based control of flywheel energy storage integrated microgrid. Sci. Rep. 2024, 14, 21550. [Google Scholar] [CrossRef] [PubMed]
- Pradhan, R.; Jena, P. An innovative fault direction estimation technique for AC microgrid. Electr. Power Syst. Res. 2023, 215, 108997. [Google Scholar] [CrossRef]
- Daraz, A.; Malik, S.A.; Azar, A.T.; Aslam, S.; Alkhalifah, T.; Alturise, F. Optimized fractional order integral-tilt derivative controller for frequency regulation of interconnected diverse renewable energy resources. IEEE Access 2022, 10, 43514–43527. [Google Scholar] [CrossRef]
- Mariam, L.; Basu, M.; Conlon, M.F. A review of existing microgrid architectures. J. Eng. 2013, 2013, 937614. [Google Scholar] [CrossRef]
- Tehrani, K.; Weber, M.; Rasoanarivo, I. Hybrid Power System Optimization for Microgrids. In Proceedings of the 2021 23rd European Conference on Power Electronics and Applications (EPE’21 ECCE Europe), Virtual, 6–10 September 2021; pp. 1–9. [Google Scholar]
- Aprilia, E.; Meng, K.; Al Hosani, M.; Zeineldin, H.H.; Dong, Z.Y. Unified power flow algorithm for standalone AC/DC hybrid microgrids. IEEE Trans. Smart Grid 2017, 10, 639–649. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Z.; Fan, M. A Newton–Raphson-based sequential power flow algorithm for hybrid AC/DC microgrids. IEEE Trans. Ind. Appl. 2021, 58, 843–854. [Google Scholar] [CrossRef]
- Kongjeen, Y.; Bhumkittipich, K. Modeling of electric vehicle loads for power flow analysis based on PSAT. In Proceedings of the 2016 13th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Chiang Mai, Thailand, 28 June–1 July 2016; pp. 1–6. [Google Scholar]
- Chaudhary, R.; Singh, V.; Mathur, A.; Meena, V.; Murari, K. Truncation-based Approximation of Autonomous Microgrid. In Proceedings of the 2024 IEEE Kansas Power and Energy Conference (KPEC), Manhattan, KS, USA, 25–26 April 2024; pp. 1–5. [Google Scholar]
- Mathur, A.; Kumari, R.; Meena, V.; Singh, V.; Azar, A.T.; Hameed, I.A. Data-driven optimization for microgrid control under distributed energy resource variability. Sci. Rep. 2024, 14, 10806. [Google Scholar] [CrossRef]
- Mumtaz, F.; Syed, M.; Al Hosani, M.; Zeineldin, H. A novel approach to solve power flow for islanded microgrids using modified Newton Raphson with droop control of DG. IEEE Trans. Sustain. Energy 2015, 7, 493–503. [Google Scholar] [CrossRef]
- Shirmohammadi, D.; Hong, H.W.; Semlyen, A.; Luo, G. A compensation-based power flow method for weakly meshed distribution and transmission networks. IEEE Trans. Power Syst. 1988, 3, 753–762. [Google Scholar] [CrossRef]
- Kumar, Y.; Meena, V.; Mathur, A.; Singh, V. Fault Detection and Localization in Distribution System using Sparse Matrix Reconstruction. In Proceedings of the 2023 International Conference on Computer, Electronics & Electrical Engineering & Their Applications (IC2E3), Srinagar Garhwal, India, 8–9 June 2023; pp. 1–6. [Google Scholar]
- Luo, G.X.; Semlyen, A. Efficient load flow for large weakly meshed networks. IEEE Trans. Power Syst. 1990, 5, 1309–1316. [Google Scholar] [CrossRef]
- Daraz, A.; Malik, S.A.; Waseem, A.; Azar, A.T.; Haq, I.U.; Ullah, Z.; Aslam, S. Automatic generation control of multi-source interconnected power system using FOI-TD controller. Energies 2021, 14, 5867. [Google Scholar] [CrossRef]
- Chang, G.; Chu, S.; Wang, H. An improved backward/forward sweep load flow algorithm for radial distribution systems. IEEE Trans. Power Syst. 2007, 22, 882–884. [Google Scholar] [CrossRef]
- Krishna, P.; Khan, B. Rank-sum-weight method based systematic determination of weights for controller tuning for automatic generation control. IEEE Access 2022, 10, 68161–68174. [Google Scholar] [CrossRef]
- Pilla, R.; Azar, A.T.; Gorripotu, T.S. Impact of flexible AC transmission system devices on automatic generation control with a metaheuristic based fuzzy PID controller. Energies 2019, 12, 4193. [Google Scholar] [CrossRef]
- Augugliaro, A.; Dusonchet, L.; Favuzza, S.; Ippolito, M.G.; Sanseverino, E.R. A backward sweep method for power flow solution in distribution networks. Int. J. Electr. Power Energy Syst. 2010, 32, 271–280. [Google Scholar] [CrossRef]
- Pompodakis, E.E.; Kryonidis, G.C.; Alexiadis, M.C. A comprehensive load flow approach for grid-connected and islanded AC microgrids. IEEE Trans. Power Syst. 2019, 35, 1143–1155. [Google Scholar] [CrossRef]
- Meena, G.; Saini, D.; Meena, V.; Mathur, A.; Singh, V. A Modified Implicit Z-Bus Method for an Unbalanced Hybrid AC-DC Microgrids. In Proceedings of the 2023 IEEE IAS Global Conference on Renewable Energy and Hydrogen Technologies (GlobConHT), Male, Maldives, 11–12 March 2023; pp. 1–6. [Google Scholar]
- Nikkhajoei, H.; Iravani, R. Steady-state model and power flow analysis of electronically-coupled distributed resource units. IEEE Trans. Power Deliv. 2006, 22, 721–728. [Google Scholar] [CrossRef]
- Ashfaq, S.; Zhang, D.; Zhang, C.; Dong, Z.Y. Load flow investigations for regionalized islanded microgrid considering frequency regulation with high renewable penetration. Electr. Power Syst. Res. 2023, 214, 108904. [Google Scholar] [CrossRef]
- Eajal, A.; Abdelwahed, M.A.; El-Saadany, E.; Ponnambalam, K. A unified approach to the power flow analysis of AC/DC hybrid microgrids. IEEE Trans. Sustain. Energy 2016, 7, 1145–1158. [Google Scholar] [CrossRef]
- Hameed, F.; Al Hosani, M.; Zeineldin, H.H. A modified backward/forward sweep load flow method for islanded radial microgrids. IEEE Trans. Smart Grid 2017, 10, 910–918. [Google Scholar] [CrossRef]
- Rao, G.K.; Jena, P. A Novel Fault Identification and Localization Scheme for Bipolar DC Microgrid. IEEE Trans. Ind. Inform. 2023, 19, 11752–11764. [Google Scholar] [CrossRef]
- Mishra, A.; Jena, P. Application of Blockchain Technology for Microgrid Restoration. IEEE Trans. Power Deliv. 2022, 38, 1810–1825. [Google Scholar] [CrossRef]
- Meena, V.; Yadav, U.; Mathur, A.; Singh, V.; Guerrero, J.M.; Khan, B. Location and size selection using hybrid Jaya-Luus-Jaakola algorithm for decentralized generations in distribution system considering demand-side management. IET Renew. Power Gener. 2023, 17, 1535–1544. [Google Scholar] [CrossRef]
- Naveen, P.; Jena, P. A robust protection scheme for multimicrogrids using fault current limiter. IEEE Trans. Ind. Appl. 2022, 58, 5763–5775. [Google Scholar] [CrossRef]
- Gangwar, T.; Padhy, N.P.; Jena, P. Storage Allocation in Active Distribution Networks Considering Life Cycle and Uncertainty. IEEE Trans. Ind. Inform. 2022, 19, 339–350. [Google Scholar] [CrossRef]
- Mansoorhoseini, P.; Mozafari, B.; Mohammadi, S. Islanded AC/DC microgrids supervisory control: A novel stochastic optimization approach. Electr. Power Syst. Res. 2022, 209, 108028. [Google Scholar] [CrossRef]
- Allam, M.A.; Hamad, A.A.; Kazerani, M. A generic modeling and power-flow analysis approach for isochronous and droop-controlled microgrids. IEEE Trans. Power Syst. 2018, 33, 5657–5670. [Google Scholar] [CrossRef]
- Nassar, M.E.; Hamad, A.A.; Salama, M.; El-Saadany, E.F. A novel load flow algorithm for islanded AC/DC hybrid microgrids. IEEE Trans. Smart Grid 2017, 10, 1553–1566. [Google Scholar] [CrossRef]
- Amritha, M.; Savier, J. Load Flow Analysis of Islanded Droop Regulated Microgrids. In Proceedings of the 2020 International Conference on Power, Instrumentation, Control and Computing (PICC), Thrissur, India, 17–19 December 2020; pp. 1–6. [Google Scholar]
- Lone, A.H.; Gupta, N. A Novel Modified Decoupled Newton-Raphson Load Flow Method with Distributed Slack Bus for Islanded Microgrids Considering Frequency Variations. Electr. Power Components Syst. 2023, 52, 678–696. [Google Scholar] [CrossRef]
- Goyal, M.; Ghosh, A.; Zare, F. Power sharing control with frequency droop in a hybrid microgrid. In Proceedings of the 2013 IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5. [Google Scholar]
- Majumder, R.; Ghosh, A.; Ledwich, G.; Zare, F. Operation and control of hybrid microgrid with angle droop controller. In Proceedings of the TENCON 2010–2010 IEEE Region 10 Conference, Fukuoka, Japan, 21–24 November 2010; pp. 509–515. [Google Scholar]
- Majumder, R.; Chaudhuri, B.; Ghosh, A.; Majumder, R.; Ledwich, G.; Zare, F. Improvement of stability and load sharing in an autonomous microgrid using supplementary droop control loop. IEEE Trans. Power Syst. 2009, 25, 796–808. [Google Scholar] [CrossRef]
- Farhadi, M.; Mohammed, O. Adaptive energy management in redundant hybrid DC microgrid for pulse load mitigation. IEEE Trans. Smart Grid 2014, 6, 54–62. [Google Scholar] [CrossRef]
- Wang, H.; Yan, Z.; Xu, X.; He, K. Probabilistic power flow analysis of microgrid with renewable energy. Int. J. Electr. Power Energy Syst. 2020, 114, 105393. [Google Scholar] [CrossRef]
- Kongjeen, Y.; Bhumkittipich, K.; Mithulananthan, N.; Amiri, I.; Yupapin, P. A modified backward and forward sweep method for microgrid load flow analysis under different electric vehicle load mathematical models. Electr. Power Syst. Res. 2019, 168, 46–54. [Google Scholar] [CrossRef]
- Abdelaziz, M.M.A.; Farag, H.E.; El-Saadany, E.F.; Mohamed, Y.A.R.I. A novel and generalized three-phase power flow algorithm for islanded microgrids using a newton trust region method. IEEE Trans. Power Syst. 2012, 28, 190–201. [Google Scholar] [CrossRef]
- Li, C.; Chaudhary, S.K.; Savaghebi, M.; Vasquez, J.C.; Guerrero, J.M. Power flow analysis for low-voltage AC and DC microgrids considering droop control and virtual impedance. IEEE Trans. Smart Grid 2016, 8, 2754–2764. [Google Scholar] [CrossRef]
- Allam, M.A.; Hamad, A.A.; Kazerani, M.; El-Saadany, E.F. A steady-state analysis tool for unbalanced islanded hybrid AC/DC microgrids. Electr. Power Syst. Res. 2017, 152, 71–83. [Google Scholar] [CrossRef]
- Xiao, Y.; Ren, C.; Han, X.; Wang, P. A generalized and mode-adaptive approach to the power flow analysis of the isolated hybrid AC/DC microgrids. Energies 2019, 12, 2253. [Google Scholar] [CrossRef]
- Wang, R.; Sun, Q.; Ma, D.; Zhang, X. The equivalent impedance characteristic analysis of the AC microgrid and its decoupled power flow calculation. Int. Trans. Electr. Energy Syst. 2019, 29, e2820. [Google Scholar] [CrossRef]
- Wang, R.; Sun, Q.; Liu, X.; Ma, D. Power flow calculation based on local controller impedance features for the AC microgrid with distributed generations. IET Energy Syst. Integr. 2019, 1, 202–209. [Google Scholar] [CrossRef]
- Morgan, M.Y.; Shaaban, M.F.; Sindi, H.F.; Zeineldin, H.H. A holomorphic embedding power flow algorithm for islanded hybrid AC/DC microgrids. IEEE Trans. Smart Grid 2022, 13, 1813–1825. [Google Scholar] [CrossRef]
- Allam, M.A.; Hamad, A.A.; Kazerani, M. A sequence-component-based power-flow analysis for unbalanced droop-controlled hybrid AC/DC microgrids. IEEE Trans. Sustain. Energy 2018, 10, 1248–1261. [Google Scholar] [CrossRef]
- Jha, B.K.; Kumar, A.; Dheer, D.K.; Singh, D.; Misra, R.K. A modified current injection load flow method under different load model of EV for distribution system. Int. Trans. Electr. Energy Syst. 2020, 30, e12284. [Google Scholar] [CrossRef]
- Sunderland, K.; Coppo, M.; Conlon, M.; Turri, R. A correction current injection method for power flow analysis of unbalanced multiple-grounded 4-wire distribution networks. Electr. Power Syst. Res. 2016, 132, 30–38. [Google Scholar] [CrossRef]
- López-Santos, O.; Salas-Castaño, M.C.; Salazar-Dantonio, D.F. Continuous Simulation of the Power Flow in AC–DC Hybrid Microgrids Using Simplified Modelling. Computation 2022, 10, 52. [Google Scholar] [CrossRef]
- Srivastava, A.K.; Kumar, A.A.; Schulz, N.N. Impact of distributed generations with energy storage devices on the electric grid. IEEE Syst. J. 2012, 6, 110–117. [Google Scholar] [CrossRef]
- Chen, Y.; Hesse, R.; Turschner, D.; Beck, H.P. Improving the grid power quality using virtual synchronous machines. In Proceedings of the 2011 International Conference on Power Engineering, Energy and Electrical Drives, Malaga, Spain, 11–13 May 2011; pp. 1–6. [Google Scholar]
- Liu, J.; Miura, Y.; Ise, T. Comparison of dynamic characteristics between virtual synchronous generator and droop control in inverter-based distributed generators. IEEE Trans. Power Electron. 2015, 31, 3600–3611. [Google Scholar] [CrossRef]
- Chen, Y.; Hesse, R.; Turschner, D.; Beck, H.P. Comparison of methods for implementing virtual synchronous machine on inverters. In Proceedings of the International Conference on Renewable Energies and Power Quality, Santiago de Compostela, Spain, 28–30 March 2012; Volume 1, pp. 1–15. [Google Scholar]
- Lee, J.O.; Kim, Y.S.; Moon, S.I. Current injection power flow analysis and optimal generation dispatch for bipolar DC microgrids. IEEE Trans. Smart Grid 2020, 12, 1918–1928. [Google Scholar] [CrossRef]
- Li, J.; Cai, H.; Yang, P.; Wei, W. A bus-sectionalized hybrid ac/dc microgrid: Concept, control paradigm, and implementation. Energies 2021, 14, 3508. [Google Scholar] [CrossRef]
- Li, C.; Chaudhary, S.K.; Vasquez, J.C.; Guerrero, J.M. Power flow analysis for droop controlled LV hybrid AC-DC microgrids with virtual impedance. In Proceedings of the 2014 IEEE PES General Meeting| Conference & Exposition, National Harbor, MD, USA, 27–31 July 2014; pp. 1–4. [Google Scholar]
- Das, B.K.; Al-Abdeli, Y.M.; Kothapalli, G. Effect of load following strategies, hardware, and thermal load distribution on stand-alone hybrid CCHP systems. Appl. Energy 2018, 220, 735–753. [Google Scholar] [CrossRef]
- Luna, A.C.; Meng, L.; Diaz, N.L.; Graells, M.; Vasquez, J.C.; Guerrero, J.M. Online energy management systems for microgrids: Experimental validation and assessment framework. IEEE Trans. Power Electron. 2017, 33, 2201–2215. [Google Scholar] [CrossRef]
- Guan, M.; Pan, W.; Zhang, J.; Hao, Q.; Cheng, J.; Zheng, X. Synchronous generator emulation control strategy for voltage source converter (VSC) stations. IEEE Trans. Power Syst. 2015, 30, 3093–3101. [Google Scholar] [CrossRef]
- Wang, P.; Jin, C.; Zhu, D.; Tang, Y.; Loh, P.C.; Choo, F.H. Distributed control for autonomous operation of a three-port AC/DC/DS hybrid microgrid. IEEE Trans. Ind. Electron. 2014, 62, 1279–1290. [Google Scholar] [CrossRef]
- Radwan, A.A.A.; Mohamed, Y.A.R.I. Networked control and power management of AC/DC hybrid microgrids. IEEE Syst. J. 2014, 11, 1662–1673. [Google Scholar] [CrossRef]
- Mohamed, Y.A.R.I.; El-Saadany, E.F. Adaptive decentralized droop controller to preserve power sharing stability of paralleled inverters in distributed generation microgrids. IEEE Trans. Power Electron. 2008, 23, 2806–2816. [Google Scholar] [CrossRef]
- Bhavana, G.; Anand, R.; Ramprabhakar, J.; Meena, V.; Jadoun, V.K.; Benedetto, F. Applications of blockchain technology in peer-to-peer energy markets and green hydrogen supply chains: A topical review. Sci. Rep. 2024, 14, 21954. [Google Scholar] [CrossRef]
- Mathur, A.; Das, B.; Pant, V. Fault analysis of unbalanced radial and meshed distribution system with inverter based distributed generation (IBDG). Int. J. Electr. Power Energy Syst. 2017, 85, 164–177. [Google Scholar] [CrossRef]
- Plet, C.A.; Graovac, M.; Green, T.C.; Iravani, R. Fault response of grid-connected inverter dominated networks. In Proceedings of the IEEE PES General Meeting, Minneapolis, MN, USA, 25–29 July 2010; pp. 1–8. [Google Scholar]
- Plet, C.A.; Green, T.C. Fault response of inverter interfaced distributed generators in grid-connected applications. Electr. Power Syst. Res. 2014, 106, 21–28. [Google Scholar] [CrossRef]
- Baskaran, J.; Naghapushanam, M.; Ganapathy, M.; Meena, P.; Meena, V.; Azar, A.T.; Hameed, I.A. Cost-effective high-gain dc-dc converter for elevator drives using photovoltaic power and switched reluctance motors. Front. Energy Res. 2024, 12, 1400651. [Google Scholar] [CrossRef]
- Rodriguez, P.; Timbus, A.V.; Teodorescu, R.; Liserre, M.; Blaabjerg, F. Flexible active power control of distributed power generation systems during grid faults. IEEE Trans. Ind. Electron. 2007, 54, 2583–2592. [Google Scholar] [CrossRef]
- Camacho, A.; Castilla, M.; Miret, J.; Vasquez, J.C.; Alarcon-Gallo, E. Flexible voltage support control for three-phase distributed generation inverters under grid fault. IEEE Trans. Ind. Electron. 2012, 60, 1429–1441. [Google Scholar] [CrossRef]
- Miret, J.; Castilla, M.; Camacho, A.; de Vicuña, L.G.; Matas, J. Control scheme for photovoltaic three-phase inverters to minimize peak currents during unbalanced grid-voltage sags. IEEE Trans. Power Electron. 2012, 27, 4262–4271. [Google Scholar] [CrossRef]
- DebBarman, S.; Namrata, K.; Kumar, N.; Meena, V. Optimising power distribution systems: Solar-powered capacitors and cost reduction through meta-heuristic methods. Int. J. Intell. Eng. Inform. 2024, 12, 188–212. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, N.; Ye, L. Fault analysis for distribution networks with current-controlled three-phase inverter-interfaced distributed generators. IEEE Trans. Power Deliv. 2015, 30, 1532–1542. [Google Scholar] [CrossRef]
- Nimpitiwan, N.; Heydt, G.T.; Ayyanar, R.; Suryanarayanan, S. Fault current contribution from synchronous machine and inverter based distributed generators. IEEE Trans. Power Deliv. 2006, 22, 634–641. [Google Scholar] [CrossRef]
- Ebrahimi, E.; Sanjari, M.J.; Gharehpetian, G.B. Control of three-phase inverter-based DG system during fault condition without changing protection coordination. Int. J. Electr. Power Energy Syst. 2014, 63, 814–823. [Google Scholar] [CrossRef]
- Darwish, A.; Abdel-Khalik, A.; Elserougi, A.; Ahmed, S.; Massoud, A. Fault current contribution scenarios for grid-connected voltage source inverter-based distributed generation with an LCL filter. Electr. Power Syst. Res. 2013, 104, 93–103. [Google Scholar] [CrossRef]
- Baran, M.E.; El-Markaby, I. Fault analysis on distribution feeders with distributed generators. IEEE Trans. Power Syst. 2005, 20, 1757–1764. [Google Scholar] [CrossRef]
- Tan, A.; Liu, W.H.; Shirmohammadi, D. Transformer and load modeling in short circuit analysis for distribution systems. IEEE Trans. Power Syst. 1997, 12, 1315–1322. [Google Scholar] [CrossRef]
- Abdel-Akher, M.; Nor, K.M. Fault analysis of multiphase distribution systems using symmetrical components. IEEE Trans. Power Deliv. 2010, 25, 2931–2939. [Google Scholar] [CrossRef]
- Chen, T.H.; Chen, M.S.; Lee, W.J.; Kotas, P.; Van Olinda, P. Distribution system short circuit analysis-A rigid approach. IEEE Trans. Power Syst. 1992, 7, 444–450. [Google Scholar] [CrossRef]
- Halpin, S.; Grigsby, L.; Gross, C.; Nelms, R. An improved fault analysis algorithm for unbalanced multi-phase power distribution systems. IEEE Trans. Power Deliv. 1994, 9, 1332–1338. [Google Scholar] [CrossRef]
- Zhang, X.; Soudi, F.; Shirmohammadi, D.; Cheng, C.S. A distribution short circuit analysis approach using hybrid compensation method. IEEE Trans. Power Syst. 1995, 10, 2053–2059. [Google Scholar] [CrossRef]
- Mao, Y.; Miu, K. Radial distribution system short circuit analysis with lateral and load equivalencing: Solution algorithms and numerical results. In Proceedings of the 2000 Power Engineering Society Summer Meeting (Cat. No. 00CH37134), Seattle, WA, USA, 16–20 July 2000; Volume 1, pp. 449–453. [Google Scholar]
- Teng, J.H. Fast short circuit analysis method for unbalanced distribution systems. In Proceedings of the 2003 IEEE Power Engineering Society General Meeting (IEEE Cat. No. 03CH37491), Toronto, ON, Canada, 13–17 July 2003; Volume 1, pp. 240–245. [Google Scholar]
- Chen, T.H.; Chen, M.S.; Inoue, T.; Kotas, P.; Chebli, E.A. Three-phase cogenerator and transformer models for distribution system analysis. IEEE Trans. Power Deliv. 1991, 6, 1671–1681. [Google Scholar] [CrossRef]
- Paz, M.C.R.; Ferraz, R.G.; Bretas, A.S.; Leborgne, R.C. System unbalance and fault impedance effect on faulted distribution networks. Comput. Math. Appl. 2010, 60, 1105–1114. [Google Scholar]
- Filomena, A.D.; Resener, M.; Salim, R.H.; Bretas, A.S. Distribution systems fault analysis considering fault resistance estimation. Int. J. Electr. Power Energy Syst. 2011, 33, 1326–1335. [Google Scholar] [CrossRef]
- Saha, S.; Aldeen, M.; Tan, C.P. Unsymmetrical fault diagnosis in transmission/distribution networks. Int. J. Electr. Power Energy Syst. 2013, 45, 252–263. [Google Scholar] [CrossRef]
- Lacroix, J.S.; Kocar, I.; Belletête, M. Accelerated computation of multiphase short circuit summary for unbalanced distribution systems using the concept of selected inversion. IEEE Trans. Power Syst. 2012, 28, 1515–1522. [Google Scholar] [CrossRef]
- Penido, D.R.R.; de Araujo, L.R.; de Carvalho Filho, M. An enhanced tool for fault analysis in multiphase electrical systems. Int. J. Electr. Power Energy Syst. 2016, 75, 215–225. [Google Scholar] [CrossRef]
- Klucznik, J. Earth wires currents calculation by tableau analysis. Electr. Power Syst. Res. 2017, 151, 329–337. [Google Scholar] [CrossRef]
- Favuzza, S.; Mitolo, M.; Moradi, S.; Musca, R.; Zizzo, G. A General Methodology for Short-circuit Calculations in Hybrid AC/DC Microgrids. IEEE Trans. Ind. Appl. 2023, 59, 2742–2749. [Google Scholar] [CrossRef]
- Kim, I. Short-circuit analysis models for unbalanced inverter-based distributed generation sources and loads. IEEE Trans. Power Syst. 2019, 34, 3515–3526. [Google Scholar] [CrossRef]
- Ou, T.C. A novel unsymmetrical faults analysis for microgrid distribution systems. Int. J. Electr. Power Energy Syst. 2012, 43, 1017–1024. [Google Scholar] [CrossRef]
- Yu, M.; Wang, Y.; Zhang, L.; Zhang, Z. DC short circuit fault analysis and protection of ring type DC microgrid. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016; pp. 1694–1700. [Google Scholar]
- Lu, X.; Wang, J.; Guerrero, J.M.; Zhao, D. Virtual-impedance-based fault current limiters for inverter dominated AC microgrids. IEEE Trans. Smart Grid 2016, 9, 1599–1612. [Google Scholar] [CrossRef]
- Zhao, M.; Zheng, X. Waveform characteristic analysis and recognition of short-circuit fault in grid-connected AC microgrid. In Proceedings of the 2019 4th International Conference on Intelligent Green Building and Smart Grid (IGBSG), Yichang, China, 6–9 September 2019; pp. 732–735. [Google Scholar]
- Eisapour-Moarref, A.; Kalantar, M.; Esmaili, M. Control strategy resilient to unbalanced faults for interlinking converters in hybrid microgrids. Int. J. Electr. Power Energy Syst. 2020, 119, 105927. [Google Scholar] [CrossRef]
- Azizpour, A.; Radmehr, M.; Firouzi, M.; Gharehpetian, G. Single AC/DC fault current limiter for both side of hybrid AC/DC microgrid. Int. J. Electron. 2022, 110, 1337–1354. [Google Scholar] [CrossRef]
- Xiao, F.; Xia, Y.; Zhang, K.; Zhang, Z.; Yin, X. Short-circuit calculation method for unbalanced distribution networks with doubly fed induction generators. Electr. Power Syst. Res. 2022, 210, 108108. [Google Scholar] [CrossRef]
- Miret, J.; Castilla, M.; Velasco, M.; Guzmán, R.; de Vicuña, L.G. Maximum current injection method for grid-forming inverters in an islanded microgrid subject to short circuits. IET Power Electron. 2023, 16, 1028–1042. [Google Scholar] [CrossRef]
- Wang, Z.; Mu, L.; Xu, Y.; Zhang, F.; Zhu, J. The fault analysis method of islanded microgrid based on the U/f and PQ control strategy. Int. Trans. Electr. Energy Syst. 2021, 31, e12919. [Google Scholar] [CrossRef]
- Teng, J.H. Unsymmetrical short-circuit fault analysis for weakly meshed distribution systems. IEEE Trans. Power Syst. 2009, 25, 96–105. [Google Scholar] [CrossRef]
- Bayindir, R.; Irmak, E.; Issi, F.; Guler, N. Short-circuit fault analysis on microgrid. In Proceedings of the 2015 International Conference on Renewable Energy Research and Applications (ICRERA), Palermo, Italy, 22–25 November 2015; pp. 1248–1252. [Google Scholar]
- Simic, N.; Strezoski, L.; Dumnic, B. Short-circuit analysis of DER-based microgrids in connected and islanded modes of operation. Energies 2021, 14, 6372. [Google Scholar] [CrossRef]
- Seyedi, Y.; Mahseredjian, J.; Karimi, H. Impact of fault impedance and duration on transient response of hybrid AC/DC microgrid. Electr. Power Syst. Res. 2021, 197, 107298. [Google Scholar] [CrossRef]
- Hooshyar, H.; Baran, M.E. Fault analysis on distribution feeders with high penetration of PV systems. IEEE Trans. Power Syst. 2012, 28, 2890–2896. [Google Scholar] [CrossRef]
- Furlaneto, R.; Kocar, I.; Grilo-Pavani, A.; Karaagac, U.; Haddadi, A.; Farantatos, E. Short circuit network equivalents of systems with inverter-based resources. Electr. Power Syst. Res. 2021, 199, 107314. [Google Scholar] [CrossRef]
- Nahas, E.W.; Abd el Ghany, H.A.; Mansour, D.E.A.; Eissa, M. Extensive analysis of fault response and extracting fault features for DC microgrids. Alex. Eng. J. 2021, 60, 2405–2420. [Google Scholar] [CrossRef]
- Fu, R.; Montross, K.C. A New Method of Coordinating ZCBs and Fuses for a Reliable Short-Circuit Protection in DC Power Networks. IEEE Access 2022, 10, 63270–63279. [Google Scholar] [CrossRef]
- Hsieh, T.Y.; Chen, T.H.; Yang, N.C.; Lee, W.J. Efficient network fault analysis method for unbalanced microgrid systems. Int. J. Electr. Power Energy Syst. 2018, 103, 89–101. [Google Scholar] [CrossRef]
- He, J.; Li, Z.; Li, W.; Zou, J.; Li, X.; Wu, F. Fast short-circuit current calculation of unbalanced distribution networks with inverter-interfaced distributed generators. Int. J. Electr. Power Energy Syst. 2023, 146, 108728. [Google Scholar] [CrossRef]
- Luka, S.; Simic, N.; Dumnic, B. Fault current study of microgrids in grid-connected and islanded modes of operation. In Proceedings of the 12th Mediterranean Conference on Power Generation, Transmission, Distribution and Energy Conversion (MEDPOWER 2020), IET, Paphos, Cyprus, 9–12 November 2020; Volume 2020, pp. 372–377. [Google Scholar]
- Casagrande, E.; Woon, W.L.; Zeineldin, H.H.; Svetinovic, D. A differential sequence component protection scheme for microgrids with inverter-based distributed generators. IEEE Trans. Smart Grid 2013, 5, 29–37. [Google Scholar] [CrossRef]
- Sortomme, E.; Venkata, S.; Mitr, J. Microgrid Protection Using Communication-Assisted Digital Relays. IEEE Trans. Power Deliv. 2010, 25, 2789–2796. [Google Scholar] [CrossRef]
- Rajaei, N.; Ahmed, M.H.; Salama, M.M.; Varma, R.K. Fault current management using inverter-based distributed generators in smart grids. IEEE Trans. Smart Grid 2014, 5, 2183–2193. [Google Scholar] [CrossRef]
- Li, X.; Dyśko, A.; Burt, G.M. Traveling wave-based protection scheme for inverter-dominated microgrid using mathematical morphology. IEEE Trans. Smart Grid 2014, 5, 2211–2218. [Google Scholar] [CrossRef]
- Elkhatib, M.E.; Ellis, A. Communication-assisted impedance-based microgrid protection scheme. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 1–5. [Google Scholar]
- Nian, H.; Kong, L. Transient modeling and analysis of VSC based DC microgrid during short circuit fault. IEEE Access 2019, 7, 170604–170614. [Google Scholar] [CrossRef]
- Zha, X.; Ning, H.; Lai, X.; Huang, Y.; Liu, F. Suppression strategy for short-circuit current in loop-type DC microgrid. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014; pp. 758–764. [Google Scholar]
- Dağ, B.; Boynueğri, A.R.; Ateş, Y.; Karakaş, A.; Nadar, A.; Uzunoğlu, M. Static modeling of microgrids for load flow and fault analysis. IEEE Trans. Power Syst. 2016, 32, 1990–2000. [Google Scholar] [CrossRef]
- Jia, K.; Bi, T.; Ren, Z.; Thomas, D.W.; Sumner, M. High frequency impedance based fault location in distribution system with DGs. IEEE Trans. Smart Grid 2016, 9, 807–816. [Google Scholar] [CrossRef]


| Ref. | Year | Architecture | ILC | PFA | SCA | ||
|---|---|---|---|---|---|---|---|
| AC | DC | AC/DC | |||||
| [3] | 2007 | ✓ | × | × | × | ✓ | × |
| [4] | 2008 | ✓ | × | × | × | ✓ | × |
| [5] | 2012 | ✓ | × | × | × | ✓ | × |
| [6] | 2017 | ✓ | ✓ | × | × | ✓ | × |
| [7] | 2017 | ✓ | × | ✓ | × | ✓ | × |
| [8] | 2018 | ✓ | × | × | × | ✓ | × |
| [9] | 2020 | ✓ | × | × | × | × | × |
| [10] | 2020 | ✓ | ✓ | × | × | × | × |
| [11] | 2021 | × | × | ✓ | ✓ | × | × |
| [12] | 2023 | × | × | ✓ | ✓ | ✓ | × |
| This review | 2024 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Ref. | Technique | Architecture | R/WM/ Is/GC | Unbalanced | ||
|---|---|---|---|---|---|---|
| AC | DC | AC/DC | ||||
| [28] | Newton–Raphson (N-R) | × | × | ✓ | Is | ✓ |
| [29] | N-R | × | × | ✓ | Is | ✓ |
| [30] | Power system analysis toolbox (PSAT) | ✓ | × | × | R | × |
| [33] | Modified Newton–Raphson (MNR) | ✓ | × | × | Is | ✓ |
| [34] | Compensation-based method | ✓ | × | × | R/WM | ✓ |
| [36] | Tree-based load flow | ✓ | × | × | WM | × |
| [38] | Improved backward–forward sweep (IBFS) | ✓ | × | × | R | ✓ |
| [41] | Backward–forward sweep (BFS) | ✓ | × | × | R/WM | ✓ |
| [42] | Implicit Z-Bus | ✓ | × | × | Is/GC | ✓ |
| [43] | Modified implicit Z-Bus | × | × | ✓ | Is/GC | ✓ |
| [44] | Conventional PF using DR | ✓ | × | × | Is/GC | × |
| [45] | Clustering-based method | ✓ | × | × | R/Is | ✓ |
| [46] | Newton trust region (NTR) | × | × | ✓ | R/Is | ✓ |
| [47] | Modified backward–forward sweep | ✓ | × | × | R/Is | × |
| [48] | Fault identification | × | ✓ | × | R | × |
| [49] | Blockchain technology | ✓ | × | × | R | × |
| [51] | Fault current limiter | ✓ | × | × | R | × |
| [52] | Mixed-integer linear programming | ✓ | × | × | R/Is | × |
| [53] | Model predictive control | × | × | ✓ | Is | ✓ |
| [54] | Sequence component-based PF | ✓ | × | × | GC | ✓ |
| [55] | Modified branch-based approach | × | × | ✓ | Is | × |
| [56] | BFS | ✓ | × | × | R/Is | ✓ |
| [57] | Modified Newton–Raphson | ✓ | × | × | Is | ✓ |
| [58] | Controlling and power sharing | × | × | ✓ | Is/GC | × |
| [59] | Angle droop control | × | × | ✓ | GC | × |
| [60] | Droop-based power sharing | ✓ | × | × | Is | × |
| [61] | Adaptive energy calculation | × | ✓ | × | GC | × |
| [62] | Global sensitivity analysis (GSA) | ✓ | × | × | Is/GC | ✓ |
| [63] | MBFS PF | ✓ | × | × | R | ✓ |
| [64] | Newton trust region (NTR) | ✓ | × | × | Is | ✓ |
| [65] | Virtual impedance-based power flow | ✓ | ✓ | × | GC | × |
| [66] | NTR | × | × | ✓ | Is | ✓ |
| [67] | Unified power flow model | × | × | ✓ | Is | ✓ |
| [68] | Impedance based | ✓ | × | × | GC | × |
| Ref. | Technique | Architecture | R/WM/ Is/GC | Unbalanced | ||
|---|---|---|---|---|---|---|
| AC | DC | AC/DC | ||||
| [69] | Local controller impedance features | ✓ | × | × | GC | × |
| [70] | Holomorphic embedding | × | × | ✓ | Is | ✓ |
| [71] | Sequence component-based PF | × | × | ✓ | Is | ✓ |
| [72] | Modified current injection method (MCIM) | ✓ | × | × | R | ✓ |
| [73] | Current injection method (CIM) | ✓ | × | × | R | ✓ |
| [74] | Multiple-input multiple-output model | × | × | ✓ | Is/GC | ✓ |
| [75] | Hybrid optimization model | ✓ | × | × | R | × |
| [76] | Virtual synchronous machine (VISMA) | ✓ | × | × | R | × |
| [77] | VSM-based control | ✓ | × | × | Is/GC | × |
| [78] | Virtual synchronous machine (VSM) | ✓ | × | × | Is | × |
| [79] | Current injection method (CIM) | × | ✓ | × | GC | ✓ |
| [80] | Bus-sectionalized method | × | × | ✓ | Is/GC | × |
| [81] | Droop control and virtual impedance | × | × | ✓ | GC | × |
| [82] | Genetic algorithm | ✓ | × | × | R | × |
| [83] | Adaptable energy management | ✓ | × | × | Is/GC | × |
| [84] | VSC control | ✓ | × | × | R | × |
| [85] | Power control | ✓ | × | × | R | × |
| [86] | Power management | × | × | ✓ | Is | × |
| [87] | Droop based | ✓ | × | × | GC | × |
| Ref. | Technique | Architecture | R/WM/ Is/GC | Unbalanced | ||
|---|---|---|---|---|---|---|
| AC | DC | AC/DC | ||||
| [20] | Delta-circuit and VICL (SCC) | ✓ | × | × | Is | ✓ |
| [21] | Fortescue approach | ✓ | × | × | R | ✓ |
| [90] | Inverter-based fault response | ✓ | × | × | GC | × |
| [91] | IIDG fault response | ✓ | × | × | GC | × |
| [93] | Power control during fault | ✓ | × | × | R/GC | × |
| [94] | Voltage source control (VSC) | ✓ | × | × | R/GC | ✓ |
| [95] | Inverter control | ✓ | × | × | R/GC | ✓ |
| [97] | Fault analysis | ✓ | × | × | GC/DS | ✓ |
| [98] | Fault calculation Z-bus matrix | ✓ | × | × | R/GC | ✓ |
| [99] | IBDG controlling | ✓ | × | × | R/GC | ✓ |
| [100] | VSC-based fault current controlling | ✓ | × | × | R/GC | ✓ |
| [101] | Distribution system fault analysis | ✓ | × | × | R/GC | × |
| [102] | Short-circuit analysis | ✓ | × | × | R/GC | × |
| [103] | Symmetrical component based | ✓ | × | × | R | ✓ |
| [104] | Phase-based system | ✓ | × | × | R | ✓ |
| [105] | Improved fault analysis algorithm | ✓ | × | × | R | ✓ |
| [106] | Hybrid compensation | ✓ | × | × | R | ✓ |
| [107] | Fault analysis | ✓ | × | × | R | ✓ |
| [117] | IBDG SCC | ✓ | × | × | R | ✓ |
| [109] | Transformer model based | ✓ | × | × | R | ✓ |
| [110] | Symmetrical component/ phase component | ✓ | × | × | R | ✓ |
| [111] | Fault resistance estimation | ✓ | × | × | R | ✓ |
| [112] | Unsymmetrical fault analysis | ✓ | × | × | R | × |
| [113] | Fault analysis | ✓ | × | × | R | ✓ |
| [118] | Hybrid compensation method | ✓ | × | × | Is/GC | ✓ |
| [119] | Current differential protection | × | ✓ | × | GC | × |
| [120] | Virtual impedance based | × | ✓ | × | Is | × |
| [121] | Wavelet energy spectrum | ✓ | × | × | GC | × |
| [122] | Fault analysis of interlinking converters | × | × | ✓ | GC | ✓ |
| [123] | Fault current limiter | × | × | ✓ | GC | × |
| [124] | DFIG-based SCC | ✓ | × | × | R | ✓ |
| [125] | MCIM | ✓ | × | × | Is | ✓ |
| [114] | CIM | ✓ | × | × | R | ✓ |
| Ref. | Technique | Architecture | R/WM/ Is/GC | Unbalanced | ||
|---|---|---|---|---|---|---|
| AC | DC | AC/DC | ||||
| [115] | Fault current calculation | ✓ | × | × | R | ✓ |
| [116] | SCC calculation IEC 61660 | × | × | ✓ | R | × |
| [126] | V/F and PQ control | ✓ | × | × | Is | ✓ |
| [127] | BIBC | ✓ | × | × | WM | ✓ |
| [128] | SCC of MG | ✓ | × | × | GC | ✓ |
| [129] | DER based | ✓ | × | × | Is/GC | ✓ |
| [130] | Fault impedance based | × | × | ✓ | R | × |
| [131] | Time-varying fault analysis | ✓ | × | × | R | × |
| [132] | Voltage-dependent network equivalents (VDNEs) | ✓ | × | × | R | × |
| [133] | Fault analysis | × | ✓ | × | GC | × |
| [134] | ZCBs and fuse based | × | ✓ | × | GC | × |
| [135] | Augmented matrix based | ✓ | × | × | GC | ✓ |
| [136] | Simple generalized minimal residual (SGMRES) | ✓ | × | × | R | ✓ |
| [137] | Fault current calculation | ✓ | × | × | Is/GC | ✓ |
| [138] | IBDG fault current calculation | ✓ | × | × | Is/GC | ✓ |
| [139] | Communication-assisted digital relays | ✓ | × | × | GC | ✓ |
| [140] | IBDG fault current calculation | ✓ | × | × | R | ✓ |
| [141] | Mathematical morphology | ✓ | × | × | R | ✓ |
| [142] | Impedance based | ✓ | × | × | GC | × |
| [143] | VSC based | × | ✓ | × | GC | × |
| [144] | SC current suppression | × | ✓ | × | GC | × |
| [145] | Static modeling approach | ✓ | × | × | GC | ✓ |
| [146] | Impedance based | ✓ | × | × | R | ✓ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meena, G.; Meena, V.; Mathur, A.; Singh, V.P.; Azar, A.T.; Hameed, I.A. Optimizing Power Flow and Stability in Hybrid AC/DC Microgrids: AC, DC, and Combined Analysis. Math. Comput. Appl. 2024, 29, 108. https://doi.org/10.3390/mca29060108
Meena G, Meena V, Mathur A, Singh VP, Azar AT, Hameed IA. Optimizing Power Flow and Stability in Hybrid AC/DC Microgrids: AC, DC, and Combined Analysis. Mathematical and Computational Applications. 2024; 29(6):108. https://doi.org/10.3390/mca29060108
Chicago/Turabian StyleMeena, Ghanshyam, Veerpratap Meena, Akhilesh Mathur, Vinay Pratap Singh, Ahmad Taher Azar, and Ibrahim A. Hameed. 2024. "Optimizing Power Flow and Stability in Hybrid AC/DC Microgrids: AC, DC, and Combined Analysis" Mathematical and Computational Applications 29, no. 6: 108. https://doi.org/10.3390/mca29060108
APA StyleMeena, G., Meena, V., Mathur, A., Singh, V. P., Azar, A. T., & Hameed, I. A. (2024). Optimizing Power Flow and Stability in Hybrid AC/DC Microgrids: AC, DC, and Combined Analysis. Mathematical and Computational Applications, 29(6), 108. https://doi.org/10.3390/mca29060108








