Shadowed Type-2 Fuzzy Sets in Dynamic Parameter Adaption in Cuckoo Search and Flower Pollination Algorithms for Optimal Design of Fuzzy Fault-Tolerant Controllers
Abstract
1. Introduction
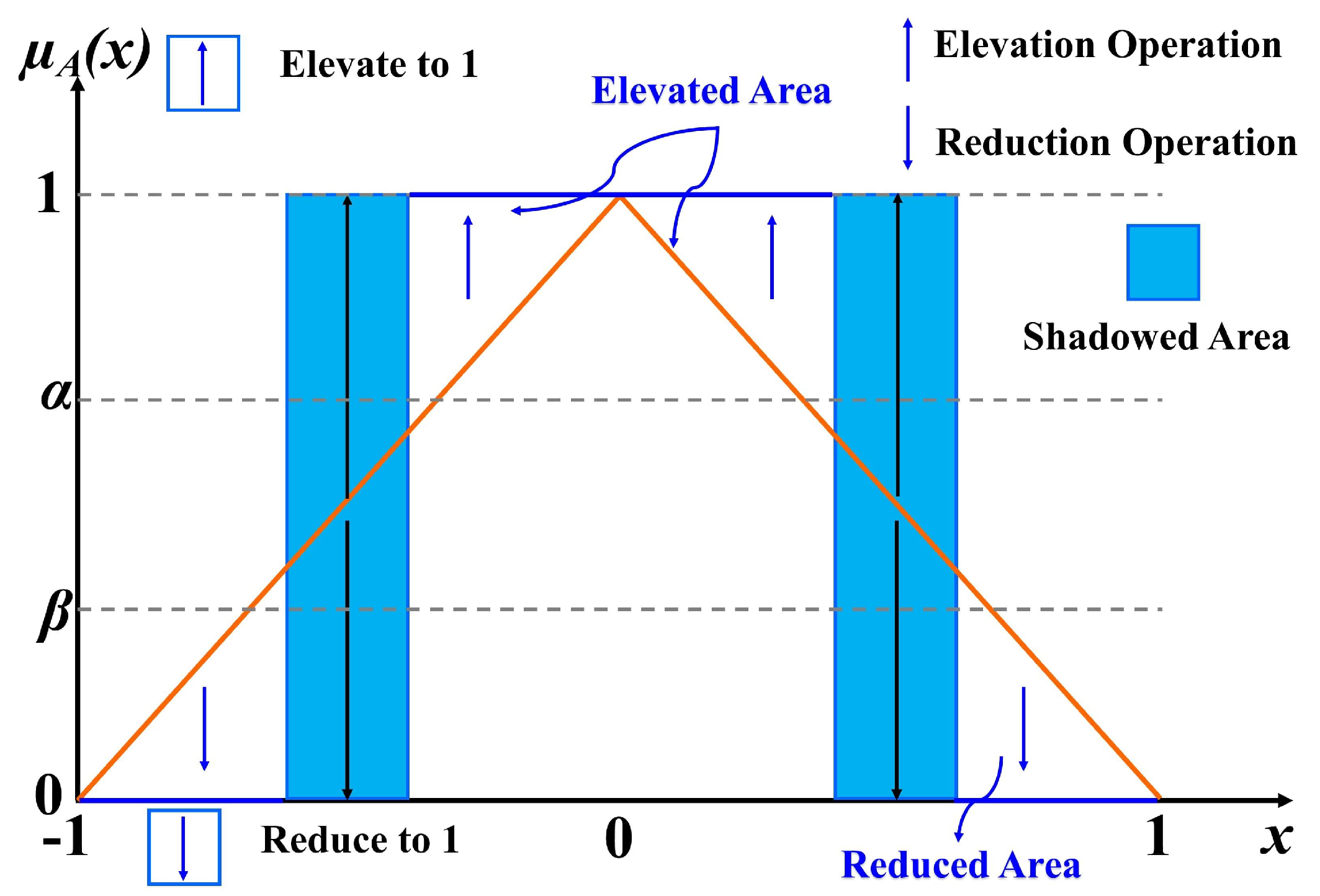
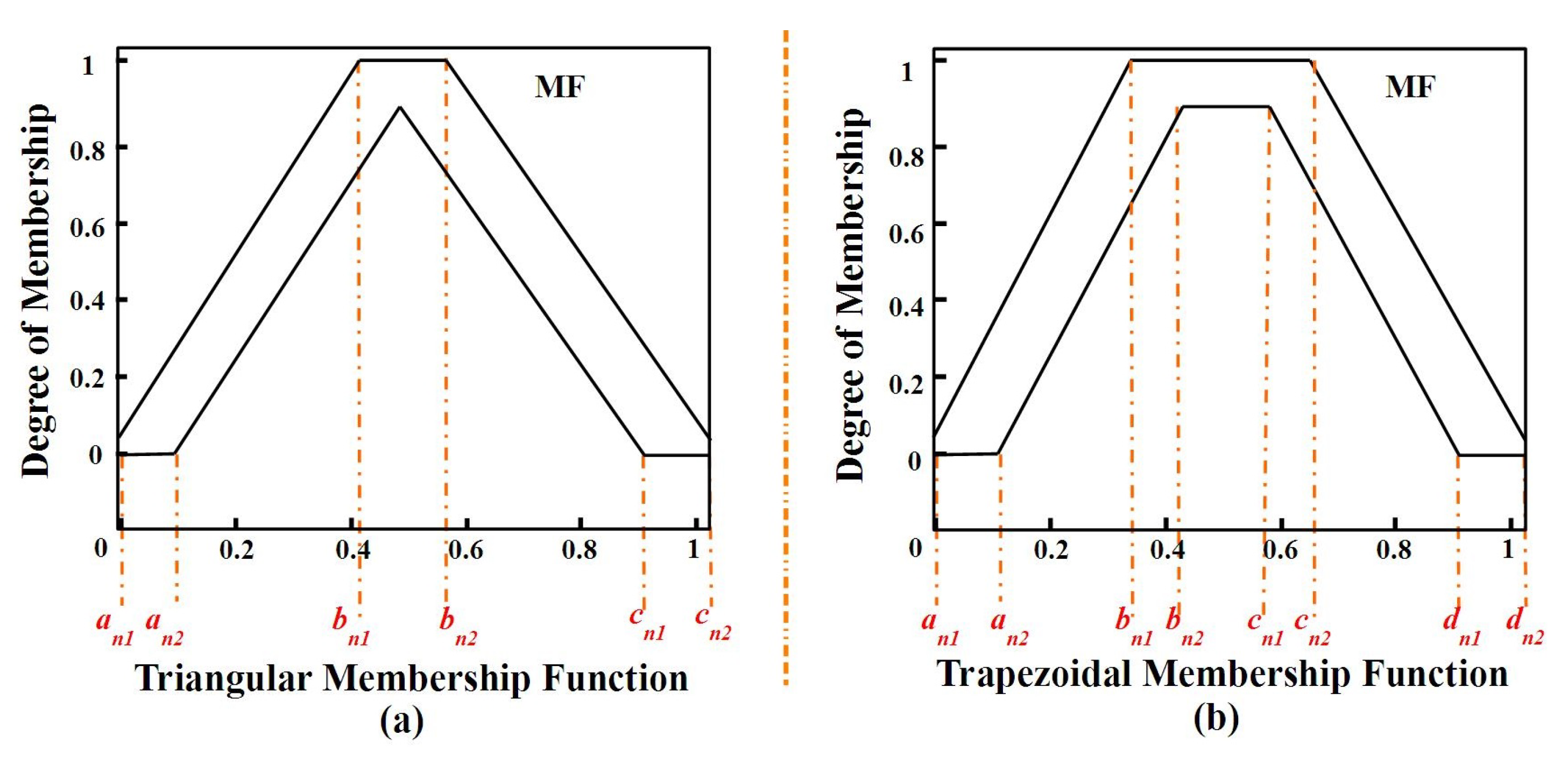
2. General Type-2 Fuzzy Sets and Shadowed Sets
General Type-2 Fuzzy Sets with Shadowed Sets
3. Background of Optimization Algorithm and Mathematical Formulation
3.1. Cuckoo Search (CS) Algorithm
- An egg, kept in a nest, represents a solution. An artificial cuckoo can lay only one egg at a time [70].
- The cuckoo bird searches for the most suitable nest to lay its eggs in to maximize the survival rate of its eggs (solution). Because of an exclusivist selection strategy, only high-quality eggs (best solutions around the optimal value) that are more similar to the host bird’s eggs have a chance to develop (next generation) and become mature cuckoos [70].
- The population (number of host nests) remains constant. The host bird can find the alien egg with a probability of (worse solutions away from the optimal value), and these eggs are thrown away or the nest is neglected and a new nest is established in a different location. Otherwise, the egg matures and lives to the next generation. Lèvy flights around the best current solutions aid in the selection of new eggs (solutions) laid by a cuckoo [70,72].
| Algorithm 1: Pseudo code for CS Algorithm [70,72] |
|
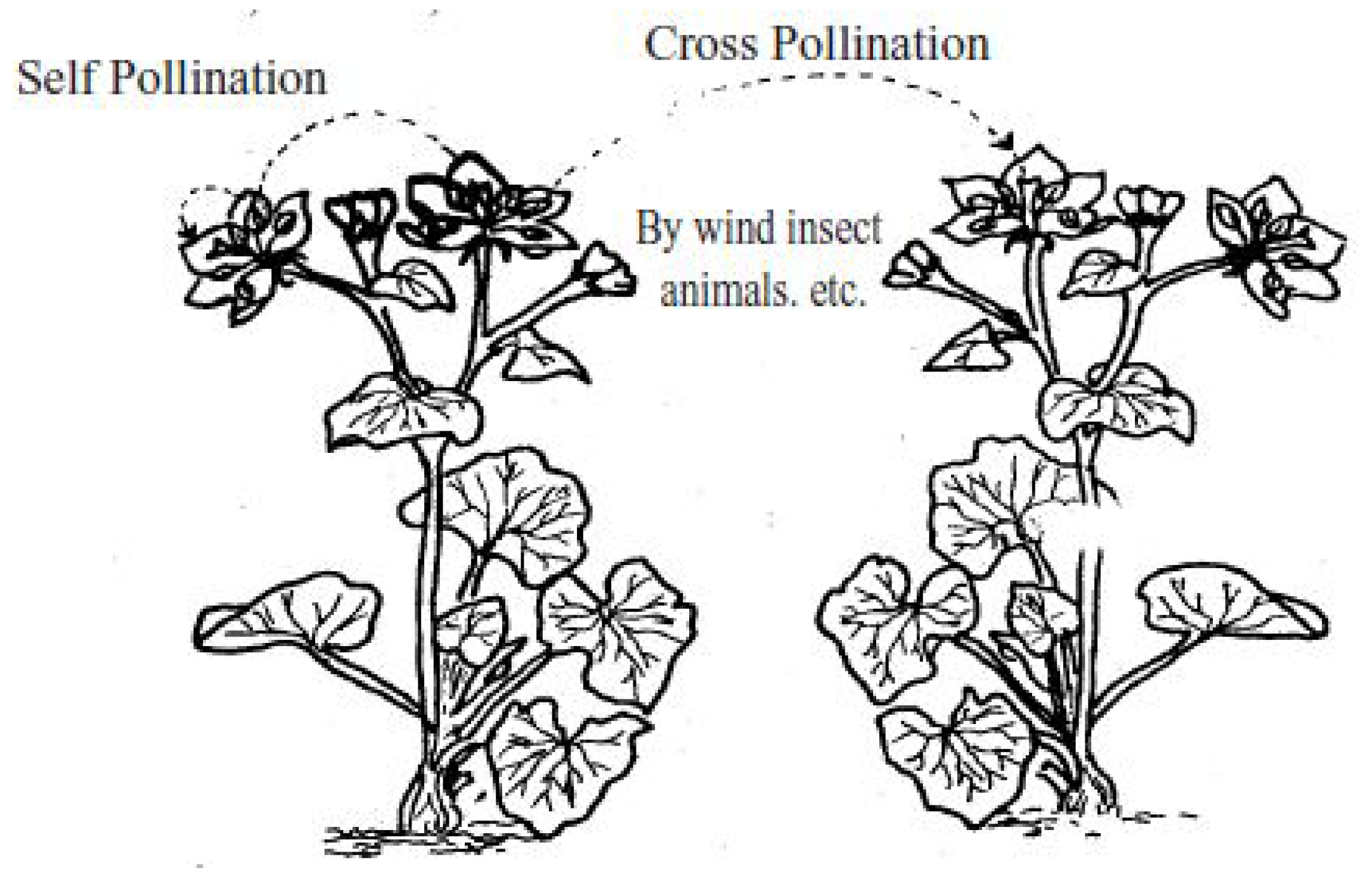
3.2. Flower Pollination
| Algorithm 2: Pseudo code for FP Algorithm [73,74] |
|
3.3. Mathematical Modeling of FPA
4. Two-Tank Conical Frustum Non-Interacting Level System with Mathematical Model
Modeling of Coupled Frustum Tank Level Control Process
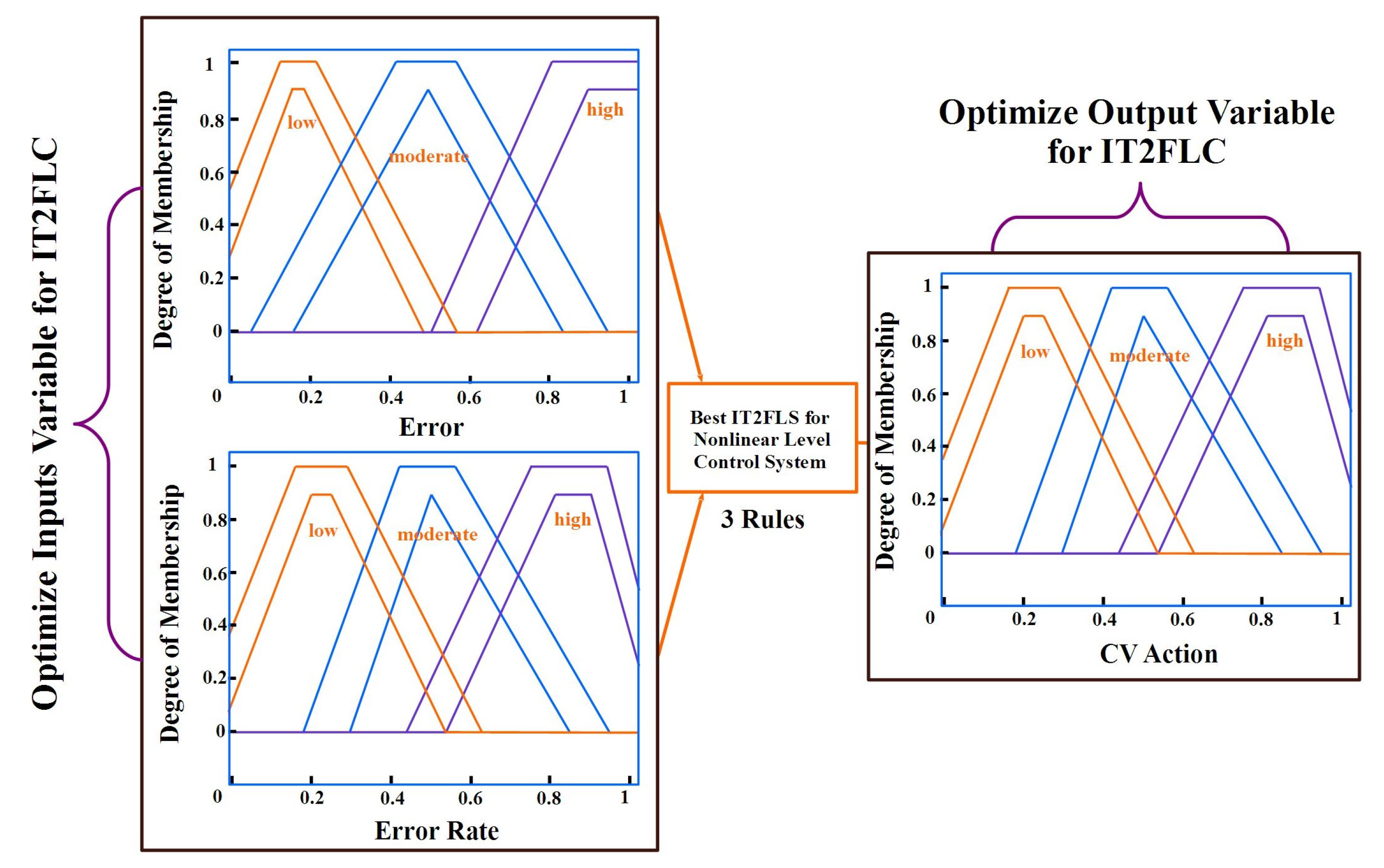
5. Proposal and Methods
- If iteration is low, then Lèvy flight (P) is low;
- If iteration is moderate, then Lèvy flight (P) is moderate;
- If iteration is high, then Lèvy flight (P) is high.
- If iteration is low, then switching Probability (P’) is low;
- If iteration is moderate, then switching Probability (P’) is moderate;
- If iteration is high, then switching Probability (P’) is high.
6. Simulation Results
Comparative Analysis and Result Discussion
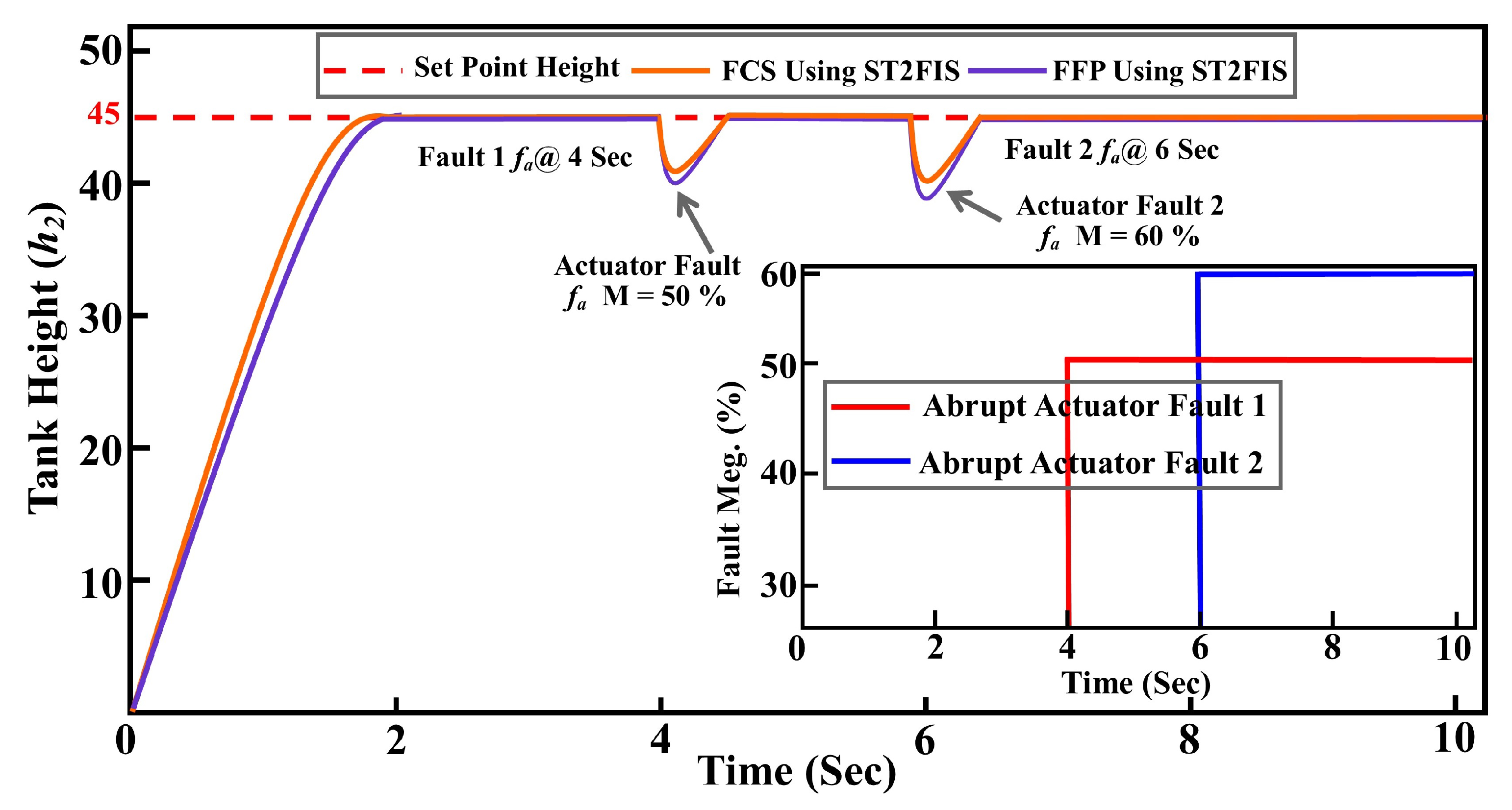
Simulation Results with Noise and Intermittent Fault
- (1)
- Interval type-2 fuzzy controller with random noise with magnitude (Gaussian random number);
- (2)
- Interval type-2 fuzzy controller with random noise and TTCFNLC system with intermittent actuator fault in main actuator with magnitude of and at time s and s respectively;
- (3)
- Interval type-2 fuzzy controller with random noise and TTCFNLC system with intermittent system component (leak) fault in bottom of the frustum tank 2 (additional flow rate ) with magnitude of and at time s and s, respectively.
7. Statistical Results and Analysis
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANNs | Artificial Neural Networks |
| ACO | Ant Colony Optimisation |
| CS | Cuckoo Search |
| CV | Control Valve |
| CPS | Cyber-Physical Systems |
| DE | Differential Evolution |
| DMs | Decision Makers |
| DOF | Degrees of Freedom |
| DTs | Decision Threes |
| EA | Elevation Area |
| FF | Feedforward |
| FP | Flower Pollination |
| FSs | Fuzzy Sets |
| FLC | Fuzzy Logic Controller |
| FISs | Fuzzy Inference Systems |
| FTS | Frustum Tank System |
| GA | Genetic Algorithm |
| GT2FS | General Type-2 Fuzzy Sets |
| GT2FIS | General Type-2 Fuzzy Inference System |
| GOA | Grasshopper Optimization Algorithm |
| GSO | Galactic Swarm Optimization |
| LFM | Lower Membership Function |
| LPFNs | Linguistic Pythagorean fuzzy numbers |
| MFs | Membership Functions |
| MSE | Mean Square Error |
| MPPT | Maximum Power Point Tracking |
| NN | Neural Network |
| PID | Proportional Integral Derivative |
| PSO | Particle swarm optimisation |
| PV | Photo Voltaic |
| RTAC | Rotational/Translational Proof-Mass Actuator |
| RA | Reduction Area |
| RL | Reinforcement Learning |
| RMSE | Root Mean Square Error |
| SA | Shadowing Area |
| SISO | Single Input Single Output |
| ST2FIS | Shadowed Type-2 Fuzzy Inference System |
| SFC | Stochastic Fractal Search |
| SVMs | Support Vector Machines |
| TTCFNLCS | Two-Tank Conical Frustum Non-Interacting Level System |
| T1FLCs | Type-1 Fuzzy Logic Controllers |
| Fault recovery time | |
| HS | Harmony Search |
| IP | Inverted Pendulum |
| IAE | Integral Absolute Error |
| ICS | Improved Cuckoo Search |
| ISE | Integral Square Error |
| ITAE | Integral Time Absolute Error |
| ITSE | Integral Time Absolute Error |
| IT2FLCs | Interval Type-2 Fuzzy Logic Controllers |
| IT2FIS | Interval Type-2 Fuzzy Inference System |
References
- Patel, H.R.; Shah, V.A. Fuzzy Logic Based Metaheuristic Algorithm for Optimization of Type-1 Fuzzy Controller: Fault-Tolerant Control for Nonlinear System with Actuator Fault. IFAC-PapersOnLine 2022, 55, 715–721. [Google Scholar] [CrossRef]
- Patel, H.R.; Shah, V.A. Comparative Analysis Between Two Fuzzy Variants of Harmonic Search Algorithm: Fuzzy Fault Tolerant Control Application. IFAC-PapersOnLine 2022, 55, 507–512. [Google Scholar] [CrossRef]
- Patel, H.R.; Raval, S.K.; Shah, V.A. A novel design of optimal intelligent fuzzy TID controller employing GA for nonlinear level control problem subject to actuator and system component fault. Int. J. Intell. Comput. Cybern. 2021, 14, 17–32. [Google Scholar] [CrossRef]
- Georgieva, A.; Jordanov, I. Global optimization based on novel heuristics, low-discrepancy sequences and genetic algorithms. Eur. J. Oper. Res. 2009, 196, 413–422. [Google Scholar] [CrossRef][Green Version]
- Ji, Y.; Zhang, K.-C.; Qu, S.-J. A deterministic global optimization algorithm. Appl. Math. Comput. 2007, 185, 382–387. [Google Scholar] [CrossRef]
- Patel, H.; Shah, V. An Optimized Intelligent Fuzzy Fractional Order TID Controller for Uncertain Level Control Process with Actuator and System Component Uncertainty. In Fuzzy Information Processing 2020; Advances in Intelligent Systems and Computing; Bede, B., Ceberio, M., De Cock, M., Kreinovich, V., Eds.; Springer: Cham, Switzerland, 2020; Volume 1337, pp. 183–195. [Google Scholar] [CrossRef]
- Verma, M.; Ghritlahre, H.K.; Chaurasiya, P.K.; Ahmed, S.; Bajpai, S. Optimization of wind power plant sizing and placement by the application of multi-objective genetic algorithm (GA) in Madhya Pradesh, India. Sustain. Comput. Inform. Syst. 2021, 32, 100606. [Google Scholar] [CrossRef]
- Patel, H.R.; Shah, V.A. A Fractional and Integer Order PID Controller for Nonlinear System: Two Non-interacting Conical Tank Process Case Study. In Advances in Control Systems and its Infrastructure; Lecture Notes in Electrical Engineering; Mehta, A., Rawat, A., Chauhan, P., Eds.; Springer: Singapore, 2020; Volume 604, pp. 37–55. [Google Scholar] [CrossRef]
- Luo, J.; Chen, H.; Zhang, Q.; Xu, Y.; Huang, H.; Zhao, X. An improved grasshopper optimization algorithm with application to financial stress prediction. Appl. Math. Model. 2018, 64, 654–668. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy logic. Computer 1988, 21, 83–93. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy logic computing with words. IEEE Trans. Fuzzy Syst. 1996, 4, 103–111. [Google Scholar] [CrossRef]
- Patel, H.R.; Shah, V.A. Fuzzy logic based passive fault tolerant control strategy for a single-tank system with system fault and process disturbances. In Proceedings of the 2018 5th International Conference on Electrical and Electronic Engineering (ICEEE), Istanbul, Turkey, 3–5 May 2018; pp. 257–262. [Google Scholar] [CrossRef]
- Patel, H.R.; Shah, V.A. A Framework for Fault-tolerant Control for an Interacting and Non-interacting Level Control System using AI. In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics ICINCO, Porto, Portugal, 29–31 July 2018; Volume 1, pp. 180–190. [Google Scholar] [CrossRef]
- Liang, Q.; Mendel, J.M. Interval type-2 fuzzy logic systems: Theory and design. IEEE Trans. Fuzzy Syst. 2000, 8, 535–550. [Google Scholar] [CrossRef]
- Du, Z.; Kao, Y.; Zhao, X. An input delay approach to interval type-2 fuzzy exponential stabilization for nonlinear unreliable networked sampled-data control systems. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 3488–3497. [Google Scholar] [CrossRef]
- Patel, H.R.; Shah, V.A. Stable fuzzy controllers via LMI approach for non-linear systems described by type-2 T–S fuzzy model. Int. J. Intell. Comput. Cybern. 2021, 14, 509–531. [Google Scholar]
- Patel, H.R.; Shah, V.A. Passive Fault-Tolerant Control Based on Interval Type-2 Fuzzy Controller for Coupled Tank System. In Proceedings of International Conference on Artificial Intelligence, Smart Grid and Smart City Applications. AISGSC 2019; Kumar, L., Jayashree, L., Manimegalai, R., Eds.; Springer: Cham, Switzerland, 2020; pp. 145–154. [Google Scholar] [CrossRef]
- Patel, H.R.; Shah, V.A. Fault Tolerant Controller Using Interval Type-2 TSK Logic Control Systems: Application to Three Interconnected Conical Tank System. In Fuzzy Techniques: Theory and Applications; IFSA/NAFIPS 2019; Advances in Intelligent Systems and Computing; Kearfott, R., Batyrshin, I., Reformat, M., Ceberio, M., Kreinovich, V., Eds.; Springer: Cham, Switzerland, 2019; Volume 1000, pp. 466–482. [Google Scholar]
- Patel, H.R.; Shah, V.A. Stable Fault Tolerant Controller Design for Takagi–Sugeno Fuzzy Model-Based Control Systems via Linear Matrix Inequalities: Three Conical Tank Case Study. Energies 2019, 12, 2221. [Google Scholar] [CrossRef]
- Patel, H.R.; Shah, V.A. Fault Tolerant Control Design Based on Takagi-Sugeno Fuzzy Logic: Application to a Three-Tank System. In Proceedings of the 11th Conference of the European Society for Fuzzy Logic and Technology (EUSFLAT 2019); Springer: Cham, Switzerland, 2019; pp. 256–266. [Google Scholar] [CrossRef]
- Patel, H.R.; Shah, V.A. Design of Interval Type 2 Fuzzy Fault-Tolerant Controller for a Non-Minimum Phase System: Application to quadruple conical tank system. In Proceedings of the 11th Conference of the European Society for Fuzzy Logic and Technology (EUSFLAT 2019); Springer: Cham, Switzerland, 2019; pp. 358–369. [Google Scholar] [CrossRef]
- Patel, H.R.; Shah, V.A. Fault Tolerant Control Using Interval Type-2 Takagi-Sugeno Fuzzy Controller for Nonlinear System. In Intelligent Systems Design and Applications; Advances in Intelligent Systems and Computing; Abraham, A., Cherukuri, A., Melin, P., Gandhi, N., Eds.; Springer: Cham, Switzerland, 2018; Volume 941, pp. 150–164. [Google Scholar]
- Mendel, J.M. Advances in type-2 fuzzy sets and systems. Inf. Sci. 2007, 177, 84–110. [Google Scholar] [CrossRef]
- Patel, H.R.; Shah, V.A. General Type-2 Fuzzy Logic Systems Using Shadowed Sets: A New Paradigm Towards Fault-Tolerant Control. In Proceedings of the 2021 Australian & New Zealand Control Conference (ANZCC), Gold Coast, Australia, 25–26 November 2021; pp. 116–121. [Google Scholar]
- Patel, H.R.; Shah, V.A. Actuator and system component fault tolerant control using interval type-2 Takagi-Sugeno fuzzy controller for hybrid nonlinear process Int. J. Hybrid Intell. Syst. 2019, 15, 143–153. [Google Scholar] [CrossRef]
- Lagunes, M.L.; Castillo, O.; Soria, J. Methodology for the optimization of a fuzzy controller using a bio-inspired algorithm. In Proceedings of the North American Fuzzy Information Processing Society Annual Conference, Cancun, Mexico, 16 October 2017; Springer: Cham, Switzerland, 2018; Volume 648, pp. 131–137. [Google Scholar]
- Lagunes, M.L.; Castillo, O.; Soria, J. Optimization of membership function parameters for fuzzy controllers of an autonomous mobile robot using the firefly algorithm. In Fuzzy Logic Augmentation of Neural and Optimization Algorithms: Theoretical Aspects and Real Applications; Studies in Computational Intelligence; Springer: Berlin, Germany, 2018; Volume 749, pp. 199–206. [Google Scholar]
- Patel, H.R. Fuzzy Based Metaheuristic Algorithm for Optimization of Fuzzy Controller: Fault Tolerant Control Application. Int. J. Intell. Comput. Cybern. 2022, 15, 599–624. [Google Scholar] [CrossRef]
- Wagner, C.; Hagras, H. A genetic algorithm based architecture for evolving type-2 fuzzy logic controllers for real world autonomous mobile robots. In Proceedings of the 2007 IEEE International Fuzzy Systems Conference, London, UK, 23–26 July 2007; pp. 1–6. [Google Scholar]
- Astudillo, L.; Castillo, O.; Melin, P.; Alanis, A.; Soria, J.; Aguilar, L.T. Intelligent control of an autonomous mobile robot using type-2 fuzzy logic. Eng. Lett. 2006, 13, 199–206. [Google Scholar]
- Wu, D.; Tan, W.W. Genetic learning and performance evaluation of interval type-2 fuzzy logic controllers. Eng. Appl. Artif. Intell. 2006, 19, 829–841. [Google Scholar] [CrossRef]
- Wu, D. On the fundamental differences between interval type-2 and type-1 fuzzy logic controllers. IEEE Trans. Fuzzy Syst. 2006, 20, 832–848. [Google Scholar] [CrossRef]
- Wu, D.; Tan, W.W. A type-2 fuzzy logic controller for the liquid-level process. In Proceedings of the 2004 IEEE International Conference on Fuzzy Systems (IEEE Cat. No. 04CH37542), Budapest, Hungary, 25–29 July 2004; pp. 953–958. [Google Scholar]
- Yang, X.-S. Nature-Inspired Metaheuristic Algorithms; Luniver Press: Beckington, UK, 2010. [Google Scholar]
- Patel, H.R.; Shah, V.A. Comparative Study of Interval Type-2 and Type-1 Fuzzy Genetic and Flower Pollination Algorithms in Optimization of Fuzzy Fractional Order PIλDμ Controllers. In Intelligent System and Computing; Yi, Y., Ed.; IntechOpen: Rijeka, Croatia, 2020. [Google Scholar] [CrossRef]
- Arqub, O.A.; Al-Smadi, M. Fuzzy conformable fractional differential equations: Novel extended approach and new numerical solutions. Soft Comput. 2020, 24, 12501–12522. [Google Scholar] [CrossRef]
- Abu Arqub, O.; AL-Smadi, M.; Momani, S. Numerical solutions of fuzzy differential equations using reproducing kernel Hilbert space method. Soft Comput. 2016, 20, 3283–3302. [Google Scholar]
- Abu Arqub, O. Adaptation of reproducing kernel algorithm for solving fuzzy Fredholm–Volterra in-tegrodifferential equations. Neural Comput. Appl. 2017, 28, 1591–1610. [Google Scholar] [CrossRef]
- Abu Arqub, O.; Singh, J.; Maayah, B.; Alhodaly, M.S. Reproducing kernel approach for numerical solutions of fuzzy fractional initial value problems under the Mittag–Leffler kernel differential operator. Math. Methods Appl. Sci. 2021. [Google Scholar] [CrossRef]
- Abu Arqub, O.; Singh, J.; Maayah, B.; Alhodaly, M.S. Adaptation of kernel functions-based approach with Atangana–Baleanu–Caputo distributed order derivative for solutions of fuzzy fractional Volterra and Fredholm integrodifferential equations. Math. Methods Appl. Sci. 2021. [Google Scholar] [CrossRef]
- Saima, H.; Mojtaba Ahmadieh, K.; Nazar Kalaf, H.; Samir Brahim, B.; Usman Amjad and Wali Khan, M. Optimization of Interval Type-2 Fuzzy Logic System using Grasshopper Optimization Algorithm for Electricity Load and Price Forecasting. Comput. Mater. Contin. 2022, 71, 3513–3531. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Saber, S.; Askar, S.S.; Abouhawwash, M. Modified Flower Pollination Algorithm for Global Optimization. Mathematics 2021, 9, 1661. [Google Scholar]
- Templos-Santos, J.L.; Aguilar-Mejia, O.; Peralta-Sanchez, E.; Sosa-Cortez, R. Parameter Tuning of PI Control for Speed Regulation of a PMSM Using Bio-Inspired Algorithms. Algorithms 2019, 12, 54. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Mohammad, N.; Sallam, K.; Moustafa, N. An Adaptive Cuckoo Search-Based Optimization Model for Addressing Cyber-Physical Security Problems. Mathematics 2021, 9, 1140. [Google Scholar] [CrossRef]
- Ali, E.M.; Abdelsalam, A.K.; Youssef, K.H.; Hossam-Eldin, A.A. An Enhanced Cuckoo Search Algorithm Fitting for Photovoltaic Systems’ Global Maximum Power Point Tracking under Partial Shading Conditions. Energies 2021, 14, 7210. [Google Scholar] [CrossRef]
- Mpanza, L.J.; Pedro, J.O. Optimised Tuning of a PID-Based Flight Controller for a Medium-Scale Rotorcraft. Algorithms 2021, 14, 178. [Google Scholar] [CrossRef]
- Rezk, H.; Fathy, A. Stochastic Fractal Search Optimization Algorithm Based Global MPPT for Triple-Junction Photovoltaic Solar System. Energies 2000, 13, 4971. [Google Scholar] [CrossRef]
- Ren, Y.; Li, H.; Lin, H.-C. Optimization of Feedforward Neural Networks Using an Improved Flower Pollination Algorithm for Short-Term Wind Speed Prediction. Energies 2019, 12, 4126. [Google Scholar] [CrossRef]
- Khan, M.S.A.; Jana, C.; Khan, M.T.; Mahmood, W.; Pal, M.; Mashwani, W.K. Extension of GRA method for multiattribute group decision making problem under linguistic Pythagorean fuzzy setting with incomplete weight information. Int. J. Intell. Syst. 2022, 37, 9726–9749. [Google Scholar] [CrossRef]
- Ali, J.; Bashir, Z.; Rashid, T.; Mashwani, W.K. A q-rung orthopair hesitant fuzzy stochastic method based on regret theory with unknown weight information. J. Ambient. Intell. Humaniz. 2022. [Google Scholar] [CrossRef]
- Kukker, A.; Sharma, R. Genetic Algorithm-Optimized Fuzzy Lyapunov Reinforcement Learning for Nonlinear Systems. Arab. J. Sci. Eng. 2020, 45, 1629–1638. [Google Scholar] [CrossRef]
- Kukker, A.; Sharma, R. Stochastic Genetic Algorithm-Assisted Fuzzy Q-Learning for Robotic Manipulators. Arab. J. Sci. Eng. 2021, 46, 9527–9539. [Google Scholar] [CrossRef]
- Kumar, A.; Sharma, R. Linguistic Lyapunov reinforcement learning control for robotic manipulators. Neurocomputing 2018, 272, 84–95. [Google Scholar] [CrossRef]
- Kumar, A.; Sharma, R. Fuzzy Lyapunov Reinforcement Learning for Non-Linear Systems. ISA Trans. 2017, 67, 151–159. [Google Scholar] [CrossRef]
- Amador-Angulo, L.; Castillo, O.; Pulido, M. Comparison of fuzzy controllers for the water tank with type-1 and type-2 fuzzy logic. In Proceedings of the 2013 Joint IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS), Edmonton, AB, Canada, 24–28 June 2013; pp. 1062–1067. [Google Scholar]
- Sola, H.B.; Fernandez, J.; Hagras, H.; Herrera, F.; Pagola, M.; Barrenechea, E. Interval Type-2 Fuzzy Sets are Generalization of Interval-Valued Fuzzy Sets: Toward a Wider View on Their Relationship. IEEE Trans. Fuzzy Syst. 2015, 23, 1876–1882. [Google Scholar] [CrossRef]
- Coupland, S.; John, R. Geometric type-1 and type-2 fuzzy logic systems. IEEE Trans. Fuzzy Syst. 2007, 15, 3–15. [Google Scholar] [CrossRef]
- Mendel, J.M.; Liu, F.; Zhai, D. α-plane representation for type2 fuzzy sets: Theory and applications. IEEE Trans. Fuzzy Syst. 2009, 17, 1189–1207. [Google Scholar] [CrossRef]
- Pedrycz, W.; Song, M. Granular fuzzy models: A study in knowledge management in fuzzy modeling. Int. J. Approx. Reason. 2012, 53, 1061–1079. [Google Scholar] [CrossRef]
- Pedrycz, W. From fuzzy sets to shadowed sets: Interpretation and computing. Int. J. Intell. Syst. 2009, 24, 48–61. [Google Scholar] [CrossRef]
- Mitra, S.; Pedrycz, W.; Barman, B. Shadowed c-means: Integrating fuzzy and rough clustering. Pattern Recognit. 2010, 43, 1282–1291. [Google Scholar] [CrossRef]
- Wijayasekara, D.; Linda, O.; Manic, M. Shadowed Type-2 Fuzzy Logic Systems. In Proceedings of the 2013 IEEE Symposium on Advances in Type-2 Fuzzy Logic Systems (T2FUZZ), Singapore, 16–19 April 2013; pp. 15–22. [Google Scholar]
- Gonzalez, C.I.; Melin, P.; Castillo, O.; Juarez, D.; Castro, J.R. Toward general type-2 fuzzy logic systems based on shadowed sets. In Advances in Fuzzy Logic and Technology; Springer: Cham, Switzerland, 2017; pp. 131–142. [Google Scholar]
- Castillo, O.; Peraza, C.; Ochoa, P.; Amador-Angulo, L.; Melin, P.; Park, Y.; Geem, Z.W. Shadowed Type-2 Fuzzy Systems for Dynamic Parameter Adaptation in Harmony Search and Differential Evolution for Optimal Design of Fuzzy Controllers. Mathematics 2021, 9, 2439. [Google Scholar] [CrossRef]
- Castillo, O.; Melin, P.; Valdez, F.; Soria, J.; Ontiveros-Robles, E.; Peraza, C.; Ochoa, P. Shadowed Type-2 Fuzzy Systems for Dynamic Parameter Adaptation in Harmony Search and Differential Evolution Algorithms. Algorithms 2019, 12, 17. [Google Scholar] [CrossRef]
- Ontiveros-Robles, E.; Melin, P. A hybrid design of shadowed type-2 fuzzy inference systems applied in diagnosis problems. Eng. Appl. Artif. Intell. 2019, 86, 43–55. [Google Scholar] [CrossRef]
- Chatterjee, K.; De, A.; Felix, T.S. Chan. Real time traffic delay optimization using shadowed type-2 fuzzy rule base. Appl. Soft Comput. 2019, 74, 226–241. [Google Scholar] [CrossRef]
- Ochoa, P.; Castillo, O.; Melin, P.; Soria, J.S. Differential Evolution with Shadowed and General Type-2 Fuzzy Systems for Dynamic Parameter Adaptation in Optimal Design of Fuzzy Controllers. Axioms 2021, 10, 194. [Google Scholar] [CrossRef]
- Yang, X.-S.; Deb, S. Cuckoo search via Lèvy flights. In Proceedings of the World Congress on Nature & Biologically Inspired Computing (NABIC ’09), Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- Walton, S.; Hassan, O.; Morgan, K.; Brown, M.R. A review of the development and applications of the Cuckoo search algorithm. In Swarm Intelligence and Bio-Inspired Computation Theory and Applications; Yang, X.-S., Cui, Z., Xiao, R., Gandomi, A.H., Karamanoglu, M., Eds.; Elsevier: San Diego, CA, USA, 2013; pp. 257–271. [Google Scholar]
- Yang, X.-S.; Deb, S. Engineering optimization by cuckoo search. Int. J. Math. Model. Numer. Optim. 2010, 1, 330–343. [Google Scholar]
- Yang, X.S. Flower pollination algorithm for global optimization. In Unconventional Computation and Natural Computation; Springer: Berlin, Germany, 2012; Volume 7445, pp. 240–249. [Google Scholar]
- Glover, B.J. Understanding Flowers and Flowering: An Integrated Approach; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Patel, H.R.; Shah, V.A. A metaheuristic approach for interval type-2 fuzzy fractional order fault-tolerant controller for a class of uncertain nonlinear system. Automatika 2022, 63, 656–675. [Google Scholar] [CrossRef]
- Patel, H.R.; Shah, V.A. Type-2 fuzzy logic applications designed for active parameter adaptation in me-taheuristic algorithm for fuzzy fault-tolerant controller. Int. J. Intell. Comput. Cybern. 2022. ahead-of-print. [Google Scholar] [CrossRef]
- Willmer, P. Pollination and Floral Ecology; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Balasubramani, K.; Marcus, K. A Study on Flower Pollination Algorithm and Its Applications. Int. J. Appl. Innov. Eng. Manag. (IJAIEM) 2014, 3, 320–325. [Google Scholar]
- Abdel-Raouf, O.; Abdel-Baset, M. A new hybrid flower pollination algorithm for solving constrained global optimization problems. Int. J. Appl. Oper.-Res. 2014, 4, 1–13. [Google Scholar]
- Raval, S.; Patel, H.R.; Patel, S.; Shah, V.A. Passive Fault-Tolerant Control Scheme for Nonlinear Level Control System with Parameter Uncertainty and Actuator Fault. In Applications of Fuzzy Techniques. NAFIPS 2022. Lecture Notes in Networks and Systems; Dick, S., Kreinovich, V., Lingras, P., Eds.; Springer: Cham, Switzerland, 2023; Volume 500, pp. 229–242. [Google Scholar] [CrossRef]
- Raval, S.; Patel, H.R.; Shah, V.A. Neural Network-Based Control Framework for SISO Uncertain System: Passive Fault Tolerant Approach. In Intelligent and Fuzzy Techniques: Smart and Innovative Solutions, INFUS 2020; Advances in Intelligent Systems and Computing; Kahraman, C., Cevik Onar, S., Oztaysi, B., Sari, I., Cebi, S., Tolga, A., Eds.; Springer: Cham, Switzerland, 2021; Volume 1197, pp. 1039–1047. [Google Scholar] [CrossRef]
- Patel, H.R.; Shah, V.A. Fault-Tolerant Controller Comparative Study and Analysis for Benchmark Two-Tank Interacting Level Control System. SN Comput. Sci. 2021, 2, 145–154. [Google Scholar] [CrossRef]
- Patel, H.R.; Shah, V.A. Integrated Design of Model-Based Passive Fault-Tolerant Control for Nonlinear Systems Based on PID and Fuzzy Control. In Soft Computing: Theories and Applications. Advances in Intelligent Systems and Computing; Pant, M., Sharma, T., Verma, O., Singla, R., Sikander, A., Eds.; Springer: Singapore, 2020; Volume 1053, pp. 155–169. [Google Scholar] [CrossRef]
- Patel, H.R.; Shah, V.A. A Novel Design of Centralized Fractional order PID Controller and its Optimal Time Domain Tuning: A hybrid two interacting conical frustum tank level process case study. In Proceedings of the Memorias del Congreso Nacional de Control Autom A¸tico (CNCA 2019), Puebla, Mexico, 23–25 October 2019; pp. 754–761. [Google Scholar]
- Patel, H.R.; Shah, V.A. Fault Detection and Diagnosis Methods in Power Generation Plants- The Indian Power Generation Sector Perspective: An Introductory Review J. Energy & Manag. 2018, 2, 31–49. [Google Scholar]
- Patel, H.R.; Shah, V.A. Passive Fault Tolerant Control System Using Feed-forward Neural Network for Two-Tank Interacting Conical Level Control System Against Partial Actuator Failures and Disturbances. IFAC-PapersOnLine 2019, 52, 141–146. [Google Scholar] [CrossRef]
- Patel, H.R.; Shah, V.A. Passive Fault-Tolerant Tracking for Nonlinear System with intermittent Fault and Time Delay. IFAC-PapersOnLine 2019, 52, 200–205. [Google Scholar] [CrossRef]
- Patel, H.R.; Shah, V.A. Passive fault-tolerant control system design with tracking control against major system faults: Application to a canonical tank level system. In Communication and Computing Systems; CRC Press: Boca Raton, FL, USA, 2019; pp. 98–104. [Google Scholar]
- Patel, H.R.; Shah, V.A. Decentralized stable and robust fault-tolerant PI plus fuzzy control of MIMO systems: A quadruple tank case study, Int. J. Smart Sens. Intell. Syst. 2019, 122, 1–20. [Google Scholar] [CrossRef]
- Lakshmanaprabu, S.K.; Wahid, N.A.; Banu Sabura, U. Design of Centralized Fractional order PI Controller for Two Interacting Conical Frustum Tank Level Process. J. Appl. Fluid Mech. 2017, 10, 1–23. [Google Scholar]
- Patel, H.R.; Shah, V.A. Fault Tolerant Control Systems: A Passive Approaches for Single Tank Level Control System J. Instrum. Control. Eng. 2018, 6, 1–8. [Google Scholar]
- Patel, H.R.; Shah, V.A. A passive fault-tolerant control strategy for a non-linear system: An application to the two tank conical non-interacting level control system. Maskay 2019, 9, 1–8. [Google Scholar] [CrossRef]
- Valdez, F.; Melin, P.; Castillo, O. An improved evolutionary method with fuzzy logic for combining particle swarm optimization and genetic algorithms. Appl. Soft Comput. 2011, 11, 2625–2632. [Google Scholar] [CrossRef]
- Olivas, F.; Valdez, F.; Melin, P.; Sombra, A.; Castillo, O. Interval type-2 fuzzy logic for dynamic parameter adaptation in a modified gravitational search algorithm. Inf. Sci. 2019, 476, 159–175. [Google Scholar] [CrossRef]
- Eftimov, T.; Korošec, P.; Seljak, B.K. A Novel Approach to statistical comparison of meta-heuristic stochastic optimization algorithms using deep statistics. Inf. Sci. 2017, 417, 186–215. [Google Scholar] [CrossRef]
- Ontiveros-Robles, E.; Melin, P.; Castillo, O. Comparative analysis of noise robustness of type 2 fuzzy logic controllers. Kybernetika 2018, 54, 175–201. [Google Scholar] [CrossRef]
















| Control Problem | Input | Output | Total Size of Vector | ||
|---|---|---|---|---|---|
| Total | Type of MFs | Total | Type of MFs | ||
| TTCFNLC Process | 3 | 2—IT2 Trapezoidal and 1—IT2 Triangular in each Input | 3 | 3—IT2 Triangular in each output | 80 |
| Algorithm | Performance Index | Simulation Scenarios | |
|---|---|---|---|
| Without Fault | With Actuator Fault 1 | ||
| CS | ITAE | ||
| ITSE | |||
| IAE | |||
| ISE | |||
| FP | ITAE | ||
| ITSE | |||
| IAE | |||
| ISE | |||
| Algorithm | Performance Index | Simulation Scenarios | |
|---|---|---|---|
| Without Fault | With Actuator Fault 1 | ||
| CS | BEST | ||
| WORST | 0.1671 | 0.2315 | |
| AVERAGE | |||
| STANDARD DEVIATION | |||
| FP | BEST | 0.2923 | |
| WORST | 0.2161 | 0.3019 | |
| AVERAGE | |||
| STANDARD DEVIATION | |||
| Algorithm | Performance Index | Simulation Scenarios | |
|---|---|---|---|
| Without Fault | With Actuator Fault | ||
| CS | BEST | ||
| WORST | |||
| AVERAGE | |||
| STANDARD DEVIATION | |||
| FP | BEST | ||
| WORST | |||
| AVERAGE | |||
| STANDARD DEVIATION | |||
| Type of Uncertainties | Fault Magnitude | Nature of Uncertainties | Time of Occurrence in Second | Metaheuristic Algorithms | |
|---|---|---|---|---|---|
| Fuzzy CS | Fuzzy FP | ||||
| in Second | |||||
| Actuator Fault 1 | 50% | Abrupt | 4 | 0.47 | 0.54 |
| Actuator Fault 2 | 60% | 6 | 0.52 | 0.57 | |
| Leak Fault 1 | 50% | Abrupt | 4 | 0.43 | 0.48 |
| Leak Fault 2 | 60% | 6 | 0.49 | 0.56 | |
| Algorithm | Performance Index | Simulation Scenarios | ||
|---|---|---|---|---|
| With Noise | With Noise and Actuator Fault 1 and 2 | With Noise and Leak Fault 1 and 2 | ||
| CS | BEST | |||
| WORST | 0.2667 | 0.2767 | 0.2709 | |
| AVERAGE | 0.1415 | 0.1607 | 0.1447 | |
| SD | ||||
| FP | BEST | |||
| WORST | 0.3093 | 0.3477 | 0.3118 | |
| AVERAGE | 0.2154 | 0.2390 | 0.2179 | |
| SD | ||||
| Algorithm | Performance Index | Simulation Scenarios | ||
|---|---|---|---|---|
| With Noise | With Noise and Actuator Fault 1 and 2 | With Noise and Leak Fault 1 and 2 | ||
| CS | BEST | 0.2675 | 0.3127 | 0.2893 |
| WORST | 0.4934 | 0.5260 | 0.5204 | |
| AVERAGE | 0.37 | 0.3957 | 0.3737 | |
| SD | ||||
| FP | BEST | 0.3142 | 0.3215 | 0.3138 |
| WORST | 0.5561 | 0.5896 | 0.5574 | |
| AVERAGE | 0.4583 | 0.4812 | 0.4610 | |
| SD | ||||
| Type of Uncertainties | Fault Magnitude | Nature of Uncertainties | Time of Occurrence in Second | Metaheuristic Algorithms | |
|---|---|---|---|---|---|
| Fuzzy CS | Fuzzy FP | ||||
| in Second | |||||
| Actuator Fault 1 | 50 % | Abrupt | 4 | 0.49 | 0.64 |
| Actuator Fault 2 | 60 % | 6 | 0.53 | 0.61 | |
| Leak Fault 1 | 50 % | Abrupt | 4 | 0.44 | 0.53 |
| Leak Fault 2 | 60 % | 6 | 0.51 | 0.59 | |
| Parameter | Value |
|---|---|
| (Claim) | |
| Level of significance | 95 % |
| A | 0.05 |
| Critical value | −1.645 |
| CS | FP | z-Value | ||
|---|---|---|---|---|
| Average | Std | Average | Std | |
| FCS ST2FIS | FPA ST2FIS | |||
| FCS Using IT2FIS vs. FPA Using IT2FIS | |
|---|---|
| Test Statistic | p-Value |
| 16.13333 | 0.000061 |
| Q = | |
| Q = 16.13333 | |
| FCS Using T1FIS vs. FPA Using T1FIS | |
|---|---|
| Test Statistic | p-Value |
| 16.13333 | 0.0000589 |
| Q = | |
| Q = 16.13333 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Patel, H.R.; Shah, V.A. Shadowed Type-2 Fuzzy Sets in Dynamic Parameter Adaption in Cuckoo Search and Flower Pollination Algorithms for Optimal Design of Fuzzy Fault-Tolerant Controllers. Math. Comput. Appl. 2022, 27, 89. https://doi.org/10.3390/mca27060089
Patel HR, Shah VA. Shadowed Type-2 Fuzzy Sets in Dynamic Parameter Adaption in Cuckoo Search and Flower Pollination Algorithms for Optimal Design of Fuzzy Fault-Tolerant Controllers. Mathematical and Computational Applications. 2022; 27(6):89. https://doi.org/10.3390/mca27060089
Chicago/Turabian StylePatel, Himanshukumar R., and Vipul A. Shah. 2022. "Shadowed Type-2 Fuzzy Sets in Dynamic Parameter Adaption in Cuckoo Search and Flower Pollination Algorithms for Optimal Design of Fuzzy Fault-Tolerant Controllers" Mathematical and Computational Applications 27, no. 6: 89. https://doi.org/10.3390/mca27060089
APA StylePatel, H. R., & Shah, V. A. (2022). Shadowed Type-2 Fuzzy Sets in Dynamic Parameter Adaption in Cuckoo Search and Flower Pollination Algorithms for Optimal Design of Fuzzy Fault-Tolerant Controllers. Mathematical and Computational Applications, 27(6), 89. https://doi.org/10.3390/mca27060089