4. Thickness and Patterns in Fractals
In this section, we investigate the connection between the thickness and patterns in sparse sets:
Definition 4. We say that a set contains a homothetic copy of P if there exist and such that .
For example, an arithmetic progression of a length N in the real line is a homothetic copy of .
The following result is well known:
Lemma 3. Any set of positive Lebesgue measures contains homothetic copies of every finite set.
Proof. Let be a finite set and .
We know by the Lebesgue Density Theorem that almost every point
satisfies
where
is the cube with a center
x and radius
r. We fix a value of
x satisfying this. Then, there exists
such that
.
By rescaling and translating the set C and the cube , we can assume . Then, we know that .
This is enough to prove that
Then, in particular,
is non-empty, and any point
y in the intersection satisfies
Note that if
and
, then
. By applying this to
and
whose norm is smaller than
, we obtain
If
, ⋯,
satisfy
for all
i, then
We apply this to
and
to obtain
□
Since a positive Lebesgue measure guarantees homothetic copies of every finite set, it is natural to ask whether a weaker notion of size guarantees copies too. A natural notion of size to consider is the Hausdorff dimension. However, Keleti [
17] proved that there exists a compact set
, with a full Hausdorff dimension one, which does not contain any arithmetic progression of a length of three. Afterward, Keleti [
18] improved this by constructing full Hausdorff dimensional compact sets in the real line, avoiding homothetic copies of triplets in any given countable collection. Maga [
19] generalized this result to the complex plane. Máthé [
20] constructed large Hausdorff dimensional compact sets avoiding polynomial patterns. In particular, he generalized Keleti’s result to a countable amount of many linear patterns. Finally, Yavicoli [
21] studied what happens “in between” a positive Lebesgue measure and Hausdorff dimension one by considering a more general notion of Hausdorff measures.
These facts indicate that Hausdorff measures and Hausdorff dimensions cannot by themselves detect the presence or absence of patterns in sets of a Lebesgue measure of zero, even in the most basic case of arithmetic progressions. Thus, it is natural to seek a different notion of size that is able to detect patterns in sets of zero Lebesgue measures.
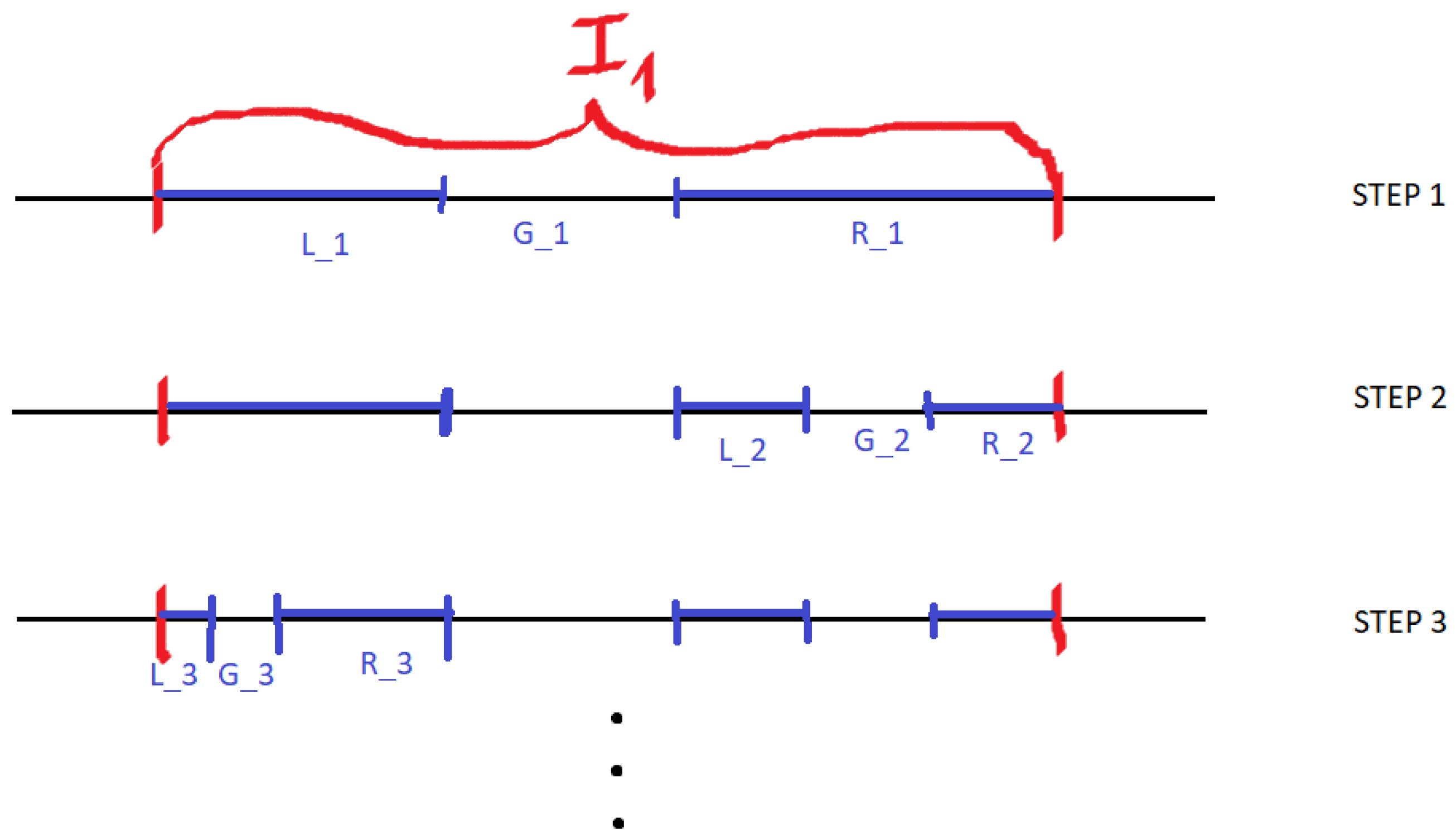
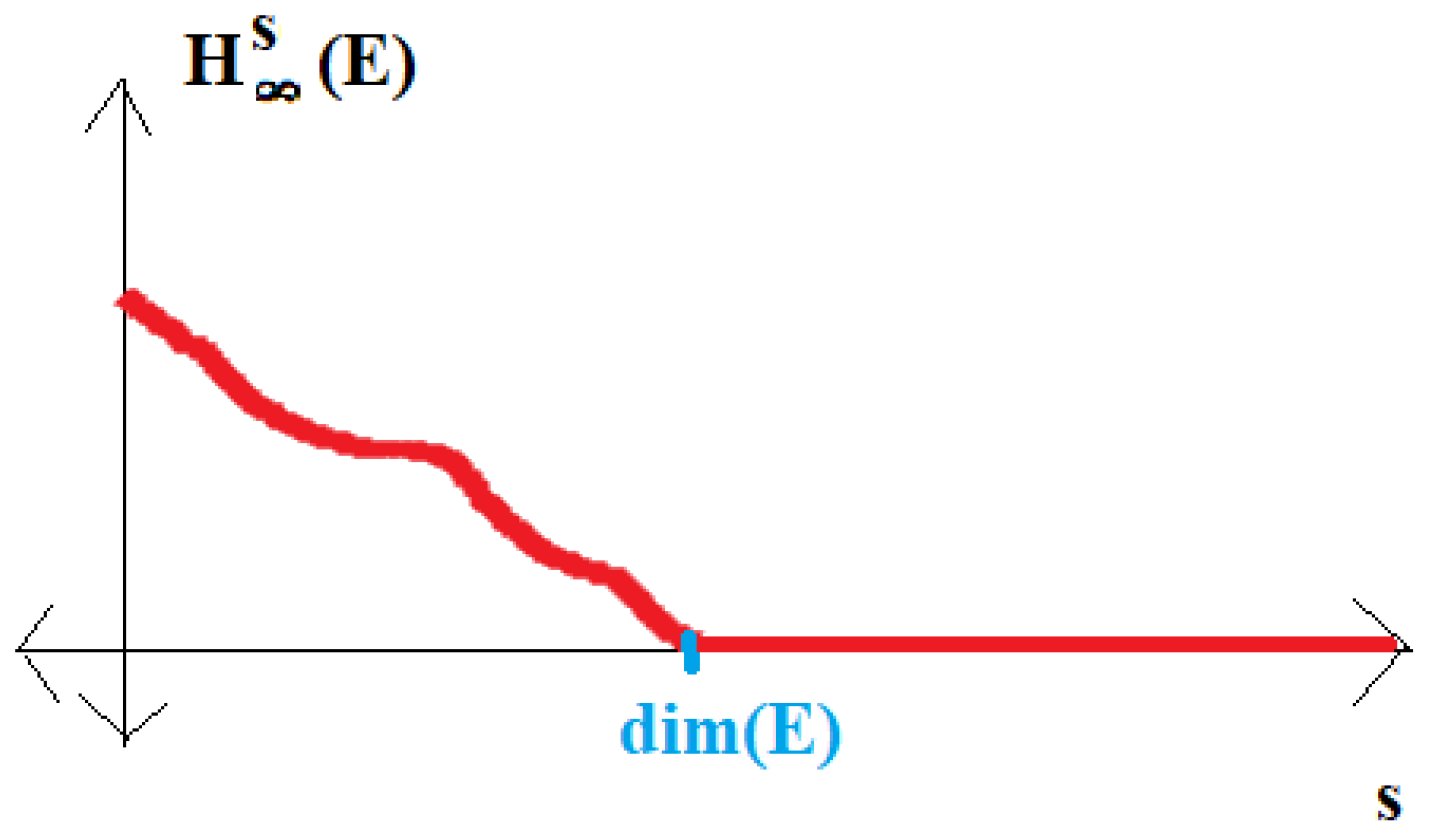
One of the ideas behind Keleti’s construction is avoiding the given proportion everywhere at some scales of the construction (see
Figure 7). This picture happens on a “zero density” set of scales. Thus, the Hausdorff dimension can still be large (at “almost all” scales, the set is large). The notion of thickness is useful to avoid such examples. Even one scale that looks like the one in
Figure 7 makes the thickness small.
Before studying the patterns in arelationship with thick sets, let us mention that the Hausdorff dimension can be useful to detect some nonlinear patterns (see [
22]) or to detect the arithmetic progressions of a length of three, assuming additional Fourier decay hypotheses, which are often not explicit or hard to check (see [
23,
24,
25]). This suggests that it is natural to try to find explicit checkable conditions on a compact set that ensure that it contains arithmetic progressions, as well as other patterns.
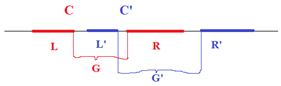
Before studying arithmetic progressions, let us consider a different pattern—distances—using Newhouse’s thickness and the Gap Lemma. We define the set of distances of a set
as
Lemma 4. Let be a compact set with and . Then, .
Proof. We know that , because and because . It remains to be seen whether any belongs to .
The sets C and satisfy the hypotheses of the Gap Lemma. Since and , the convex hulls of C and intersect, and each set cannot be contained in a gap of the other set. Finally, using and the invariance of the thickness under translation, we obtain . By the Gap Lemma, there is , and thus (which means that because ). □
Now, we are going to see that, unlike the Hausdorff dimension, the set of large thicknesses contains three-term progressions:
Proposition 1. Let be a compact set with . Then, C contains an arithmetic progression of a length of three.
Proof. Since the thickness of the compact set and arithmetic progression are invariant under homothetic functions, we can assume that .
This is the idea: if we prove that , then there are such that . Then, . The problem is that a priori, we could have . To avoid this issue we, are going to consider two disjoint subsets of C (A and B below) and prove that .
Let
be the longest gap of
C. Since
, then
. The set
consists of two intervals:
and
. We can assume that
Otherwise, we would work with instead.
Let and . Since we want to show that , we want to understand .
Claim:
Clearly,
, and so we need to see the other inclusion. We have that
and
Observe that holds because is the largest gap (otherwise, this may not be true since, in general, the thickness is not well behaved with respect to intersections).
Analogously with
, we have
We are going to apply the Gap Lemma to and for any . Let us see whether the assumptions are satisfied.
Note that
where the last equivalence holds, since we assume
.
Then, we have the following:
is not contained in a gap of . This is true because, since , . Analogously, is not contained in a gap of A.
, since we are considering values of .
.
Then, the Gap Lemma yields that for all , there is , and then , giving the claim.
Claim:
We are going to prove that, in fact, (note that ).
Since
, we know that
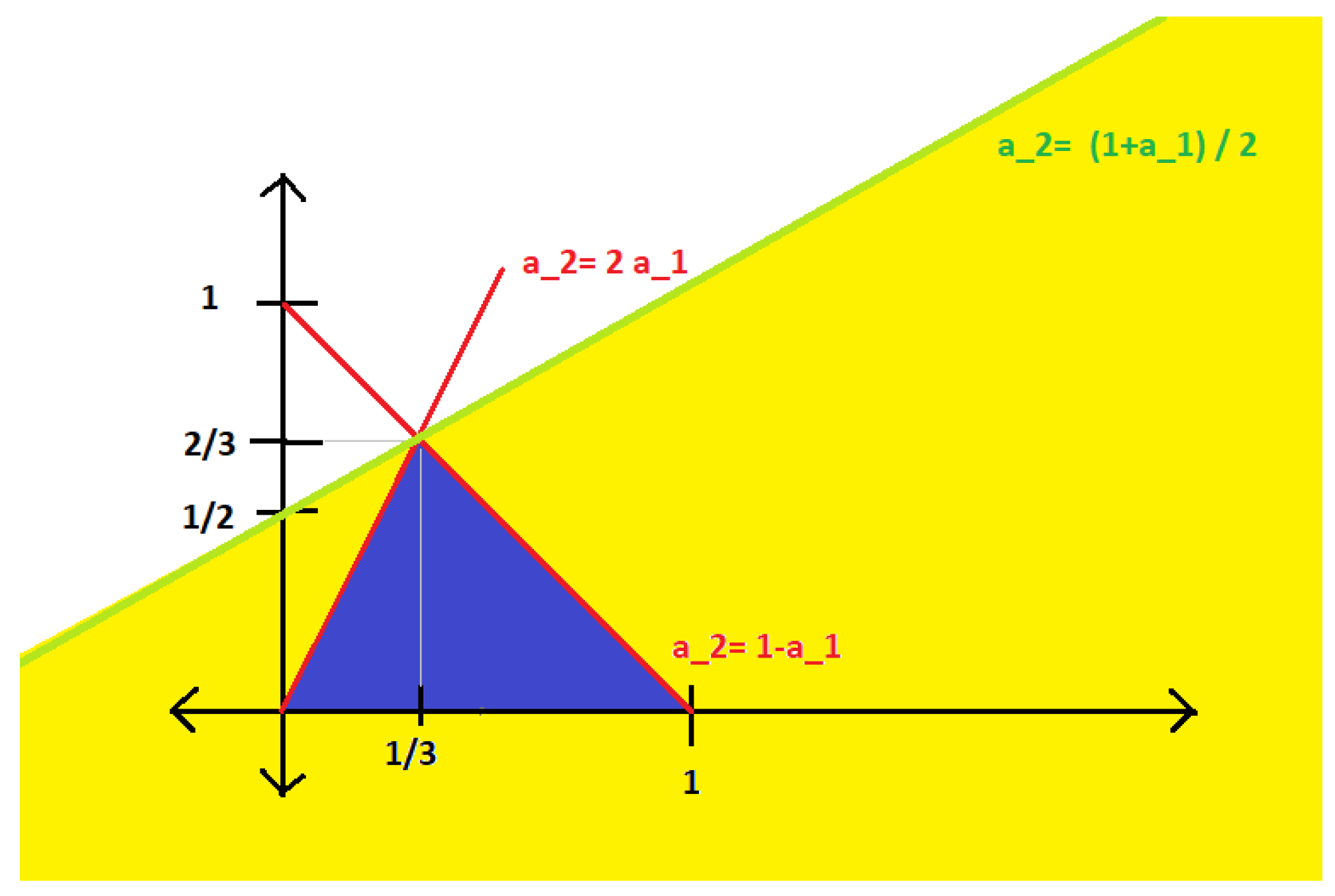
Where are the pairs that we are working with?
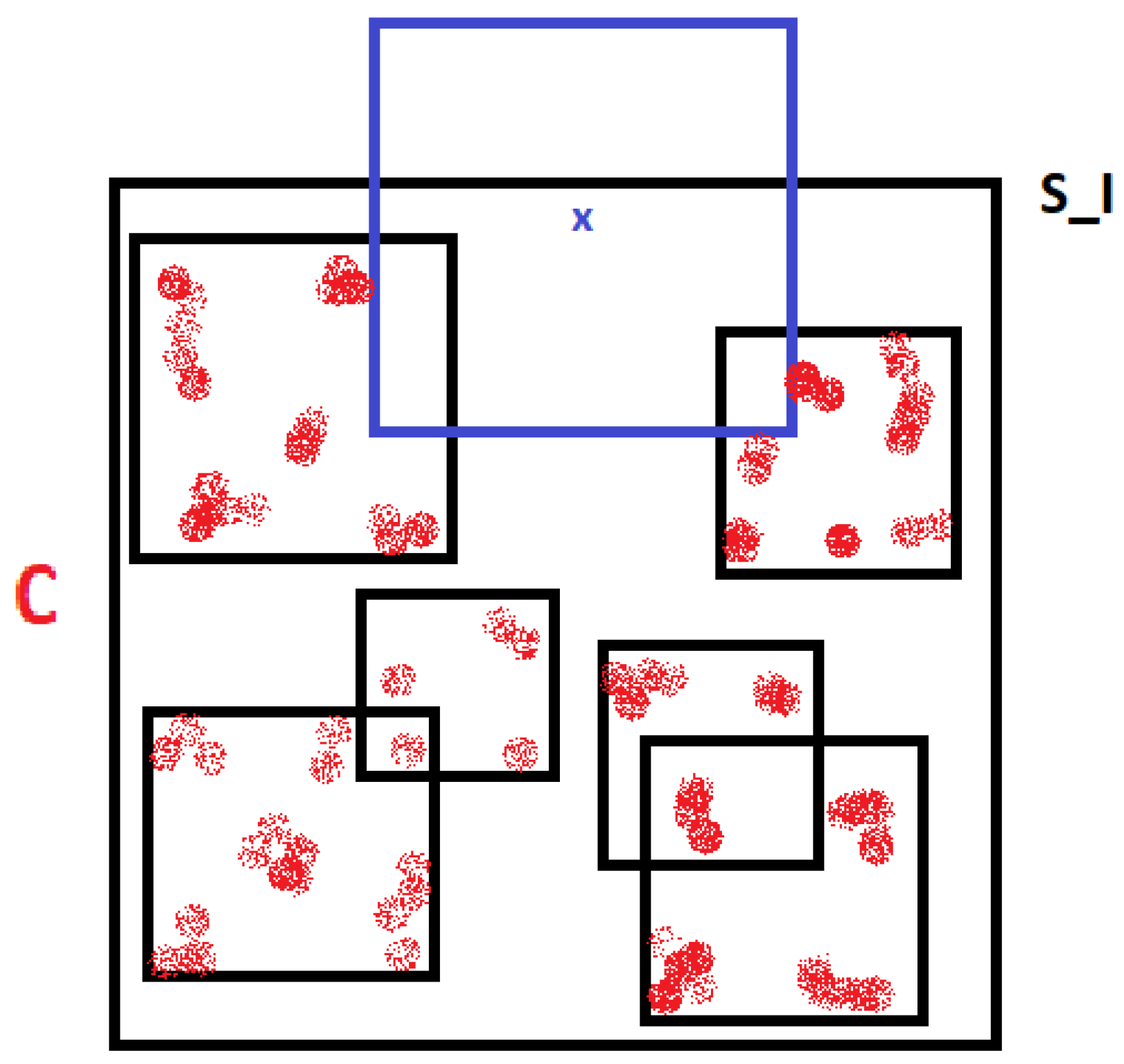
As we can see in
Figure 8, the blue region of pairs
is contained in the yellow region
. In particular, we must have
so that
, as claimed.
We have seen that C contains an arithmetic progression . This is indeed a non-degenerate progression since and A and B are disjoint, so the proof is complete. □
What about longer arithmetic progressions? For example, what is the length of the longest arithmetic progression that is contained in the middle Cantor set?
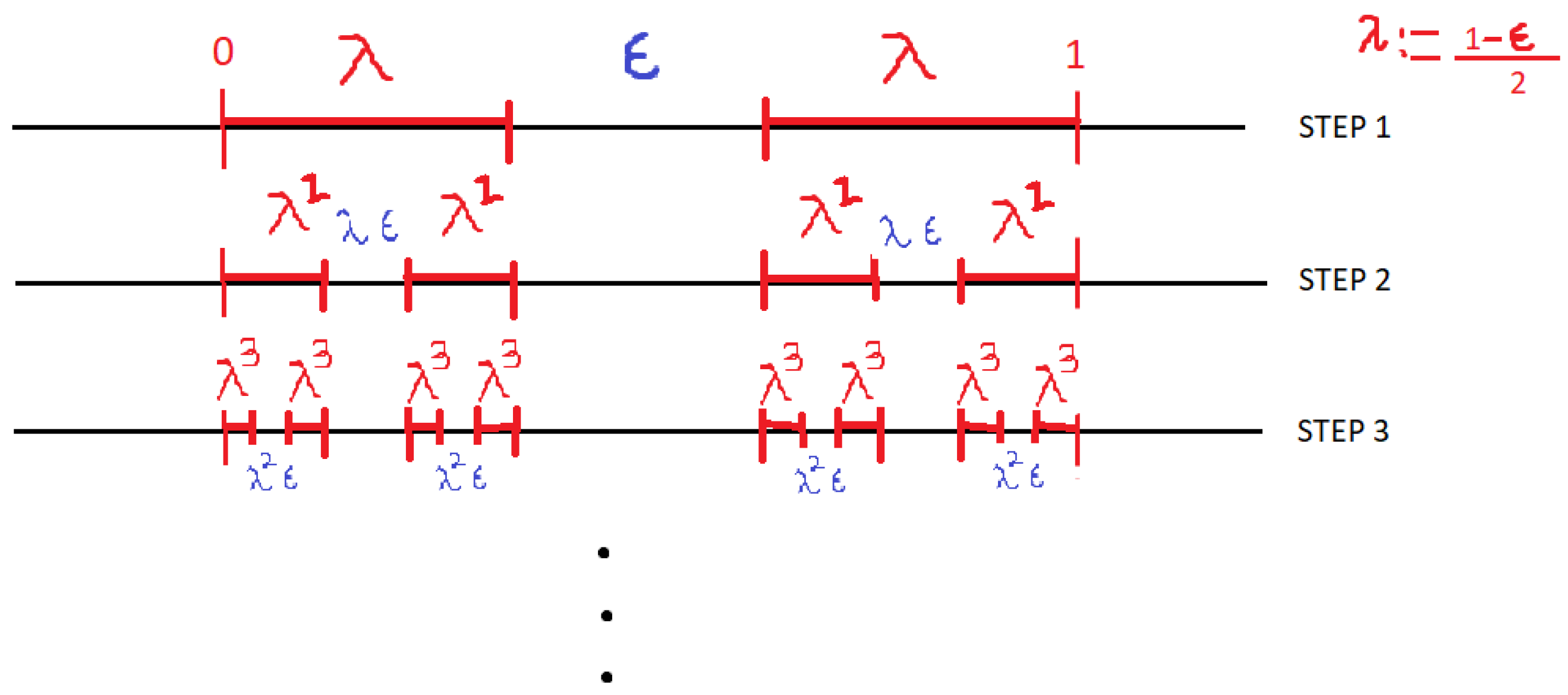
Lemma 5. The middle ε Cantor set does not contain an arithmetic progression of a length .
Proof. Take . The length of any interval of step k of the construction is (for ), and the length of any gap of the step k of the construction is (for ). Assume that there is an arithmetic progression , (with ) contained in . Then, by self-similarity, there is a first step such that the arithmetic progression is contained in an interval of step k but splits in step . Hence, and . Therefore, , and thus . □
Finding the lower bounds for the length of the longest arithmetic progression in
is more difficult. Broderick, Fishman and Simmons [
26] proved the following result:
Theorem 3 (Broderick, Fishman and Simmons).
For when sufficiently small, the middle ε Cantor set contains an arithmethic progression of a length , where c is a very small constant.
By the two previous results, we know that for
to be sufficiently small, then
The precise asymptotic behavior remains an open problem.
We will not give a proof of Theorem 3. The very rough idea behind the proof is as follows:
Then, the existence of arithmetic progressions of a length n is reduced to proving that intersections of certain n sets are non-empty. Unfortunately, the Gap Lemma does not generalize in any simple way to intersections of three or more sets, and for this reason, the authors use a different approach: the potential game, which is a game of the Schmidt type.
The classical Schmidt game was defined in 1966 by Wolfgang Schmidt to study badly approximable numbers, and since then, many variants of the original game have been developed, mainly to study problems in diophantine approximation.
As a general idea, the potential game is a game in which there are certain rules and two players: Bob, who decides where we are going to zoom in, and Alice, who decides what to erase there. Bob has limits on how far to zoom in, and Alice has limits on how much to erase. There are also special sets called winning sets, which are subsets of the “board game”. A set W is winning if Alice has a strategy guaranteeing that if she does not erase the limit point of convergence for Bob’s moves during the game, then that point belongs to W. Being a winning set (for certain parameters) can be considered another notion of a “large size” for the set.
Broderick, Fishman and Simmons showed that a slight modification of a middle Cantor set is a winning set with certain parameters. Then, they used the intersections of the winning sets (for certain other parameters) and found a result that gave a (positive) lower bound for the Hausdorff dimension of a winning set inside certain balls. In particular, the intersection was non-empty.
As a remark, winning sets for the classical Schmidt’s game and many variants have a full Hausdorff dimension. This is not the case for the potential game (with fixed parameters). This makes it useful for studying fractal sets that do not have a full Hausdorff dimension.
We will define now the potential game in a restricted context (on the real line, where Alice is able to erase neighborhoods of points and the game can be extended to higher dimensions and more general sets).
Definition 5 (Potential game in
).
Given and , Alice and Bob play the potential game in under the following rules:
For each , Bob plays first, and then Alice plays.
On the mth turn, Bob plays a closed ball . The first ball must satisfy . The following moves must satisfy and for every .
On the mth turn, Alice responds by choosing and erasing a finite or countably infinite collection of balls with radii . Alice’s collection must satisfy the following: Alice is not allowed to erase any set or, equivalently, to pass her turn.
Bob must ensure that .
There exists a single pointcalled the outcome of the game.
We say a set is an -winning set if Alice has a strategy guaranteeing that The potential game has several elementary but very useful properties:
Lemma 6 (Countable intersection property).
Let J be a countable index set, and for each , let be an -winning set, where .
Then, the set is -winning, where (assuming that the series converges).
To see this, it is enough to consider the following strategy for Alice: in the turn
m, she plays the union over
j of all the strategies of turn
m. For each
j, we know that for each turn
m, we have
. Now, we can see that playing all the strategies together is legal. In turn
m, we have
Lemma 7
(Monotonicity). If S is -winning and , , and , then S is -winning.
Indeed, one can check that Alice can answer in the game using her strategy from the game:
Lemma 8 (Invariance under similarities).
Let be a similarity with a contraction ratio λ. Then, a set S is -winning if and only if the set is -winning.
This follows by mapping Alice’s strategy with f.
In [
10], we established a new connection between Schmidt’s games and thickness in the real line and generalized the result with the findings of Broderick, Fishman and Simmons:
Theorem 4. Let be a compact set. Then, C contains a homothetic copy of every set P with at mostelements. Moreover, for each such set P, the compact set C contains for some and a set of x positive Hausdorff dimensions. Note that this result gives non-trivial information only when , which requires the thickness to be larger than some large absolute constant. The main usefulness of the theorem is for large values of . Theorem 4 generalizes the results of Broderick, Fishman and Simmons, since is a compact set with a thickness and the arithmetic progression is a homothetic copy of .
Let us see the main ideas behind the proof of Theorem 4. Given a finite set
, we have the following:
Then, to guarantee a pattern of a size
n, we need to check that a certain intersection of
n sets is non-empty (in fact, the proof shows that the intersection has a positive Hausdorff dimension count). We know from Lemma 6 that winning sets have certain stability under intersections. It is not obvious that winning sets intersect a given interval, but Broderick, Fishman and Simmons ([
26], Theorem 5.5) proved that, depending on the parameters, the intersection of a winning set with an interval is not only nonempty but has a positive Hausdorff dimension count. While [
26] (Theorem 5.5) involves some non-explicit constants, in the context relevant to Theorem 4, this result was made completely explicit in [
10] (Theorem 19).
What remains to prove Theorem 4 is the link between thick sets and winning sets. This is provided by the following result:
Proposition 2. Let C be a compact set with and . Then, is -winning for all .
Proof. In order to prove that a set S is winning, we have to see that Alice is able to erase the complement of S where Bob is zooming in.
If Bob plays B, how does Alice respond? Let be the sequence of complementary open gaps of S, ordered by non-increasing length.
Alice’s strategy: If there exists such that B intersects and , then Alice erases if it is a legal movement. In any other case (if B does not intersect any gap of S or if ), Alice does not erase anything.
To show that this strategy is winning, suppose that Alice does not erase
during the game. We want to see that
. Let us make a counter-assumption that
. Then, there exists
n such that
. We will show that Alice erases
at some stage of the game (which is a contradiction). By definition,
for all
, and we assumed
. Thus, we have
Since
, we have that
, and we also know that
. Thus, we take
to be the smallest integer such that
Then,
. Indeed, we find the following:
Recall that we proved that
, while
. Hence, we have
Since is the first gap intersecting , the gap is uniquely defined (there are not two gaps that Alice should erase in the same turn). In conclusion, it is legal for Alice to erase in the th turn, and her strategy specifies that she does so. □
For a sketch of proof of Theorem 4, we can assume without loss of generality that
and also that the pattern with
n elements is
. We define
Using Propositions 2, 6, 7 and 8, we find that
is
-winning for all
and all
. We define
and take
,
and
, which is an interval of a length
. Then, by applying [
10] (Theorem 19) (which is a very technical result from where we obtain the constant
), one finds the following condition:
if
Therefore, to guarantee the presence of a homothetic copy of a set of a size n, it is sufficient that n satisfies the hypothesis of the theorem.
For those values of
n, we have seen
. For each
, using
, we have
Since is disjoint from and , we have that .
Thus, is a translated copy of the given finite set, which is contained in C.