Experimental and Numerical Investigation of the In-Plane Compression of Corrugated Paperboard Panels

Abstract

Finite element analysis (FEA) has been proven as a useful design tool to model corrugated paperboard boxes, and is capable of accurately predicting load capacity. The in-plane deformation, however, is usually significantly underpredicted. To investigate this discrepancy, a panel compression test jig, that implemented simply supported boundary conditions, was built to test individual panels. The panels were then modelled using non-linear FEA with a linear material model. The results show that the in-plane deformation was still underpredicted, but a general improvement was seen. Three discrepancies were identified. The first was that the panels showed an initial region of low stiffness that was not present in the FEA results. This was attributed to imperfections in the panels and jig. Secondly, the experimental results reported a lower stiffness than the FEA. Applying an initial imperfection in the shape of the first buckling mode shape was found to reduce the FEA stiffness. Thirdly, the panels showed a decrease in stiffness near failure, which was not seen in the FEA. A bi-linear material model was investigated and holds the potential to improve the results. Box compression tests were performed on a Regular Slotted Container (RSC) with the same dimensions as the tested panel. The box displaced 13.1 mm compared to 3.5 mm for the panel. There was an initial region of low stiffness, which accounted for 7 mm of displacement compared to 0.5 mm for the panels. Thus, box complexities such as horizontal creases should be included in finite element (FE) models to accurately predict the in-plane deformation, while a bi-linear (or any other non-linear) material model may be useful for panel compression.

1. Introduction

Corrugated paperboard is one of the most widely used packaging materials for various reasons. It is inexpensive, has a high strength-to-weight ratio and is environmentally friendly [1]. Corrugated boxes are widely used to transport various goods, from fresh food to industrial equipment [2]. During transport, these boxes may undergo various loads such as compressive loading, vibrational loading, cyclic loading due to changing environmental conditions, etc. Changeable conditions and different loading mechanisms are only some of the difficulties in determining the strength of a box. Aspects such as the presence of hand/ventilation holes, the type of box (RCS, Bliss, telescopic, etc.) and flute size all play an important role [3].

Box strength can be determined using empirical relations or numerical analysis. McKee’s equation, as proposed by [4], is the most prominent empirical relation. This relation is, however, only valid in very specific cases. Other authors have tried to improve the accuracy, but most involve just fitting an equation to a limited data set [5,6]. A more general equation was proposed; however, it lacks the simplicity of application the McKee equation has [7]. Due to the increase in computing power, numerical analysis using finite element methods (FEM) has become increasingly more popular to estimate the strength of a box and can accelerate design time. Once a valid model is obtained, several designs of boxes can be tested without the need for physically testing each design.

Finite element analysis (FEA) was used to investigate the effect that size, shape, and location of ventilation and handholes have on box strength to find the optimal design [8]. The effect of different indentation shapes on box strength was analysed [9]. FEA was used to analyse different edge crush test (ECT) methods [10].

It has been observed that FEA models can very accurately predict the failure load of boxes, but are typically less accurate when it comes to in-plane displacement and out-of-plane displacement [11]. One reason for this is suspected to be due to creases. An investigation of paperboard packages (boxes) showed that the middle segment has a higher stiffness than the upper and lower segments [12]. The difference in stiffness was attributed to the horizontal creases. Digital image correlation (DIC) was used to show that about 5% of the crosshead displacement, measured by a compression tester, can be attributed to pure in-plane compression, while the rest of the crosshead displacement is concentrated around the top and bottom horizontal creases [13]. A test fixture was built to investigate eccentricity in loading caused by creases [14]. An 80 mm wide 220 mm long sample was creased 70 mm from the end folded to a 90° angle and clamped. The 70 mm vertical portion displaced up to about 4 mm before failing in an axial compression test. Again, a large portion of this displacement is attributed to the presence of a crease.

Literature on individual panels is less common, likely since it is not a standardized test. Jigs for panel compression were designed by [15,16] using 290 mm × 400 mm and 400 mm × 400 mm panels respectively. Both studies were aimed at investigating out-of-plane displacement. Recently, Ref. [17] developed a new design that included flaps to have a single panel that is more representative of an entire box. The test jig as designed by [16] was also used by other authors, to measure changes in the thickness of the panel by using DIC set-ups on both sides of the panel [18] and to investigate global and local buckling [1,19]. None of these studies, however, have compared panel compression to box compression.

In this study, panel compression of a 400 mm × 400 mm panel, using a test jig similar to that of [16], is compared to an FEA simulation of the 400 mm × 400 mm panel and box compression of a 400 mm × 400 mm × 400 mm RSC. DIC was also used to capture the out-of-plane deformation of both the panel and the box. Lastly, empirical equations were compared to experimental values.

2. Materials and Methods

All tests were conducted using 250 KL (kraft liner)/150C-SC (semi-chemical)/250 KL C-flute corrugated paperboard. Samples were cut using a Kongsberg cutter with a powerhead attachment and conditioned at standard testing conditions (23 °C and 50% relative humidity (RH)) for at least 24 h as per ISO 187.

2.1. Edge Crush Test

The ECT is one of the most performed tests on corrugated paperboard and is used to determine the compressive strength of the combined board, typically in the CD. This value is used in the popular McKee formula to determine box strength. Various industry standards for this test are available and studies have been conducted to compare the different methods [20]. In this study, the Tappi T 838 (circular necked down) method was used.

A Testing Machines Inc. (TMI) crush tester (model 17–56) and clamp were used to perform the ECT. The failure load is reported by the machine and can be used to calculate the ECT value as:

$$ECT=\frac{F_{max}}{w},$$

(1)

where w is the load-bearing width of the specimen at the necked down region and F_max is the failure load.

2.2. Bending Stiffness Test

The bending stiffness can be estimated by using experimental results from tensile tests of the individual sheets and a homogenization process to extract the equivalent bending stiffness matrix of the board [21]. Alternatively, a three- or four-point bending test can be performed. Four-point is the preferred method for corrugated board as it provides a shear-free section of board between the supports closest to the centre of the specimen [22]. Bending stiffness tests were performed as part of a bigger study, thus the results were available and analytical methods were not required [23]. The bending stiffness tests were also used to verify the finite element (FE) model and in the long McKee equation.

Four-point bending tests were performed, according to the ISO 5628 standard, with an Instron universal tester with a four-point bending fixture, Figure 1. Additionally, a Hottinger Baldwin Messtechnik (HBM) S2M (200 N) loadcell, HBM WA100 (100 mm) linear variable differential transducer (LVDT), HBM Quantum X MX440B and Catman Easy data acquisition software were used. The bottom (support) anvils were spaced 200 mm apart and the top (load) anvils were placed 340 mm apart, leaving a 70 mm free length at each end.

The displacement rate was set to 12.7 mm/min. The load-displacement curve was recorded and the initial linear segment (as similarly defined for panels, see Figure 10) of the curve can be used to determine the bending stiffness as follows:

$${\mathrm{S}}_{\mathrm{b}}=\frac{1}{16}\left(\frac{P}{Y}\right)\left(\frac{L^3}{w}\right)\left(\frac{a}{L}\right),$$

(2)

where P is the load, Y is the displacement, L is the distance between supports, a is the free length (between support and load pins) and w is the sample width.

2.3. Panel Compression

Since panel compression is not a standardized test, examples available in the literature were used as guidelines on how to perform the test and design the jig to implement simply supported (rolling) boundary conditions [15,16]. One aspect that was found lacking in the literature was the adjustability of the jig. As part of a bigger study, the jig was designed to accommodate panels of various widths, heights, and thicknesses. Simply supported boundary conditions on the vertical edges can be accomplished by using knife edge supports [16]. The horizontal edges are more complex. A panel with simply supported boundary conditions would require non-uniform edge rotation. The knife edge supports on the vertical edges work for this as they only need to prevent out-of-plane displacement, and there is no load application perpendicular to the vertical edges. The horizontal edge has a load applied perpendicular to the edge as well. To apply the load uniformly without restricting rotation, a flat surface that can rotate is required, but a single surface would enforce uniform edge rotation. To allow non-uniform edge rotation, adjustable sectioned slotted rollers were used on the horizontal edges. The jig used is shown in Figure 2a.

For this paper, only 400 mm × 400 mm panels compressed in the cross direction (CD) will be considered. The larger study, however, considered 200 mm × 200 mm, 300 mm × 300 mm and 400 mm × 400 mm panels compressed in both the machine direction (MD) and CD [23]. The actual samples were cut 15 mm wider than square to allow lateral movement and prevent the samples from slipping out of the jig. The corners were also chamfered to prevent localised damage at the rollers (geometry shown in Figure 3). To perform the test, an Instron universal tester fitted with the panel compression jig was used, with the displacement rate set to 12.7 mm/min, Figure 2a. To capture the out-of-plane deformation, a stereo DIC set-up was also used. The DIC set-up, Figure 2b, consisted of a computer with LaVision StrainMaster software (version 1.3.0), two light-emitting diode (LED) lights, two 5-megapixel charge-coupled device (CCD) cameras, and a control unit. The cameras were placed such that the sample occupied most of the field of vision, and the aperture was set to f/1.6 and digitally adjusted further for optimal exposure in the StrainMaster software. The set-up was calibrated for each test with a calibration plate. For the test, the image frequency was set to 5 Hz. To use the DIC equipment, a speckle pattern was sprayed onto the panels with white and black spray paint.

2.4. Finite Element Modeling

Since the individual sheets were not tested, material data established by [11] were used as an initial set of material properties—

Table 1. Initial material properties [11].

Material Property	250 KL	150C-SC	150C-SC Homogenised
E1 (MPa)	6695	4709	27
E2 (MPa)	2310	2918	235
E3 (MPa)	35	25	3000
ν12	0.5	0.37	0.02
ν13	0.01	0.01	0.01
ν23	0.01	0.01	0.01
G12 (MPa)	1522	1435	21
G13 (MPa)	122	86	3
G23 (MPa)	66	83	14

. These properties were used to create detailed and homogenised models of the four-point bending and panel compression tests. The core homogenisation process that was used is presented in Appendix A. Quarter symmetry was used for all models. MSC Marc and Mentat [24] was used to perform all analyses. For the detailed models, the flute shape was assumed as sinusoidal, and the liners were connected to the core by sharing nodes at the flute crests [16]. For the homogeneous models, the composite function in Mentat was used to simplify the homogenised core and liners into one layer [24]. Four-node-thick shell elements with full integration were used for both the detailed and homogenised models. Friction was not considered, and node-to-segment contact was used. A wavelength of 7.7 mm [11] and board thickness of 4.17 mm (measured) were used. The sheet thickness of the 150C-SC and 250 KL was 251 μm and 345 μm, respectively [11].

Note that in the model, point-wise contact between the flute and the liners was assumed, which in reality is a contact area. This would slightly reduce the modelled stiffness of the board when compared to experiments.

2.4.1. Bending Test

For the bending models (MD and CD), symmetry along the x-axis fixed the Ty, Rx and Rz rigid body modes (where T is translation and R is rotation) and symmetry along the y-axis fixed the Tx, Ry and Rz rigid body modes. The final rigid body mode, Tz, was restricted by defining touching contact between the sample and the load and support pins (modelled as rigid bodies). The load was incrementally applied with a negative z-displacement control on the load pin, using adaptive multi-criteria stepping and a linear timetable. A linear material model and the Tsai-Wu failure criterion were used to define the material model. The parameters used to define the criterion are shown in

Table 2. Measured paper sheet strength properties [11].

Sheet	σ1,t (MPa)	σ1,c (MPa)	σ2,t (MPa)	σ2,c (MPa)
150C-SC	45.3 ± 2.4	30.7 ± 1.7	22.1 ± 1.4	17.5 ± 1.1
250 KL	68.0 ± 2.9	23.3 ± 1.4	24.1 ± 1.7	12.9 ± 1.2

, where σ is the failure stresses in tension and compression. A non-linear static analysis with the large strain formulation and a full Newton–Raphson iterative procedure was used. The final model consisted of 131,528 nodes and 135,600 elements.

2.4.2. Panel Compression

For the panel compression models, the material properties adjusted to the bending test were used (reported in Table 6). The sample itself was modelled using the same process as for the bending models, with the exception that a 1 mm element size was used for the detailed model instead of 0.5 mm. This model was much larger than the bending models and increasing the mesh size saved computational time. However, the mesh size was still sufficiently converged to produce accurate results (from a mesh convergence study on the bending models). The resulting model consisted of 141,424 nodes and 151,104 elements. A 2 mm mesh was still used for the homogenised model (10,605 nodes and 10,400 elements). The symmetry conditions again fixed the Tx, Ty, Rx, Rz, Ry, and Rz degrees of freedom. Tz was fixed along the edges of the panel to represent the test jig.

Since the board in the detailed model had an inherent thickness, a single load surface would enforce uniform edge rotation. To rectify this, ten solids (similar to the rollers of the jig) with possible rotation in the x-axis were used for load application—Figure 4. The “rollers” had to be separated to properly result in non-uniform edge rotation. It was, however, not necessary to use “rollers” to apply the load for the homogeneous model. Since the shell thickness could be ignored for the contact condition between the load surface and the sample, non-uniform edge rotation was automatically allowed. Thus, a single load surface was used for the homogeneous model, Figure 5.

Two analyses were performed on both the detailed and homogenised models—one to determine the buckling load and mode shape and another to determine the failure load, as well as in-plane- and out-of-plane displacement. For the first case (buckling analysis), a non-linear static structural analysis with large strain enabled, followed by a buckling analysis (eigenvalue problem), was performed. For the second case (failure analysis), a non-linear static structural analysis with large strain enabled, as in the previous case, was followed by a transient (dynamic with implicit time integration) analysis. Since the nodes of the homogenised model were exactly zero, i.e., a perfectly flat panel, an additional step was added to the failure analysis of the homogenised model to ensure that the panel will buckle, as seen with experimental data. An initial geometric imperfection was introduced by first applying a small load to the sample using a static analysis, followed by a buckling analysis, and extracting the first buckling mode shape (normalised). The mode shape was then used to apply an out-of-plane displacement perturbation with a certain scale (0.001 mm in this case) to the panel, followed by the failure analysis as described.

When looking at panel or box behaviour, there are two important points on the load-displacement curve. One is the point where buckling occurs, and since the post-buckling behaviour is stable [16], the second point is where the box fails. The theoretical buckling load per unit width can be calculated as [15]:

$$P_{cr}={\pi }^2\left[\frac{d^2{D}_{11}}{w^4}+\frac{2\left(D_{12}+2D_{66}\right)}{w^2}+\frac{D_{22}}{d^2}\right],$$

(3)

where D_i,j is the bending stiffness, w is the panel width and d is the panel height. The failure load can be calculated as:

$$P_l=w\left[k{P}_{cr}^{1-b}EC{T}^b\right],$$

(4)

by setting k and b (empirical constants) to 0.5 and 0.76, respectively [4].

2.5. Box Compression

The box compression test (BCT) is used to determine the load-bearing capacity of a box. This is the only way to truly know what the strength of a box is, but it requires production and is thus not an efficient method to determine box strength. The TAPPI T 804 standard was used to test 400 mm × 400 mm × 400 mm boxes. As with the material tests, 250KL/150C-SC/250KL C-flute board samples from the exact same batch were used and conditioned in a standard atmosphere (23 ± 1 °C and 50 ± 2% RH) for at least 24 h before testing [25].

The test was performed using a Lansmont Squeezer compression tester. The tester has fixed and swivel platen options, but a fixed platen setup was used. The DIC system, as described above, was also used to measure the out-of-plane displacement. The box blanks were glued with hot glue at the manufacturer’s joint. Flaps were bent directly to the final position and unsealed. A panel, away from the manufacturer’s joint, was spray-painted with a black and white speckle pattern for the DIC. Ten boxes were tested in total, of which five boxes were folded to have the speckle pattern on a panel with top flaps (flaps were above those of the side panels, Figure 6a) and five with the speckle pattern on bottom flaps (flaps were beneath those of the side panels, Figure 6b). A preload of 223 N was applied and the displacement rate was set to 12.7 mm/min.

The BCT strength can be estimated with the popular McKee formula, using either the long or short form (Equations (5) and (6), respectively).

$$BCT=a\cdot EC{T}^b{\left(\sqrt{D_{11}{D}_{22}}\right)}^{1-b}{Z}^{2b-1},$$

(5)

$$BCT=5.874ECT{t}^{0.508}{Z}^{0.492}\approx 5.87ECT\sqrt{tZ},$$

(6)

where a and b are empirical constants equal to 2.028 and 0.746, respectively [4], Z is the perimeter and t is the board thickness.

3. Results and Discussion

3.1. ECT

The results for the ECT are shown in

Table 3. ECT results.

Direction	Number of Samples	Average Force (N)	ECT Strength (kN/m)
CD	20	298.3 ± 11.6	11.75 ± 0.46

. A similar value (10 kN/m) was reported by [26] for the same board specification. A significantly lower value (7.2 kN/m) was reported by [11], but the author used a different testing standard, ISO 3037, which used a rectangular specimen and not a neck-down specimen. Similar differences between standards have been noted by [10].

3.2. Bending Stiffness

The results of the four-point bending test are shown in Figure 7 and

Table 4. Four-point bending test results.

Direction	Pmax (N)	Ymax (mm)	Sb (N⋅m)
Four-point CD	58.6 ± 2.4	14.3 ± 0.5	8.0 ± 0.3
Four-point MD	41.6 ± 3.5	3.5 ± 0.4	20.8 ± 1.1

. The bending stiffness was larger in the MD, while the failure load and maximum displacement were larger in the CD [22]. Similar results were obtained by [26] for the same board specification.

3.3. Panel Compression

The results for the panel compression tests are shown in Figure 8 and

Table 5. Panel compression results.

Panel	Pmax (kN)	Ymax (mm)	Wmax (mm)	Stiffness (kN/mm)	Pnorm (kN/m)
ECT CD	-	-	-	-	11.74
400 mm CD CH	2.07 ± 0.07	3.5 ± 0.3	13.9	1.00	5.18
400 mm CD DIC	2.07 ± 0.07	1.6 ± 0.2	13.9	3.62	5.18

. Note that two in-plane displacement curves are given in Figure 8a. The crosshead (CH) displacement curve is the displacement as measured by the Instron, while the DIC curve was obtained from the DIC data. For the DIC curve, two points on the panel, one at the top and one at the bottom, initially 360 mm apart, were identified, and the difference in vertical displacement between these two points was recorded (see Figure 9 for the approximate location of these points). The DIC curve reported 54% less displacement and can be considered a more accurate representation of displacement, purely due to in-plane compression and bending, since the DIC is not affected by settling [13]. This method of displacement measurement does, however, have one drawback. Since part of the panel is covered by the rollers and the DIC data do not go to the edge of the rollers, about 40 mm of the sample (10%) is not considered in this measurement, which was accounted for by adjusting the displacement using the actual length of the panel.

The out-of-plane displacement was measured at the centre of the panel as this was the most consistent way to report the displacement, but the maximum displacement may be located away from the centre of the board, especially at failure—see Figure 9a. The typical displacement pattern before failure is also shown in Figure 9b.

The panel stiffness (slope of the linear portion of each curve) and a normalised force (maximum force divided by panel width) was also calculated (Table 5). The linear portion was defined as the portion after the initial low-stiffness region and before the final low-stiffness region—Figure 10. The slope was calculated by selecting two points in this region such that R² > 0.99. The DIC panel stiffness was 3.6 kN/m, compared to 1 kN/m for the crosshead displacement curve. The ECT strength was included for reference, but it should be noted that the ECT had different boundary conditions (clamped horizontal edges) than the panel compression (simply supported). Compared to the ECT, the 400 mm panels were about 49% weaker. The decrease in strength is due to buckling failure rather than pure material failure.

The panels failed as expected, i.e., localised failure in the corner region—see Figure 9a and Figure 11. A crease formed in the corners and then propagated towards the centre of the panel at an angle of approximately 45° [18,19].

3.4. Finite Element Modelling

3.4.1. Bending

A mesh convergence study was performed on the detailed and homogenised models, and it was concluded that a 0.5 mm and 2 mm mesh (size of elements), respectively, showed reasonable convergence. A sensitivity analysis was performed on several of the material properties with the bending models, according to which these material properties were adjusted (

Table 6. Bending-adjusted material properties.

Material Property	250 KL	150C-SC	150C-SC Homogenised
E1 (MPa)	7699	4709	32
E2 (MPa)	2541	2918	246
E3 (MPa)	35	25	3000
ν12	0.5	0.37	0.03
ν13	0.01	0.01	0.01
ν23	0.01	0.01	0.01
G12 (MPa)	1583	1492	24.6
G13 (MPa)	122	86	2.7
G23 (MPa)	66	83	13

) until there was good agreement with the experimental data (within 4%, see

Table 7. Bending stiffness comparison of experimental data and adjusted detailed- and homogeneous model.

Model		Four-Point CD	Four-Point MD
Experimental	Stiffness (N·m)	8.0	20.8
Adjusted detailed model	Stiffness (N·m)	8.2	21.2
	Error	2.8%	1.6%
Adjusted homogeneous model	Stiffness (N·m)	7.7	21.2
	Error	3.5%	1.8%

).

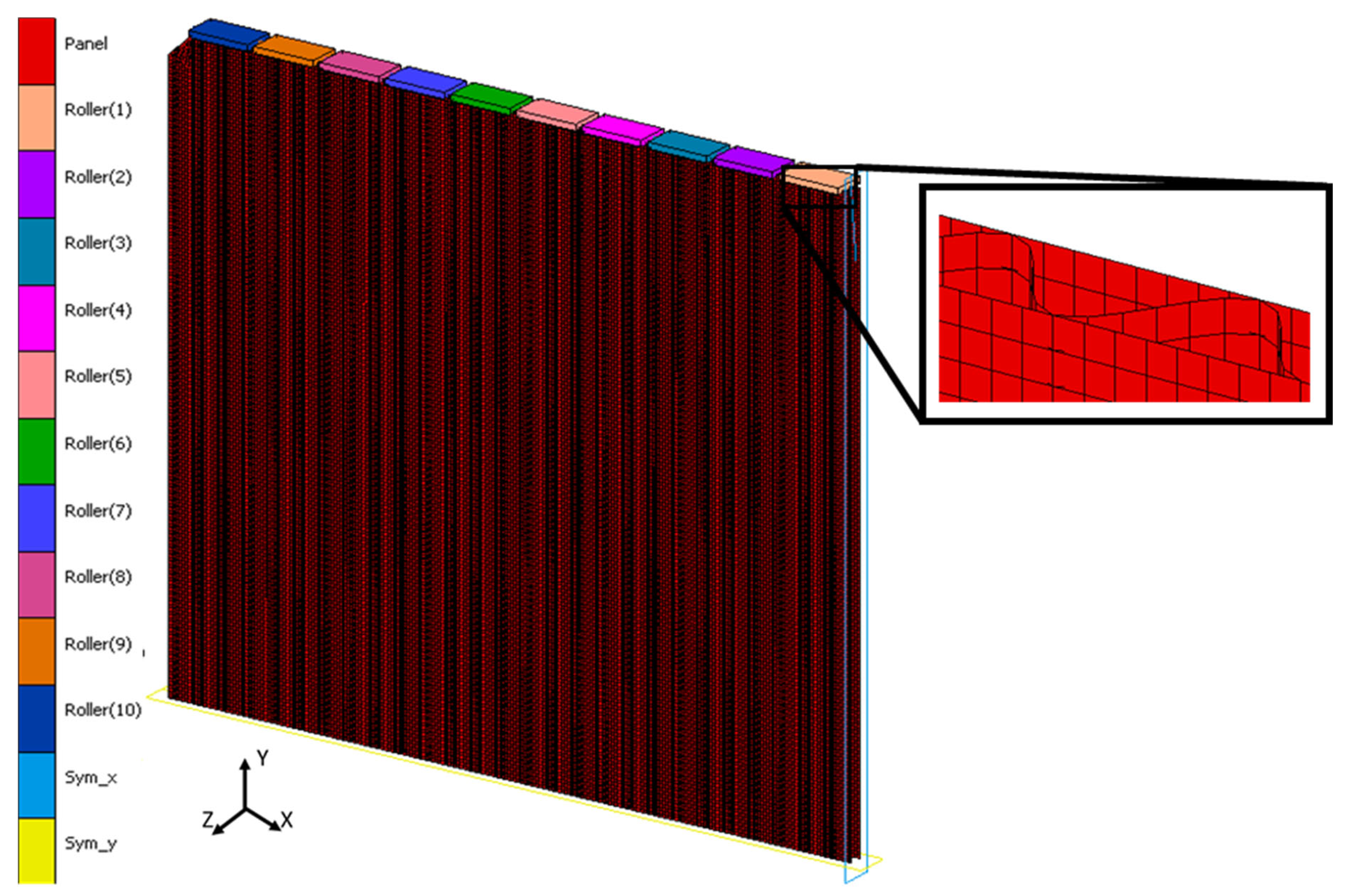
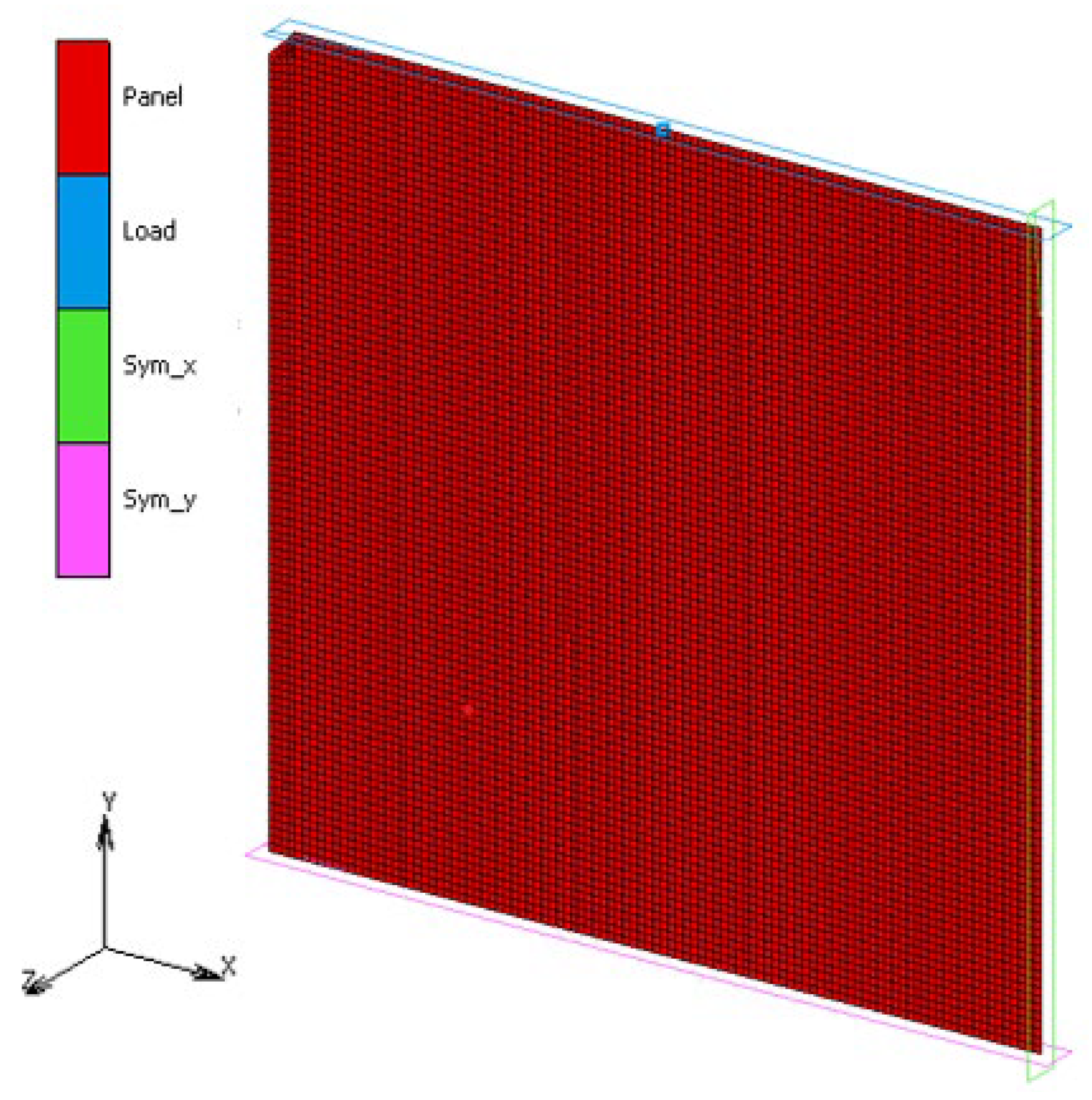
3.4.2. Panel Compression

The results for the panel compression simulations are shown in

Table 8. Comparison of the 400 mm panel behaviour for experimental and FEA values.

Method	Buckling Load (N)	Failure Load (N)	In-Plane Displacement (Failure) (mm)	Out-of-Plane Displacement (Failure) (mm)
Experimental	N\A	2071	3.5 (CH), 1.6 (DIC)	13.9
FEA detail	1310	2209	1.25	11.45
Error	-	6.7%	64.6% (CH), 21.9% (DIC)	17.6%
FEA homogeneous (0.001 mm perturbation)	1352	2220	1.31	11.60
Error	-	7.2%	62.9% (CH), 18.1% (DIC)	16.5%

and Figure 12 and Figure 13, and have been compared to experimental data. Note that the material parameters from Table 6 were used to perform the analyses.

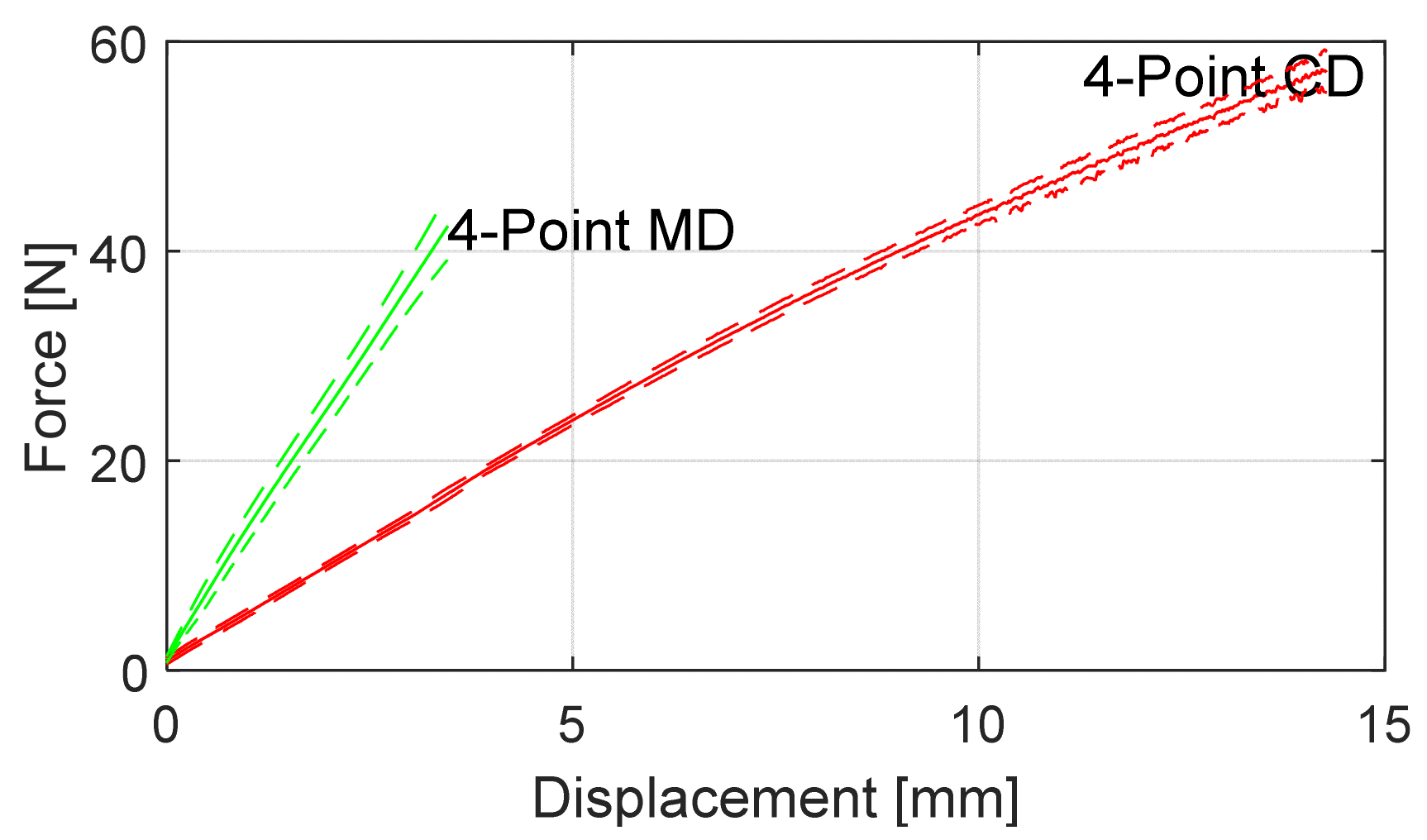
There was a 3% difference in the buckling load between the detailed and homogeneous models, while the failure load, and maximum in-plane and out-of-plane displacements, differed by 0.5%, 4.8% and 1.3%, respectively. Overall, there is a good correlation with the detailed and homogeneous models. The homogeneous model predicted a slightly higher failure load and displacements (in-plane and out-of-plane), while the detailed model had a slightly higher panel stiffness.

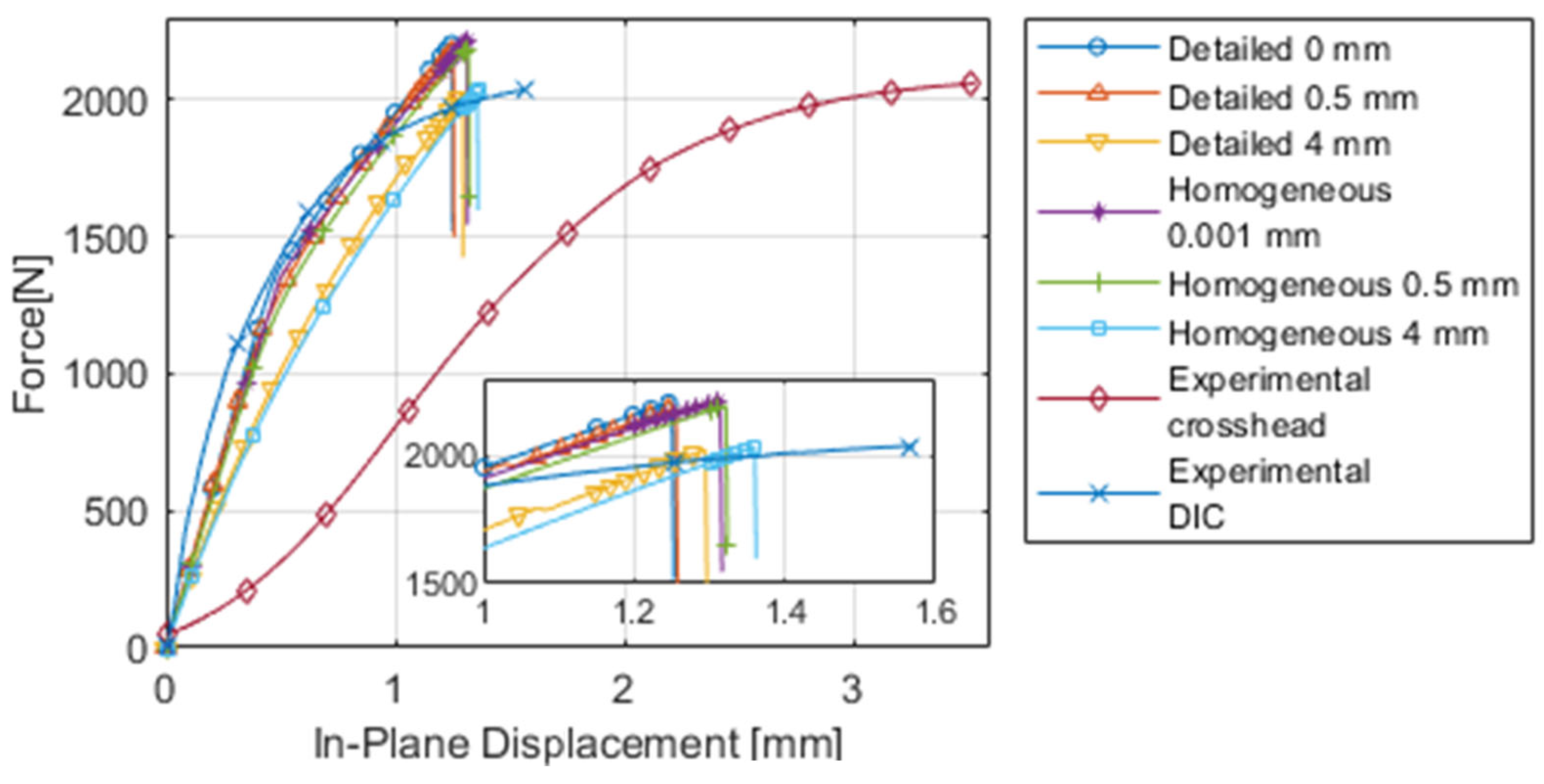
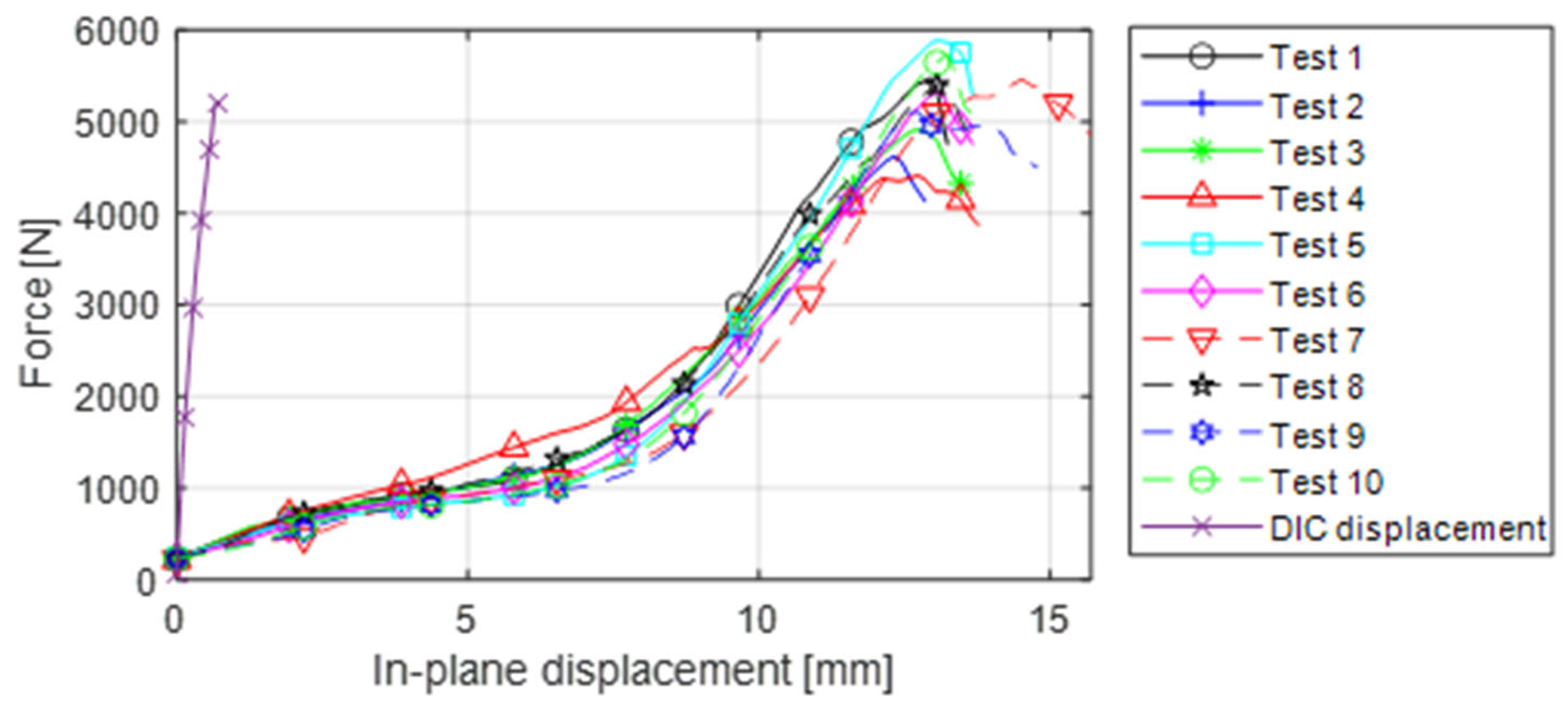
As seen in Figure 12 and Figure 13, a 0.5 mm and 4 mm perturbation was also applied to the detailed and homogenised models. Since the experimental panels were not perfectly flat, the influence of different size perturbations was investigated. A larger perturbation resulted in an increased in-plane displacement, while out-of-plane displacement and failure load decreased. The load-displacement curves also became smoother with a larger perturbation, i.e., there was no clear kink (buckling event) in the curves as was seen with no (or small) perturbations. The 4 mm perturbation curves (Figure 12 and Figure 13) seem to match the stiffness of the experimental (crosshead) data better than the other models, both in terms of in-plane and out-of-plane displacements. No (or small) perturbations matched the stiffness of the DIC experimental data well in terms of in-plane displacement.

Considering Figure 12, the experimental (crosshead) curve initially had low stiffness and then started to stiffen up before the stiffness decreased at the end. The FEA results do not reflect this initial low-stiffness region. This is likely caused by the localised crushing of the panel edges, where the edges and rollers are not perfectly parallel. It could also be due to settling if the panels are not perfectly square. This observation is supported by the DIC experimental curve which, like the FEA results, does not show a low-stiffness region.

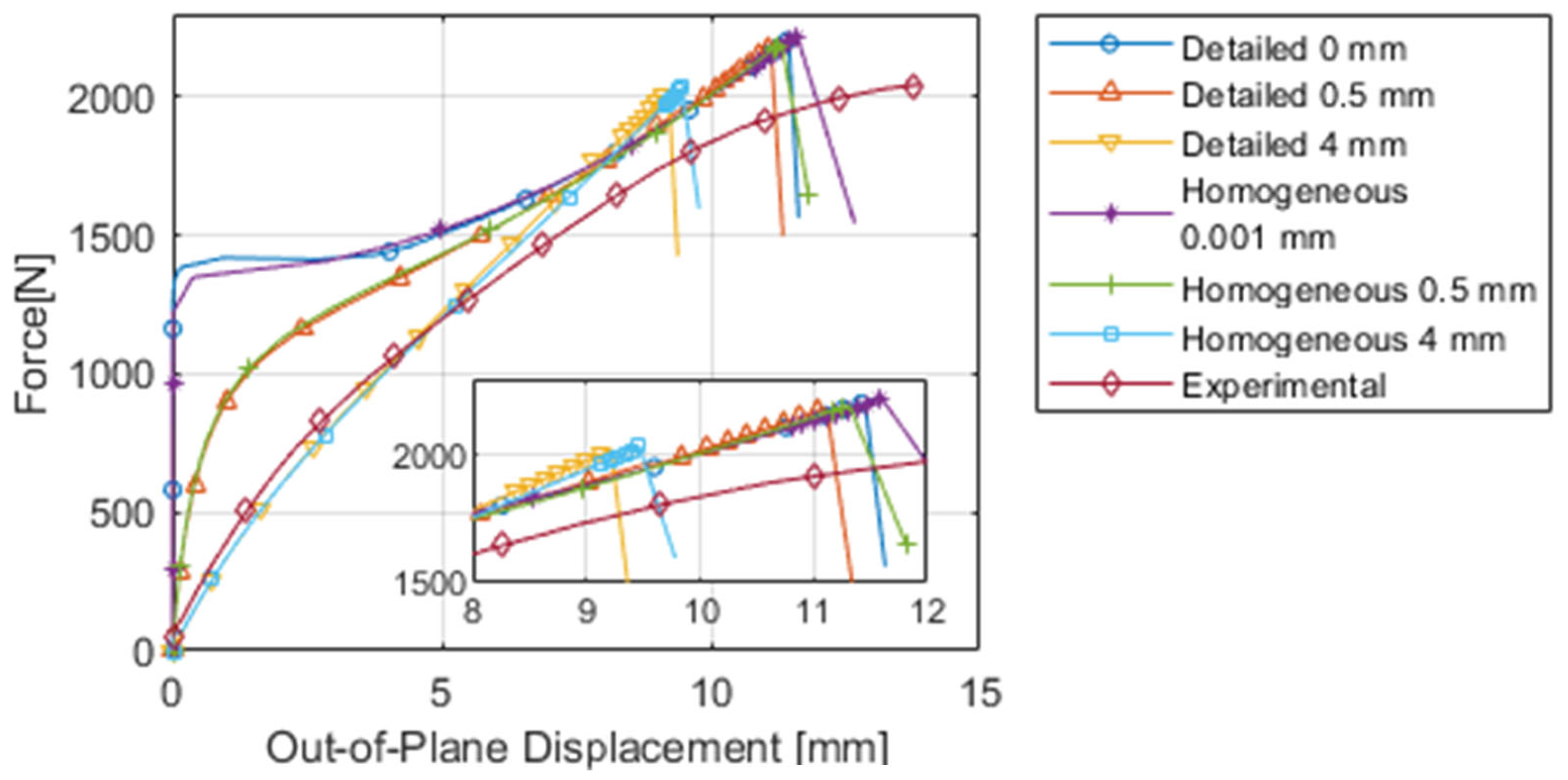
The linear portion of the experimental (crosshead) curve had a lower stiffness than the FEA curves with a small perturbation (Figure 12). It is seen that an initial imperfection, in the form of the first buckling mode shape, can decrease the stiffness of the FEA model in this region, suggesting the tested panels had some form of an initial imperfection that reduced the stiffness. From Figure 13, the same conclusion can be drawn for the out-of-plane deformation curve. When the samples were first received, there was no visible warping, but after spray-painting the samples for DIC purposes, there was visible warping. The precise severity is unknown, since the warpage was not measured, but from a visual inspection, we can see they fell within the range of 0.5 mm to 2 mm. Using a white kraft liner instead of brown will minimise the amount of paint needed for a speckle pattern, and thus minimise warpage. The DIC experimental curve, however, is slightly stiffer than the FEA with small (or no) perturbation. This would suggest that even after initial settling (the low stiffness region), there are still imperfections, causing the crosshead displacement to give different results than the DIC displacement.

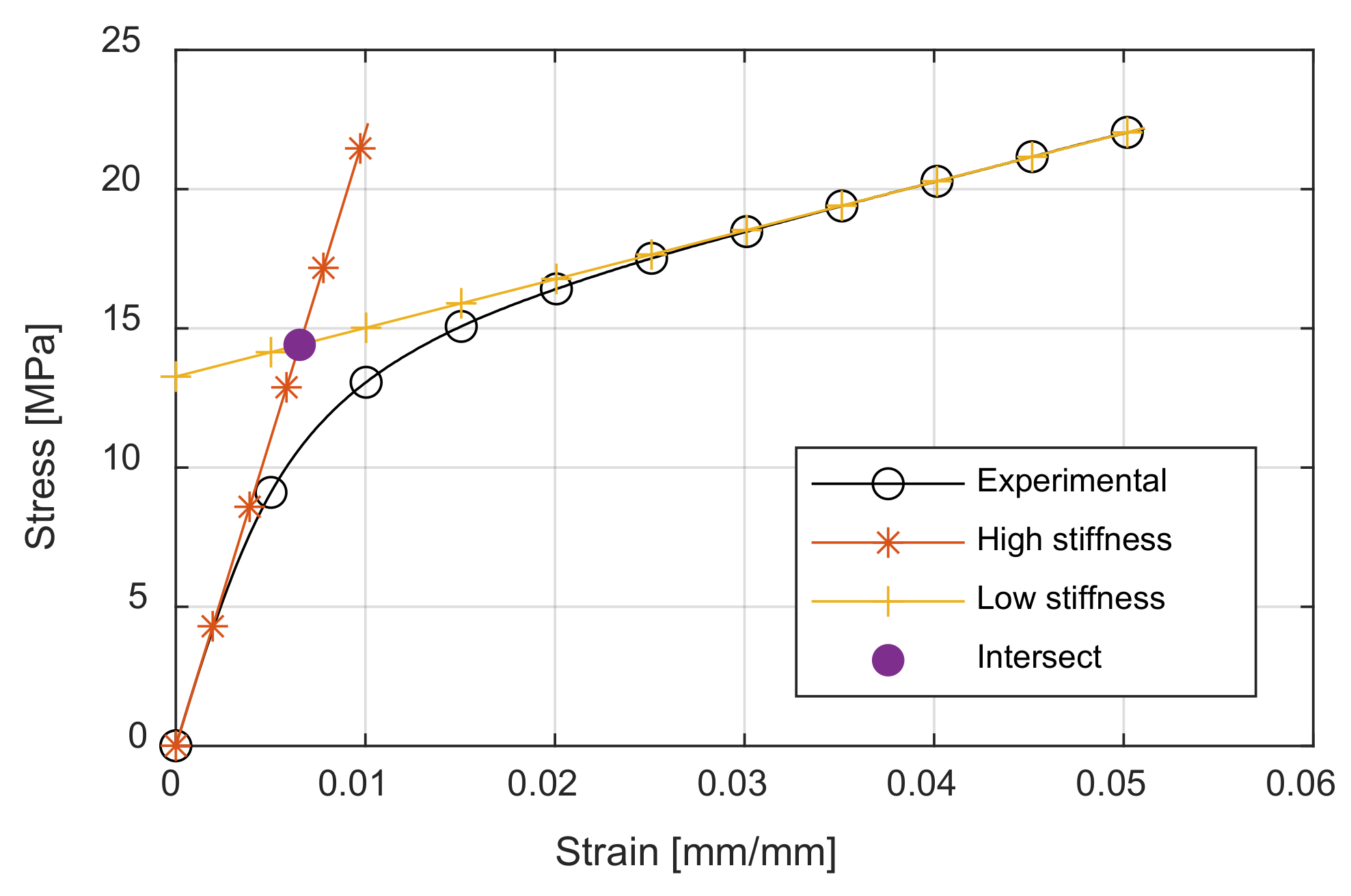
Looking at the final portion of the experimental curves in Figure 12 and Figure 13, a decrease in stiffness is seen that is not captured in the FEA results. A decrease in stiffness is also seen in tensile tests performed on individual paper sheets—see Figure 14 [11]. The behaviour of the individual paper sheets (tested by [11]) is approximately bi-linear (Figure 14); thus, the use of a bi-linear material model [27] with Hill’s yield criterion was investigated.

Since a nonlinear material model was not considered by [11], whose data for individual sheets were used, all the required test data were not available, and some assumptions had to be made to implement Hill’s criterion. Hill’s yield criterion is not the most appropriate as it does not account for paper’s different strengths in tension and compression; however, other authors have used Hill’s criterion [28,29]. More applicable yield criteria have been investigated [30], but would require even more assumptions to implement. The bi-linear material model thus serves as a feasibility study rather than a means of drawing clear conclusions.

Hill’s criterion would typically be determined using test data from the directions 0°, 45° and 90° relative to the “rolling” direction. The yield function, as proposed in 1948 (referred to as Hill-48), for plane stress is given as [31]:

$$2f\left(\sigma \right)=\left(G+H\right){\sigma }_x^2+\left(F+H\right){\sigma }_y^2-2H{\sigma }_x{\sigma }_y+2N{\tau }_{xy}^2=1,$$

(7)

where F, G, H and N describe the anisotropy and may be determined in two ways. One is with R-values (or Lankford coefficients, defined as the strain ratio of the testing direction and thickness direction) along the 0°, 90° and 45° directions:

$$\frac{H}{G}=R_0,\hspace{1em}\frac{F}{G}=\frac{R_0}{R_{90}},\hspace{1em}\frac{N}{G}=\left(R_{45}+\frac{1}{2}\right)\left(\frac{R_0}{R_{90}}+1\right).$$

(8)

The other is by using yield stresses along the 0°, 90° and 45° directions, and either R₀ or R₉₀. For R₀, the parameters may be given as:

$$H=\frac{R_0}{\left(1+R_0\right){\sigma }_0^2},\hspace{1em}G=\frac{H}{R_0},\hspace{1em}F=\frac{1}{{\sigma }_{90}^2}, N=\frac{2}{{\sigma }_{45}^2}-\frac{\left(G+F\right)}{2}.$$

(9)

However, the implementation in MSC Marc is slightly different [24]. The anisotropy parameters are defined in terms of yield ratios, and these yield ratios are the input parameters, defined as:

$$YRDIR\left(1\right)=\frac{{\sigma }_0}{{\sigma }_{av}}, YRDIR\left(2\right)=\frac{{\sigma }_{90}}{{\sigma }_{av}}, YRDIR\left(3\right)=\frac{{\sigma }_N}{{\sigma }_{av}},$$

(10)

$$YRSHR\left(1\right)=YRDIR\left(3\right)\sqrt{\frac{3}{2R_{45}+1}},\hspace{1em}YRSHR\left(2\right)=YRSHR\left(3\right)=1$$

(11)

where σ_N is the yield stress in the thickness direction and σ_av is the initial yield stress:

$${\sigma }_N={\sigma }_0\sqrt{\frac{R_{90}\left(1+R_0\right)}{R_0+R_{90}}}={\sigma }_{90}\sqrt{\frac{R_0\left(1+R_{90}\right)}{R_0+R_{90}}},$$

(12)

$${\sigma }_{av}=\frac{{\sigma }_0+2{\sigma }_{45}+{\sigma }_{90}}{4}.$$

(13)

Since the R-values and σ₄₅ were unknown, some assumptions had to be made. It was assumed that σ₄₅ was equal to σ₉₀, and the strain at σ₄₅ was equal to the strain at σ₀, based on the failure trends seen in [32]. It was also assumed that the R-values were large, since the strain in the thickness direction was assumed small compared to the in-plane directions, i.e., plane stress [16].

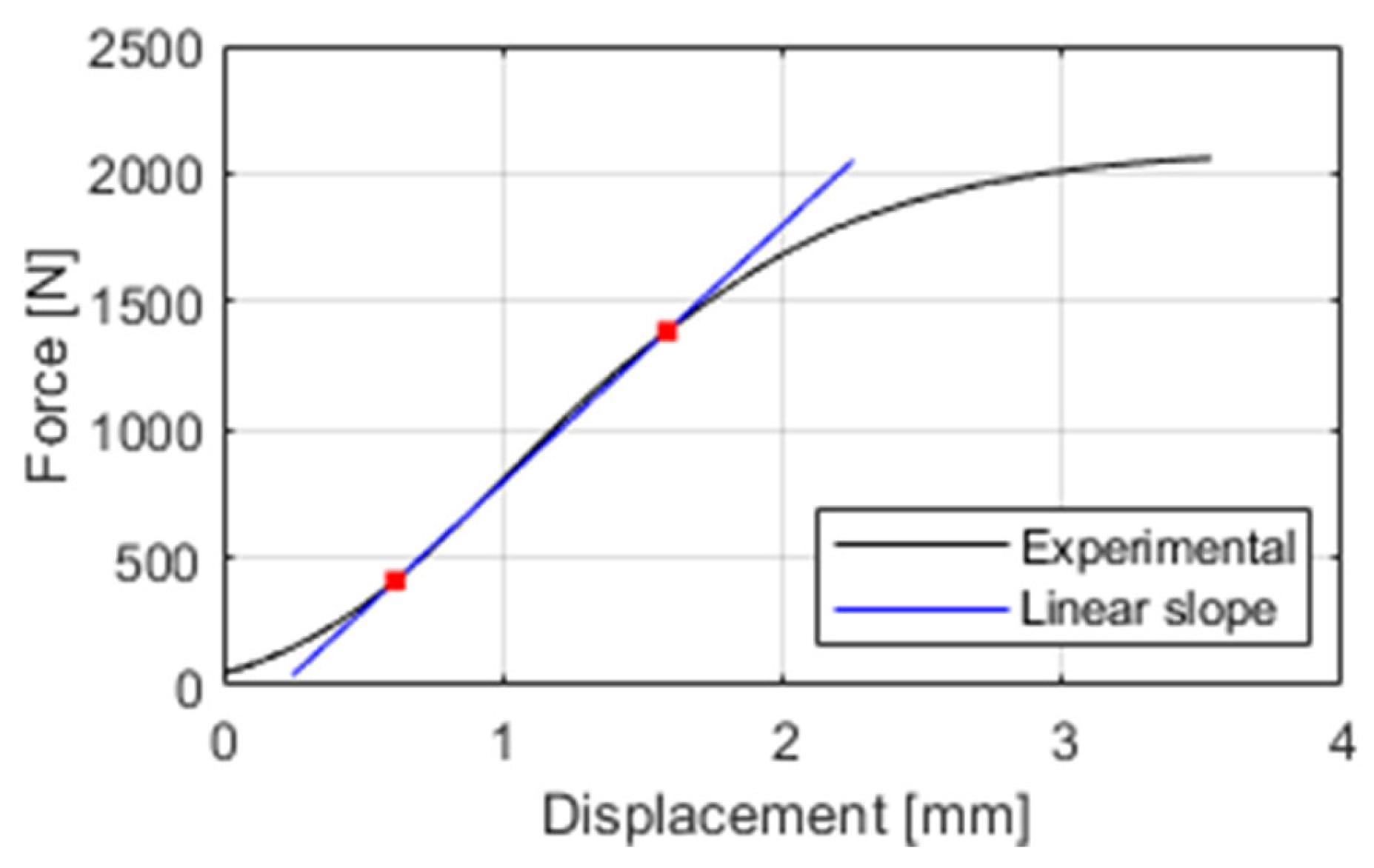
Thus, the σ_N was large, and finally, since R and σ_N were large, YRSHR (1) was approximated as 1. σ₀ and σ₉₀ were estimated from Figure 14 by fitting a linear slope to the high- and low-stiffness regions (see Figure 15) and taking the intersect as the yield strength (

Table 9. Paper yield strengths.

Paper Type	σ0 (MPa)	σ45 (MPa)	σ90 (MPa)	σavg (MPa)
150C-SC	26.11	18.87	18.87	20.68
250KL	32.65	14.02	14.02	18.68

).

The bi-linear model was only considered for the detailed model. The bending adjusted material properties were used and the yield criterion was defined using the values in Table 9. Since paper is stronger in tension than compression and the yield criterion was based on tensile data, it was expected that material failure, as defined by the Tsai-Wu failure criterion, may occur before plastic deformation (yielding). Thus, the Tsai-Wu failure criterion was not activated for the bi-linear model. A non-linear static structural analysis with large strain enabled, followed by a transient (dynamic with implicit time integration) analysis, was performed.

The load–displacement curves are shown in Figure 16. Plastic deformation started at a much larger load than the experimental failure load, as expected, but the decrease in stiffness seen in both the in-plane and out-of-plane response was similar to what was seen in the final portion of the experimental curves. To investigate how the panel would respond to a lower yield criterion, the values in Table 9 were reduced by 30%. A 40% reduction in tensile yield values was used by [28] to model ECT behaviour based on values reported in the literature, but since this section is only a feasibility study, 30% was deemed acceptable. The overall response was similar to the original bi-linear curves, but the sample yielded at a smaller load—Figure 16 (bi-linear 70% curve). This shows that including bi-linear behaviour can improve the FEA results. Paper testing with the intention of using a bi-linear model should provide the necessary data for more accurate material parameters, and thus even better results.

Determining the buckling and failure loads of the panel with FEA has been discussed above. Further, experimentally, the failure load is obvious, but the buckling load is less obvious, and will thus not be included in the following discussion (experimentally, there is no clear buckling event, as seen in the FEA results—see Figure 12 and Figure 13).

Table 10. Comparison of the 400 mm × 400 mm (415 mm × 400 mm in brackets) panel behaviour for experimental, theoretical and FEA values.

Method	Buckling Load (N)	Failure Load (N)	In-Plane Displacement (Failure) (mm)	Out-of-Plane Displacement (Failure) (mm)
Experimental	N\A	2071	3.5 (CH), 1.6 (DIC)	13.9
Theoretical	1351 (1281)	1742 (1769)	N\A	N\A
Error	N\A	15.9% (14.6%)	N\A	N\A
FEA detail	1310	2209	1.25	11.45
Error	3.0% (2.3%)	6.7%	64.6% (CH), 21.9% (DIC)	17.6%
FEA homogeneous (0.001 mm)	1352	2220	1.31	11.60
Error	0.1% (5.5%)	7.2%	62.9% (CH), 18.1% (DIC)	16.5%

compares the panel behaviour based on experimental, theoretical and FEA results. The buckling load, failure load and in- and out-of-plane displacements at failure are considered. For the theoretical values, two sample sizes were used, 400 mm × 400 mm and 415 mm × 400 mm. The 400 mm × 400 mm sample represents the ideal geometry and box dimensions. The 415 mm × 400 mm sample represents the overall dimensions of the physical samples, even though only 400 mm of the horizontal edges was loaded, and the vertical supports were 400 mm wide. Values relating to the 415 mm × 400 mm sample size are bracketed (see Table 10). Error-values compare experimental values to the relevant method, except for the buckling load, where the error values are related to the theoretical buckling load. Note as well that, for the in-plane displacement, two values are given, i.e., crosshead (CH) and DIC displacement.

The FEA buckling loads corresponded well with the theoretical buckling load for both sample sizes, within 5.5%. The theoretical failure load does not correspond well with the experimental value, and is about 15% smaller. This deviation is not outside the margins seen in the literature [4,33], but it is towards the limits. The FEA failure load corresponded well to the experimental values, and was about 7% larger. A closer correlation to the experimental values (3%) was reported by [11], but 7% is not uncommon [19,34].

The FEA out-of-plane displacement was about 17% less than the experimental values, which is in line with the 18% reported by [11]. The FEA in-plane deformation is about 63% less than the experimental (CH) value. Even though this is not very accurate, it is a much better correlation than is typically seen for FEA results of BCT [9,11], and the in-plane deformation may in some cases not even be reported [1,34]. However, the FEA results are only about 20% less when looking at the DIC displacement. Further, the FEA and DIC curves (see Figure 12) only differ largely in the final portion of the curve (which may be caused by yielding). Thus, the FEA is less inaccurate than expected when looking at the DIC displacement. Looking purely at crosshead displacement should be carefully considered when complexities such as settling and imperfect panels are not considered in the FEA model.

3.5. Box Compression Test

The in-plane load–deformation curve (Figure 17) shows that the tests were repeatable with consistent results. The initial response of the curve showed a relatively low stiffness up to a displacement of about 7 mm, after which the stiffness significantly increased, up to the failure displacement of about 13 mm [11,13]. A DIC displacement curve was extracted using the procedure described previously. Again, the displacement extracted from the DIC data was significantly smaller than the crosshead displacement, at 95% less (a similar observation was made by [13]). The stiffness for this curve was also much larger (11,054 N/mm) than seen with the crosshead (CH) displacement (163 N/mm and 865 N/mm for the low- and high-stiffness regions respectively,

Table 11. BCT test data.

BCT (N)	Y (mm)	W (mm)	Stiffness, High (N/mm)	Stiffness, Low (N/mm)
5267 ± 464	13.1 ± 0.6 (CH) 0.7 ± 0.1 (DIC)	11.3 ± 1.6	865.4 (CH) 11,054 (DIC)	163.0 (CH)

), and about three times larger than seen for a single panel using the DIC displacement (3620 N/mm). However, this should be expected, as a box has a perimeter equal to four panels (stiffnesses in parallel).

Considering the CH displacement curve, the box’s lower initial stiffness, up to approximately 7 mm, could be attributed to the differences in the panel and the box, namely, creases, flaps and possibly different boundary conditions during testing [12,13]. Note that the panel compression also had a lower initial stiffness, Figure 4. However, this was only for the first 0.5 mm of displacement, and could be attributed to the compression and settling of the panel in the clamped region.

A BCT model by [11] predicted a vertical displacement of almost 1 mm before failure, while the physical box displaced 7 mm (CH). In this study, a panel compression model predicted a vertical displacement of 1.25 mm, while the physical panel displaced 3.5 mm (CH) and a comparable box displaced 13 mm (CH). The DIC displacements for these were, however, 1.6 mm and 0.7 mm, respectively. Thus, the pure in-plane compression from the DIC results is similar to the FEA results.

The out-of-plane load-displacement curves are shown in Figure 18 (only nine curves shown as the DIC data for test 1 were lost). The first five samples tested (only four shown, test 2 to test 5) had top-flap panels facing the DIC camera, while the latter five had bottom flaps facing the DIC camera. From Figure 18, bottom-flap boxes initially bowed out a lot faster and then stiffened up, while the top-flap boxes behaved initially stiffer and then started to bow out more at about half of the maximum load. This can likely be attributed to the unsealed flaps. As pressure was applied to the top flaps, the bottom flaps sank into the open box. The movement of the bottom flaps could cause the panels to bow out. Note that the load displacement path of test 2 is significantly different from the other tests. Test 2 failed with a full wave in the CD, instead of a half wave as expected, see Figure 20b. This was likely due to an initial imperfection caused by the spray paint, and therefore this test was excluded from the results in Table 11.

Comparing the load versus out-of-plane displacement curves of the boxes (Figure 18) to that of the panels (Figure 8), the panel curves match the top-flap boxes much better than the bottom-flap boxes. This may be due to top-flap panels carrying more load than bottom-flap panels. Top-flap panels were found to carry about 20% more load than bottom-flap panels [35]. This is another complexity within boxes that is typically not modelled. The effect of sealed versus unsealed flaps could also contribute to the different displacement paths.

The BCT strength (Table 11) measured for the box was considerably lower than the combined strength of four panels, 5267 N versus 8284 N, with a difference of 36%. However, the vertical displacement of the box was significantly larger than that of a single panel, 13.1 mm versus 3.5 mm, i.e., a factor of 3.7. The out-of-place displacement was about 18% less for boxes than single panels (11.3 mm versus 13.9 mm).

The failure pattern observed in the boxes followed the typical pattern expected [9,26]. Creases formed in the corners and propagated towards the centre of the panel at an angle of about 45°—see Figure 19. The typical out-of-plane displacement pattern just before failure is shown in Figure 20a.

Comparing the out-of-plane behaviour of a box (Figure 20a) to a panel (Figure 9b), one can see that a panel had a more uniform displacement pattern, roughly in the shape of a square with rounded edges with increasing displacement towards the centre. The box, on the other hand, formed more of an upright rectangle. This shape was also reported by [9]. This difference was likely due to the presence of vertical and horizontal creases. The vertical supports remained at the same location during panel compression tests, which allowed lateral movement within the supports. For a box, the “vertical support” is the corner regions that are connected to other panels, thus each panel affects those next to it.

Table 12. Comparison of analytical and experimental BCT strength.

Method	BCT Load (N)	Error (%)
Experimental	5 267	N\A
McKee long	5 321	1.0
McKee short	5 632	6.9

compares the experimental BCT strength with values from the McKee formulas. The long form corresponded well with the experimental value. Given that McKee, in deriving his formula, assumed the exact same type of box as used here (RSC box with square panels and without any ventilation or hand holes), this was expected. The short form did not correspond that well, but fell within the range of accuracy stated by [4].

4. Conclusions

The detailed FE model of a 400 mm square panel compressed in the CD showed a good correlation with the experimental failure load, but was 7% larger. At the point of failure, the out-of-plane displacement was under-predicted by 17% and the in-plane displacement was under-predicted by 65% compared to the CH (crosshead). However, DIC (digital image correlation) data were also used to extract the in-plane displacement to eliminate any unknown factors, such as settling of the panel and misalignment in the clamped area. This resulted in a 54% smaller displacement being recorded, which meant that the FEA error was only 20%. Thus, care should be taken when comparing FEA results to CH displacement when local effects are not accounted for.

The homogenised panel compression model provided similar results but required an initial imperfection, in the shape of the first buckling mode, to induce buckling. The effect of the initial imperfection was investigated by varying the size of the imperfection. A larger imperfection led to a decrease in failure load and out-of-plane displacement, while the in-plane displacement increased. This behaviour was observed for both the detailed and the homogenised models. A 4 mm imperfection was found to improve the out-of-plane load-displacement path, suggesting that the panel had a similar imperfection at the start of the test, possibly due to the spray paint that was applied for DIC purposes. When looking at the in-plane response, the models with small or no imperfections corresponded better with the DIC displacement, while the 4 mm imperfection matched the stiffness in the linear portion of the CH curve quite well.

Box compression tests showed that four panels combined carried 57% more load than a single box. This could be largely attributed to the box’s flaps. The boxes were tested with top-flap panels and bottom-flap panels facing a DIC set-up, and the load versus out-of-plane displacement curves were very different. Bottom-flap panels bowed out initially before stiffening up, while top-flap panels were initially very stiff. The initial bowing of the bottom flap panels could be due to the rotation of the flaps. The top-flap panels and panel compression tests had similar load–displacement paths, which might be due to top-flap panels carrying more load. The decrease in stiffness seen at the end of panel compression tests was not seen with the BCT. Since the boxes carried less load than four panels combined, it could indicate that the boxes failed due to global buckling before the onset of local failure. When comparing the CH and DIC in-plane displacement, it was seen that the DIC displacement was 95% less than the CH displacement. This suggests that only 5% of the CH displacement was due to pure in-plane compression, while 95% could be contributed to settling, flaps, creases and any other form of localised crushing.

The results showed that the FE-predicted in-plane displacement was more accurate than that of a complete box. On the other hand, the accuracies of the predicted failure load and out-of-plane displacement were similar for the panel and a box. The FEA correlated even better when DIC was used to measure in-plane displacement instead of relying on the crosshead displacement. Thus, to improve the in-plane displacement for boxes (and panels) modelled by FEA, the creases, flaps and any other imperfections must be included in the model. Furthermore, a non-linear material model may improve the in-plane displacement predictions for individual panels, but may be redundant for boxes due to the lower load carried by boxes. Investigating tubes first may also be beneficial, as the effects of the flaps and creases will be eliminated.