Abstract
The impacts of Stefan blowing along with slip and Joule heating on hybrid nanofluid (HNF) flow past a shrinking cylinder are investigated in the presence of thermal radiation. Using the suitable transformations, the governing equations are converted into ODEs, and the MATLAB tool bvp4c is used to solve the resulting equations. As Stefan blowing increases, temperature and concentration profiles are accelerated but the velocity profile diminishes and also the heat transfer rate improves up to 25% as thermal radiation upsurges. The mass transfer rate diminishes as increasing Stefan blowing. The Sherwood number, the Nusselt number, and the skin friction coefficient are numerically tabulated and graphs are also plotted. The outcomes are conscientiously and thoroughly discussed.
1. Introduction
Most scientists, engineers, and researchers are very much interested in the boundary layer flow, heat, and mass transfer towards a stretching/shrinking cylinder because of the numerous applications which include the extraction of metals, annealing, extrusion process, pipe industry, copper wire thinning, etc. Nanofluid comes into existence when we add a little amount of nano-sized particles into base fluids. The term nanofluid was first instituted by Choi and Eastman [1], to enhance the heat transfer rate. Furthermore, studies have shown that a significant increment in the heat transfer rate of nanofluid is attained when two different nanoparticles (HNF) are used. The earlier experimental works utilized hybrid nanoparticles that were considered by Turcu et al. [2] and Jana et al. [3]. They stated that, although Al2O3 has low thermal conductivity, there is a good chemical inertness in alumina that could maintain the stability of HNF. Additionally, Takabi et al. [4] researched HNF flow containing Al2O3-Cu nanoparticles in a sinusoidal corrugated enclosure.
Early on, Crane [5] emphasized flow towards a stretching plat. Waini et al. [6] inspected HNF flow past a stretching (shrinking) cylinder and concluded that the inclusion of nanoparticles heat transfer rate improved. Wang [7] researched stagnation flow past a shrinking sheet. Waini et al. [8] researched HNF flow past a shrinking cylinder with surface heat flux. Similar research was carried out by Awaludin et al. [9]. Work on viscid flow due to shrinking cylinders with non-uniform radius was conducted by Ali et al. [10]. Jagan et al. [11] investigated thermal radiative Jeffrey nano liquid flow past a stretching cylinder. Natural convection in a linearly heated vertical porous annulus was examined by Sankar et al. [12]. Heat transfer and HNF flow towards stretching/shrinking horizontal cylinder work carried out by Rashid et al. [13]. Girish et al. [14] Developed buoyant convection in vertical porous annuli with unheated entry and exit.
After claiming the improved thermal upshot of nanoparticles, this contribution reflects the thermal enhancement of graphene oxide (GO) and molybdenum disulphide (MoS2) nanoparticles over a vertically moving plate with help of a fractional approach. Chu et al. [15] examined MHD mixed convection in HNF flow over a cylinder with shape factor and scrutinized that the blade-shaped nanoparticles have a maximum temperature and brick-shaped nanoparticles have a low temperature. Khan et al. [16] researched stagnation point flow impinging on a radially permeable moving rotating disk with Go-MoS2 nanoparticles.
According to theory, Joule heating is the development of heat as a result of resistive loss during the change in electric to thermal state. This method is mainly used in cartridge heaters, MHD (magnetohydrodynamics) thrusters, electrical and electronic devices, and so on. Wahid et al. [17] researched by using Joule heating flow towards a shrinking sheet. Alarabi et al. [18] researched HNF flow towards a shrinking (stretching) cylinder with joule heating. Khashi et al. [19] examined HNF flow toward a shrinking cylinder with Joule heating. To direct the MHD flow toward a stretched cylinder, Jagan et al. [20] considered velocity slip.
A careful review of the literature disclosed that the thermal radiation effect tangled in various engineering processes including thermal engineering storage, nuclear turbines, spectroscopy, and so on. Yashkun et al. [21] observed the HNF flow towards a shrinking /stretching sheet with thermal radiative. Pal et al. [22] investigated radiative heat and mass transfer of nanofluid flow over a stretching/shrinking sheet. Waini et al. [23] inspected thermal radiative flow toward a shrinking cylinder by using two different nanoparticles. Numerical simulations of HNF flow towards a shrinking cylinder with the effect of thermal radiative were inspected by Aladdin et al. [24]. Eswaramoorthi et al. [25] researched thermal radiative bioconvective nanofluid in a stratified medium by using gyrostatic microorganisms.
Stefan blowing effect relates the velocity and species (concentration) field. A blowing effect develops on an impervious surface. Uddin et al. [26] evaluated the numerical outcomes for nano liquid flow with Stefan blowing. Casson fluid moving toward a shrinking sheet with effects of Stefan blowing and velocity slip analyzed by Lund et al. [27]. Cattaneo-Christov model on nanofluid flow with Stefan blowing analyzed by Ali et al. [28]. Rana et al. [29] examined HNF flow towards a stretched cylinder with MHD and Stefan blowing effects.
The current work examines the effects of previously unstudied phenomena on HNF flow, including Stefan blowing, thermal radiation, Joule heating, and velocity slip. By examining heat and mass transmission while stagnation point, thermal radiation, Stefan blowing, and joule heating effects are present, this current work shows its novelty. The main study is in industrial systems such as drying and purifying processes. The pertinent physical quantities for various parameters are also shown via tables and graphs.
2. Mathematical Formulation
The HNF flow over a shrinking cylinder with radius a = 1 as shown in Figure 1. Here, the surface and free stream velocity are respectively and , where c1 and c2 are constants and L is the characteristic length. is the magnetic field applied in the opposite flow direction and the radiative heat flux is defined as . The impacts of Stefan blowing, stagnation point, thermal radiative, Joule heating, and velocity slip are contemplated. The following assumptions are taken

Figure 1.
Physical model.
- The flow is steady, laminar, and 2D-dimensional.
- The flow is incompressible.
- The cylinder is shrinking with uniform velocity along the x-direction.
The equations that govern the HNF flow are described (refer to Waini et al. [6,23]):
Continuity Equation
Momentum Equation
Temperature Equation
Concentration Equation
associated boundary conditions are (refer to Waini et al. [6] Rana et al. [29]):
where u and v are the corresponding x- and r-axis velocity components and T denotes fluid temperature. In addition, Table 1 presents the physical properties of base fluid (H2O) and nanoparticles, while Table 2 provides the physical relations of the HNF. Here, the nanoparticle volume fraction of Graphene oxide (Go) and Molybdenum disulfide (MoS2) are symbolized by and respectively as follows

Table 1.
The thermophysical properties. (refer to Waini et al. [6] and Raza et al. [30]).

Table 2.
Correlations of HNF (referring to Waini et al. [6,23]).
Similarity transformation (referring to Awaludin et al. [9]) are introduced:
By using similarity transformation (7), one obtains:
subjected to:
where Stefan blowing parameter, local Reynolds number, velocity slip, magnetic parameter, Eckert number, thermal radiation, Prandtl number, Schmidt number, curvature parameter, , , , and .
The physical quantities are
with the skin friction coefficient Cf, Nusselt number Nu and Sherwood number Sh (referring to Waini et al. [23]).
Inserting (7) and (13) into Equation (12), one obtains.
3. Numerical Method
Equations (8) to (11) are numerically solved using the boundary value problem solver MATLAB (bvp4c) package which is a finite difference code that implements the 3-stage Lobatto IIIa formula as explained by Waini et al. [6].
Equation (8) is translated into:
Equation (9) converts:
Equation (10) is written as:
with the boundary conditions:
The bvp4c MATLAB package is then used to solve Equations (15)–(22), yielding the required solutions.
4. Results and Discussion
In this present study, flow behavior is examined for various parameters by taking = = 0.02. In Table 3, the current findings were compared with Wang [7] and Waini et al. [8] and are consistent with the literature stated above. Table 4 provides the numerical results for skin friction, the Nusselt number, and the Sherwood number by fixing = 0.02 and Pr = 6.2.

Table 3.
Comparison results where Sb = λ = M = Ec = Rd = Sc = K = 0 and when Pr = 6.2.

Table 4.
Numerical results of Cf, Nu, and Sh when = 0.02 and Pr = 6.2.
From Figure 2a, rising Stefan blowing decreases the velocity profile. Infer that an upsurge in Stefan blowing from the surface to free stream which slows down the speed of HNF as it moves towards the surface due to mass diffusion. With the upsurge of Stefan blowing, the temperature and concentration profiles accelerated and are blown further away from the surface to ambient temperature and ambient concentration. Physically, species diffusion is energized by the inclusion of nanoparticles (tiny particles) in base fluid (water). In turn, the temperature and concentration profiles increase (see Figure 2b,c).
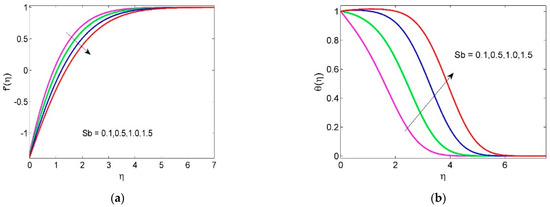

Figure 2.
Impacts of Sb on , and .
Figure 3a demonstrates that by rising values of the curvature parameter (λ), the velocity profile intensifies slightly. The radius of the cylinder is inversely proportional to the curvature parameter by definition, a rise in the λ implies a decrease in the cylinder radius. The profile of temperature declines due to increasing λ. As the increase in λ, the flatness of the shrinking surface rises, consequently, the flow velocity accelerates, and the profile of temperature decreases because the resistance between the fluid layer reduces (see Figure 3b).

Figure 3.
Impacts of λ on and .
According to Figure 4a, the profile of velocity is enhanced with larger values of M because the magnetic property has a substantial effect on nanoparticles interaction with the electromagnetic field. Additionally, nanoparticles respond strongly to the magnetic field since they are in sync with the electromagnetic field. Since the magnetic field assists the fluid flow, it drives the nanoparticles toward the cylinder surface. This lively process reduces the temperature as well as the concentration field (see Figure 4b,c).
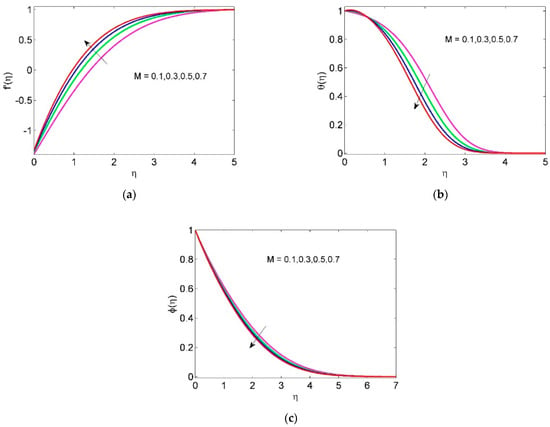
Figure 4.
Impacts of M on , and .
Figure 5a observed that as thermal radiation Rd rises, the temperature profile initially declines, but after moving far from the surface, the temperature profile exhibits the opposite trend. Because thermal radiation more is dominant than thermal conduction. The temperature profile rises due to an increase in Eckert number as depicted in Figure 5b. Physically, an increase in Ec converts kinetic energy into internal energy by work that is conducted against viscous fluid stress, which rises the temperature field.

Figure 5.
Impacts of Rd and Ec on .
Figure 6a shows that the rising slip parameter increases the velocity profile. Moreover, a rise in the velocity slip allows fluid to slip over the cylinder surface, which consequently speeds up fluid flow at the boundary. Figure 6b, demonstrates the temperature profile decreases as the slip parameter upsurges, which reduces the thickness of the thermal boundary layer.

Figure 6.
Impacts of A on and .
Figure 7a witnessed that by raising the nanoparticle volume fraction of up to 2%, the velocity profile diminishes. In general, an increase in the nanoparticle volume fraction causes resistance in the fluid flow, which slows down the velocity field. The temperature profile upsurges as increasing up to 2% (see Figure 7b). In turn, this is due to the thermal conductivity of HNF elevates, and as a consequence fluid temperature rises.

Figure 7.
Impacts of on and .
Figure 8a,b, display the increasing nanoparticle volume fraction of and up to 2% versus Stefan blowing and shrinking state, the skin friction coefficient upsurges. In general, nanoparticle volume fractions produce less resistance at the cylinder surface due to the random motion of HNF/nanoparticles.

Figure 8.
Impacts of and against ε and Sb on Cf.
Heat transfer rate increases against shrinking parameter and Stefan blowing when a rise in the nanoparticle volume fraction of and up to 2% as compared to regular fluid ( = = 0). Physically, an upsurge in the and against shrinking parameter and Stefan blowing leads to the thermal conductivity accelerated, which causes a rise in the heat transfer rate. This is due to the synergistic effects of HNF (see Figure 9a,b).

Figure 9.
Impacts of and against ε and Sb on Nu.
Figure 10a shows Nusselt number Nu upsurges as thermal radiation increases. Physically, thermal radiation increases the thermal conductivity of the fluid, which boosts the heat transfer rate. With an increase in Stefan blowing Sb, the mass transfer rate decreases. Physically, due to intermolecular force between nanoparticles the diffusion causes from ambient concentration to surface concentration (see Figure 10b).
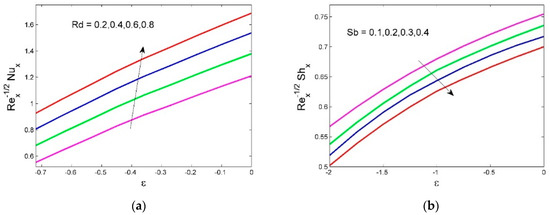
Figure 10.
Impacts of Rd against ε on Nu and Sb against ε on Sh.
5. Conclusions
The present study addressed the impacts of Stefan blowing, Joule heating, and thermal radiation on HNF flow over a shrinking cylinder has been expertise.
The following potential limitations are accomplished:
- Since water is used as the base fluid in our model, the Schmidt number is fixed.
- Surface velocity is always less than zero.
- The Prandtl number has a range from 1.7 to 13.7 which is based on the base fluid.
The consequences of the current study are recorded as follows:
- There is an augmentation in temperature as well as concentration profiles due to the presence of Stefan blowing, but the velocity profile falls.
- The magnetic and curvature parameters cause a reduction in the temperature and concentration profiles and a rise in the velocity profile.
- The temperature profile rises due to an increase in Eckert number and thermal radiation parameter.
- The velocity profile rises as the magnetic field increases but decreases the thermal and concentration boundary layer.
- The heat transfer rate is improved by the thermal radiation parameter and shrinking case when ε < 0.
- With higher Stefan blowing, heat transmission increases but the mass transfer rate decreases in the presence of 2% of nanoparticles/HNF.
Author Contributions
Conceptualization, J.K. and S.S.; methodology, J.K.; software, J.K. and M.K.N.; validation, J.K.; formal analysis, J.K., S.S. and M.K.N.; investigation, J.K. and M.K.N.; resources, J.K.; writing—original draft preparation, J.K. and M.K.N.; writing—review and editing, J.K. and M.K.N.; visualization, J.K.; supervision, J.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
In this manuscript, the following abbreviations are used.
| HNF | hybrid nanofluid |
| MHD | Magnetohydrodynamics |
Nomenclature
| u,v | velocity components along x- and r-axes (m s−1) |
| L | characteristic length (m) |
| ww | surface velocity (m s−1) |
| ue | free stream velocity (m s−1) |
| Tw | surface temperature (K) |
| Cw | surface concentration (mol m3) |
| T∞ | ambient temperature (K) |
| D | mass diffusivity (m2 s−1) |
| C∞ | ambient concentration (mol m3) |
| Cs | concentration susceptibility |
| qr | heat flux (kg m2 s3) |
| kT | thermal diffusion ratio |
| Cp | specific heat (kg−1 J) |
| k* | mean absorption coefficient (cm−1) |
| T | the temperature of the fluid (K) |
| a | cylinder radius (cm) |
| k | thermal conductivity (W m−1 K−1) |
| C | fluid concentration (mol m3) |
| Rd | thermal radiation parameter |
| B0 | strength of magnetic field (A m−1) |
| Ec | Eckert number |
| M | Magnetic parameter |
| Pr | Prandtl number |
| Sc | Schmidt number |
| Cf | skin friction coefficient |
| Sb | Stefan blowing parameter |
| A | velocity slip parameter |
| Re | local Reynolds number |
| Nu | local Nusselt number |
| Sh | local Sherwood number |
| Greek symbols | |
| ν | kinematic viscosity (m2 s−1) |
| σ | electrical conductivity (S m−1) |
| μ | dynamic viscosity (m2 s−1) |
| ρ | the density of the fluid (kg m−3) |
| ε | shrinking parameter (<0) |
| σ* | Stefan-Boltzmann constant (W m−2 K−4) |
| Subscripts | |
| ∞ | ambient |
| f | base fluid |
| nf | nanofluid |
| hnf | hybrid nanofluid |
References
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Argonne National Lab (ANL): Argonne, IL, USA, 1995.
- Turcu, R.; Darabont, A.; Nan, A.; Aldea, N.; Macovei, D.; Bica, D.; Vekas, L. New polypyrrole-multiwall carbon nanotubes hybrid materials. J. Optoelectron. Adv. Mater. 2006, 8, 643–647. [Google Scholar]
- Jana, S.; Salehi Khojin, A.; Zhong, W.H. Enhancement of fluid thermal conductivity by the addition of single and hybrid nano-additives. Thermochim. Acta 2007, 462, 45–55. [Google Scholar] [CrossRef]
- Takabi, B.; Salehi, S. Augmentation of the heat transfer performance of a sinusoidal corrugated enclosure by employing hybrid nanofluid. Adv. Mech. Eng. 2014, 6, 147059. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plate. Z. Angew. Math. Phys. ZAMP 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Hybrid nanofluid flow towards a stagnation point on a stretching/shrinking cylinder. Sci. Rep. 2020, 10, 9296. [Google Scholar] [CrossRef]
- Wang, C.Y. Stagnation Flow towards a Shrinking Sheet. Int. J. Non-Linear Mech. 2008, 43, 377–382. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Hybrid Nanofluid Flow on a Shrinking Cylinder with Prescribed Surface Heat Flux. Int. Numer. Methods Heat Fluid Flow 2020, 31, 1987–2004. [Google Scholar] [CrossRef]
- Awaludin, I.S.; Ahmad, R.; Ishak, A. On the stability of the flow over a shrinking cylinder with prescribed surface heat flux. Propuls. Power Res. 2020, 9, 181–187. [Google Scholar] [CrossRef]
- Ali, A.; Marwat, D.N.K.; Asghar, S. Viscous Flow over a Stretching (Shrinking) and Porous Cylinder of Non-Uniform Radius. Adv. Mech. Eng. 2019, 11, 168781401987984. [Google Scholar] [CrossRef]
- Jagan, K.; Sivasankaran, S.; Bhuvaneswari, M.; Rajan, S.; Makinde, O.D. Soret and Dufour effect on MHD Jeffrey nanofluid flow towards a stretching cylinder with triple stratification, radiation and slip. Defect Diffus. Forum 2018, 387, 523–533. [Google Scholar] [CrossRef]
- Sankar, M.; Kiran, S.; Sivasankaran, S. Natural Convection in a Linearly Heated Vertical Porous Annulus. J. Phys. Conf. Ser. 2018, 1139, 012018. [Google Scholar] [CrossRef]
- Rashid, U.; Liang, H.; Ahmad, H.; Abbas, M.; Iqbal, A.; Hamed, Y.S. Study of (Ag and TiO2)/Water Nanoparticles Shape Effect on Heat Transfer and Hybrid Nanofluid Flow toward Stretching Shrinking Horizontal Cylinder. Results Phys. 2021, 21, 103812. [Google Scholar] [CrossRef]
- Girish, N.; Sankar, M.; Makinde, O.D. Developing Buoyant Convection in Vertical Porous Annuli with Unheated Entry and Exit. Heat Transf. 2020, 49, 2551–2576. [Google Scholar] [CrossRef]
- Chu, Y.-M.; Nisar, K.S.; Khan, U.; Daei Kasmaei, H.; Malaver, M.; Zaib, A.; Khan, I. Mixed Convection in MHD Water-Based Molybdenum Disulfide-Graphene Oxide Hybrid Nanofluid through an Upright Cylinder with Shape Factor. Water 2020, 12, 1723. [Google Scholar] [CrossRef]
- Khan, U.; Zaib, A.; Ishak, A.; Waini, I.; Abdel-Aty, A.-H.; Sheremet, M.A.; Yahia, I.S.; Zahran, H.Y.; Galal, A.M. Agrawal Axisymmetric Rotational Stagnation-Point Flow of a Water-Based Molybdenum Disulfide-Graphene Oxide Hybrid Nanofluid and Heat Transfer Impinging on a Radially Permeable Moving Rotating Disk. Nanomaterials 2022, 12, 787. [Google Scholar] [CrossRef]
- Wahid, N.S.; Arifin, N.M.; Pop, I.; Bachok, N.; Hafidzuddin, M.E.H. MHD stagnation-point flow of nanofluid due to a shrinking sheet with melting, viscous dissipation and Joule heating effects. Alex. Eng. J. 2022, 61, 12661–12672. [Google Scholar] [CrossRef]
- Alarabi, T.H.; Rashad, A.M.; Mahdy, A. Homogeneous–Heterogeneous Chemical Reactions of Radiation Hybrid Nanofluid Flow on a Cylinder with Joule Heating: Nanoparticles Shape Impact. Coatings 2021, 11, 1490. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Waini, I.; Arifin, N.M.; Pop, I. Unsteady Squeezing Flow of Cu–Al2O3/Water Hybrid Nanofluid in a Horizontal Channel with Magnetic Field. Sci. Rep. 2021, 11, 14128. [Google Scholar] [CrossRef]
- Jagan, K.; Sivasankaran, S. Soret & Dufour and Triple Stratification Effect on MHD Flow with Velocity Slip towards a Stretching Cylinder. Math. Comput. Appl. 2022, 27, 25. [Google Scholar] [CrossRef]
- Yashkun, U.; Zaimi, K.; Abu Bakar, N.A.; Ishak, A.; Pop, I. MHD Hybrid Nanofluid Flow over a Permeable Stretching/Shrinking Sheet with Thermal Radiation Effect. Int. J. Numer. Methods Heat Fluid Flow 2020, 31, 1014–1031. [Google Scholar] [CrossRef]
- Pal, D.; Mandal, G.; Vajravalu, K. Soret and Dufour Effects on MHD Convective–Radiative Heat and Mass Transfer of Nanofluids over a Vertical Non-Linear Stretching/Shrinking Sheet. Appl. Math. Comput. 2016, 287–288, 184–200. [Google Scholar] [CrossRef]
- Waini, I.; Khan, U.; Zaib, A.; Ishak, A.; Pop, I. Inspection of TiO2-CoFe2O4 Nanoparticles on MHD Flow toward a Shrinking Cylinder with Radiative Heat Transfer. J. Mol. Liq. 2022, 361, 119615. [Google Scholar] [CrossRef]
- Aladdin, N.A.L.; Bachok, N.; Rosali, H.; Wahi, N.; Abd Rahmin, N.A.; Arifin, N.M. Numerical Computation of Hybrid Carbon Nanotubes Flow over a Stretching/Shrinking Vertical Cylinder in Presence of Thermal Radiation and Hydromagnetic. Mathematics 2022, 10, 3551. [Google Scholar] [CrossRef]
- Eswaramoorthi, S.; Jagan, K.; Sivasankaran, S. MHD Bioconvective Flow of a Thermally Radiative Nanoliquid in a Stratified Medium Considering Gyrotactic Microorganisms. J. Phys. Conf. Ser. 2020, 1597, 012001. [Google Scholar] [CrossRef]
- Uddin, M.J.; Alginahi, Y.; Bég, O.A.; Kabir, M.N. Numerical Solutions for Gyrotactic Bioconvection in Nanofluid-Saturated Porous Media with Stefan Blowing and Multiple Slip Effects. Comput. Math. Appl. 2016, 72, 2562–2581. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Raza, J.; Khan, I.; Sherif, E.-S.M. Effects of Stefan Blowing and Slip Conditions on Unsteady MHD Casson Nanofluid Flow over an Unsteady Shrinking Sheet: Dual Solutions. Symmetry 2020, 12, 487. [Google Scholar] [CrossRef]
- Ali, B.; Hussain, S.; Abdal, S.; Mehdi, M.M. Impact of Stefan Blowing on Thermal Radiation and Cattaneo–Christov Characteristics for Nanofluid Flow Containing Microorganisms with Ablation/Accretion of Leading Edge: FEM Approach. Eur. Phys. J. Plus 2020, 135, 821. [Google Scholar] [CrossRef]
- Rana, P.; Makkar, V.; Gupta, G. Finite element study of bio-convective Stefan blowing Ag-MgO/water hybrid nanofluid induced by stretching cylinder utilizing non-Fourier and non-Fick’s laws. Nanomaterials 2021, 11, 1735. [Google Scholar] [CrossRef]
- Raza, A.; Khan, S.U.; Khan, M.I.; Farid, S.; Muhammad, T.; Khan, M.I.; Galal, A.M. Fractional order simulations for the thermal determination of graphene oxide (GO) and molybdenum disulphide (MoS2) nanoparticles with slip effects. Case Stud. Therm. Eng. 2021, 28, 101453. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).