Theoretical and Computational Results of a Memory-Type Swelling Porous-Elastic System
Abstract
:1. Introduction
- We produce some numerical experiments to illustrate the energy decay results, for this purpose, we develop a second-order numerical scheme to solve the problem (4) based on finite element discretization and the Crank–Nicolson method in time that has the property to be unconditionally stable.
- The result is significant to engineers and architects as it might help to attenuate the harmful effects of swelling soils swiftly.
2. Assumptions
3. Technical Lemmas
4. The Main Result
- (1)
- Let , , are constants, and a is chosen so that is satisfied; thenThus, under the assumptions of Theorem 1, we conclude that the solution of (4) satisfies, for two constants , the energy estimate
- (2)
- For , for , , and a is chosen so that condition is satisfied, thenThus, under the assumptions of Theorem 1, we conclude that the solution of (4) satisfies, for some constant , the energy estimate
- (3)
- Consider the following relaxation function,for , and a is chosen so that hypothesis remains valid. Thenwhere b is a fixed constant, , which satisfies . Thus, under the assumptions of Theorem 1, we conclude that the solution of (4) satisfies, for some constant and , the energy estimate
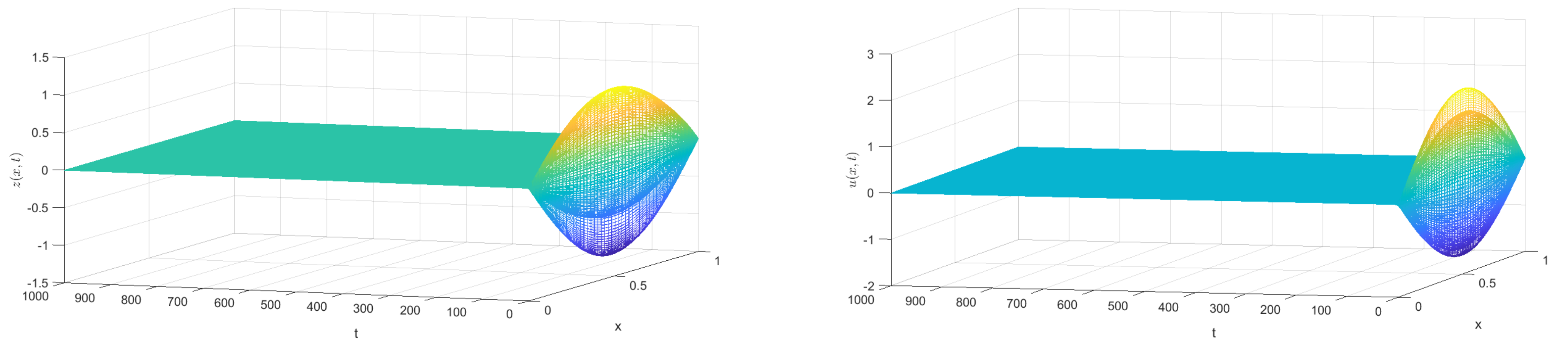
5. Numerical Tests
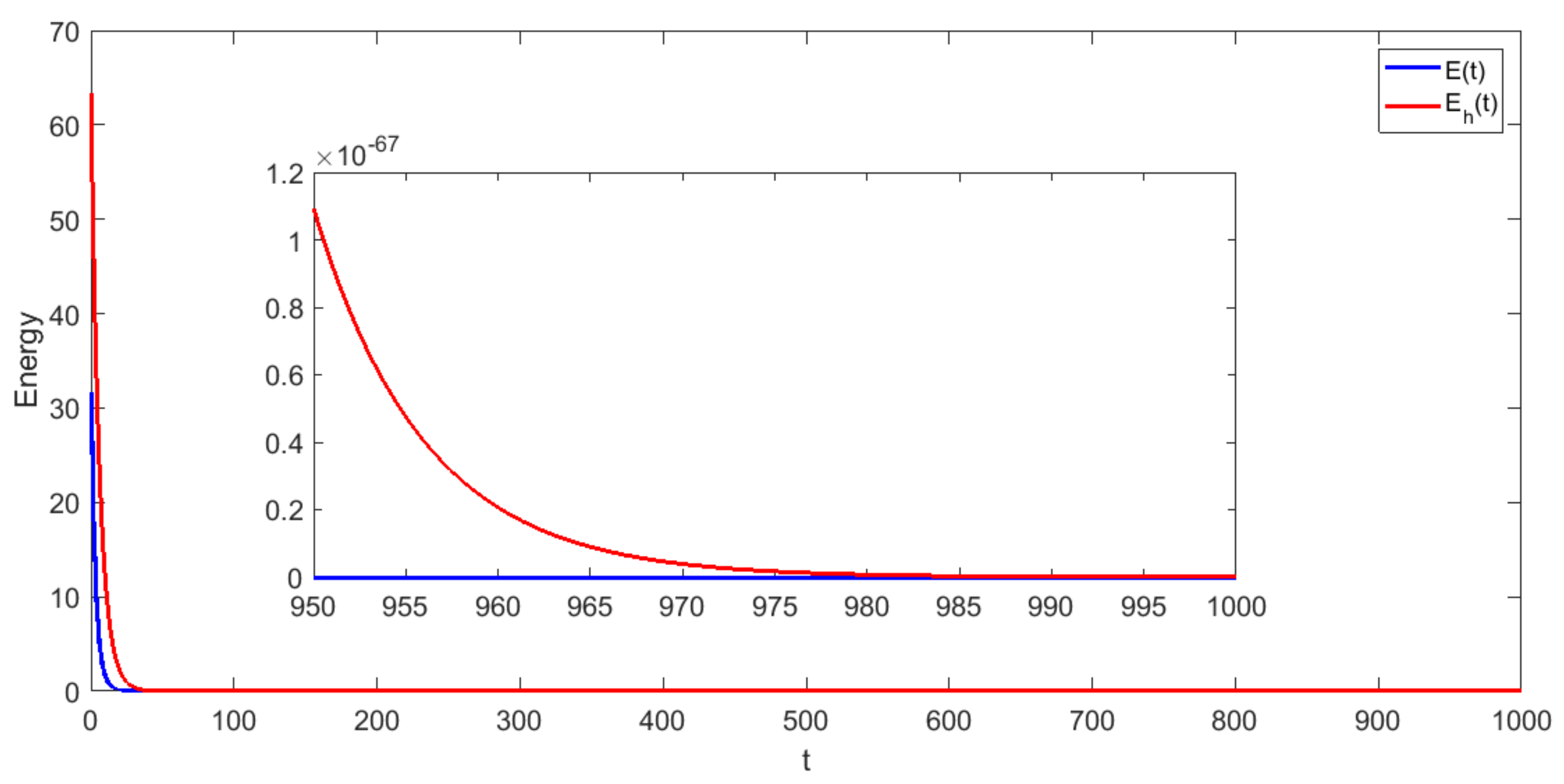
- Test 1: For the first numerical test, we choose the following entries:and the relaxation functionThus, under the assumptions of Theorem 1, the solution of (4) satisfies the energy estimatewhere C is a constant depends on the energy at .
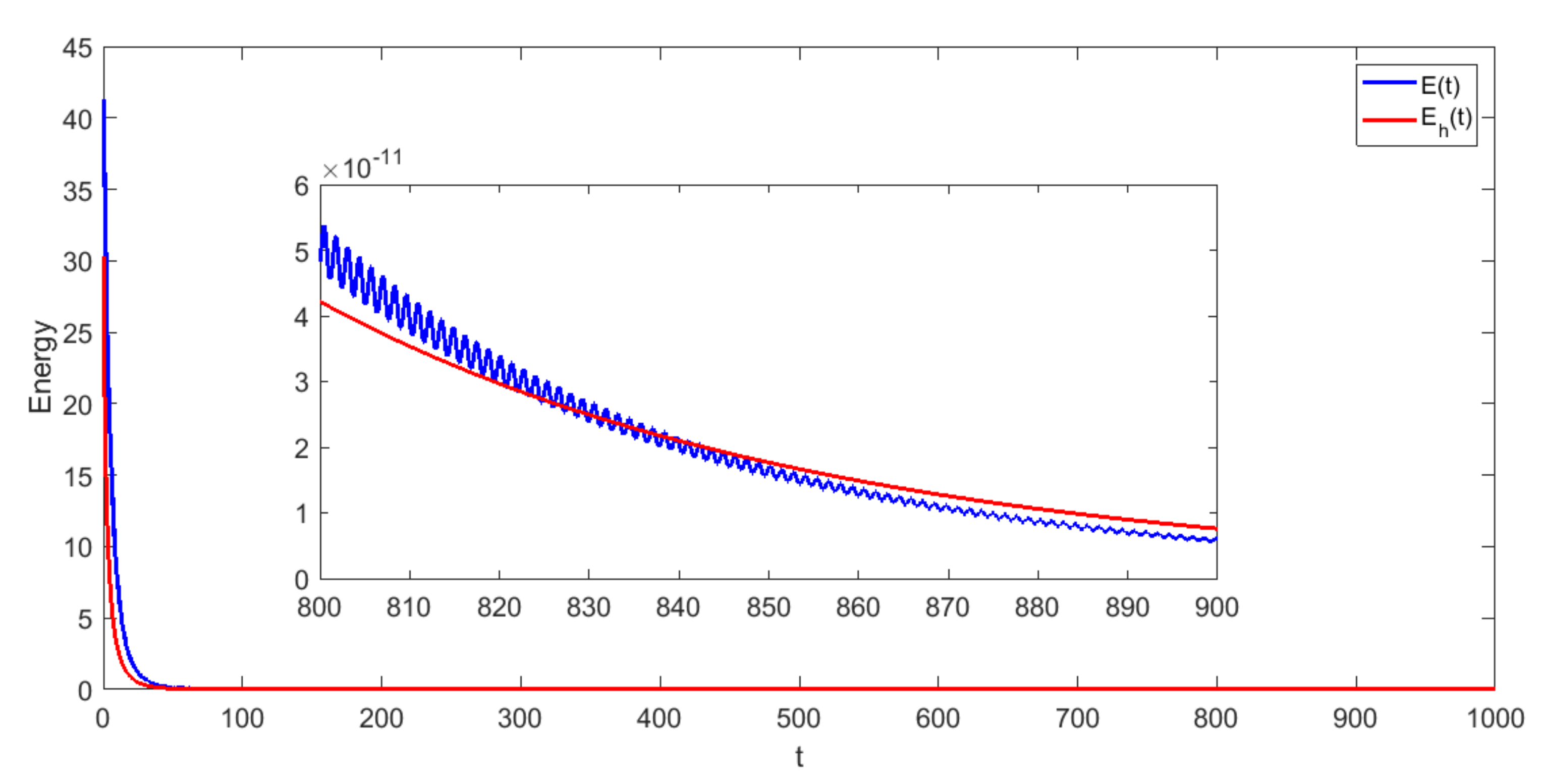
- Test 2: In the second numerical test, we consider the following entries so that condition is satisfiedand the following relaxation functionThen, under the assumptions of Theorem 1, the solution of (4) satisfies the energy estimatewhere C is a constant depends on the energy at .
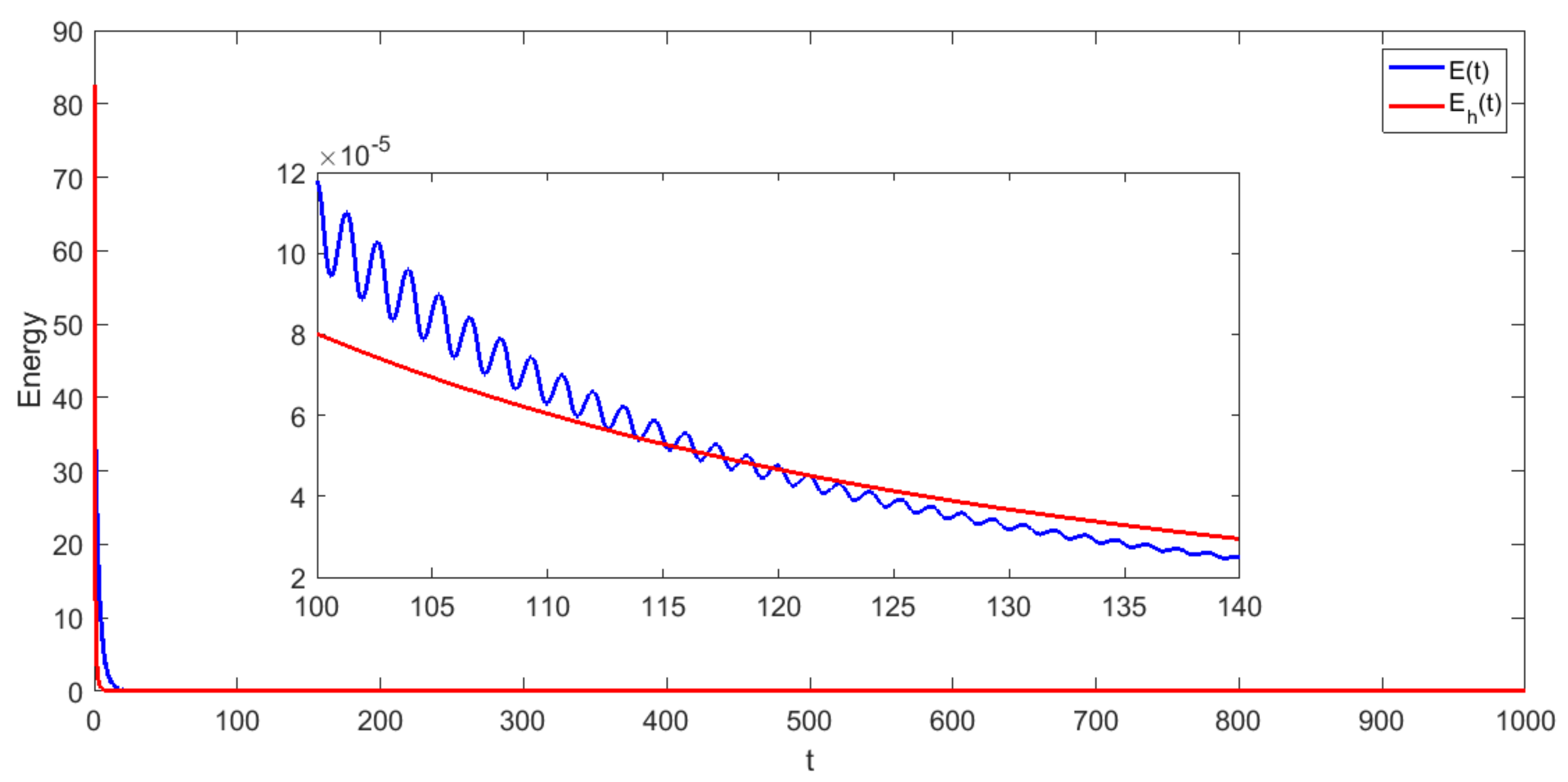
- Test 3: For last test, we consider the third case of Example 1 with the same entries of Test 1 and with an polynomial relaxation functionUnder the assumptions of Theorem 1, the solution of (4) satisfies the energy estimatewhere C is a constant depends on the energy at .
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Coduto, D.P. Geotechnical Engineering: Principles and Practices; Prentice Hall: Hoboken, NJ, USA, 1999. [Google Scholar]
- Holtz, R.D.; Kovacs, W.D.; Sheahan, T.C. An Introduction to Geotechnical Engineering; Prentice-Hall: Englewood Cliffs, NJ, USA, 1981; Volume 733. [Google Scholar]
- Kalantari, B. Construction of Foundations on Expansive Soils; University of Missouri Columbia: Columbia, MI, USA, 1991. [Google Scholar]
- Hung, V. Hidden Disaster. In University News; University of Saska Techwan: Saskatoon, SK, Canada, 2003. [Google Scholar]
- Freitas, M.M.; Ramos, A.J.; Santos, M.L. Existence and Upper-Semicontinuity of Global Attractors for Binary Mixtures Solids with Fractional Damping. Appl. Math. Optim. 2019, 83, 1353–1385. [Google Scholar] [CrossRef]
- Karalis, T. On the elastic deformation of non-saturated swelling soils. Acta Mech. 1990, 84, 19–45. [Google Scholar] [CrossRef]
- Handy, R.L. A stress path model for collapsible loess. In Genesis and Properties of Collapsible Soils; Springer: Berlin/Heidelberg, Germany, 1995; pp. 33–47. [Google Scholar]
- Leonard, R. Expansive Soils Shallow Foundation; Regent Centre, University of Kansas: Lawrence, KS, USA, 1989. [Google Scholar]
- Jones, L.D.; Jefferson, I. Expansive Soils. In ICE Manual of Geotechnical Engineering Vol 1: Geotechnical Engineering Principles, Problematic Soils and Site Investigation (ICE Manuals); ICE Publishing: London, UK, 2012; pp. 413–441. [Google Scholar]
- Bowles, J.E. Foundation Design and Analysis; McGraw-Hill: New York, NY, USA, 1982. [Google Scholar]
- Kalantari, B. Engineering significant of swelling soils. Res. J. Appl. Sci. Eng. Technol. 2012, 4, 2874–2878. [Google Scholar]
- Krauklis, A.E.; Gagani, A.I.; Echtermeyer, A.T. Prediction of orthotropic hygroscopic swelling of fiber-reinforced composites from isotropic swelling of matrix polymer. J. Compos. Sci. 2019, 3, 10. [Google Scholar] [CrossRef] [Green Version]
- Sinchuk, Y.; Pannier, Y.; Gueguen, M.; Tandiang, D.; Gigliotti, M. Computed-tomography based modeling and simulation of moisture diffusion and induced swelling in textile composite materials. Int. J. Solids Struct. 2018, 154, 88–96. [Google Scholar] [CrossRef]
- Ieşan, D. On the theory of mixtures of thermoelastic solids. J. Therm. Stress. 1991, 14, 389–408. [Google Scholar] [CrossRef]
- Quintanilla, R. Exponential stability for one-dimensional problem of swelling porous elastic soils with fluid saturation. J. Comput. Appl. Math. 2002, 145, 525–533. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.M.; Guo, B.Z. On the stability of swelling porous elastic soils with fluid saturation by one internal damping. IMA J. Appl. Math. 2006, 71, 565–582. [Google Scholar] [CrossRef]
- Ramos, A.; Freitas, M.; Almeida, D., Jr.; Noé, A.; Santos, M.D. Stability results for elastic porous media swelling with nonlinear damping. J. Math. Phys. 2020, 61, 101505. [Google Scholar] [CrossRef]
- Apalara, T.A. General stability result of swelling porous elastic soils with a viscoelastic damping. Z. Angew. Math. Phys. 2020, 71, 200. [Google Scholar] [CrossRef]
- Pamplona, P.X.; Rivera, J.E.M.; Quintanilla, R. Stabilization in elastic solids with voids. J. Math. Anal. Appl. 2009, 350, 37–49. [Google Scholar] [CrossRef] [Green Version]
- Magaña, A.; Quintanilla, R. On the time decay of solutions in porous-elasticity with quasi-static microvoids. J. Math. Anal. Appl. 2007, 331, 617–630. [Google Scholar] [CrossRef] [Green Version]
- Muñoz-Rivera, J.; Quintanilla, R. On the time polynomial decay in elastic solids with voids. J. Math. Anal. Appl. 2008, 338, 1296–1309. [Google Scholar] [CrossRef] [Green Version]
- Soufyane, A. Energy decay for porous-thermo-elasticity systems of memory type. Appl. Anal. 2008, 87, 451–464. [Google Scholar] [CrossRef]
- Messaoudi, S.A.; Fareh, A. General decay for a porous-thermoelastic system with memory: The case of nonequal speeds. Acta Math. Sci. 2013, 33, 23–40. [Google Scholar] [CrossRef]
- Apalara, T.A. General decay of solutions in one-dimensional porous-elastic system with memory. J. Math. Anal. Appl. 2019, 469, 457–471. [Google Scholar] [CrossRef]
- Apalara, T.A. A general decay for a weakly nonlinearly damped porous system. J. Dyn. Control Syst. 2019, 25, 311–322. [Google Scholar] [CrossRef]
- Feng, B.; Apalara, T.A. Optimal decay for a porous elasticity system with memory. J. Math. Anal. Appl. 2019, 470, 1108–1128. [Google Scholar] [CrossRef]
- Feng, B.; Yin, M. Decay of solutions for a one-dimensional porous elasticity system with memory: The case of non-equal wave speeds. Math. Mech. Solids 2019, 24, 2361–2373. [Google Scholar] [CrossRef]
- Casas, P.S.; Quintanilla, R. Exponential decay in one-dimensional porous-thermo-elasticity. Mech. Res. Commun. 2005, 32, 652–658. [Google Scholar] [CrossRef] [Green Version]
- Santos, M.; Campelo, A.D.S.; Almeida Júnior, D.A. On the decay rates of porous elastic systems. J. Elast. 2017, 127, 79–101. [Google Scholar] [CrossRef]
- Apalara, T.A. General stability of memory-type thermoelastic Timoshenko beam acting on shear force. Contin. Mech. Thermodyn. 2018, 30, 291–300. [Google Scholar] [CrossRef]
- Ammar-Khodja, F.; Benabdallah, A.; Rivera, J.M.; Racke, R. Energy decay for Timoshenko systems of memory type. J. Differ. Equ. 2003, 194, 82–115. [Google Scholar] [CrossRef] [Green Version]
- Al-Mahdi, A.M.; Al-Gharabli, M.M.; Guesmia, A.; Messaoudi, S.A. New decay results for a viscoelastic-type Timoshenko system with infinite memory. Z. Angew. Math. Phys. 2021, 72, 22. [Google Scholar] [CrossRef]
- Al-Mahdi, A.M.; Al-Gharabli, M.M.; Alahyane, M. Theoretical and numerical stability results for a viscoelastic swelling porous-elastic system with past history. AIMS Math. 2021, 6, 11921–11949. [Google Scholar] [CrossRef]
- Alabau-Boussouira, F.; Cannarsa, P. A general method for proving sharp energy decay rates for memory-dissipative evolution equations. Comptes Rendus Math. 2009, 347, 867–872. [Google Scholar] [CrossRef] [Green Version]
- Mustafa, M.I. Optimal decay rates for the viscoelastic wave equation. Math. Methods Appl. Sci. 2018, 41, 192–204. [Google Scholar] [CrossRef]
- Jin, K.P.; Liang, J.; Xiao, T.J. Coupled second order evolution equations with fading memory: Optimal energy decay rate. J. Differ. Equ. 2014, 257, 1501–1528. [Google Scholar] [CrossRef]
- Arnold, V. Mathematical Methods of Classical Mechanics; Springer: Berlin, Germany; New York, NY, USA, 1989. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Mahdi, A.M.; Al-Gharabli, M.M.; Alahyane, M. Theoretical and Computational Results of a Memory-Type Swelling Porous-Elastic System. Math. Comput. Appl. 2022, 27, 27. https://doi.org/10.3390/mca27020027
Al-Mahdi AM, Al-Gharabli MM, Alahyane M. Theoretical and Computational Results of a Memory-Type Swelling Porous-Elastic System. Mathematical and Computational Applications. 2022; 27(2):27. https://doi.org/10.3390/mca27020027
Chicago/Turabian StyleAl-Mahdi, Adel M., Mohammad M. Al-Gharabli, and Mohamed Alahyane. 2022. "Theoretical and Computational Results of a Memory-Type Swelling Porous-Elastic System" Mathematical and Computational Applications 27, no. 2: 27. https://doi.org/10.3390/mca27020027
APA StyleAl-Mahdi, A. M., Al-Gharabli, M. M., & Alahyane, M. (2022). Theoretical and Computational Results of a Memory-Type Swelling Porous-Elastic System. Mathematical and Computational Applications, 27(2), 27. https://doi.org/10.3390/mca27020027





