Design of a Nonhomogeneous Nonlinear Synchronizer and Its Implementation in Reconfigurable Hardware

Abstract

In this work, a generalization of a synchronization methodology applied to a pair of chaotic systems with heterogeneous dynamics is given. The proposed control law is designed using the error state feedback and Lyapunov theory to guarantee asymptotic stability. The control law is used to synchronize two systems with different number of scrolls in their dynamics and defined in a different number of pieces. The proposed control law is implemented in an FPGA in order to test performance of the synchronization schemes.

1. Introduction

Dynamical systems that exhibit chaotic behavior have proven to be very useful in science and engineering, for this same reason it is important to look for implementation alternatives that are fast and reliable. FPGAs are a very useful technology for these types of needs, due to their flexibility and the user friendly programming approach.

Since the discovery of systems with chaotic behavior, multiple analysis have been carried out [1,2,3,4], and the topic of synchronization of this class of systems has been a highly studied topic during the last 30 years [5]. This is due to the mistaken perception that this class of systems cannot be synchronized due to the complexity of their dynamics. This myth vanished in 1983 thanks to Yamada and Fujisaka [6] where a methodology for the synchronization of two chaotic systems using bidirectional coupling is presented, meanwhile in 1990 Pecora and Carroll [7] proposed the synchronization of the drive and response systems with different initial conditions. Since then, a wide series of alternative methodologies for the synchronization of chaotic systems have been developed [8,9,10,11,12,13,14,15,16] and thanks to this methodologies, a vast quantity of possible applications have been found in science and engineering, from physics [17,18], optics [19,20], biology [21,22,23], chemistry [24,25] and specially in the branch of secure communications [26,27,28].

A wide variety of chaotic systems have been implemented in circuits [29,30,31,32,33], this class of circuit implementations have certain disadvantages, such as the fact that they need very large changes in case the system wants to be modified. FPGAs have shown great flexibility in this regard [34,35,36] and although the original system changes, the only significant change is the reprogramming of the FPGA, which represents a great advantage when working on prototyping of new applications, a situation that represents cost savings and implementation times.

The aim of this work is to generalize a master–slave synchronization methodology in order to synchronize two chaotic systems with heterogeneous dynamics, which means that the master system and the slave system do not need to present the same behavior through time and it is not necessary that they are defined in the same number of parts, for example, the master system can be a system defined as a piecewise system, with n parts, while the slave system can be defined in a single part, with a single domain. In addition to this, the implementation of the most representative synchronization scheme is carried out in an FPGA, which allows these schemes to be used in multiple different applications.

The rest of this work is divided in the following way: in Section 2 the systems with which we will work are presented and a brief description of them is given; in Section 3, four different synchronization schemes are presented, including the methodology; in Section 4 the implementation of one of the schemes in an FPGA is presented and the results obtained are shown; finally, in Section 5 the conclusions are presented.

2. Preliminaries

This section presents in a non exhaustive way the dynamical systems that will be used in the rest of the paper.

2.1. The Generalized Lorenz System

Consider the generalized Lorenz system (GLS) defined in [37] as

$$\dot{x}=\left(\begin{array}{ccc}{a}_{11}& a_{12}& 0\\ a_{21}& a_{22}& 0\\ 0& 0& a_{33}\end{array}\right)x+x_1\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& -1\\ 0& 1& 0\end{array}\right)x,$$

(1)

where $x={(x_1,x_2,x_3)}^T$. Four typical chaotic systems can be specified from (1): (i) Classical Lorenz system with $a_{12}=-a_{11}=a$, $a_{21}=c$, $a_{22}=-1$ and $a_{33}=-b$; ($ii$) Chen system with $a_{12}=-a_{11}=a$, $a_{21}=c-a$, $a_{22}=c$ and $a_{33}=-b$; ($iii$) Lü system using $a_{12}=-a_{11}=a$, $a_{21}=0$, $a_{22}=c$ and $a_{33}=-b$; ($iv$) Unified chaotic system with $a_{12}=-a_{11}=25+\eta$, $a_{21}=28-35\eta$, $a_{22}=29\eta -1$ and $a_{33}=-\frac{8+\eta }{3}$, where $a,b,c\in {\mathbb{R}}^{+}$ and $\eta \in [0,1]$.

2.2. Unstable Dissipative Systems

Now consider a unstable dissipative system (UDS) defined in [38] as

$$\dot{\chi }=A\chi +B,$$

(2)

where $\chi ={({\chi }_1,{\chi }_2,{\chi }_3)}^T$, $A={\left({\alpha }_{ij}\right)}_{j=1}^3$ and B contains the switching law of the form

$$B=\left\{\begin{array}{ccc}{B}_1\hfill & if& \chi \in D_1,\\ B_2\hfill & if& \chi \in D_2,\\ ⋮\hfill & ⋮& ⋮\\ B_k\hfill & if& \chi \in D_k,\end{array}\right.$$

(3)

with $B_k={(b_{k1},b_{k2},b_{k3})}^T$. It is possible to define two types of UDS, and two types of correspond equilibria.

Definition 1.

(Campos-Cantón et al. [39]) A system given by (2) with eigenvalues ${\lambda }_i$, $i=1,2,3$, satisfying ${\sum }_{i=1}^3{\lambda }_i<0$. Then, the system is said to be:

(i) 

An UDS Type I, if one eigenvalue is negative real and the other two are complex conjugate with a positive real part.

(ii) 

An UDS Type II, if one eigenvalue is positive real and the other two are complex conjugate with a negative real part.

For the equilibria, their two types are defined accordingly. In Definition 1, item $\left(i\right)$ implies that the UDS Type I is dissipative in one of its components but oscillatory unstable in the other two, while item $\left(ii\right)$ implies that an UDS Type II is dissipative and oscillatory in two of their components but unstable in the other one. Some chaotic dynamical systems may relate to these two types of UDS around equlibria, systems as the ones in [29,40,41,42] can be characterized through a combination of UDS Type I and Type II.

3. Synchronization Scheme

The synchronization scheme diagram is depicted the Figure 1. The output X of the master FPGA is the input of the slave FPGA, the controller takes this input X and the output Y of the slave system inside of the slave FPGA and compensates the slave system output, which means that $\underset{t\to \infty }{\lim }|Y-X|=0$.

The rest of this section presents four master–slave synchronization schemes.

3.1. Master UDS–Slave GLS

Consider the master system as

$$\dot{\chi }=\left(\begin{array}{ccc}{\alpha }_{11}& {\alpha }_{12}& {\alpha }_{13}\\ {\alpha }_{21}& {\alpha }_{22}& {\alpha }_{23}\\ {\alpha }_{31}& {\alpha }_{32}& {\alpha }_{33}\end{array}\right)\chi +\left(\begin{array}{c}{b}_{k_1}\\ b_{k2}\\ b_{k3}\end{array}\right),$$

(4)

while the slave system is defined as

$$\dot{x}=\left(\begin{array}{ccc}{a}_{11}& a_{12}& 0\\ a_{21}& a_{22}& 0\\ 0& 0& a_{33}\end{array}\right)x+x_1\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& -1\\ 0& 1& 0\end{array}\right)x+u,$$

(5)

where $u={(u_1,u_2,u_3)}^T$. The error vector is defined as $e=x-\chi$, and is possible to obtain

$$\dot{e}=\left(\begin{array}{ccc}{a}_{11}& a_{12}& 0\\ a_{21}& a_{22}& 0\\ 0& 0& a_{33}\end{array}\right)x+x_1\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& -1\\ 0& 1& 0\end{array}\right)x-\left(\begin{array}{ccc}{\alpha }_{11}& {\alpha }_{12}& {\alpha }_{13}\\ {\alpha }_{21}& {\alpha }_{22}& {\alpha }_{23}\\ {\alpha }_{31}& {\alpha }_{32}& {\alpha }_{33}\end{array}\right)\chi -\left(\begin{array}{c}{b}_{k1}\\ b_{k2}\\ b_{k3}\end{array}\right)+u.$$

(6)

In order to stabilize the error system, the proposed Lyapunov function is

$$V=\frac{1}{2}\left(e_1^2+e_2^2+e_3^2\right),$$

(7)

whose derivative is

$$\begin{array}{cc}\dot{V}=\hfill & e_1\left(a_{11}{x}_1+a_{12}{x}_2-{\alpha }_{11}{\chi }_1-{\alpha }_{12}{\chi }_2-{\alpha }_{13}{\chi }_3-b_{k1}+u_1\right)+e_2\left(a_{21}{x}_1+a_{22}{x}_2-x_1{x}_3\right.\hfill \\ \hfill & \left.-{\alpha }_{21}{\chi }_1-{\alpha }_{22}{\chi }_2-{\alpha }_{23}{\chi }_3-b_{k2}+u_2\right)+e_3\left(a_{33}{x}_3+x_1{x}_2-{\alpha }_{31}{\chi }_1-{\alpha }_{32}{\chi }_2-{\alpha }_{33}{\chi }_3\right.\hfill \\ \hfill & \left.-b_{k3}+u_3\right),\hfill \end{array}$$

(8)

which allows to design the control law u as

$$u=-Pe-\left(\begin{array}{ccc}{\alpha }_{11}& {\alpha }_{12}& {\alpha }_{13}\\ {\alpha }_{21}& {\alpha }_{22}& {\alpha }_{23}\\ {\alpha }_{31}& {\alpha }_{32}& {\alpha }_{33}\end{array}\right)\chi -\left(\begin{array}{c}{b}_{k1}\\ b_{k2}\\ b_{k3}\end{array}\right)+\left(\begin{array}{ccc}{a}_{11}& a_{12}& 0\\ a_{21}& a_{22}& 0\\ 0& 0& a_{33}\end{array}\right)x+x_1\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& -1\\ 0& 1& 0\end{array}\right)x,$$

(9)

where $e={(e_1,e_2,e_3)}^T$ is the error vector, and $P=P^T=\mathrm{diag}\{p_1^2,p_2^2,p_3^2\}$ is a diagonal matrix of parameters selected to ensure negativeness of (8).

3.2. Master GLS–Slave UDS

For this scheme the master system is considered as

$$\dot{x}=\left(\begin{array}{ccc}{a}_{11}& a_{12}& 0\\ a_{12}& a_{22}& 0\\ 0& 0& a_{33}\end{array}\right)x+x_1\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& -1\\ 0& 1& 0\end{array}\right)x,$$

(10)

while the slave system is

$$\dot{\chi }=\left(\begin{array}{ccc}{\alpha }_{11}& {\alpha }_{12}& {\alpha }_{13}\\ {\alpha }_{21}& {\alpha }_{22}& {\alpha }_{23}\\ {\alpha }_{31}& {\alpha }_{32}& {\alpha }_{33}\end{array}\right)\chi +\left(\begin{array}{c}{b}_{k1}\\ b_{k2}\\ b_{k3}\end{array}\right)+u.$$

(11)

The error vector is defined as $e=\chi -x$, consequently the error dynamics are represented by

$$\dot{e}=\left(\begin{array}{ccc}{\alpha }_{11}& {\alpha }_{12}& {\alpha }_{13}\\ {\alpha }_{21}& {\alpha }_{22}& {\alpha }_{23}\\ {\alpha }_{31}& {\alpha }_{32}& {\alpha }_{33}\end{array}\right)\chi +\left(\begin{array}{c}{b}_{k1}\\ b_{k2}\\ b_{k3}\end{array}\right)-\left(\begin{array}{ccc}{a}_{11}& a_{12}& 0\\ a_{12}& a_{22}& 0\\ 0& 0& a_{33}\end{array}\right)x-x_1\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& -1\\ 0& 1& 0\end{array}\right)x+u.$$

(12)

Similarly to the previous scheme, the proposed Lyapunov function is

$$V=\frac{1}{2}\left(e_1^2+e_2^2+e_3^2\right),$$

(13)

while in this scheme the derivative results in

$$\begin{array}{cc}\dot{V}=\hfill & e_1\left({\alpha }_{11}{\chi }_1+{\alpha }_{12}{\chi }_2+{\alpha }_{13}{\chi }_3+b_{k1}-a_{11}{x}_1-a_{12}{x}_2+u_1\right)+e_2\left({\alpha }_{21}{\chi }_1+{\alpha }_{22}{\chi }_2+{\alpha }_{23}{\chi }_3\right.\hfill \\ \hfill & \left.-a_{21}{x}_1-a_{22}{x}_2+x_1{x}_3+b_{k2}+u_2\right)+e_3\left({\alpha }_{31}{\chi }_1+{\alpha }_{32}{\chi }_2+{\alpha }_{33}{\chi }_3-a_{33}{x}_3-x_1{x}_2+b_{k3}\right.\hfill \\ \hfill & \left.+u_3\right).\hfill \end{array}$$

(14)

Under the before considerations, the proposed control law is

$$u=-Pe-\left(\begin{array}{ccc}{\alpha }_{11}& {\alpha }_{12}& {\alpha }_{13}\\ {\alpha }_{21}& {\alpha }_{22}& {\alpha }_{23}\\ {\alpha }_{31}& {\alpha }_{32}& {\alpha }_{33}\end{array}\right)\chi -\left(\begin{array}{c}{b}_{k1}\\ b_{k2}\\ b_{k3}\end{array}\right)+\left(\begin{array}{ccc}{a}_{11}& a_{12}& 0\\ a_{12}& a_{22}& 0\\ 0& 0& a_{33}\end{array}\right)x+x_1\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& -1\\ 0& 1& 0\end{array}\right)x,$$

(15)

where, in the same form as before $P=P^T=\mathrm{diag}\{p_1^2,p_2^2,p_3^2\}$ is a matrix of parameters selected to ensure the negativeness of (14).

3.3. Master GLS–Slave GLS

The master system for this synchronization scheme is

$$\dot{x}=\left(\begin{array}{ccc}{a}_{11}& a_{12}& 0\\ a_{21}& a_{22}& 0\\ 0& 0& a_{33}\end{array}\right)x+x_1\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& -1\\ 0& 1& 0\end{array}\right)x,$$

(16)

However, in this scheme the slave system is defined as

$$\dot{y}=\left(\begin{array}{ccc}{b}_{11}& b_{12}& 0\\ b_{21}& b_{22}& 0\\ 0& 0& b_{33}\end{array}\right)y+y_1\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& -1\\ 0& 1& 0\end{array}\right)y+u,$$

(17)

Once again, $u={(u_1,u_2,u_3)}^T$ is the controller. The error is defined as $e=y-x$, and its dynamics is given by

$$\dot{e}=\left(\begin{array}{ccc}{b}_{11}& b_{12}& 0\\ b_{21}& b_{22}& 0\\ 0& 0& b_{33}\end{array}\right)y-\left(\begin{array}{ccc}{a}_{11}& a_{12}& 0\\ a_{21}& a_{22}& 0\\ 0& 0& a_{33}\end{array}\right)x+\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& -1\\ 0& 1& 0\end{array}\right)\left(y_{1}y-x_{1}x\right)+u.$$

(18)

In order to stabilize the error dynamics, the proposed Lyapunov function is

$$V={\displaystyle \frac{1}{2}}\left(e_1^2+e_2^2+e_3^2\right),$$

(19)

where the derivative is

$$\begin{array}{cc}\dot{V}=\hfill & e_1\left(b_{11}{y}_1+b_{12}{y}_2-a_{11}{x}_1-a_{12}{x}_2+u_1\right)+e_2\left(b_{21}{y}_1+b_{22}{y}_2-a_{21}{x}_1-a_{22}{x}_2-y_1{y}_3\right.\hfill \\ \hfill & \left.+x_1{x}_3+u_2\right)+e_3\left(b_{33}{y}_3-a_{33}{x}_3+y_1{y}_2-x_1{x}_2+u_3\right),\hfill \end{array}$$

(20)

which allows to design the controll law u as

$$u=-Pe-\left(\begin{array}{ccc}{b}_{11}& b_{12}& 0\\ b_{21}& b_{22}& 0\\ 0& 0& b_{33}\end{array}\right)y+\left(\begin{array}{ccc}{a}_{11}& a_{12}& 0\\ a_{21}& a_{22}& 0\\ 0& 0& a_{33}\end{array}\right)x-\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& -1\\ 0& 1& 0\end{array}\right)\left(y_{1}y-x_{1}x\right).$$

(21)

3.4. Master UDS–Slave UDS

Finally, the master system for this scheme is

$$\dot{\chi }=\left(\begin{array}{ccc}{\alpha }_{11}& {\alpha }_{12}& {\alpha }_{13}\\ {\alpha }_{21}& {\alpha }_{22}& {\alpha }_{23}\\ {\alpha }_{31}& {\alpha }_{32}& {\alpha }_{33}\end{array}\right)\chi +\left(\begin{array}{c}{b}_{k1}\\ b_{k2}\\ b_{k3}\end{array}\right),$$

(22)

and the slave system is of the form

$$\dot{\phi }=\left(\begin{array}{ccc}{\beta }_{11}& {\beta }_{12}& {\beta }_{13}\\ {\beta }_{21}& {\beta }_{22}& {\beta }_{23}\\ {\beta }_{31}& {\beta }_{32}& {\beta }_{33}\end{array}\right)\phi +\left(\begin{array}{c}{c}_{k1}\\ c_{k2}\\ c_{k3}\end{array}\right)+u.$$

(23)

The dynamics of the error $\phi -\chi$ is given by

$$\dot{e}=\left(\begin{array}{ccc}{\beta }_{11}& {\beta }_{12}& {\beta }_{13}\\ {\beta }_{21}& {\beta }_{22}& {\beta }_{23}\\ {\beta }_{31}& {\beta }_{32}& {\beta }_{33}\end{array}\right)\phi -\left(\begin{array}{ccc}{\alpha }_{11}& {\alpha }_{12}& {\alpha }_{13}\\ {\alpha }_{21}& {\alpha }_{22}& {\alpha }_{23}\\ {\alpha }_{31}& {\alpha }_{32}& {\alpha }_{33}\end{array}\right)\chi +\left(\begin{array}{c}{c}_{k1}\\ c_{k2}\\ c_{k3}\end{array}\right)-\left(\begin{array}{c}{b}_{k1}\\ b_{k2}\\ b_{k3}\end{array}\right)+u,$$

(24)

and once again, the proposed Lyapunov function is

$$V={\displaystyle \frac{1}{2}}\left(e_1^2+e_2^2+e_3^2\right),$$

(25)

with derivative

$$\begin{array}{cc}\dot{V}=\hfill & e_1\left({\beta }_{11}{\phi }_1+{\beta }_{12}{\phi }_2+{\beta }_{13}{\phi }_3-{\alpha }_{11}{\chi }_1-{\alpha }_{12}{\chi }_2-{\alpha }_{13}{\chi }_3+c_{k1}-b_{k1}+u_1\right)+e_2\left({\beta }_{21}{\phi }_1\right.\hfill \\ \hfill & +\left.{\beta }_{22}{\phi }_2+{\beta }_{23}{\phi }_3-{\alpha }_{21}{\chi }_1-{\alpha }_{22}{\chi }_2-{\alpha }_{23}{\chi }_3+c_{k2}-b_{k2}+u_2\right)+e_3\left({\beta }_{31}{\phi }_1+{\beta }_{32}{\phi }_2\right.\hfill \\ \hfill & \left.+{\beta }_{33}{\phi }_3-{\alpha }_{31}{\chi }_1-{\alpha }_{32}{\chi }_2-{\alpha }_{33}{\chi }_3+c_{k3}-b_{k3}+u_3\right).\hfill \end{array}$$

(26)

Consequently, the proposed control law is

$$u=-Pe-\left(\begin{array}{ccc}{\beta }_{11}& {\beta }_{12}& {\beta }_{13}\\ {\beta }_{21}& {\beta }_{22}& {\beta }_{23}\\ {\beta }_{31}& {\beta }_{32}& {\beta }_{33}\end{array}\right)\phi +\left(\begin{array}{ccc}{\alpha }_{11}& {\alpha }_{12}& {\alpha }_{13}\\ {\alpha }_{21}& {\alpha }_{22}& {\alpha }_{23}\\ {\alpha }_{31}& {\alpha }_{32}& {\alpha }_{33}\end{array}\right)\chi -\left(\begin{array}{c}{c}_{k1}\\ c_{k2}\\ c_{k3}\end{array}\right)+\left(\begin{array}{c}{b}_{k1}\\ b_{k2}\\ b_{k3}\end{array}\right).$$

(27)

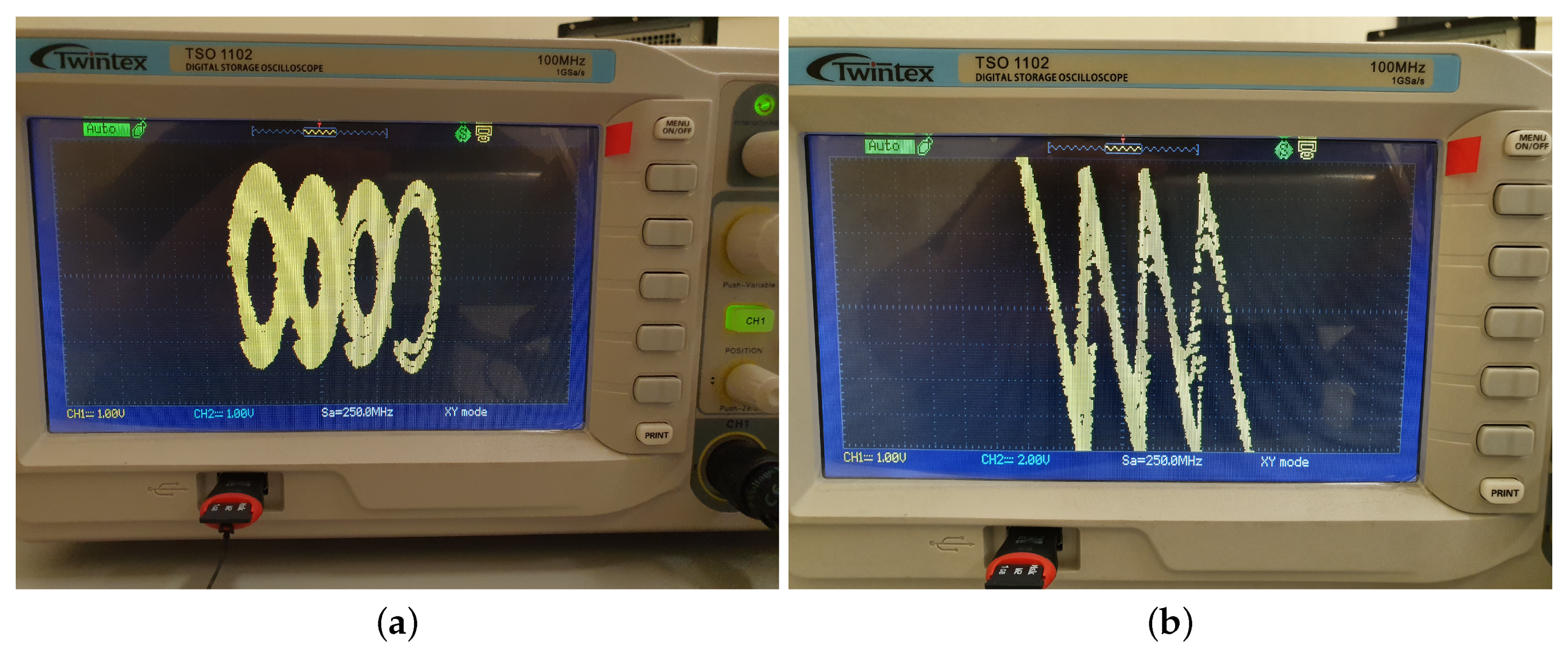
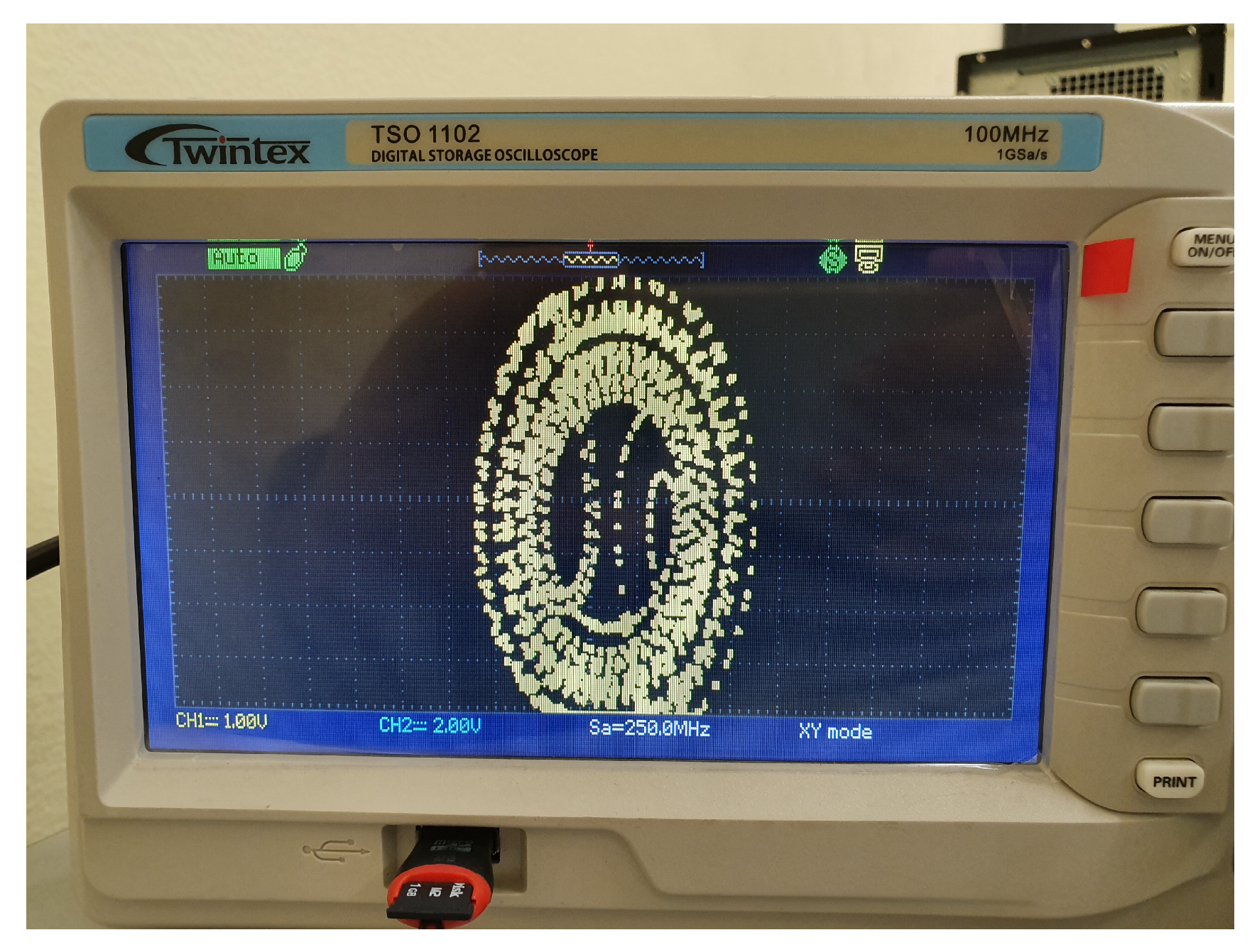
4. Results

For the implementation of the synchronization scheme, the selected piecewise UDS given in [43] presents a four scrolls attractor and it is defined as

$$\dot{\chi }=\left(\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ -35.139& -8.23& -3.7\end{array}\right)\chi +\left(\begin{array}{c}0\\ 0\\ B_k\end{array}\right),$$

(28)

where $B_k$ is given by

$$B_k=\left\{\begin{array}{ccc}21.0834\hfill & \mathrm{if}& {\chi }_1>0.5,\\ 14.055\hfill & \mathrm{if}& 0.3<{\chi }_1\le 0.5,\\ 7.0278\hfill & \mathrm{if}& 0.1<{\chi }_1\le 0.3,\\ 0\hfill & \mathrm{if}& {\chi }_1\le 0.1,\end{array}\right.$$

(29)

and the slave system is

$$\dot{x}=\left(\begin{array}{ccc}-16& 16& 0\\ 45.6& -1& 0\\ 0& 0& -4\end{array}\right)x+x_1\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& -1\\ 0& 1& 0\end{array}\right)x+u.$$

(30)

Using the synchronization scheme described in the Section 3.1, the control law is defined as

$$u=-Pe-\left(\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ -35.139& -8.23& -3.7\end{array}\right)\chi -\left(\begin{array}{c}0\\ 0\\ B_k\end{array}\right)+\left(\begin{array}{ccc}-16& 16& 0\\ 45.6& -1& 0\\ 0& 0& -4\end{array}\right)x+x_1\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& -1\\ 0& 1& 0\end{array}\right)x,$$

(31)

which will be implemented in a SPARTAN–3AN FPGA Starter Kit board from Xilinx, the general scheme can be appreciated in the Figure 2. It can be seen that in (a) the SPARTAN–3AN starter kit board in which the master system is implemented; in (b) the slave system is implemented with the control law (31); in (c) the Digital to Analog Converter (DAC) can be observed and in (d) the output data is acquired.

In order to implement the synchronization scheme in the SPARTAN–3AN starter kit, the Simulink^® toolbox: Xilinx System Generator was used. In the Figure 3 can be observed the classical Lorenz system without any kind of control, implemented in Simulink^® using this toolbox as example.

When implementing the master system in the FPGA, it is possible to acquire the output signal using the DAC from the National Instruments module NI–6211. With this is possible to obtain the plane projections $({\chi }_1,{\chi }_2)$ and ${\chi }_{1,2}$ vs. t, this can be appreciated in the Figure 4. This is also applicable to the projection on the plane (${\chi }_1,{\chi }_3$), as can be seen in the Figure 5. The projections (${\chi }_2,{\chi }_3$) are shown in the Figure 6, and the FPGA resources utilized by the master system is presented in

Table 1. FPGA utilization summary for the master 4–scrolls UDS.

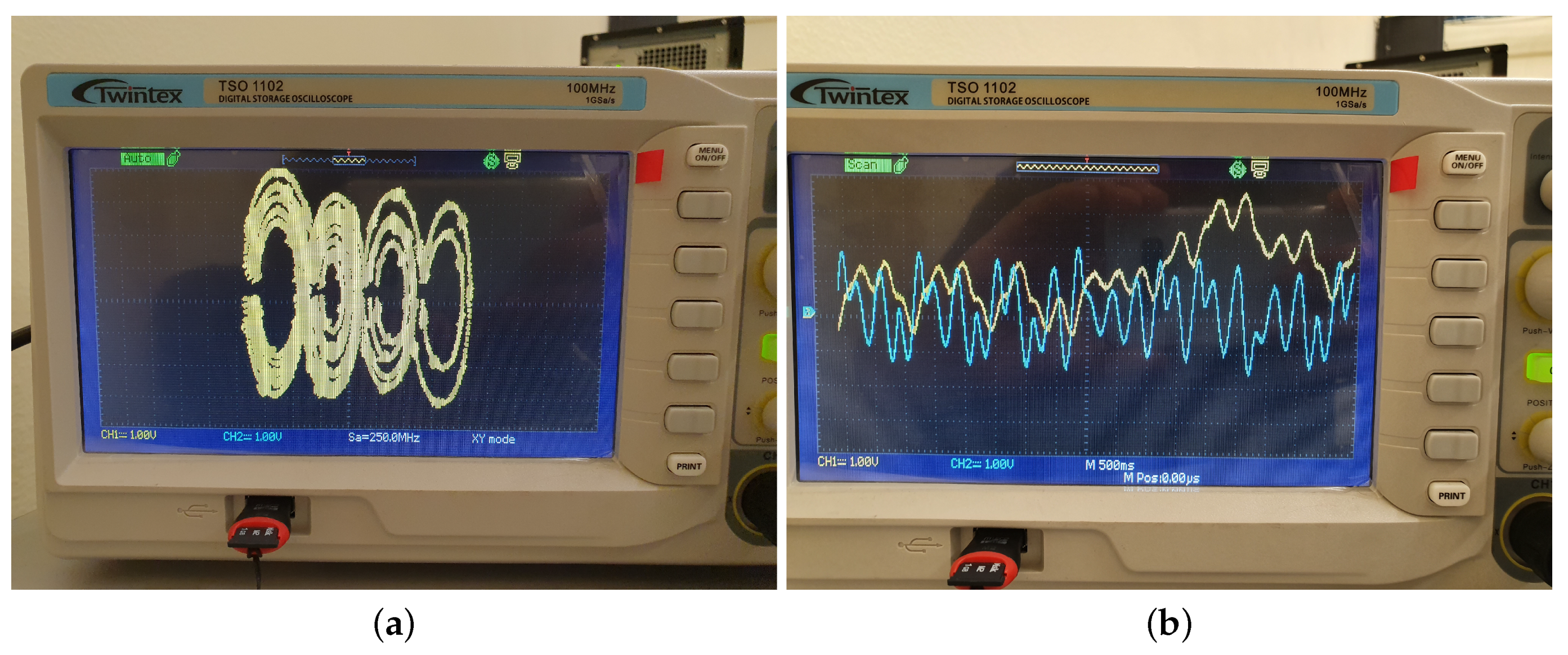
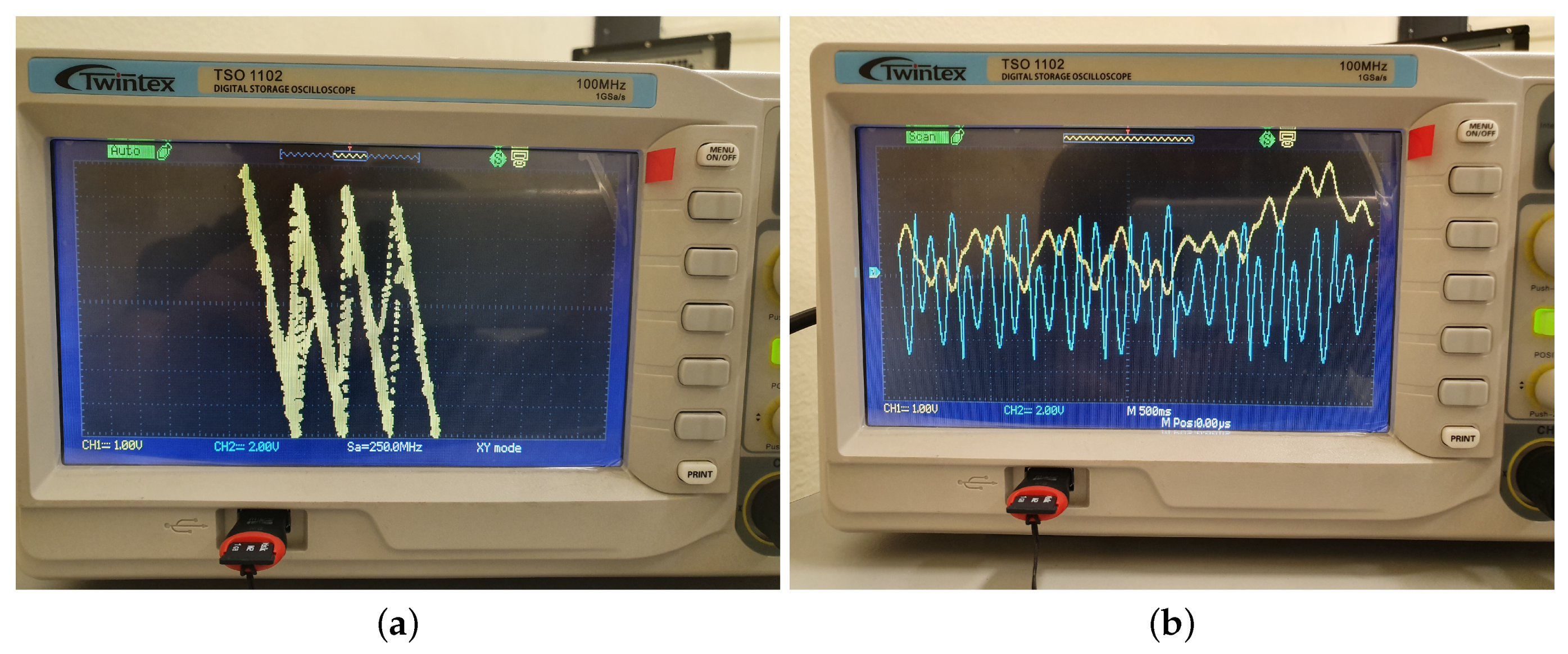
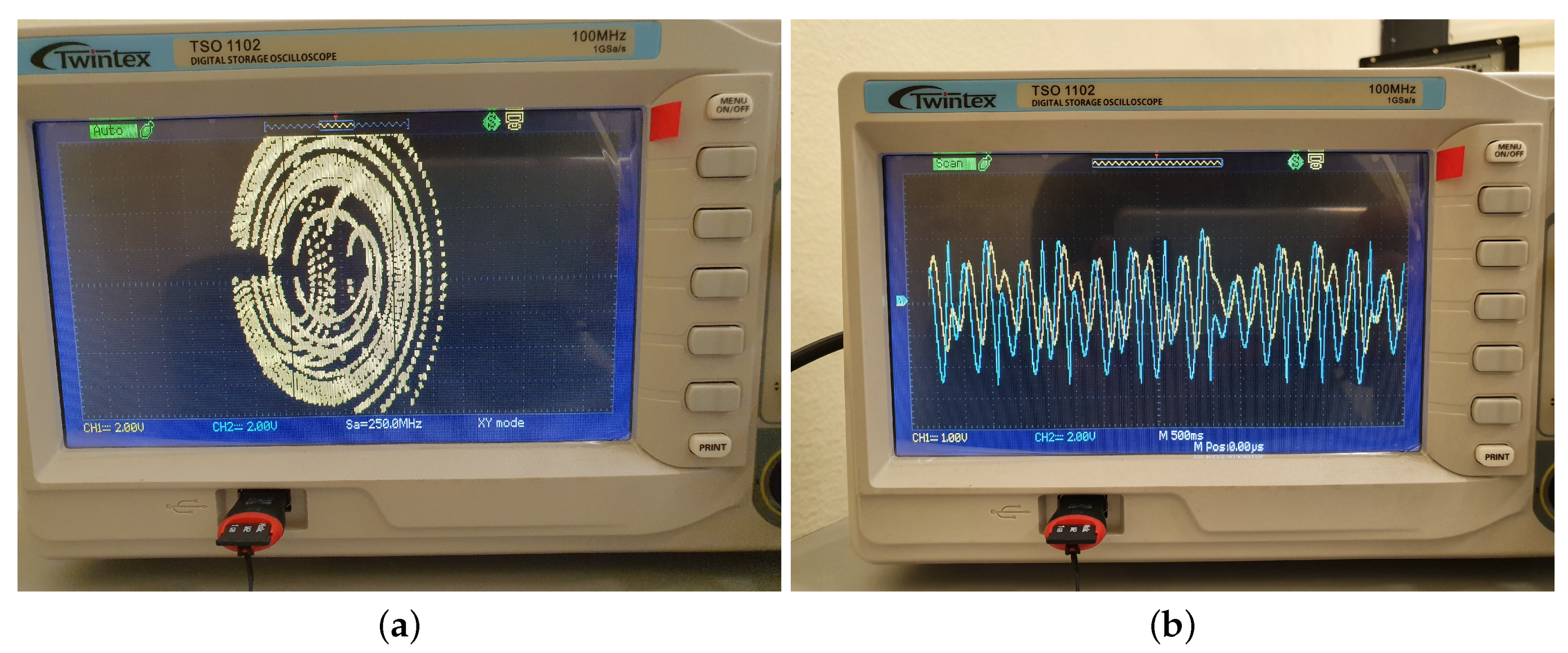
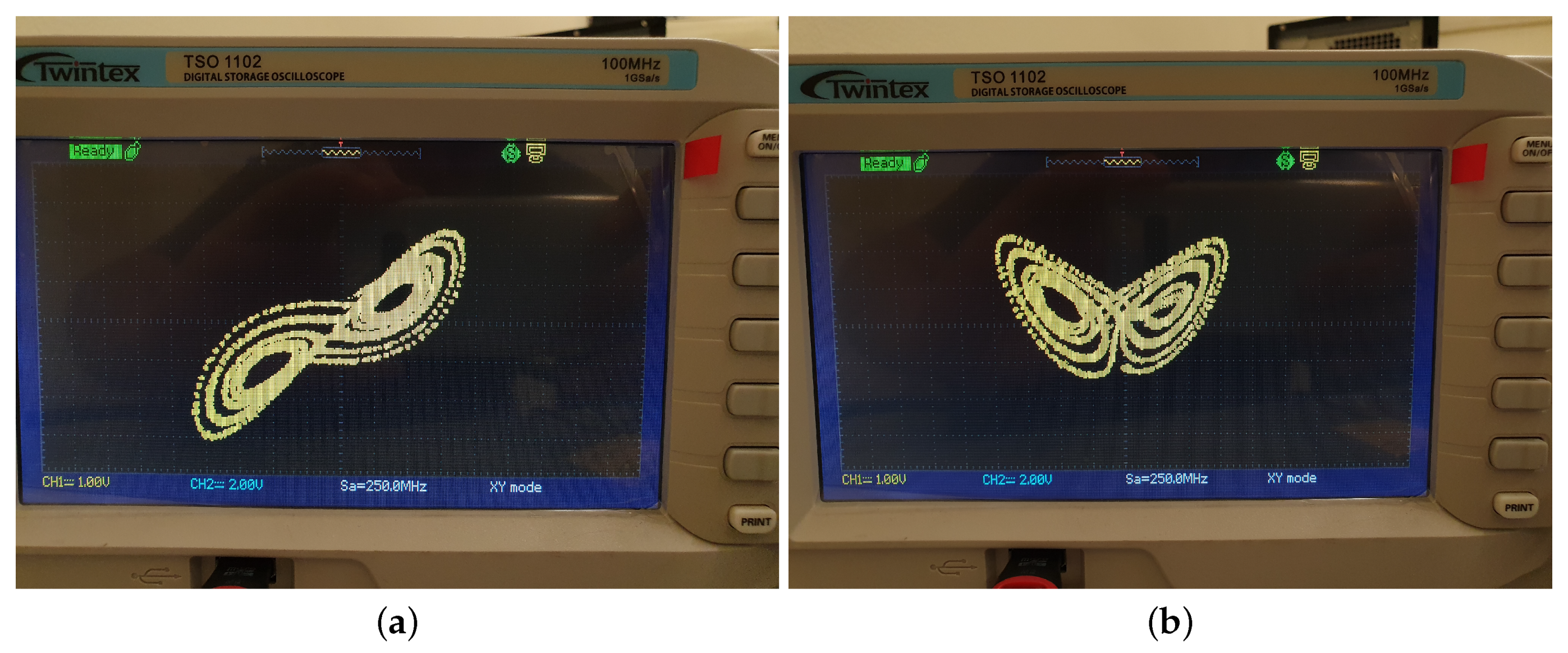
Resources	Used	Available	Utilization
Number of Slice Flip Flops	159	11,776	$1\%$
Number of 4 input LUTs	4177	11,776	$35\%$
Number of occupied Slices	2473	5888	$42\%$
Total Number of 4 input LUTs	4467	11,776	$37\%$
Number of bounded IOBs	145	372	$38\%$
Number of BUFGMUXs	1	24	$4\%$

.

For the uncontrolled slave system, both of the projections on the planes $(x_1,x_2)$ and $(x_1,x_3)$ were obtained and they can be seen in Figure 7. The projections on the plane $(x_2,x_3)$ are depicted in Figure 8. It is important to highlight that the slave system arises a two-scroll attractor while the master system presents four scrolls. Consequently, once implemented the control law, the slave system will change its dynamics undergoing a four-scroll attractor behavior with the shape of the master systems’s phase portrait. The FPGA utilization summary for the slave system is presented in

Table 2. FPGA utilization summary for the uncontrolled Lorenz slave system.

Resources	Used	Available	Utilization
Number of Slice Flip Flops	170	11,776	$1\%$
Number of 4 input LUTs	2373	11,776	$20\%$
Number of occupied Slices	1491	5888	$25\%$
Total Number of 4 input LUTs	2677	11,776	$22\%$
Number of bounded IOBs	53	372	$14\%$
Number of BUFGMUXs	1	24	$4\%$
Number of MULT18X18SIOs	18	20	$90\%$

.

For the synchronized slave system, both of the projections on the planes $(x_1,x_2)$ and $(x_1,x_3)$ were obtained and they can be observed in the Figure 9. The projections on the plane $(x_2,x_3)$ are depicted in the Figure 10. It is easy to see that the two-scroll slave system in fact adopted the master system behavior presenting four scrolls. The resource utilization of the FPGA is shown in the

Table 3. FPGA utilization summary for the controlled Lorenz slave system.

Resources	Used	Available	Utilization
Number of Slice Flip Flops	332	11,776	$3\%$
Number of 4 input LUTs	5550	11,776	$56\%$
Number of occupied Slices	2964	5888	$67\%$
Total Number of 4 input LUTs	7244	11,776	$62\%$
Number of bounded IOBs	194	372	$52\%$
Number of BUFGMUXs	2	24	$8\%$
Number of MULT18X18SIOs	20	20	$100\%$

, the utilization increases compared with the master and the uncontrolled slave, this is due to the integration of the controller u. This proves that in a low cost, entry-level FPGA like the SPARTAN–3AN the system are possible to implement by taking in consideration that the utilization of the FPGA exceeds the $60\%$ of the resources. For the MULTI18X18IOs of the system the utilization is $100\%$, this problem can be avoided by implementing the synchronization scheme in a more powerful FPGA.

5. Conclusions

A synchronization scheme for systems with heterogeneous chaotic behavior was implemented in an FPGA, this synchronization scheme can synchronize a pair of chaotic systems defined by a different number of pieces, is possible to apply the scheme to UDSs which is a kind of generalization for synchronization of piecewise systems with different quantities of pieces on the master and slave systems, which allows the use in a wide variety of applications in science and engineering. The synchronization scheme gives to the slave system a the dynamics of the master system. The synchronization scheme is designed taking into account the error system between the master and the slave, adding a parameter matrix P that controls the synchronization speed, whenever the parameter is adequate. The controller guarantees a fast synchronization with a minimum error.