1. Introduction
Linear differential equations of the form
are ubiquitous in many branches of physics, chemistry and mathematics. Here,
U is a real or complex
matrix, and
is a sufficiently smooth matrix to ensure the existence of solutions. Perhaps the most important example corresponds to the Schrödinger equation for the evolution operator in quantum systems with a time-dependent Hamiltonian
, in which case
. Particular cases include spin dynamics in magnetic resonance (Nuclear Magnetic Resonance—NMR, Electronic Paramagnetic Resonance—EPR, Dynamic Nuclear Polarization—DNP, etc.) [
1,
2,
3], electron-atom collisions in atomic physics, pressure broadening of rotational spectra in molecular physics, control of chemical reactions with driving induced by laser beams, etc. When the time-dependence of the Hamiltonian is periodic, as occurs, for instance, in periodically driven quantum systems, atomic quantum gases in periodically driven optical lattices, etc. [
4,
5], the Floquet theorem [
6] relates
with a constant Hamiltonian. More specifically, it implies that the evolution operator is factorized as
, with
a periodic time-dependent matrix and
F a constant matrix. This theorem has been widely used in problems of solid state physics, in NMR, in the quantum simulation of systems with time-independent Hamiltonians by periodically driven quantum systems, etc. [
7]. The Average Hamiltonian Theory is also closely related with this result, and the effective Hamiltonian is an important tool in the description of the system [
8,
9].
In general, Equation (
1) cannot be solved in closed form, and so different approaches have been proposed along the years to obtain approximations, both analytic and numerical. Among the former, we can mention the standard perturbation theory, the average Hamiltonian theory, and the Magnus expansion [
5,
8,
10]. Concerning the second approach, different numerical algorithms have been applied to obtain solutions on specific time intervals [
11,
12,
13].
In this work, we will concentrate on different techniques providing analytic approximations to the solution of (
1) that also share some of its most salient qualitative features. In particular, if (
1) represents the Schrödinger equation, it is well known that
is unitary for all
t, and this guarantees that its elements represent probabilities of transition between the different states of the system. However, it happens that not every approximate scheme (either analytic or numerical) renders unitary matrices and, thus, the physical description they provide is unreliable, especially for large integration times.
The Magnus expansion [
14] presents the remarkable feature that it allows one to express the solution as the exponential of a series,
, so that, even when the series
is truncated, the corresponding approximation is still unitary when applied to the Schrödinger equation. More generally, if (
1) is defined in a Lie group
, then it provides an approximate solution also belonging to
. Moreover, it has also been used to construct efficient numerical integration algorithms also preserving this feature [
12,
15].
When
periodically depends on time with period
T, the Magnus expansion does not explicitly provide the structure of the solution ensured by the Floquet theorem, i.e.,
. with
periodic and
F a constant matrix. Nevertheless, it can be conveniently generalized to cover also this situation, in such a way that the matrix
is expressed as the exponential of a series of periodic terms. The resulting approach (the so-called Floquet–Magnus expansion [
10]) has been used during the last years in a variety of physical problems [
4,
5,
7,
16].
Very often, the coefficient matrix in (
1) is of the form
, where
is constant,
, and
is a (small) parameter. In other words, one is dealing with a time-dependent perturbation of a solvable problem defined by
. In that case, several perturbative procedures exist to construct
as a power series in
, either directly (by applying standard perturbation techniques in the interaction picture defined by
) or taking into account the structure ensured by the Floquet theorem and constructing both matrices
and
F as power series [
9]. Of course, if
and
is also constructed as a power series in
, then the qualitative properties of the solution are inherited by the approximations (in particular, they are unitary in quantum evolution problems) [
17].
An alternative manner of viewing the Floquet theorem is to interpret the matrix
, provided that it is invertible, as a time-periodic transformation to a new set of coordinates where the new evolution equation has a constant coefficient matrix
F, so that
is the exact solution in the new coordinates. In the language of Quantum Mechanics, this corresponds to a change of picture. This interpretation leads to the important mathematical notion of a
reducible system: according to Lyapunov, the general system (
1) is called reducible if there exists a matrix
which together with
is bounded on
, such that the system obtained from (
1) by applying the linear transformation defined by
has constant coefficients [
18]. In this sense, if
is a periodic matrix, then (
1) is reducible by means of a periodic matrix. The situation is not so clear; however, when
is quasi-periodic or almost periodic: although several general results exist ensuring reducibility [
19,
20,
21], there are also examples of irreducible systems [
22].
In this work, we pursue and generalize this interpretation to show that all of the above mentioned exponential perturbative treatments can be considered as particular instances of a generic change of variables applied to the original differential equation. The idea of making a coordinate change to analyze a problem arises of course in many application settings, ranging from canonical (or symplectic) transformations in classical mechanics (based either on generating functions expressed in terms of mixed, old and new, variables [
23], or on the Lie-algebraic setting [
24,
25]) to changes of picture and unitary transformations in quantum mechanics. What we intend here is to show that several widely used perturbative expansions in quantum mechanics can be indeed derived from the same basic principle using different variations of a unique ansatz based on a generic linear transformations of coordinates. We believe that this interpretation sheds new light into the different expansions and, moreover, allows one to elaborate a unique procedure for analyzing a given problem and compare in an easy way how they behave in practice.
It is important to remark that all the procedures considered here (with the exception of course of the standard perturbation theory) preserve by construction the unitarity of the solution when (
1) refers to the Schrödinger equation. More generally, the approximations obtained evolve in the same matrix Lie group as the exact solution of the differential Equation (
1).
2. Coordinate Transformations and Linear Systems
To begin with, let us consider the most general situation of a linear differential equation
with
a
matrix whose entries are integrable functions of
t. Notice that
in (
1) can be considered the fundamental matrix of (
2). We analyze a change of variables
transforming the original system (
2) into
where the matrix
F adopts some desirable form. Because we are interested in preserving qualitative properties of (
2), we impose an additional requirement for the transformation, namely, it has to be of the form
so that
. Thus, in particular, if (
2) is the Schrödinger equation with Hamiltonian
,
is skew-Hermitian.
It is clear that the transformation (
4) is completely determined once the generator
is obtained. An evolution equation for
is obtained by introducing (
4) in (
2) and also taking into account (
3) as
The derivative of a matrix exponential can be written as [
26]
where the symbol
stands for the (everywhere convergent) power series
Here
,
, and
denotes the usual commutator. By inserting (
6) into (
5), one gets
where
If we invert the
operator given by (
7), we get from (
8) the formal identity
Now, taking into account that
it is clear that
A more convenient way of expressing this identity is obtained by recalling that
where
are the Bernoulli numbers, so that (
9) reads
With more generality, we can assume that both
and
are power series of some appropriate parameter
,
and, thus, the generator
will be also a power series,
The successive
can be determined by inserting (
11) and (
12) into Equation (
10) and equating terms of the same power in
. Thus, one obtains the following recursive procedure:
where
Of course, although the change of variables
is completely general, it is only worth to be considered if Equation (
3) is simpler to solve than (
2). In the following we analyze several ways of choosing
F fulfilling this basic requirement, and how, in this way, we are able to recover different exponential perturbative expansions.
3. Magnus Expansion
The simplest choice one can imagine of is taking
or, in other words, one is looking for a linear transformation rendering the original system (
2) into
with trivial solution
. A sufficient condition for the reducibility of Equation (
2) to (
15) is [
18]
where
. If this is the case, from (
4),
where
is determined from (
10) with
, i.e.,
This, of course, corresponds to the well known Magnus expansion for the solution
of (
2) [
14,
26]. The terms
are then determined by the recursion (
14) by taking
. If we take
and
in (
11), then we get the familiar recursive procedure [
26]
whence the successive terms
are obtained by integration. An explicit expression for
involving only independent nested commutators can be obtained by working out this recurrence and using the class of bases proposed by Dragt and Forest [
27] for the Lie algebra generated by the operators
. Specifically, one has [
28]
where
is a permutation of
and
corresponds to the number descents of
. We recall that
has a descent in
i if
,
. Notice that the argument in the last term is fixed to
, and one considers all of the permutations in
. Moreover, the series (
12) converges in this case in the interval
, such that
and the sum
satisfies
[
26]. Here,
denotes the spectral norm, characterized as
.
The Magnus expansion has a long history as a tool to approximate solutions in a wide spectrum of fields in Physics and Chemistry, from atomic and molecular physics to Nuclear Magnetic Resonance to Quantum Electrodynamics (see [
26] and references therein). Additionally, in computational mathematics, it has been used to construct efficient algorithms for the numerical integration of differential equations within the widest field of geometric numerical integration [
12,
13,
15]. Recently, it has also been used in the treatment of dissipative driven two-level systems [
29].
4. Floquet–Magnus Expansion
The Magnus expansion can be, in principle applied for any particular time dependence in
, as long as the integrals in
can be computed or conveniently approximated. When
in (
2) is periodic in
t with period
T; however, other changes of variables may be more suitable. According to Floquet’s theorem, the original system is reducible to a system with a constant coefficient matrix
F, whose eigenvalues (the so-called characteristic exponents) determine the asymptotic stability of the solution
. In addition, the linear transformation is periodic with the same period
T [
6].
In our general framework, then, it makes sense to determine a change of variables
in such a way that
F in (
3) is constant, so that
and
is periodic. Proceeding as before, if we take
and
in (
11), the procedure (
13)–(
14) simplifies to
and
Notice that, in general,
depends on the previously computed
,
,
, so that equations (
21) can be solved recursively, as follows. First, we determine
and
by taking the average of
A and
, respectively, over one period
T,
and then compute the integrals
respectively, thus ensuring that
is periodic with the same period
T. This results in the well known Floquet–Magnus expansion for the solution of (
2),
originally introduced in [
10] and subsequently applied in different areas [
4,
5,
7,
16]. In the context of periodic quantum mechanical problems,
is called the effective Hamiltonian of the problem. This expansion presents the great advantage that, in addition to preserving unitarity as the Magnus expansion, also allows one to determine the stability of the system by analyzing the eigenvalues of
F.
As shown in [
10], the resulting series for
is absolutely convergent at least for
, such that
The procedure can be easily generalized to quasi-periodic problems [
30]. We recall that
is quasi-periodic in
t with frequencies
if
, where
is
-periodic with respect to
and
for
. In that case, we can write
where
and
[
31].
In this case,
is also quasi-periodic (by induction) and we take
the limiting mean value of
, independent of the particular value of
a. In consequence,
and
is also quasi-periodic with the same basic frequencies as
.
7. Concluding Remarks
The subject of the perturbative treatment of linear systems of time-dependent differential equations has a long history in physics and mathematics. In physics, in particular, it plays a fundamental role in the study of the evolution of quantum systems. Among the different procedures, the so-called exponential perturbation algorithms have the relevant property of preserving the unitary character of the evolution. More in general, the approximations they provide belong to the same Lie group than the exact solution of the problem. Archetypical examples of exponential perturbation theories are the Magnus expansion since its inception in the 1950s and, more recently, the Floquet–Magnus expansion, several quantum averaging procedures and a generalization of the well known Hori–Deprit perturbation theory of classical mechanics. Each of these algorithms has been derived in an independent way and it is not always easy to establish connections and common points between them.
The present paper tries to bridge this gap by showing that all of them can be seen in fact as the result of linear changes of coordinates expressed as the exponential of a certain series whose terms can be obtained recursively. In addition to the Magnus and Floquet–Magnus expansions, other techniques can also be incorporated into our general framework, including the quantum averaging method and the Lie–Deprit perturbative algorithm. In the process, we have also considered a novel approach, namely an exponential transformation rendering the original system into another one in which the perturbation is removed. The resulting approximations preserve whatever qualitative features the exact solution may possess (unitarity, orthogonality, symplecticness, etc.). Even the standard perturbation theory in the interaction picture is recovered in this setting when the exponential defining the transformation is truncated.
With this same framework one might of course consider other exponential transformations, and this would automatically lead to new perturbation formalisms that might be particularly adapted to the problem at hand. For instance, we could choose
as a diagonal time-dependent matrix, so that equation (
3) is easy to solve, and construct the corresponding generator
. We believe that the proposed framework sheds new light into nature of the different expansions and allows one to create a unique procedure to analyze a given problem, obtaining all of the expansions by choosing appropriately the coefficient matrix in the new variables. Moreover, it also allows one to determine in an easy way what is the best algorithm for a given problem. This feature has been illustrated in this work by applying the procedure to two simple examples.
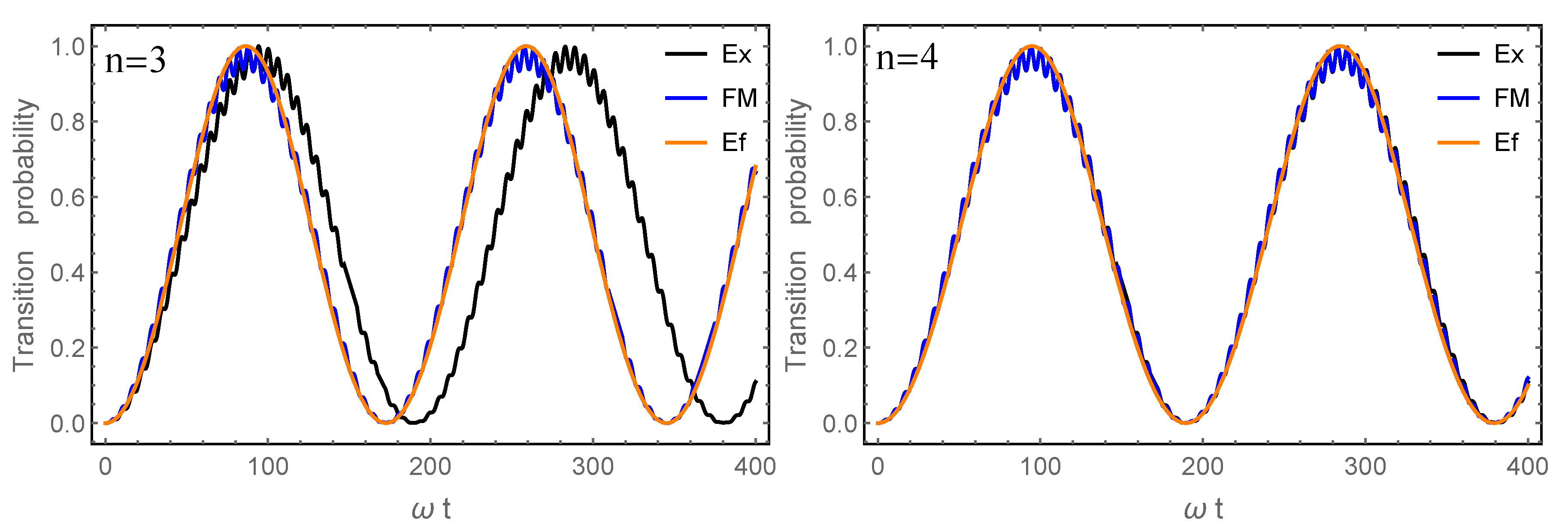
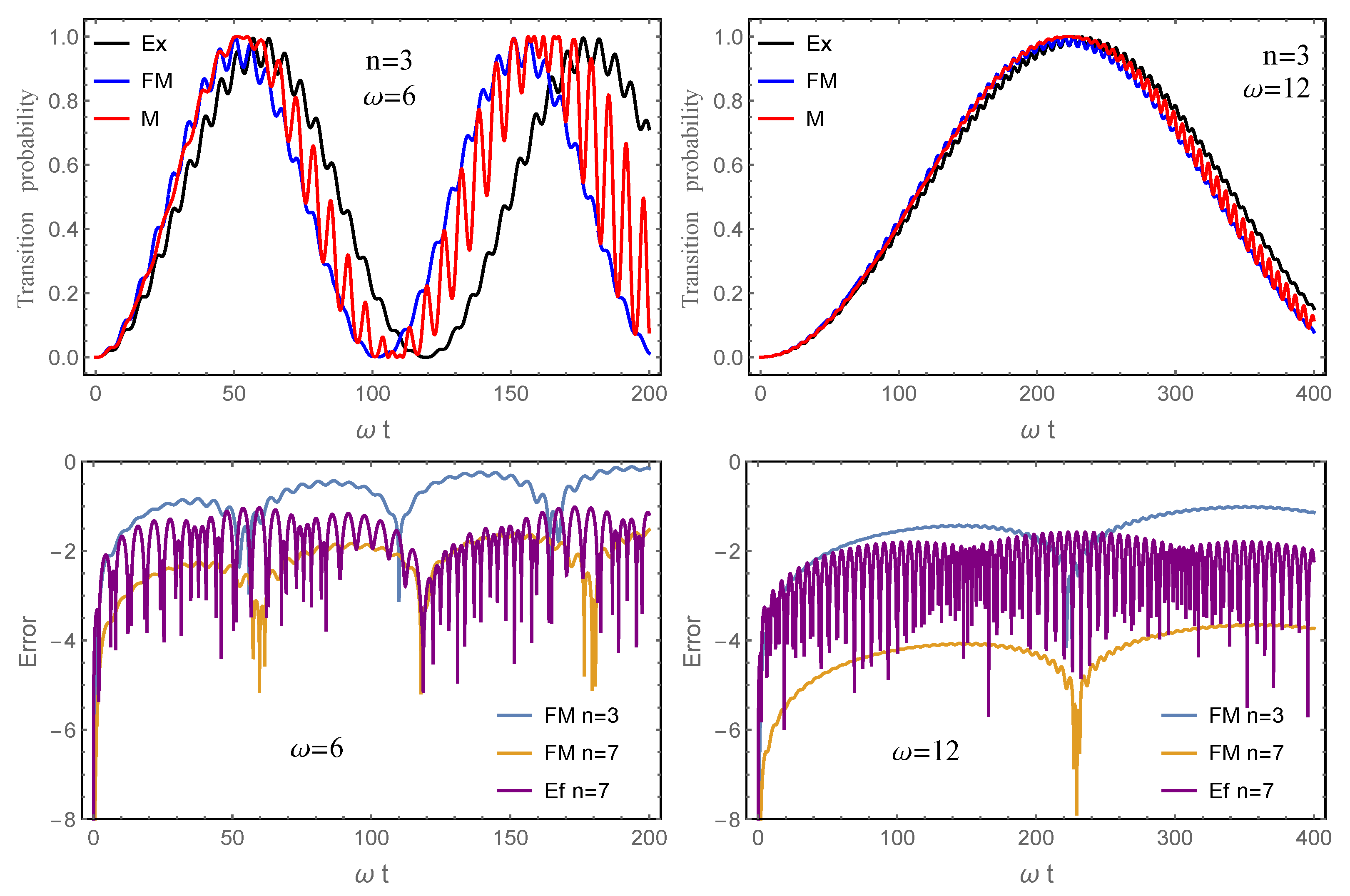
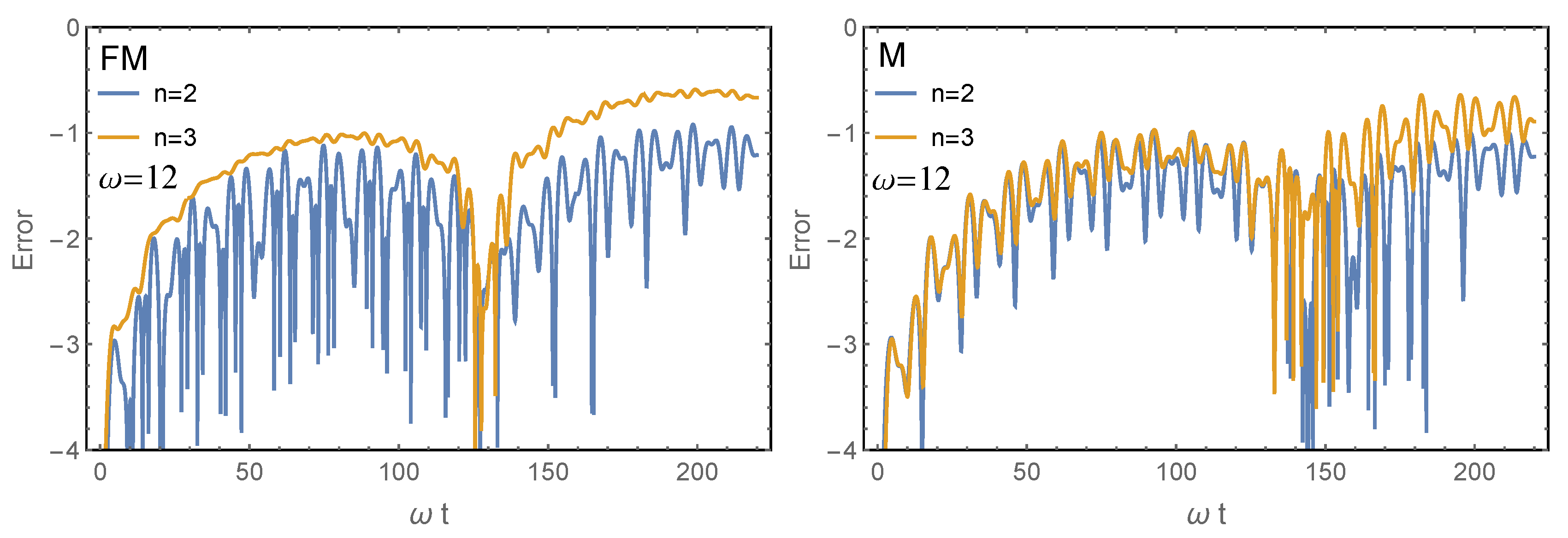
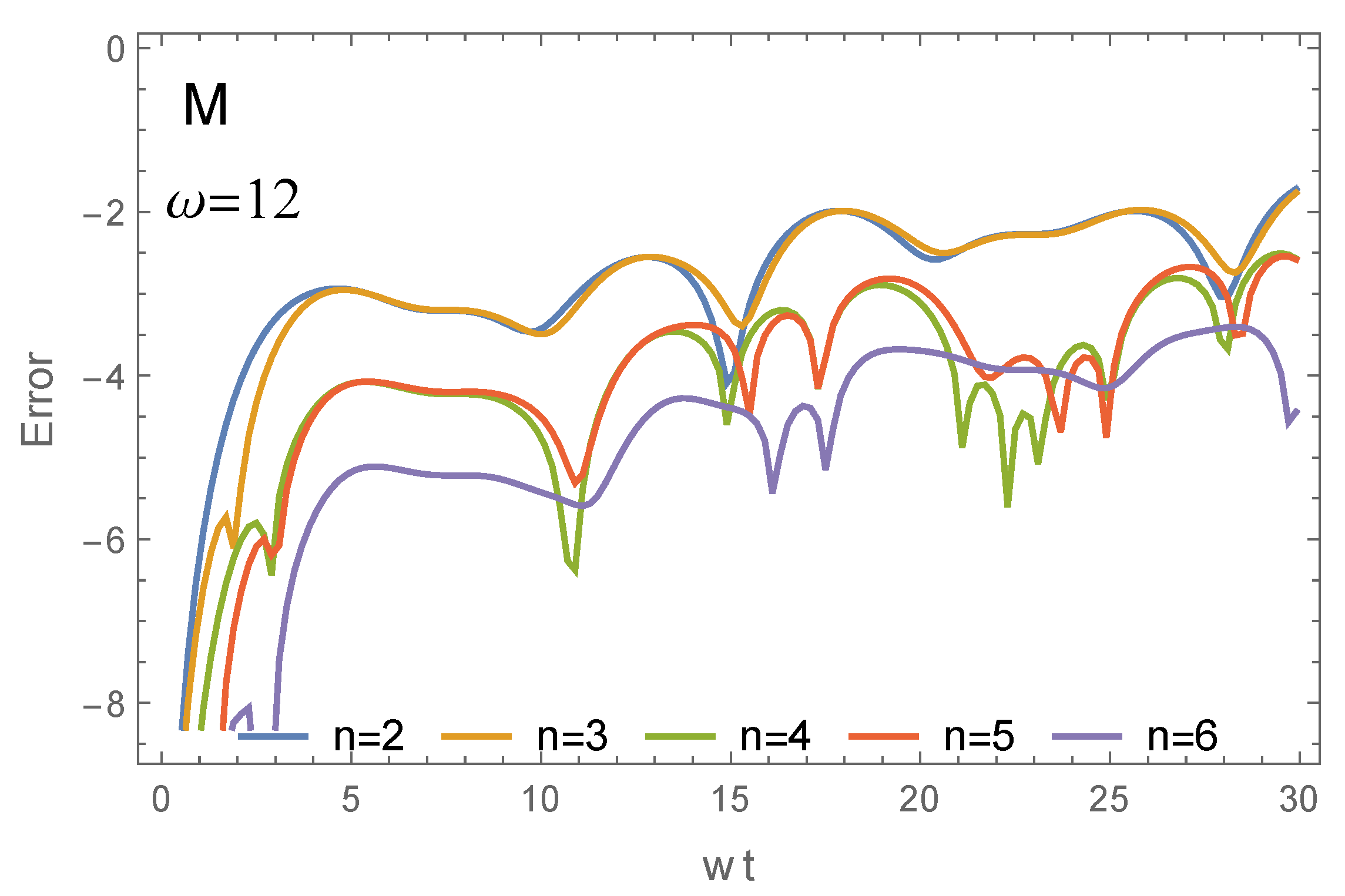
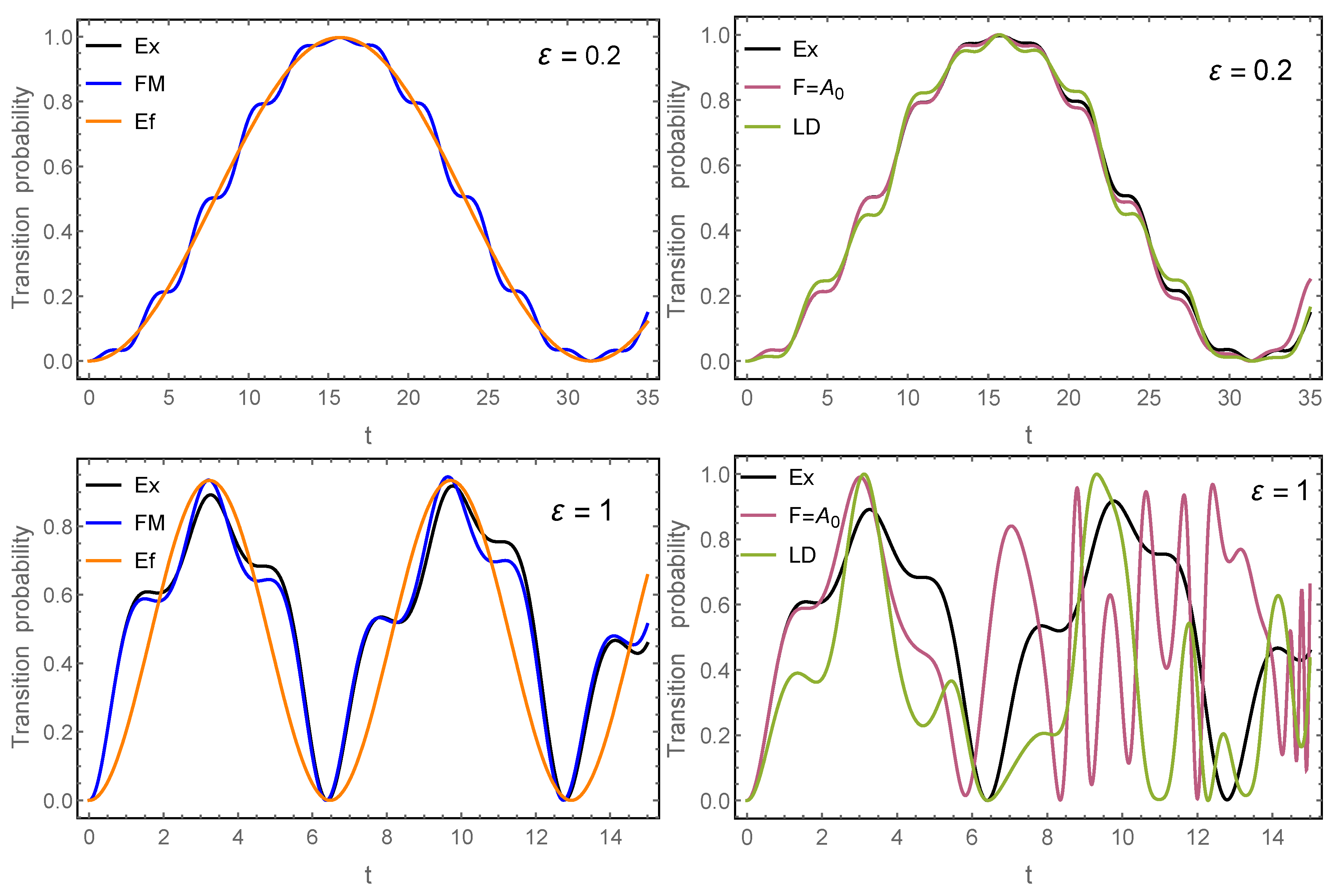
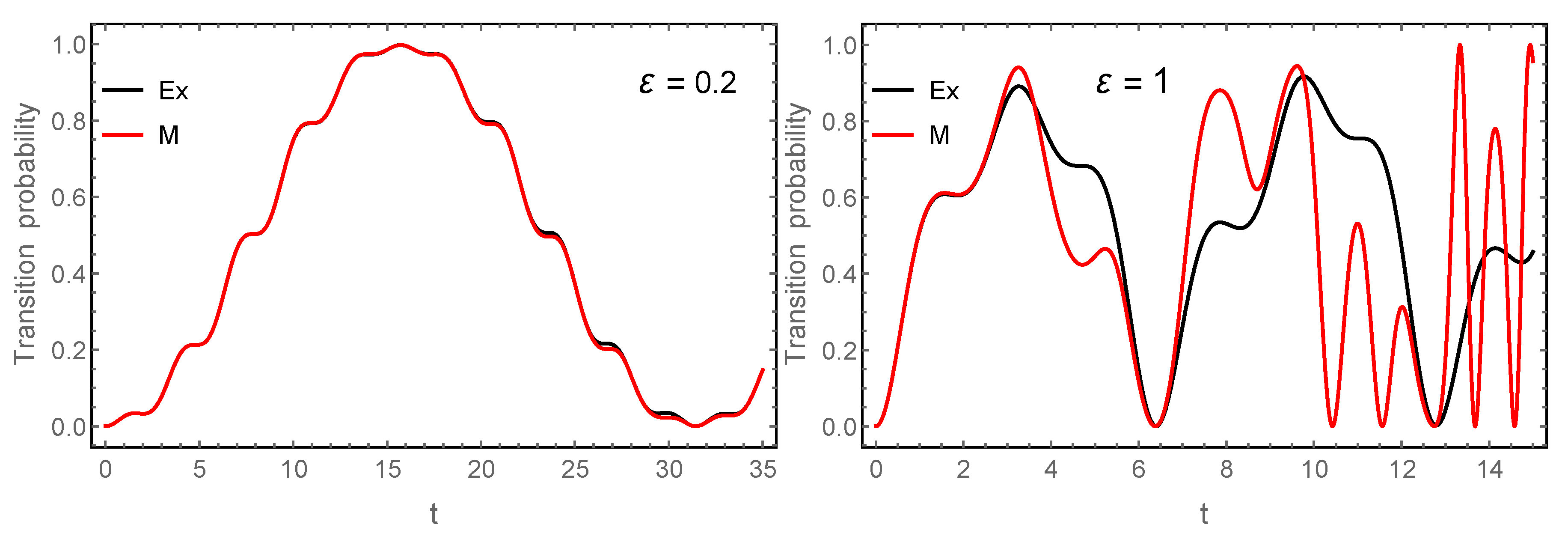
We have seen, in particular, that for problems with a periodic time dependence, the Floquet–Magnus expansion leads to more accurate results over longer time intervals, even for perturbed problems of the form in the interaction picture, unless the parameter is exceedingly small, in which other purely perturbative procedures are competitive. It would be interesting to check whether this conclusion remains valid for more involved problems.
The interested reader may find useful the file available in [
41] containing the
Mathematica implementation of the techniques exposed here for the quantum mechanical problem describing the Bloch–Siegert dynamics.
In this paper we have always taken
, but it is clear that we can also take instead
as the image by the transformation of
. In that case, the solution is factorized as
where, obviously, the recurrences for determining
and
F are slightly different from those collected here. The final results can also vary, as shown in [
33].
Although only examples of quantum mechanics have been considered here, the formalism of this paper can be applied in fact to any explicitly time-dependent linear system of differential equations. This might include the treatment of open quantum systems described by a non-Hermitian Hamiltonian operator [
42]. This will be the subject of future research.