Permanent-Magnet Eddy-Current Losses: A Global Revision of Calculation and Analysis
Abstract
1. Introduction
1.1. Context of this Paper
- Induction furnace: The rapid variation in the magnetic field generates very large eddy-currents, and the heat produced is sufficient to melt a metal;
- Electric brakes: The brakes expose the wheels (metal) to a magnetic field, which generates eddy-currents. The magnetic interaction between the applied field and the eddy-currents acts to slow the wheels down.
- Detection of flaws and cracks in materials.
1.2. Objective of This Paper
2. Sources of PM Losses
2.1. Slotting Effect
2.2. Winding Distribution
2.3. Supply and Control
2.4. PM Hysteresis Losses
3. Calculation of PM Losses
3.1. Two-Dimensional Analytical Models
3.2. Three-Dimensional Analytical Models
3.3. Finite-Elements Analysis
- FE magneto-static method with analytical post-processing:Loss was calculated analytically from the numerically-obtained flux density values. The inducing effect was neglected, as well as the eddy-current reaction field.
- FE magneto-static method:FEA software was used to calculate directly the PMs losses without the need for additional post-processing. The reaction field was not considered.
- FE magneto-dynamic method:The time-stepping method solved Maxwell’s equation for a moving rotor and for any current waveform. It took into account the eddy-current reaction field, but it was very time consuming.
3.4. Hybrid Models
4. PM Loss Reduction
4.1. PM Segmentation
4.2. Rotor Shape
4.3. Material Type Effect
4.4. Spatial Filter
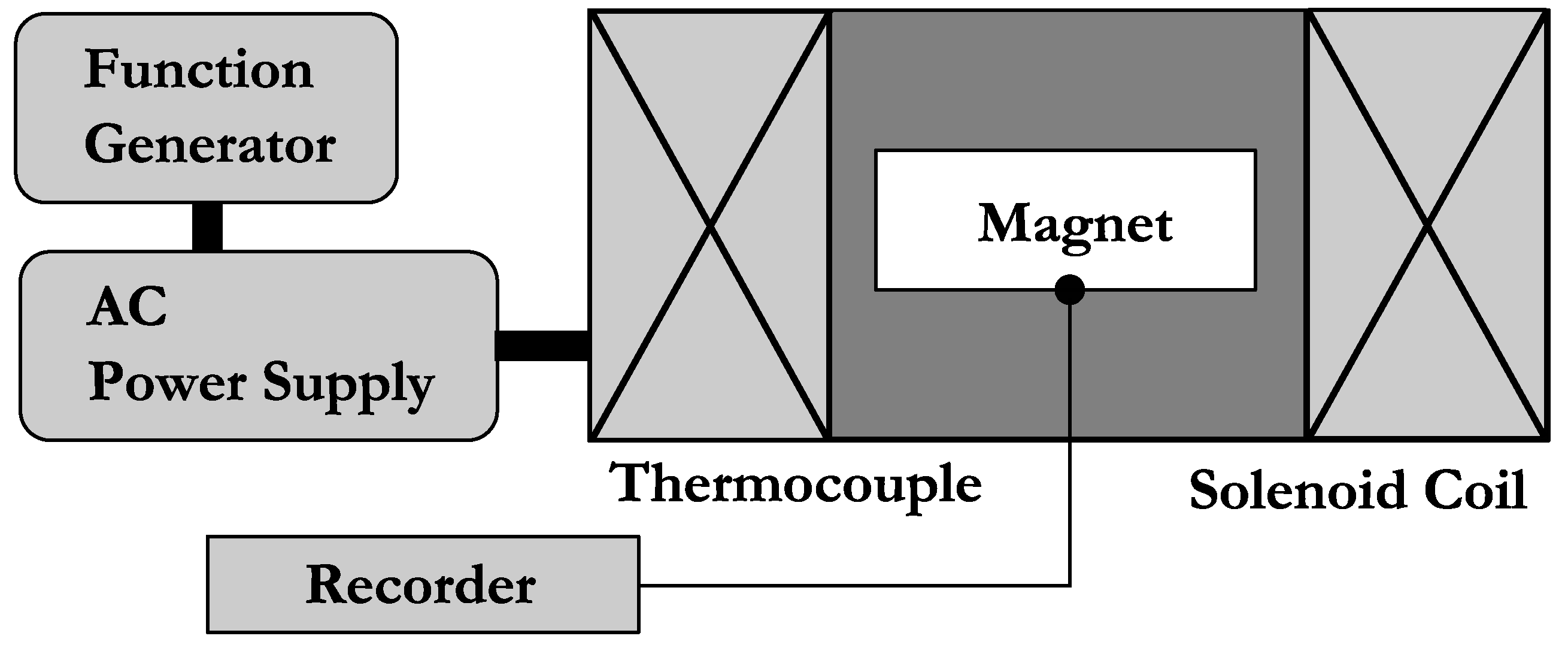
5. PM Loss Measurement
6. Thermal Analysis
7. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Stoll, R.L. The Analysis of Eddy Currents; Oxford University Press: Oxford, UK, 1974. [Google Scholar]
- Cassat, A.; Espanet, C.; Coleman, R.; Burdet, L.; Leleu, E.; Torregrossa, D.; M’Boua, J.; Miraoui, A. A practical solution to mitigate vibrations in industrial PM motors having concentric windings. IEEE Trans. Ind. Appl. 2012, 48, 1526–1538. [Google Scholar] [CrossRef]
- Ouamara, D.; Dubas, F.; Randi, S.A.; Benallal, M.N.; Espanet, C. Electromagnetic Comparison of 3-, 5- and 7-Phases Permanent-Magnet Synchronous Machines: Mild Hybrid Traction Application. Mediterr. J. Model. Simul. 2016, 6, 012–022. [Google Scholar]
- Huang, W.Y.; Bettayeb, A.; Kaczmarek, R.; Vannier, J.C. Optimization of magnet segmentation for reduction of eddy-current losses in permanent magnet synchronous machine. IEEE Trans. Energy Convers. 2010, 25, 381–387. [Google Scholar] [CrossRef]
- Belahcen, A.; Arkkio, A. Permanent magnets models and losses in 2D FEM simulation of electrical machines. In Proceedings of the 19th International Conference on Electrical Machines, Rome, Italy, 6–8 September 2010. [Google Scholar] [CrossRef]
- Alexandrova, J.; Jussila, H.; Nerg, J.; Pyrhönen, J. Comparison between models for eddy-current loss calculations in rotor surface-mounted permanent magnets. In Proceedings of the 19th International Conference on Electrical Machines, Rome, Italy, 6–8 September 2010. [Google Scholar] [CrossRef]
- Tessarolo, A. A survey of state-of-the-art methods to compute rotor eddy-current losses in synchronous permanent magnet machines. In Proceedings of the 2017 IEEE Workshop on Electrical Machines Design, Control and Diagnosis, Nottingham, UK, 20–21 April 2017; pp. 12–19. [Google Scholar] [CrossRef]
- Boules, N. Impact of slot harmonics on losses of high-speed permanent magnet machines with a magnet retaining ring. Electr. Mach. Power Syst. 1981, 6, 527–539. [Google Scholar] [CrossRef]
- Bouillault, F.; Razek, A. Eddy-currents due to stator teeth in synchronous machine rotors. IEEE Trans. Magn. 1984, 20, 1939–1941. [Google Scholar] [CrossRef]
- Abu Sharkh, S.M.; Harris, M.R.; Irenji, N.T. Calculation of rotor eddy-current loss in high-speed pm alternators. In Proceedings of the Eighth International Conference on Electrical Machines and Drives, Cambridge, UK, 1–3 September 1997; pp. 170–174. [Google Scholar] [CrossRef]
- Hor, P.; Zhu, Z.; Howe, D. Eddy-current loss in a moving-coil tubular permanent magnet motor. IEEE Trans. Magn. 1999, 35, 3601–3603. [Google Scholar] [CrossRef]
- Wills, D.A.; Kamper, M.J. Analytical prediction of rotor eddy-current loss due to stator slotting in PM machines. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 12–16 September 2010; pp. 992–995. [Google Scholar] [CrossRef]
- Dubas, F.; Espanet, C. Semi-Analytical Solution of 2D Rotor Eddy-Current Losses due to the Slotting Effect in SMPMM. In Proceedings of the 17th Conference on the Computation of Electromagnetic Fields, Florianópolis, Brazil, 22–26 November 2009; pp. 20–25. [Google Scholar]
- Markovic, M.; Perriard, Y. A simplified determination of the permanent magnet (PM) eddy-current losses due to slotting in a PM rotating motor. In Proceedings of the International Conference on Electrical Machines and Systems (ICEMS), Wuhan, China, 17–20 October 2008; pp. 309–313. [Google Scholar]
- Bode, C.; Canders, W.R. Advanced calculation of eddy-current losses in PMSM with tooth windings. In Proceedings of the XIX International Conference on Electrical Machines, Rome, Italy, 6–8 September 2010; Volume 1, pp. 1–6. [Google Scholar] [CrossRef]
- de la Barriere, O.; Hlioui, S.; Ben Ahmed, H.; Gabsi, M. An Analytical Model for the Computation of No-Load Eddy-Current Losses in the Rotor of a Permanent Magnet Synchronous Machine. IEEE Trans. Magn. 2016, 52, 1–13. [Google Scholar] [CrossRef]
- Fang, Z.X.; Zhu, Z.Q.; Wu, L.J.; Xia, Z.P. Simple and accurate analytical estimation of slotting effect on magnet loss in fractional-slot surface-mounted PM machines. In Proceedings of the 2012 XXth International Conference on Electrical Machines, Marseille, France, 2–5 September 2012; Volume 37, pp. 464–470. [Google Scholar] [CrossRef]
- Nair, S.S.; Wang, J.; Chin, R.; Chen, L.; Sun, T. Analytical Prediction of 3D Magnet Eddy Current Losses in Surface Mounted PM Machines Accounting Slotting Effect. IEEE Trans. Energy Convers. 2017, 32, 414–423. [Google Scholar] [CrossRef]
- Wu, L.J.; Zhu, Z.Q.; Staton, D.; Popescu, M.; Hawkins, D. Analytical model for predicting magnet loss of surface-mounted permanent magnet machines accounting for slotting effect and load. IEEE Trans. Magn. 2012, 48, 107–117. [Google Scholar] [CrossRef]
- Nagarkatti, A.K.; Mohammed, O.A.; Demerdash, N.A. Special Losses in Rotors of Electronically Commutated Brushless DC Motors Induced by Non-Uniformly Rotating Armature MMFS. IEEE Power Eng. Rev. 1982, PER-2, 33. [Google Scholar] [CrossRef]
- Deng, F. Improved analytical modeling of commutation losses including space harmonic effects in permanent magnet brushless DC motors. In Proceedings of the 1997 IEEE International Electric Machines and Drives Conference Record, Milwaukee, WI, USA, 18–21 May 1997; pp. WB2/4.1–WB2/4.3. [Google Scholar] [CrossRef]
- Deng, F. Commutation-caused eddy-current losses in permanent-magnet brushless DC motors. IEEE Trans. Magn. 1997, 33, 4310–4318. [Google Scholar] [CrossRef]
- Atallah, K.; Howe, D.; Mellor, P.; Stone, D. Rotor loss in permanent-magnet brushless AC machines. IEEE Trans. Ind. Appl. 2000, 36, 1612–1618. [Google Scholar] [CrossRef]
- Zhu, Z.; Ng, K.; Schofield, N.; Howe, D. Improved analytical modelling of rotor eddy-current loss in brushless machines equipped with surface-mounted permanent magnets. IEE Proc. Electr. Power Appl. 2004, 151, 641. [Google Scholar] [CrossRef]
- Ishak, D.; Zhu, Z.; Howe, D. Eddy-current loss in the rotor magnets of permanent-magnet brushless machines having a fractional number of slots per pole. IEEE Trans. Magn. 2005, 41, 2462–2469. [Google Scholar] [CrossRef]
- Dubas, F.; Espanet, C.; Miraoui, A. Field Diffusion Equation in High-Speed Surface-Mounted Permanent Magnet Motors, Parasitic Eddy-Current Losses. In Proceedings of the 6th International Symposium on Advanced Electromechanical Motion Systems, Lausanne, Switzerland, 27–29 September 2005; pp. 1–6. [Google Scholar]
- Nakano, M.; Kometani, H.; Kawamura, M. A study on Eddy-current losses in rotors of surface permanent-magnet synchronous machines. IEEE Trans. Ind. Appl. 2006, 42, 429–435. [Google Scholar] [CrossRef]
- Bianchi, N.; Bolognani, S.; Fomasiero, E. A General Approach to Determine the Rotor Losses in Three-Phase Fractional-Slot PM Machines. In Proceedings of the 2007 IEEE International Electric Machines & Drives Conference, Antalya, Turkey, 3–5 May 2007; Volume 1, pp. 634–641. [Google Scholar] [CrossRef]
- Bianchi, N.; Fornasiero, E. Impact of MMF Space Harmonic on Rotor Losses in Fractional-Slot Permanent-Magnet Machines. IEEE Trans. Energy Convers. 2009, 24, 323–328. [Google Scholar] [CrossRef]
- Bianchi, N.; Fornasiero, E. Index of rotor losses in three-phase fractional-slot permanent magnet machines. IET Electr. Power Appl. 2009, 3, 381. [Google Scholar] [CrossRef]
- Bianchi, N.; Bolognani, S.; Fornasiero, E. An Overview of Rotor Losses Determination in Three-Phase Fractional-Slot PM Machines. IEEE Trans. Ind. Appl. 2010, 46, 2338–2345. [Google Scholar] [CrossRef]
- Li, J.; Choi, D.W.; Son, D.H.; Cho, Y.H. Effects of MMF Harmonics on Rotor Eddy-Current Losses for Inner-Rotor Fractional Slot Axial Flux Permanent Magnet Synchronous Machines. IEEE Trans. Magn. 2012, 48, 839–842. [Google Scholar] [CrossRef]
- El-Refaie, A.; Shah, M.; Qu, R.; Kern, J. Effect of Number of Phases on Losses in Conducting Sleeves of Surface PM Machine Rotors Equipped With Fractional-Slot Concentrated Windings. IEEE Trans. Ind. Appl. 2008, 44, 1522–1532. [Google Scholar] [CrossRef]
- Fornasiero, E.; Bianchi, N.; Bolognani, S. Slot Harmonic Impact on Rotor Losses in Fractional-Slot Permanent-Magnet Machines. IEEE Trans. Ind. Electron. 2012, 59, 2557–2564. [Google Scholar] [CrossRef]
- Dajaku, G.; Gerling, D. Eddy-current loss minimization in rotor magnets of PM machines using high-efficiency 12-teeth/10-slots winding topology. In Proceedings of the 2011 International Conference on Electrical Machines and Systems, Beijing, China, 20–23 August 2011. [Google Scholar] [CrossRef]
- Aslan, B.; Semail, E.; Legranger, J. Analytical model of magnet eddy-current volume losses in multi-phase PM machines with concentrated winding. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; Volume L, pp. 3371–3378. [Google Scholar] [CrossRef]
- Aslan, B.; Semail, E.; Legranger, J. General Analytical Model of Magnet Average Eddy-Current Volume Losses for Comparison of Multiphase PM Machines With Concentrated Winding. IEEE Trans. Energy Convers. 2014, 29, 72–83. [Google Scholar] [CrossRef]
- Li, J.; Xu, Y.; Zou, J.; Wang, Q.; Liang, W. Analysis and Reduction of Magnet Loss by Deepening Magnets in Interior Permanent-Magnet Machines With a Pole/Slot Ratio of 2/3. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- van der Veen, J.; Offringa, L.; Vandenput, A. Minimising rotor losses in high-speed high-power permanent magnet synchronous generators with rectifier load. IEE Proc. Electr. Power Appl. 1997, 144, 331–337. [Google Scholar] [CrossRef]
- Polinder, H.; Hoeijmakers, M. Eddy-current losses in the segmented surface-mounted magnets of a PM machine. IEE Proc. Electr. Power Appl. 1999, 146, 261–266. [Google Scholar] [CrossRef]
- Zhu, Z.; Ng, K.; Schofield, N.; Howe, D. Analytical prediction of rotor eddy-current loss in brushless machines equipped with surface-mounted permanent magnets. I. Magnetostatic field model. In Proceedings of the Fifth International Conference on Electrical Machines and Systems, Shenyang, China, 18–20 August 2001; Volume 2, pp. 806–809. [Google Scholar] [CrossRef]
- Schofield, N.; Ng, K.; Zhu, Z.Q.; Howe, D. Parasitic rotor losses in a brushless permanent magnet traction machine. In Proceedings of the Eighth International Conference on Electrical Machines and Drives, Cambridge, UK, 1–3 September 1997; pp. 200–204. [Google Scholar]
- Deng, F.; Nehl, T. Analytical modeling of eddy-current losses caused by pulse-width-modulation switching in permanent-magnet brushless direct-current motors. IEEE Trans. Magn. 1998, 34, 3728–3736. [Google Scholar] [CrossRef]
- Bellara, A.; Bali, H.; Belfkira, R.; Amara, Y.; Barakat, G. Analytical Prediction of Open-Circuit Eddy-Current Loss in Series Double Excitation Synchronous Machines. IEEE Trans. Magn. 2011, 47, 2261–2268. [Google Scholar] [CrossRef]
- Sergeant, P.; Van den Bossche, A. Segmentation of Magnets to Reduce Losses in Permanent-Magnet Synchronous Machines. IEEE Trans. Magn. 2008, 44, 4409–4412. [Google Scholar] [CrossRef]
- Marashi, A.N.; Abbaszadeh, K.; Alam, F.R. Analysis and reduction of magnet eddy-current losses in surface mounted permanent magnet machines. In Proceedings of the 2014 22nd Iranian Conference on Electrical Engineering (ICEE), Tehran, Iran, 20–22 May 2014; pp. 782–786. [Google Scholar] [CrossRef]
- Jumayev, S.; Merdzan, M.; Boynov, K.O.; Paulides, J.J.H.; Pyrhonen, J.; Lomonova, E.A. The Effect of PWM on Rotor Eddy-Current Losses in High-Speed Permanent Magnet Machines. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Cheng, M.; Zhu, S. Calculation of PM Eddy Current Loss in IPM Machine Under PWM VSI Supply With Combined 2D FE and Analytical Method. IEEE Trans. Magn. 2017, 53, 1–12. [Google Scholar] [CrossRef]
- Yamazaki, K.; Abe, A. Loss Investigation of Interior Permanent-Magnet Motors Considering Carrier Harmonics and Magnet Eddy Currents. IEEE Trans. Ind. Appl. 2009, 45, 659–665. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Chen, Y.; Howe, D.; Gliemann, J.H. Rotor Eddy Current Loss in Single-Phase Permanent Magnet Brushless DC Motor. In Proceedings of the 2007 IEEE Industry Applications Annual Meeting, New Orleans, LA, USA, 23–27 September 2007; pp. 537–543. [Google Scholar] [CrossRef]
- Yamazaki, K.; Fukushima, Y.; Sato, M. Loss Analysis of Permanent-Magnet Motors with Concentrated Windings—Variation of Magnet Eddy-Current Loss Due to Stator and Rotor Shapes. IEEE Trans. Ind. Appl. 2009, 45, 1334–1342. [Google Scholar] [CrossRef]
- Ding, X.; Mi, C. Modeling of eddy-current loss in the magnets of permanent magnet machines for hybrid and electric vehicle traction applications. In Proceedings of the 2009 IEEE Vehicle Power and Propulsion Conference, Dearborn, MI, USA, 7–10 September 2009; Volume 20, pp. 419–424. [Google Scholar] [CrossRef]
- Jumayev, S.; Borisavljevic, A.; Boynov, K.; Lomonova, E.A.; Pyrhonen, J. Analysis of rotor eddy-current losses in slotless high-speed permanent magnet machines. In Proceedings of the 2014 16th European Conference on Power Electronics and Applications, Lappeenranta, Finland, 26–28 August 2014. [Google Scholar] [CrossRef]
- Hemeida, A.; Sergeant, P.; Vansompel, H. Comparison of Methods for Permanent Magnet Eddy-Current Loss Computations with and without Reaction Field Considerations in Axial Flux PMSM. IEEE Trans. Magn. 2015, 51, 1–11. [Google Scholar] [CrossRef]
- Qazalbash, A.A.; Sharkh, S.M.; Irenji, N.T.; Wills, R.G.; Abusara, M.A. Rotor Eddy Current Power Loss in Permanent Magnet Synchronous Generators Feeding Uncontrolled Rectifier Loads. IEEE Trans. Magn. 2014, 50, 1–9. [Google Scholar] [CrossRef]
- Balamurali, A.; Lai, C.; Mollaeian, A.; Loukanov, V.; Kar, N.C. Analytical Investigation Into Magnet Eddy Current Losses in Interior Permanent Magnet Motor Using Modified Winding Function Theory Accounting for Pulsewidth Modulation Harmonics. IEEE Trans. Magn. 2016, 52, 1–5. [Google Scholar] [CrossRef]
- Narjes, G.; Ponick, B. Novel Method for the Determination of Eddy Current Losses in the Permanent Magnets of a High-Speed Synchronous Machine. In Proceedings of the 2018 XIII International Conference on Electrical Machines (ICEM), Alexandroupoli, Greece, 3–6 September 2018; pp. 1285–1290. [Google Scholar] [CrossRef]
- Fukuma, A.; Kanazawa, S.; Miyagi, D.; Takahashi, N. Investigation of AC loss of permanent magnet of SPM motor considering hysteresis and eddy-current losses. IEEE Trans. Magn. 2005, 41, 1964–1967. [Google Scholar] [CrossRef]
- Pyrhonen, J.; Ruoho, S.; Nerg, J.; Paju, M.; Tuominen, S.; Kankaanpaa, H.; Stern, R.; Boglietti, A.; Uzhegov, N. Hysteresis Losses in Sintered NdFeB Permanent Magnets in Rotating Electrical Machines. IEEE Trans. Ind. Electron. 2015, 62, 857–865. [Google Scholar] [CrossRef]
- Petrov, I.; Egorov, D.; Link, J.; Stern, R.; Ruoho, S.; Pyrhonen, J. Hysteresis Losses in Different Types of Permanent Magnets Used in PMSMs. IEEE Trans. Ind. Electron. 2017, 64, 2502–2510. [Google Scholar] [CrossRef]
- Egorov, D.; Petrov, I.; Pyrhonen, J.; Link, J.; Stern, R. Hysteresis Loss in Ferrite Permanent Magnets in Rotating Electrical Machinery. IEEE Trans. Ind. Electron. 2018, 65, 9280–9290. [Google Scholar] [CrossRef]
- Sikora, R.; Purczynski, J.; Lipinski, W.; Gramz, M. Use of variational methods to the eddy-currents calculation in thin conducting plates. IEEE Trans. Magn. 1978, 14, 383–385. [Google Scholar] [CrossRef]
- Davey, K.; Turner, L. Prediction of transient eddy-current fields using surface impedance methods. IEEE Trans. Magn. 1989, 25, 4156–4158. [Google Scholar] [CrossRef]
- Polinder, H.; Hoeijmakers, M. Eddy-current losses in the permanent magnets of a PM machine. In Proceedings of the 1997 Eighth International Conference on Electrical Machines and Drives, Cambridge, UK, 1–3 September 1997; pp. 138–142. [Google Scholar]
- Spooner, E.; Williamson, A. Parasitic Losses in Modular Permanent-Magnet Generators. IEE Proc. Electr. Power Appl. 1998, 145, 485–496. [Google Scholar] [CrossRef]
- Wang, J.; Atallah, K.; Chin, R.; Arshad, W.M.; Lendenmann, H. Rotor Eddy-Current Loss in Permanent-Magnet Brushless AC Machines. IEEE Trans. Magn. 2010, 46, 2701–2707. [Google Scholar] [CrossRef]
- Zhu, Z.; Ng, K.; Schofield, N.; Howe, D. Analytical Prediction of Rotor Eddy Current Loss in Brushless Machines Equipped with Surface-Mounted Permanent Magnets. II: Accounting for Eddy Current Reaction Field. In Proceedings of the Fifth International Conference on Electrical Machines and Systems, Shenyang, China, 18–20 August 2001; Volume 2, pp. 810–813. [Google Scholar] [CrossRef]
- Markovic, M.; Perriard, Y. An Analytical Determination of Eddy-Current Losses in a Configuration With a Rotating Permanent Magnet. IEEE Trans. Magn. 2007, 43, 3380–3386. [Google Scholar] [CrossRef]
- Miljavec, D.; Zidarič, B. Eddy-current losses in permanent magnets of the BLDC machine. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2007, 26, 1095–1104. [Google Scholar] [CrossRef]
- Markovic, M.; Perriard, Y. Analytical Solution for Rotor Eddy-Current Losses in a Slotless Permanent-Magnet Motor: The Case of Current Sheet Excitation. IEEE Trans. Magn. 2008, 44, 386–393. [Google Scholar] [CrossRef]
- Wang, J.; Papini, F.; Chin, R.; Arshad, W.M.; Lendenmann, H. Computationally efficient approaches for evaluation of rotor eddy current loss in permanent magnet brushless machines. In Proceedings of the 2009 International Conference on Electrical Machines and Systems, Tokyo, Japan, 15–18 November 2009. [Google Scholar] [CrossRef]
- Tariq, A.R.; Nino-Baron, C.E.; Strangas, E.G. Iron and Magnet Losses and Torque Calculation of Interior Permanent Magnet Synchronous Machines Using Magnetic Equivalent Circuit. IEEE Trans. Magn. 2010, 46, 4073–4080. [Google Scholar] [CrossRef]
- Nuscheler, R. Two-dimensional analytical model for eddy-current rotor loss calculation of PMS machines with concentrated stator windings and a conductive shield for the magnet. In Proceedings of the XIX International Conference on Electrical Machines, Rome, Italy, 6–8 September 2010. [Google Scholar] [CrossRef]
- Bettayeb, A.; Jannot, X.; Vannier, J.C. Analytical calculation of rotor magnet eddy-current losses for high speed IPMSM. In Proceedings of the XIX International Conference on Electrical Machines, Rome, Italy, 6–8 September 2010. [Google Scholar] [CrossRef]
- Yoshida, Y.; Nakamura, K.; Ichinokura, O. A Method for Calculating Eddy Current Loss Distribution Based on Reluctance Network Analysis. IEEE Trans. Magn. 2011, 47, 4155–4158. [Google Scholar] [CrossRef]
- Yoshida, Y.; Nakamura, K.; Ichinokura, O. Basic examination of eddy-current loss estimation in SPM motor based on electric and magnetic networks. In Proceedings of the 2012 XXth International Conference on Electrical Machines, Marseille, France, 2–5 September 2012; Volume 48, pp. 1586–1591. [Google Scholar] [CrossRef]
- Hemeida, A.; Sergeant, P. Analytical modeling of eddy-current losses in Axial Flux PMSM using resistance network. In Proceedings of the 2014 International Conference on Electrical Machines (ICEM), Berlin, Germany, 2–5 September 2014; pp. 2688–2694. [Google Scholar] [CrossRef]
- Wu, L.J.; Zhu, Z.Q.; Staton, D.; Popescu, M.; Hawkins, D. Analytical Modeling and Analysis of Open-Circuit Magnet Loss in Surface-Mounted Permanent-Magnet Machines. IEEE Trans. Magn. 2012, 48, 1234–1247. [Google Scholar] [CrossRef]
- Pyrhonen, J.; Jussila, H.; Alexandrova, Y.; Rafajdus, P.; Nerg, J. Harmonic Loss Calculation in Rotor Surface Permanent Magnets—New Analytic Approach. IEEE Trans. Magn. 2012, 48, 2358–2366. [Google Scholar] [CrossRef]
- Rahideh, A.; Korakianitis, T. Analytical magnetic field distribution of slotless brushless permanent magnet motors – Part I. Armature reaction field, inductance and rotor eddy-current loss calculations. IET Electr. Power Appl. 2012, 6, 628. [Google Scholar] [CrossRef]
- Arumugam, P.; Hamiti, T.; Gerada, C. Estimation of Eddy Current Loss in Semi-Closed Slot Vertical Conductor Permanent Magnet Synchronous Machines Considering Eddy Current Reaction Effect. IEEE Trans. Magn. 2013, 49, 5326–5335. [Google Scholar] [CrossRef]
- Gotovac, G.; Lampic, G.; Miljavec, D. Analytical Model of Permeance Variation Losses in Permanent Magnets of the Multipole Synchronous Machine. IEEE Trans. Magn. 2013, 49, 921–928. [Google Scholar] [CrossRef]
- Dubas, F.; Rahideh, A. Two-Dimensional Analytical Permanent-Magnet Eddy-Current Loss Calculations in Slotless PMSM Equipped With Surface-Inset Magnets. IEEE Trans. Magn. 2014, 50, 54–73. [Google Scholar] [CrossRef]
- Martin, F.; Zaim, M.E.H.; Tounzi, A.; Bernard, N. Improved Analytical Determination of Eddy Current Losses in Surface Mounted Permanent Magnets of Synchronous Machine. IEEE Trans. Magn. 2014, 50, 1–9. [Google Scholar] [CrossRef]
- Paradkar, M.; Bocker, J. 2D analytical model for estimation of eddy-current loss in the magnets of IPM machines considering the reaction field of the induced eddy currents. In Proceedings of the 2015 IEEE International Electric Machines & Drives Conference (IEMDC), Coeur d’Alene, ID, USA, 10–13 May 2015; pp. 1096–1102. [Google Scholar] [CrossRef]
- Pfister, P.D.; Yin, X.; Fang, Y. Slotted Permanent-Magnet Machines: General Analytical Model of Magnetic Fields, Torque, Eddy Currents, and Permanent-Magnet Power Losses Including the Diffusion Effect. IEEE Trans. Magn. 2016, 52, 1–13. [Google Scholar] [CrossRef]
- Qazalbash, A.A.; Sharkh, S.M.; Irenji, N.T.; Wills, R.G.; Abusara, M.A. Rotor eddy loss in high-speed permanent magnet synchronous generators. IET Electr. Power Appl. 2015, 9, 370–376. [Google Scholar] [CrossRef]
- Mirzaei, M.; Binder, A.; Funieru, B.; Susic, M. Analytical Calculations of Induced Eddy Currents Losses in the Magnets of Surface Mounted PM Machines With Consideration of Circumferential and Axial Segmentation Effects. IEEE Trans. Magn. 2012, 48, 4831–4841. [Google Scholar] [CrossRef]
- Masmoudi, A.; Masmoudi, A. 3D Analytical Model With the End Effect Dedicated to the Prediction of PM Eddy-Current Loss in FSPMMs. IEEE Trans. Magn. 2015, 51, 1–11. [Google Scholar] [CrossRef]
- Paradkar, M.; Bocker, J. 3D analytical model for estimation of eddy-currentlosses in the magnets of IPM machine considering the reaction field of the induced eddy currents. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 2862–2869. [Google Scholar] [CrossRef]
- Chen, L.; Wang, J.; Nair, S.S. An Analytical Method for Predicting 3D Eddy Current Loss in Permanent Magnet Machines Based on Generalized Image Theory. IEEE Trans. Magn. 2016, 52, 1–11. [Google Scholar] [CrossRef]
- Nair, S.S.; Wang, J.; Chen, L.; Chin, R.; Manolas, I.; Svechkarenko, D. Prediction of 3D High-Frequency Eddy Current Loss in Rotor Magnets of SPM Machines. IEEE Trans. Magn. 2016, 52, 1–10. [Google Scholar] [CrossRef]
- Nair, S.S.; Wang, J.; Chen, L.; Chin, R.; Manolas, I.; Svechkarenko, D. Computationally Efficient 3D Eddy Current Loss Prediction in Magnets of Interior Permanent Magnet Machines. IEEE Trans. Magn. 2016, 52, 1–10. [Google Scholar] [CrossRef]
- Nair, S.S.; Wang, J.; Chen, L.; Chin, R.; Manolas, I.; Svechkarenko, D. Computationally efficient 3D rotor eddy-current loss prediction in permanent magnet machines. In Proceedings of the 2016 XXII International Conference on Electrical Machines (ICEM), Lausanne, Switzerland, 4–7 September 2016; pp. 1426–1432. [Google Scholar] [CrossRef]
- Chin, R.; Chen, L.; Manolas, I.; Wang, J.; Nair, S.; Svechkarenko, D. 3D Analytical Slotting-Effect Model for Magnet Loss Prediction in SPM Machines. In Proceedings of the 8th IET International Conference on Power Electronics, Machines and Drives (PEMD 2016), Glasgow, UK, 19–21 April 2016. [Google Scholar]
- Nair, S.S.; Chen, L.; Wang, J.; Chin, R.; Manolas, I.; Svechkarenko, D. Computationally efficient 3D analytical magnet loss prediction in surface mounted permanent magnet machines. IET Electr. Power Appl. 2017, 11, 9–18. [Google Scholar] [CrossRef]
- Mecrow, B.; Masterman, J.M. Determination of Rotor Eddy Current Losses in Permanent Magnet Machines. In Proceedings of the Sixth International Conference on Electrical Machines and Drives, Oxford, UK, 8–10 September 1993; pp. 299–304. [Google Scholar]
- Kamiya, Y.; Onuki, T. 3D eddy-current analysis by the finite element method using double nodes technique. IEEE Trans. Magn. 1996, 32, 741–744. [Google Scholar] [CrossRef]
- Kawase, Y.; Ota, T.; Fukunaga, H. 3D eddy-current analysis in permanent magnet of interior permanent magnet motors. IEEE Trans. Magn. 2000, 36, 1863–1866. [Google Scholar] [CrossRef]
- Yoshida, K.; Hita, Y.; Kesamaru, K. Eddy-current loss analysis in PM of surface-mounted-PM SM for electric vehicles. IEEE Trans. Magn. 2000, 36, 1941–1944. [Google Scholar] [CrossRef]
- Yamazaki, K.; Watari, S. Loss analysis of permanent-magnet motor considering carrier harmonics of PWM inverter using combination of 2D and 3D finite-element method. IEEE Trans. Magn. 2005, 41, 1980–1983. [Google Scholar] [CrossRef]
- Pang, Y.; Zhu, Z.; Howe, D.; Iwasaki, S.; Deodhar, R.; Pride, A. Eddy Current Loss in the Frame of a Flux-Switching Permanent Magnet Machine. IEEE Trans. Magn. 2006, 42, 3413–3415. [Google Scholar] [CrossRef]
- Al-Naemi, F.I.; Moses, A.J. FEM Modeling of Rotor Losses in PM Motors. J. Magn. Magn. Mater. 2006, 304, 794–797. [Google Scholar] [CrossRef]
- Deak, C.; Petrovic, L.; Binder, A.; Mirzaei, M.; Irimie, D.; Funieru, B. Calculation of eddy-current losses in permanent magnets of synchronous machines. In Proceedings of the 2008 International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Ischia, Italy, 11–13 June 2008; Volume 30, pp. 26–31. [Google Scholar] [CrossRef]
- Yamazaki, K.; Kanou, Y. Rotor Loss Analysis of Interior Permanent Magnet Motors Using Combination of 2D and 3D Finite Element Method. IEEE Trans. Magn. 2009, 45, 1772–1775. [Google Scholar] [CrossRef]
- Ruoho, S.; Santa-Nokki, T.; Kolehmainen, J.; Arkkio, A. Modeling Magnet Length In 2D Finite-Element Analysis of Electric Machines. IEEE Trans. Magn. 2009, 45, 3114–3120. [Google Scholar] [CrossRef]
- Fadriansyah, T.; Strous, T.D.; Polinder, H. Axial segmentation and magnets losses of SMPM machines using 2D FE method. In Proceedings of the 2012 XXth International Conference on Electrical Machines, Marseille, France, 2–5 September 2012; pp. 577–581. [Google Scholar] [CrossRef]
- Yang, X.; Patterson, D.; Hudgins, J.; Colton, J. FEA estimation and experimental validation of solid rotor and magnet eddy-current loss in single-sided axial flux permanent magnet machines. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013; pp. 3202–3209. [Google Scholar] [CrossRef]
- El-Hasan, T. Rotor eddy-current determination using finite element analysis for High-Speed Permanent Magnet Machines. In Proceedings of the 2014 IEEE 23rd International Symposium on Industrial Electronics (ISIE), Istanbul, Turkey, 1–4 June 2014; pp. 885–889. [Google Scholar] [CrossRef]
- Li, J.; Choi, D.W.; Cho, C.H.; Koo, D.H.; Cho, Y.H. Eddy-Current Calculation of Solid Components in Fractional Slot Axial Flux Permanent Magnet Synchronous Machines. IEEE Trans. Magn. 2011, 47, 4254–4257. [Google Scholar] [CrossRef]
- Okitsu, T.; Matsuhashi, D.; Muramatsu, K. Method for Evaluating the Eddy Current Loss of a Permanent Magnet in a PM Motor Driven by an Inverter Power Supply Using Coupled 2D and 3D Finite Element Analyses. IEEE Trans. Magn. 2009, 45, 4574–4577. [Google Scholar] [CrossRef]
- Okitsu, T.; Matsuhashi, D.; Gao, Y.; Muramatsu, K. Coupled 2D and 3D Eddy Current Analyses for Evaluating Eddy Current Loss of a Permanent Magnet in Surface PM Motors. IEEE Trans. Magn. 2012, 48, 3100–3103. [Google Scholar] [CrossRef]
- Vansompel, H.; Sergeant, P.; Dupré, L. Effect of segmentation on eddy-current loss in permanent-magnets of axial-flux PM machines using a multilayer-2D–2D coupled model. In Proceedings of the 2012 XXth International Conference on Electrical Machines, Marseille, France, 2–5 September 2012; pp. 228–232. [Google Scholar] [CrossRef]
- Vansompel, H.; Sergeant, P.; Dupré, L. A Multilayer 2D–2D Coupled Model for Eddy Current Calculation in the Rotor of an Axial-Flux PM Machine. IEEE Trans. Energy Convers. 2012, 27, 784–791. [Google Scholar] [CrossRef]
- Steentjes, S.; Boehmer, S.; Hameyer, K. Permanent Magnet Eddy-Current Losses in 2D FEM Simulations of Electrical Machines. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Schmidt, E.; Kaltenbacher, M.; Wolfschluckner, A. Eddy-current losses in permanent magnets of surface mounted permanent magnet synchronous machines—Analytical calculation and high order finite element analyses. e & i Elektrotechnik und Informationstechnik 2017, 134, 148–155. [Google Scholar] [CrossRef][Green Version]
- Chen, Q.; Liang, D.; Jia, S.; Wan, X. Analysis of Multi-Phase and Multi-Layer Factional-Slot Concentrated-Winding on PM Eddy Current Loss Considering Axial Segmentation and Load Operation. IEEE Trans. Magn. 2018, 54, 1–6. [Google Scholar] [CrossRef]
- Saban, D.M.; Lipo, T.A. Hybrid Approach for Determining Eddy-Current Losses in High-Speed PM Rotors. In Proceedings of the 2007 IEEE International Electric Machines & Drives Conference, Antalya, Turkey, 3–5 May 2007; Volume 1, pp. 658–661. [Google Scholar] [CrossRef]
- Niu, S.; Chau, K.T.; Li, J.; Li, W. Eddy-Current Analysis of Double-Stator Inset-Type Permanent Magnet Brushless Machines. IEEE Trans. Appl. Supercond. 2010, 20, 1097–1101. [Google Scholar] [CrossRef]
- Madina, P.; Poza, J.; Ugalde, G.; Almandoz, G. Magnet eddy-current loss calculation method for segmentation analysis on permanent magnet machines. In Proceedings of the 2011 14th European Conference on Power Electronics and Applications (EPE 2011), Birmingham, UK, 30 August–1 September 2011; pp. 1–9. [Google Scholar]
- Lee, S.-Y.; Jung, H.-K. Eddy-current loss analysis in the rotor of permanent magnet traction motor with high power density. In Proceedings of the 2012 IEEE Vehicle Power and Propulsion Conference, Seoul, South Korea, 9–12 October 2012; pp. 210–214. [Google Scholar] [CrossRef]
- Zhang, P.; Sizov, G.Y.; He, J.; Ionel, D.M.; Demerdash, N.A.O. Calculation of Magnet Losses in Concentrated-Winding Permanent-Magnet Synchronous Machines Using a Computationally Efficient Finite-Element Method. IEEE Trans. Ind. Appl. 2013, 49, 2524–2532. [Google Scholar] [CrossRef]
- Wu, X.; Wrobel, R.; Mellor, P.H.; Zhang, C. A computationally efficient PM power loss derivation for surface-mounted brushless AC PM machines. In Proceedings of the 2014 International Conference on Electrical Machines (ICEM), Berlin, Germany, 2–5 September 2014; Volume 105, pp. 17–23. [Google Scholar] [CrossRef]
- Wu, X.; Wrobel, R.; Mellor, P.H.; Zhang, C. A Computationally Efficient PM Power Loss Mapping for Brushless AC PM Machines With Surface-Mounted PM Rotor Construction. IEEE Trans. Ind. Electron. 2015, 62, 7391–7401. [Google Scholar] [CrossRef]
- Benlamine, R.; Dubas, F.; Randi, S.A.; Lhotellier, D.; Espanet, C. 3D Numerical Hybrid Method for PM Eddy-Current Losses Calculation: Application to Axial-Flux PMSMs. IEEE Trans. Magn. 2015, 51, 1–10. [Google Scholar] [CrossRef]
- Daanoune, A.; Lateb, R.; da Silva, J. Semi analytical model for eddy current losses calculation in high speed permanent magnet synchronous machines. In Proceedings of the International Conference on Electrical Machines and Systems (ICEMS), Chiba, Japan, 13–16 November 2016; pp. 1–6. [Google Scholar]
- Gerlach, T.; Rabenstein, L.; Dietz, A.; Kremser, A.; Gerling, D. Determination of eddy-current losses in permanent magnets of SPMSM with concentrated windings: A hybrid loss calculation method and experimental verification. In Proceedings of the 2018 Thirteenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte-Carlo, Monaco, 10–12 April 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Toda, H.; Xia, Z.; Wang, J.; Atallah, K.; Howe, D. Rotor Eddy-Current Loss in Permanent Magnet Brushless Machines. IEEE Trans. Magn. 2004, 40, 2104–2106. [Google Scholar] [CrossRef]
- Ede, J.D.; Atallah, K.; Jewell, G.W.; Wang, J.B.; Howe, D. Effect of Axial Segmentation of Permanent Magnets on Rotor Loss in Modular Permanent-Magnet Brushless Machines. IEEE Trans. Ind. Appl. 2007, 43, 1207–1213. [Google Scholar] [CrossRef]
- Mirzaei, M.; Binder, A.; Deak, C. 3D analysis of circumferential and axial segmentation effect on magnet eddy-current losses in permanent magnet synchronous machines with concentrated windings. In Proceedings of the XIX International Conference on Electrical Machines, Rome, Italy, 6–8 September 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Nuscheler, R. Two-dimensional analytical model for eddy-current loss calculation in the magnets and solid rotor yokes of permanent magnet synchronous machines. In Proceedings of the 2008 18th International Conference on Electrical Machines, Vilamoura, Portugal, 6–9 September 2008; pp. 1–6. [Google Scholar] [CrossRef]
- Yamazaki, K.; Shina, M.; Kanou, Y.; Miwa, M.; Hagiwara, J. Effect of Eddy Current Loss Reduction by Segmentation of Magnets in Synchronous Motors: Difference Between Interior and Surface Types. IEEE Trans. Magn. 2009, 45, 4756–4759. [Google Scholar] [CrossRef]
- Klotzl, J.; Pyc, M.; Gerling, D. Permanent magnet loss reduction in PM-machines using analytical and FEM calculation. In Proceedings of the SPEEDAM 2010, Pisa, Italy, 14–16 June 2010; pp. 98–100. [Google Scholar] [CrossRef]
- Wills, D.A.; Kamper, M.J. Reducing PM eddy-current rotor losses by partial magnet and rotor yoke segmentation. In Proceedings of the XIX International Conference on Electrical Machines, Rome, Italy, 6–8 September 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Li, B.; Li, M. Calculation and Analysis of Permanent Magnet Eddy Current Loss Fault with Magnet Segmentation. Math. Probl. Eng. 2016, 2016, 1–6. [Google Scholar] [CrossRef]
- Madina, P.; Poza, J.; Ugalde, G.; Almandoz, G. Analysis of non-uniform circumferential segmentation of magnets to reduce eddy-current losses in SPMSM machines. In Proceedings of the 2012 XXth International Conference on Electrical Machines, Marseille, France, 2–5 September 2012; Volume 14, pp. 79–84. [Google Scholar] [CrossRef]
- Yamazaki, K.; Fukushima, Y. Effect of Eddy-Current Loss Reduction by Magnet Segmentation in Synchronous Motors With Concentrated Windings. IEEE Trans. Ind. Appl. 2011, 47, 779–788. [Google Scholar] [CrossRef]
- Moriyasu, S.; Endo, K. The Ripple Loss at the Rotor Surface of Synchronous Machines. IEEE Trans. Power Apparatus Syst. 1980, PAS-99, 2393–2399. [Google Scholar] [CrossRef]
- Chaithongsuk, S.; Takorabet, N.; Kreuawan, S. Reduction of Eddy-Current Losses in Fractional-Slot Concentrated-Winding Synchronous PM Motors. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Yamazaki, K.; Kanou, Y.; Fukushima, Y.; Ohki, S.; Nezu, A.; Ikemi, T.; Mizokami, R. Reduction of Magnet Eddy-Current Loss in Interior Permanent-Magnet Motors With Concentrated Windings. IEEE Trans. Ind. Appl. 2010, 46, 2434–2441. [Google Scholar] [CrossRef]
- Yamazaki, K.; Kitayuguchi, K. Teeth shape optimization of surface and interior permanent-magnet motors with concentrated windings to reduce magnet eddy-current losses. In Proceedings of the International Conference on Electrical Machines and Systems, Incheon, South Korea, 10–13 October 2010; pp. 990–995. [Google Scholar]
- Sharkh, S.M.; Qazalbash, A.A.; Irenji, N.T.; Wills, R.G. Effect of slot configuration and airgap and magnet thicknesses on rotor electromagnetic loss in surface PM synchronous machines. In Proceedings of the 2011 International Conference on Electrical Machines and Systems, Beijing, China, 20–23 August 2011. [Google Scholar] [CrossRef]
- Bode, C.; May, H. Optimized Reduction of Parasitic Eddy Current Losses in High Speed Permanent Magnet Motors based on 2D and 3D Field Calculations. In Proceedings of the XV ISEF, International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering, Madeira, Portugal, 1–3 September 2011. [Google Scholar]
- Belli, Z.; Mekideche, M.R. Optimization of magnets segmentation for eddy-current losses reduction in permanent magnets electrical machines. In Proceedings of the 2013 Eighth International Conference and Exhibition on Ecological Vehicles and Renewable Energies (EVER), Monte Carlo, Monaco, 27–30 March 2013; Volume 34, pp. 1–7. [Google Scholar] [CrossRef]
- Alberti, L.; Fornasiero, E.; Bianchi, N. Impact of the Rotor Yoke Geometry on Rotor Losses in Permanent-Magnet Machines. IEEE Trans. Ind. Appl. 2012, 48, 98–105. [Google Scholar] [CrossRef]
- Yamazaki, K.; Kato, Y.; Ikemi, T.; Ohki, S. Reduction of Rotor Losses in Multilayer Interior Permanent-Magnet Synchronous Motors by Introducing Novel Topology of Rotor Flux Barriers. IEEE Trans. Ind. Appl. 2014, 50, 3185–3193. [Google Scholar] [CrossRef]
- Choi, G.; Jahns, T.M. Reduction of Eddy-Current Losses in Fractional-Slot Concentrated-Winding Synchronous PM Machines. IEEE Trans. Magn. 2016, 52, 1. [Google Scholar] [CrossRef]
- Jara, W.; Lindh, P.; Tapia, J.A.; Petrov, I.; Repo, A.K.; Pyrhonen, J. Rotor Eddy Current Losses Reduction in an Axial Flux Permanent Magnet Machine. IEEE Trans. Ind. Electron. 2016, 63, 1. [Google Scholar] [CrossRef]
- Cho, H.W.; Jang, S.M.; Choi, S.K. A Design Approach to Reduce Rotor Losses in High-Speed Permanent Magnet Machine for Turbo-Compressor. IEEE Trans. Magn. 2006, 42, 3521–3523. [Google Scholar] [CrossRef]
- Etemadrezaei, M.; Wolmarans, J.J.; Polinder, H.; Ferreira, J.A. Precise calculation and optimization of rotor eddy-current losses in high speed permanent magnet machine. In Proceedings of the 2012 XXth International Conference on Electrical Machines, Marseille, France, 2–5 September 2012; pp. 1399–1404. [Google Scholar] [CrossRef]
- Ma, J.; Zhu, Z.Q. Magnet eddy-current loss reduction in a 3-slot 2-pole permanent magnet machine. In Proceedings of the 2017 IEEE International Electric Machines and Drives Conference (IEMDC), Miami, FL, USA, 21–24 May 2017. [Google Scholar] [CrossRef]
- Gilbert, A. A method of measuring loss distribution in electrical machines. Proc. IEE A Power Eng. 1961, 108, 239. [Google Scholar] [CrossRef]
- Aoyama, Y.; Miyata, K.; Ohashi, K. Simulations and experiments on eddy-current in Nd-Fe-B magnet. IEEE Trans. Magn. 2005, 41, 3790–3792. [Google Scholar] [CrossRef]
- Yamazaki, K.; Shina, M.; Miwa, M.; Hagiwara, J. Investigation of Eddy Current Loss in Divided Nd–Fe–B Sintered Magnets for Synchronous Motors Due to Insulation Resistance and Frequency. IEEE Trans. Magn. 2008, 44, 4269–4272. [Google Scholar] [CrossRef]
- Alberti, L.; Fornasiero, E.; Bianchi, N.; Bolognani, S. Rotor Losses Measurements in an Axial Flux Permanent Magnet Machine. IEEE Trans. Energy Convers. 2011, 26, 639–645. [Google Scholar] [CrossRef]
- Liu, D.; Jassal, A.; Polinder, H.; Ferreira, J. Validation of eddy-current loss models for permanent magnet machines with fractional-slot concentrated windings. In Proceedings of the 2013 International Electric Machines & Drives Conference, Chicago, IL, USA, 12–15 May 2013; Volume 16, pp. 678–685. [Google Scholar] [CrossRef]
- Liu, Z.; Binns, K.; Low, T. Analysis of eddy-current and thermal problems in permanent magnet machines with radial-field topologies. IEEE Trans. Magn. 1995, 31, 1912–1915. [Google Scholar] [CrossRef]
- Zhao, N.; Zhu, Z.Q.; Liu, W. Rotor Eddy Current Loss Calculation and Thermal Analysis of Permanent Magnet Motor and Generator. IEEE Trans. Magn. 2011, 47, 4199–4202. [Google Scholar] [CrossRef]
- Huang, Z.; Fang, J.; Liu, X.; Han, B. Loss Calculation and Thermal Analysis of Rotors supported by Active Magnetic Bearings for High-speed Permanent Magnet Electrical Machines. IEEE Trans. Ind. Electron. 2015, 63, 2027–2035. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ouamara, D.; Dubas, F. Permanent-Magnet Eddy-Current Losses: A Global Revision of Calculation and Analysis. Math. Comput. Appl. 2019, 24, 67. https://doi.org/10.3390/mca24030067
Ouamara D, Dubas F. Permanent-Magnet Eddy-Current Losses: A Global Revision of Calculation and Analysis. Mathematical and Computational Applications. 2019; 24(3):67. https://doi.org/10.3390/mca24030067
Chicago/Turabian StyleOuamara, Daoud, and Frédéric Dubas. 2019. "Permanent-Magnet Eddy-Current Losses: A Global Revision of Calculation and Analysis" Mathematical and Computational Applications 24, no. 3: 67. https://doi.org/10.3390/mca24030067
APA StyleOuamara, D., & Dubas, F. (2019). Permanent-Magnet Eddy-Current Losses: A Global Revision of Calculation and Analysis. Mathematical and Computational Applications, 24(3), 67. https://doi.org/10.3390/mca24030067





