Investigation of Details in the Transition to Synchronization in Complex Networks by Using Recurrence Analysis
Abstract
1. Introduction
2. Rulkov Map
3. Connection Architecture
- the network is expanded by the addition of new nodes;
- the nodes added preferentially build connections to nodes that are already well-connected.
4. Quantifiers
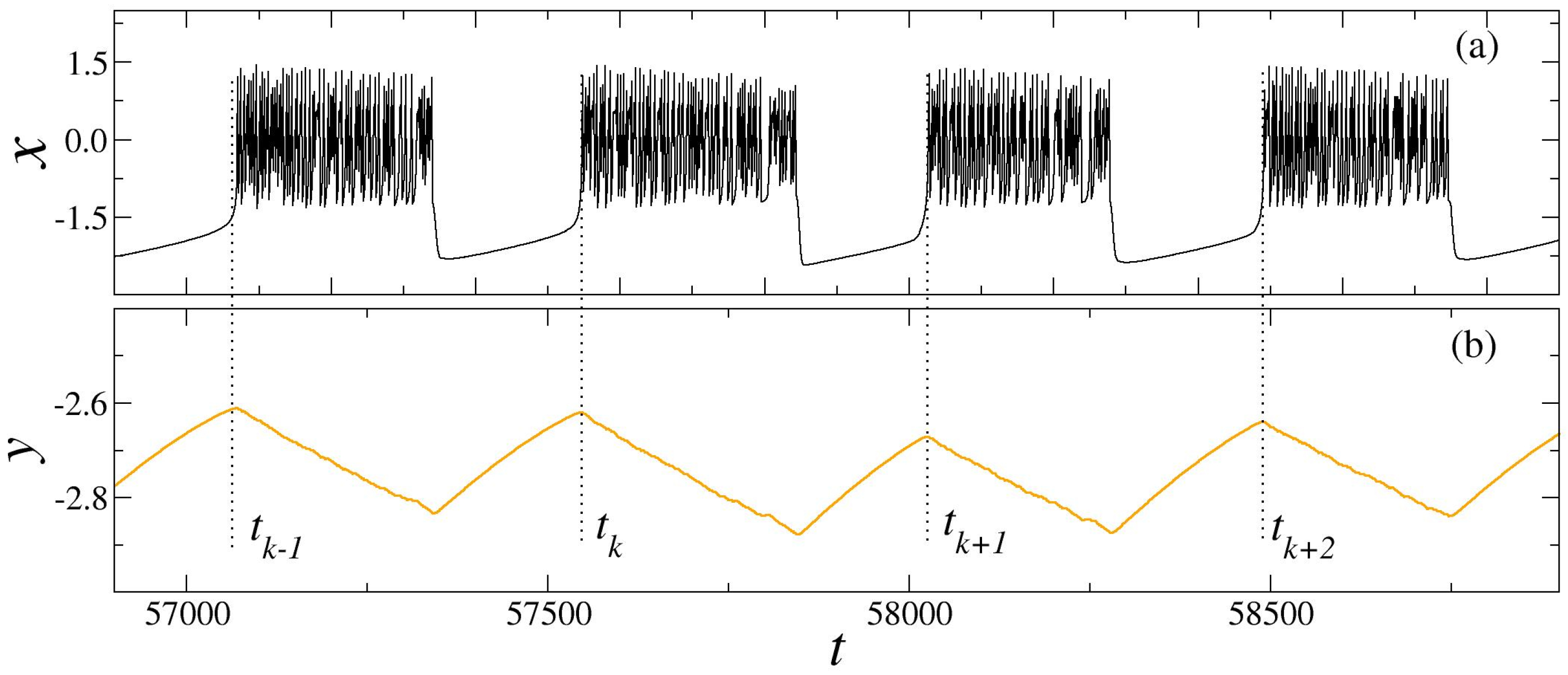
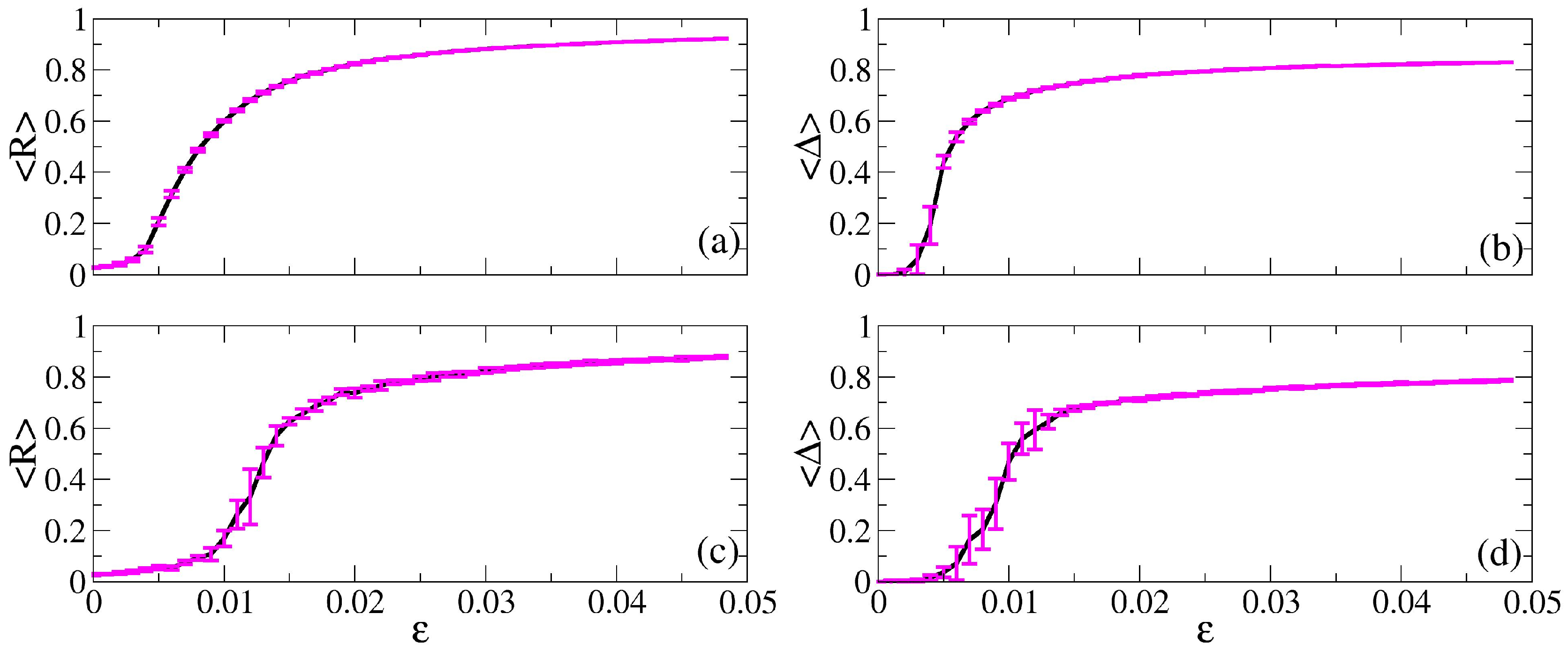
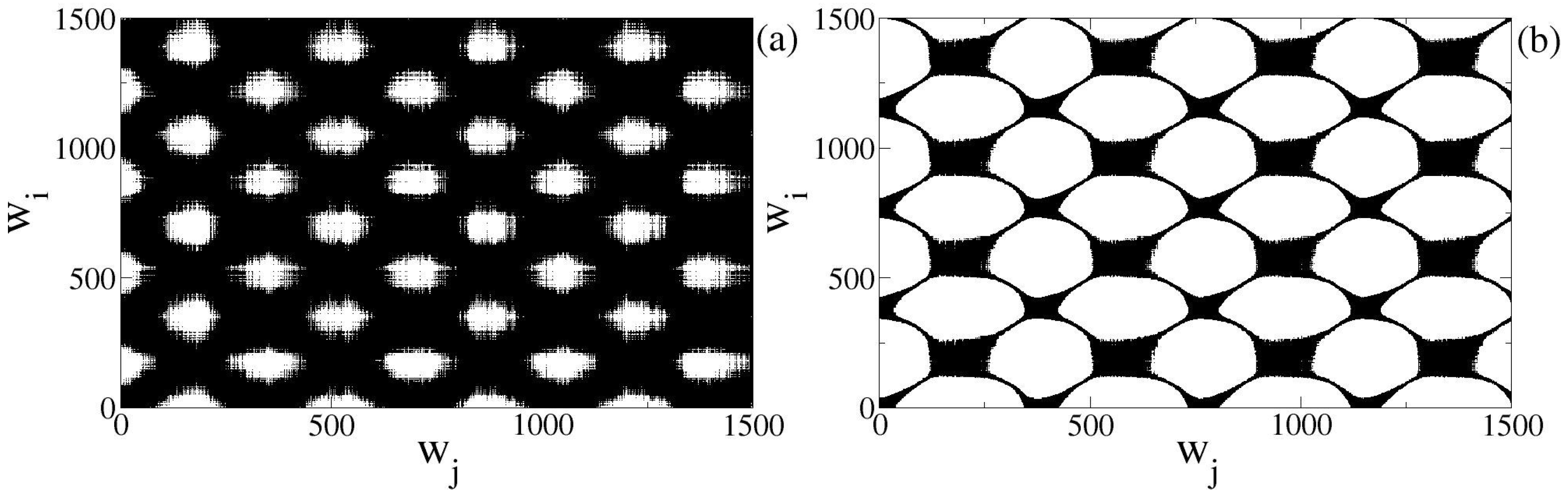
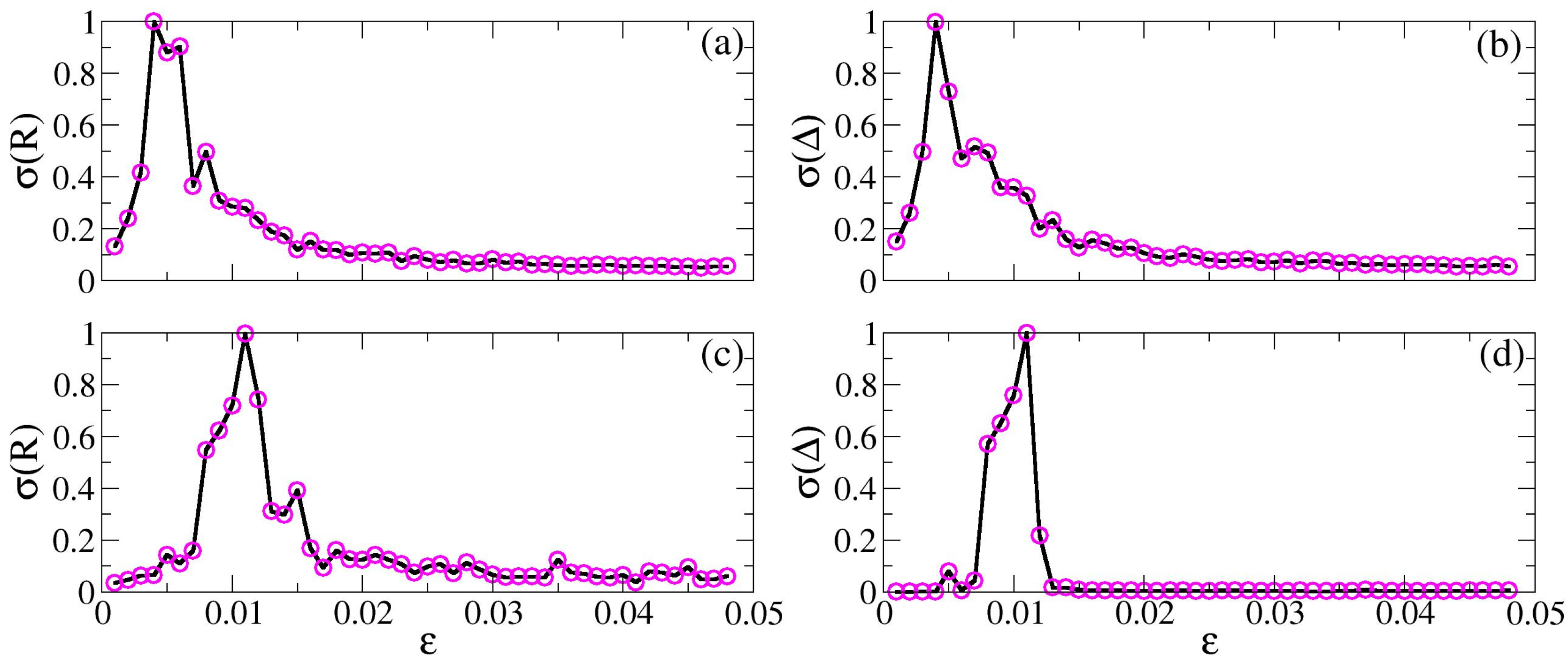
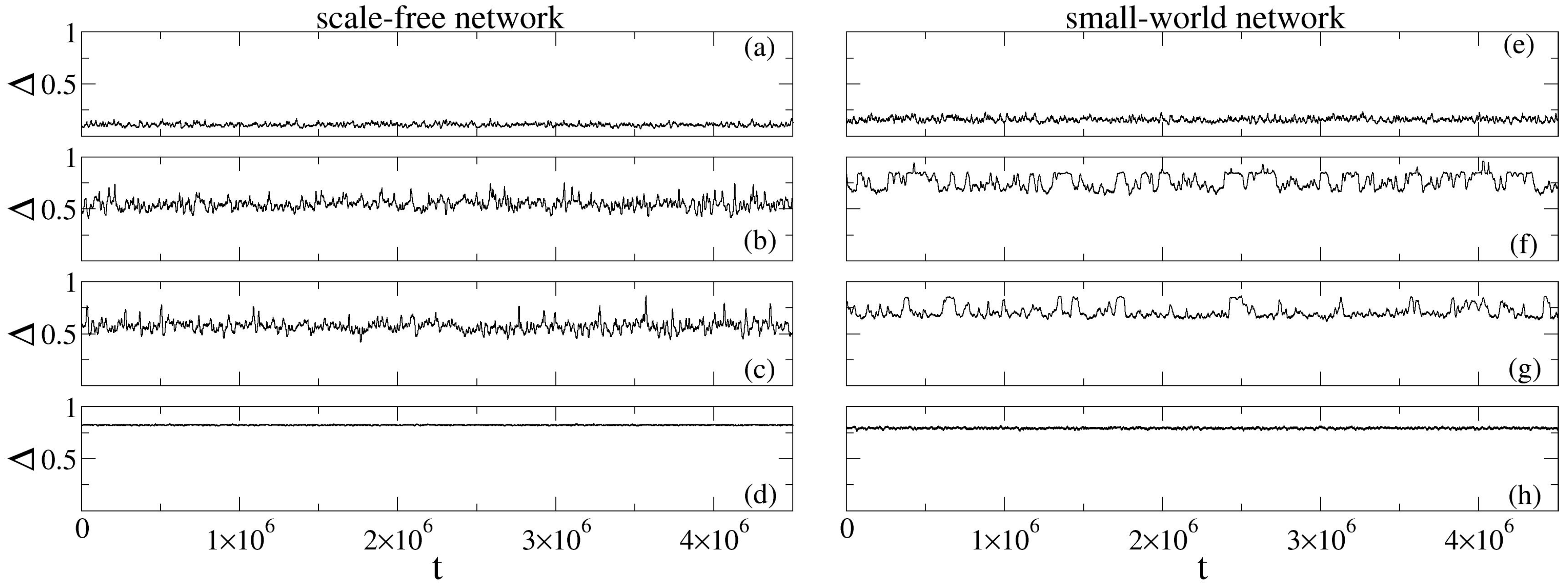
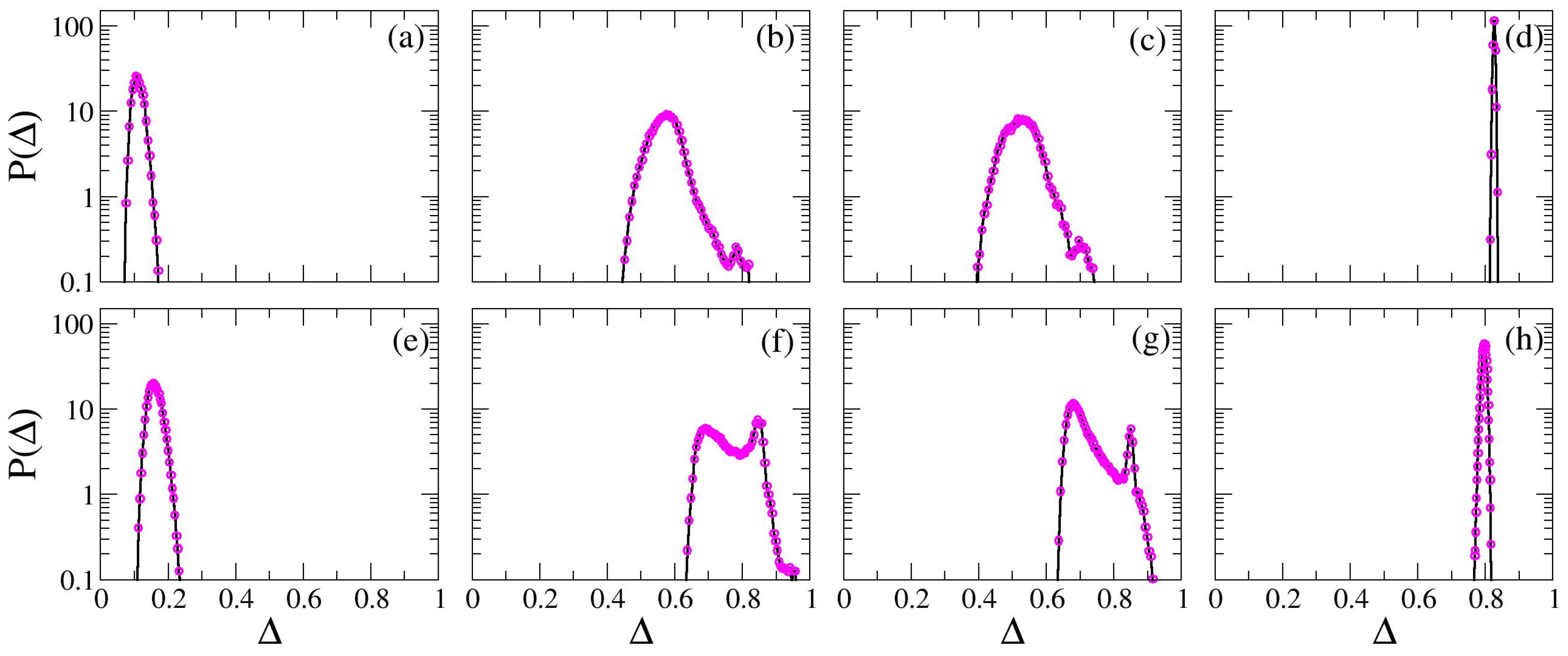
5. Results and Discussions
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Strogatz, S.H. Exploring complex networks. Nature 2001, 410, 268–276. [Google Scholar] [CrossRef]
- Bullmore, E.; Sporns, O. Complex brain networks: Graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 2009, 10, 186. [Google Scholar] [CrossRef] [PubMed]
- Kuramoto, Y. Chemical Oscillations, Waves, and Turbulence; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Rubido, N.; Cabeza, C.; Kahan, S.; Ávila, G.R.; Marti, A.C. Synchronization regions of two pulse-coupled electronic piecewise linear oscillators. Eur. Phys. J. D 2011, 62, 51–56. [Google Scholar] [CrossRef]
- Ottino-Löffler, B.; Strogatz, S.H. Kuramoto model with uniformly spaced frequencies: Finite-N asymptotics of the locking threshold. Phys. Rev. E 2016, 93, 062220. [Google Scholar] [CrossRef]
- Etémé, A.S.; Tabi, C.B.; Mohamadou, A. Firing and synchronization modes in neural network under magnetic stimulation. Commun. Nonlinear Sci. Numer. Simul. 2019, 72, 432–440. [Google Scholar] [CrossRef]
- Ferrari, F.A.S.; Viana, R.L. Building phase synchronization equivalence between coupled bursting neurons and phase oscillators. J. Phys. Commun. 2018, 2, 025014. [Google Scholar] [CrossRef]
- Hilgetag, C.C.; Kaiser, M. Lectures in Supercomputational Neuroscience: Dynamics in Complex Brain Networks; Springer: Berlin, Germany, 2008. [Google Scholar]
- Budzinski, R.C.; Boaretto, B.R.R.; Rossi, K.L.; Prado, T.L.; Kurths, J.; Lopes, S.R. Nonstationary transition to phase synchronization of neural networks induced by the coupling architecture. Phys. A Stat. Mech. Appl. 2018, 507, 321–334. [Google Scholar] [CrossRef]
- Batista, C.A.S.; Viana, R.L.; Ferrari, F.A.S.; Lopes, S.R.; Batista, A.M.; Coninck, J.C.P. Control of bursting synchronization in networks of Hodgkin-Huxley-type neurons with chemical synapses. Phys. Rev. E 2013, 87, 042713. [Google Scholar] [CrossRef] [PubMed]
- Boaretto, B.R.R.; Budzinski, R.C.; Prado, T.L.; Kurths, J.; Lopes, S.R. Suppression of anomalous synchronization and nonstationary behavior of neural network under small-world topology. Phys. A Stat. Mech. Appl. 2018, 497, 126–138. [Google Scholar] [CrossRef]
- Batista, C.A.S.; Lopes, S.R.; Viana, R.L.; Batista, A.M. Delayed feedback control of bursting synchronization in a scale-free neuronal network. Neural Netw. 2010, 23, 114–124. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Wang, J.; Liu, Q.; Deng, B.; Wei, X. Delayed feedback control of bursting synchronization in small-world neuronal networks. Neurocomputing 2013, 99, 178–187. [Google Scholar] [CrossRef]
- Ferrari, F.A.S.; Viana, R.L.; Reis, A.S.; Iarosz, K.C.; Caldas, I.L.; Batista, A.M. A network of networks model to study phase synchronization using structural connection matrix of human brain. Phys. A Stat. Mech. Appl. 2018, 496, 162–170. [Google Scholar] [CrossRef]
- Protachevicz, P.R.; Borges, R.R.; da Silva Reis, A.; Borges, F.S.; Iarosz, K.C.; Caldas, I.L.; Lameu, E.L.; Macau, E.E.N.; Viana, R.L.; Sokolov, I.M.; et al. Synchronous behaviour in network model based on human cortico-cortical connections. Physiol. Meas. 2018, 39, 7. [Google Scholar] [CrossRef]
- Yamamoto, H.; Kubota, S.; Shimizu, F.A.; Hirano-Iwata, A.; Niwano, M. Effective subnetwork topology for synchronizing interconnected networks of coupled phase oscillators. Front. Comput. Neurosci. 2018, 12, 17. [Google Scholar] [CrossRef]
- Mugnaine, M.; Reis, A.S.; Borges, F.S.; Borges, R.R.; Ferrari, F.A.S.; Iarosz, K.C.; Caldas, I.L.; Lameu, E.L.; Viana, R.L.; Szezech, J.D.; et al. Delayed feedback control of phase synchronisation in a neuronal network model. Eur. Phys. J. Spec. Top. 2018, 227, 1151–1160. [Google Scholar] [CrossRef]
- Budzinski, R.C.; Boaretto, B.R.R.; Prado, T.L.; Lopes, S.R. Phase synchronization and intermittent behavior in healthy and Alzheimer-affected human-brain-based neural network. Phys. Rev. E 2019, 99, 022402. [Google Scholar] [CrossRef] [PubMed]
- Lameu, E.L.; Batista, C.A.S.; Batista, A.M.; Iarosz, K.; Viana, R.L.; Lopes, S.R.; Kurths, J. Suppression of bursting synchronization in clustered scale-free (rich-club) neuronal networks. Chaos Interdiscip. J. Nonlinear Sci. 2012, 22, 043149. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Gardenes, J.; Moreno, Y.; Arenas, A. Paths to synchronization on complex networks. Phys. Rev. Lett. 2007, 98, 034101. [Google Scholar] [CrossRef]
- Zhang, X.; Boccaletti, S.; Guan, S.; Liu, Z. Explosive synchronization in adaptive and multilayer networks. Phys. Rev. Lett. 2015, 114, 038701. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Zou, Y.; Boccaletti, S.; Liu, Z. Explosive synchronization as a process of explosive percolation in dynamical phase space. Sci. Rep. 2014, 4, 5200. [Google Scholar] [CrossRef]
- Varshney, L.R.; Chen, B.L.; Paniagua, E.; Hall, D.H.; Chklovskii, D.B. Structural Properties of the Caenorhabditis elegans Neuronal Network. PLOS Comput. Biol. 2011, 7, e1001066. [Google Scholar] [CrossRef]
- He, Y.; Chen, Z.J.; Evans, A.C. Small-world anatomical networks in the human brain revealed by cortical thickness from MRI. Cereb. Cortex 2007, 17, 2407–2419. [Google Scholar] [CrossRef] [PubMed]
- Stam, C.J.; Van Straaten, E.C.W. The organization of physiological brain networks. Clin. Neurophysiol. 2012, 123, 1067–1087. [Google Scholar] [CrossRef]
- Budzinski, R.C.; Boaretto, B.R.R.; Prado, T.L.; Lopes, S.R. Detection of nonstationary transition to synchronized states of a neural network using recurrence analyses. Phys. Rev. E 2017, 96, 012320. [Google Scholar] [CrossRef]
- Xu, K.; Maidana, J.P.; Castro, S.; Orio, P. Synchronization transition in neuronal networks composed of chaotic or non-chaotic oscillators. Sci. Rep. 2018, 8, 8370. [Google Scholar] [CrossRef]
- Blasius, B.; Montbrió, E.; Kurths, J. Anomalous phase synchronization in populations of nonidentical oscillators. Phys. Rev. E 2003, 67, 035204. [Google Scholar] [CrossRef]
- Prado, T.L.; Lopes, S.R.; Batista, C.A.S.; Kurths, J.; Viana, R.L. Synchronization of bursting Hodgkin–Huxley-type neurons in clustered networks. Phys. Rev. E 2014, 90, 032818. [Google Scholar] [CrossRef]
- Boaretto, B.R.R.; Budzinski, R.C.; Prado, T.L.; Kurths, J.; Lopes, S.R. Neuron dynamics variability and anomalous phase synchronization of neural networks. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 106304. [Google Scholar] [CrossRef]
- Galuzio, P.P.; Lopes, S.R.; Viana, R.L. Two-state on-off intermittency caused by unstable dimension variability in periodically forced drift waves. Phys. Rev. E 2011, 84, 056211. [Google Scholar] [CrossRef]
- Newman, M.E.J. The structure and function of complex networks. SIAM Rev. 2003, 45, 167–256. [Google Scholar] [CrossRef]
- Liu, W.; Wu, Y.; Xiao, J.; Zhan, M. Effects of frequency-degree correlation on synchronization transition in scale-free networks. Europhys. Lett. 2013, 101, 38002. [Google Scholar] [CrossRef]
- Rulkov, N.F. Regularization of synchronized chaotic bursts. Phys. Rev. Lett. 2001, 86, 183. [Google Scholar] [CrossRef] [PubMed]
- Coombes, S.; Bressloff, P.C. Bursting: The Genesis of Rhythm in the Nervous System; World Scientific: Singapore, 2005. [Google Scholar]
- Feudel, U.; Neiman, A.; Pei, X.; Wojtenek, W.; Braun, H.A.; Huber, M.; Moss, F. Homoclinic bifurcation in a Hodgkin–Huxley model of thermally sensitive neurons. Chaos Interdiscip. J. Nonlinear Sci. 2000, 10, 231–239. [Google Scholar] [CrossRef]
- Braun, H.A.; Dewald, M.; Schäfer, K.; Voigt, K.; Pei, X.; Dolan, K.; Moss, F. Low-dimensional dynamics in sensory biology 2: Facial cold receptors of the rat. J. Comput. Neurosci. 1999, 7, 17–32. [Google Scholar] [CrossRef] [PubMed]
- Gerstner, W.; Kistler, W.M. Spiking Neuron Models: Single Neurons, Populations, Plasticity; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Newman, M.E.J.; Watts, D.J. Scaling and percolation in the small-world network model. Phys. Rev. E 1999, 60, 7332–7342. [Google Scholar] [CrossRef]
- Barabási, A.; Albert, R.; Jeong, H. Scale-free characteristics of random networks: the topology of the world-wide web. Phys. A Stat. Mech. Appl. 2000, 281, 69–77. [Google Scholar] [CrossRef]
- Marwan, N.; Romano, M.C.; Thiel, M.; Kurths, J. Recurrence plots for the analysis of complex systems. Phys. Rep. 2007, 438, 237–329. [Google Scholar] [CrossRef]
- Zou, Y.; Donner, R.V.; Marwan, N.; Donges, J.F.; Kurths, J. Complex network approaches to nonlinear time series analysis. Phys. Rep. 2019, 787, 1–97. [Google Scholar] [CrossRef]
- Prado, T.d.L.; dos Santos Lima, G.Z.; Lobão-Soares, B.; do Nascimento, G.C.; Corso, G.; Fontenele-Araujo, J.; Kurths, J.; Lopes, S.R. Optimizing the detection of nonstationary signals by using recurrence analysis. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 085703. [Google Scholar] [CrossRef]
- Corso, G.; Prado, T.D.L.; Lima, G.Z.S.; Kurths, J.; Lopes, S.R. Quantifying entropy using recurrence matrix microstates. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 083108. [Google Scholar] [CrossRef]
- Lima, G.Z.S.; Lopes, S.R.; Prado, T.L.; Lobao-Soares, B.; do Nascimento, G.C.; Fontenele-Araujo, J.; Corso, G. Predictability of arousal in mouse slow wave sleep by accelerometer data. PLoS ONE 2017, 12, e0176761. [Google Scholar] [CrossRef]
- Neves, F.M.; Viana, R.L.; Pie, M.R. Recurrence analysis of ant activity patterns. PLoS ONE 2017, 12, e0185968. [Google Scholar] [CrossRef] [PubMed]
- Rulkov, N.F. Modeling of spiking-bursting neural behavior using two-dimensional map. Phys. Rev. E 2002, 65, 041922. [Google Scholar] [CrossRef] [PubMed]
- Borges, R.R.; Borges, F.S.; Lameu, E.L.; Batista, A.M.; Iarosz, K.C.; Caldas, I.L.; Viana, R.L.; Sanjuán, M.A.F. Effects of the spike timing-dependent plasticity on the synchronisation in a random Hodgkin–Huxley neuronal network. Commun. Nonlinear Sci. Numer. Simul. 2016, 34, 12–22. [Google Scholar] [CrossRef]
- Kandel, E.R.; Schwartz, J.H.; Jessell, T.M.; Siegelbaum, S.A.; Hudspeth, A.J. Principles of Neural Science; McGraw-Hill: New York, NY, USA, 2000. [Google Scholar]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Lo, C.Y.; Wang, P.N.; Chou, K.H.; Wang, J.; He, Y.; Lin, C.P. Diffusion tensor tractography reveals abnormal topological organization in structural cortical networks in Alzheimer’s disease. J. Neurosci. 2010, 30, 16876–16885. [Google Scholar] [CrossRef]
- Chialvo, D.R. Critical brain networks. Phys. A Stat. Mech. Appl. 2004, 340, 756–765. [Google Scholar] [CrossRef]
- Eguiluz, V.M.; Chialvo, D.R.; Cecchi, G.A.; Baliki, M.; Apkarian, A.V. Scale-free brain functional networks. Phys. Rev. Lett. 2005, 94, 018102. [Google Scholar] [CrossRef]
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar]
- Hagberg, A.; Schult, D.; Swart, P. Exploring network structure, dynamics, and function using NetworkX. In Proceedings of the 7th Python in Science Conference, Pasadena, CA, USA, 19–24 August 2008; pp. 11–16. [Google Scholar]
- Boccara, N. Modeling Complex Systems; Springer Science & Business Media: New York, NY, USA, 2010. [Google Scholar]
- Albert, R.; Barabási, A. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47–97. [Google Scholar] [CrossRef]
- Sporns, O.; Zwi, J.D. The small world of the cerebral cortex. Neuroinformatics 2004, 2, 145–162. [Google Scholar] [CrossRef]
- Rosenblum, M.G.; Pikovsky, A.S.; Kurths, J. Phase synchronization of chaotic oscillators. Phys. Rev. Lett. 1996, 76, 1804. [Google Scholar] [CrossRef] [PubMed]
- Boccaletti, S.; Kurths, J.; Osipov, G.; Valladares, D.; Zhou, C. The synchronization of chaotic systems. Phys. Rep. 2002, 366, 1–101. [Google Scholar] [CrossRef]
- Bar-Yam, Y. Dynamics of Complex Systems; Addison-Wesley: Reading, MA, USA, 1997. [Google Scholar]
- Ivanchenko, M.V.; Osipov, G.V.; Shalfeev, V.D.; Kurths, J. Phase Synchronization in Ensembles of Bursting Oscillators. Phys. Rev. Lett. 2004, 93, 134101. [Google Scholar] [CrossRef] [PubMed]
- Lameu, E.L.; Yanchuk, S.; Macau, E.E.N.; Borges, F.S.; Iarosz, K.C.; Caldas, I.L.; Protachevicz, P.R.; Borges, R.R.; Viana, R.L.; Szezech, J.D., Jr.; et al. Recurrence quantification analysis for the identification of burst phase synchronisation. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 085701. [Google Scholar] [CrossRef]
- Santos, M.S.; Szezech, J.D., Jr.; Batista, A.M.; Caldas, I.L.; Viana, R.L.; Lopes, S.R. Recurrence quantification analysis of chimera states. Phys. Lett. A 2015, 379, 2188–2192. [Google Scholar] [CrossRef]
- Eckmann, J.P.; Kamphorst, S.O.; Ruelle, D. Recurrence plots of dynamical systems. Europhys. Lett. 1987, 4, 973. [Google Scholar] [CrossRef]
- Grabow, C.; Hill, S.M.; Grosskinsky, S.; Timme, M. Do small worlds synchronize fastest? Europhys. Lett. 2010, 90, 48002. [Google Scholar] [CrossRef]
- Budzinski, R.C.; Boaretto, B.R.R.; Prado, T.L.; Lopes, S.R. Synchronization domains in two coupled neural networks. Commun. Nonlinear Sci. Numer. Simul. 2019, 75, 140–151. [Google Scholar] [CrossRef]
- Galuzio, P.P.; Lopes, S.R.; Viana, R.L. Two-State On-Off Intermittency and the Onset of Turbulence in a Spatiotemporally Chaotic System. Phys. Rev. Lett. 2010, 105, 055001. [Google Scholar] [CrossRef]
- Shanahan, M. Metastable chimera states in community-structured oscillator networks. Chaos Interdiscip. J. Nonlinear Sci. 2010, 20, 013108. [Google Scholar] [CrossRef] [PubMed]
- Uhlhaas, P.J.; Singer, W. Neural synchrony in brain disorders: relevance for cognitive dysfunctions and pathophysiology. Neuron 2006, 52, 155–168. [Google Scholar] [CrossRef] [PubMed]
- Lasemidis, L.D.; Sackellares, J.C. Chaos Theory and Eilepsy. The Neuroscientist 1996, 2, 118–126. [Google Scholar] [CrossRef]
- Galvan, A.; Wichmann, T. Pathophysiology of parkinsonism. Clin. Neurophysiol. 2008, 119, 1459–1474. [Google Scholar] [CrossRef]
- Dinstein, I.; Pierce, K.; Eyler, L.; Solso, S.; Malach, R.; Behrmann, M.; Courchesne, E. Disrupted neural synchronization in toddlers with autism. Neuron 2011, 70, 1218–1225. [Google Scholar] [CrossRef] [PubMed]
- Aron, L.; Yankner, B.A. Neural synchronization in Alzheimer’s disease. Nature 2016, 540, 207–208. [Google Scholar] [CrossRef] [PubMed]
- Iaccarino, H.F.; Singer, A.C.; Martorell, A.J.; Rudenko, A.; Gao, F.; Gillingham, T.Z.; Mathys, H.; Seo, J.; Kritskiy, O.; Abdurrob, F.; et al. Gamma frequency entrainment attenuates amyloid load and modifies microglia. Nature 2016, 540, 230–235. [Google Scholar] [CrossRef] [PubMed]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Budzinski, R.C.; Boaretto, B.R.R.; Prado, T.L.; Lopes, S.R. Investigation of Details in the Transition to Synchronization in Complex Networks by Using Recurrence Analysis. Math. Comput. Appl. 2019, 24, 42. https://doi.org/10.3390/mca24020042
Budzinski RC, Boaretto BRR, Prado TL, Lopes SR. Investigation of Details in the Transition to Synchronization in Complex Networks by Using Recurrence Analysis. Mathematical and Computational Applications. 2019; 24(2):42. https://doi.org/10.3390/mca24020042
Chicago/Turabian StyleBudzinski, Roberto C., Bruno Rafael Reichert Boaretto, Thiago L. Prado, and Sergio Roberto Lopes. 2019. "Investigation of Details in the Transition to Synchronization in Complex Networks by Using Recurrence Analysis" Mathematical and Computational Applications 24, no. 2: 42. https://doi.org/10.3390/mca24020042
APA StyleBudzinski, R. C., Boaretto, B. R. R., Prado, T. L., & Lopes, S. R. (2019). Investigation of Details in the Transition to Synchronization in Complex Networks by Using Recurrence Analysis. Mathematical and Computational Applications, 24(2), 42. https://doi.org/10.3390/mca24020042




