Abstract
Parametric high-fidelity simulations are of interest for a wide range of applications. However, the restriction of computational resources renders such models to be inapplicable in a real-time context or in multi-query scenarios. Model order reduction (MOR) is used to tackle this issue. Recently, MOR is extended to preserve specific structures of the model throughout the reduction, e.g., structure-preserving MOR for Hamiltonian systems. This is referred to as symplectic MOR. It is based on the classical projection-based MOR and uses a symplectic reduced order basis (ROB). Such an ROB can be derived in a data-driven manner with the Proper Symplectic Decomposition (PSD) in the form of a minimization problem. Due to the strong nonlinearity of the minimization problem, it is unclear how to efficiently find a global optimum. In our paper, we show that current solution procedures almost exclusively yield suboptimal solutions by restricting to orthonormal ROBs. As a new methodological contribution, we propose a new method which eliminates this restriction by generating non-orthonormal ROBs. In the numerical experiments, we examine the different techniques for a classical linear elasticity problem and observe that the non-orthonormal technique proposed in this paper shows superior results with respect to the error introduced by the reduction.
1. Introduction
Simulations enable researchers of all fields to run virtual experiments that are too expensive or impossible to be carried out in the real world. In many contexts, high-fidelity models are indispensable to represent the simulated process accurately. These high-fidelity simulations typically come with the burden of a large computational cost such that an application in real time or an evaluation for many different parameters is impossible respecting the given restrictions of computational resources at hand. Model order reduction (MOR) techniques can be used to reduce the computational cost of evaluations of the high-fidelity model by approximating these with a surrogate reduced-order model (ROM) [1].
One class of high-fidelity models are systems of ordinary differential equations (ODEs) with a high order, i.e., a high dimension in the unknown variable. Such models typically arise from fine discretizations of time-dependent partial differential equations (PDEs). Since each point in the discretization requires one or multiple unknowns, fine discretizations with many discretization points yield a system of ODEs with a high order. In some cases, the ODE system takes the form of a finite-dimensional Hamiltonian system. Examples are linear elastic models [2] or gyro systems [3].
Symplectic MOR [4] allows for deriving a ROM for high-dimensional Hamiltonian systems by lowering the order of the system while maintaining the Hamiltonian structure. Thus, it is also referred to as structure-preserving MOR for Hamiltonian systems [5]. Technically speaking, a Petrov–Galerkin projection is used in combination with a symplectic reduced-order basis (ROB).
For a data-driven generation of the ROB, the conventional methods, e.g., the Proper Orthogonal Decomposition (POD) [1] is not suited since they do not necessarily compute a symplectic ROB. To this end, the referenced works introduce the Proper Symplectic Decomposition (PSD) which is a data-driven basis generation technique for symplectic ROBs. Due to the high nonlineariy of the optimization problem, an efficient solution strategy is yet unknown for the PSD. The existing PSD methods (Cotangent Lift, Complex Singular Value Decomposition (Complex SVD)), a nonlinear programming approach [4] and a greedy procedure introduced in [5]) each restrict to a specific subset of symplectic ROBs from which they select optimal solutions which might be globally suboptimal.
The present paper classifies the existing symplectic basis generation techniques in two classes of methods which either generate orthonormal or non-orthonormal bases. To this end, we show that the existing basis generation techniques for symplectic bases almost exclusively restrict to orthonormal bases. Furthermore, we prove that Complex SVD is the optimal solution of the PSD on the set of orthonormal, symplectic bases. During the proof, an alternative formulation of the Complex SVD for symplectic matrices is introduced. To leave the class of orthonormal, symplectic bases, we propose a new basis generation technique, namely the PSD SVD-like decomposition. It is based on an SVD-like decomposition of arbitrary matrices introduced in [6].
This paper is organized in the following way: Section 2 is devoted to the structure-preserving MOR for autonomous and non-autonomous, parametric Hamiltonian systems and thus introduces symplectic geometry, Hamiltonian systems and symplectic MOR successively. The data-driven generation of a symplectic ROB with PSD is discussed in Section 3. The numerical results are presented and elaborated in Section 4 exemplified by a Lamé–Navier type elasticity model which we introduce at the beginning of that section together with a short comment on the software that is used for the experiments. The paper is summarized and concluded in Section 5.
2. Symplectic Model Reduction
Symplectic MOR for autonomous Hamiltonian systems is introduced in [4]. We repeat the essentials for the sake of completeness and to provide a deeper understanding of the methods used. In the following, describes parameters of the system from the parameter set . We might skip the explicit dependence on the parameter vector if it is not relevant in this specific context.
2.1. Symplectic Geometry in Finite Dimensions
Definition 1 (Symplectic form over ).
Let be a finite-dimensional vector space over . We consider a skew-symmetric and non-degenerate bilinear form , i.e., for all , it holds
The bilinear form is called symplectic form on and the pair is called symplectic vector space.
It can be shown that is necessarily of even dimension [7]. Thus, is isomorphic to which is why we are restricted to and write instead of as follows. In context of the theory of Hamiltonians, refers to the phase space which consists, in the context of classical mechanics, of position states of the configuration space and momentum states which form together the state .
It is guaranteed [7] that there exists a basis such that the symplectic form takes the canonical structure
where is the identity matrix, is the matrix of all zeros and is called Poisson matrix. Thus, we restrict to symplectic forms of the canonical structure in the following. For the Poisson matrix, it holds for any
These properties are intuitively understandable as the Poisson matrix is a -dimensional, rotation matrix and the matrix can be interpreted as a rotation by in this context.
Definition 2 (Symplectic map).
Let , , be a linear mapping for and . We call A a linear symplectic map and a symplectic matrix with respect to and if
where is the canonical symplectic form on (and is equal to if ).
Let be an open set and a differentiable map on U. We call a symplectic map if the Jacobian matrix is a symplectic matrix for every .
For a linear map, it is easy to check that condition (3) is equivalent to the preservation of the symplectic form, i.e., for all
Now, we give the definition of the so-called symplectic inverse which will be used in Section 2.3.
Definition 3 (Symplectic inverse).
For each symplectic matrix , we define the symplectic inverse
The symplectic inverse exists for every symplectic matrix and it holds the inverse relation
2.2. Finite-Dimensional, Autonomous Hamiltonian Systems
To begin with, we introduce the Hamiltonian system in a finite-dimensional, autonomous setting. The non-autonomous case is discussed subsequently in Section 2.4.
Definition 4 (Finite-dimensional, autonomous Hamiltonian system).
Let be a scalar-valued function that we require to be continuously differentiable in the first argument and which we call Hamiltonian (function). Hamilton’s equation is an initial value problem with the prescribed initial data , which describes the evolution of the solution for all with
where is called the Hamiltonian vector field. The triple is referred to as the Hamiltonian system. We denote the flow of a Hamiltonian system as the mapping that evolves the initial state to the corresponding solution of Hamilton’s equation
where indicates that it is the solution with the initial data .
The two characteristic properties of Hamiltonian systems are (a) the preservation of the Hamiltonian function and (b) the symplecticity of the flow which are presented in the following two propositions.
Proposition 1 (Preservation of the Hamiltonian).
The flow of Hamilton’s equation preserves the Hamiltonian function .
Proof.
We prove the assertion by showing that the evolution over time is constant for any due to
□
Proposition 2 (Symplecticity of the flow).
Let the Hamiltonian function be twice continuously differentiable in the first argument. Then, the flow of a Hamiltonian system is a symplectic map.
Proof.
See ([8], Chapter VI, Theorem 2.4). □
2.3. Symplectic Model Order Reduction for Autonomous Hamiltonian Systems
The goal of MOR [1] is to reduce the order, i.e., the dimension, of high dimensional systems. To this end, we approximate the high-dimensional state with
with the reduced state , the reduced-order basis (ROB) , the reconstructed state and the reduced space . The restriction to even-dimensional spaces and is not necessary for MOR in general but is required for the symplectic MOR in the following. To achieve a computational advantage with MOR, the approximation should introduce a clear reduction of the order, i.e., .
For Petrov–Galerkin projection-based MOR techniques, the ROB is accompanied by a projection matrix which is chosen to be biorthogonal to , i.e., . The reduced-order model (ROM) is derived with the requirement that the residual vanishes in the space spanned by the columns of the projection matrix, i.e., in our case
where is the vector of all zeros. Due to the biorthogonality, this is equivalent to
In the context of symplectic MOR, the ROB is chosen to be a symplectic matrix (3) which we call a symplectic ROB. Additionally, the transposed projection matrix is the symplectic inverse and the projection in (7) is called a symplectic projection or symplectic Galerkin projection [4]. The (possibly oblique) projection reads
In combination, this choice of and guarantees that the Hamiltonian structure is preserved by the reduction which is shown in the following proposition.
Proposition 3 (Reduced autonomous Hamiltonian system).
Let be a symplectic ROB with the projection matrix . Then, the ROM (7) of a high-dimensional Hamiltonian system is a Hamiltonian system on with the canonical symplectic form and the reduced Hamiltonian function for all .
Proof.
First, we remark that the symplectic inverse is a valid biorthogonal projection matrix since it fulfils . To derive the Hamiltonian form of the ROM in (7), we use the identity
which makes use of the properties (2) of the Poisson matrix. It follows with (5), (7) and (8)
where the last step follows from the chain rule. Thus, the evolution of the reduced state takes the form of Hamilton’s equation and the resultant ROM is equal to the Hamiltonian system . □
Corollary 1 (Linear Hamiltonian system).
Hamilton’s equation is a linear system in the case of a quadratic Hamiltonian with symmetric and
The evolution of the reduced Hamiltonian system reads
with the reduced Hamiltonian function .
Remark 1.
We emphasise that the reduction of linear Hamiltonian systems follows the pattern of the classical projection-based MOR approaches [9] to derive the reduced model with and which allows a straightforward implementation in existing frameworks.
Since the ROM is a Hamiltonian system, it preserves its Hamiltonian. Thus, it can be shown that the error in the Hamiltonian is constant [4]. Furthermore, there are a couple of results for the preservation of stability ([5], Theorem 18), ([4], Section 3.4.) under certain assumptions on the Hamiltonian function.
Remark 2 (Offline/online decomposition).
A central concept in the field of MOR for parametric systems is the so-called offline/online decomposition. The idea is to split the procedure in a possibly costly offline phase and a cheap online phase where the terms costly and cheap refer to the computational cost. In the offline phase, the ROM is constructed. The online phase is supposed to evaluate the ROM fast. The ultimate goal is to avoid any computations that depend on the high dimension in the online phase. For a linear system, the offline/online decomposition can be achieved if , and allow a parameter-separability condition [9].
Remark 3 (Non-linear Hamiltonian systems).
If the Hamiltonian function is not quadratic, the gradient is nonlinear. Thus, the right-hand side of the ODE system (i.e., the Hamiltonian vector field) is nonlinear. Nevertheless, symplectic MOR, technically, can be applied straightforwardly. The problem is that, without further assumptions, an efficient offline/online decomposition cannot be achieved which results in a low or no reduction of the computational costs. Multiple approaches [10,11] exist which introduce an approximation of the nonlinear right-hand side to enable an efficient offline/online decomposition.
For symplectic MOR, the symplectic discrete empirical interpolation method (SDEIM) was introduced ([4], Section 5.2.) and ([5], Section 4.2.) to preserve the symplectic structure throughout the approximation of the nonlinear terms. The performace of these methods is discussed in in [4,5] for typical examples like the sine-Gordon equation or the nonlinear Schrödinger equation.
Remark 4 (MOR for port-Hamiltonian systems).
Alternatively to symplectic MOR with a snapshot-based basis generation method, MOR for so-called port-Hamiltonian systems can be used [12,13]. The projection scheme of that approach does not require symplecticity of the ROB but instead approximates the gradient of the Hamiltonian with the projection matrix . That alternative approach, like symplectic MOR, preserves the structure of the Hamiltonian equations, but, contrary to symplectic MOR, might result in a non-canonical symplectic structure in the reduced system.
2.4. Finite-Dimensional, Non-Autonomous Hamiltonian Systems
The implementation of non-autonomous Hamiltonian systems in the symplectic framework is non-trivial as the Hamiltonian might change over time. We discuss the concept of the extended phase space [14] in the following, which redirects the non-autonomous Hamiltonian system to the case of an autonomous Hamiltonian system. The model reduction of these systems is discussed subsequently in Section 2.5.
Definition 5 (Finite-dimensional, non-autonomous Hamiltonian system).
Let be a scalar-valued function function that is continuously differentiable in the second argument. A non-autonomous (or time-dependent) Hamiltonian system is of the form
We therefore call a time-dependent Hamiltonian function.
A problem for non-autonomous Hamiltonian systems occurs as the explicit time dependence of the Hamiltonian function introduces an additional variable, the time, and the carrier manifold becomes odd-dimensional. As mentioned in Section 2.1, symplectic vector spaces are always even-dimensional which is why a symplectic description is no longer possible. Different approaches are available to circumvent this issue.
As suggested in ([15], Section 4.3), we use the methodology of the so-called symplectic extended phase space ([14], Chap. VI, Section 10) to redirect the non-autonomous system to an autonomous system. The formulation is based on the extended Hamiltonian function with
Technically, the time is added to the extended state with and the corresponding momentum is chosen such that the extended system is an autonomous Hamiltonian system.
This procedure requires the time-dependent Hamiltonian function to be differentiable in the time variable. Thus, it does for example not allow for the description of loads that are not differentiable in time in the context of mechanical systems. This might, e.g., exclude systems that model mechanical contact since loads that are not differentiable in time are required.
2.5. Symplectic Model Order Reduction of Non-Autonomous Hamiltonian Systems
For the MOR of the, now autonomous, extended system, only the original phase space variable is reduced. The time and the corresponding conjugate momentum are not reduced. To preserve the Hamiltonian structure, a symplectic ROB is used for the reduction of analogous to the autonomous case. The result is a reduced extended system which again can be written as a non-autonomous Hamiltonian system with the time-dependent Hamiltonian for all .
An unpleasant side effect of the extended formulation is that the linear dependency on the additional state variable (see (11)) implies that the Hamiltonian cannot have strict extrema. Thus, the stability results listed in [4,5] do not apply if there is a true time-dependence in the Hamiltonian . Nevertheless, symplectic MOR in combination with a non-autonomous Hamiltonian system shows stable results in the numerical experiments.
Furthermore, it is important to note that only the extended Hamiltonian is preserved throughout the reduction. The time-dependent Hamiltonian is not necessarily preserved throughout the reduction, i.e., but potentially .
3. Symplectic Basis Generation with the Proper Symplectic Decomposition (PSD)
We introduced the symplectic MOR for finite-dimensional Hamiltonian systems in the previous section. This approach requires a symplectic ROB which is yet not further specified. In the following, we discuss the Proper Symplectic Decomposition (PSD) as a data-driven basis generation approach. To this end, we classify symplectic ROBs as orthogonal and non-orthogonal. The PSD is investigated for these two classes in Section 3.1 and Section 3.2 separately. For symplectic, orthogonal ROBs, we prove that an optimal solution can be derived based on an established procedure, the PSD Complex SVD. For symplectic, non-orthogonal ROBs, we provide a new basis generation method, the PSD SVD-like decomposition.
We pursue the approach to generate an ROB from a collection of snapshots of the system [16]. A snapshot is an element of the so-called solution manifold which we aim to approximate with a low-dimensional surrogate
where is a solution of the full model (5), is the ROB and is the solution of the reduced system (7). In [4], the Proper Symplectic Decomposition (PSD) is proposed as a snapshot-based basis generation technique for symplectic ROBs. The idea is to derive the ROB from a minimization problem which is suggested in analogy to the very well established Proper Orthogonal Decomposition (POD, also Principal Component Analysis) [1].
Classically, the POD chooses the ROB to minimize the sum over squared norms of all residuals of the orthogonal projection of the single snapshots measured in the 2-norm with the constraint that the ROB is orthogonal, i.e.,
In contrast, the PSD requires the ROB to be symplectic instead of orthogonal, which is expressed in the reformulated constraint. Furthermore, the orthogonal projection is replaced by the symplectic projection which results in
We summarize this in a more compact (matrix-based) formulation in the following definition.
Definition 6 (Proper Symplectic Decomposition (PSD)).
Given snapshots , we denote the snapshot matrix as . Find a symplectic ROB which minimizes
We denote the minimization problem (14) in the following as , where is the given snapshot matrix.
The constraint in (14) ensures that the ROB is symplectic and thus guarantees the existence of the symplectic inverse . Furthermore, the matrix-based formulation (14) is equivalent to the vector-based formulation presented in (13) due to the properties of the Frobenius norm .
Remark 5 (Interpolation-based ROBs).
Alternatively to the presented snapshot-based basis generation techniques, interpolation-based ROBs might be used. These aim to interpolate the transfer function of linear problems (or the linearized equations of nonlinear problems). For the framework of MOR of port-Hamiltonian systems (see Remark 4), there exists an interpolation-based basis generation technique ([13], Section 2.2.). In the scope of our paper, we focus on symplectic MOR and snapshot-based techniques.
3.1. Symplectic, Orthonormal Basis Generation
The foremost problem of the PSD is that there is no explicit solution procedure known so far due to the high nonlinearity and possibly multiple local optima. This is an essential difference to the POD as the POD allows to find a global minimum by solving an eigenvalue problem [1].
Current solution procedures for the PSD restrict to a certain subset of symplectic matrices and derive an optimal solution for this subset which might be suboptimal in the class of symplectic matrices. In the following, we show that this subclass almost exclusively restricts to symplectic, orthonormal ROBs.
Definition 7 (Symplectic, orthonormal ROB).
We call an ROB symplectic, orthonormal (also orthosymplectic, e.g., in [5]) if it is symplectic w.r.t. and and is orthonormal, i.e., the matrix has orthonormal columns
In the following, we show an alternative characterization of a symplectic and orthonormal ROB. Therefore, we extend the results given, e.g., in [17] for square matrices in the following Proposition 4 to the case of rectangular matrices . This was also partially addressed in ([4], Lemma 4.3.).
Proposition 4 (Characterization of a symplectic matrix with orthonormal columns).
The following statements are equivalent for any matrix
- (i)
- is symplectic with orthonormal columns,
- (ii)
- is of the form
- (iii)
- is symplectic and it holds .
We remark that these matrices are characterized in [4] to be elements in where is the symplectic Stiefel manifold and is the Stiefel manifold.
Proof.
“(i) ⇒ (ii)”: Let be a symplectic matrix with orthonormal columns. We rename the columns to with and . The symplecticity of the matrix written in terms of and reads
Expressed in terms of the columns of the matrices , this condition reads for any
and the orthonormality of the columns of implies
For a fixed , it is easy to show with that is of unit length
Thus, and are both unit vectors which fulfill . By the Cauchy–Schwarz inequality, it holds if and only if the vectors are parallel. Thus, we infer , which is equivalent to . Since this holds for all , we conclude that is of the form proposed in (15).
“(ii) ⇒ (iii)”: Let be of the form (15). Direct calculation yields
which shows that is symplectic. Thus, the symplectic inverse exists. The following calculation shows that it equals the transposed
“(iii) ⇒ (i)”: Let be symplectic with . Then, we know that has orthonormal columns since
□
Proposition 4 essentially limits the symplectic, orthonormal ROB to be of the form (15). Later in the current section, we see how to solve the PSD for ROBs of this type. In Section 3.2, we are interested in ridding the ROB of this requirement to explore further solution methods of the PSD.
As mentioned before, the current solution procedures for the PSD almost exclusively restrict to the class of symplectic, orthonormal ROBs introduced in Proposition 4. This includes the Cotangent Lift [4], the Complex SVD [4], partly the nonlinear programming algorithm from [4] and the greedy procedure presented in [5]. We briefly review these approaches in the following proposition.
Proposition 5 (Symplectic, orthonormal basis generation).
The Cotangent Lift (CT), Complex SVD (cSVD) and the greedy procedure for symplectic basis generation all derive a symplectic and orthonormal ROB. The nonlinear programming (NLP) admits a symplectic, orthonormal ROB if the coefficient matrix in ([4], Algorithm 3) is symplectic and has orthonormal columns, i.e., it is of the form . The methods can be rewritten with , where the different formulations of read
where
- (i)
- (ii)
- are the basis vectors selected by the greedy algorithm,
- (iii)
- is an ROB computed from CT or cSVD and , , stems from the coefficient matrix computed by the NLP algorithm.
Proof.
All of the listed methods derive a symplectic ROB of the form which satisfies (15). By Proposition 4, these ROBs are each a symplectic, orthonormal ROB. □
In the following, we show that PSD Complex SVD is the solution of the PSD in the subset of symplectic, orthonormal ROBs. This was partly shown in [4] which yet lacked the final step that, restricting to orthonormal, symplectic ROBs, a solution of solves and vice versa. This proves that the PSD Complex SVD is not only near optimal in this set but indeed optimal. Furthermore, the proof we show is alternative to the original and naturally motivates an alternative formulation of the PSD Complex SVD which we call the POD of in the following. To begin with, we reproduce the definition of PSD Complex SVD from [4].
Definition 8 (PSD Complex SVD).
We define the complex snapshot matrix
which is derived with the imaginary unit . The PSD Complex SVD is a basis generation technique that requires the auxiliary complex matrix to fulfil
and builds the actual ROB with
The solution of (18) is known to be based on the left-singular vectors of which can be explicitly computed with a complex version of the SVD.
We emphasize that we denote this basis generation procedure as PSD Complex SVD in the following to avoid confusions with the usual complex SVD algorithm.
Proposition 6 (Minimizing PSD in the set of symplectic, orthonormal ROBs).
Given the snapshot matrix , we augment this with “rotated” snapshots to . We assume that is such that we obtain a gap in the singular values of , i.e., . Then, minimizing the PSD in the set of symplectic, orthonormal ROBs is equivalent to the following minimization problem
Clearly, this is equivalent to the POD (12) applied to the snapshot matrix . We, thus, call this procedure the POD of in the following. A minimizer can be derived with the SVD as it is common for POD [1].
Proof.
The proof proceeds in three steps: we show
- (i)
- that is a pair of left- and right-singular vectors of to the singular value if and only if also is a pair of left- and right-singular vectors of to the same singular value ,
- (ii)
- that a solution of the POD of is a symplectic, orthonormal ROB, i.e., ,
- (iii)
- that the POD of is equivalent to the PSD for symplectic, orthonormal ROBs.
We start with the first step (i). Let be a pair of left- and right-singular vectors of to the singular value . We use that the left-singular (or right-singular) vectors of are a set of orthonormal eigenvectors of (or ). To begin with, we compute
where we use . Thus, we can reformulate the eigenvalue problems of and, respectively, as
Thus, is necessarily another pair of left- and right-singular vectors of with the same singular value . We infer that the left-singular vectors , , ordered by the magnitude of the singular values in a descending order can be written as
For the second step (ii), we remark that the solution of the POD is explicitly known to be any matrix which stacks in its columns left-singular vectors of the snapshot matrix with the highest singular value [1]. Due to the special structure (21) of the singular vectors for the snapshot matrix , a minimizer of the POD of necessarily adopts this structure. We are allowed to rearrange the order of the columns in this matrix and thus the result of the POD of can always be rearranged to the form
Note that it automatically holds that and since, in both products, we use the left-singular vectors from the columns of the matrix from (21) which is known to be orthogonal from properties of the SVD. Thus, (15) holds and we infer from Proposition 4 that the POD of indeed is solved by a symplectic, orthonormal ROB.
For the final step (iii), we define the orthogonal projection operators
Both are idempotent and symmetric, thus . Due to , it further holds
Thus, it follows
and with
where we use in the last step that for two matrices , for , it holds for the Frobenius norm .
Since it is equivalent to minimize a function or a multiple of it for any positive constant , minimizing is equivalent to minimizing . Additionally, for an ROB of the form , the constraint of orthonormal columns is equivalent to the requirements in (15). Thus, to minimize the PSD in the class of symplectic, orthonormal ROBs is equivalent to the POD of (19). □
Remark 6.
We remark that, in the same fashion as the proof of step (iii) in Proposition 6, it can be shown that, restricting to symplectic, orthonormal ROBs, a solution of is a solution of and vice versa, which is one detail that was missing in [4] to show the optimality of PSD Complex SVD in the set of symplectic, orthonormal ROBs.
We next prove that PSD Complex SVD is equivalent to POD of from (19) and thus also minimizes the PSD in the set of symplectic, orthonormal bases. To this end, we repeat the optimality result from [4] and extend it with the results of the present paper.
Proposition 7 (Optimality of PSD Complex SVD).
Let denote the set of symplectic bases with the structure . The PSD Complex SVD solves in .
Proof.
See ([4], Theorem 4.5). □
Proposition 8 (Equivalence of POD of Ys and PSD Complex SVD).
PSD Complex SVD is equivalent to the POD of . Thus, PSD Complex SVD yields a minimizer of the PSD for symplectic, orthonormal ROBs.
Proof.
By Proposition 7, PSD Complex SVD minimizes (19) in the set of symplectic bases with the structure . Thus, (16) holds with which is equivalent to the conditions on required in (15). By Proposition 4, we infer that equals the set of symplectic, orthonormal bases.
Furthermore, we can show that, in the set , a solution of is a solution of and vice versa (see Remark 6). Thus, PSD Complex SVD minimizes the PSD for the snapshot matrix in the set of orthonormal, symplectic matrices and PSD Complex SVD and the POD of solve the same minimization problem. □
We emphasize that the computation of a minimizer of (19) via PSD Complex SVD requires less memory storage than the computation via POD of . The reason is that the complex formulation uses the complex snapshot matrix which equals floating point numbers while the solution with the POD of method artificially enlarges the snapshot matrix to which are floating point numbers. Still, the POD of might be computationally more efficient since it is a purely real formulation and thereby does not require complex arithmetic operations.
3.2. Symplectic, Non-Orthonormal Basis Generation
In the next step, we want to give an idea how to leave the class of symplectic, orthonormal ROBs. We call a basis generation technique symplectic, non-orthonormal if it is able to compute a symplectic, non-orthonormal basis.
In Proposition 5, we briefly showed that most existing symplectic basis generation techniques generate a symplectic, orthonormal ROB. The only exception is the NLP algorithm suggested in [4]. It is able to compute a non-orthonormal, symplectic ROB. The algorithm is based on a given initial guess which is a symplectic ROB, e.g., computed with PSD Cotangent Lift or PSD Complex SVD. Nonlinear programming is used to leave the class of symplectic, orthonormal ROBs and derive an optimized symplectic ROB with the symplectic coefficient matrix for some . Since this procedure searches a solution spanned by the columns of , it is not suited to compute a global optimum of the PSD which we are interested in the scope of this paper.
In the following, we present a new, non-orthonormal basis generation technique that is based on an SVD-like decomposition for matrices presented in [6]. To this end, we introduce this decomposition in the following. Subsequently, we present first theoretical results which link the symplectic projection error with the “singular values” of the SVD-like decomposition which we call symplectic singular values. Nevertheless, the optimality with respect to the PSD functional (14) of this new method is yet an open question.
Proposition 9 (SVD-like decomposition
[6]). Any real matrix can be decomposed as the product of a symplectic matrix , a sparse and potentially non-diagonal matrix and an orthogonal matrix with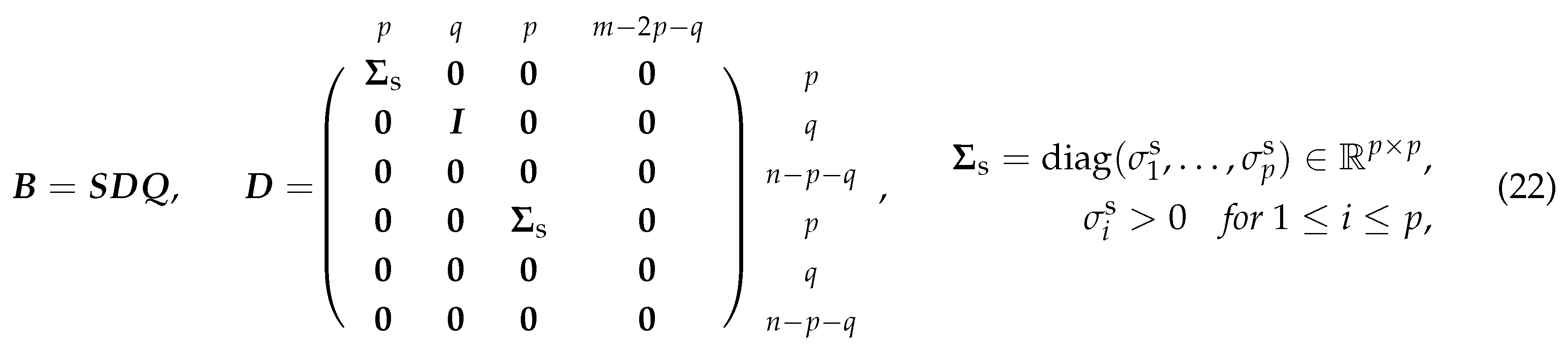 with and and where we indicate the block row and column dimensions in by small letters. The diagonal entries , , of the matrix are related to the pairs of purely imaginary eigenvalues of with
with and and where we indicate the block row and column dimensions in by small letters. The diagonal entries , , of the matrix are related to the pairs of purely imaginary eigenvalues of with
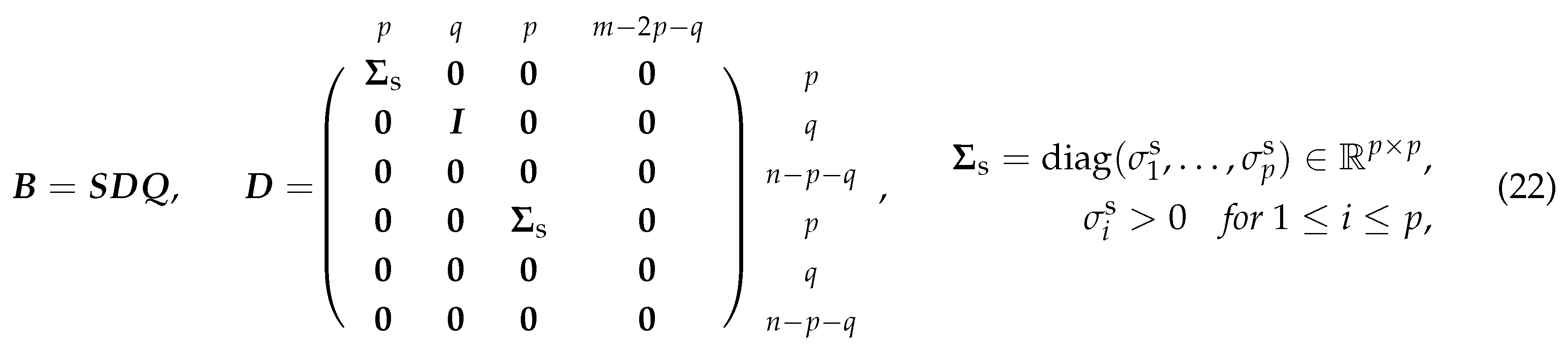 with and and where we indicate the block row and column dimensions in by small letters. The diagonal entries , , of the matrix are related to the pairs of purely imaginary eigenvalues of with
with and and where we indicate the block row and column dimensions in by small letters. The diagonal entries , , of the matrix are related to the pairs of purely imaginary eigenvalues of withRemark 7 (Singular values).
We call the diagonal entries , , of the matrix from Proposition 9 in the following the symplectic singular values. The reason is the following analogy to the classical SVD.
The classical SVD decomposes as where , are each orthogonal matrices and is a diagonal matrix with the singular values on its diagonal , . The singular values are linked to the real eigenvalues of with . Furthermore, for the SVD, it holds due to the orthogonality of and , respectively, and .
A similar relation can be derived for an SVD-like decomposition from Proposition 9. Due to the structure of the decomposition (22) and the symplecticity of , it holds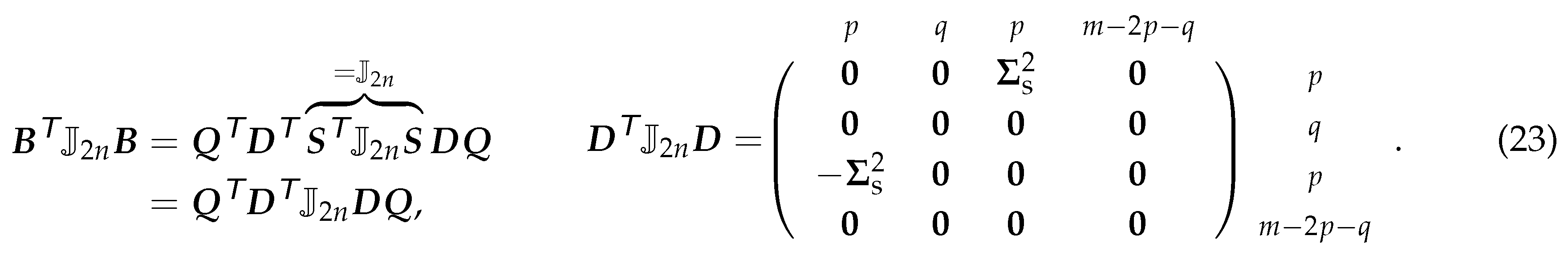 This analogy is why we call the diagonal entries , , of the matrix symplectic singular values.
This analogy is why we call the diagonal entries , , of the matrix symplectic singular values.
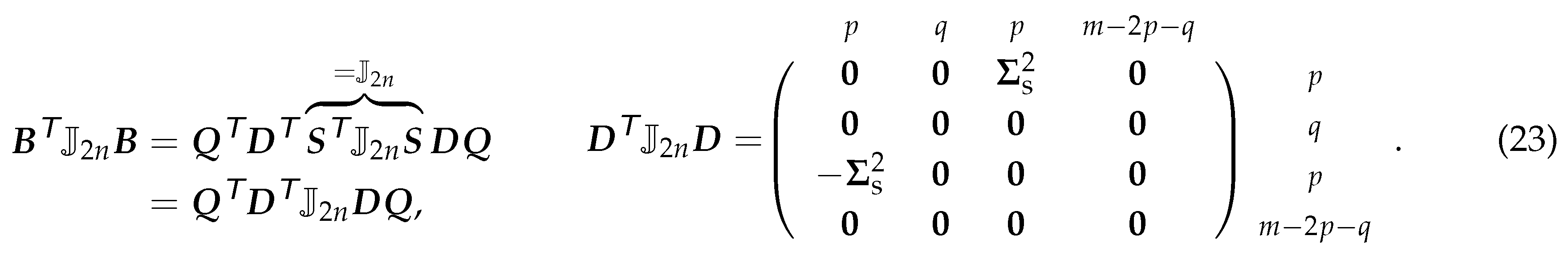 This analogy is why we call the diagonal entries , , of the matrix symplectic singular values.
This analogy is why we call the diagonal entries , , of the matrix symplectic singular values.The idea for the basis generation now is to select pairs of columns of in order to compute a symplectic ROB. The selection should be based on the importance of these pairs which we characterize by the following proposition by linking the Frobenius norm of a matrix with the symplectic singular values.
Proposition 10.
Let with an SVD-like decomposition with from Proposition 9. The Frobenius norm of can be rewritten as
where is the i-th column of for . In the following, we refer to each as the weighted symplectic singular value.
Proof.
We insert the SVD-like decomposition and use the orthogonality of to reformulate
which is equivalent to (24). □
It proves true in the following Proposition Proposition 11 that we can delete single addends in (24) with the symplectic projection used in the PSD if we include the corresponding pair of columns in the ROB. This will be our selection criterion in the new basis generation technique that we denote PSD SVD-like decomposition.
Definition 9 (PSD SVD-like decomposition).
We compute an SVD-like decomposition (22) as of the snapshot matrix and define as in Proposition 9. In order to compute an ROB with columns, find the k indices which have large contributions in (24) with
To construct the ROB, we choose the k pairs of columns from corresponding to the selected indices such that
The special choice of the ROB is motivated by the following theoretical result which is very analogous to the results known for the classical POD in the framework of orthogonal projections.
Proposition 11 (Projection error by neglegted weighted symplectic singular values).
Let be an ROB constructed with the procedure described in Definition 9 to the index set with from Proposition 9. The PSD functional can be calculated by
which is the cumulative sum of the squares of the neglected weighted symplectic singular values.
Proof.
Let be an ROB constructed from an SVD-like decomposition of the snapshot matrix with the procedure described in Definition 9. Let be defined as in Proposition 9 and be the set of indices selected with (25).
For the proof, we introduce a slightly different notation of the ROB . The selection of the columns of is denoted with the selection matrix based on
which allows us to write the ROB as the matrix–matrix product . Furthermore, we can select the neglected entries with .
We insert the SVD-like decomposition and the representation of the ROB introduced in the previous paragraph in the PSD which reads
where we use the orthogonality of and the symplecticity of in the last step. We can reformulate the product of Poisson matrices and the selection matrix as
Thus, we can further reformulate the PSD as
where are the weighted symplectic singular values from (24). In the last step, we use that the resultant diagonal matrix in the braces sets all rows of with indices to zero for . Thus, the last step can be concluded analogously to the proof of Proposition 10.
A direct consequence of Proposition 11 is that the decay of the PSD functional is proportional to the decay of the sum over the neglected weighted symplectic singular values from (24). In the numerical example Section 4.2.1, we observe an exponential decrease of this quantities which induces an exponential decay of the PSD functional. □
Remark 8 (Computation of the SVD-like decomposition).
To compute an SVD-like decompostion (22) of , several approaches exist. The original paper [6] derives a decomposition based on the product which is not good for a numerical computation since errors can arise from cancellation. In [3], an implicit version is presented that does not require the computation of the full product but derives the decomposition implicitly by transforming . Furthermore, Ref. [18] introduces an iterative approach to compute an SVD-like decomposition which computes parts of an SVD-like decomposition with a block-power iterative method. In the present case, we use the implicit approach [3].
To conclude the new method, we display the computational steps in Algorithm 1. All methods in this algorithm are standard MATLAB® functions except for SVD_like_decomp which is supposed to return the matrices , , and integers of the SVD-like decomposition (22). The matrix is not required and thus, replaced with ∼ as usual in MATLAB® notation.
| Algorithm 1: PSD SVD-like decomposition in MATLAB® notation. | |
| Input: snapshot matrix , size of the ROB | |
| Output: symplectic ROB | |
| 1 | // compute SVD-like decomposition, Q is not required |
| 2 | // extract symplectic singular values |
| 3 | // compute squares of the 2-norm of each column of S |
| 4 | // weighted sympl. singular values |
| 5 | // append weighted symplectic singular values |
| 6 | // find indices of k highest weighted symplectic singular values |
| 7 | // select columns with indices and |
3.3. Interplay of Non-Orthonormal and Orthonormal ROBs
We give further results on the interplay of non-orthonormal and orthonormal ROBs. The fundamental statement in the current section is the Orthogonal SR decomposition [6,19].
Proposition 12 (Orthogonal SR decomposition).
For each matrix with , there exists a symplectic, orthogonal matrix , an upper triangular matrix and a strictly upper triangular matrix such that
We remark that a similar result can be derived for the case [6], but it is not introduced since we do not need it in the following.
Proof.
Let with . We consider the QR decomposition
where is an orthogonal matrix and is upper triangular. The original Orthogonal SR decomposition ([19], Corollary 4.5.) for the square matrix states that we can decompose as a symplectic, orthogonal matrix , an upper triangular matrix , a strictly upper triangular matrix and two (possibly) full matrices
Since is upper triangular, it does preserve the (strictly) upper triangular pattern in and and we obtain the (strictly) upper triangular matrices from
□
Based on the Orthogonal SR decomposition, the following two propositions prove bounds for the projection errors of PSD which allows an estimate for the quality of the respective method. In both cases, we require the basis size to satisfy or , respectively. This restriction is not limiting in the context of symplectic MOR as in all application cases .
Similar results have been presented in ([20], Proposition 3.11) for PSD Cotangent Lift. In comparison to these results, we are able to extend the bound to the case of PSD Complex SVD and thereby improve the bound for the projection error by a factor of .
Proposition 13.
Let be a minimizer of POD with basis vectors and be a minimizer of the PSD in the class of orthonormal, symplectic matrices with basis vectors. Then, the orthogonal projection errors of and satisfy
Proof.
The Orthogonal SR decomposition (see Proposition 12) guarantees that a symplectic, orthogonal matrix and exist with . Since both matrices and are orthogonal and , we can show that yields a lower projection error than with
Let be a minimizer of the PSD in the class of symplectic, orthonormal ROBs. By definition of , it yields a lower projection error than . Since both ROBs are symplectic and orthonormal, we can exchange the symplectic inverse with the transposition (see Proposition 4, (iii)). This proves the assertion with
□
Proposition 13 proves that we require at most twice the number of basis vectors to generate a symplectic, orthonormal basis with an orthogonal projection error at least as small as the one of the classical POD. An analogous result can be derived in the framework of a symplectic projection which is proven in the following proposition.
Proposition 14.
Assume that there exists a minimizer of the general PSD for a basis size with potentially non-orthonormal columns. Let be a minimizer of the PSD in the class of symplectic, orthogonal bases of size . Then, we know that the symplectic projection error of is less than or equal to the one of , i.e.,
Proof.
Let be a minimizer of PSD with . By Proposition 12, we can determine a symplectic, orthogonal matrix and with . Similar to the proof of Proposition 13, we can bound the projection errors. We require the identity
With this identity, we proceed analogously to the proof of Proposition 13 and derive for a minimizer of PSD in the class of symplectic, orthonormal ROBs
□
Proposition 14 proves that we require at most twice the number of basis vectors to generate a symplectic, orthonormal basis with a symplectic projection error at least as small as the one of a (potentially non-orthonormal) minimizer of PSD.
4. Numerical Results
The numerical experiments in the present paper are based on a two-dimensional plane strain linear elasticity model which is described by a Lamé–Navier equation
for and with the density , the Lamé constants , the external force and Dirichlet boundary conditions on and Neumann boundary conditions on . We apply non-dimensionalization (e.g., ([21], Chapter 4.1)), apply the Finite Element Method (FEM) with piecewise linear Lagrangian ansatz functions on a triangular mesh (e.g., [22]) and rewrite the system as a first-order system to derive a quadratic Hamiltonian system (see Corollary 1) with
where is the vector of displacement DOFs, is the vector of linear momentum DOFs, is the stiffness matrix, is the inverse of the mass matrix and is the vector of external forces.
We remark that a Hamiltonian formulation with the velocity DOFs instead of the linear momentum DOFs is possible if a non-canonical symplectic structure is used. Nevertheless, in ([4], Remark 3.8.), it is suggested to switch to a formulation with a canonical symplectic structure for the MOR of Hamiltonian systems.
In order to solve the system (27) numerically with a time-discrete approximation for each of time steps , , a numerical integrator is required. The preservation of the symplectic structure in the time-discrete system requires a so-called symplectic integrator [8,23]. In the context of our work, the implicit midpoint scheme is used in all cases for the sake of simplicity. Higher-order symplectic integrators exist and could as well be applied.
Remark 9 (Modified Hamiltonian).
We remark that, even though the symplectic structure is preserved by symplectic integrators, the Hamiltonian may be modified in the time-discrete system compared to the original Hamiltonian. In the case of a quadratic Hamiltonian (see Corollary 1) and a symplectic Runge–Kutta integrator, the modified Hamiltonian equals the original Hamiltonian since these integrators preserve quadratic first integrals. For further details, we refer to ([8], Chapter IX.) or ([24], Sections 5.1.2 and 5.2).
The model parameters are the first and second Lamé constants with which varies between cast iron and steel with approx. chromium ([25], App. E 1 Table 1). The density is set to . The non-dimensionalization constants are set to , , . The geometry is a simple cantilever beam clamped on the left side with a force applied to the right boundary (see Figure 1). The time interval is chosen to be with and which is one oscillation of the beam. For the numerical integration, time steps are used.
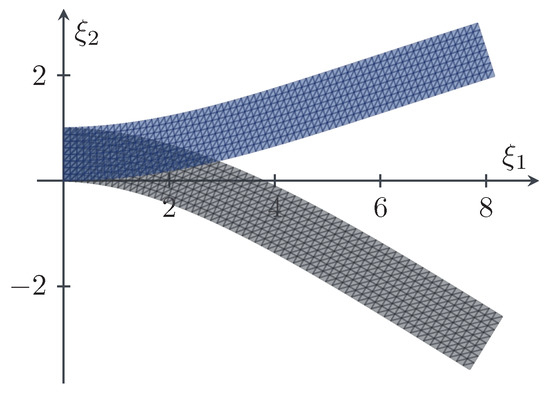
Figure 1.
An exaggerated illustration of the displacements of the non-autonomous beam model (a) at the time with the maximum displacement (gray) and (b) at the final time (blue).
The symplectic MOR techniques examined are PSD Complex SVD (Definition 8), the greedy procedure [5] and the newly introduced PSD SVD-like decomposition (Definition 9). The MOR techniques that do not necessarily derive a symplectic ROB are called non-symplectic MOR techniques in the following. The non-symplectic MOR techniques investigated in the scope of our numerical results are the POD applied to the full state (POD full state) and a POD applied to the displacement and linear momentum states separately (POD separate states). To summarize the basis generation methods, let us enlist them in Table 1 where and denote the SVD and the complex SVD, respectively.

Table 1.
Basis generation methods used in the numerical experiments in summary, where we use the MATLAB® notation to denote the selection of the first k columns of a matrix, e.g., in .
All presented experiments are generalization experiments, i.e., we choose nine different training parameter vectors on a regular grid to generate the snapshots and evaluate the reduced models for 16 random parameter vectors that are distinct from the nine training parameter vectors. Thus, the number of snapshots is . The size of the ROB is varied in steps of 20 with .
Furthermore, all experiments consider the performance of the reduced models based on the error introduced by the reduction. We do not compare the computational cost of the different basis generation techniques in the offline-phase since the current (non-optimized) MATLAB® implementation of the SVD-like decomposition does not allow a meaningful numerical comparisons of offline-runtimes as the methods using a MATLAB®-internal, optimized SVD implementation will be faster.
The software used for the numerical experiments is RBmatlab (https://www.morepas.org/software/rbmatlab/) which is an open-source library based on the proprietary software package MATLAB® and contains several reduced simulation approaches. An add-on to RBmatlab is provided in the Supplementary Materials of the current paper which includes all the additional code to reproduce the results of the present paper. The versions used in the present paper are RBmatlab 1.16.09 and MATLAB® 2017a.
4.1. Autonomous Beam Model
In the first model, we load the beam on the free end (far right) with a constant force which induces an oscillation. Due to the constant force, the discretized system can be formulated as an autonomous Hamiltonian system. Thus, the Hamiltonian is constant and its preservation in the reduced models can be analysed. All other reduction results are very similar to the non-autonomous case and thus are exclusively presented for the non-autonomous case in the following Section 4.2.
Preservation over Time of the Modified Hamiltonian in the Reduced Model
In the following, we investigate the preservation of the Hamiltonian of our reduced models. With respect to Remark 9, we mean the preservation over time of the modified Hamiltonian. Since the Hamiltonian is quadratic in our example and the implicit midpoint is a symplectic Runge-Kutta integrator, the modified Hamiltonian equals the original which is why we speak of “the Hamiltonian” in the following.
We present in Figure 2 the count of the total 240 simulations which show a preservation (over time) of the reduced Hamiltonian in the reduced model. The solution of a reduced simulation preserves the reduced Hamiltonian over time if for all discrete times , where is a parameter-dependent normalization factor. The heat map shows that no simulation in the non-symplectic case preserves the Hamiltonian, whereas the symplectic methods all preserve the Hamiltonian which is what was expected from theory.

Figure 2.
Heat map which shows the preservation of the reduced Hamiltonian in the reduced model in x of y cases ().
In Figure 3, we exemplify the non-constant evolution of the reduced Hamiltonian for three non-symplectic bases generated by POD separate states with different basis sizes and one selected test parameter . It shows that, in all three cases, the Hamiltonian starts to grow exponentially.
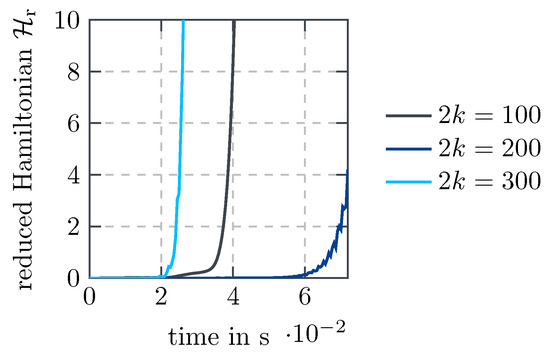
Figure 3.
Evolution of the reduced Hamiltonian for POD separate states for a selected parameter .
4.2. Non-Autonomous Beam Model
The second model is similar to the first one. The only difference is that the force on the free (right) end of the beam is loaded with a time-varying force. The force is chosen to act in phase with the beam. The time dependence of the force necessarily requires a non-autonomous formulation which requires in the framework of the Hamiltonian formulation a time-dependent Hamiltonian function which we introduced in Section 2.4.
We use the model to investigate the quality of the reduction for the considered MOR techniques. To this end, we investigate the projection error, i.e., the error on the training data, the orthogonality and symplecticity of the ROB and the error in the reduced model for the test parameters.
4.2.1. Projection Error of the Snapshots and Singular Values
The projection error is the error on the training data collected in the snapshot matrix , i.e.,
It is a measure for the approximation qualities of the ROB based on the training data. Figure 4 (left) shows this quantity for the considered MOR techniques and different ROB sizes . All basis generation techniques show an exponential decay. As expected from theory, POD full state minimizes the projection error for the orthonormal basis generation techniques (see Table 1). PSD SVD-like decomposition shows a lower projection error than the other PSD methods for and yields a similar projection error for . Concluding this experiment, one might expect the full-state POD to yield decent results or even the best results. The following experiments prove this expectation to be wrong.
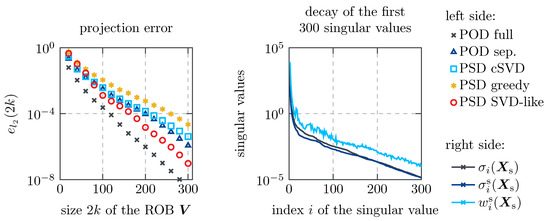
Figure 4.
Projection error (left) and decay of the singular values from Remark 7 and (24) (right).
The decay of (a) the classical singular values , (b) the symplectic singular values (see Remark 7) and (c) the weighted symplectic singular values (see (24)) sorted by the magnitude of the symplectic singular values is displayed in Figure 4 (right). All show an exponential decrease. The weighting introduced in (24) for does not influence the exponential decay rate of . The decrease in the classical singular values is directly linked to the exponential decrease of the projection error of POD full state due to properties of the Frobenius norm (see [1]). A similar result was deduced in the scope of the present paper for PSD SVD-like decomposition and the PSD functional (see Proposition 11).
4.2.2. Orthonormality and Symplecticity of the Bases
To verify the orthonormality and the symplecticity numerically, we consider the two functions
which are zero/numerically zero if and only if the basis is orthonormal or symplectic, respectively. In Figure 5, we show both values for the considered basis generation techniques and RB sizes.
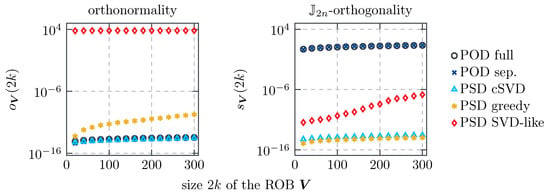
Figure 5.
The orthonormality (left) and the -orthogonality (right) from (28).
The orthonormality of the bases is in accordance with the theory. All procedures compute symplectic bases except for PSD SVD like-decomposition. PSD greedy shows minor loss in the orthonormality which is a known issue for the -orthogonalization method used (modified symplectic Gram–Schmidt procedure with re-orthogonalization [26]). However, no major impact on the reduction results could be attributed to this deficiency in the scope of this paper.
In addition, the symplecticity (or -orthogonality) of the bases behaves as expected. All PSD methods generate symplectic bases, whereas the POD methods do not. A minor loss of symplecticity is recorded for PSD SVD-like decomposition which is objected to the computational method that is used to compute an SVD-like decomposition. Further research on algorithms for the computation of an SVD-like decomposition should improve this result. Nevertheless, no major impact on the reduction results could be attributed to this deficiency in the scope of this paper.
4.2.3. Relative Error in the Reduced Model
We investigate the error introduced by MOR in the reduced model based on 16 test parameters distinct from the training parameters. The error is measured in the relative ∞-norm in time and space
where indicates the size of the ROB , is one of the test parameters, is the solution of the full model (5) and is the solution of the reduced model (7). This error is used for testing purposes only since it requires the computation of the full solution . It may be instead estimated in the online phase with an a posteriori error estimator as, e.g., in [9,27].
To display the results for all 16 test parameters at once, we use box plots in Figure 6. The box represents the -quartile, the median and the -quartile. The whiskers indicate the range of data points which lay within times the interquartile range (IQR). The crosses show outliers. For the sake of a better overview, we truncated relative errors above .
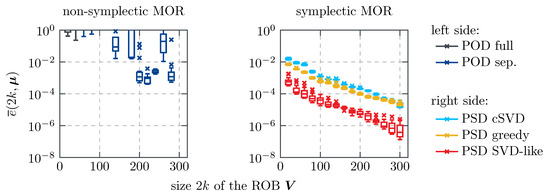
Figure 6.
Relative error in the reduced model.
The experiments show that the non-symplectic MOR techniques show a strongly non-monotonic behaviour for an increasing basis size. For many of the basis sizes, there exists a parameter which shows crude approximation results which lay above relative error. The POD full state is unable to produce results with a relative error below .
On the other hand, the symplectic MOR techniques show an exponentially decreasing relative error. Furthermore, the IQRs are much lower than for the non-symplectic methods. We stress that the logarithmic scale of the y-axis distorts the comparison of the IQRs—but only in favour of the non-symplectic methods. The low IQRs for the symplectic methods show that the symplectic MOR techniques derive a reliable reduced model that yields good results for any of the 16 randomly chosen test parameters. Furthermore, none of the systems shows an error above —for PSD SVD-like decomposition, this bound is , i.e., one magnitude lower.
In the set of the considered symplectic, orthogonal MOR techniques, PSD greedy shows the best result for most of the considered ROB sizes. This superior behaviour of PSD greedy in comparison to PSD complex SVD is unexpected since PSD greedy showed inferior results for the projection error in Section 4.2.1. This was also observed in [5].
Within the set of investigated symplectic MOR techniques, PSD SVD-like decomposition shows the best results followed by PSD greedy and PSD complex SVD. While the two orthonormal procedures show comparable results, PSD SVD like-decomposition shows an improvement in the relative error. Comparing the best results of either PSD greedy or PSD complex SVD with the worst result of PSD SVD-like decomposition considering the 16 different test parameters for a fixed basis size—which is pretty much in favour of the orthonormal basis generation techniques—, the improvement of PSD SVD-like decomposition ranges from factor to with a mean of .
5. Conclusions
We gave an overview of autonomous and non-autonomous Hamiltonian systems and the structure-preserving model order reduction (MOR) techniques for these kinds of systems [4,5,15]. Furthermore, we classified the techniques in orthonormal and non-orthonormal procedures based on the capability to compute a symplectic, (non-)orthonormal reduced order basis (ROB). To this end, we introduced a characterization of rectangular, symplectic matrices with orthonormal columns. Based thereon, an alternative formulation of the PSD Complex SVD [4] was derived which we used to prove the optimality with respect to the PSD functional in the set of orthonormal, symplectic ROBs. As a new method, we presented a symplectic, non-orthonormal basis generation procedure that is based on an SVD-like decomposition [6]. First theoretical results show that the quality of approximation can be linked to a quantity we referred to as weighted symplectic singular values.
The numerical examples show advantages for the considered linear elasticity model for symplectic MOR if a symplectic integrator is used. We were able to reduce the error introduced by the reduction with the newly introduced non-orthonormal method.
We conclude that non-orthonormal methods are able to derive bases with a lower error for both, the training and the test data. However, it is still unclear if the newly introduced method computes the global optimum of the PSD functional. Further work should investigate if a global optimum of the PSD functional can be computed with an SVD-like decomposition.
Furthermore, the application of symplectic MOR techniques in real-time scenarios and multi-query context should be further extended. This includes inverse problems or uncertainty quantification which often require solutions of the model for many different parameters. A suitable framework for uncertainty quantification in combination with symplectic MOR is, e.g., the approach discussed in [28].
Supplementary Materials
The following are available at https://www.mdpi.com/2297-8747/24/2/43/s1.
Author Contributions
Conceptualization, P.B., A.B., and B.H.; methodology, P.B. and A.B.; software, P.B.; validation, P.B.; formal analysis, P.B.; investigation, P.B.; resources, B.H.; data curation, P.B.; writing–original draft preparation, P.B.; writing–review and editing, A.B. and B.H.; visualization, P.B.; supervision, A.B. and B.H.; project administration, B.H.; and funding acquisition, B.H.
Funding
This research was partly funded by the German Research Foundation (DFG) Grant No. HA5821/5-1 and within the GRK 2198/1.
Acknowledgments
We thank the German Research Foundation (DFG) for funding this work. The authors thank Dominik Wittwar for inspiring discussions. The valuable input of the anonymous reviewers is acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Benner, P.; Ohlberger, M.; Cohen, A.; Willcox, K. Model Reduction and Approximation; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2017. [Google Scholar]
- Buchfink, P. Structure-Preserving Model Order Reduction of Hamiltonian Systems for Linear Elasticity. ARGESIM Rep. 2018, 55, 35–36. [Google Scholar] [CrossRef]
- Xu, H. A Numerical Method for Computing an SVD-like Decomposition. SIAM J. Matrix Anal. Appl. 2005, 26, 1058–1082. [Google Scholar] [CrossRef]
- Peng, L.; Mohseni, K. Symplectic Model Reduction of Hamiltonian Systems. SIAM J. Sci. Comput. 2016, 38, A1–A27. [Google Scholar] [CrossRef]
- Maboudi Afkham, B.; Hesthaven, J.S. Structure Preserving Model Reduction of Parametric Hamiltonian Systems. SIAM J. Sci. Comput. 2017, 39, A2616–A2644. [Google Scholar] [CrossRef]
- Xu, H. An SVD-like matrix decomposition and its applications. Linear Algebra Its Appl. 2003, 368, 1–24. [Google Scholar] [CrossRef]
- Cannas da Silva, A. Lectures on Symplectic Geometry; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Hairer, E.; Wanner, G.; Lubich, C. Geometric Numerical Integration: Structure-Preserving Algorithms for Ordinary Differential Equations; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Haasdonk, B.; Ohlberger, M. Efficient Reduced Models and A-Posteriori Error Estimation for Parametrized Dynamical Systems by Offline/Online Decomposition. Math. Comput. Model. Dyn. Syst. 2011, 17, 145–161. [Google Scholar] [CrossRef]
- Barrault, M.; Maday, Y.; Nguyen, N.C.; Patera, A.T. An ‘empirical interpolation’ method: Application to efficient reduced-basis discretization of partial differential equations. C. R. Math. 2004, 339, 667–672. [Google Scholar] [CrossRef]
- Chaturantabut, S.; Sorensen, D.C. Discrete Empirical Interpolation for nonlinear model reduction. In Proceedings of the 48th IEEE Conference on Decision and Control (CDC) Held Jointly with the 2009 28th Chinese Control Conference, Shanghai, China, 15–18 December 2009; pp. 4316–4321. [Google Scholar] [CrossRef]
- Beattie, C.; Gugercin, S. Structure-preserving model reduction for nonlinear port-Hamiltonian systems. In Proceedings of the 2011 50th IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2011; pp. 6564–6569. [Google Scholar] [CrossRef]
- Chaturantabut, S.; Beattie, C.; Gugercin, S. Structure-Preserving Model Reduction for Nonlinear Port-Hamiltonian Systems. SIAM J. Sci. Comput. 2016, 38, B837–B865. [Google Scholar] [CrossRef]
- Lanczos, C. The Variational Principles of Mechanics; Dover Books on Physics; Dover Publications: Mineola, NY, USA, 1970. [Google Scholar]
- Maboudi Afkham, B.; Hesthaven, J.S. Structure-Preserving Model-Reduction of Dissipative Hamiltonian Systems. J. Sci. Comput. 2018. [Google Scholar] [CrossRef]
- Sirovich, L. Turbulence the dynamics of coherent structures. Part I: coherent structures. Q. Appl. Math. 1987, 45, 561–571. [Google Scholar] [CrossRef]
- Paige, C.; Loan, C.V. A Schur decomposition for Hamiltonian matrices. Linear Algebra Appl. 1981, 41, 11–32. [Google Scholar] [CrossRef]
- Agoujil, S.; Bentbib, A.H.; Kanber, A. An iterative method for computing a symplectic SVD-like decomposition. Comput. Appl. Math. 2018, 37, 349–363. [Google Scholar] [CrossRef]
- Bunse-Gerstner, A. Matrix factorizations for symplectic QR-like methods. Linear Algebra Appl. 1986, 83, 49–77. [Google Scholar] [CrossRef]
- Peng, L.; Mohseni, K. Structure-Preserving Model Reduction of Forced Hamiltonian Systems. arXiv 2016, arXiv:1603.03514. [Google Scholar]
- Langtangen, H.P.; Pedersen, G.K. Scaling of Differential Equations, 1st ed.; Springer International Publishing: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Ern, A.; Guermond, J.L. Finite Element Interpolation. In Theory and Practice of Finite Elements; Springer: New York, NY, USA, 2004; pp. 3–80. [Google Scholar] [CrossRef]
- Bhatt, A.; Moore, B. Structure-preserving Exponential Runge–Kutta Methods. SIAM J. Sci. Comput. 2017, 39, A593–A612. [Google Scholar] [CrossRef]
- Leimkuhler, B.; Reich, S. Simulating Hamiltonian Dynamics; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar] [CrossRef]
- Oechsner, M.; Kloos, K.H.; Pyttel, B.; Berger, C.; Kübler, M.; Müller, A.K.; Habig, K.H.; Woydt, M. Anhang E: Diagramme und Tabellen. In Dubbel: Taschenbuch für den Maschinenbau; Grote, K.H., Feldhusen, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 324–357. [Google Scholar] [CrossRef]
- Al-Aidarous, E. Symplectic Gram–Schmidt Algorithm with Re-Orthogonalization. J. King Abdulaziz Univ. Sci. 2011, 23, 11–20. [Google Scholar] [CrossRef]
- Ruiner, T.; Fehr, J.; Haasdonk, B.; Eberhard, P. A-posteriori error estimation for second order mechanical systems. Acta Mechanica Sinica 2012, 28, 854–862. [Google Scholar] [CrossRef]
- Attia, A.; Ştefănescu, R.; Sandu, A. The reduced-order hybrid Monte Carlo sampling smoother. Int. J. Numer. Methods Fluids 2016, 83, 28–51. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).