1. Introduction
The behavior of large ensembles of out of equilibrium units is far from being completely understood. Recently, some bridges have been built to connect the dynamics of individual units with the collective state of a network (see, for example, [
1,
2,
3,
4]). This line of work has a long and rich history that includes the pioneering work of Art Winfree, who presented the first mathematical models built to describe the synchronization between biological oscillators [
5,
6]. Yoshiki Kuramoto also made important advances in this line of work. He proposed a simple model for the behavior of a large set of coupled oscillators, interacting pairwise through a sinusoidal function of their phase differences [
7,
8]. In this approach, the collective behavior of the system is described in terms of a single complex number: its amplitude accounts for the phase-coherence of the population of oscillators, and its phase stands for the average phase. In a typical statistical approach, the assumption is that this problem can be well approximated by a continuous system, described in terms of a density function of phase and time. This density represents the distribution of oscillators that, at a given time, present a given phase
.
Ott and Antonsen proposed an approach to this problem that turned out to be a breakthrough in the field [
9,
10]. In that work, the authors studied the dynamics of a network of coupled oscillators. Each oscillator was described in terms of its phase. The continuity equation satisfied by the density describing the state of the network was decomposed in modes, and under a specific set of hypotheses, the amplitudes of the modes were found to be linked by a simple function. In this way, knowing the dynamics of the first mode was enough to reconstruct the behavior of the infinite set of modes. Moreover, with this approach, it is possible to show that an order parameter describing the synchronicity of the network might obey a low dimensional system of ordinary differential equations (the order dependent on the complexity of the network).
This reduction in the dimensionality of the system of equations for the mode amplitudes was only a good approach if the interaction between the units could be written in terms of specific functional forms, such us the Kuramoto coupling term (a sinusoidal function of the difference between the interacting phases). It also worked if the units presented excitable dynamics before coupling and if the coupling was modeled in terms of “pulse” functions [
11]. Due to the similarity in their dynamics, this framework is generally used to model neural networks. The coupling describes the input current into the excitable units
I as:
which will account for the contributions to the current
I by the
j units, as their phases pass the value
(defined as the phase in which the neurons “spike”). Even if the dynamics of the individual units before the coupling was excitable, the couplings previously described are not the most natural ones to model synapses. In order to overcome this difficulty, Montbrió and collaborators derived independently exact equations to describe macroscopically networks of spiking units [
12,
13]. They were interested in the mechanisms of individual spike generation, and how they introduce an effective coupling between the mean membrane potential and the spiking rate, two biophysically relevant macroscopic quantities. In this approach, the firing rate is a good approximation of the global synaptic current for fast synapses. Moreover, to account for slower synapses, they proposed that the global synaptic activation
S would be ruled by:
where
R stands for the spiking rate (the number of spikes occurring per unit of time) [
12]. This approach led the authors to show that inhibitory, all-to-all coupled excitable units can display oscillations. This is a result that a Wilson-Cowan-like phenomenological model cannot reproduce [
14].
In the first part of this work (
Section 2), we build on these previous efforts by modeling the global synaptic activation as the sum of synaptic currents which present a maximum that is delayed with respect to the spike responsible for its occurrence. This is an important feature of the synaptic interaction that is not reproduced by previous models. Biophysical models of the synaptic interaction (nonlinear kinetic models [
15]) have solutions that display this delay. Nevertheless, it is not known how to achieve an analytical macroscopic description of the system with these nonlinear equations describing the synaptic interactions. In this work, we present a model capable of reproducing this realistic feature of the synaptic coupling, but which is also compatible with the analytic calculation of macroscopic quantities for the network.
The ideas proposed by Ott and Antonsen were successfully applied to study the
N→∞ limit in different kinds of networks of coupled units [
16,
17,
18,
19,
20,
21]. In cases where the composing elements of the system are excitable, such as neurons, an order parameter describing the synchrony of the network can indicate a highly synchronous state either because the units are spiking in phase, or because the units are quiescent near each other [
22]. To account not only for its synchrony but also for its level of activity, different quantities have been proposed to describe the global state of a network. Yet, these quantities are not unrelated. In recent work, it has been shown that the spiking rate of the network can be analytically expressed as a function of its synchrony [
11]. A different approach was followed by Montbrió et al., who formulated a model for a network of quadratic integrate-and-fire units (QIF) in terms of its average voltage and its firing rate [
23]. Both approaches (a network of phase oscillators and a network of QIF neurons) have been proven to be equivalent. Yet, despite the clear interpretation of the firing rate as a variable describing the state of a network, its direct measurement constitutes a challenge, as it requires recording the individual activity of every neuron in the network. In the second part of this work (
Section 3 and
Section 4), we discuss how the macroscopic variable defined in
Section 2 compares to the local field potential (LFP), and we test this relationship using measurements in an actual nervous system.
2. Macroscopic Evolution of a Set of Excitable Units
Let us assume a network of
N excitable units whose dynamics are described in terms of the phases
, obeying:
where
defines the degree of excitability of the
unit,
the coupling strength between the units, and
stands for the average synaptic current between the units. This model is known as the theta neuron model, and it is a simple one-dimensional model for the spiking of a neuron [
24]. The variable
lies on the unit circle and ranges between 0 and
. When
the neuron “spikes”, that is, it produces an action potential.
As we show in
Appendix A, when taking the continuous limit, the order parameter
, obeys the following dynamical rule:
with
, where each
describes the synaptic current contributed by a neuron spiking at
and
and
are the mean and width of a Lorentzian distribution for
, the excitability distribution function of the population (see details in
Appendix A). If we assume that each synaptic current can be represented by a function:
we can write a two-dimensional linear dynamical system having this function as a solution [
25], which reads:
Since these equations are linear, the global variable
S will satisfy the same equations, with the activity
(the total number of spikes taking place per unit of time) as the forcing term. This can be expressed in terms of the order parameter as (see detailed calculation in
Appendix A):
In this way, the network of coupled units can be macroscopically described by the following system:
In this calculation, we have assumed a unique population of neurons (for example all excitatory ones), with parameters distributed in a Lorentzian way (mean excitability parameter
), and with all the units coupled among each other with a unique strength described by
. For this simple architecture, we illustrate the different solutions of the problem in
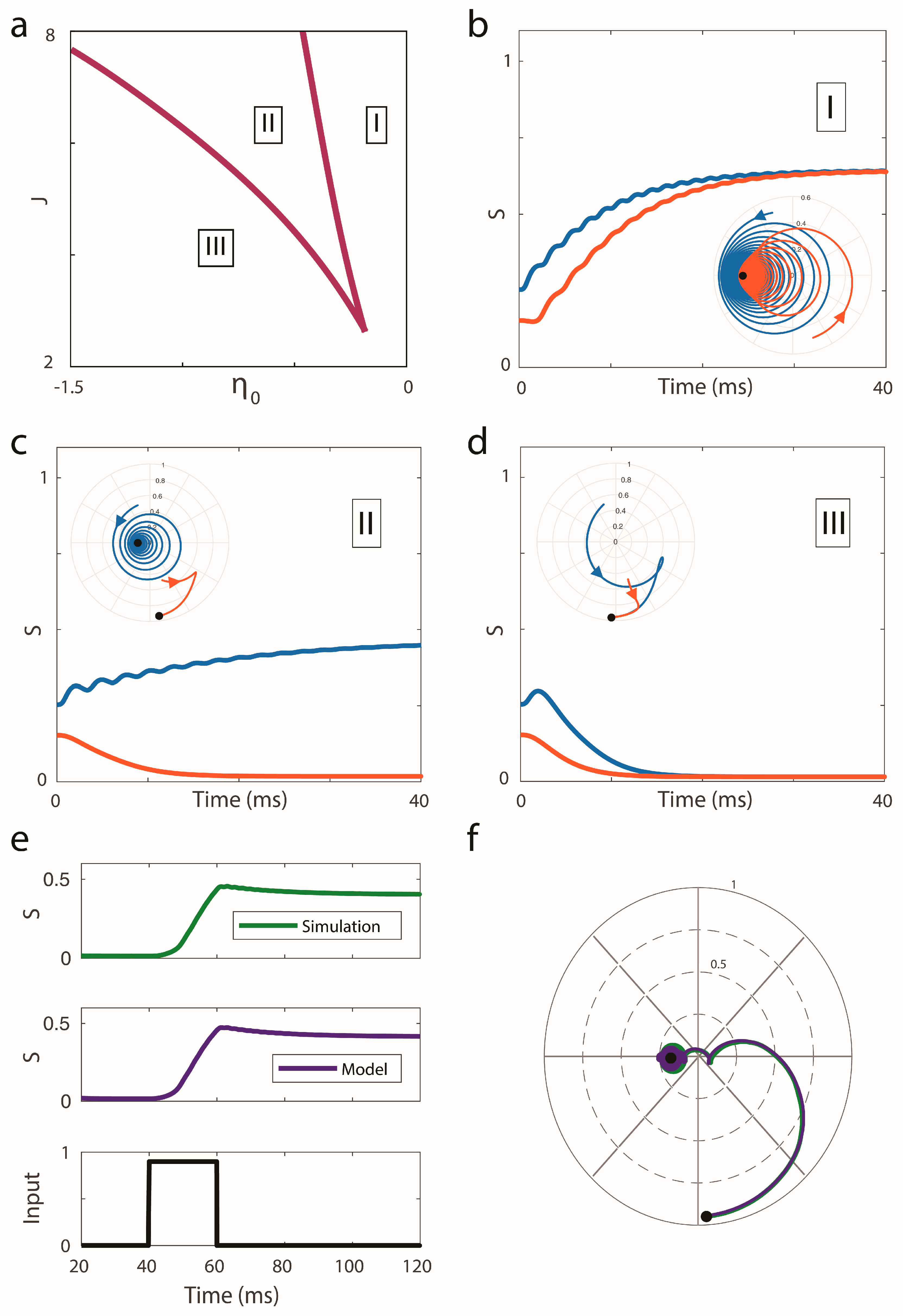
Figure 1. The calculations used to write these equations are presented in
Appendix A.
The panel (a) in
Figure 1 displays three different regions of the parameter space (
), for a problem in which
and
. The three panels displayed in b–d correspond to simulations for different initial conditions, showing that regions I and III present a unique stationary attracting solution. Region II presents bi-stability. This result is consistent with what is expected from simple additive models [
26]. Panels (e) and (f) in
Figure 1, show the agreement between this macroscopic description of the system, and a simulation of 15,000 oscillators, whose dynamics are ruled by our original set of equations. The rate used to drive the system was computed as the number of oscillators crossing the value
, divided by the total number of oscillators and the time step
.
Notice that in our description, the variable z describes the system´s synchronicity, and the variable
represents the global synaptic activation of the network. The individual synaptic currents are in fact the result of nonlinear processes. But since the functional form
is a most successful fit for a synaptic current [
15], we use a linear model for its generation. This allows us to add the equations for each synaptic component in order to come up with an equation of the global synaptic activation. Remarkably, synaptic activity is often acknowledged as the most important source of extracellular current flow [
27]. In the next sections, we will show that it is possible to use electrophysiological measurements as a starting point to compute a variable that can be a proxy for the synaptic activation.
3. An Experimental System
Synaptic currents are conjectured to contribute in a substantial way to the LFP since extracellular currents from many individual compartments must overlap in time to induce a measurable signal. This requires pertinent events to be slow [
27]. In general, complex neural architectures involve both excitatory and inhibitory neurons. This poses a problem for reconstructing the origin of any given fluctuation in the LFP. However, synchronous action potentials from many neurons can contribute substantially at specific temporal instances, particularly in the cases where the structure of the network allows us to have inhibitory and excitatory neurons spiking out of phase. Songbirds have been shown to present this out-of-phase spiking between excitatory and inhibitory neurons [
28]. We will thus investigate a system with complex neural architecture but for which, during some time intervals, mostly one class of neurons are active. We will then concentrate on those time intervals and investigate whether a reconstructed global synaptic activity can approximate the recorded LFP.
Songbirds have highly specialized brain regions to generate and process the signals that are involved in song production and perception. In a specific region of the telencephalon (known as the nucleus HVC, an old acronism at present used as a proper name), some neurons are active during song production. Interestingly, those neurons also spike when the bird is asleep or anesthetized if it is exposed to a recording of its own song (e.g., [
29]). Moreover, a neuron that spikes at a specific temporal instance when producing song will spike at about the same temporal instance when the anesthetized or sleeping bird listens to the song recording [
30]. This paradigm motivates the study of auditory-elicited responses in the HVC and its link to the coding of vocal production.
For the data presented in this work, extracellular recordings of neural activity were conducted on urethane-anesthetized canaries (
Serinus canaria). Surgery was performed to access the neural nuclei HVC and insert a multi-electrode array (A1 × 32, Neuronexus Technologies, Inc.). This array contained 32 aligned electrodes, separated
from each other. Neural activity was monitored online using proprietary INTAN software to control an Intan RHD2000 acquisition board. To study auditory responses in HVC, the experimental protocol consisted of presenting three different auditory stimuli (BOS, bird’s own song; CON, the song of an adult male conspecific; REV, its own song in reverse). Each protocol consisted of twenty randomized presentations of each stimulus (for more detailed methods, see [
31]). These methods are the standard paradigm to study selectivity in the neuronal nucleus HVC. Signals were sampled at 20 kHz and the hardware filtering was set between 0.1 Hz and 5000 Hz.
Recordings were analyzed using custom-built software. Low-frequency components due to synaptic currents were isolated from the high-frequency spiking activity due to action potentials elicited by neurons near each recording site. The slow signals commonly referred to as LFP were obtained using a low-pass zero-phase Butterworth IIR digital filter on the raw data (4th order, cutoff frequency: 300 Hz). For spiking activity, the filter used was a high-pass zero-phase Butterworth IIR digital filter (4th order, cutoff frequency: 500 Hz).
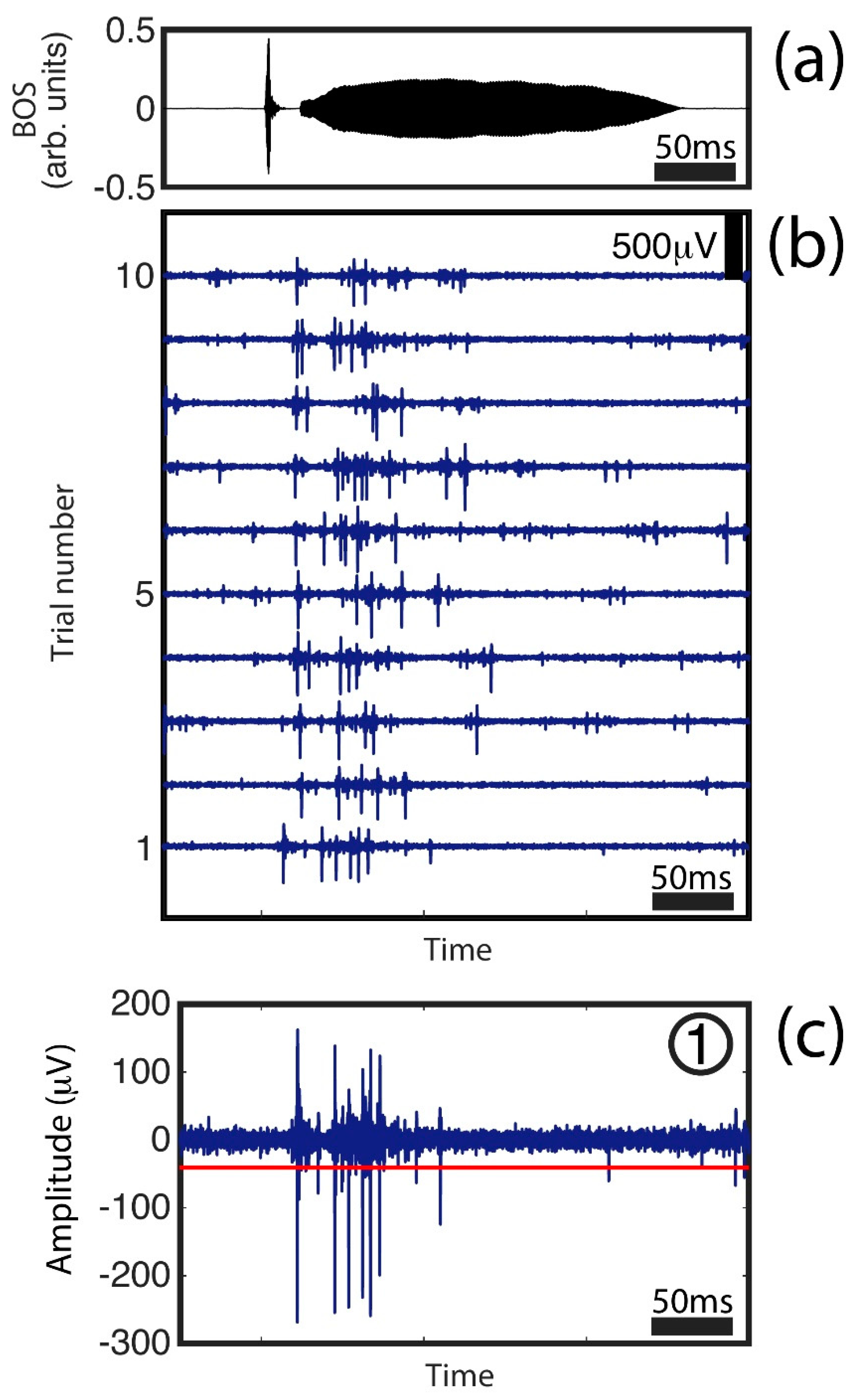
Figure 2 shows examples of the high-pass filtered data from one protocol. These traces represent the neural response to auditory presentations of the bird’s own song. In
Figure 2a, we show the sound signal from a single canary syllable (part of the auditory stimulus that was presented to the anesthetized bird). In
Figure 2b, we show a segment from 10 traces of high-pass filtered data. These traces correspond to the recorded activity in one channel of the neural probe for 10 presentations of the bird’s own song. In
Figure 2c, we show a magnified example of presentation 1 in
Figure 2b and the threshold used for spike detection. As can be seen from the different traces in
Figure 2b,c, there are multiple spikes of different amplitudes. This is an indicator that the electrode is registering multiunit activity (i.e., spikes from different neurons located at different positions from the electrode). As we are registering extracellular spikes, the amplitude registered by the electrode decays with distance. For additional details on the recording of neural ensembles, see [
32]. A simple characterization of the overall neural response to the stimulus is given by the multiunit activity histogram, which is computed by thresholding the signal, detecting the times at which each spike occurred and binning the activity in 15 ms windows.
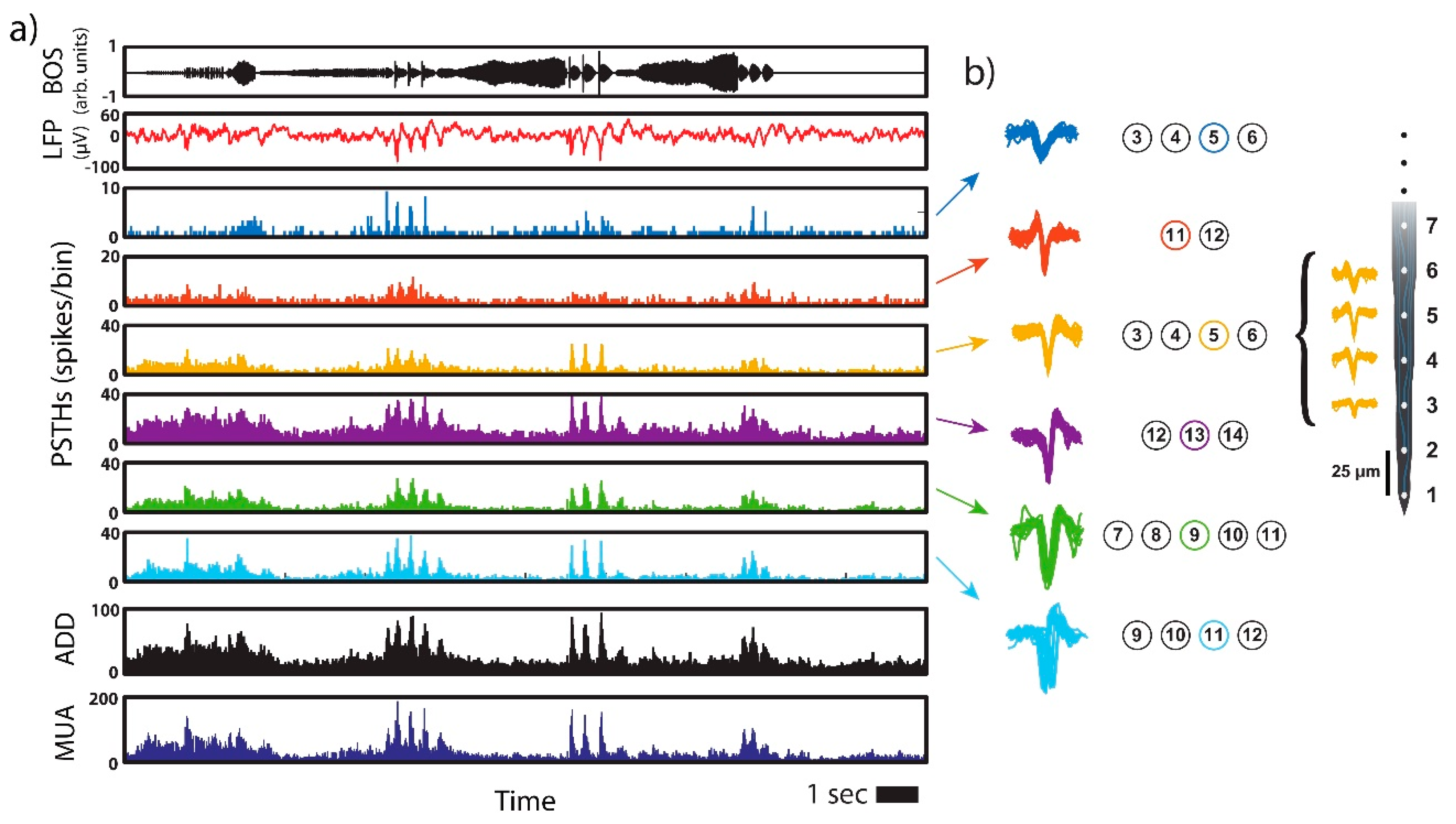
Figure 3 illustrates the results from the protocol from which the segment shown in
Figure 2 was extracted. The top panel in
Figure 3a shows the BOS recording presented to the anesthetized bird. The average LFP trace (trial-averaged for 20 trials and channel-averaged for the 32 channels) is shown in the second panel. This average was computed to consider all the synaptic currents in the recording, which is required for comparison with the global synaptic activation
S that we will reconstruct from these data. Since this signal represents the average, note that peaks arise both from the robustness in the response (trial-average) and from the synchronization of multiple channels (channel-average).
Single neuron activity was also recovered from the recordings. A spike-sorting algorithm (Phy, [
33]) identifies the temporal instances where different neurons are spiking by conducting a principal component analysis (PCA) on detected spike shapes. For the data shown in
Figure 3, identified neurons are plotted with different colors (see
Figure 3b). The same neuron could be registered simultaneously in more than one channel (as an example, we show in
Figure 3b the yellow spike shape registered in several channels of the multi-electrode). The circles to the right of each set of spike shapes indicate the channels where that neuron was registered. We have also color-outlined the circles representing the maximum amplitude channel, which correspond to the spike shapes shown. Binning the spike times for each neuron with 15 ms bins, we get the time traces displayed in the insets 3–8 in
Figure 3a (post-stimulus time histograms or PSTH). Peaks within each of these signals account for the response robustness at a given temporal instance and the presence of higher activation levels in response to the song. Notice that, additionally, whenever these time traces show peaks, their positions coincide, meaning that there is a degree of synchronization among units in the part of the neural network that is being sampled in these recordings.
Only neurons that respond mostly to the bird´s own song (BOS) were taken into account in our analysis. Some neurons present brief bursts of activity at a few instances during the production of a specific syllable type. Other neurons spike in a tonic-like fashion. Comparison between these firing patterns [
34], and results from another species (zebra finches,
Taeniopygia guttata [
35]), suggests that the first type might be projection neurons, while the second class might correspond to inhibitory interneurons. Projection neurons are excitatory neurons [
36]. Neurons shown in
Figure 3 are putative projection neurons, since they present bursts of activity at specific instances within the song.
4. Reconstructing the Dynamics for S from the Data
The single-channel multiunit activity recorded when the anesthetized bird is exposed to its own song, summed over the different repetitions, presents clear peaks at specific temporal instances (see
Figure 3). We have also found that at least close to the peaks, this MUA is similar to the summed activity of several different neurons detected by the multi-electrode at different depths of the nucleus HVC (compare MUA and ADD in
Figure 3a). All these neurons spiking at the same temporal instances are of the same kind (either excitatory or inhibitory), and therefore will contribute additively to the average synaptic current. In this way, we can define a threshold for the multiunit activity, and identify the times
where spikes are detected (as was shown in
Figure 2c). With that sequence of times
, we can add the functions for each synaptic event
:
and build a proxy for the average synaptic current, at least close to the instances where the multiunit activity has peaks. Using a parsimonious estimation for excitatory synapses of
, [
15] we generate this synthetic activation
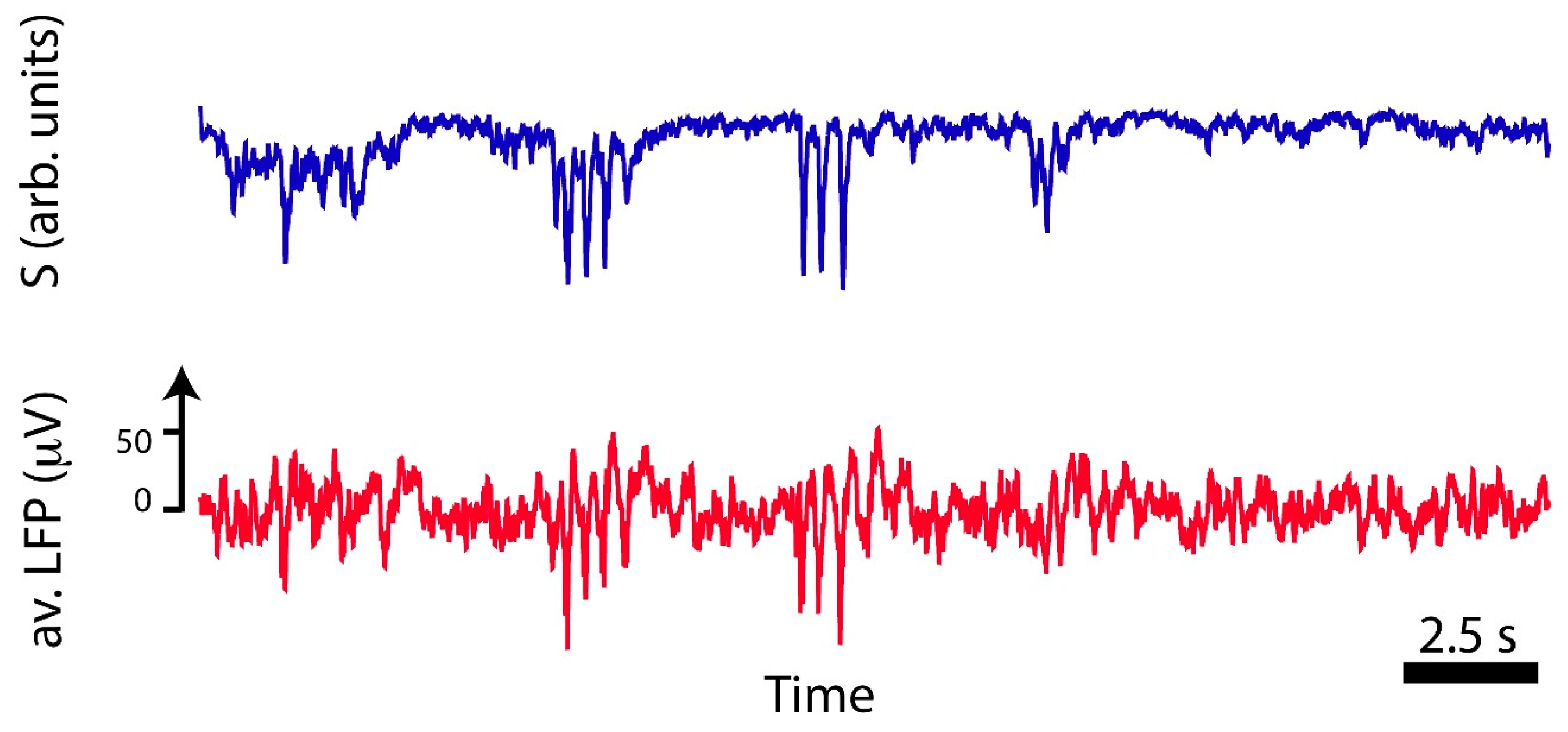
S, and compare the signal with the local field potential. The result is shown in
Figure 4. In blue (top panel), the trace shows
S as reconstructed from the spiking times and the red trace (bottom panel) is the LFP obtained from the recordings (also shown in
Figure 3a). These two traces share some temporal features: the instances where
S presents peaks correspond to the peaks found in the LFP. However, the LFP presents additional variations that
S does not capture. Most probably, this is because
S is reconstructed with a binned version of the high-passed data, where only the instances of the supra-threshold spiking activity were considered. This, in turn, yields a time trace for
S that presents small fluctuations, while the measured LFP presents additional variations arising from the background electrical activity. Finally, to measure the similarity between the two, we computed the average Pearson correlation between the two signals in shifting windows of 1.0 s, and we got
, with correlation values reaching
in the regions with the peaks. This informs that the reconstructed
S is more reliable in the case where synchronous firing has occurred, such that an emerging pattern can be observed from the data.
5. Discussion
In recent years, it has been shown that, in the infinite size limit, certain systems of globally coupled phase oscillators can display macroscopic features that obey low dimensional dynamics. That class of systems includes excitable systems, and therefore it is natural to inquire about its consequences in neuroscience, studying how large sets of neurons synchronize to generate behavior. Different functional forms describing the interaction between the units were studied in order to achieve an analytic macroscopic description of a network. In this work, we built a model for the global synaptic activation of a neural network, by adding functions that represented realistic synaptic currents. In particular, each synaptic current had a maximum that was delayed with respect to the maximum of the spike responsible for its occurrence. This led us to propose a two-dimensional linear model for each current, and therefore a two-dimensional model for the global activation, with the firing rate as its driving force. We computed and integrated the differential equations satisfied by quantities that describe the network macroscopically. Then, we simulated the networks directly and computed the same observables, finding a remarkable agreement.
It has been pointed out that in physiological situations, synaptic activity is often the most important source of extracellular current flow. This is because many events need to contribute to induce a measurable signal, which privileges slow events as synaptic currents. The effect is amplified if large synchrony exists. We tested the hypothesis that a global synaptic activation, reconstructed from the spikes detected by a multi-electrode assuming an excitatory nature, could approximate the LFP at some temporal instances. We did it for a system which presents an architecture far more complex than the one used to introduce our model. Nevertheless, we restrained our analysis to temporal intervals where large synchronic events of neurons of a single type are expected and found that, for those time intervals, the LFP data and the computed synaptic activation were highly correlated.
It is possible to obtain a significant amount of information from a dynamical system by measuring some or even one of its variables. For example, it has been shown that it is possible to reconstruct the topology of a dynamical system that displays chaotic behavior by building an embedding from one of the system´s variables [
37]. Moreover, for some systems, it is possible to reconstruct their ruling equations by operating on one measured variable [
38]. In this way, the similarity between LFP (measurable) and the synaptic global activation (used in our macroscopic models) suggests a path to build bridges between macroscopic models for large sets of excitable units and experimental data.