An Efficient Semi-Analytical Solution of a One-Dimensional Curvature Equation that Describes the Human Corneal Shape
Abstract
:1. Introduction
2. Description of the Method
2.1. Construction of Green’s Function
2.2. Green-Picard Fixed Point Iteration
2.3. Green-Mann Fixed Point Iteration
3. Convergence Analysis
4. Results and Discussions
- The zero-order solution based on the hyperbolic cosine function [2]:
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Corsato, C.; De Coster, C.; Omari, P. The Dirichlet problem for a prescribed anisotropic mean curvature equation: existence, uniquness and regularity of solutons. J. Differ. Equ. 2016, 260, 4572–4618. [Google Scholar] [CrossRef]
- Okrasiński, W.; Płociniczak, Ł. A nonlinear mathematical model of the corneal shape. Nonlinear Anal. Real World Appl. 2012, 13, 1498–1505. [Google Scholar]
- Płociniczak, Ł.; Okrasiński, W.; Nieto, J.J.; Domínguez, O. On a nonlinear boundary value problem modeling corneal shape. J. Math. Anal. Appl. 2014, 414, 461–471. [Google Scholar]
- He, J. A remark on “A nonlinear mathematical model of the corneal shape”. Nonlinear Anal. Real World Appl. 2012, 13, 2863–2865. [Google Scholar] [CrossRef]
- Płociniczak, Ł.; Griffiths, G.W.; Schiesser, W.E. ODE/PDE analysis of corneal curvature. Comput. Biol. Med. 2014, 53, 30–41. [Google Scholar]
- Coelho, I.; Corsato, C.; Omari, P. A one-dimensional prescribed curvature equation modeling the corneal shape. Bound. Value Probl. 2014, 2014, 127. [Google Scholar] [CrossRef] [Green Version]
- Griffiths, G.W.; Płociniczak, Ł.; Schiesser, W.E. Analysis of cornea curvature using radial basis functions—Part I: Methodology. Comput. Biol. Med. 2016, 77, 274–284. [Google Scholar] [CrossRef]
- Okrasiński, W.; Płociniczak, Ł. Solution estimates for a system of nonlinear integral equations arising in optometry. J. Integral Equ. Appl. 2018, 30, 167–179. [Google Scholar]
- Anderson, K.; El-Sheikh, A.; Newson, T. Application of structural analysis to the mechanical behaviour of the cornea. J. R. Soc. Interface 2014, 1, 3–15. [Google Scholar] [CrossRef]
- Ahmed, E. Finite element modeling of corneal biomechanical behavior. J. Refract. Surg. 2010, 26, 289–300. [Google Scholar]
- Iskander, D.R.; Collins, M.J.; Davis, B. Optimal modeling of corneal surfaces by Zernike polynomials. IEEE Trans. Biomed. Eng. 2001, 48, 87–95. [Google Scholar] [CrossRef] [PubMed]
- Okrasiński, W.; Płociniczak, Ł. Bessel function model of corneal topography. Appl. Math. Comput. 2013, 223, 436–443. [Google Scholar] [Green Version]
- Jang, B. Two-point boundary value problems by the extended Adomian decomposition method. J. Comput. Appl. Math. 2008, 219, 253–262. [Google Scholar] [CrossRef] [Green Version]
- Lu, J. Variational iteration method for solving two-point boundary value problems. J. Comput. Appl. Math. 2007, 207, 92–95. [Google Scholar] [CrossRef] [Green Version]
- Abukhaled, M. Variational iteration method for nonlinear singular two-point boundary value problems arising in human physiology. J. Math. 2013, 2013, 720134. [Google Scholar] [CrossRef]
- Chen, C.L.; Liu, Y.C. Solution of two-boundary-value problems using the differential transformation method. J. Opt. Theory Appl. 1998, 99, 23–35. [Google Scholar] [CrossRef]
- Abukhaled, M.; Khuri, S.A.; Sayfy, A. A numerical approach for solving a class of singular boundary value problems arising in physiology. Int. J. Numer. Anal. Model. 2011, 8, 353–363. [Google Scholar]
- Żur, K.K. Green’s function approach to frequency analysis of thin circular plates. Bull. Polish Acad. Sci. Tech. Sci. 2016, 64, 181–188. [Google Scholar] [CrossRef] [Green Version]
- Żur, K.K. Green’s function for frequency analysis of thin annular plates with nonlinear variable thickness. Appl. Math. Model. 2016, 40, 3601–3619. [Google Scholar] [CrossRef]
- Żur, K.K. Green’s function in frequency analysis of circular thin plates of variable thickness. J. Theor. Appl. Mech. 2015, 53, 873–884. [Google Scholar] [CrossRef]
- Żur, K.K. Quasi-Green’s function approach to free vibration analysis of elastically supported functionally graded circular plates. Comput. Struct. 2018, 183, 600–610. [Google Scholar] [CrossRef]
- Żur, K.K. Free vibration analysis of elasticically supported functionally graded annular plates via quasi-Green’s function method. Compos. Part B 2018, 144, 37–55. [Google Scholar] [CrossRef]
- Andrade, F.M. Exact Green’s function for rectangular potentials and its application to quasi-bound states. Phys. Lett. A 2014, 378, 1461–1468. [Google Scholar] [CrossRef]
- Ahyoune, S.; Sieiro, J.; Carrasco, T.; Vidal, N.; López-Villegasa, J.; Roca, E.; Fernández, F. Quasi-static PEEC planar solver using a weighted combination of 2D and 3D analytical Green’s functions and a predictive meshing generator. Integration 2018, 63, 322–341. [Google Scholar] [CrossRef]
- Abukhaled, M. Green’s Function Iterative Method for Solving a Class of Boundary Value Problems Arising in Heat Transfer. Appl. Math. Inf. Sci. 2017, 11, 229–234. [Google Scholar] [CrossRef]
- Abukhaled, M. Green’s Function Iterative Approach for Solving Strongly Nonlinear Oscillators. Comput. Nonlinear Dyn. 2017, 12, 051021. [Google Scholar] [CrossRef]
- Abukhaled, M.; Khuri, S.A. A semi-analytical solution of amperometric enzymatic reactions based on Green’s functions and fixed point iterative schemes. Electroanal. Chem. 2017, 792, 66–71. [Google Scholar] [CrossRef]
- Kafri, H.Q.; Khuri, S.A. Bratu’s problem: A novel approach using fixed-point iterations and Green’s functions. Comput. Phys. Commun. 2016, 198, 97–104. [Google Scholar] [CrossRef]
- Atkinson, K.; Han, W. Theoretical Numerical Analysis: A Functional Analysis Framework, 3rd ed.; Springer: Berlin, Germany, 2009. [Google Scholar]
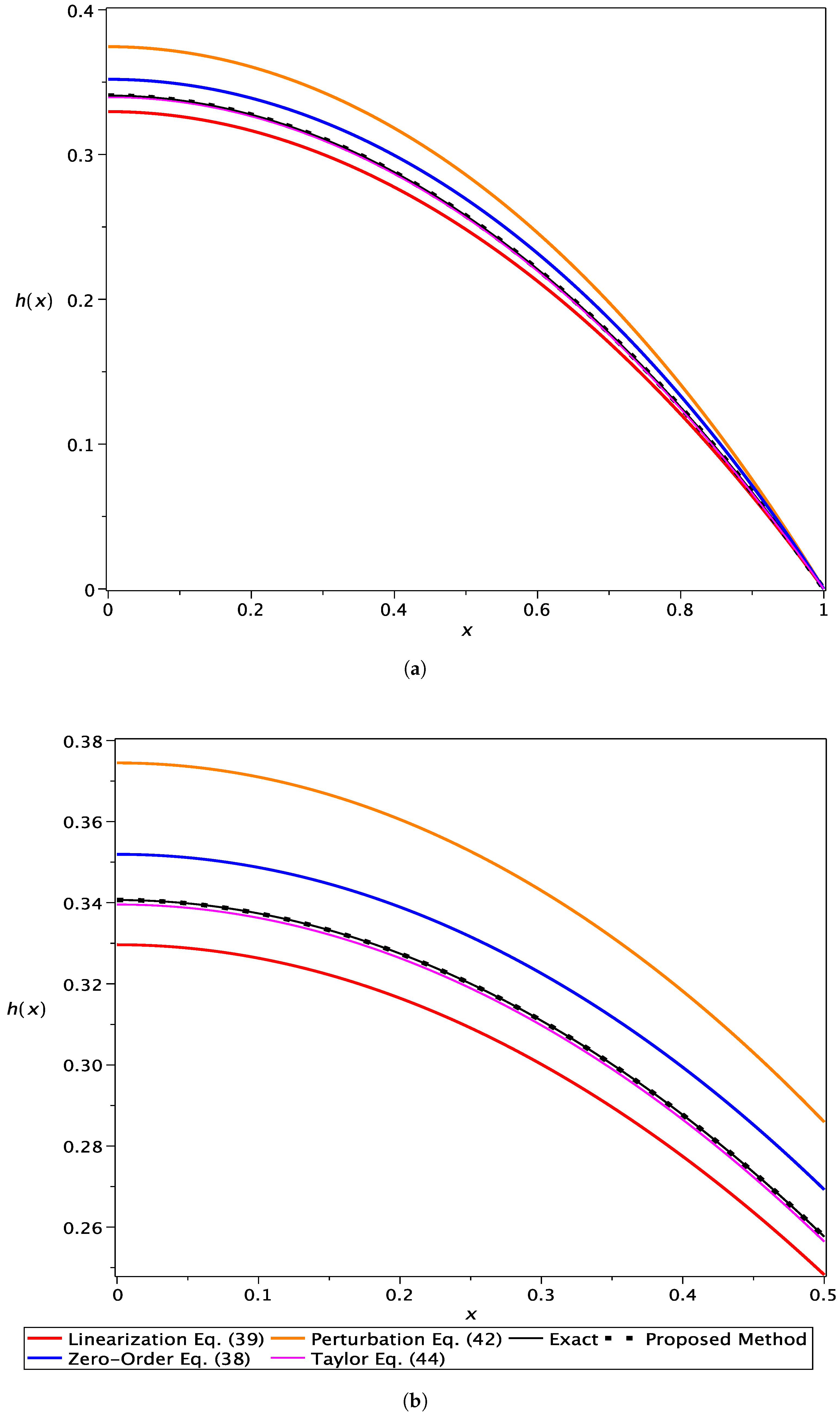
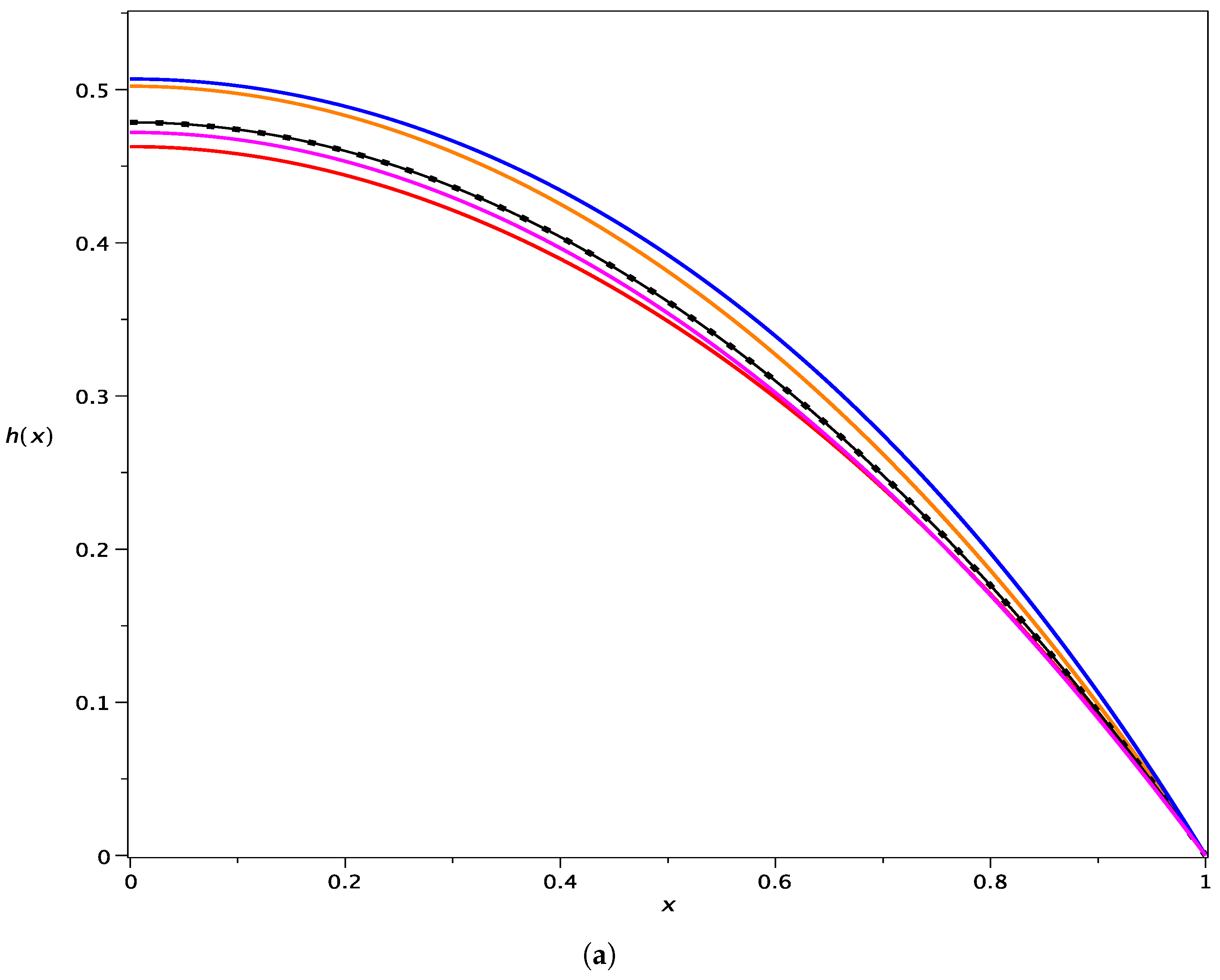
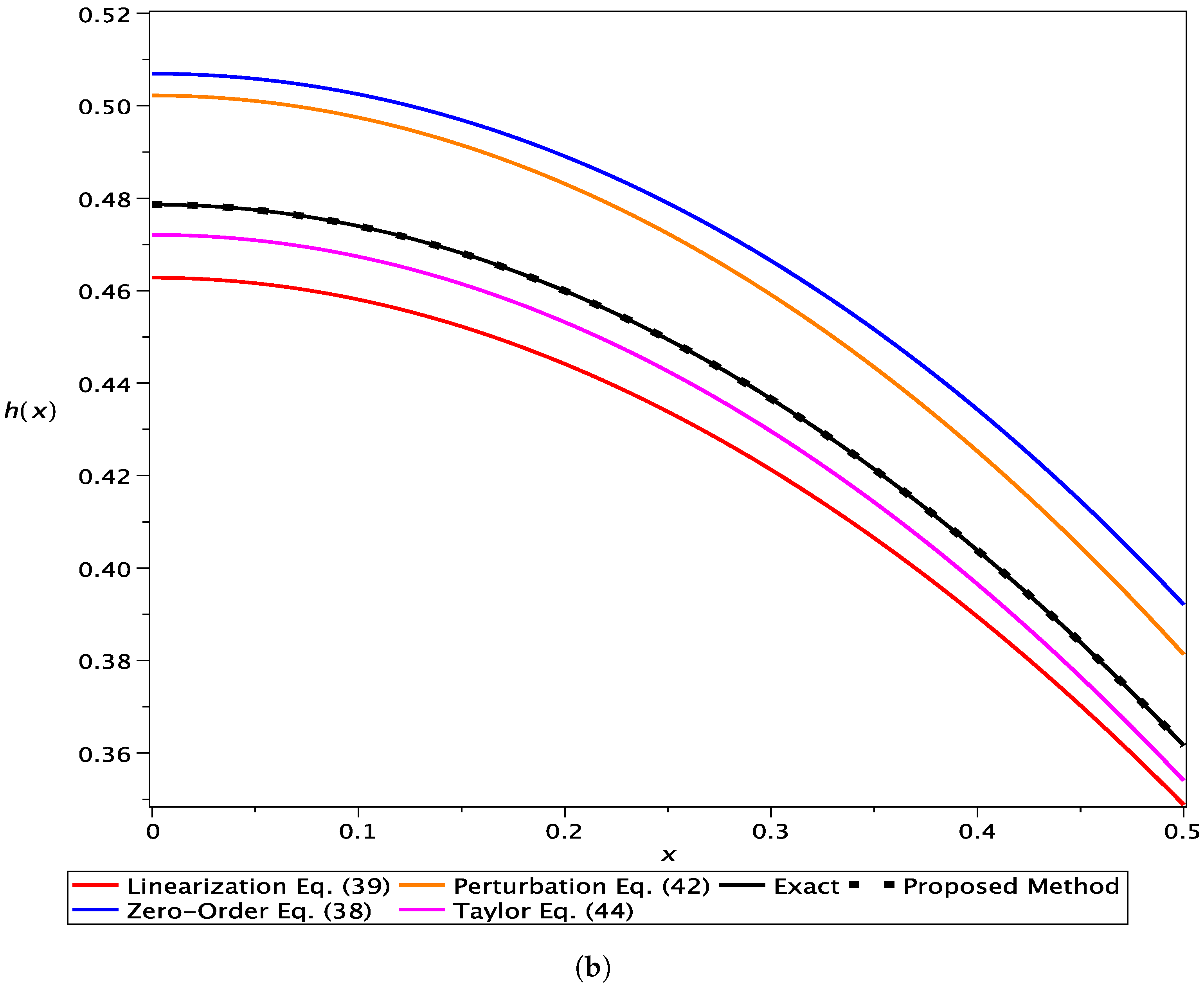
| x | Proposed Method h5 | Taylor Equation (45) | Linearization Equation (40) | Zero-Order Equation (39) | Perturbation Equation (43) |
|---|---|---|---|---|---|
| 0.0 | 0.00005 | 0.32318 | 3.23315 | 3.31177 | 9.93049 |
| 0.1 | 0.00002 | 0.32800 | 3.27178 | 3.36031 | 9.97343 |
| 0.2 | 0.00004 | 0.34291 | 3.35877 | 3.50557 | 10.10180 |
| 0.3 | 0.00005 | 0.36958 | 3.46262 | 3.74615 | 10.31389 |
| 0.4 | 0.00005 | 0.41066 | 3.56295 | 4.07985 | 10.60702 |
| 0.5 | 0.00005 | 0.46910 | 3.64695 | 4.50375 | 10.97761 |
| 0.6 | 0.00005 | 0.55066 | 3.70707 | 5.01426 | 11.42121 |
| 0.7 | 0.00004 | 0.65862 | 3.73951 | 5.60723 | 11.93270 |
| 0.8 | 0.00007 | 0.79862 | 3.74304 | 6.27816 | 12.50642 |
| 0.9 | 0.00018 | 0.97608 | 3.71836 | 7.02218 | 13.13624 |
| x | Proposed Method h5 | Taylor Equation (45) | Linearization Equation (40) | Zero-Order Equation (39) | Perturbation Equation (43) |
|---|---|---|---|---|---|
| 0.0 | 0.00023 | 1.36905 | 3.30851 | 5.91347 | 4.92646 |
| 0.1 | 0.00021 | 1.39359 | 3.35215 | 6.01828 | 4.95513 |
| 0.2 | 0.00016 | 1.46981 | 3.43570 | 6.33032 | 5.03704 |
| 0.3 | 0.00012 | 1.60514 | 3.51105 | 6.84277 | 5.16019 |
| 0.4 | 0.00007 | 1.81087 | 3.55219 | 7.54513 | 5.30551 |
| 0.5 | 0.00001 | 2.10070 | 3.54752 | 8.42437 | 5.44798 |
| 0.6 | 0.00007 | 2.48944 | 3.49474 | 9.46589 | 5.55769 |
| 0.7 | 0.00017 | 2.99174 | 3.39741 | 10.65448 | 5.60064 |
| 0.8 | 0.00027 | 3.62121 | 3.26263 | 11.97477 | 5.53921 |
| 0.9 | 0.00029 | 4.38984 | 3.09960 | 13.41166 | 5.33237 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abukhaled, M.; Khuri, S. An Efficient Semi-Analytical Solution of a One-Dimensional Curvature Equation that Describes the Human Corneal Shape. Math. Comput. Appl. 2019, 24, 8. https://doi.org/10.3390/mca24010008
Abukhaled M, Khuri S. An Efficient Semi-Analytical Solution of a One-Dimensional Curvature Equation that Describes the Human Corneal Shape. Mathematical and Computational Applications. 2019; 24(1):8. https://doi.org/10.3390/mca24010008
Chicago/Turabian StyleAbukhaled, Marwan, and Suheil Khuri. 2019. "An Efficient Semi-Analytical Solution of a One-Dimensional Curvature Equation that Describes the Human Corneal Shape" Mathematical and Computational Applications 24, no. 1: 8. https://doi.org/10.3390/mca24010008
APA StyleAbukhaled, M., & Khuri, S. (2019). An Efficient Semi-Analytical Solution of a One-Dimensional Curvature Equation that Describes the Human Corneal Shape. Mathematical and Computational Applications, 24(1), 8. https://doi.org/10.3390/mca24010008




