An Analytical Study of Adversely Affecting Radiation and Temperature Parameters on a Magnetohydrodynamic Elasto-viscous Fluid
Abstract
1. Introduction
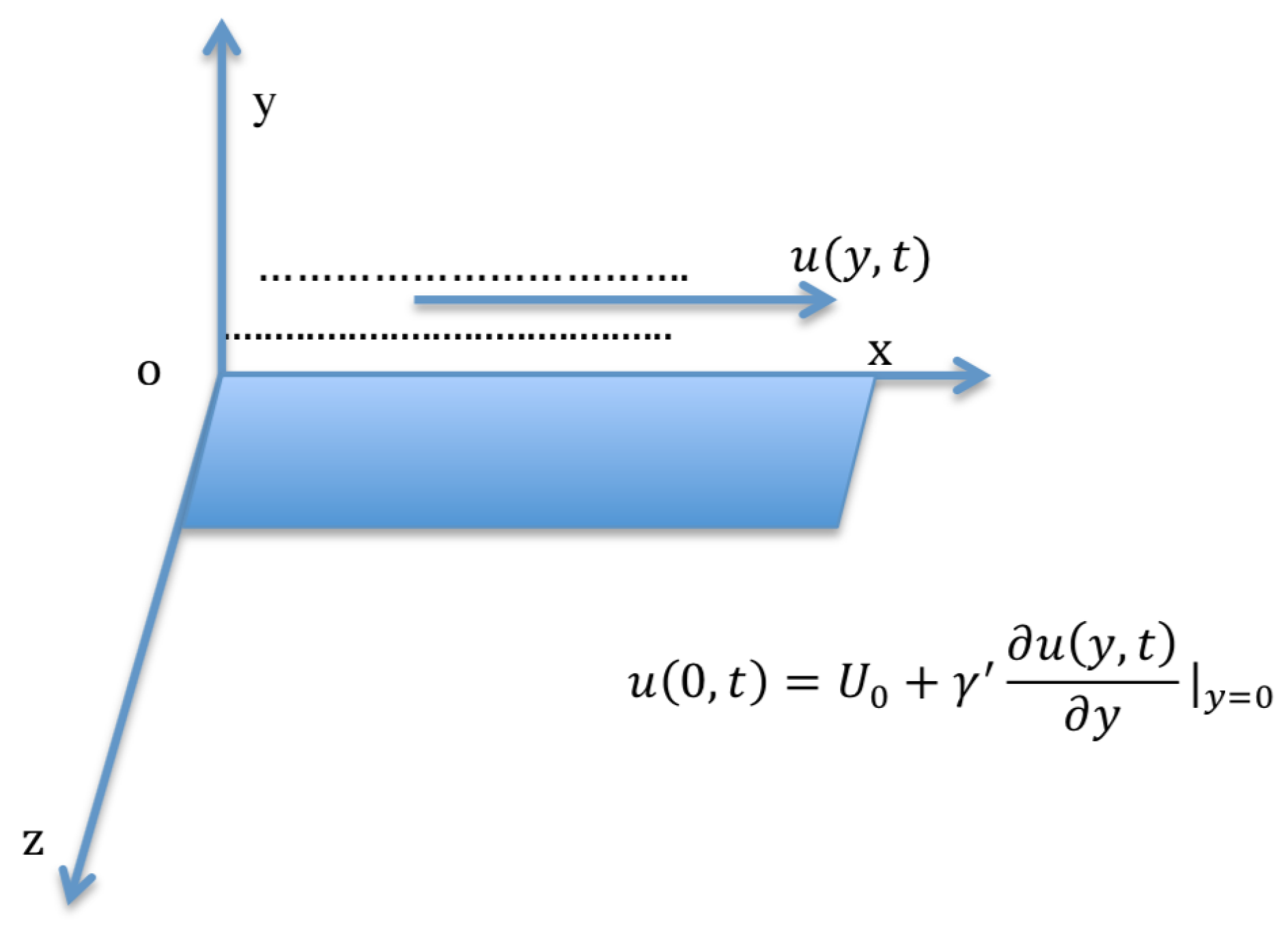
2. Mathematical Construction of the Problem
3. Mathematical Solutions
4. Limiting Cases
4.1. Newtonian Fluid
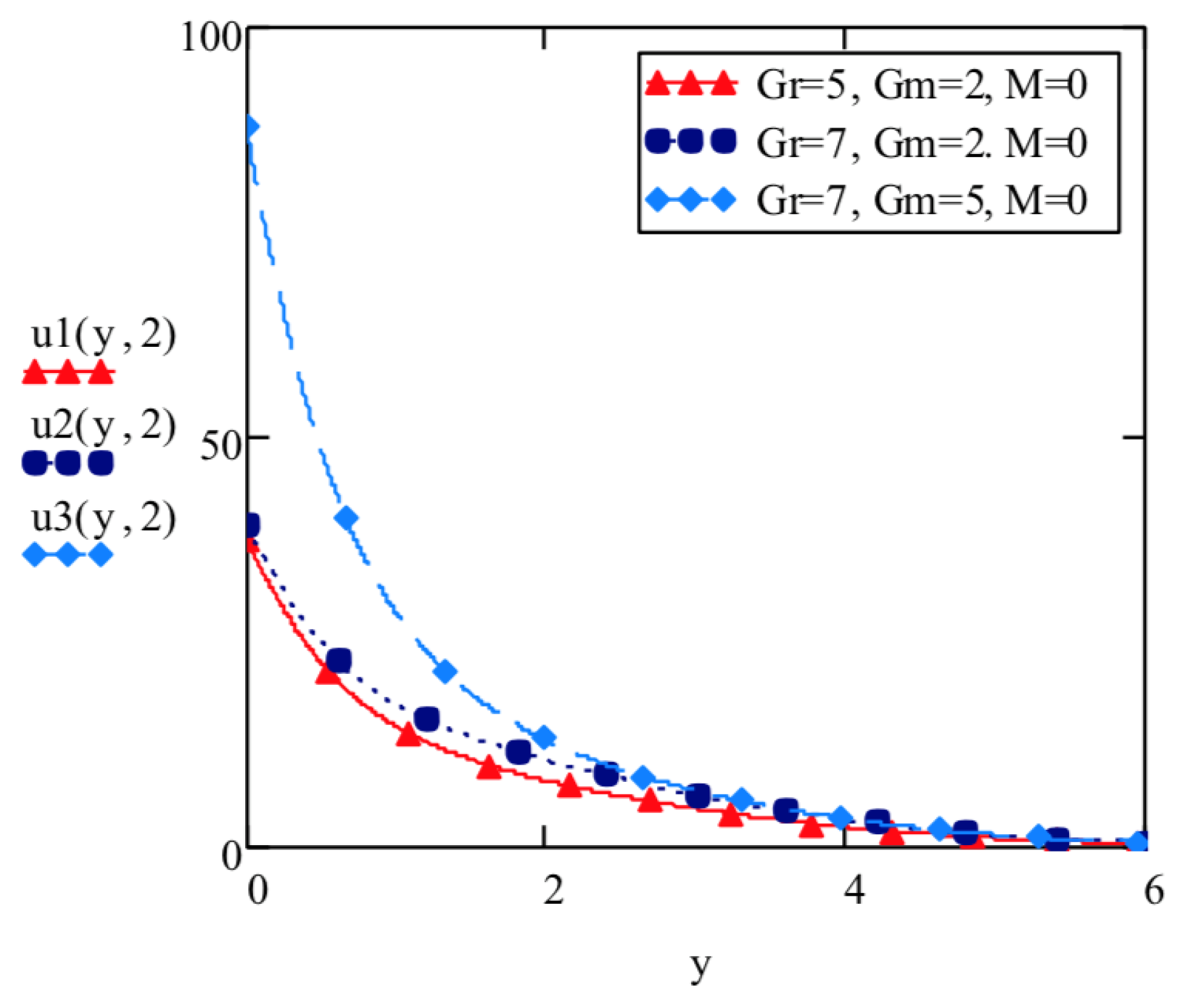
4.2. Absence of Magnetic Field ()
4.3. Constant Temperature on the Boundary
4.4. Constant Velocity on Boundary
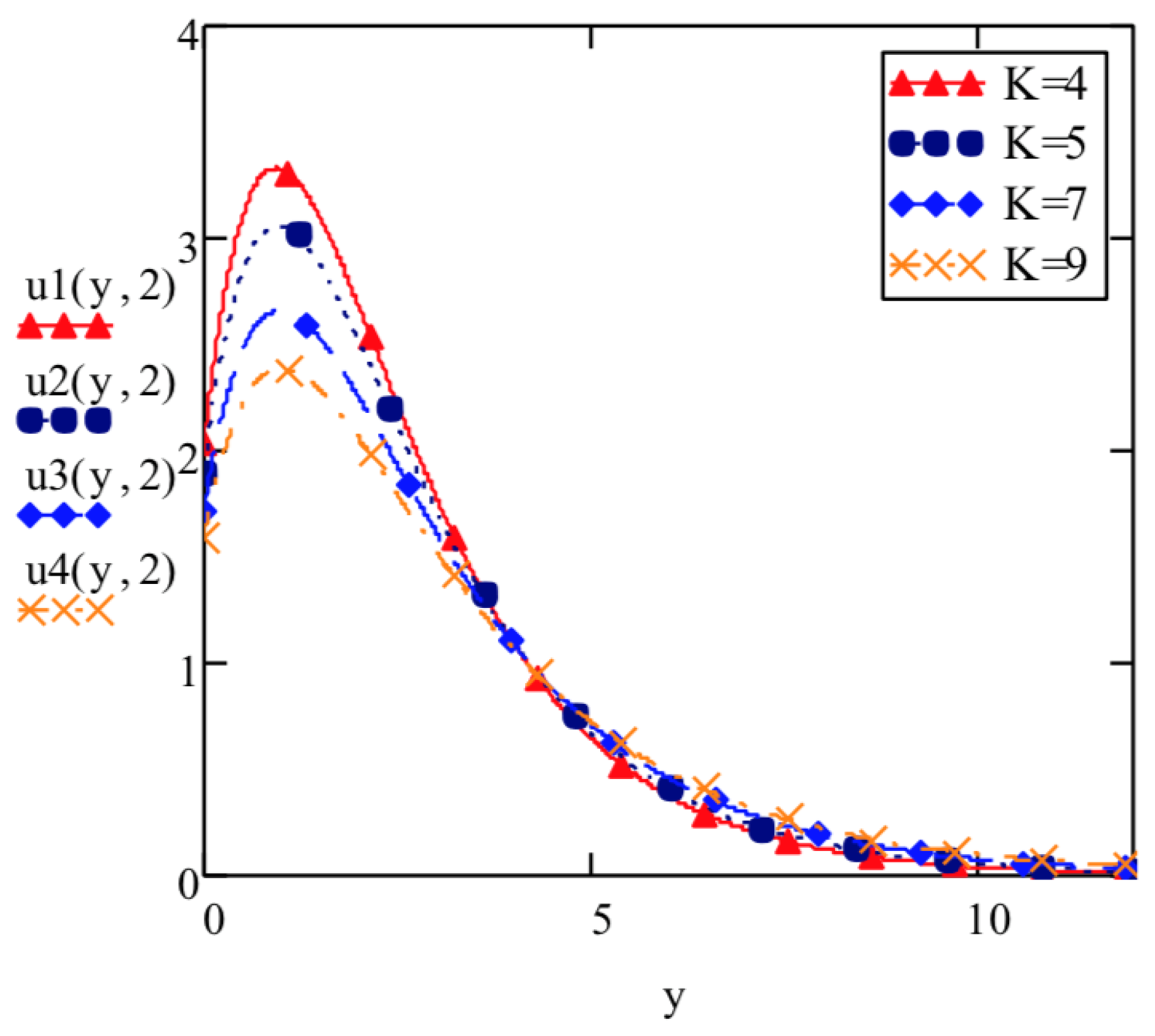
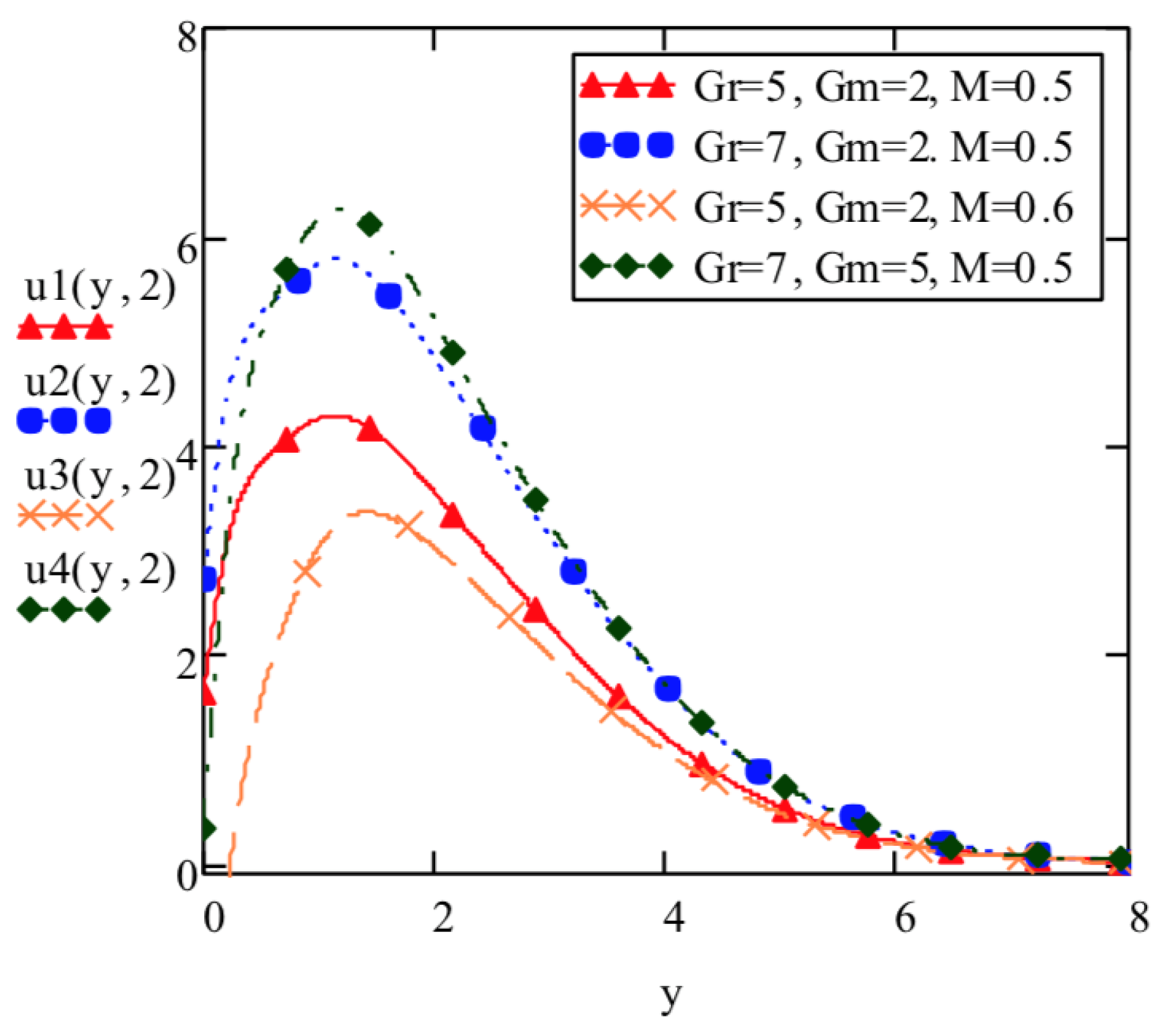
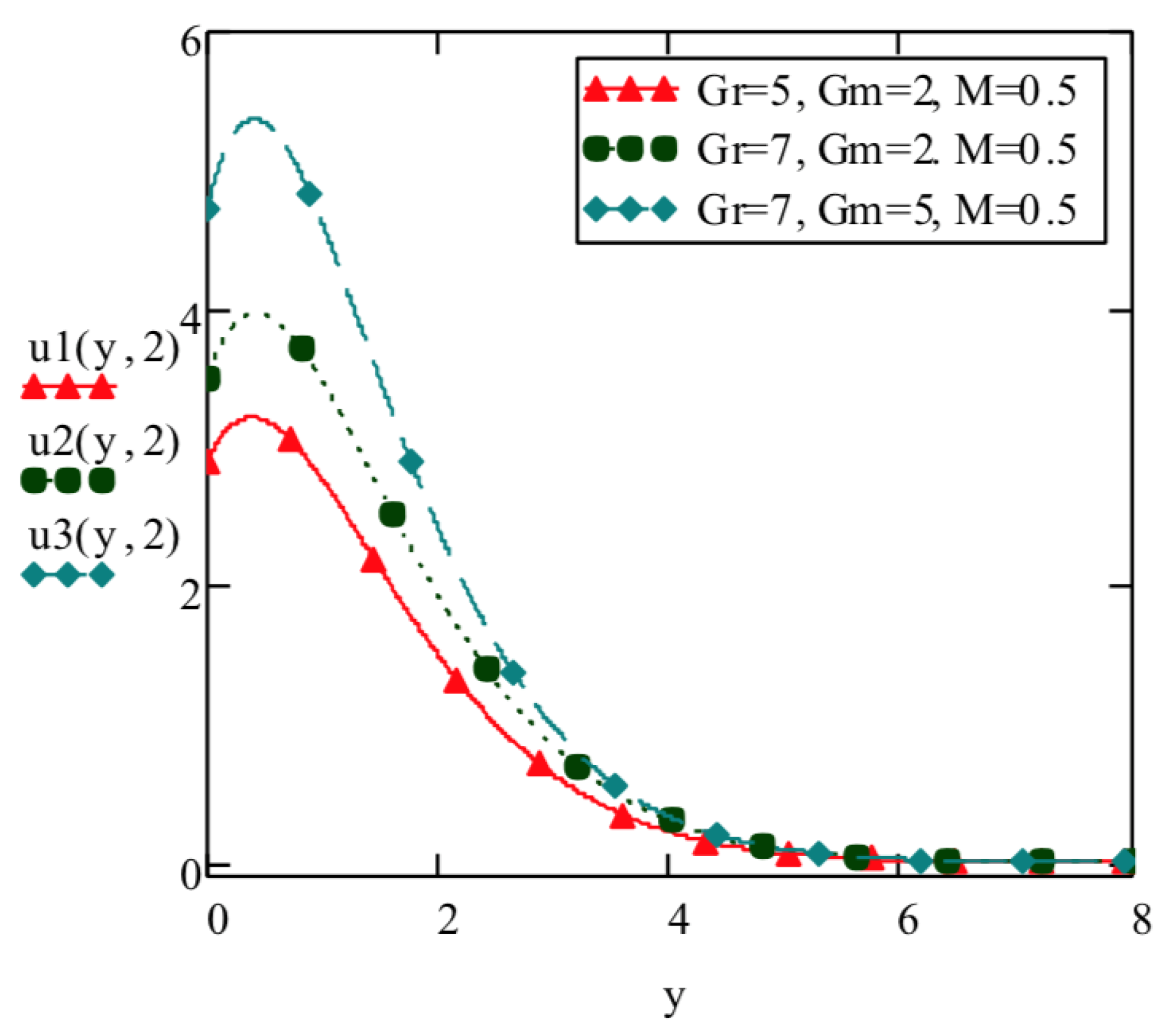
5. Discussion
6. Conclusions
- Unlike the usual adoption of numerical solutions approach for elasto-viscous fluid models, exact closed-form solutions of velocity, temperature and mass concentration have been determined and have shown to meet initial and boundary conditions.
- Expressions of velocity for no-slip and timed provision of temperature on boundary were obtained. An observation of slip-parameter’s strength and temporal temperature boundary condition hindering the speed of flow was substantiated through graphical analysis.
- Validation of current results was approached through retrieving Newtonian fluid velocity expression and graphical profiles by considering very small value of elasto-viscous parameter ().
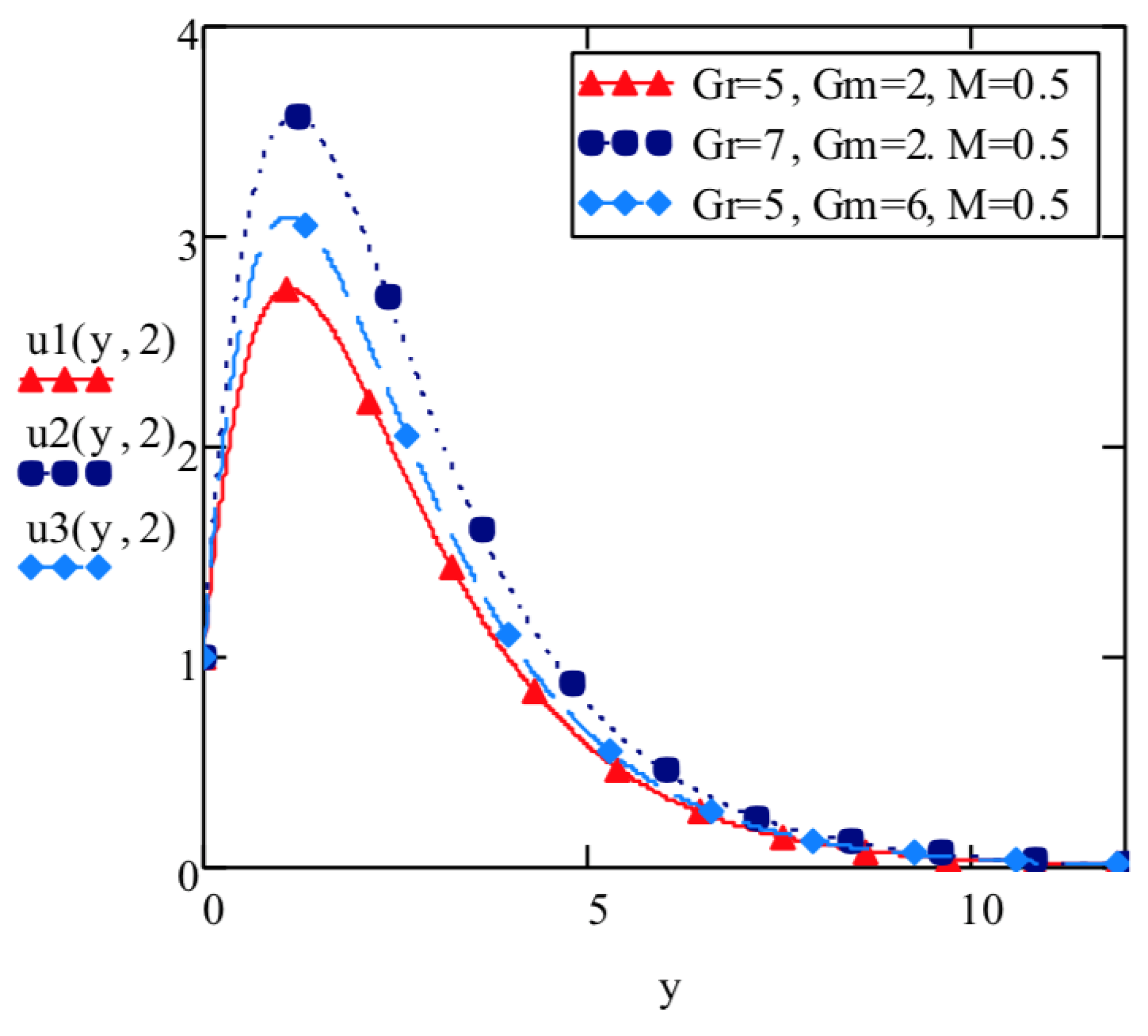
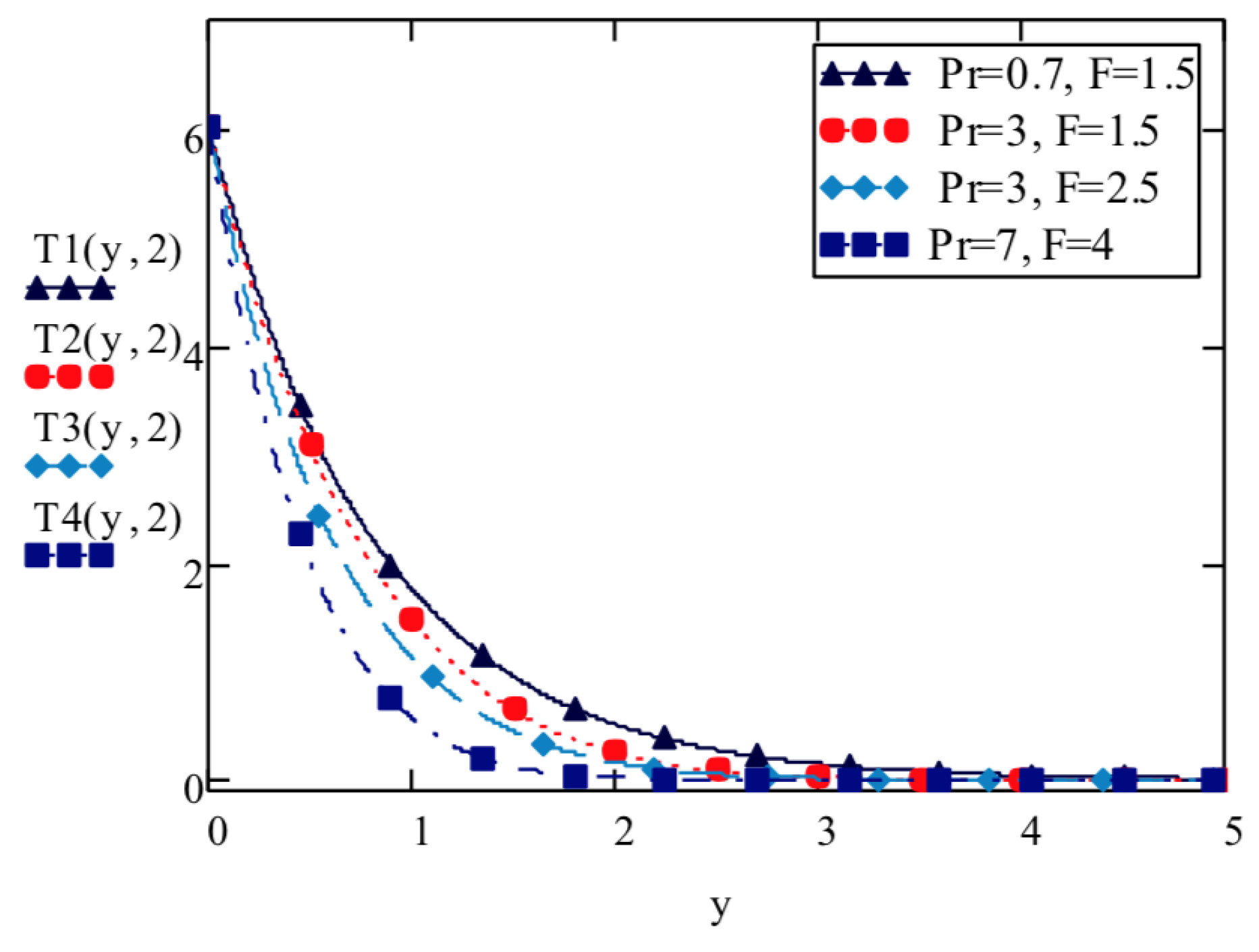
- Elasto-viscous fluid velocity increases with increase in thermal Grashof number and mass Grashof number and decreases with increase in Prandtl number , Schmidt number , Hartmann number M and thermal radiation parameter F.
- Temperature of fluid is inversely related with F and .
- Mass concentration of fluid increases with decrease in and vice-versa.
- Increasing the strength of elatso-viscous parameter K hinders the smooth flow as would be suggested by empowered viscous forces and thus decreases the flow velocity and vice-versa.
- To validate the accuracy of analytical expressions, we have generated numerical solutions for concentration of fluid. The comparison of analytical and numerical solutions points to an absolute error of order .
Conflicts of Interest
Nomenclature
| Symbols | Description | SI Units |
| u(y,t) | velocity | m/s |
| T(y,t) | temperature | K |
| C(y,t) | mass concentration | kg/m |
| density of fluid | kg/m | |
| kinematic viscosity | m/s | |
| electrical conductivity | S/m | |
| thermal conductivity | J/(s·m·K) | |
| specific heat at constant pressure | J/(kg·K) | |
| radiation heat flux | J/(s·m) | |
| thermal expansion coefficient | 1/K | |
| mass expansion coefficient | m/kg | |
| g | gravitational acceleration | m/s |
| D | mass diffusion coefficient | m/s |
| M | Hartmann number | dimensionless |
| thermal Grashof number | dimensionless | |
| mass Grashof number | dimensionless | |
| F | thermal radiation parameter | J/(s·m) |
| Prandtl number | dimensionless | |
| Schmidt number | dimensionless | |
| frequency of oscillation | 1/s |
Appendix A
References
- Abraham, F.; Behr, M.M.H. Shape optimization in steady blood flow: A numerical study of non-Newtonian effects. Comput. Methods Biomech. Biomed. Eng. 2005, 8, 127–137. [Google Scholar] [CrossRef]
- Boghosian, M.; Cassel, K.; Hammes, M.; Funaki, B.; Kim, S.; Qian, X.; Wang, X.; Dhar, P.; Hines, J. Hemodynamics in the cephalic arch of a brachiocephalic fistula. Med. Eng. Phys. 2014, 36, 822–830. [Google Scholar] [CrossRef]
- Ersoy, H.V. MHD Flow of a Second Order/Grade Fluid Due to Noncoaxial Rotation of a Porous Disk and the Fluid at Infinity. Math. Comput. Appl. 2010, 15, 354–363. [Google Scholar] [CrossRef]
- Srinivasacharya, D.; Mendu, U. Thermal radiation and chemical reaction effects on magnetohydrodynamic free convection heat and mass transfer in a micropolar fluid. Turk. J. Eng. Environ. Sci. 2014, 38, 184–196. [Google Scholar]
- Zhang, C.; Zheng, L.; Zhang, X.; Chen, G. MHD flow and radiation heat transfer of nanofluids in porous media with variable surface heat flux and chemical reaction. Appl. Math. Model. 2015, 39, 165–181. [Google Scholar] [CrossRef]
- Zeeshan, A.; Ijaz, N.; Abbas, T.; Ellahi, R. The sustainable characteristic of Bio-bi-phase flow of peristaltic transport of MHD Jeffery fluid in human body. Sustainability 2018, 10, 2671. [Google Scholar] [CrossRef]
- Samad, M.A.; Mohebujjaman, M. MHD heat and mass transfer free convection flow along a vertical stretching sheet in presence of magnetic field with heat Generation. Res. J. Appl. Sci. Eng. Tech. 2009, 1, 98–106. [Google Scholar]
- Khaleque, S.T.; Samad, M.A. Effects of radiation, heat generation and viscous dissipation on MHD free convection flow along a stretching sheet. Res. J. Appl. Sci. Eng. Tech. 2010, 2, 368–377. [Google Scholar]
- Zahan, I.; Samad, M.A. Radiative heat and mass transfer of an MHD free convection flow along a stretching sheet with chemical reaction, heat generation and viscous dissipation. Dhaka Univ. J. Sci. 2010, 61, 27–34. [Google Scholar] [CrossRef]
- Uddi, Z.; Kumarb, M. MHD heat and mass transfer free convection flow near the lower stagnation point of an isothermal cylinder imbedded in porous domain with the presence of radiation. Jord. J. Mech. Ind. Eng. 2011, 5, 133–138. [Google Scholar]
- Huang, C.; Zhang, Y. Calculation of high-temperature insulation parameters and heat transfer behaviors of multilayer insulation by inverse problems method. Chin. J. Aeronaut. 2014, 27, 791–796. [Google Scholar] [CrossRef]
- Rashid, M.M.; Rostami, B.; Freidoonimehr, N.; Abbasbandy, S. Free convective heat and mass transfer for MHD fluid flow over a permeable vertical stretching sheet in the presence of the radiation and buoyancy effects. Ain Shams Eng. J. 2014, 5, 901–912. [Google Scholar] [CrossRef]
- Seth, G.S.; Hussain, S.M.; Sarkar, S. Hydromagnetic natural convection flow with heat and mass transfer of a chemically reacting and heat absorbing fluid past an accelerated moving vertical plate with ramped temperature and ramped surface concentration through a porous medium. J. Egypt. Math. Soc. 2015, 23, 197–207. [Google Scholar] [CrossRef]
- Wu, L. Mass transfer induced slip effect on viscous gas flows above a shrinking/stretching sheet. Int. J. Heat Mass Transf. 2015, 93, 17–22. [Google Scholar] [CrossRef]
- Nayak, M.K.; Dash, G.C.; Singh, L.P. Unsteady radiative MHD free convective flow and mass transfer of a viscoelastic fluid past an inclined porous plate. Arab. J. Sci. Eng. 2015, 40, 3029–3039. [Google Scholar] [CrossRef]
- Dawar, A.; Shah, Z.; Idrees, M.; Khan, W.; Islam, S.; Gul, T. Impact of Thermal Radiation and Heat Source/Sink on Eyring–Powell Fluid Flow over an Unsteady Oscillatory Porous Stretching Surface. Math. Comput. Appl. 2018, 23, 20. [Google Scholar] [CrossRef]
- Ellahi, R.; Alamri, S.Z.; Basit, A.; Majeed, A. Effects of MHD and slip on heat transfer boundary layer flow over a moving plate based on specific entropy generation. J. Taibah Univ. Sci. 2018, 12, 476–482. [Google Scholar] [CrossRef]
- Yildiz, B.; Kazimi, M.S. Efficiency of hydrogen production systems using alternative nuclear energy technologies. Int. J. Hydrog. Energy 2006, 31, 77–92. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Abbas, T.; Rashidi, M.M.; Ali, M.; Yang, Z. Entropy generation on MHD Eyring–Powell nanofluid through a permeable stretching surface. Entropy 2016, 18, 224. [Google Scholar] [CrossRef]
- Hussain, F.; Ellahi, R.; Zeeshan, A. Mathematical models of electro-magnetohydrodynamic multiphase flows synthesis with nano-sized hafnium particles. Appl. Sci. 2018, 8, 275. [Google Scholar] [CrossRef]
- Erdogan, M.E. A note on an unsteady flow of a viscous fluid due to an oscillating plane wall. Int. J. Non-Linear Mech. 2001, 35, 1–6. [Google Scholar] [CrossRef]
- Hayat, T.; Siddiqui, A.M.; Asghar, S. Some simple flows of an Oldroyd-B fluid. Int. J. Eng. Sci. 2001, 39, 135–147. [Google Scholar] [CrossRef]
- Fetecau, C.; Fetecau, C. Starting solutions for some unsteady unidirectional flows of a second grade fluid. Int. J. Eng. Sci. 2005, 43, 781–789. [Google Scholar] [CrossRef]
- Fetecau, C.; Fetecau, C. Starting solutions for the motion of a second grade fluid due to longitudinal and torsional oscillations of a circular cylinder. Int. J. Eng. Sci. 2006, 44, 788–796. [Google Scholar] [CrossRef]
- Yao, Y.; Liu, Y. Some unsteady flows of a second grade fluid over a plane wall. Nonlin. Anal. Real World Appl. 2010, 11, 4442–4450. [Google Scholar] [CrossRef]
- Vieru, D.; Fetecau, C.; Sohail, A. Flow due to a plate that applies an accelerated shear to a second grade fluid between two parallel walls perpendicular to the plate. Z. Angew. Math. Phys. 2011, 62, 161–172. [Google Scholar] [CrossRef]
- Fetecau, C.; Fetecau, C.; Rana, M. General solutions for the unsteady flow of second-grade fluids over an infinite plate that applies arbitrary shear to the fluid. Z. Naturforschung 2011, 66, 753–759. [Google Scholar] [CrossRef]
- Fetecau, C.; Vieru, D.; Fetecau, C. Effect of side walls on the motion of a viscous fluid induced by an infinite plate that applies an oscillating shear stress to the fluid. Cent. Eur. J. Phys. 2011, 9, 816–824. [Google Scholar] [CrossRef]
- Soundalgekar, V.M. Free convection effects on the flow past a vertical oscillating plate. Astrophys. Space Sci. 1979, 66, 165–172. [Google Scholar] [CrossRef]
- Soundalgekar, V.M.; Akolkar, S.P. Effects of free convection currents and mass transfer on flow past a vertical oscillating plate. Astrophys. Space Sci. 1983, 89, 241–254. [Google Scholar] [CrossRef]
- Gupta, P.S.; Gupta, A.S. Radiation Effect on hydromagnetic convection in a vertical channel. Int. J. Heat Mass Trans. 1974, 17, 1437–1442. [Google Scholar] [CrossRef]
- Soundalgekar, V.M.; Lahurikar, R.M.; Pohanerkar, S.G.; Birajdar, N.S. Effects of mass transfer on the flow past an oscillating infinite vertical plate with constant heat flux. Thermophys. Aeromech. 1994, 1, 119–124. [Google Scholar]
- Fetecau, C.; Rana, M.; Fetecau, C. Radiative and porous effects on free convection flow near a vertical plate that applies shear stress to the fluid. Zeitschrift für Naturforschung A 2012, 68, 130–138. [Google Scholar] [CrossRef]
- Deka, R.K.; Neog, B.C. Combined effects of thermal radiation and chemical reaction on free convection flow past a vertical plate in porous medium. Adv. Appl. Fluid Mech. 2009, 6, 181–195. [Google Scholar]
- Shahid, N. A study of heat and mass transfer in a fractional MHD flow over an infinite oscillating plate. SpringerPlus 2015, 4, 640. [Google Scholar] [CrossRef]
- Shahid, N. Effects of thermal radiation and mass diffusion on MHD flow over a vertical plate applying time-dependent shear to the fluid. Neural Parallel Sci. Comput. 2016, 24, 431–452. [Google Scholar]
- Singh, A.K.; Singh, A.K.; Singh, N.P. Heat and mass transfer in MHD flow of a viscous fluid past a vertical plate under oscillatory suction velocity. Indian J. Pure Appl. Math. 2003, 34, 429–433. [Google Scholar]
- Chen, C.H. Combined heat and mass transfer in MHD free convection from a vertical surface with Ohmic heating and viscous dissipation. Int. J. Eng. Sci. 2004, 42, 699–713. [Google Scholar] [CrossRef]
- Aboeldahab, E.M.; Elbarbary, E.M.E. Hall current effect magneto-hydrodynamics free convection flow past a semi.-infinite vertical plate with mass transfer. Int. J. Eng. Sci. 2001, 39, 1641–1652. [Google Scholar] [CrossRef]
- Sharma, B.K.; Chaudhary, R.C. Hydromagnetic unsteady mixed convection and mass transfer flow past a vertical plate immersed in a porous medium with Hall effect. Eng. Trans. 2005, 56, 3–23. [Google Scholar]
- Raju, R.S.; Reddy, G.J.; Rao, J.A.; Rashidi, M.M.; Gorla, R.S.R. Analytical and numerical study of unsteady MHD free convection flow over an exponentially moving vertical plate with heat absorption. Int. J. Therm. Sci. 2016, 107, 303–315. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Bagheri, S.; Momoniat, E.; Freidoonimehr, N. Entropy analysis of convective MHD flow of third grade non-Newtonian fluid over a stretching sheet. Ain Shams Eng. J. 2017, 8, 77–85. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Abbas, M.A.; Rashidi, M.M. A robust numerical method for solving stagnation point flow over a permeable shrinking sheet under the influence of MHD. Appl. Math. Comput. 2018, 316, 381–389. [Google Scholar] [CrossRef]
- Shahid, N. Role of a Structural Parameter in Modelling Blood Flow Through a Tapering Channel. Bound. Value Probl. 2018, 2018, 84. [Google Scholar] [CrossRef]
- Landau, L.D.; Llfshltz, E.M. Fluid Mechanics; Elsevier: New York, NY, USA, 1978. [Google Scholar]
- Stehfest, H. Algorithm 368: Numerical inversion of Laplace transform. Commun. ACM 1979, 13, 47–49. [Google Scholar] [CrossRef]

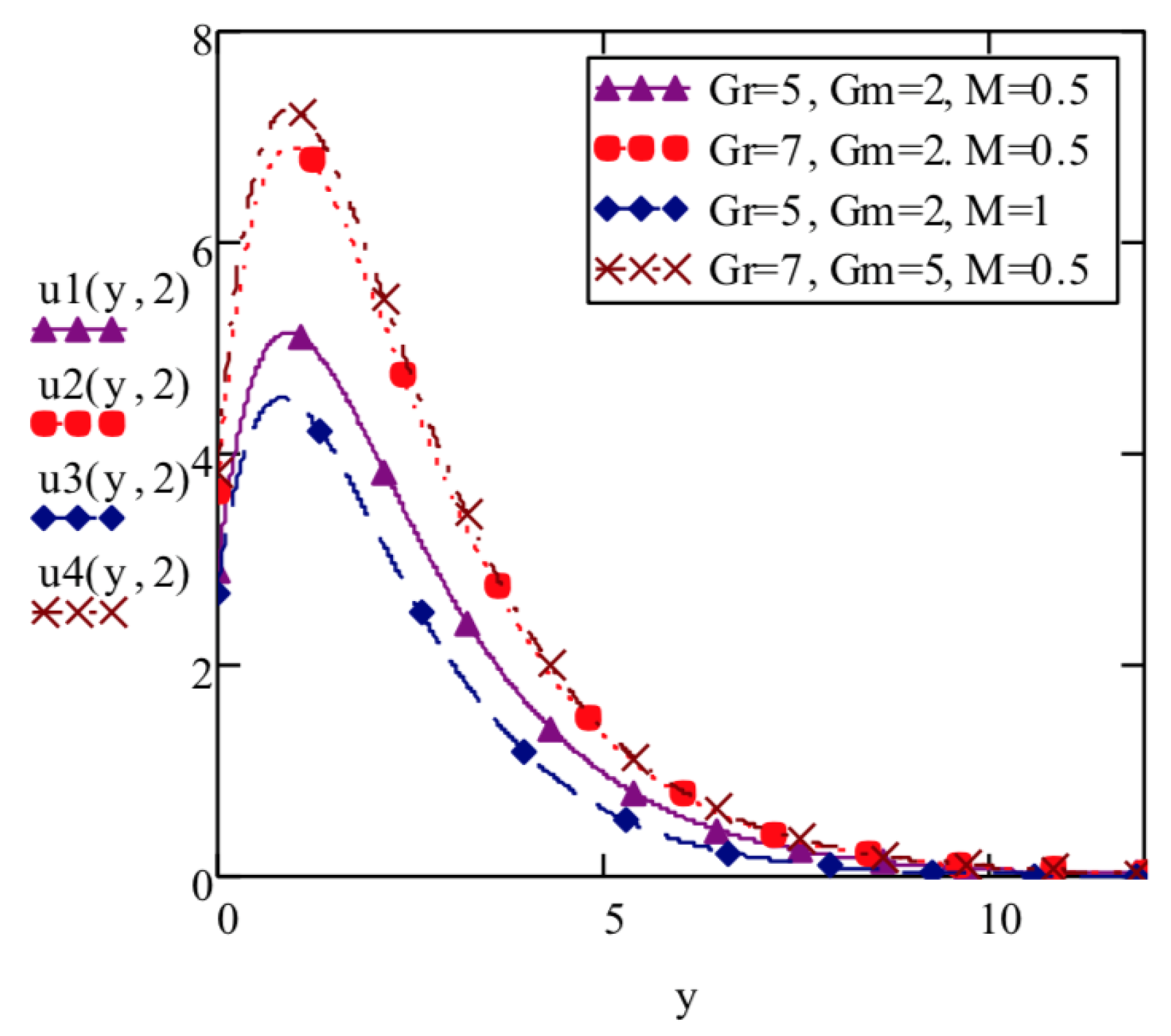
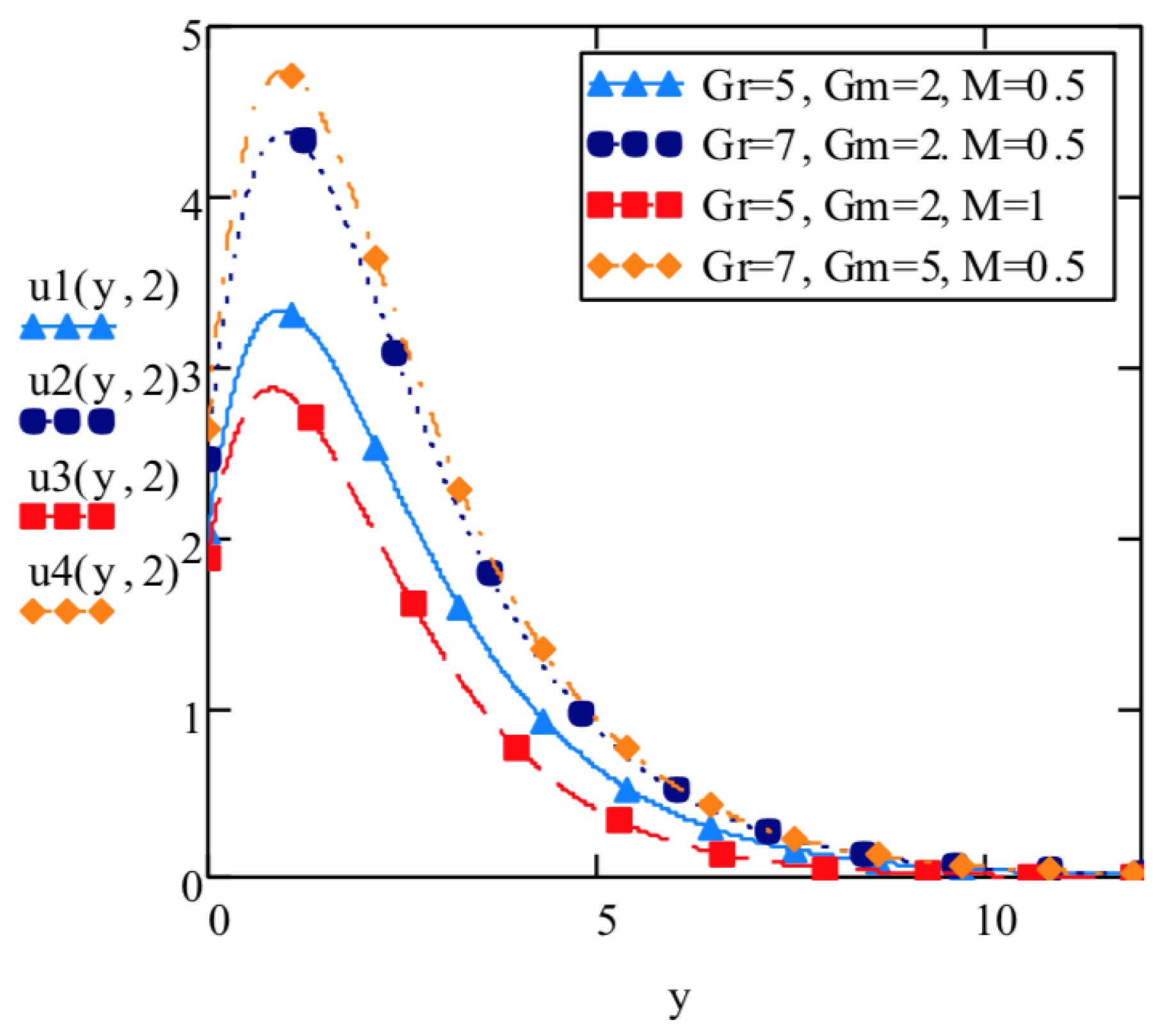

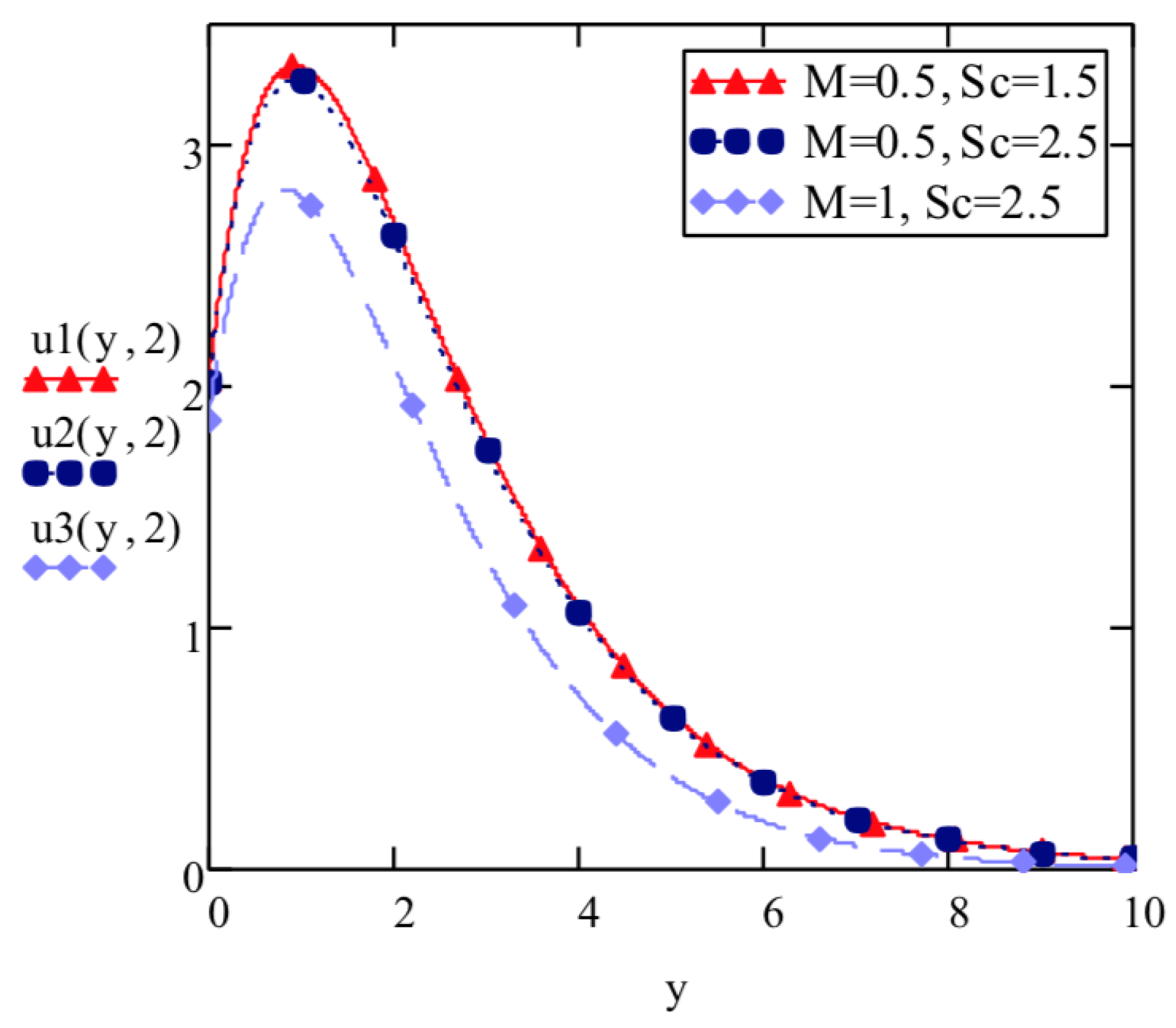

| y | —Equation (19) | —Equation (17) | |
|---|---|---|---|
| 0 | 5 | 5.00001 | |
| 0.1 | 4.66656 | 4.66658 | |
| 0.2 | 4.35403 | 4.35404 | |
| 0.3 | 4.06119 | 4.0612 | |
| 0.4 | 3.7869 | 3.78691 | |
| 0.5 | 3.53007 | 3.53008 | |
| 0.6 | 3.28967 | 3.28968 | |
| 0.7 | 3.06472 | 3.06473 | |
| 0.8 | 2.8543 | 2.8543 | |
| 0.9 | 2.65753 | 2.65754 | |
| 1 | 2.47359 | 2.47359 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahid, N. An Analytical Study of Adversely Affecting Radiation and Temperature Parameters on a Magnetohydrodynamic Elasto-viscous Fluid. Math. Comput. Appl. 2019, 24, 31. https://doi.org/10.3390/mca24010031
Shahid N. An Analytical Study of Adversely Affecting Radiation and Temperature Parameters on a Magnetohydrodynamic Elasto-viscous Fluid. Mathematical and Computational Applications. 2019; 24(1):31. https://doi.org/10.3390/mca24010031
Chicago/Turabian StyleShahid, Nazish. 2019. "An Analytical Study of Adversely Affecting Radiation and Temperature Parameters on a Magnetohydrodynamic Elasto-viscous Fluid" Mathematical and Computational Applications 24, no. 1: 31. https://doi.org/10.3390/mca24010031
APA StyleShahid, N. (2019). An Analytical Study of Adversely Affecting Radiation and Temperature Parameters on a Magnetohydrodynamic Elasto-viscous Fluid. Mathematical and Computational Applications, 24(1), 31. https://doi.org/10.3390/mca24010031





