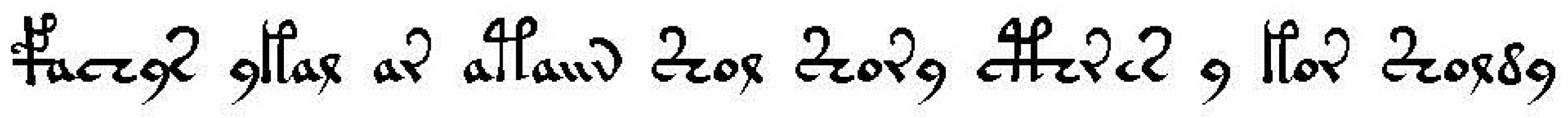1. Introduction
Hidden Markov models (HMMs) are a particular kind of a Bayesian network obtained by combining a Hidden Markov layer and a second layer of outputs that depends probabilistically on the hidden states of the first layer [
1,
2]. This model has proven a very versatile and useful tool in many applications of artificial intelligence, among others: (i) modeling of biological sequences of proteins and DNA [
3]; (ii) speech recognition systems [
4]; (iii) data compression and pattern recognition [
5]; and (iv) object tracking in video sequences [
6]. Of particular interest to us are the early studies in which HMMs were used to analyze a large body of text, in that case of English (the so-called “Brown Corpus”), considered as a sequence of letters without any previous assumption on the linguistic structure of the text or the meaning of the letters [
1,
4,
7]. Depending on the number of hidden states, thanks to this work, light was shed on the linguistic structure of English in the model. For example, for two hidden states, the basic division among vowels and consonants was recovered as the most natural basic pattern of the English language [
7]. As many more states were taken into account, it was discovered a structure including the initial and final letters of a word, vowel followers and preceders, etc. This elucidates the purely statistical nature of a language and it shows that HMMs can be an insightful tool in mathematical and computational linguistics.
Applications of HMMs to the field of Natural Language Processing (NLP) has also flourished in recent years as its has been shown for different layers of NLP such as speech tagging and morphological analysis. By using this approach, successful results for many languages such as Arabic and Persian have been obtained [
8,
9]. For these reasons, it seems promising to extend these analyses to other sources of text that still cannot be deciphered because they are written in an unknown script and with a unique linguistic structure. Among the candidates to this challenge, the medieval codex known as Voynich manuscript stands out [
10].
Discovered by the Polish–Lithuanian book dealer W. Voynich in 1912, it has remained an enigma of historical cryptography since then. For a detailed introduction to the manuscript’s history and attempts of decipherment until 1978, the interested reader can find more information in M. d’Imperio’s monograph [
11] and on Zandbergen’s website [
10]. It is generally believed by history researchers that this book could have belonged to emperor Rudolph II of Baviera until his death in 1612. This was stated in a letter addressed to the XVIIth century scholar Athanasius Kircher that was found by Voynich himself inside the manuscript. The history of the ownership of the manuscripthas been elucidated throughout the years. It is also known that it was property of the Jesuits and it was kept at the “Collegio Romano” since the last decade of the XVIIth century until the end of the XIXth century when it was moved to Frascati where Voynich acquired it.
Modern physics and chemistry analyses have allowed establishing some rigorous facts. Firstly, in 2009, some samples of ink and paint were taken from the manuscript and analyzed by X-ray spectroscopy and X-ray diffraction techniques showing that these inks and pigments were totally compatible with those used by scribes at the last epoch of the Middle Ages [
12]. The same year, a radiocarbon dating of the parchment was carried out by researchers at the University of Arizona [
13]. They found that with a
probability the parchment corresponds to the period between 1404 and 1438. This places the manuscript in the first half of the fifteen century. It is also clear that the text was added after the drawing of the figures in the manuscript because it usually surrounds these figures very closely.
An image of the first line in the Voynich manuscript is shown in
Figure 1. The total set of individual characters depends on some ambiguities in counting but it seems that there are 36 characters in the set as recognized by the Currier alphabet, some of them far more frequent than other. Others alphabets, such as the European Voynich Alphabet (EVA), consider only 25 characters (ignoring the rare ones). Although the symbols seem strange, and not immediately associated with any known alphabet ancient or modern, a closer inspection reveals a similarity with Latin, Arabic numerals and, specially, some Latin abbreviations very common throughout the Middle Ages [
14]. Anyway, these clues have helped little in finding an accepted decipherment of the text.
Among the possible solutions to this riddle, there have been four main proposals:
It is a manuscript written in an extinct natural language with an exotic alphabet [
15].
It is the encipherment of a known language (possibly Latin, German or other Indo-European language but nobody is sure [
11]).
It is a hoax consisting of asemic writing with the objective of making the book strange and valuable to collectors of antiquities [
16].
It is a modern fabrication (perhaps by its discoverer, W. Voynich) [
10].
From these hypotheses, the last one seems excluded by modern physicochemical analyses but the other three may still be considered open. The paper is organized as follows. In
Section 2, we discuss the basics of Hidden Markov Models and its application to linguistic analysis.
Section 3 is devoted to the application of HMMs to the Voynich manuscript and the information we may deduce from this. Finally, the paper ends with a discussion on the meaning of the findings of the paper and guidelines for future work in
Section 4.
2. Hidden Markov Models
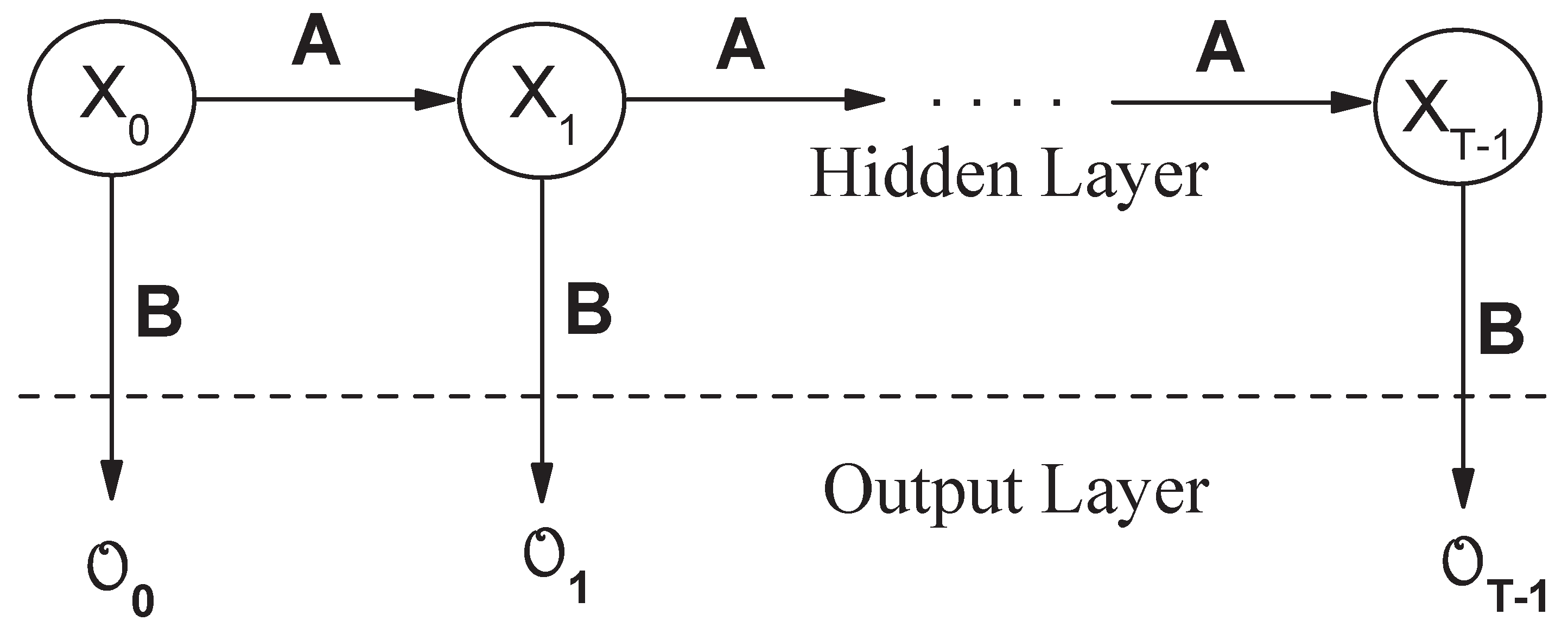
In this section, we provide a quick summary of the basic concepts and algorithms for HMMs. In
Figure 2, we show the structure of a HMM. The Markov process (
Figure 2) is characterized by a sequence
of internal states selected among a total of
N. The transition among these states is performed according to the probabilities of a transition matrix
in such a way that the element
denotes the probability of performing a transition from the internal
i state to the state
j. We can also denote the different internal states as
, with
.
The second layer we have plotted in
Figure 2 corresponds to the observations. The sequence of observations is then denoted by
and they can be chosen among a total of
M possible observation symbols. The relation between the Markov process layer and the observation layer is also probabilistic because, given an internal state
, the probability for observing the symbol
k is
. These elements constitute a row stochastic matrix,
.
The problem we want to address is the following: Suppose we have a given sequence of observations,
, consisting of a series of symbols from a total of
M. If we assume that there are
N internal states in the model, the objective is to find the model
(where
is the distribution of initial states) that provides the best fit of the observation data. The standard technique in HMMs to evaluate this optimum model makes use of a forward algorithm and a backward algorithm described as follows. In the description of the algorithms, we closely follow the pedagogical presentation by Stamp [
1].
2.1. The Forward Algorithm
Firstly, we are interested in evaluating the following probability:
i.e., the probability that the sequence of observations up to time
t is given by
and the internal state at time
t is
for a given model
. Then, for
, we have that:
where
, 1,
…,
. The reason is that
is the probability that the initial internal state is
, and
is the probability that, given that the internal state is
, we have the observation
. It is the easy to check that the recursion expression for
is given by:
Here, is the transition probability from the inner state j to the inner state i. This algorithm is also called -pass.
2.2. The Backward Algorithm
The backward algorithm, or
-pass, is proposed for the efficient evaluation of the following probability:
This means that we are interested in finding the probability that the sequence of observations from time to the end is and the inner state at time t is . The algorithm is constructed as follows:
In the first place, we define for , 1, …, .
Then, for
,
,
…, 0 we define the recursive relation:
We use these two algorithms, the forward and the backward, to find the standard algorithm that can be used to reestimate the model and make it approach its optimum.
2.3. Reestimating The Model
Our objective now is to reevaluate the model in such a way that the optimum parameters that fit the observations are found. These parameters are the elements of the matrices and as well as those in the vector corresponding to the initial distribution of internal states, . We need now an algorithm to reestimate the model in such a way that the probability of the observation sequence, , given the model , is maximized.
The idea of the algorithm begins with the definition of the following probability for a given model and a given observation sequence:
This is the probability of finding the internal states
and
at times
t and
for the observation sequence
and the model
. Using now the standard relations for conditional probabilities and the definitions of the
and
probabilities in Equations (
1) and (
4), we have:
for time
, 1,
…,
. We also define the sum over the index
j, i.e., the probability of finding the inner state
at time
t for a given model and observation sequence:
With these definitions and expressions, we can now propose the evolution algorithm for the reestimation of the parameters:
We initialize the model . It is a common practice to choose the elements according to the uniform distribution: , , and but these values must be randomized to avoid that the algorithm becomes stuck at a local maximum.
We calculate the parameters
,
,
and
by applying the corresponding expressions in Equations (
3), (
5), (
7) and (
8).
For
, 1,
…,
and
, 1,
…,
we reestimate the elements of the transition matrix,
, as follows:
For
, 1,
…,
and
, 1,
…,
we compute the new values for the elements of the observation probability matrix as follows:
Here, the sum in the numerator is restricted to those instants of time in which the observation symbol is the
kth.
Finally, we compute the probability of the given observation sequence, i.e., (obtained as the sum of for all the inner state values, i). If this probability increases (with respect to the previous value), the model updating is performed again. However, in practice, the algorithm is run for a given number of steps or until the probability does not increases more than a selected tolerance.
Another issue with this algorithm is that the
-pass and
-pass evaluations may easily lead to underflow. To avoid this problem, a normalization by the sum over
j of
is performed. For further details on HMMs the interested reader may check the references [
1].
2.4. Applications to Linguistics of HMM and Other Network Models
Before the application of this particular model to the examples in the next section, we briefly review some relevant studies concerning the use of networks in linguistics. Although computational linguistics is as old as computers themselves, the field of natural language processing (NLP) started to take off in the 1980s with the development of statistical machine translation [
17], machine learning algorithms and neural networks [
18]. More recently, NLP has received an important advance within the broader field of Deep Learning [
19]. Hidden Markov Models (HMM) also played a role in these developments: Baum and Petrie in their seminal paper laid the foundations of the theory of HMM in 1966 [
20], which took form in the late 1960s and early 1970s [
21,
22]. The forward–backward algorithm described in this section was proposed in this early studies and it is usually known as the Baum–Welch algorithm. As mentioned before, in 1980, Cave and Neuwirth applied HMMs to study the structure of a set of texts in English (known as “Brown Corpus”), which allowed them to derive useful conclusions about the role of individual letters [
1,
7]. Word alignment was also studied in connection with statistical translation by using a HMM by Vogel et al. [
23]. More recent applications of HMM to linguistics include part-of-speech tagging, i.e., the labeling of the different words according to their grammatical category [
8,
9]. The Baum–Welch algorithm has also been used to identify spoken phrases in VoIP calls [
24]. HMM are used in speech recognition since the seminal work of Baker in 1975 [
25]. Nowadays, Long Short-Term Deep Neural Networks are the current paradigm in this field due to their capacity tospot long term dependencies [
26]. Networks have also proven very useful in the development of the so-called word adjacency model, as shown by Amancio [
27] and Nebil et al. [
28]. This paradigm has been applied to the classification of artificially generated manuscripts in contrasts to genuine ones by observing their topological properties [
29]. The dynamics of word co-occurrence in networks has also allowed identifying the author of a given manuscript [
30]. It is known that this adjacency model captures, mainly, syntactical features of texts [
31]. The algorithm to find the optimum model for HMM is also oriented to identify the basic syntactical features concerning the probability sequences of individual letters. Nothing can be said about the semantics, although it can certainly help in a Rosetta stone approach to decode a particular manuscript written in an unknown language, such as the Voynich manuscript [
15]. The adjacency model has also been used to analyze the Voynich manuscript [
32] with similar conclusions to the ones deduced in this paper: that the manuscript is mostly compatible with a natural language instead of a random text.
3. Results
In this section, we discuss the application of the algorithm discussed in the previous section to several cases. First, we consider the case of a text in English and we implement the model optimization algorithm to classify the letters of the alphabet (after removing all the punctuation signs) into two classes corresponding to the inner states of the HMM. It is shown that these classes are clearly associated with the vowels and the consonants in English and this provides the basic phonemic structure of the language. Testing the algorithm with a known language gives us the necessary confidence to apply it to the Voynich manuscript.
In both applications (to a text in English and to the Voynich manuscript), we only used two hidden states. This raises the question about the advisability of this particular choice, instead of a larger number of hidden states. As the main objective was to show that these texts can be partitioned in different sets of symbols that are different in their statistical properties, selecting
seems the simpler choice. Moreover, in earlier applications to other books (such as the “Brown Corpus”, which it is a compilation of roughly one million words with texts ranging from science to literature or religion), this choice was proven to be successful in the identification of the vowels and consonants [
7]. More hidden states were considered by Cave and Neuwirth in their seminal application of HMM to language and they even obtained some conclusions for
to
. Nevertheless, this was done with the advantage of dealing with a known language. Proving the existence of, at least, two different sets of letters in the Voynich manuscript is already a useful conclusion. If we take into account that the alphabet and the language are completely unknown in this case, this could help linguistics in their research to unveil some meaning in the words of the manuscript. Only after some globally accepted success is achieved in this endeavor the study of the convergence of the HMM model for
could be done with some possibility of interpretation.
3.1. Application to The Quixote
We applied the model evolution algorithm for HMM with
and
. Therefore, we considered 26 letters and the space as output symbols. The text of the Quixote in plain ASCII can be freely downloaded from the Gutenberg’s project website [
33]. This is the English translation of the original Spanish version. As a data pre-processing stage, we transformed all the upper-case letters to lower-case and removed the punctuation signs with the exception of the spaces among subsequent words. This way, we obtained a sequence of 5,693,310 characters but, to our purpose, we restricted ourselves to the first 100,000 characters.
As initial transition matrix, we chose:
and the distribution of initial hidden states was given at the start of the algorithm by
The observation probability matrix was obtained by randomizing the equal probability assumption:
for every
j. For example, we could multiply
by a random number in the interval
. However, we must verify the condition that the total probability for a given inner state
j and all the possible observation outcomes is normalized to one:
and this was accomplished by imposing this condition to define the last value
for the
Mth state,
.
The algorithm was then implemented in Mathematica using lists and the model evolution was run for 200 steps with 100,000 characters from the book, pre-processed to retain only the letters and removing all the punctuation signs (see the
supplementary material accompanying this paper for Mathematica code). Results were also checked using other independent implementations of the code in C
[
34].
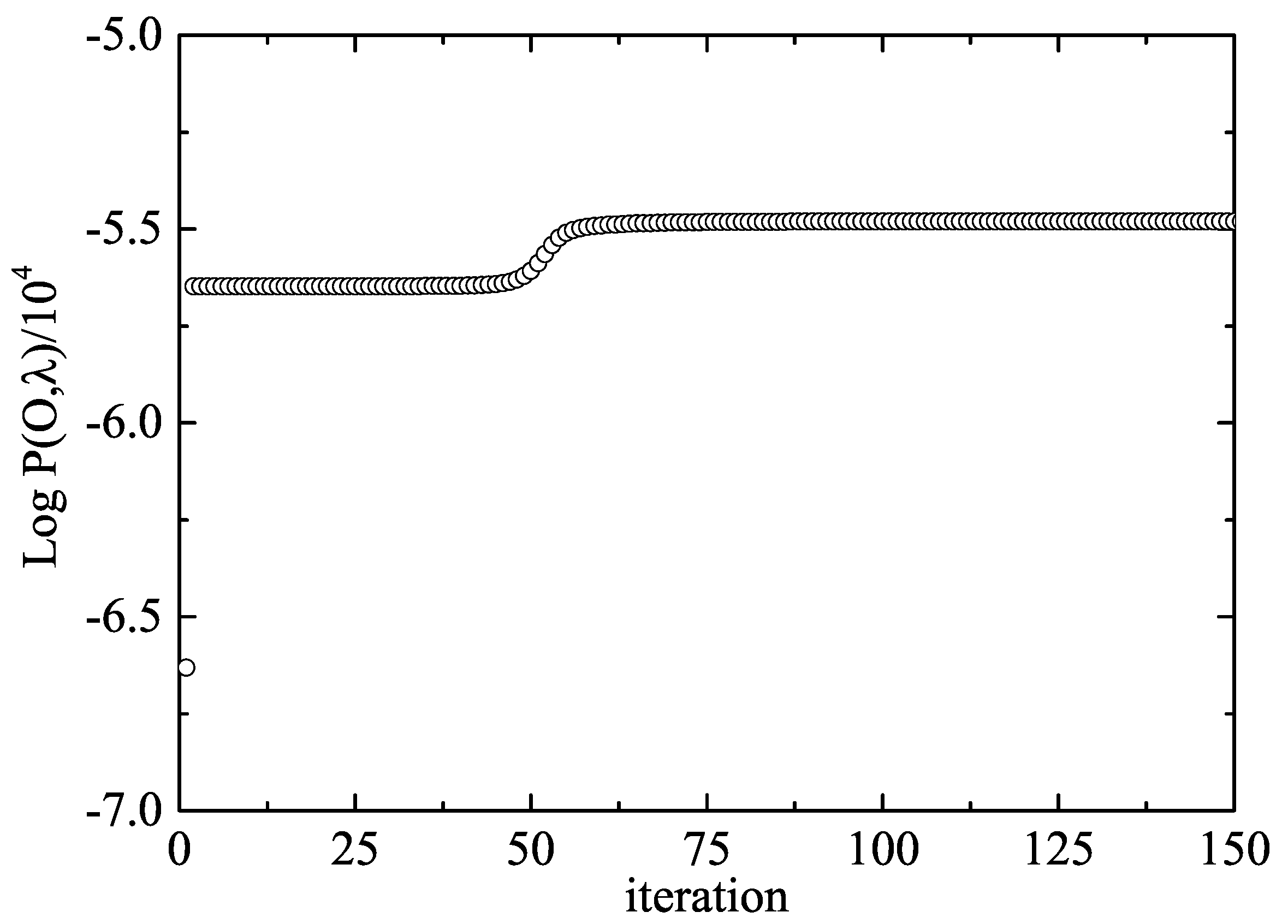
Firstly, we noticed that the algorithm converged after around 100 iterations, as deduced from the evolution of the logarithm of the observation sequence probability for the given model
. This is shown in
Figure 3. However, the convergence may seem peculiar because this probability only started raising after iteration 50 and settled to a “plateau” in a few iterations after that. This could be an indication of a small basin of attraction for the fixed point we were looking for. The topography of the landscape for this particular problem would require further investigation.
From the results in this figure, we conclude that convergence was achieved after only 60 steps and that further iterations only improve the results very slightly. The final transition matrix we found is given as follows:
with an initial distribution of initial states given by:
Transition matrices with large off-diagonal elements are also found using other texts such as the “Brown Corpus” [
7]. This compilation contains a million words with texts ranging from religion to science, including also some novels. Consequently, the conclusions we derived from a single book are already supported for a variety of texts in English from the early study of Cave and Neuwirth [
7]. The form of the transition matrix in Equation (
14) is already pointing towards the existence of two categories of letters (the inner states of the HMM). These categories are, obviously, the vowels and the consonants and this statement is reinforced by the values of the observation probability matrix,
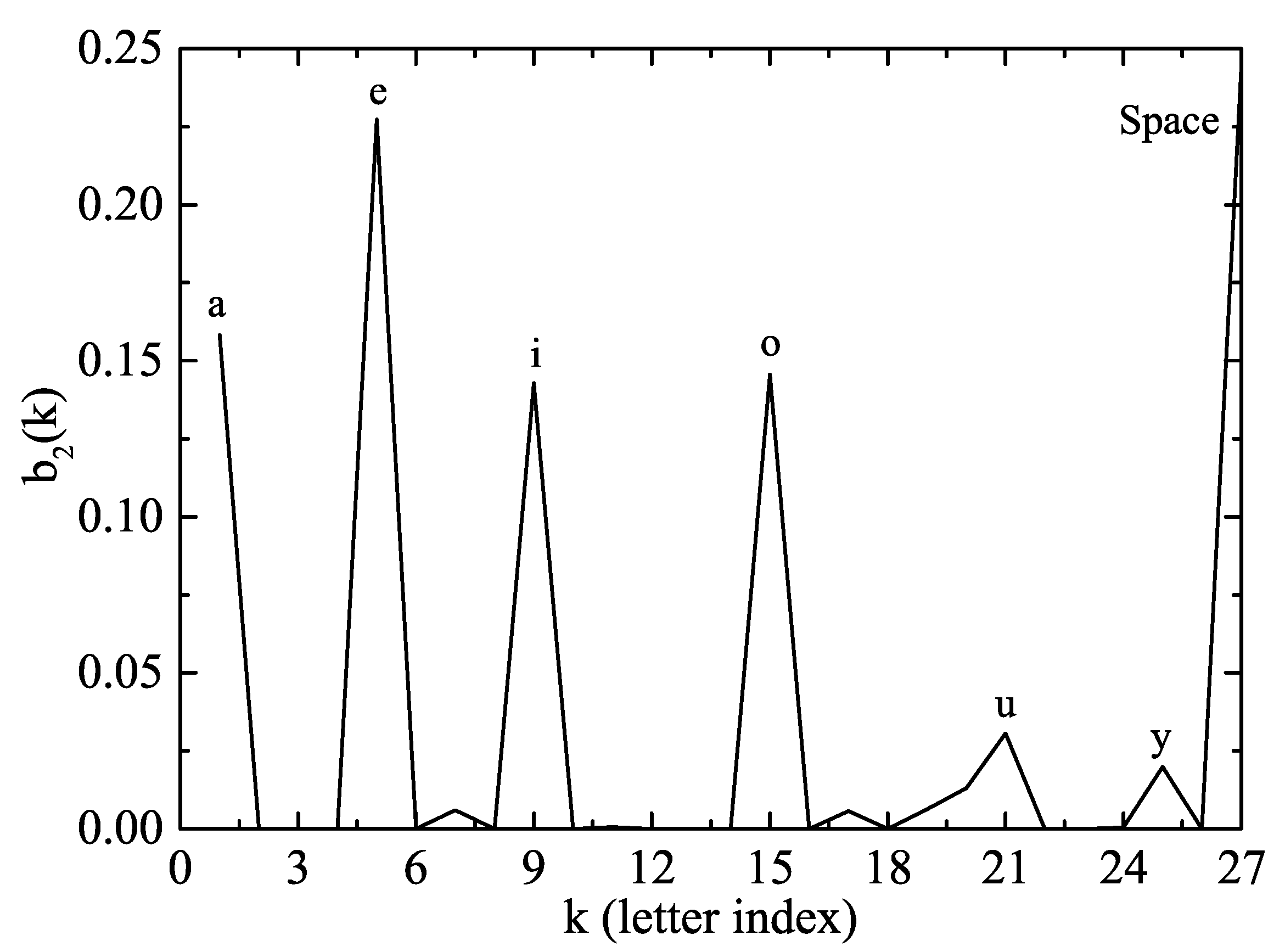
. In our case, the inner state 2 has been identified as the vowels, as clearly shown in
Figure 4 where a peak of probability is found for every vowel.
From the results in
Figure 4, we could also derive some interesting conclusions:
The most frequent vowel in the English language is “e”.
The space among words has the structural function of a vowel, although it has no associated sound.
The letter “y” is mostly a vowel in the English language. Indeed, the Oxford Dictionary classifies it as a vowel in some cases (“myth”), a semivowel in others (“yes”) or forming a diphthong (as in “my”) [
35].
In rigor, these conclusions would be valid only for the Quixote but they have also been checked for other books (in particular the “Brown Corpus” book compilation). Thus, it is not unjustified to apply them to the English language in general. Similar conclusions can also be deduced for the consonants. It is also remarkable that the results in
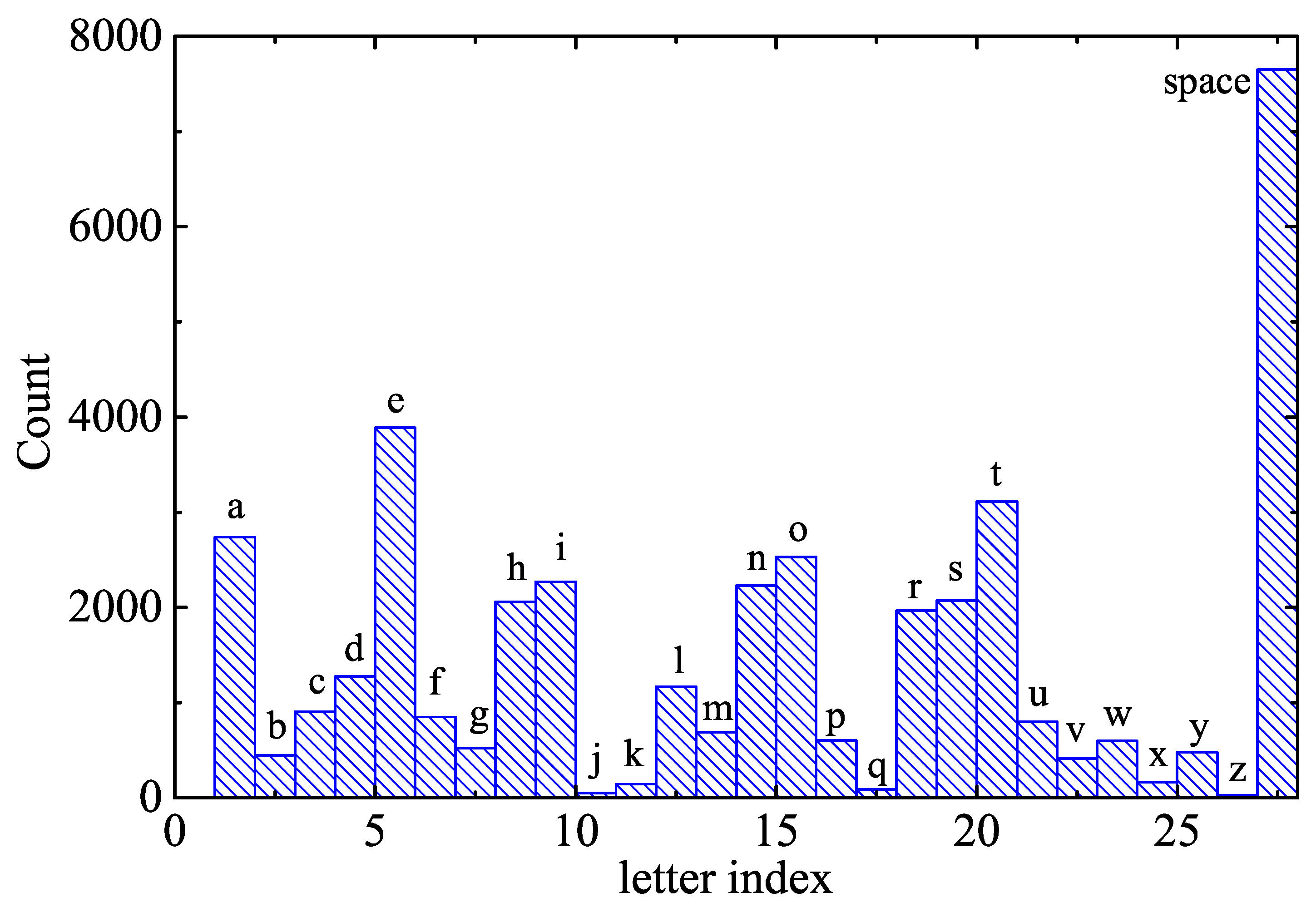
Figure 4 cannot be deduced from simple frequency analysis. The histogram of the letters obtained from the Quixote’s text is shown in
Figure 5.
We see that the vowel “e” is still the most frequent letter in the English language (not only the most frequent vowel) but the second most frequent letter is “t”. Thus, there is no clear pattern in the histogram to separate vowels from consonants. This ability of HMM make them a very powerful tool in computational linguistics.
Finally, we should emphasize that this experiment was performed by starting with particular forms of the transition matrix,
, and the initial distribution vector,
, as given in Equations (
11) and (
12). The observation probability matrix was also chosen in a random way as described above. It is possible that, in some cases, the evolution algorithm for the HMM may find a local minima and be sensitive to initial values instead of converging to the global minima we are looking for. Indeed, a solution with
defined as a 2-by-2 identity matrix is always stable and can be approached by certain initial conditions. For these reasons, it is convenient to check the sensitivity of our results to initial conditions by performing several runs of the program. To check the convergence of the algorithm, we chose different initial conditions, in which
and
were randomly selected as follows:
where
x,
y, and
z are random real numbers in the interval
. After performing 10 simulations with 200 runs, we found that the average transition matrix is given by:
Notice that both the matrices in Equations (
14) and (
18), are unstable as the off-diagonal elements are larger than the diagonal ones. However, this stationary state of the algorithm is coherent with previous results obtained with other texts [
7]. This means that two hidden states can be identified in the symbols of the book (corresponding to vowels and consonants) and that the transitions take place mainly from consonants to vowels and vice versa. This is precisely what happens in natural languages. A transition matrix equal, or approximately equal, to the identity matrix would not separate the states and it is not relevant to this linguistic application.
3.2. Application to the Voynich Manuscript
After the successful implementation of the HMM technique for the Quixote, we thus turned again to our problem of analyzing the Voynich manuscript. Several transcriptions of this manuscript are available but the most popular is the one based upon the so-called European Voynich Alphabet (EVA), as developed by Zandbergen and Landini. Although there is an extended version, which includes the less common symbols in the Voynich manuscript, the basic version uses 26 letters of the English alphabet (excluding “w”) to make a correspondence with the most abundant symbols in Voynichese. The correspondence among the EVA code and the Voynich symbol is given in the table of
Figure 6.
At this point, it is also necessary to explain why we chose this particular alphabet instead of the other alternatives. The main reasons are its popularity and the fact that many transcriptions are available for it. Otherwise, some specialists would argue that some symbol combinations in this alphabet, such as “ch” and “sh”(corresponding to the so-called “pedestals”) should be considered as one single character each [
10]. On the other hand, the combinations “in” and “iin” are also candidates for representing letters, although, in some other cases, “i” could be a single character. This is another problem that computational analyses could help to solve [
36].
This way, a transcription of the whole Voynich manuscript has been performed in such a way that it can be used in computational analysis. These transcriptions are available in several sites, as discussed by Zandbergen [
10]. In particular, we used Takahashi’s transcription developed in 1999. Of course, some pre-processing was required before applying the HMM algorithm because this file includes some information about each line, including the folium number (recto or verso) and the number of the line within each page of the manuscript. After removing this information, we were left with a set of EVA characters separated by dots. These dots correspond to the spaces between words in the original manuscript. The total number of characters (including spaces) we used for the simulation is 228,836. Convergence of the algorithm was also very fast, as in the case of the English text analyzed in
Section 3.1, and, when we used more than 50,000 characters, the results were stable and showed no dependence on the total length of the sequence,
T. This is a convincing argument in favor of the consistency of the results.
We started with the same initial conditions as those given in Equations (
11) and (
12) for the transition matrix and the distribution of the state
. The probability matrix for the observation states (the Voynich characters) was randomized in the usual way explained in
Section 3.1. In this particular example, we used the first 100,000 characters in the Voynich manuscript and 200 iteration steps. The final transition matrix is similar to those of natural languages (because the off-diagonal elements are larger than the diagonal ones):
and the distribution of initial states was given by:
After performing the same randomization of initial conditions as we saw for the example of the Quixote, we found an average transition matrix of the form:
which confirms that the result in Equation (
19) is close to the asymptotic fixed point we were looking for.
We can also see that Equation (
20) indicates that the first character of the manuscript is associated with a consonant sound. The most interesting results are, however, those obtained with the observation probability matrix, which clearly separate two kinds of characters to be associated with vowel and consonant phonemes, as occurred in the case of the Quixote. In
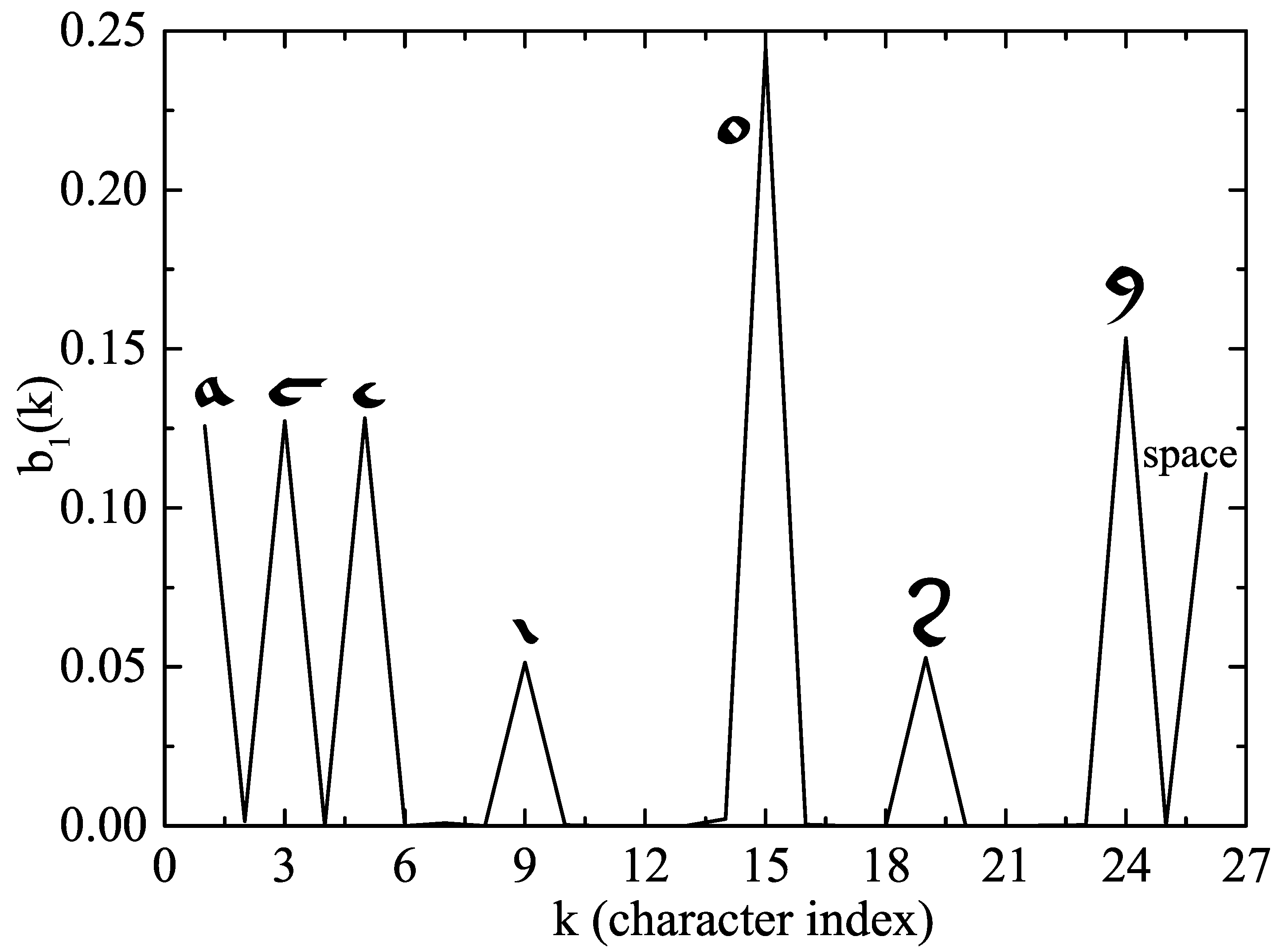
Figure 7, we show the probability of obtaining each character when the hidden state is 1.
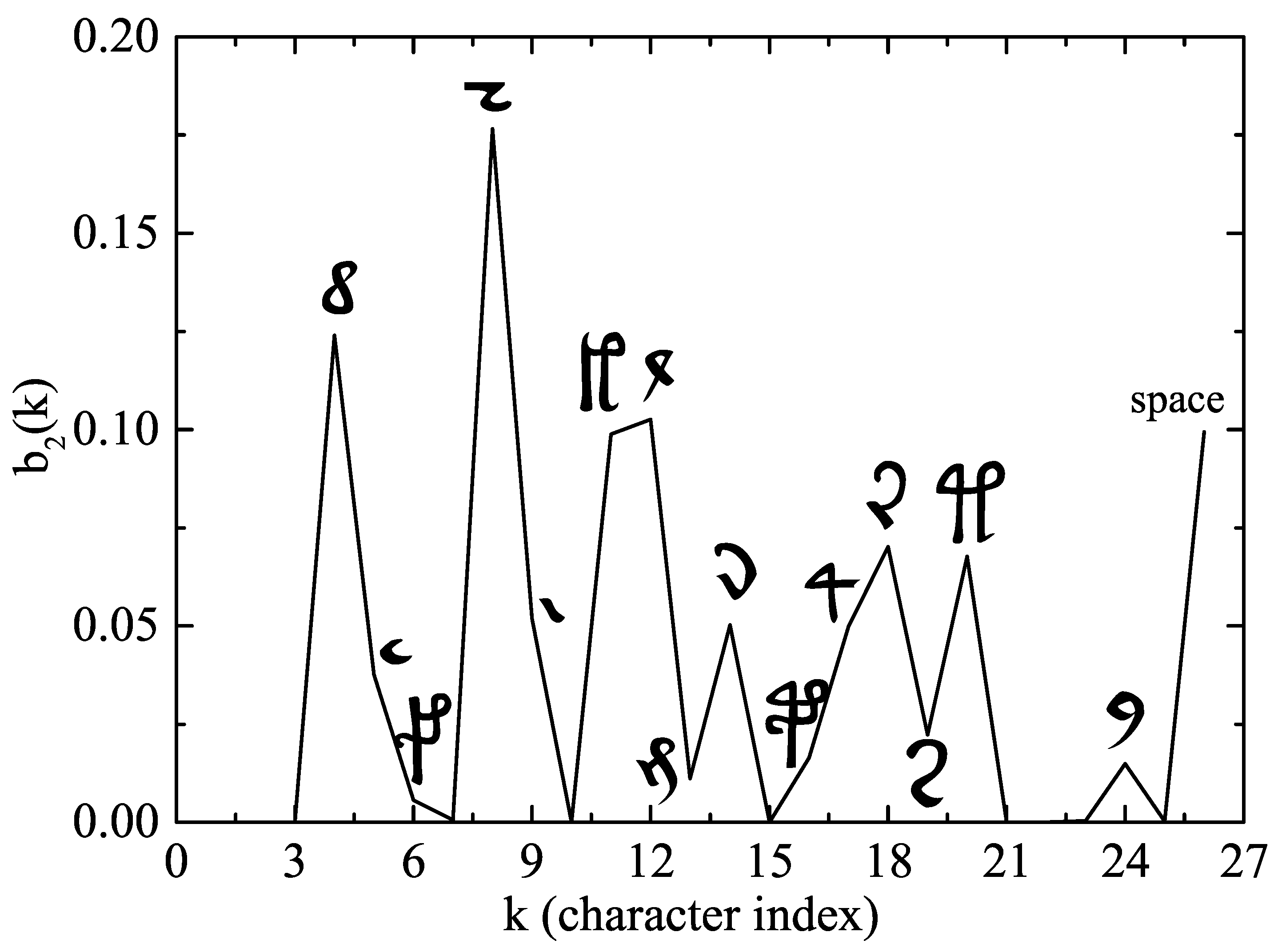
The probabilities for hidden state 2 are given in
Figure 8. We see that a set of very conspicuous peaks were obtained in both cases, but there were fewer in the result shown in
Figure 7, which could mean that the symbols corresponding to those peaks are associated with vowel’s phonemes. On the other hand, this correspondence is not as strong as in the case of the English text of
Section 3.1 because there are symbols with noticeable probability that appear in both figures (in particular, the EVA symbols “e”, “i”, “s” and “y”). Perhaps, the most simple explanation for the absence of a clear separation among vowels and consonants in these four cases is that we are confronted with another example of letters that can function as both vowels and consonants as in the case of “y” in English. However, for the Voynich manuscript, we have four letters with this capacity and this is a peculiarity whose meaning we cannot unravel for the moment. Another possibility is that the Voynich alphabet is some kind of abjad but this hypothesis is not so clear because in abjads the letters that appear in the text are always a vowel or a consonant (although some vowels are left out). This could have an effect in the transition matrix but it is not evident that it would produce an ambiguity in the classification of those letters in the hidden states, one or two. Further research into HMM applied to languages with abjad’s alphabets, such as Arabic, should be necessary to clarify this point.
Nevertheless, the appearance of high peaks in
Figure 7 also suggests the existence of vowel symbols in the manuscript so this abjad would be impure. Bax also suggested in 2014 [
15] that this is the case after proposing a provisional decoding of some words in the manuscripts associated with plants and a constellation. In the next section, we discuss this intriguing possibility.
4. Discussion
Although a lot of research effort has been devoted to understanding the Voynich manuscript, we still lack a consensual opinion about the nature of the writing it contains. Early efforts by Friedman, Tiltman, Currier and Bennett, among others [
10,
11] helped to elucidate some features of the manuscript and exclude the hypothesis of a simple substitution cipher. The interest in the application of mathematical and computational methods to the Voynich manuscript is maintained nowadays, as shown by recent publications [
32,
37].
The main result of this paper is the evidence of the existence of two states associated with the symbols in the manuscript that could correspond to consonants and vowels. This reaffirms to the conclusions of Amancio et al. [
32] and Montemurro et al. [
37] of the existence of word co-occurrences and keywords in the same proportion than natural languages.
The recent proof of the old age of the “vellum” by carbon-dating places this manuscript in the first half of the XVth century and all other tests are very compatible with an origin in the Middle Ages [
12,
13]. Anyway, although a forgery by Voynich or other recent author is excluded, some authors support the idea that this object was fabricated in the Middle Ages with a pecuniary intention by making it similar, in appearance, to a real, but enciphered, text [
16]. As said before, statistical measurements carried out by Amancio et al. in 2013 [
32] show that the Voynich manuscript is incompatible with shuffled texts and, moreover, that certain keywords appear throughout the manuscript. These keywords organize in patterns of semantic networks, as shown by Montemurro et al. [
37]. These conclusions, and those of this paper, make the hypothesis of a fake more unlikely but a clever fake designed to simulate a human language with the adequate transition among letters cannot completely be excluded.
Other authors, as most researchers in the past, think that the text is enciphered in some way. Hauer and Kondrak assumed that the manuscript was written in some abjad’s alphabet using some transposition of letters or anagramming [
38]. These assumptions are very strong and their conclusions of a relation to Hebrew have been widely dismissed.
In this paper, we use the conservative approach of applying the standard technique of HMM for the linguistic analysis of the manuscript. We have shown that a division among vowels and consonant phonemes is very clear in the resulting observation probability matrix but that some characters (such as the EVA symbols “e”, “i”, “s” and “y”) could participate in the vowel and consonant natures, either because they are semivowels or because there is an implicit vowelling in them as in impure abjad’s alphabets. A positional dependence of the vowelling as in abugida’s alphabets cannot be excluded. In abugida’s alphabets, some vowels are written but, sometimes, they are attached as part of the consonant, which makes the analysis more difficult. Further research with HMM into languages with these alphabets would be necessary to obtain a reliable conclusion.
In any case, we found some characters in the script that very possibly represent vowel’s phonemes: “a”, “c”, “e”, “o” and “y” in the EVA notation (see
Figure 6). There are also some exclusively consonant phonemes, such as “d”, “h”, “k”, “l” or “t” in the EVA’s notation.
The idea of using HMM to analyze the Voynich manuscript has already been proposed by other authors but their results have not been published officially in scientific journals. For example, Zandbergen discussed his application of HMM to the manuscript on a webpage [
36]. His conclusions are similar to those found in this present paper. Another study was performed by Reddy and Knight [
39]. However, they indicated that their algorithm separates vowels and consonants in an odd fashion because one of the states always corresponds to the last symbol in a letter. Anyway, their explanations are cursory and they did not describe their algorithm in enough detail to allow for a reproduction of their results. Much earlier, D’Imperio wrote a paper about the use of an algorithm called PTAH at the National Security Agency [
40]. Although we can infer from her discussion that the algorithm is some kind of HMM and that the results obtained from a five-state model are compatible with our results, it is difficult to compare her algorithm with the one discussed here because PTAH is still classified. On the other hand, implementations with a higher-state HMM could provide useful information if the linguistics provide some agreement about the possible translation of some words.
It also seems interesting that Prof. Bax in 2014 [
15] identified some names of plants and the constellation Taurus in the manuscript and that his associations with phonemes are similar to the one discussed in this paper. In
Figure 9, we show some of these associations for the words “Taurus”, “Coriander” and “Juniper” (in Arabic).
Although these associations are considered very preliminary, even by its author, the similarity with our identification of vowels and consonants is striking. Thus, we can gain some confidence that a serious scholarship effort could enhance these identifications and provide a sure path for further research. In any case, we must stress that the identifications performed by Bax are not generally accepted but, at least, they show that our mapping of vowels and consonants allows for some meaningful words to appear.
Although other possibilities might still be open, we have increasing support of the view that the text in the manuscript is neither a hoax nor an intentional cipher but a genuine language written in an unknown script. Notwithstanding this progress, we are still far from identifying the language because it could even be a dead tongue, for which the script was devised. Further analysis including more states could help if the decoding of the manuscript adds further evidence to these preliminary conclusions. We hope that this work stimulates further research by expert linguists that could shed additional light into this ancient enigma.