Evolution of an Exponential Polynomial Family of Discrete Dynamical Systems
Abstract
1. Introduction
2. Exponential Polynomial Family of DDS
3. Analysis of the Family
3.1. Perturbed Linear Case,
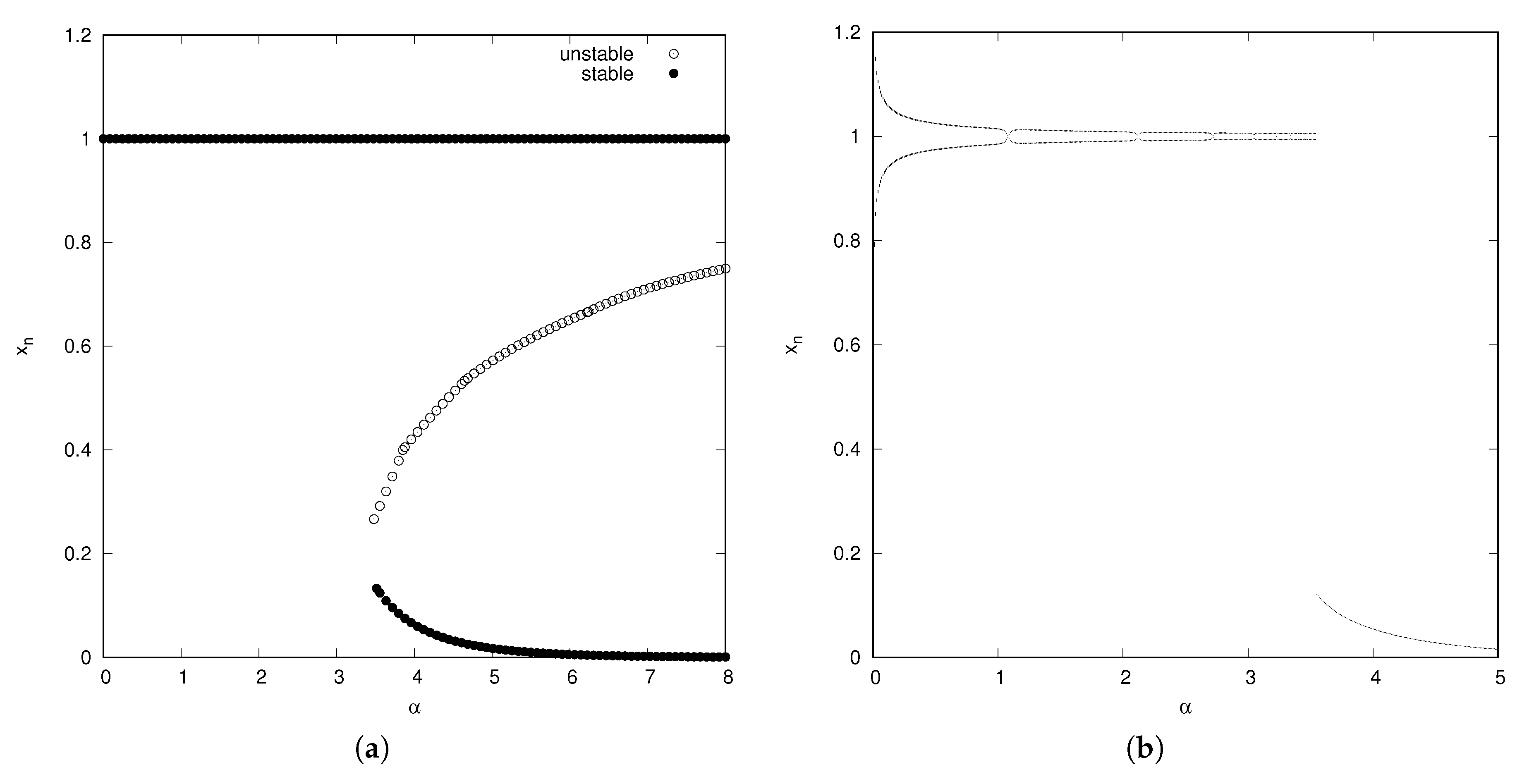
3.2. Basic Exponential Polynomial Case,
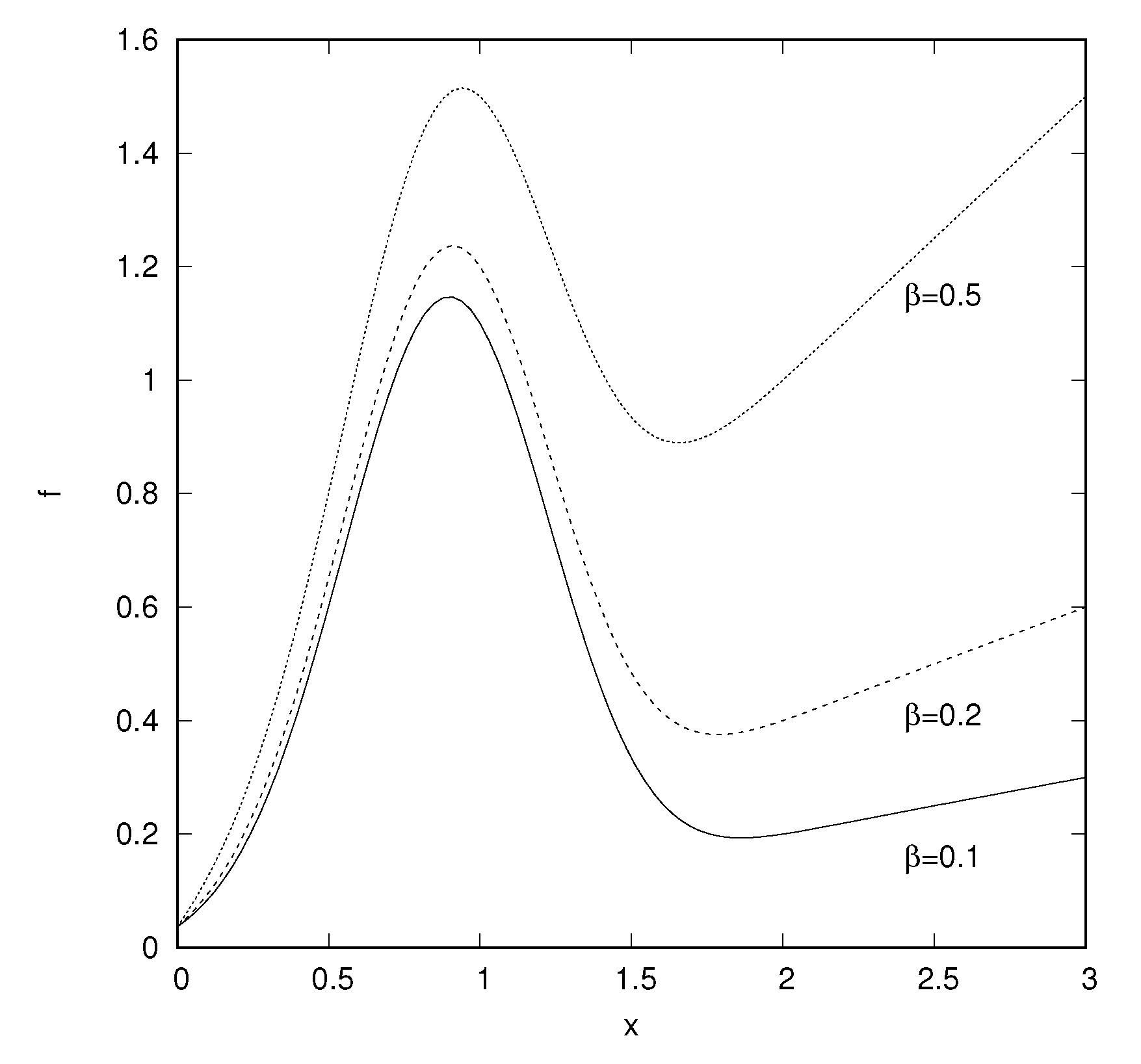
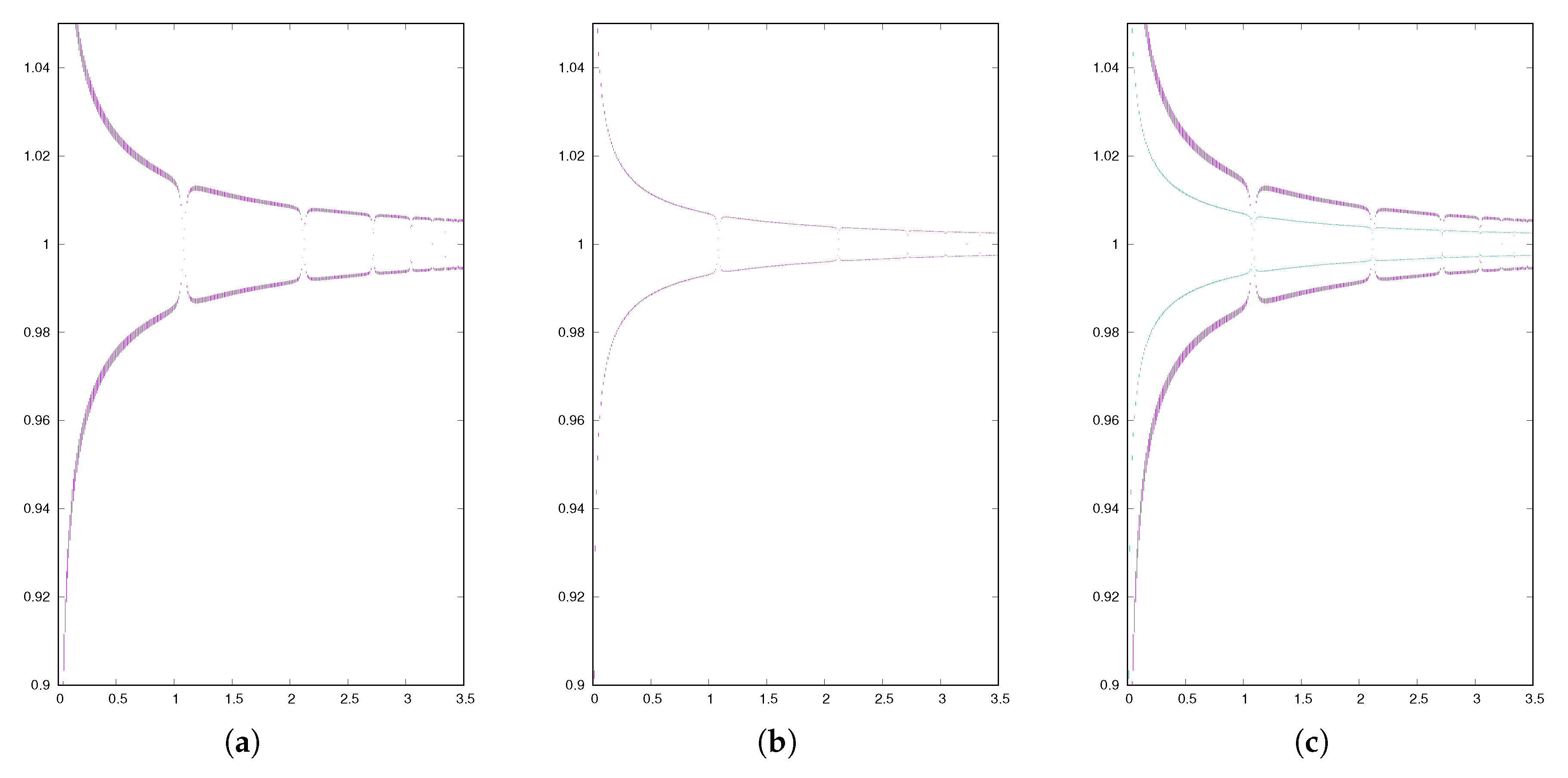
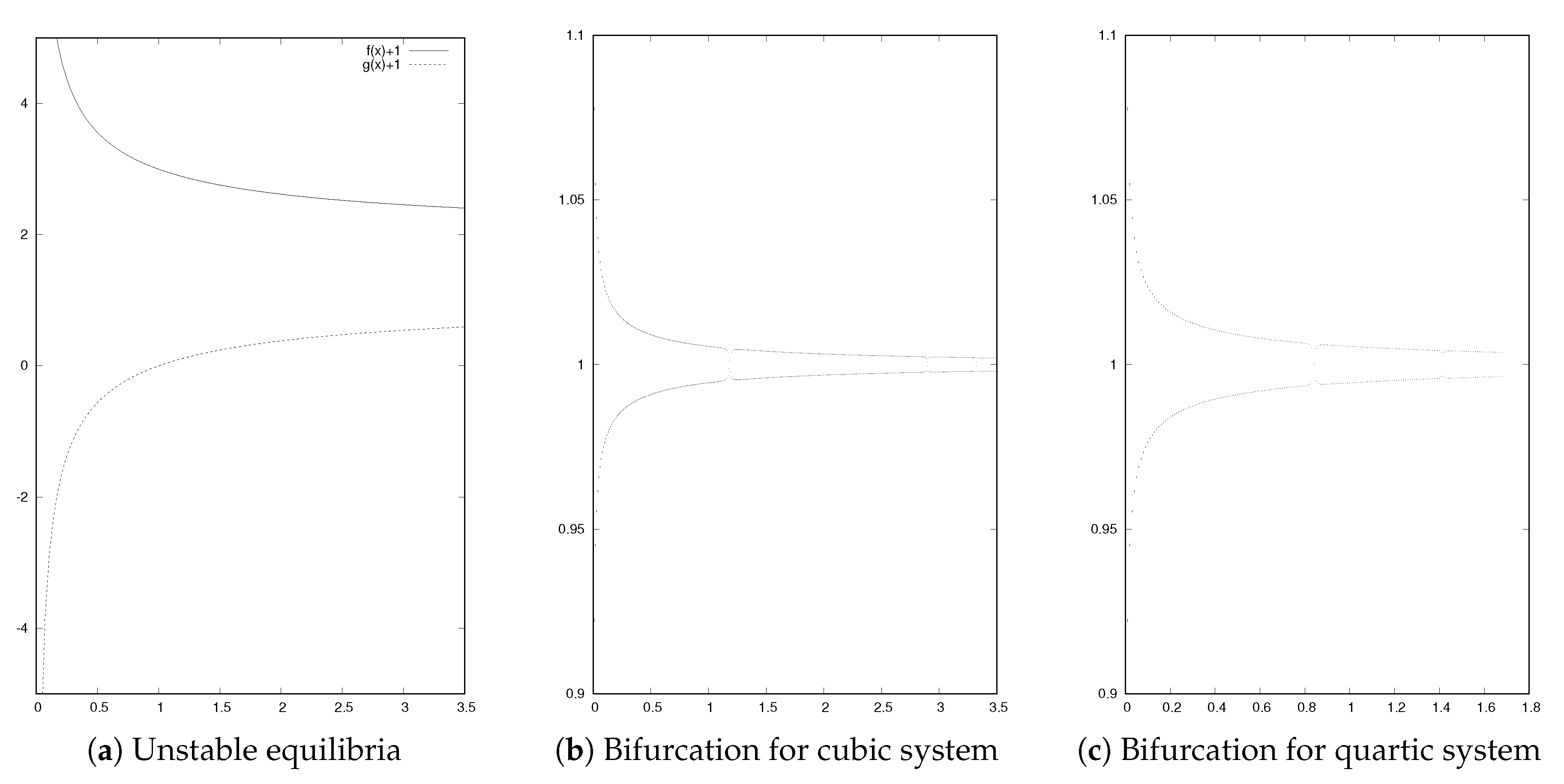
3.3. Mixed Case
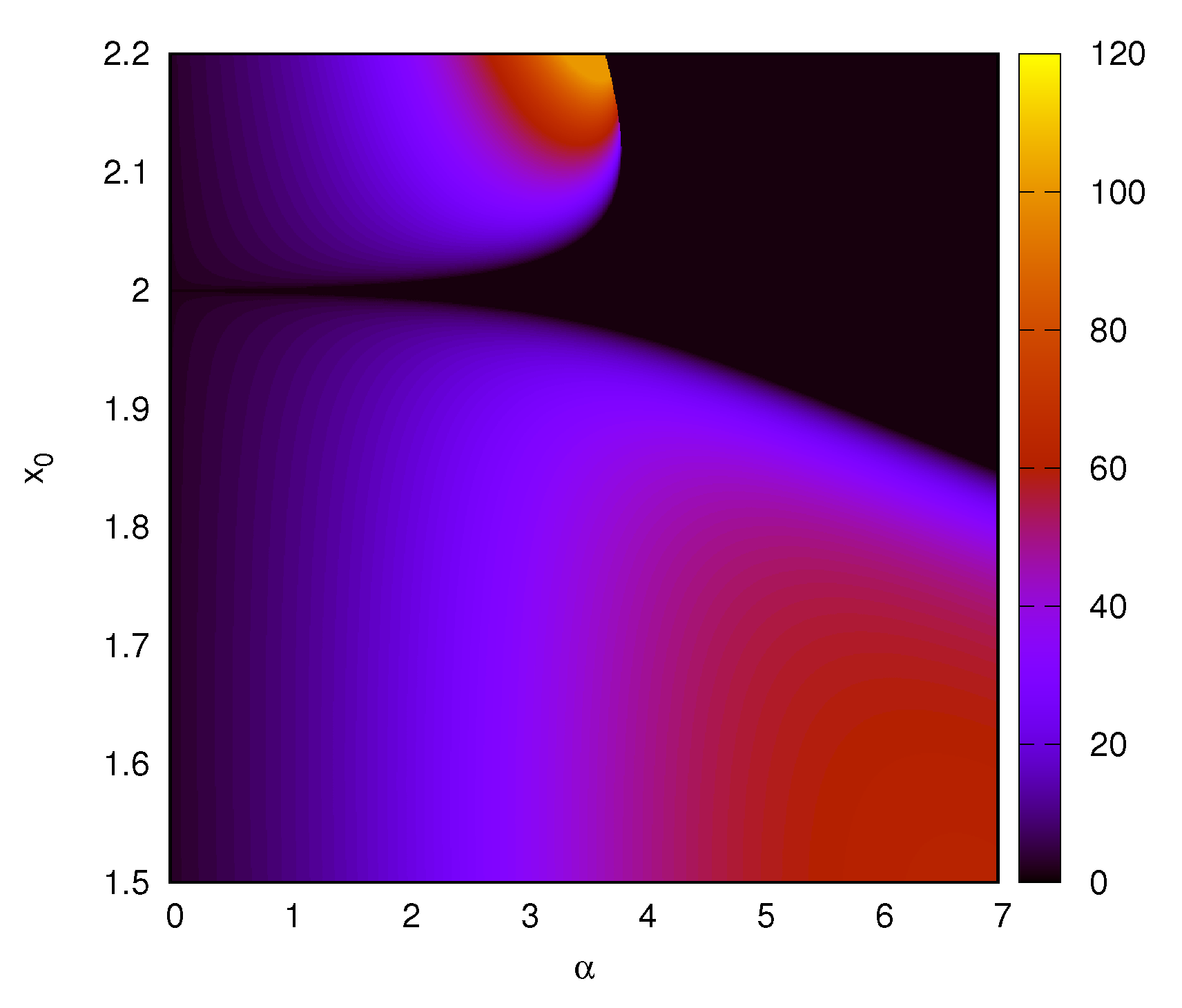
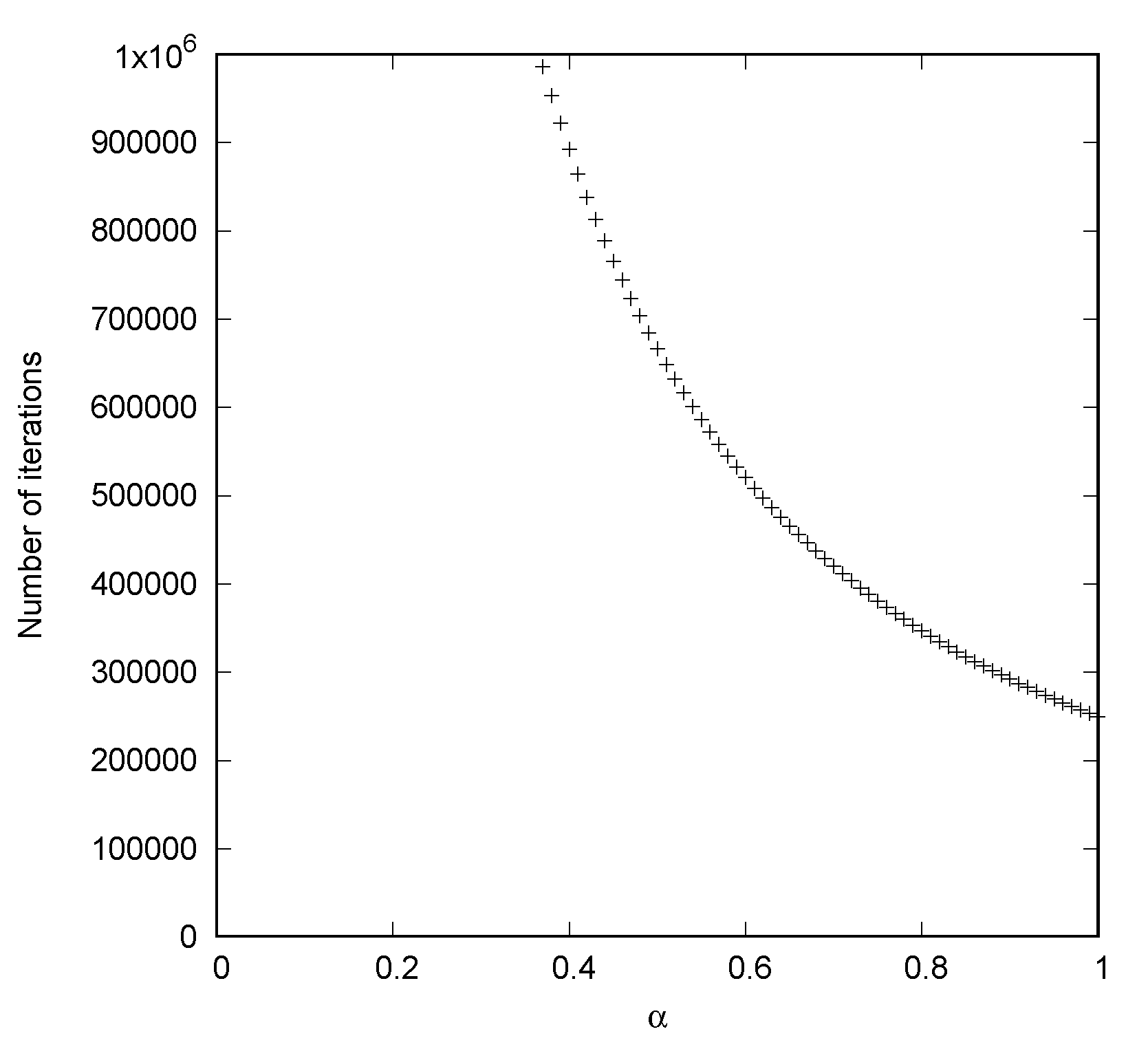
4. Transient Behavior for the Case
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Arenas, A.J.; González-Parra, G.; Chen-Charpentier, B.M. A nonstandard numerical scheme of predictor– corrector type for epidemic models. Comput. Math. Appl. 2010, 59, 3740–3749. [Google Scholar] [CrossRef]
- Kojouharov, H.V.; Dimitrov, D.T. Compatible Discretizations for Continuous Dynamical Systems. AIP Conf. Proc. 2008, 1067, 28–37. [Google Scholar]
- Shreiber, D.I.; Barocas, V.H.; Tranquillo, R.T. Temporal variations in cell migration and traction during fibroblast-mediated gel compaction. Biophys. J. 2003, 84, 4102–4114. [Google Scholar] [CrossRef]
- Zaliapin, I.; Semenova, I.; Kashina, A.; Rodionov, V. Multiscale trend analysis of microtubule transport in melanophores. Biophys. J. 2005, 88, 4008–4016. [Google Scholar] [CrossRef] [PubMed]
- Simson, R.; Sheets, E.D.; Jacobson, K. Detection of temporary lateral confinement of membrane proteins using single-particle tracking analysis. Biophys. J. 1995, 69, 989–993. [Google Scholar] [CrossRef]
- Fujiwara, T.; Ritchie, K.; Murakoshi, H.; Jacobson, K.; Kusumi, A. Phospholipids undergo hop diffusion in compartmentalized cell membrane. J. Cell Biol. 2002, 157, 1071–1081. [Google Scholar] [CrossRef]
- Fiutak, J.; Mizerski, J.Z. Transient behaviour of laser. Phys. B 1980, 39, 347–352. [Google Scholar] [CrossRef]
- Tang, C.; Telle, J.; Ghizoni, C. Transient effects in wavelength-modulated dye lasers. Appl. Phys. Lett. 1975, 26, 534–537. [Google Scholar] [CrossRef]
- Krapivsky, P.L.; Redner, S.; Ben-Naim, E. A Kinetic View of Statistical Physics; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Castellano, C.; Fortunato, S.; Loreto, V. Statistical physics of social dynamics. Rev. Mod. Phys. 2009, 81, 591. [Google Scholar] [CrossRef]
- Chowdhury, D.; Santen, L.; Schadschneider, A. Statistical Physics of Vehicular Traffic and Some Related Systems. Phys. Rep. 2000, 329, 199–329. [Google Scholar] [CrossRef]
- Hinton, E. The dynamic transient analysis of axisymmetric circular plates by finite element method. J. Sound Vib. 1976, 46, 465–472. [Google Scholar] [CrossRef]
- Kunow-Baumhauer, A. The response of a beam subjected to a transient pressure wave load. J. Sound Vib. 1984, 92, 491–506. [Google Scholar] [CrossRef]
- Hastings, A. Transients: The key to long-term ecological understanding? Trends. Ecol. Evol. 2004, 19, 39–45. [Google Scholar] [CrossRef] [PubMed]
- Van Geest, G.; Coops, H.; Scheffer, M.; van Nes, E. Long Transients Near the Ghost of a Stable State in Eutrophic Shallow Lakes with Fluctuating Water Levels. Ecosystems 2007, 10, 37–47. [Google Scholar] [CrossRef]
- Schaffer, W.M.; Kendall, B.; Tidd, C.W.; Olsen, L.F. Transient periodicity and episodic predictability in biological dynamics. IMA J. Math. Appl. Med. Biol. 1993, 10, 227–247. [Google Scholar] [CrossRef]
- Fisher, R.S.; Boas, W.E.; Blume, W.; Elger, C.; Genton, P.; Lee, P.; Engel, J. Epileptic Seizures and Epilepsy: Definitions Proposed by the International League Against Epilepsy (ILAE) and the International Bureau for Epilepsy (IBE). Epilepsia 2005, 46, 470–472. [Google Scholar] [CrossRef]
- Grüne, L.; Stieler, M. Asymptotic stability and transient optimality of economic MPC without terminal conditions. J. Process Control 2014, 24, 1187–1196. [Google Scholar] [CrossRef]
- Solis, F.; Jódar, L. Nonisolated slow convergence in discrete dynamical systems. Appl. Math. Lett. 2004, 17, 597–599. [Google Scholar] [CrossRef]
- Solis, F.; Felipe, R. Slow convergence of Maps. Nonlinear Stud. 2001, 8, 389–392. [Google Scholar]
- Weidner, P. The Durand-Kerner method for trigonometric and exponential polynomials. Computing 1988, 40, 175–179. [Google Scholar] [CrossRef]
- Schock, E. Approximate solution of ill-posed equations: Arbitrarily slow convergence vs. superconvergence. In Constructive Methods for the Practical Treatment of Integral Equations; Birkhäuser: Basel, Switzerland, 1985; pp. 234–243. [Google Scholar]
- Braun, M. Differential Equations and Their Applications: An Introduction to Applied Mathematics; Springer: New York, NY, USA, 2013; Volume 15. [Google Scholar]
- Dunham, C.B. Chebyshev approximation by exponential-polynomial sums. J. Comput. Appl. Math. 1979, 5, 53–57. [Google Scholar] [CrossRef]
- Viswanathan, K.S. Statistical mechanics of a one-dimensional lattice gas with exponential-polynomial interactions. Comm. Math. Phys. 1976, 47, 131–141. [Google Scholar] [CrossRef]
- Boyadzhiev, K.N. Exponential Polynomials, Stirling Numbers, and Evaluation of Some Gamma Integrals. Abstr. Appl. Anal. 2009, 2009, 168672. [Google Scholar] [CrossRef]
- Mayoral, E.; Robledo, A. Multifractality and nonextensivity at the edge of chaos of unimodal maps. Phys. A 2004, 340, 219–226. [Google Scholar] [CrossRef]
- Andrecut, M.; Ali, M.K. Robust chaos in smooth unimodal maps. Phys. Rev. E 2001, 64, 025203–025205. [Google Scholar] [CrossRef] [PubMed]
- Jensen, R.V.; Ma, L.K.H. Nonuniversal behavior of asymmetric unimodal maps. Phys. Rev. A 1985, 31, 3993–3995. [Google Scholar] [CrossRef]
- Hao, B.L. Universal Slowing-Down Exponent Near Periodic-Doubling Bifurcation Points. Phys. Lett. A 1981, 86, 267–268. [Google Scholar] [CrossRef]
- San Martín, J.; Porter, M.A. Convergence Time towards Periodic Orbits in Discrete Dynamical Systems. PLoS ONE 2014, 9, e92652. [Google Scholar] [CrossRef] [PubMed]
- Solis, F.; Chen, B.; Kojouharov, H. A classification of slow convergence near parametric periodic points of discrete dynamical systems. Int. J. Comput. Math. 2016, 93, 1011–1021. [Google Scholar] [CrossRef]


© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Solis, F. Evolution of an Exponential Polynomial Family of Discrete Dynamical Systems. Math. Comput. Appl. 2019, 24, 13. https://doi.org/10.3390/mca24010013
Solis F. Evolution of an Exponential Polynomial Family of Discrete Dynamical Systems. Mathematical and Computational Applications. 2019; 24(1):13. https://doi.org/10.3390/mca24010013
Chicago/Turabian StyleSolis, Francisco. 2019. "Evolution of an Exponential Polynomial Family of Discrete Dynamical Systems" Mathematical and Computational Applications 24, no. 1: 13. https://doi.org/10.3390/mca24010013
APA StyleSolis, F. (2019). Evolution of an Exponential Polynomial Family of Discrete Dynamical Systems. Mathematical and Computational Applications, 24(1), 13. https://doi.org/10.3390/mca24010013




