1. Introduction
Engineering design and product development using shape optimization can be a very daunting task, especially if the design approach is experimental, where cost and time constraints usually limit the number of prototypes that are possible to construct and test. Moreover, it is required to have an in-depth know-how of the problem being studied to choose which configurations to analyze. In this view, the continuous development of numerical methods and the increase in computing performance have suggested the use of simulation software able to model complex multi-physics problems and optimize the design space, thereby reducing the costs related to prototypes, physical experiments, and field/operational tests.
Proprietary numerical simulation tools allow very detailed analysis, but their use often requires the acquisition of expensive licenses. An alternative to commercial software is the use of free and open-source technology (e.g., GNU General Public License, BSD license, MIT license). This type of software licensing model gives users the freedom to use, read, write, and redistribute the source code, with no price tag attached. More importantly, open-source software has the same capabilities as their commercial counterparts, and it is mature enough so that it can be used in the design and certification process of new products.
With this in mind, we address in this manuscript the implementation of an open-source framework for shape optimization. In particular, we focus our attention on fluid dynamics problems applied to ship design. Nevertheless, the same methodology can be used in any engineering field. In doing so, essentially four tasks need to be addressed:
How to efficiently and accurately simulate the physics involved.
How to modify the geometry or mesh.
How to search the optimal configuration.
How to interface the applications involved in the optimization loop.
In the context of naval architecture design, the adoption of shape optimization using numerical simulations is not new. The advantages of hull optimization and related devices optimization (such as propellers and hydrofoils) have been demonstrated by several authors. Many design optimization approaches have been used in the design of traditional propellers [
1,
2], unconventional propulsion systems [
3,
4], appendages [
5], and the optimization of the entire hull shape [
6,
7]. Recently, a lot of development has been done on the design of unconventional vessels with special mission profiles, from the standard mono-hull shapes [
8,
9], to unconventional multi-hulls [
10,
11], or hulls with special shapes, such as the Small Waterplane Area Twin Hull or SWAT [
12]. However, even if these design methods have reached a satisfactory maturity level, the hull shape optimization is still confined to the research level due to its high complexity.
One of the main drawbacks of shape optimization for complex industrial applications is the large computational times required to get the outcomes. In naval architecture design (where we are mainly interested in evaluating resistance and seakeeping, among other things), this is usually overcome by the use of highly efficient low-fidelity or medium-fidelity methods, such as the boundary element methods (BEM). However, such approaches are not able to predict the wave pattern generated by the ship, do not include viscous effects, or neglect other nonlinear behaviors (which can be important in order to obtain a proper performance prediction for certain ships). Even though successful applications with low-fidelity methods have been previously reported in the literature [
10], the adoption of high-fidelity solvers (such as finite volume method or finite element method solvers) in the design loop can increase the accuracy and reliability of the design process. In this field, many studies have been conducted, for example, Serani et al. [
13] successfully used a viscous solver for addressing the shape optimization of a high-speed catamaran with excellent results; however, the computational cost in terms of CPU time (for the whole optimization loop and each single simulation) and the complexity of the optimization loop was too big to be implemented by a manufacturer (particularly small ones, which have limited resources). In light of this, innovative optimization methods to simplify and speed up the entire optimization process are under investigation, such as multi-level optimization [
14], surrogate-based optimization [
15], proper orthogonal decomposition and dynamic mode decomposition [
16], machine learning for interactive design and fluid dynamics simulations [
17], data-driven simulations and optimization [
18], and generative design [
19].
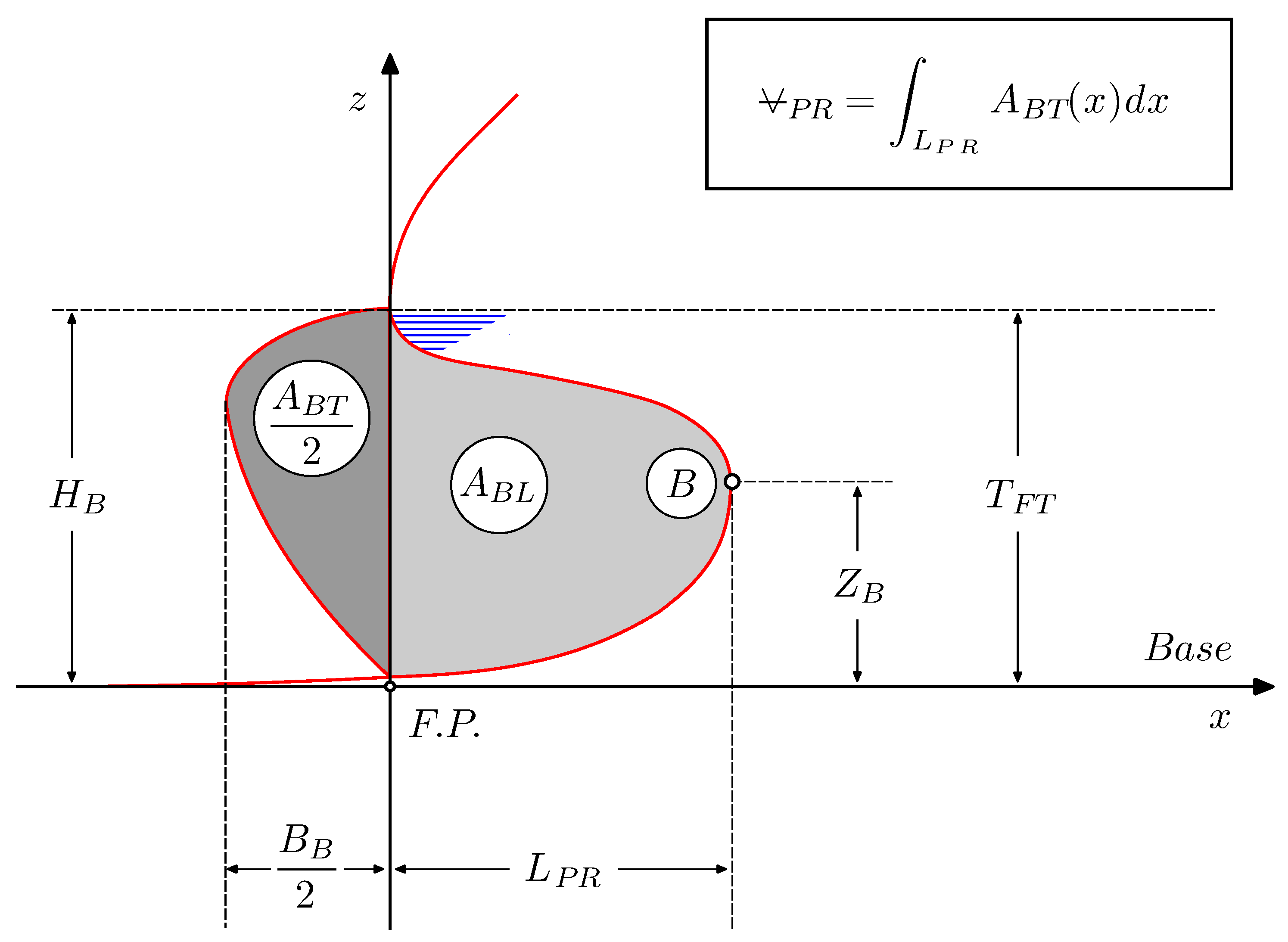
In the shipbuilding industry, the bulbous bow shape is usually designed to reduce the ship wave-making resistance. The hull drag resistance can be split into three main contributions: the wave-making drag, the friction drag, and the wake drag. Depending on the ship speed, the contribution of each component to the total resistance value can be drastically different. Considering the present case, the wave-making component is one of the most important; therefore, its reduction by optimizing the bulbous bow shape can give a not negligible contribution to the whole design (for example, a reduction of some percentage of the fuel consumption). Following the guidelines proposed by Kracht [
20], the bulbous bow shape can be defined by six non-dimensional parameters. With the goal of decreasing the computational cost by reducing the design space, and at the same time being able to represent the bulbous bow shape without losing geometrical information, only two design parameters are considered in this study. Nevertheless, the proposed approach can be extended to more complex cases where, for instance, one is interested in having more local control of the bulbous bow shape by using more design variables. Previous work addressing bulbous bow optimization using computational fluid dynamics (CFD) can be found in References [
21,
22,
23,
24,
25]. The aforementioned sources show the benefits of CFD optimization, but most of them fail in explaining the importance of the application interfacing tool, automation of the loop, and real-time analytics.
Hereafter, we propose a vertical work-flow that could potentially simplify and automate the design and optimization process. All the tools used in this work are open-source, and this translates to cost savings, as no commercial licenses are used. To generate the domain mesh and to compute the hydrodynamic resistance of the hull (including the bulbous bow), we used the multi-physics solver OpenFOAM [
26] (version 5.0). To create new geometry candidates, we used the free-form deformation application MiMMO [
27]. To reduce the number of optimization iterations and to get an initial screening of the design space, we used surrogate-based optimization. The optimization algorithms and the code coupling interface is provided through the Dakota library [
28] (version 6.7). Finally, all the real-time data analytics, quantitative post-processing, and data analytics were performed using Python and bash scripting. Previous attempts in coupling OpenFOAM and Dakota to deal with shape optimization problems are described in References [
29,
30,
31,
32,
33,
34,
35,
36], but none of them have addressed how to interface different applications in an optimization loop (besides OpenFOAM and Dakota), how to deal with concurrent simulations, work-flow automation, fault-tolerant loops, real-time data analytics, and the importance of knowledge extraction. We aim at coupling all tools needed for shape optimization studies in a streamlined work-flow, with a high degree of automation and flexibility, and using efficient optimization techniques that allow engineers to explore, exploit, and optimize the design space from a limited number of training observations.
2. Description of the Optimization Framework and Optimization Strategy
In a typical shape optimization study, many applications can live together (e.g., solid modeler, shape morpher, mesh generator, multi-physics solver, optimizer, knowledge extraction tools, coupling utilities, and so on), making the optimization loop very difficult to set up, monitor, and control. Moreover, the optimization loop must be fault tolerant, that is, in the event of an unexpected failure of the system (hardware or software), the user should be able to restart from a previously saved state. The optimizer should also be flexible, in the sense that it should provide a variety of optimization methods, design of experiment techniques, and code coupling interfaces to different simulation software and programming languages. Finally, to reduce the long execution times inherent to computational fluid dynamics (CFD) optimization studies, the optimization loop should be able to work in parallel and deploy many simulations at the same time. Furthermore, everything should be done without overwhelming the user. We aim at addressing the findings and recommendations reported in the NASA contractor report
“CFD Vision 2030 Study: A Path to Revolutionary Computational Aerosciences” [
37], where the authors state:
“A single engineer/scientist must be able to conceive, create, analyze, and interpret a large ensemble of related simulations in a time-critical period (e.g., 24 hours), without individually managing each simulation, to a pre-specified level of accuracy”.
In this work, we successfully coupled many applications used in traditional CFD work-flows to efficiently conduct general CFD optimization studies. We used the library Dakota [
28,
38] as the optimizer and application interface tool. The Dakota library provides a flexible and extensible interface between simulation codes and iterative analysis methods. This library contains many gradient-based methods and derivative-free methods for design optimization studies, uncertainty quantification, and parameter estimation capabilities. Dakota also contains many design of experiment methods to conduct sensitivity studies. With Dakota, the user is not obliged to use the optimization and space exploration methods implemented on it: one can easily interface Dakota with a third-party optimization library. The library also offers restart capabilities and solution monitoring. Most important, it is software neutral, in the sense that it can interface any application that it is able to parse input/output files via a command line interface.
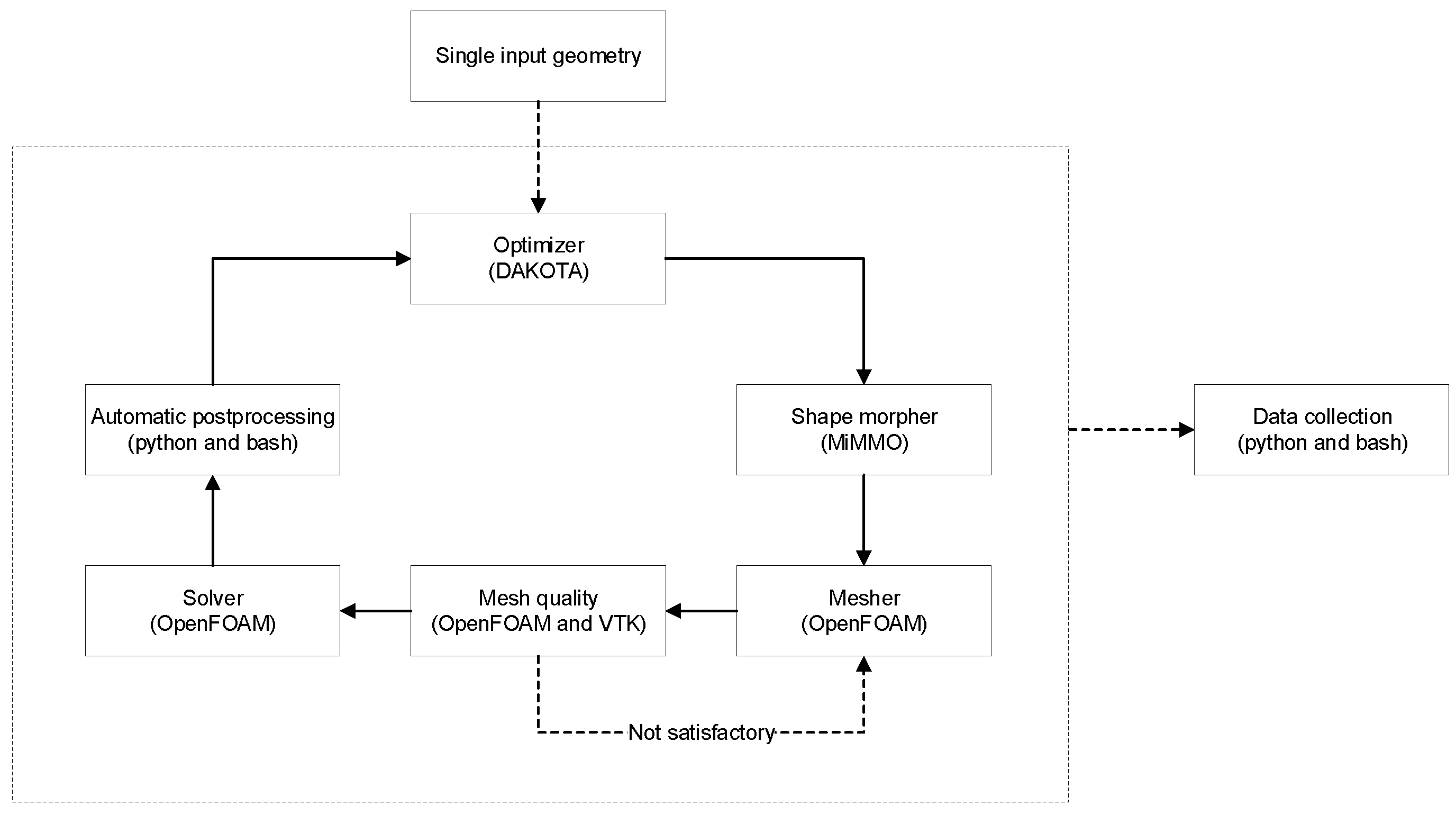
The optimization loop is illustrated in
Figure 1. In this work-flow, the starting point is the initial geometry which is manipulated with a free-form deformation tool to generate new shapes. The MiMMO library [
27], which uses radial basis functions (RBF) to shape the geometry [
39,
40,
41,
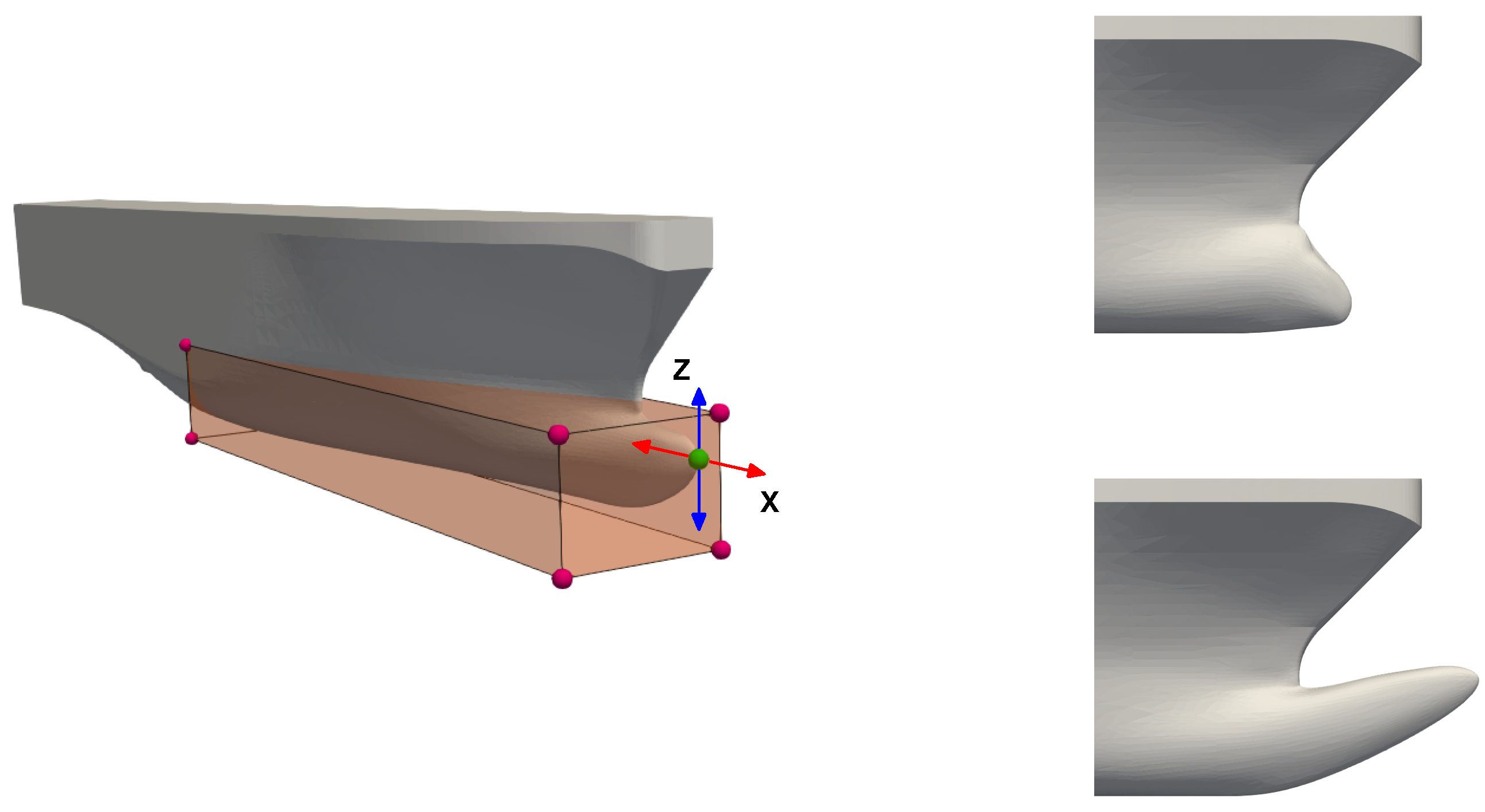
42], was used as geometry manipulation tool. With MiMMO, the user is only asked to define a series of control points, these control points are then moved in the design space, and together with the RBF function, they generate a smooth displacement field that represents the new geometry. To have more control over the deformation, the user can define a deformable region using a control box. Then, the continuity between the region to be deformed and the area labeled as undeformed is ensured by using continuous level set functions. In
Figure 2, we illustrate the original geometry (left image), where we highlight the control points and the selection box used to deform the base geometry. In this figure (right image), we also show two deformed geometries. In the figure depicted, we only used one control point to deform the geometry, but more control points can be used with no problem. It is worth mentioning that in this framework, we only take one initial geometry. Then, starting from this geometry, we can generate many variations of it. In general, the shape morphing task is computationally inexpensive. We would like to emphasize that, at this point, any geometry manipulation tool can be used; the main reasons in using MiMMO are that the input files used by this library can be easily parameterized and it also offers mesh morphing capabilities (which are not discussed in this manuscript).
After generating the input geometry, we can move to the meshing phase. To mesh the computational domain, we used the meshing tools distributed with the open-source OpenFOAM library [
26,
43], namely, blockMesh and snappyHexMesh. These tools generate high-quality hexahedral-dominant meshes and can be easily parameterized. The whole meshing process is fully automatic and, to some extent, fault tolerant. During the meshing stage, we always monitored the quality of the far-field mesh, the quality of the inflation layers close to the body, and the transition between regions with different cell sizes. In the case of mesh quality problems (such as high non-orthogonality, high skewness, too aggressive expansion ratios between cells, or discontinuous inflation layers in critical areas), the mesh was automatically recomputed using more robust predefined parameters, which generates better meshes but at the cost of a higher cell count. The meshing parameters were determined using the original geometry, and two additional geometries representing the worst case scenarios (highly deformed bulbs). The possibility of using the meshing tools in parallel and concurrently allowed us to obtain fast outcomes.
All the numerical simulations were conducted using the open-source OpenFOAM library [
26,
43], which is a multi-physics solver based on the cell-centered finite volume method. This library has been extensively validated, counts with a wide community, is highly scalable in parallel architectures, and the simulation setup can be easily parameterized. As soon as the optimization loop was started, the simulations did not require continuous user supervision. Several quantities of interest (QoI) were sampled during each computation, and in the case of anomalies (such as high oscillations in the forces, unbounded quantities, or mass imbalance), the simulation parameters were automatically changed to a more robust and stable discretization scheme. The default and modified solver parameters were determined after conducting an extensive validation of the solver (as explained in
Section 4). All the simulations were run in parallel, and as the optimization method used did not require the computation of gradients, we were able to run many simulations concurrently. The whole framework was deployed in an out-of-the-box workstation, with 16 cores and 128 GB of RAM. As all the tools used require only publicly available compilers and libraries, the same framework can be easily deployed in distributed memory HPC architectures.
At this point, we need to define the optimization strategy. One major obstacle to the use of optimization in CFD is the long CPU times of the simulations and, depending on the method used, the need for computing gradients or the need for running a large number of simulations to obtain the design space sensitivities. Therefore, due to the long computational times and the lack of analytic gradients, optimization in CFD is a slow iterative-converging task. With this in mind, we need to choose an optimization method that is reliable, computationally affordable, and will meet our deadlines.
Gradient-based methods have good converging rates, but they require the computation of the gradients (and depending o the method used, they might require the computation of the Hessians), and in the presence of a large design space these quantities can be very expensive to compute. Gradient-based methods also require some basic knowledge of the problem, as well as some input parameters (e.g., starting point in the parameter space, bounds of the design variables, iterative and gradients tolerances, how to compute the derivatives, and so on), and they do not give much information regarding the global behavior of the design space. Additionally, they do not guarantee the convergence to a global optimal value. On the other hand, global derivative-free methods have slow convergence rates, but they are more likely to converge to the global optimal value than local methods. Also, since they do not require the computation of the gradients, they behave quite well in the presence of numerical noise. However, to reach the optimal value, they need to perform a large number of function evaluations, which can impose serious time limitations, especially if we are running unsteady CFD simulations.
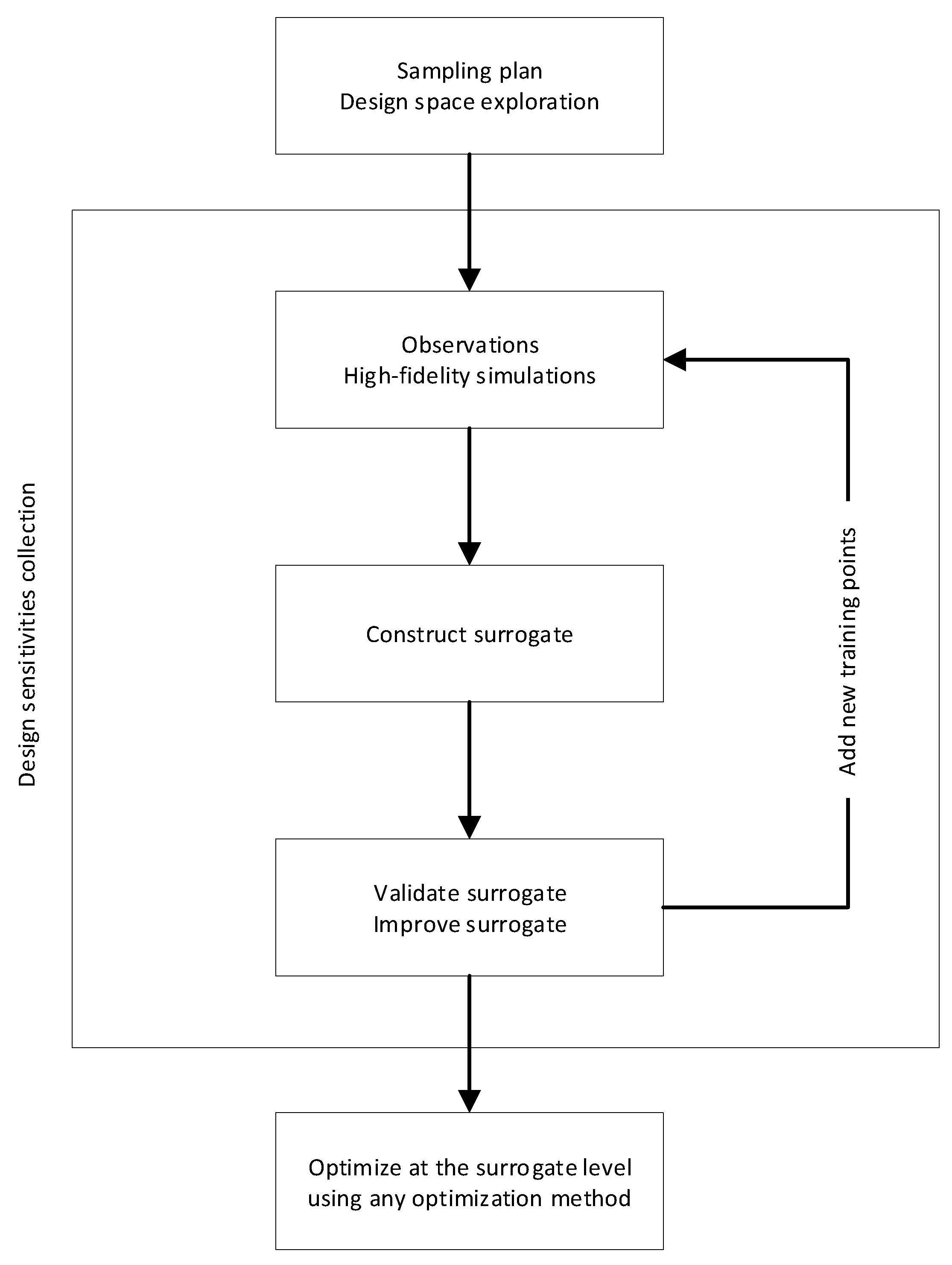
Another approach to conduct optimization is the so-called surrogate-based optimization (SBO), which is the method used in this study. The SBO method consists of constructing a mathematical model (also known as a surrogate, response surface, meta-model, emulator) from a limited number of observations (CFD simulations, in our case). After building the surrogate, the optimization can be performed at this level. Furthermore, during the design space exploration process, SBO provides a better global understanding of the problem, allowing the use of exploratory data analysis techniques and machine learning methods to get more insight, discover hidden patterns, and detect anomalies in the design space. In
Figure 3, we illustrate the basic work-flow of the SBO method. The work-flow is rather simple; we start by conducting a limited number of simulations (design space exploration). After gathering the information at the design points, we can use those observations to construct the mathematical model or surrogate. At this point, we can validate the surrogate by comparing the values obtained from the high-fidelity simulations against the predicted values using the surrogate, or we can refine the surrogate by adding more training points. After building, validating, and improving the meta-model, we can use any optimization method to find the optimal value. Working at the surrogate level is orders of magnitude faster than working at the high-fidelity level [
44].
It is important to mention that more sophisticated SBO techniques exist, such as efficient global optimization (EGO), gradient-enhanced meta-models, and adaptive sampling response surfaces [
38,
44,
45,
46,
47]. We did not use any of those state-of-the-art SBO approaches, because we were more interested in showing that complicated code coupling and complex optimization studies using traditional meta-models methods could be achieved using the Dakota library. However, the library gives the possibility to use EGO and gradient-enhanced Kriging emulators; if these methods are not enough, the user can add an external library to the optimization loop.
As already stated, surrogate models are inexpensive approximate models that are intended to capture the salient features of expensive high-fidelity experiments or observations. To construct the surrogate or meta-model, many methods are available, just to name a few: polynomial regression, Kriging interpolation, radial basis functions, neural networks, adaptive splines, and so on. In this work, we used Kriging interpolation, which is an interpolation method for which the interpolated values are modeled by a Gaussian process [
44,
48]. The implementation details of the Kriging interpolation method used in this work (universal Kriging), can be found in References [
38,
44,
45,
48,
49,
50,
51,
52]. In the Kriging interpolation method, the meta-model is forced to pass by all the observations, and in the presence of noise in the response, the surrogate can be smoothed. Kriging interpolation is well fitted for engineering design optimization problems which usually are nonlinear, multivariate, multi-modal, and noisy.
To get a better idea of how the SBO method works, let us use a toy function to go through every step of the work-flow. We will use the Branin function, which is defined as follows:
this equation with the given bounds has three minima, located at
where the minimum value in the three locations is equal to
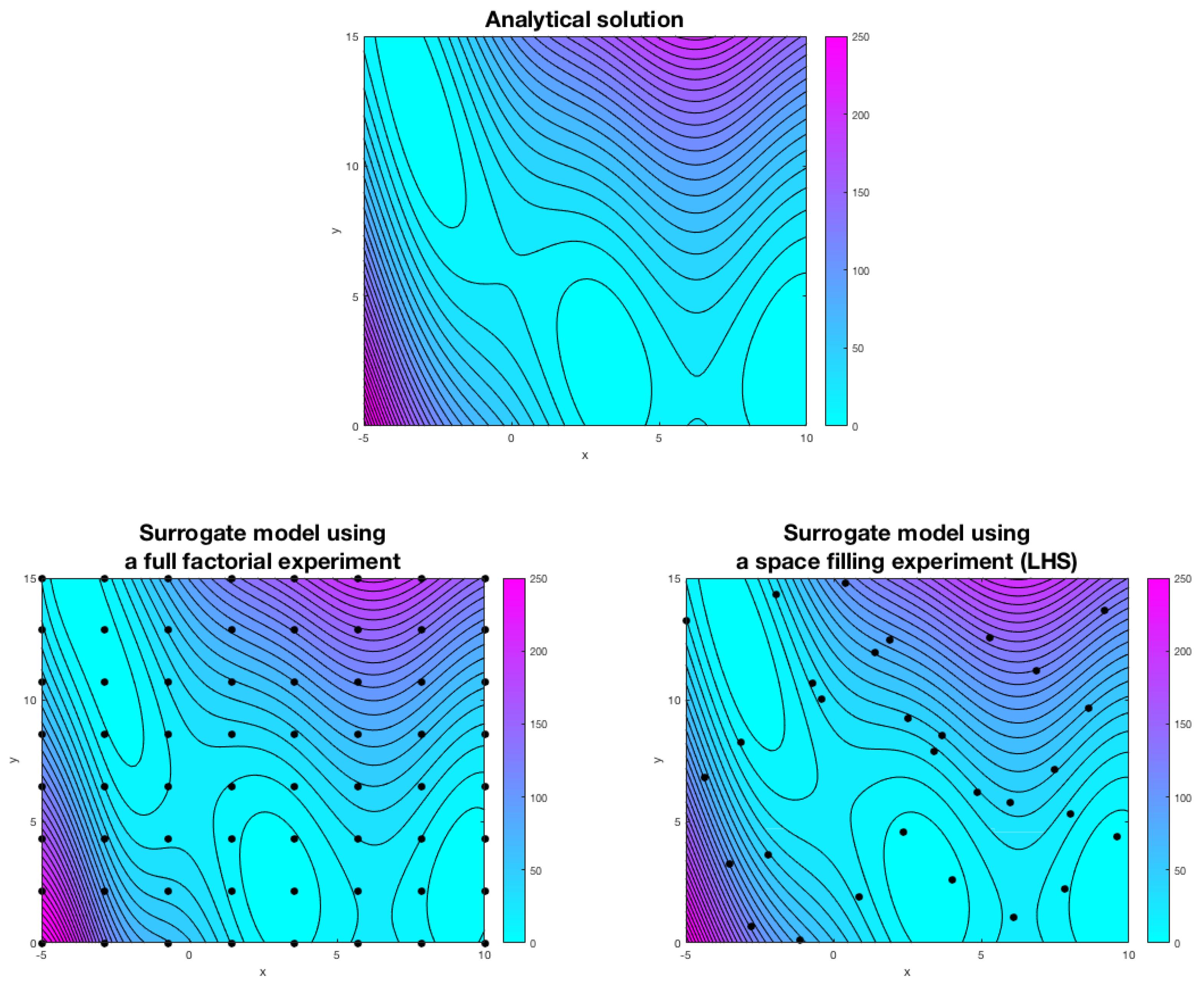
The Branin function (which is highly nonlinear and multi-modal) can easily represent the output of a CFD study. In SBO, the first step consists of exploring the design space in a precise and economical way. In
Figure 4, we present the output of two sampling methods, namely, a full-factorial experiment and a space-filling experiment using Latin hypercube sampling (LHS) [
44]. In each point illustrated in
Figure 4 (bottom images), high-fidelity function evaluations were computed.
The next step consists of generating the surrogate model using the information gathered from the sampling plan. In
Figure 4, we show the surrogates for both sampling experiments and the analytical solution. As it can be seen, there is no discernible difference between both models and the analytical solution, and this is an indication that the models are accurate. However, to construct a well-fitted surrogate, the full-factorial experiment needs more observation points (especially in high multi-dimensional cases, where the number of experiments increases to the power of the number of design variables), and this translates into higher computing times. It is clear that the quality of the surrogate depends on the number of observations; therefore, if at this point we observe differences between the meta-model and the analytical solution, we can add new points and compute a better surrogate. In SBO, the model can be trained as we gather the data, and we can even use multi-fidelity models and a mixture of physical experiments and computational experiments to construct the surrogate. Finally, after constructing the meta-model, we can conduct the optimization study at the surrogate level using any optimization method.
To demonstrate the advantages of using SBO, we compared its performance against the performance of a gradient-based method (method of feasible directions [
53]), and a derivative-free method (single-objective genetic algorithm or SOGA [
54]). All methods used were able to find the three minima; the main difference was the number of iterations used and the information provided by the user to start the optimization algorithm. The gradient-based method used 217 high-fidelity function evaluations, where we used a multi-start technique in which multiple start locations were given (this was needed in order to find the multiple minima), and we computed the gradients using forward differences. The derivative-free method used 1200 high-fidelity iterations and did not require any input information from the user (we used the recommended default parameters). Finally, the SBO method used 30 high-fidelity observations (space-filling experiment). These observations were used to construct the meta-model, then, at the surrogate level, derivative-free and gradient-based methods were used to find the minimum. The SBO method has the added value of showing information about the global design space.
As a final example, let us use the high-dimensional Rosenbrock function to demonstrate the ability of the SBO method in dealing with multivariate problems. The Rosenbrock function can be written in general form as
this equation with the given bounds has one global minimum, defined as follows:
To conduct the SBO study, we proceed in the same way as for the Branin function. At the high-fidelity level, we used two gradient-based methods, namely, the method of feasible directions [
53] and the quasi-Newton BFGS update method [
55]. Both methods converged to the global minimum, but the BFGS method showed a better convergence rate. At the surrogate level we used three methods: two gradient-based methods (same methods as in the high-fidelity study) and one derivative-free method, namely, the DIRECT method (DIvide a hyperRECTangle [
56]). The surrogate was constructed using 500 observations, which roughly correspond to the same number of function evaluations in the best case of the high-fidelity optimization studies (refer to
Table 1). It is noteworthy that as we have a mathematical representation of the design space, the gradients were computed analytically during the SBO study.
The outcome of this SBO study is presented in
Table 1. As it can be seen in this table, at the surrogate level, we get values close to the global minimum; but, due to a noisy and under-fitted surrogate, the optimal value is under-predicted. We can also observe that the values of the design variables 4–6 are a little bit over-predicted, but in general they follow the trend of the high-fidelity values. One way to improve the results could be to construct a better surrogate by using a larger number of observations. However, as the number of observations will be much higher than the number of function evaluations in the best case of the high-fidelity optimization studies, the use of SBO is not very attractive, especially if the computation of the QoI is expensive. Another way to improve the surrogate is by using infilling, which consists of adding new points to the training set and then reconstructing the surrogate. For example, we can add a new point in the location of the predicted optimal value and a few new points in areas where high nonlinearities are observed or are close to the optimal value, recompute the surrogate, and find the new optimal value. It is worth mentioning that we also used 200 experiments to conduct the SBO study, but due to the coarseness of the space-filling sampling, the surrogate was under-fitted; therefore, the optimization studies failed to converge or give similar trends to the ones shown in
Table 1.
Another advantage of SBO is that we can use exploratory data analysis and machine learning techniques to interrogate the data obtained during the design space exploration stage. These techniques can be used for knowledge extraction and anomaly detection. In
Figure 5, we show one of the many plots that can be used to visualize the data [
57,
58]. This plot is called a scatter matrix, and in one single illustration, it shows the correlation information, the data distribution (using histograms and scatterplots), and regression models of the responses of the QoI. The reader should be aware that, in the context of design space exploration, exploratory data analysis and machine learning methods should not be used with biased data, e.g., data coming from a gradient-based or derivative-free optimization study.
By conducting a quick inspection of the scatterplot matrix displayed in
Figure 5, we can see evidence that the data is distributed uniformly in the design space (meaning that the sampling plan is unbiased), and this is evidenced by the diagonal of the plot. By looking at the scatterplot of the experiments (lower triangular part of the matrix), we see the distribution of the data in the design space. If at this point we observe regions in the design space that remain unexplored, we can simply add new training points to cover those areas. In the case of outliers (anomalies), we can remove them from the dataset with no major inconvenience. However, we should be aware that outliers are telling us something, so it is a good idea to investigate the cause and effect of the outliers. In the upper triangular part of the plot, the correlation information is shown (Spearman correlation, in this case). This information tells us how correlated or uncorrelated the data are. For example, by looking at the last row of the plot that shows the response of the QoI, if we see a strong correlation between two variables, it is clear that this variable cannot be excluded from the study. The opposite is also true, that is, uncorrelated variables can be excluded from the study; therefore, the complexity of the problem is reduced. One should be aware that for data exclusion using correlation information, we should use the response of the QoI and not the design space distribution of the sampling plan. For a well-designed experiment, the design space distribution is uncorrelated. Additionally, the last row of the scatter matrix plot also shows the regression model (a quadratic model, in this case). As can be seen, this simple plot can be used to gather a deep understanding of the problem.
To close the optimization framework discussion, we would like to stress the fact that the optimization loop implemented is fault tolerant, so in the event of hardware or software failure, the optimization task can be restarted from the last saved state. Moreover, during the optimization loop, all the data monitored are made available immediately to the user, even when running multiple simulations at the same time (real-time data analytics). Therefore, anomalies and trends can be detected in real time, and corrections/decisions can be made.
4. Calibration and Validation of the Solver
The purpose of this section is twofold. First, we validate the solver against the experimental data available, and secondly, we calibrate the parameters of the solver and the mesher. In other words, we look for the best parameters to be used during the optimization study, and in the case of meshing or convergence problems, these parameters are automatically adjusted without user intervention.
In
Table 3, we list the cell count and average
of the coarse and fine mesh used in this study. We used at least five inflation layers to resolve the boundary layer, and we targeted for a
value between 40 and 200. The results obtained from transient simulations and steady simulations using the LTS method are displayed in
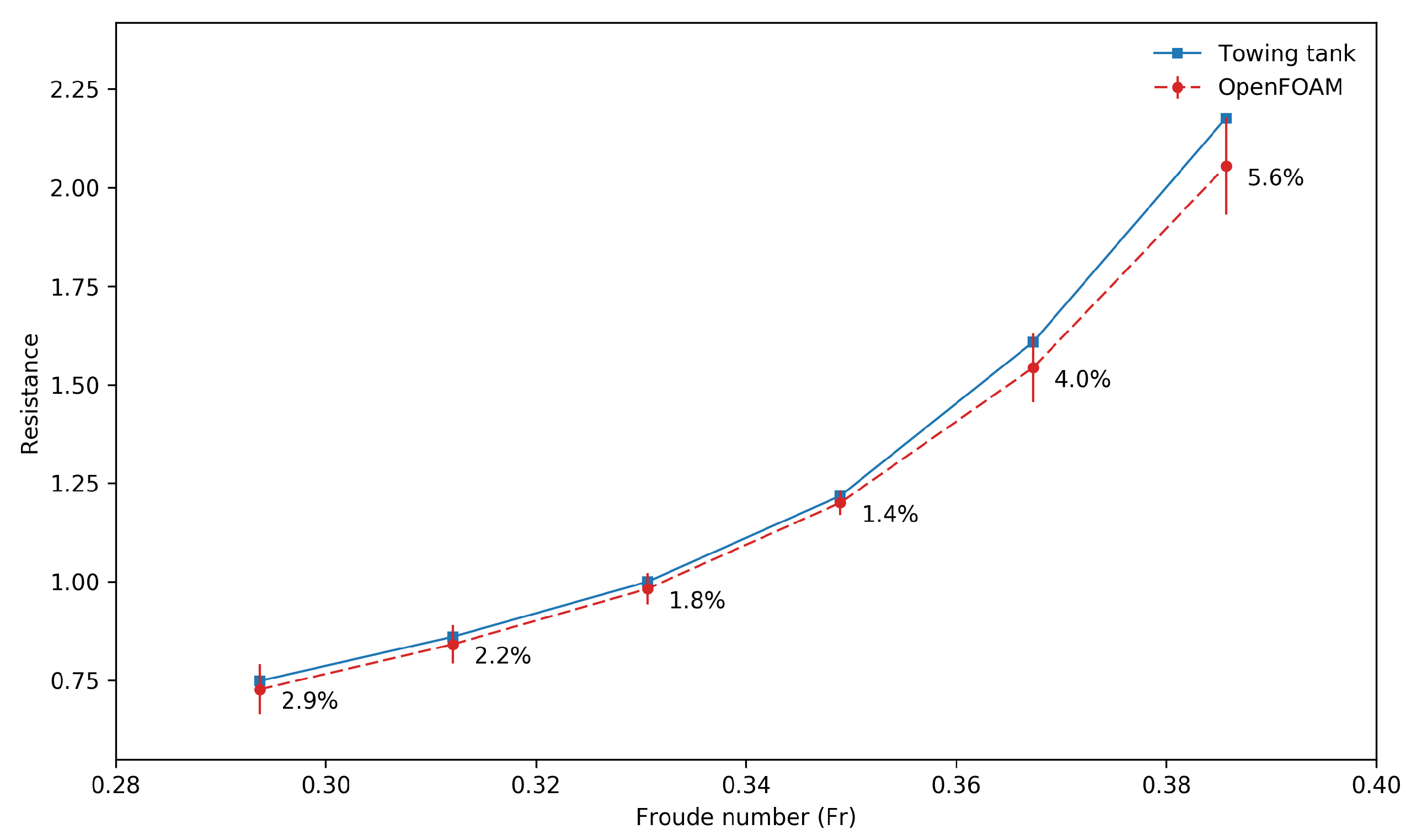
Figure 9. The results illustrated correspond to the base geometry and a Froude number equal to 0.331. Due to the intellectual property of the experimental data, from this point on, all the results are normalized using as a reference the experimental value corresponding to this operating condition.
In
Figure 9, we can observe that the outcome of the steady simulations using both meshes are in good agreement with the experimental values. Both solutions reached a steady state approximately after 4000 iterations. Nevertheless, we let the simulations run for longer times to ascertain that we reached good iterative convergence. Regarding the unsteady simulations, we can see that the simulation using the fine mesh reached periodic iterative convergence after approximately 40,000 iterations. On the other hand, the unsteady simulation using the coarse mesh reached a periodic iterative convergence after about 20,000 iterations. However, the results are slightly over-predicted due to numerical diffusion and turbulence model uncertainties. For the unsteady simulations, the time-step was chosen in such a way that the maximum CFL number is equal to 2, whereas, for the steady simulations (where we used the LTS method), the CFL number was gradually increased until reaching the value of 0.9.
In
Table 4, we show the percentage error (computed with respect to the experimental data) and the CPU time measured at 8000 iterations for each simulation plotted in
Figure 9. From these results, it becomes clear why it is important to find steady solutions when conducting optimization studies in CFD. If we had conducted this optimization study using an unsteady solver, the computing time of each simulation would have been about 2 times the computing time of the corresponding steady simulation (for the same number of iterations); therefore, the total computing time of the optimization loop would have been at least 2 times higher.
In
Figure 10, we present the normalized resistance as a function of the Froude number. The results reported were obtained using the coarse mesh and the LTS method. In the figure, a good agreement with the experimental results is observed up to a value of
, then, the percentage error starts to increase, and this is mainly due to the fixed trim condition assumption used in this study. Moreover, the prototype is not meant to operate at such high Froude numbers, which corresponds to off-design conditions. In the light of this optimization study, where we know there are many uncertainties involved, errors of this order of magnitude are acceptable given the assumptions that were taken. Also, these discrepancies can be neglected because it is reasonable to consider that this error is constant for each bulb shape to be simulated and is, therefore, irrelevant for the optimization loop.
Based on these results, we decided to use the coarse mesh as the base mesh, and in the case of mesh quality problems, the domain mesh was automatically recomputed using improved meshing parameters. As for the iterative method concerns, all the simulations were executed using the LTS method, and if proper iterative convergence was reached, the simulations were automatically stopped at 8000 iterations or until statistically stable results were obtained. These choices allowed us to obtain fast outcomes with good accuracy.
5. Results and Discussion
Hereafter, we discuss the results obtained from the surrogate-based optimization study. All the simulations presented in this section were conducted at a Froude number of 0.294. We would like to stress that to get the optimization loop started, we only need one input geometry. Then, this geometry is deformed by the shape morpher to generate new candidates. Also, the whole optimization framework was deployed using asynchronous simulations: that is, we executed many parallel simulations at the same time. Everything was controlled using the application coupling interface provided by Dakota. The average time of each simulation was between 4 and 5 hours.
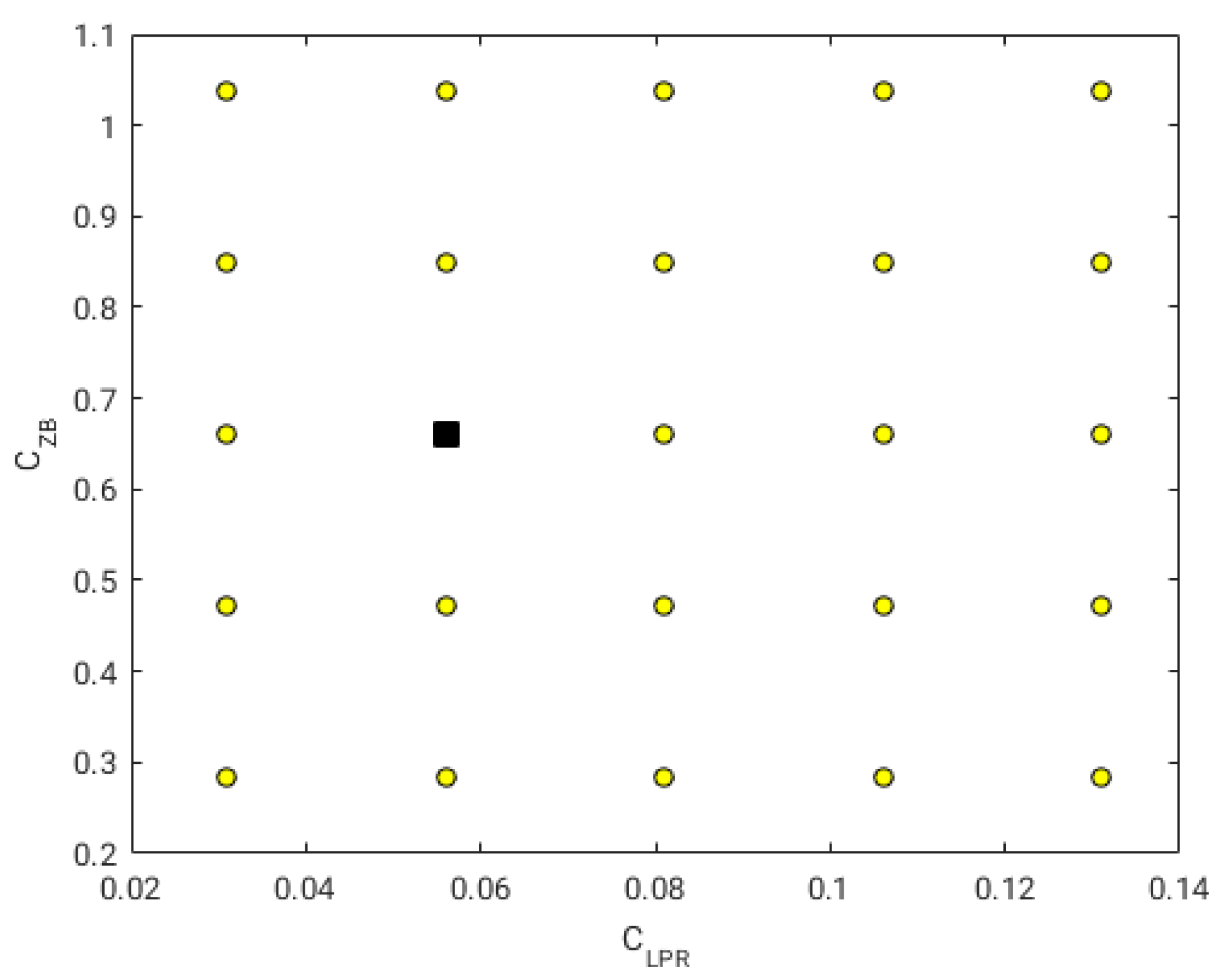
As discussed previously, the first step when conducting SBO studies is to generate a sampling plan of the design space. The sampling plan should cover the design space in a uniform and well-distributed way, without leaving large areas unexplored; also, it should be cheap to compute. It is clear that the more information we gather during the initial sampling, the better the surrogate will be, but at the cost of longer computing times. In this study, we used a full-factorial experiment, where we conducted 25 experiments uniformly spaced in the design space. In
Figure 11, we illustrate the sampling plan, where the uniform spaced points represent the locations where the high-fidelity computations were computed. The sampling plan illustrated in
Figure 11 was chosen because it is inexpensive to compute (as we reduced the number of design variables to two), and it explores design points without missing too much information between observations.
The next step in our work-flow is to construct the surrogate (or meta-model) after conducting the high-fidelity simulations at the sampling locations. In this study, we used Kriging interpolation [
38,
44,
45,
48,
49,
50,
51,
52], which has been demonstrated to be a very reliable and accurate interpolation method when conducting SBO studies. The only drawback of this method (if it can be considered a drawback) is that it forces the meta-model to pass by all the points of the sampling plan; therefore, in the presence of numerical noise, we can have surrogates with many valleys and peaks that can make the optimization task difficult when using gradient-based methods. Nevertheless, as we are working at the surrogate level, we can use derivative-free methods which behave better in the presence of numerical noise.
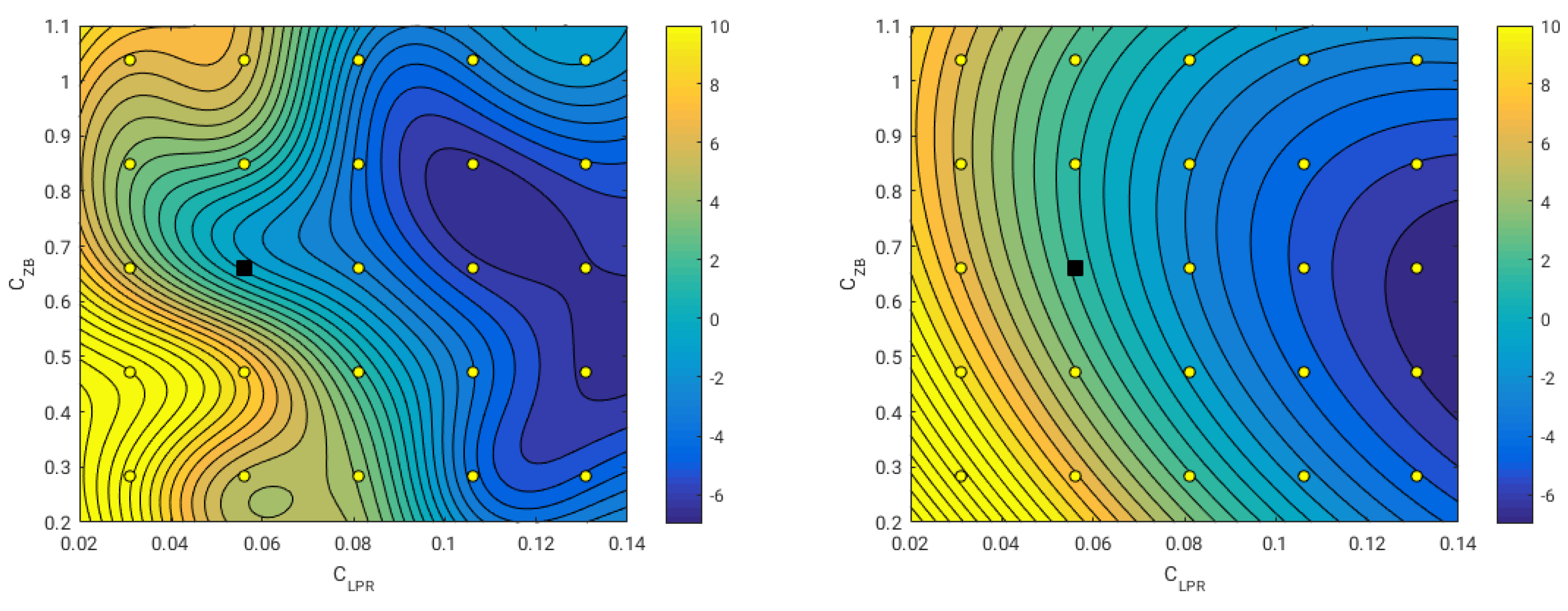
In
Figure 12, we illustrate two surrogates obtained during this study. In the figure, the surrogate in the left image was constructed using Kriging interpolation, and the one in the right image was build using a second-order polynomial function. The color scale represents the resistance variation in reference to the original geometry (where negative values indicate resistance reduction and positive values indicate resistance increment). As it can be seen, the Kriging model managed to capture the nonlinearities of the design space; we can even distinguish a valley region where the optimal solution (or solutions) might be located. On the other hand, the polynomial model is very smooth; however, it is not very accurate (it does not capture the nonlinearities). Nevertheless, it gives us a rough idea of how the design space behaves.
At this stage, we already have a surrogate of the design space, or in other words, a mathematical representation of the design space. Our next tasks consist of validating the surrogate and conducting the optimization study at the surrogate level. The validation merely consists of computing the predicted value at the surrogate level in a location that has not been included in the sampling plan. Then, this value can be compared with the value obtained using high-fidelity simulations in the same location, and the percentage error can be computed. The optimization consists of doing the actual optimization at the surrogate level. Remember, as we are working using a mathematical representation of the design space, we can use any optimization method, disregarding how expensive it can be.
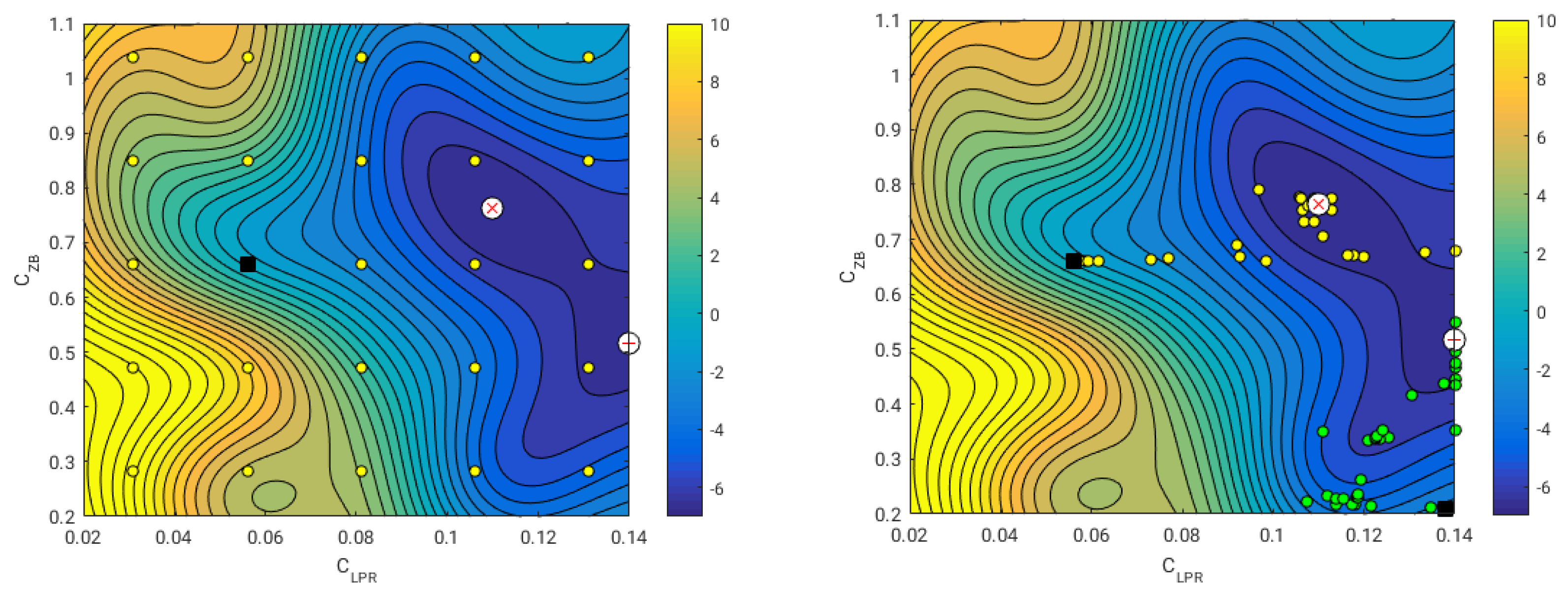
In this study, we found a global minimum and a local minimum; this situation is illustrated in
Figure 13. These results suggest that there is a bifurcation in the valley region, where the global minimum is obtained when increasing the value of the design variable
, and the local minimum is obtained when decreasing the value of the design variable
. Notice also that as we increase the value of the design variable
, smaller increments of the design variable
are required in order to obtain larger resistance reduction. In
Figure 13 (right image), we show the iterative path followed by the optimization algorithm when starting from two different initial positions, where each optimization task used about 40 iterations (function evaluations and gradient evaluations). As we used a gradient-based method to optimize the surrogate (method of feasible directions [
53]), it is clear that we need to start the optimization algorithm from different initial locations if we want to find the global and local minima. If we were to perform this study by directly resorting to high-fidelity simulations, the number of simulations would be much higher than the number of simulations used during the sampling plan.
As previously mentioned, the SBO method gives the possibility of conducting an initial screening (or visualization) of the design space. This initial screening can be extremely helpful, especially when dealing with high multi-dimensional optimization problems. By screening the surrogate, designers can explore and exploit the surrogate in a more efficient way. Different optimal candidates can be immediately identified through the subjective opinion of the designer or on the basis of external constraints (such as manufacturing process, increased weight due to the added surface, the volume of the new bulb, structural loads, clearances, and so on), without the need of resorting to high-fidelity simulations (with the exception of the validation of the surrogate).
To demonstrate the validity of the surrogate, in
Table 5, we show the numerical values of the resistance reduction and the percentage error between the surrogate value and the high-fidelity simulations outcome. The values presented in this table were measured in five different points; namely, the global minimum, the local minimum, and three points in the proximity of the global and local minima. From the table, we observe that all values listed effectively reduce the resistance. We also observe that the percentage error between the surrogate level and the high-fidelity level is about 2% for the global and local minima cases. On the other hand, for the values measured in the vicinity of the global and local minima, the percentage error is much larger, and this is presumably because in this region the nonlinearities are more significant.
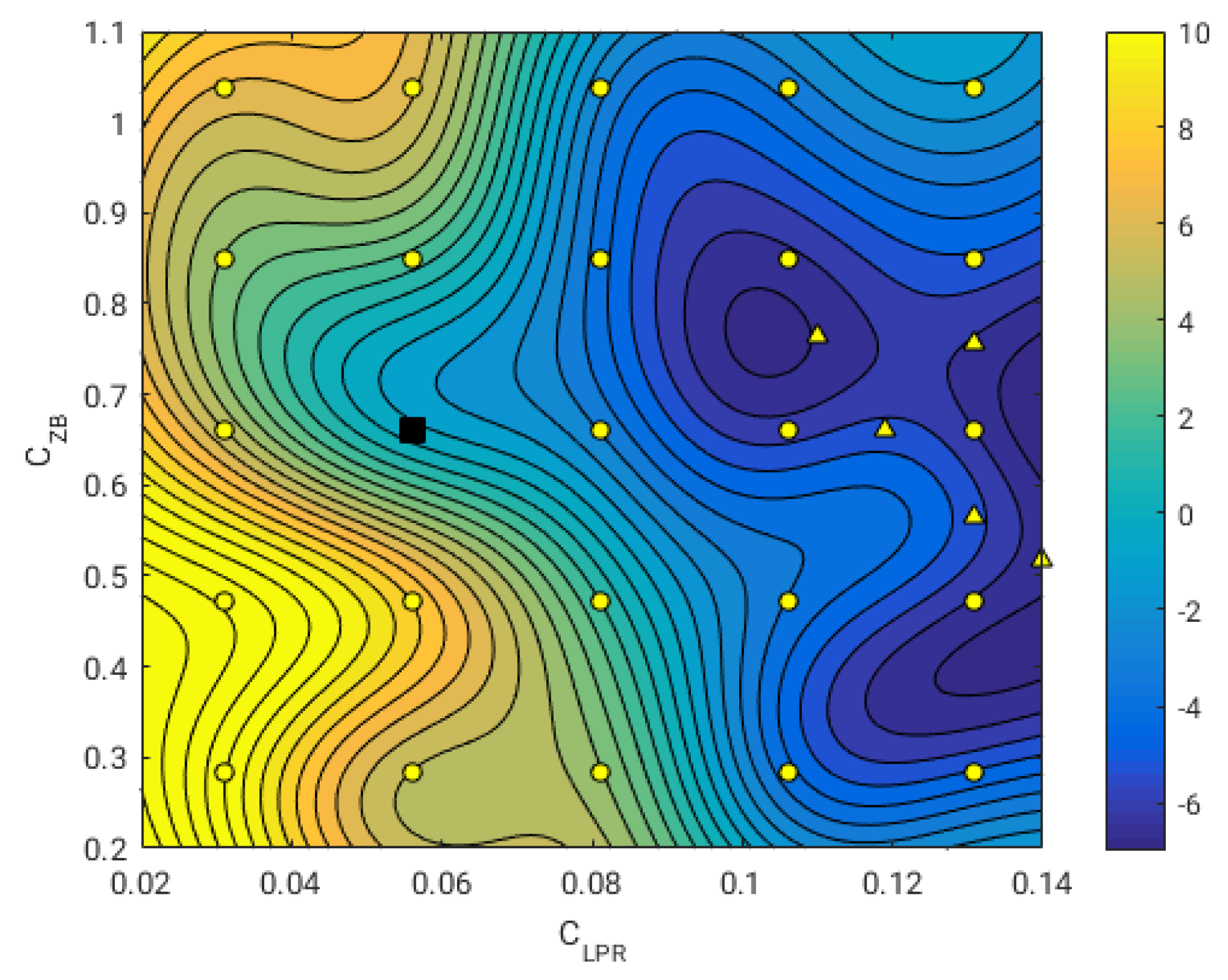
We can also improve the surrogate by adding new points to it (this is known as infilling). For example, we can add the points listed in
Table 5 (
and
) and recompute a new surrogate (and optimal values). This situation is illustrated in
Figure 14, where the triangle symbols represent the new training points. In the surrogate pictured in the figure, we are able to capture with more details the behavior of the design space close to the region where the global minimum is located. Also, we still can see the bifurcation, where there is a clear optimal solution when we increase the value of
; however, when decreasing the value
, the location of the new minimum is not very clear. It may be necessary to add a new training point in this region in order to get a better surrogate. Nevertheless, the resistance reduction values in this region are smaller; therefore, we can focus our attention on the cases where we increase the value of
.
For completeness, in
Figure 15, we show the shape of the optimal bulbs at the design conditions corresponding to the global minimum and the local minimum. From all the results presented in this section, it is clear that surrogate-based optimization is an effective design tool for engineering design. However, the user should be cautious when constructing the surrogate, because the whole method depends on the quality of the meta-model. It is always recommended to validate the surrogate, do infilling using the optimal solutions, and add a couple of extra points in areas where high nonlinearities are observed or are close to the optimal values.